درسنامه کامل فیزیک دوازدهم ریاضی
تعداد بازدید : 497.67kخلاصه نکات فیزیک دوازدهم ریاضی - درسنامه شب امتحان فیزیک دوازدهم ریاضی - جزوه شب امتحان فیزیک دوازدهم ریاضی نوبت اول
حرکت شناسی
فصل 1 : حرکت بر خط راست
حرکت شناسی
حركت و سكون يک امر نسبی هستند يعنی نسبت به دستگاه خاصی سنجيده می شوند هرگاه فاصله جسمی با گذشت زمان نسبت به يک مبدأ تغيير كند جسم نسبت به آن مبدأ دارای حركت می باشد.
انواع حرکت
1) حركت با سرعت ثابت (حركت يكنواخت(
2) حركت تند شونده و (شتابدار يا كند شونده(
مبدا حرکت
1) مبدأ مكان
نقطه ای اختياری بر روی محور مكان است. (\(x = 0\) )
2) مبدأ زمان
لحظه شروع حركت (\({t_0}\)) يا لحظه ای كه از آن پس حركت را بررسی می كنيم.
مکان اولیه
موضع يا مكان متحرک را در لحظه ی \({t_0} = 0\) مكان اوليه \({x_0}\) می نامند . اگر متحرک در مبدا زمان در مبدا مكان باشد مكان اوليه ی آن صفر است. (\({x_0} = 0\) )
مسیر حرکت
مكان هندسی نقاطی است كه جسم ضمن حركت از آن نقاط عبور می كند .
حرکت بر روی خط راست
در اين حركت راستای بردار جابه جايی و بردار های مكان منطبق بر مسير حركت است. بزرگی بردار مكان در هر لحظه ، فاصله ی متحرک را از مبدأ مكان نشان می دهد مطابق شكل زير مسير حركت جسمی بر روی محور xنمايش داده شده است مكان جسم در اين شكل با بردار d مشخص شده است.
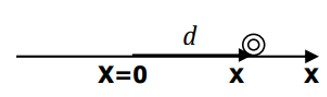
(\(d = xi\) ) بزرگی بردار مکان و(\(d = \Delta x = x - {x_0}\) )
بردار جا به جایی
بردار جابه جايی بين دو لحظه \({t_1}\) و \({t_2}\) برداری است كه ابتدای آن مكان متحرک در لحظه \({t_1}\) و انتهای آن مكان متحرک در لحظه \({t_2}\) می باشد.
بردار جابه جايی به مبدأ مكان و به شكل مسير حركت بستگی ندارد يعنی با تغيير مبدأ، تغيير نمی كند لذا نسبی نيست. (به بردار جابه جايی بردار تغيير مكان نيز می گويند.)
مكان متحرک
درحركت روی خط راست مكان متحرک عددی جبری است مانندx يا y كه جای متحرک را نسبت به مبدا مشخص می كند.
مثال
در شكل زير مسير حركت متحركی بر روی خط راست نشان داده شده است، مطلوب است:
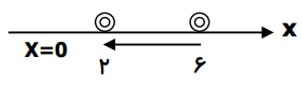
الف) رسم بردار جا به جایی
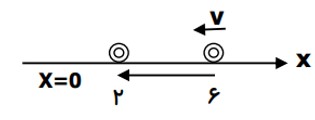
ب) محاسبه بزرگی جا به جایی
\(d = \Delta x = {x_2} - {x_1} = 2 - 6 = - 4m\)
تفاوت مسافت طی شده با جا به جایی
مسافت (L) راهی است كه متحرک می پيمايد و كميتی نرده ای است يعنی فـقط مقدار دارد (جهت ندارد) ولی جابه جايی (d) فاصله مستقيم بين مبدأ و مقصد است و كميتی برداری است.
هر گاه متحركی يک مسيری را برود و دو باره به مكان اوليه اش باز گردد ؛ جا به جايی آن صفر خواهد شد.
مثال
متحرکی از مکان \(x = - 4m\) تا مکان \(x = + 6m\) جا به جا می شود و سپس به مکان \(x = - 4m\) یر می گردد، مسافت طی شده و جا به جایی این متحرک به ترتیب چند متر است؟
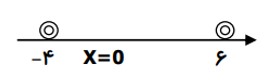
\(\begin{array}{l}L = 10 + 10 = 20m\\\Delta x = {x_3} - {x_1} = - 4 - ( - 4) = 0\end{array}\)
در حركت روی خط راست هرگاه متحرک در يک جهت حركت كند و بازگشتی وجود نداشته باشد مسافت پيموده شده با اندازه ی جابه جايی برابر است .
بازه ی زمانی
به فاصله زمانی بين دو لحظه از يک رويداد گفته می شود وبا نشان داده می شود.
مثال
متحرکی از لحظه \(t = 2s\) تا \(t = 6s\) به اندازه ی 20 مترجابه جا می شود زمان حركت (\(\Delta t\) ) چقدر بوده است؟
\(\Delta t = {t_2} - {t_1} = 4s\)
نمودار مکان-زمان
منحنی تغییرات \(x = f(t)\) نمودار مکان-زمان خوانده می شود غالباً محور افقی زمان و محور قائم مكان جسم را نشان می دهد. به كمک اين نمودار می توان مشخص کرد:
1) مكان متحرک در هر لحظه
2) مسافت
3) جا به جايی
4) مدت زمان حركت
5) تندی متوسط سرعت متوسط در هر بازه ی زمانی
6) تندی لحظه ای
7) جهت حرکت روی محور
8) علامت شتاب دار
درشكل های زير چند نمونه از اين نمودارها نشان داده شده است .
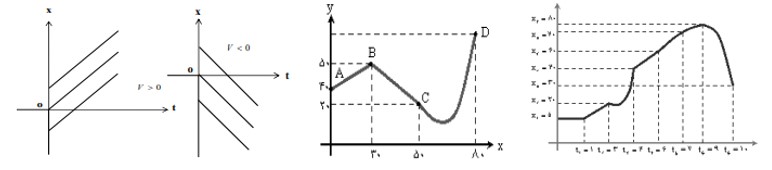
1 حركت را تعريف كنيد.
تغییر مکان یک جسم طی گذشت زمان نسبت به یک مرجع لخت، حرکت در فیزیک به معنی تغییر مکان جسم در ارتباط با زمان است .حرکت در فیزیک از نیرو ناشی می شود و با مفاهیم سرعت، شتاب، جا به جایی و زمان مرتبط است. بنا بر قانون اول نیوتن، سرعت یک جسم تنها در حالتی تغییر می کند که نیرویی به آن وارد شود.
حرکت همیشه بر اساس یک مرجع بررسی می شود و اگر مرجع ثابتی وجود نداشته باشد حرکت مطلق قابل مشاهده نیست، بنا بر همین استدلال، باید از حرکت نسبی سخن گفت. در این نگاه اگر چیزی بنا به یک مرجع ثابت باشد، به شکل نسبی در حال حرکت نسبت به مراجع دیگر است و به همین دلیل ادعا می شود که در جهان، همه چیز حرکت می کند.
2 بردار مكان چيست؟
برداری که ابتدای ان مبدا مختصات و انتهای ان مکان جسم باشد.
- آزمون آنلاین تمامی دروس پایه ریاضی
- گام به گام تمامی دروس پایه ریاضی
- ویدئو های آموزشی تمامی دروس پایه ریاضی
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ریاضی
- فلش کارت های آماده دروس پایه ریاضی
- گنجینه ای جامع از انشاء های آماده پایه ریاضی
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ریاضی
تندی
فصل 1 : حرکت بر خط راست
تندی
تندی و سرعت متوسط
نسبت مسافت طی شده توسط متوسط تندی زمان را مدت متحرک به می گويند. و نسبت جابجايی متحرک به زمان طی شده را سرعت متوسط می گويند.
تندی متوسط (\({s_{av}} = \frac{l}{{\Delta t}}\) )
سرعت متوسط (\({v_{av}} = \frac{d}{{\Delta t}}\) )
1 سرعت متوسط كميتی برداری است در حالی كه تندی متوسط كميتی نرده ای می باشد.
2 یکای سرعت در SI متر بر ثانیه (\(\frac{m}{s}\) ) است ولی یکاهای (\(\frac{{cm}}{s}\) ) و (\(\frac{{km}}{h}\) ) نیز برای سرعت به کار برده می شوند.
3 برای تبديل واحد سرعت از متر بر ثانيه به كيلومتر بر ساعت يا بلعكس به اين صورت عمل می كنيم:
\(\begin{array}{l}\frac{{km}}{h} \div 3/6 \to \frac{m}{s}\\\frac{m}{s} \times 3/6 \to \frac{{km}}{h}\end{array}\)
تعیین سرعت متوسط به کمک نمودار مکان-زمان
سرعت متوسط بين دو نقطه از نمودار مكان-زمان برابر شيب خطی است كه آن دو نقطه را به يكديگر وصل می كند.
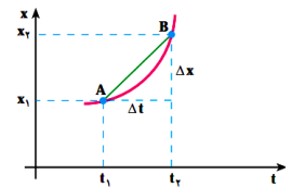
\(\frac{{\Delta x}}{{\Delta t}} = V\)
تندی لحظه ای و سرعت لحظه ای
لحظه، يعنی يک زمان بسيار كوچک
- تندی متحرک در هر لحظه از زمان را تندی لحظه ای می گويند.
- تندی كه تندی سنج اتومبيل نشان می دهد تندی لحظه ای اتومبيل می باشد.
- سرعت لحظه ای برداری است كه مماس بر مسير حركت و در جهت حركت می باشد.
1 اگر سرعت لحظه ای مثبت باشد متحرک در جهت محور مكان و اگر منفی باشد متحرک در خلاف جهت محور مكان حركت می كند.
2 هرگاه علامت سرعت عوض شود متحرک تغيير جهت می دهد و شرط اينكه متحركی نسبت به مسير اوليه خود تغيير جهت دهد (برگردد يا ساكن شود) آن است كه سرعتش صفر شود.
تعیین سرعت لحظه ای به کمک نمودار مكان-زمان
درنمودار مكان زمان شكل مقابل اگر \(\Delta t\) فوق العاده كوچک شود نقطه B خيلی به A نزديک می شود و در نهايت خط AB در نقطه A برنمودار مماس می شود.
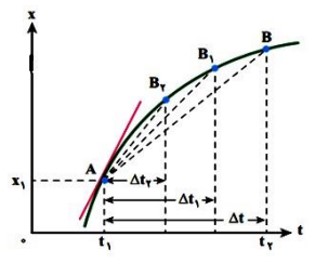
سرعت در هر لحظه برابر شیب خط مماس بر نمودار مكان– زمان در آن لحظه است.
هر گاه مماس بر نمودار مكان-زمان موازی و يا منطبق بر محور زمان باشد سرعت در آن لحظه ، برابر صفر است كه مربوط به ماكزيمم يا مينيمم منحنی است .
حرکت یكنواخت روی خط راست
هرگاه سرعت لحظه ای متحركی كه بر روی خط راست حركت می كند در تمام لحظه ها يكسان باشد، حركت آن يكنواخت ناميده می شود. در حركت يكنواخت متحرک در زمان های مساوی مسافت های مساوی را طی می كند به عبارت ديگر ، حركت يكنواخت به حركتی گويند كه در طول مسير، بردار سرعت ثابت بماند يعنی علاوه بر ثابت ماندن مقدار سرعت بايد جهت سرعت نيز ثابت بماند.
نكات مهم حرکت یكنواخت
1) در اين نوع حركت سرعت متوسط با سر عت لحظه ای برابر است. (\(V = V\) )
2) شيب نمودار مكان زمان چنين حركتی كه همان سرعت است همواره ثابت است.
3) در اين نوع حركت مكان متحرک تابعی از زمان حركت آن است: \(x = f(t)\) و اين تابع نسبت به زمان، از درجه ی اول است يعنی نمودار (مكان-زمان) آن يک خط راست است .
رابطه ی مكان زمان یا معادله حرکت
معادله حركت يک رابطه رياضی بين مكان متحرک (X) و زمانی كه متحرک به اين مكان رسيده است يعنی (t) می باشد بوسيله اين معادله می توان مكان متحرک را در هر لحظه تعيين كرد.
اگر فاصله متحرک تا مبدأ در لحظه \(t = 0\) برابر \({x_0}\) و در لحظه t برابر x باشد:
معادله حرکت یکنواخت
\(V = \frac{{\Delta x}}{{\Delta t}} = \frac{{{x_2} - {x_1}}}{{{t_2} - {t_1}}} \to V = \frac{{{x_2} - {x_0}}}{{{t_2} - {t_0}}} \to x = Vt + {x_0}\)
مثال
متحرکی بر روی مسیر مستقیم در مبداء زمان از نقطه (\( - 5m\) ) مطابق شکل در حال حرکت می باشد اگر سرعت آن ثابت و برابر (\(15\frac{m}{s}\) ) باشد، مکان آن را در زمان \(t = 20s\) تعیین کنید.
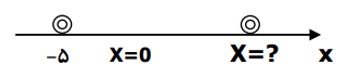
\(\begin{array}{l}x = Vt + {x_0}\\x = 15t + ( - 5) \to x = 15t - 5 \to x = 15 \times 20 - 5 = 295m\end{array}\)
نمودار سرعت-زمان
با داشتن سرعت در زمان های مختلف می توانيم اين نمودار را رسم كنيم. محور افقی را زمان و محور قائم را سرعت اختيار می كنيم.اگر متحرک با سرعت ثابت روی خط راست حركت كند نمودار سرعت زمان آن مطابق شكل مقابل خواهد بود.
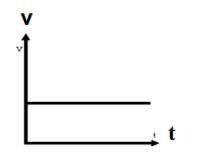
اگر سرعت متحرک ثابت نباشد نمودار سرعت زمان آن ممكن است مطابق شكل های زير باشد .

سطح محصور بين نمودار سرعت-زمان و محور زمان در بازه ی زمانی\(\Delta t\) برابر با جابه جايی متحرک (\(\Delta x\) ) است . اگر اين مساحت در بالای محور زمان باشد جابه جايی مثبت و اگر در زير محور زمان باشد جابه جايی منفی است .
1تندی متوسط و سرعت متوسط را با یکدیگر مقایسه کنید؟
تندی متوسط نسبت مسافت به زمان و کمیت نرده ای است. سرعت متوسط نسبت جا به جایی به زمان و کمیت برداری است. همچنین سرعت متوسط در یک بازه زمانی، برابر با شیب خطی است که دو نقطه نمودار مکان-زمان مربوط به ابتدا و انتهای آن بازه را به یکدیگر وصل می کند.
2در چه صورت اندازه سرعت متوسط یک متحرک با تندی متوسط آن برابر است؟
وقتی اندازه مسافت با جابه جایی برابر باشند، به عبارت دیگر اگر جهت سرعت تغییر نکند.
شتاب
فصل 1 : حرکت بر خط راست
شتاب
حرکت شتابدار
در مواردی كه سرعت متحرک تغيير می كند می گوييم حركت شتاب دار يا غير يكنواخت است. يعنی ميزان جابجايی در زمان های مساوی با هم برابر نيست.
ما چه وقت احساس شتاب می كنيم؟
- زمانی كه روی پدال گاز فشار می دهيم.
- وقتی كه ترمز می كنيم.
- وقتی كه حول يک ميدان درحال دور زدن هستيم و...
در حركت شتاب دار جهت و يا اندازه سرعت و يا هر دو می تواند تغيير كند مثال درحركت بر روی مسير خميده جهت سرعت الزاما تغيير می كند يعنی در حركت بر روی مسير منحنی، حتی اگر بزرگی سرعت هم تغيير نكند حركت شتابدار است .
عوامل ایجاد کننده شتاب
1) تغيير در سرعت متحرک
2) تغيير در جهت حركت
شتاب متوسط
شتاب متوسط برابر تغيير سرعت در واحد زمان است و با \({a_{av}}\) نشان مي دهند و یکای آن (\(\frac{m}{{{s^2}}}\) ) است.
\(a = \frac{{\Delta V}}{{\Delta t}} = \frac{{{V_2} - {V_1}}}{{{t_2} - {t_1}}}\)
نکات مهم شتاب
- شتاب يک كميت برداری است. يعنی هم مقدار و هم جهت دارد.
- شتاب يعنی در هر ثانيه يک مقدار ثابت بر سرعت اضافه يا كم می شود.
- در مواردی كه بزرگی سرعت متحرک يا جهت بردار سرعت تغيير كند حركت شتاب دار است.
- در صورتی كه متحرک ساكن يا با سرعت ثابت در مسير مستقيم حركت كند شتاب آن صفر است.
- در صورتی كه سرعت متحرک مرتبا كاهش يابد يعنی ترمز كند شتاب آن منفی است.
- درفرمول شتاب هميشه سرعت نهايی ازسرعت اوليه كم می شود پس اگر \({V_2} - {V_1}\) مثبت باشد، شتاب مثبت و اگر منفی باشد شتاب منفی است.
مثال
متحركی بروی خط راست از حال سكون شروع به حركت نموده و پس از 5 ثانيه سرعتش به \(20\frac{m}{s}\) می رسد، شتاب حرکت آن را حساب کنید.
\(a = \frac{{\Delta V}}{{\Delta t}} = \frac{{V - {V_0}}}{{\Delta t}} = \frac{{20 - 0}}{5} = 4\frac{m}{{{s^2}}}\)
تعیین شتاب متوسط به کمک نمودار سرعت-زمان
شتاب متوسط بين دو لحظه برابر شيب خطی است كه نمودار سرعت زمان را در آن دو لحظه قطع می كند.
\(\alpha = a = \frac{{\Delta V}}{{\Delta t}}\)
شتاب لحظه ای
شتابی كه متحرک در هر لحظه دارد شتاب لحظه ای گويند.
شیب خط مماس بر نمودار سرعت-زمان در هر لحظه برابر شتاب لحظه ای است و هر قدر اين شيب بيشتر باشد شتاب نيز بيشتر است .
حرکت تند شونده وکند شونده
در حركت شتاب دار با شتاب ثابت روی خط راست هرگاه بردار شتاب هم جهت با بردار سرعت باشد حركت تند شونده است (\(av\rangle 0\) ) در اين نوع حركت قدر مطلق سرعت متحرک رو به افزايش می باشد و هرگاه بردار شتاب درخلاف جهت بردار سرعت باشد حركت كند شونده و قدرمطلق سرعت به تدريج كاهش می يابد: (\(av\langle 0\) )
اگر a وv هم علامت باشند حركت تند شونده در غير اين صورت حركت كند شونده است .
حرکت شتاب دار با شتاب ثابت روی خط راست
هرگاه متحركی روی خط راست حركت كند و تغيير سرعت آن در هر فاصله زمانی مساوی ، يكسان باشد شتاب متحرک ثابت است در اين نوع حركت (يعنی حركت با شتاب ثابت) شتاب متوسط بين هر دو لحظه دلخواه با شتاب متحرک در هر لحظه برابر است.
معادلات حرکت با شتاب ثابت
1) شتاب متوسط و لحظه ای
\(1)\alpha = a = \frac{{\Delta V}}{{\Delta t}}\)
2) سرعت متوسط
\(\begin{array}{l}2)V = \frac{{\Delta x}}{{\Delta t}}\\2')V = \frac{{{V_1} + {V_2}}}{2}\\2'')V = \frac{1}{2}at + {V_0}\end{array}\)
3) معادله سرعت-زمان
\(3)v = at + {v_0}\)
4) معادله مکان-زمان (معادله حرکت)
\(4)x = \frac{1}{2}a{t^2} + {v_0}t + {x_0}\)
5) معادله مستقل از زمان
\(5){v^2} - {v_0}^2 = 2a\Delta x\)
6) معادله مستقل از شتاب
\(6)\Delta x = \frac{{v + {v_0}}}{2}\Delta t\)
جا به جایی متحرک در t ثانیه n ام حرکت
اگر متحرکی با شتاب ثابت a و با سرعت اولیه \({V_0}\) روی خط راست در حال حرکت باشد جا به جایی متحرک در t ثانیه n ام حرکت از رابطه زیر بدست می آید:
\(\Delta x = \frac{1}{2}a{t^2}(2n - 1) + {V_0}t \to t = 1s \to \Delta x = \frac{1}{2}a(2n - 1) + {V_0}\)
مثال
جسمی از حال سکون با شتاب ثابت \(10\frac{m}{{{s^2}}}\) شروع به حرکت می کند، مسافت پیموده شده در ثانیه چهارم چند متر است؟
\(\begin{array}{l}{V_0} = 0\\a = 10\frac{m}{{{s^2}}}\\t = 1s\\n = 4\\\Delta x = ?\\\Delta x = \frac{1}{2}a(2n - 1) + {V_0} \to \Delta x = \frac{1}{2} \times 10 \times (2 \times 4 - 1) + 0\\\Delta x = 35m\end{array}\)
جا به جایی متحرک در n ثانیه ی آخر حرکت و در ثانیه آخر حرکت از رابطه های زیر بدست می آید:
\(\Delta x = \frac{1}{2}an(2t - n) + n{V_0} \to n = 1 \to \Delta x = \frac{1}{2}a(2t - 1) + {V_0}\)
نمودار مکان-زمان در حرکت با شتاب ثابت روی خط راست
چون معادله حركت شتابدار ثابت از درجه 2 است؛ لذا نمودار مكان-زمان آن يک سهمی است اگر دهانه نمودار به سمت بالا باشد شتاب مثبت و اگر به سمت پايين باشد شتاب منفی است. درشكل های زير چند نمونه از اين نمودارها نشان داده شده است .
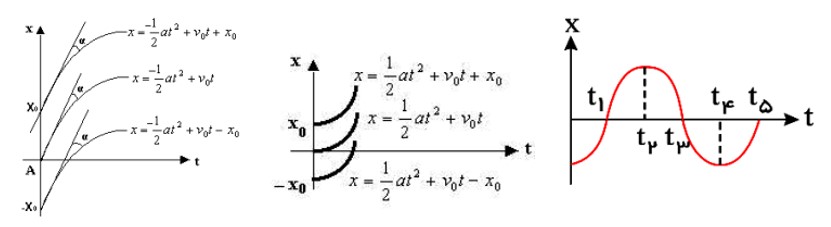
نمودار سرعت - زمان در حرکت با شتاب ثابت روی خط راست
چون معادله سرعت (\(v = at + {v_0}\) ) نسبت به زمان از درجه يک است بنابراين سرعت متحرک به طور خطی با زمان تغيير می كند يعنی نمودار سرعت-زمان اين نوع حركت به صورت يک خط راست است كه شيب آن برابر شتاب ثابت حركت است.
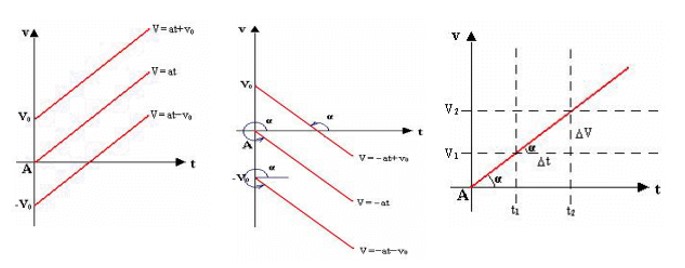
\(\alpha = a = \frac{{\Delta v}}{{\Delta t}}\)
سطح زير نمودار سرعت-زمان در حركت شتاب دار ثابت نيز اندازه جا به جايی را نشان می دهد.
نمودار شتاب-زمان
- هرنقطه از نمودار , شتاب متحرک را در يک لحظه ی دلخواه نشان می دهد.
- مساحت سطح محصور بين نمودار تا محور زمان برابر تغيير سرعت متحرک است كه اگر بالای محور زمان باشد \(\Delta v\) مثبت و اگر زير محور باشد \(\Delta v\) منفی است.
دو متحرک همزمان از یک نقطه در مسیری یکسان به حرکت در می آیند. سرعت متحرک اول در هر لحظه از متحرک دوم بیشتر است. آیا ممکن است سرعت متوسط متحرک دوم در یک بازه زمانی دلخواه بیشتر از اولی باشد؟
بله، در صورتی که مسیر خط راست نباشد؛ ممکن است جابه جایی در یک بازه زمانی برای جسم دوم بیشتر از اولی باشد و سرعت متوسط جسم دوم بزرگتر از اول شود. به عنوان مثال حرکت یک متحرک روی مسیر راست و مستقیم که برگشت هم داشته باشد، و همچنین حرکت روی مسیر دایره ای بهترین مثال ها برای توجیه این پرسش هستند. دو شناگر را تصور کنید که در مسیر رفت و برگشت یک استخر مسابقه می دهند، وقتی شناگر اول به محل اولیه برگردد سرعت متوسط آن صفر می شود در صورتی که شناگر دوم که آهسته تر حرکت می کرد سرعت متوسط آن صفر نخواهد شد.
دینامیک
فصل 2 : دینامیک و حرکت دایره ای
دینامیک
ديناميک به بررسی علت حركت می پردازد.
ويژگی های نيرو:
- نيرو حاصل بر هم كنش يا اثر متقابل دو جسم بر يكديگر است.
- نيرو كميتی برداری است كه يكای آن نيوتن (N) است.
- اثر نيرو بر يک جسم به شكل های مختلف مانند شروع به حركت كردن، توقف، كم و زياد شدن اندازه ی سرعت، تغيير جهت سرعت و تغيير شكل جسم ، خود را نشان می دهد.
محاسبه نیروی خالص
1) اگر دو بردار با يكديگر هم جهت باشند؛
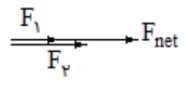
\(1){F_{net}} = {F_1} + {F_2}\)
2) اگر دو بردار خلاف جهت يكديگر باشند؛
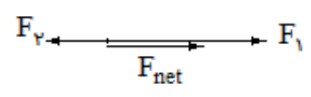
\(2){F_{net}} = \left| {{F_1} - {F_2}} \right|\)
3) اگر دو بردار عمود بر هم باشند؛
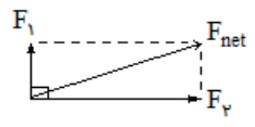
\(3){F_{net}} = \sqrt {F_1^2 + F_2^2} \)
4) اگر دو بردار هم اندازه و عمود بر هم باشند؛
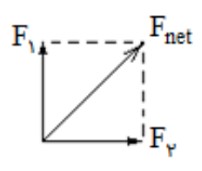
\(4){F_{net}} = \sqrt 2 {F_1}\)
روش حل مسائل ديناميک
به ترتيب زير عمل كنيد:
- رسم تمام نيروهای وارد بر جسم.
- انتخاب محورهای مختصات مناسب (در صورتی كه حركت شتاب دار باشد بهتر است يكی از محورها در جهت شتاب حركت باشد)
- نوشتن قانون اول يا دوم نيوتن روی محور های x و y به طور جداگانه و حل مسأله.
- آزمون آنلاین تمامی دروس پایه ریاضی
- گام به گام تمامی دروس پایه ریاضی
- ویدئو های آموزشی تمامی دروس پایه ریاضی
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ریاضی
- فلش کارت های آماده دروس پایه ریاضی
- گنجینه ای جامع از انشاء های آماده پایه ریاضی
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ریاضی
قوانین حرکت نیوتون
فصل 2 : دینامیک و حرکت دایره ای
قوانین حرکت نیوتون
1) قانون اول نیوتون
يک جسم، حالت سكون يا حركت با سرعت ثابت خود را حفظ می كند مگر آنكه نيروی خالص غير صفری به آن وارد شود.
به عبارت ديگر:
\({F_{net}} = 0\) اگر جسم ساکن باشد یا حرکت یکنواخت روی خط راست انجام دهد.
اگر به جسمی به طور هم زمان چند نيرو اثر كند و اين نيرو ها اثر يكديگر را خنثی كنند ( برآيند نيروها صفر باشد) می گوييم نيروهای وارد بر جسم متوازن است.
لختی
هنگامی كه نيروی خالص وارد بر جسم صفر باشد، جسم حالت سكون يا حركت يكنواخت خود را حفظ می كند، به اين خاصيت لختی گفته می شود.
2) قانون دوم نیوتون
هر گاه برجسمی نيروی خالصی وارد شود، جسم تحت تأثير آن نيرو شتاب می گيرد كه اين شتاب با نيروی خالص وارد بر جسم نسبت مستقيم دارد و در همان جهت نيروی خالص است و با جرم جسم نسبت وارون دارد:
\({F_{net}} = ma\) اگر جسم حرکت شتاب دار داشته باشد. (سرعت جسم تغییر کند)
بر اساس قانون دوم نيوتن می توان گفت جهت بردار شتاب يک جسم ، هم جهت با برآيند نيروهای وارد بر جسم است.
3) قانون سوم نیوتون
هرگاه جسمی به جسم ديگر نيرو وارد كند، جسم دوم نيز به جسم اول نيرويی هم اندازه و هم راستا در خلاف جهت وارد می كند. (نيروها ی كنش و واكنش با هم برابرند و درخلاف جهت يكديگر)
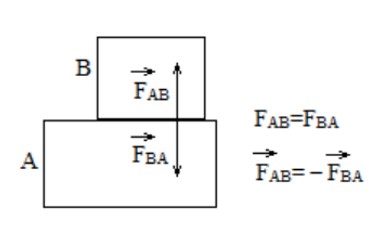
1 نيروی كنش و واكنش به دو جسم وارد می شود و برآيند گيری از آن ها اشتباه است.
2 نيروی كنش و واكنش اثرهای يكسانی بر اجسام ندارند.
3 نيروی كنش و واكنش هم نوعند.
دو شخص به جرم هاي \(75Kg\) و یا \(50Kg\) با كفش های چرخ دار در يک سالن مسطح و صاف روبه روی هم ايستاده اند. شخص اول با نيروي \(120N\) شخص دوم را به طرف راست هل می دهد، اگر اصطكاک قابل چشم پوشی باشد،
الف) شتاب که شخص دوم چند \(\frac{m}{{{s^2}}}\) می شود؟
\({F_{12}} = {m_2}{a_2} \to {a_2} = \frac{{{F_{12}}}}{{{m_2}}} \to {a_2} = \frac{{120}}{{50}} \to {a_2} = 2/4\frac{m}{{{s^2}}}\)
ب) جهت شتاب شخص اول چقدر و به كدام سمت است؟
\(\begin{array}{l}{F_{12}} = - {F_{21}}\\{a_1} = \frac{{ - {F_{21}}}}{{{m_1}}} \to {a_1} = \frac{{ - 120}}{{75}}i \to {a_1} = - 1/6\frac{m}{{{s^2}}}i\end{array}\)
برخی از نیرو های خاص
فصل 2 : دینامیک و حرکت دایره ای
نیروی وزن
وزن يک جسم روی زمين ، نيروی گرانشی است كه از طرف زمين بر جسم وارد می شود، كه به صورت زير قابل محاسبه است:
\(W = mg\)
1 جهت نيروی وزن و شتاب گرانشی همواره به طرف مركز زمين است.
2 جرم يک جسم در مكان های مختلف ثابت است اما وزن آن به مقدار g در آن مكان بستگی دارد.
نیروی عمودی سطح
نيرويی كه از طرف سطح به اجسام روی آن و به صورت عمود بر سطح وارد می شود، نيروی عمودی سطح (نيروی عمودی تكيه گاه) ناميده می شود. (این نیرو با \({F_N}\) نمایش داده می شود)
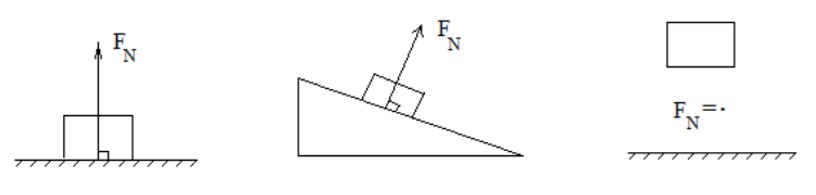
نيروی عمودی سطح ناشی از تغيير شكل سطح تماس دو جسم است. (هنگامی كه اجسام روی سطوح بسيار سخت قرار می گيرند سطح مانند اسفنج تغيير شكل دارد. اين تغيير شكل مربوط به نيروهای بين مولكولی است)
نیروی اصطکاک
وقتی تلاش می كنيم جسمی را روی سطحی به حركت در آوريم، چه جسم حركت كند و چه ساكن بماند، با مقاومتی از طرف سطح روبه رو می شويم كه به آن نيروی اصطكاک می گوييم.
انواع نیروی اصطکاک
الف) نيروی اصطكاک ايستايی (\({f_s}\))
هنگامی كه نيرويی برای حركت دادن جسم روی سطح وارد می شود، اما جسم حركت نكند، نيرويی كه از طرف سطح در مقابل حركت وارد می شود ، نيروی اصطكاک ايستايی ناميده می شود:
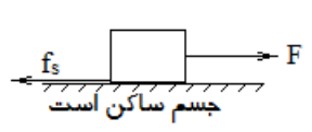
\({f_s} = F\)
ب) نیروی اصطکاک در آستانه ی حرکت (\({f_{s\max }}\) )
اين نيرو، نوعی نيروی اصطكاک ايستايی است، هنگامی كه نيرويی بر جسم وارد شود و آن را در آستانه ی حركت قرار دهد (يعنی جسم هنوز شروع به حركت نكرده است اما با تغيير ناچيزی در شرايط جسم شروع به حركت كند)، نيرويی كه در برابر حركت جسم مقاومت می كند، نيروی اصطكاک در آستانه ی حركت ناميده می شود و در واقع اين نيرو بيشينه ی نيروی اصطكاک ايستايی است:
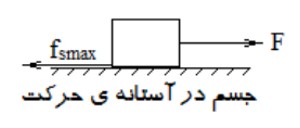
\(\begin{array}{l}{f_{s\max }} = F\\{f_{s\max }} = {\mu _s}{F_N}\end{array}\)
\({\mu _s}\) ضریب اصطکاک ایستایی
\({F_N}\) نیروی عمودی تکیه گاه
طراحی آزمايش برای تعيين ضريب اصطكاک ايستايی جسم با سطح:
ابتدا مانند تصوير به نيروسنج متصل به جسم را به تدريج می كشيم تا جسم در آستانه حركت قرار گيرد. (يعنی با ضربه كوچكی شروع به حركت نمايد)

در اين لحظه عدد نيرو سنج را می خوانيم در اين وضعيت عددی كه نيروسنج نشان می دهد (F) همان نيروی اصطكاک آستانه حركت (\({f_{s\max }}\) ) است. با رابطه زير ضريب اصطكاک ايستايی را محاسبه می كنيم:
\({f_{s\max }} = F \to {\mu _s}{F_N} = F \to {\mu _s}mg = F \to {\mu _s} = \frac{F}{{mg}}\)
پ) نیروی اصطکاک جنبشی (\({f_K}\) )
نيرويی است كه از طرف سطح در خلاف جهت حركت بر اجسام متحرک وارد می شود:
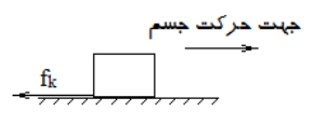
\({f_K} = {\mu _K}{F_N}\)
\({\mu _K}\) ضریب اصطکاک جنبشی
\({F_N}\) نیروی عمودی تکیه گاه
1 ضريب اصطكاک ايستايی (\({\mu _s}\) ) و ضريب اصطكاک جنبشی (\({\mu _K}\) ) به مشخصات فيزيكی دو سطح تماس (مانند جنس دو سطح تماس، ميزان صافی يا زبری آن ها و . . . )بستگی دارند.
2 برای دو سطح تماس معين \({\mu _K} \le {\mu _s}\) و \({f_K} \le {f_{s\max }}\) است.
3 نمودار نيروی اصطكاک بر حسب نيرويی كه جسم را می كشد به صورت زير است:
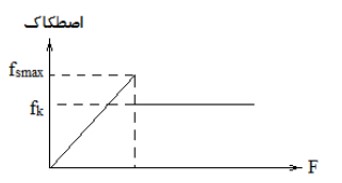
در مسائلی كه مشخص نيست جسم ساكن است يا متحرک، ابتدا با رابطه ی \({f_{s\max }} = {\mu _s}{F_N}\) ، بيشينه ی اصطكاک ايستايی را محاسبه می كنيم و سپس آن را با نيروی كشش وارد بر جسم (نيروی خلاف جهت اصطكاک) مقايسه می كنيم و به موارد زير توجه می كنيم:
- اگر نيروی كشش بزرگتر از \({f_{s\max }}\) باشد، آنگاه جسم حرکت می کند و در نتیجه اصطکاک سطح از نوع \({f_K}\) است.
- اگر نيروی كشش کوچکتر از \({f_{s\max }}\) باشد، آنگاه جسم ساکن است و در نتیجه اصطکاک سطح از نوع \({f_s}\) است.
- اگر نيروی كشش برابر با \({f_{s\max }}\) باشد، آنگاه جسم در آستانه ی حرکت است و در نتیجه اصطکاک سطح از نوع \({f_{s\max }}\) است.
نیروی واکنش سطح
برآيند نيروهايی كه از طرف سطح به جسم وارد می شوند (برآيند نيروی اصطكاک و نيروی عمودی تكيه گاه) نيروی واكنش سطح ناميده می شود:
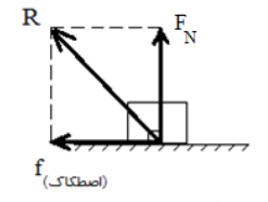
\(R = \sqrt {f_{fri}^2 + F_N^2} \)
(fri) بخشی از کلمه (Friction) به معنای اصطکاک است.
نیروی مقاومت شاره
وقتی جسمی در يک شاره (مايع يا گاز) قرار دارد و نسبت به آن حركت می كند از طرف شاره نيرويی در خلاف جهت حركت جسم ، به آن وارد می شود كه به آن نيروی مقاومت شاره می گويند و معمولاً آن را با \({f_D}\) نشان می دهند.
1 نيروی مقاومت شاره به بزرگی جسم، تندی آن و . . . بستگی دارد و هر چه اندازه جسم بزرگتر باشد يا تندی آن بيش تر شود نيروی مقاومت شاره نيز بيش تر می شود.
2 اگر جسم در هوا حركت كند، به جای نيروی مقاومت شاره ، اصطلاح نيروی مقاومت هوا به كار برده می شود.
تندی حدی
هنگام سقوط آزاد جسمی مانند چتر نجات يا قطرات باران، تندی جسم كاهش می يابد تا اينكه نيروی مقاومت هوا با وزن جسم هم اندازه شده و پس از آن جسم با تندی ثابتی به طرف پايين حركت می كند. به اين تندی ثابت تندی حدی گفته می شود.
نیروی شناوری
نيروی بالا سويی كه از طرف شاره به جسم شناور يا غوطه ور در شاره وارد می شود، نيروی شناوری گفته می شود که با \({F_b}\) نشان می دهند.
نیروی کشسانی فنر
اگر فنر را بكشيم يا فشرده كنيم، فنر نيرويی به طرف نقطه ی تعادل به جسم وارد می كند كه به آن نيروی فنر گفته می شود و با \({F_e}\) نمايش داده می شود كه جهت آن از جسم به سمت بيرون و در راستای فنر است و با رابطه ی زير محاسبه می گردد:
\({F_e} = k\Delta x\)
K ثابت فنر یا ضریب سختی فنر (\(\frac{N}{m}\) )
\(\Delta x\) تغییر طول فنر (m)
قانون هوک
نسبت نيروی وارد شده به فنر به تغيير طول آن همواره مقدار ثابتی است.
عوامل مؤثر بر ضريب سختی فنر عبارتند از:
- اندازه فنر
- شکل فنر
- جنس فنر
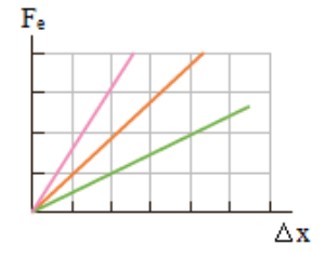
در نمودار نيروی فنر بر حسب تغيير طول فنر هر چه شيب نمودار بيش تر باشد ثابت فنر بيشتر و فنر سخت تر است.
طراحی آزمايش برای تعيين ضريب سختی فنر
فنری با طول اوليه مشخص را مانند تصوير از يک نقطه به طور قائم آويزان می كنيم و به سر ديگر آن جسمی به جرم m وصل می كنيم. پس از رسيدن فنر به حالت تعادل ، تغيير طول فنر (\(\Delta x\) ) را حساب كرده و از رابطه زير ثابت فنر به دست می آيد:
\(K\Delta x = mg \to K = \frac{{mg}}{{\Delta x}}\)
نیروی کشش طناب
هنگامی كه با يک طناب جسمی را می كشيم ، طناب نيز با نيرويی جسم را می كشد كه به آن نيروی كشش ريسمان گفته می شود و جهت آن از جسم به سمت بيرون و در راستای طناب است و اين نيرو با نماد T نشان داده می شود.
تمرین
1فنری به طول \(20cm\) و ثابت\(40\frac{N}{{cm}}\) را از سقف یک آسانســور آویزان کرده و جسمی به جرم \(2Kg\) را به انتهای فنـر وصل می کنیم. اگر آسانسور با شتاب ثابت \(2\frac{m}{{{s^2}}}\) به طرف بالا شروع به حرکت کند، طول فنر چند سانتی متر می شود؟ (\(g = 10\frac{m}{{{s^2}}}\) )
\(\begin{array}{l}{F_e} - mg = ma \to kx = m(g + a) \to 40x = 2 \times 12\\x = \frac{{24}}{{40}} = 0/6cm \to x = {L_2} - {L_1} \to {L_2} = x + {L_1} \to {L_2} = 20/6cm\end{array}\)
2جسمی به جرم \(200Kg\) روی زمین قرار دارد. جسم را توسط یک نیروی افقی به طرف راست می کشیم. اگر ضریب اصطکاک جسم با زمین \(0/3\) ، نیروی مقاومت هوا در برابر حرکت 300 نیوتن و شتاب حرکت جسم \(2\frac{m}{{{s^2}}}\) باشد، نیروی افقی چند نیوتن است؟ (\(g = 10\frac{m}{{{s^2}}}\) )
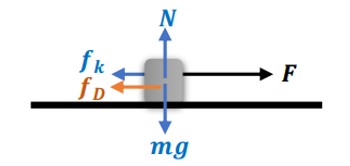
\(\begin{array}{l}{f_k} = {\mu _k}{F_N} = {\mu _k}mg = 0/3 \times 2000 = 600N\\F - {f_D} - {f_k} = ma \to F = ma + {f_D} + {f_k}\\F = 400 + 300 + 600 = 1300N\end{array}\)
مسائل آسانسور
فصل 2 : دینامیک و حرکت دایره ای
مسائل آسانسور
در اينگونه مسائل بايد توجه داشته باشيد كه شتاب اجسام داخل آسانسور همان شتاب خود آسانسور است، به مثال های زير كه برای كابل آسانسور نوشته شده است توجه كنيد: ( توصيه می كنيم كه جهت محور y را جهت شتاب آسانسور فرض كنيد)
1) اگر شتاب آسانسور رو به بالا باشد:
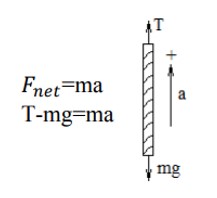
2) اگر شتاب آسانسور رو به پايين باشد:
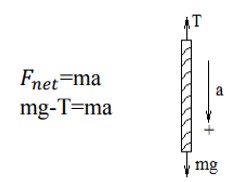
وزن ظاهری اجسام داخل آسانسور
نيروی عمودی تكيه گاه (\({F_N}\) ) كه از طرف كف آسانسور بر اجسام داخل آسانسور وارد می شود همان وزن ظاهری جسم داخل آسانسور با محتوياتش است .
جسمی به جرم \(3Kg\) را به انتهای فنری با ثابت \(50\frac{N}{{cm}}\) بسته ایم و فنر را از سقف یک آسانسور آویزان می کنیم. اگر آسانسور با شتاب ثابت به طرف بالا شروع به حرکت کند و تغییر طول فنر \(0/72cm\) باشد، اندازه شتاب آسانسور چقدر است؟ (\(g = 10\frac{m}{{{s^2}}}\) )
\(\begin{array}{l}{F_e} - mg = ma \to kx = m(g + a) \to 50 \times 0/72 = 30 + 3a\\36 - 30 = 3a \to a = 2\frac{m}{{{s^2}}}\end{array}\)
- آزمون آنلاین تمامی دروس پایه ریاضی
- گام به گام تمامی دروس پایه ریاضی
- ویدئو های آموزشی تمامی دروس پایه ریاضی
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ریاضی
- فلش کارت های آماده دروس پایه ریاضی
- گنجینه ای جامع از انشاء های آماده پایه ریاضی
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ریاضی
تکانه
فصل 2 : دینامیک و حرکت دایره ای
تکانه
حاصل ضرب جرم جسم در سرعتش تكانه ناميده می شود.
بردار تکانه (\(\vec P = m\vec V\) )
اندازه ی تکانه (\(P = mV\) )
تكانه كميتی برداری است و بردار آن هم جهت با بردار سرعت جسم است.
تغييرات تكانه، به صورت زير به دست می آيد:
بردار تغییرات تکانه (\(\Delta \vec P = m\Delta \vec V\) )
اندازه ی تغییرات تکانه (\(\Delta P = m\Delta V\) )
رابطه ی تكانه و قانون دوم نيوتن (رابطه ی نيرو و تغييرات تكانه)
بردار نیروی خالص
\({\vec F_{av}} = \frac{{\Delta \vec P}}{{\Delta t}}\)
اندازه ی بردار نیروی خالص
\({F_{av}} = \frac{{\Delta P}}{{\Delta t}}\)
1 شيب خط واصل بين دو نقطه در نمودار P-t نيروی متوسط وارد بر جسم است.
2 شيب خط مماس بر نمودار P-t در هر لحظه ، نيروی وارد بر جسم در آن لحظه است.
3 مساحت زير نمودار F-t برابر تغييرات تكانه ی جسم (\(\Delta P\)) است.
انرژی جنبشی با تكانه رابطه ای به صورت زير است:
\(K = \frac{{{P^2}}}{{2m}}\)
تکانه (\(\frac{{Kg \times m}}{s}\) )
نیروی گرانشی
فصل 2 : دینامیک و حرکت دایره ای
نیروی گرانشی
نيروی جاذبه بين دو جسم دارای جرم نيروی گرانشی ناميده می شود. (طبق قانون سوم نيوتن اين دو يک جفت نيروی كنش-واكنش را تشكيل می دهند)
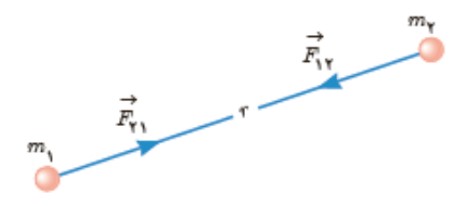
تعريف قانون عمومی گرانش
نيروی گرانش ميان دو ذره با حاصل ضرب جرم دو ذره نسبت مستقيم و با مربع فاصله ی آن ها از يكديگر نسبت وارون دارد:
\(F = \frac{{G{m_1}{m_2}}}{{{r^2}}},G = 6/67 \times {10^{ - 11}}\frac{{N \times {m^2}}}{{K{g^2}}}\)
جزئيات بيش تر در رابطه با نيروی وزن
با توجه به اينكه نيروی وزن نوعی نيروی گرانش محسوب می شود، بايد با حالت های زير برای نيروی وزن آشنا باشيد:
1) نيروی وزن در سطح زمين
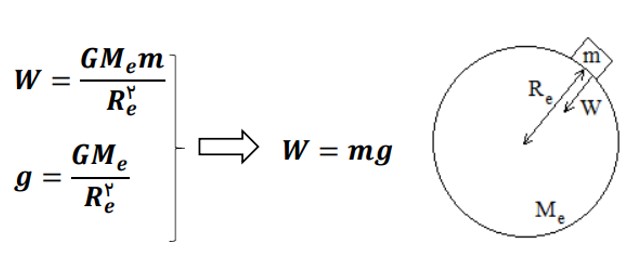
\({M_e}\) جرم کره زمین
\({{\mathop{\rm R}\nolimits} _e}\) شعاع کره زمین
\(g\) شتاب گرانش در سطح زمین
2) نيروی وزن در ارتفاع معينی از سطح زمين
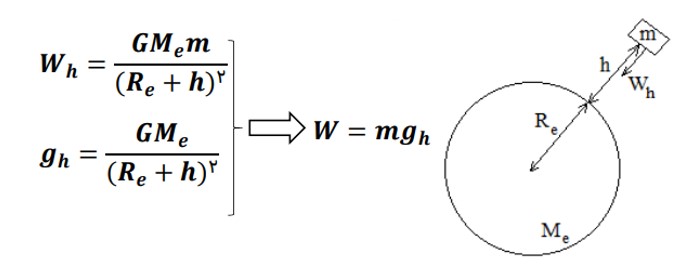
\({M_e}\) جرم کره زمین
\({{\mathop{\rm R}\nolimits} _e}\) شعاع کره زمین
H ارتفاع از سطح زمین
\({g_h}\) شتاب گرانش در سطح زمین
3) نیروی وزن در کرات و سیارات دیگر
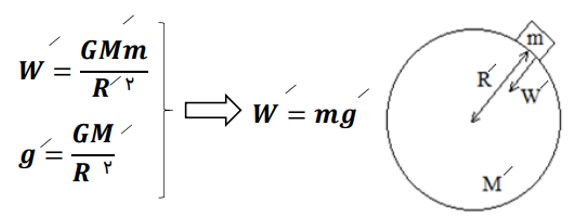
\(M'\) جرم سیاره
\(R'\) شعاع سیاره
\(g'\) شتاب گرانش در سطح سیاره
سیاره ای به شعاع \({10^4}\) کیلومتر و جرم \(2 \times {10^{25}}\) به دور خود می چرخد. شتاب گرانشی در سطح این سیاره چند \(\frac{m}{{{s^2}}}\) است؟ (\(G = 6/7 \times {10^{ - 11}}\frac{{N{m^2}}}{{K{g^2}}}\) )
\(g = \frac{{GM}}{{{r^2}}} \to g = \frac{{6/7 \times {{10}^{ - 11}} \times 2 \times {{10}^{25}}}}{{{{({{10}^7})}^2}}} \to g = 13/4\frac{m}{{{s^2}}}\)
حرکت دایره ای یکنواخت
فصل 2 : دینامیک و حرکت دایره ای
حرکت دایره ای یکنواخت
حركت جسمی روی يک دايره يا بخشی از آن كه با تندی ثابت انجام می شود حركت دايره ای يكنواخت نام دارد.
همان طور كه قبل تر گفته شد در هر مسيری بردار سرعت مماس بر مسير است.
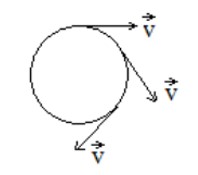
در حركت دايره ای يكنواخت اندازه سرعت ( تندی) ثابت است اما جهت بردار سرعت تغيير می كند، بنابراين يک حركت شتاب دار محسوب می شود.
در حركت دايره ای يكنواخت ذره در بازه های زمانی برابر، مسافت های يكسانی را طی می كند. (زيرا در زمان های مساوی زاويه ها ی يكسانی را می چرخد)
دوره تناوب در حركت دايره ای يكنواخت
زمان لازم برای پيمودن يک دور محيط دايره را دوره ی تناوب (دوره) می نامند، كه با فرمول های زير محاسبه می گردد:
\(\begin{array}{l}T = \frac{{2\pi r}}{V}\\T = \frac{t}{N}\end{array}\)
r)) شعاع دايره
V)) اندازه ی سرعت
t)) زمان كل گردش ها
N)) تعداد كل گردش ها
T)) دوره يا زمان تناوب
بسامد در حركت دايره ای يكنواخت
تعداد گردش ها در هر ثانيه است كه به صورت زير محاسبه می گردد:
\(f = \frac{N}{t}\)
محاسبه ی زاويه ای كه ذره در يک بازه ی زمانی روی دايره می چرخد:
اين زاويه برحسب راديان به صورت زير به دست می آيد:
\(\Delta \theta = \frac{{2\pi }}{T}\Delta t\)
شتاب مركز گرا در حركت دايره ای يكنواخت
همانطور كه گفته شد در حركت دايره ای يكنواخت، اندازه ی سرعت ثابت است اما جهت آن دائم تغيير می كند به همين دليل اين حركت يک حركت شتاب دار است، شتاب حركت همواره به سمت مركز دايره است و اندازه ی آن به صورت زير محاسبه می شود:
\(\begin{array}{l}{a_c} = \frac{{{V^2}}}{r}\\{a_c} = \frac{{4{\pi ^2}r}}{{{T^2}}}\end{array}\)
قانون دوم نيوتن در حركت دايره ای يكنواخت
از آنجا كه شتاب يک جسم را نيروی خالص وارد بر آن ايجاد می كند و شتاب جسم همواره در راستا و جهت نيروی خالص وارد بر جسم است، بنابراين در اين حركت همواره يک نيروی خالص رو به مركز دايره وجود دارد كه به آن نيروی مركز گرا گفته می شود:
\(\begin{array}{l}{F_{net}} = m{a_c} \to {F_{net}} = \frac{{m{V^2}}}{r}\\{F_{net}} = m{a_c} \to {F_{net}} = \frac{{4{\pi ^2}rm}}{{{T^2}}}\end{array}\)
در رابطه ی فوق به جاي \({F_{net}}\) می توان برآیند نیرو های وارد بر جسم در راستای شعاع دایره را نوشت. )در واقع نيروی مركز گرا نوع جديدی از نيرو نيست و نيروهايی مانند كشش ريسمان، نيروی فنر، اصطكاک و . . . می توانند همان نيروی مركزگرا باشند.)
حرکت ماهواره ای
حركت ماهواره ها و كره ی ماه به دور كره ی زمين را حركت ماهواره ای می گويند، تنها نيرويی كه بر چنين اجرامی وارد می شود نيروی گرانش است (\({F_r} = {W_h}\) )، بنابراين شتاب مركز گرا نيز همان شتاب گرانش است و برای حركت های ماهواره ای روابطی به صورت زير می توان نوشت:
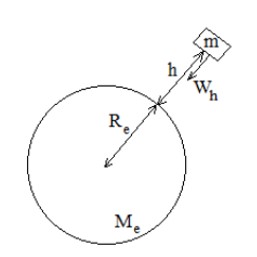
\(\begin{array}{l}{a_c} = {g_h} \to \frac{{{V^2}}}{r} = \frac{{G{M_e}}}{{{{({{\mathop{\rm R}\nolimits} _e} + h)}^2}}}\\{a_c} = {g_h} \to \frac{{4{\pi ^2}r}}{{{T^2}}} = \frac{{G{M_e}}}{{{{({{\mathop{\rm R}\nolimits} _e} + h)}^2}}}\\ \to r = {{\mathop{\rm R}\nolimits} _e} + h\end{array}\)
1 با توجه به روابط فوق، برای سرعت حركت ماهواره رابطه ای به صورت زير می توان اثبات نمود:
\(V = \sqrt {\frac{{G{M_e}}}{{{{\mathop{\rm R}\nolimits} _e} + h}}} \)
2 با توجه به روابط فوق، برای دوره تناوب حركت ماهواره ای رابطه ای به صورت زير می توان اثبات نمود:
\(T = 2\pi \sqrt {\frac{{{{({{\mathop{\rm R}\nolimits} _e} + h)}^3}}}{{G{M_e}}}} \)
ماهواره ای با تندی \(6 \times {10^3}\frac{m}{s}\) روی یک مدار تقریباً دایره ای به دور زمین می چرخد. اگر جرم ماهواره \(200Kg\) و فاصله آن از مرکز زمین \(9000Km\) باشد، نیروی گرانشی ای که زمین بر ماهواره وارد می کند را حساب کنید.
\(F = \frac{{m{V^2}}}{r} \to F = \frac{{200 \times {{(6 \times {{10}^3})}^2}}}{{9 \times {{10}^6}}} = 800N\)
- آزمون آنلاین تمامی دروس پایه ریاضی
- گام به گام تمامی دروس پایه ریاضی
- ویدئو های آموزشی تمامی دروس پایه ریاضی
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ریاضی
- فلش کارت های آماده دروس پایه ریاضی
- گنجینه ای جامع از انشاء های آماده پایه ریاضی
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ریاضی
چرخه
فصل 3 : نوسان و موج
چرخه
تكرار منظم يک حركت چرخه يا سيكل نوسان گفته می شود.
انواع نوسان ها
نوسان ها به دو دسته ی زير تقسيم می شوند:
1) نوسان دوره ای
نوسان هايی كه را كه هر چرخه ی آن در دورهای ديگر تكرار می شود نوسان دوره ای می نامند. مانند (مانند ضرب آهنگ (ریتم)، قلب انسان)
2) نوسان غیر دوره ای
نوسان روی خط راست
يک رفت و برگشت نوسانگر، نوسان ناميده می شود. هر نوسان دارای 4 قسمت به شكل زير است:
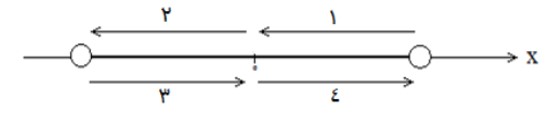
دوره تناوب
مدت زمان يک نوسان (چرخه)، دوره تناوب حركت ناميده می شود، كه به صورت زير محاسبه می گردد:
\(T = \frac{t}{N}\)
بسامد(فركانس)
تعداد نوسان های انجام شده (تعداد چرخه) در هر ثانيه بسامد ناميده می شود كه به صورت زير محاسبه می گردد:
\(f = \frac{N}{t}\)
دوره تناوب و بسامد رابطه ای به صورت زير دارند:
\(f = \frac{1}{T}\) یا \(T = \frac{1}{f}\)
حركت هماهنگ ساده (SHM)
به نوسان های سينوسی، حركت هماهنگ ساده گفته می شود.
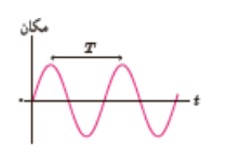
حركت هماهنگ ساده، مبنايی برای درک هر نوع نوسان دوره ای ديگر است زيرا در سطوح بالاتر نشان داده می شود كه هر نوسان دوره ای را می توان مجموعی از نوسان های سينوسی در نظر گرفت.
حركت نوسانی وزنه-فنر
يک نمونه معروف از حركت هماهنگ ساده است. اگر فرض كنيم نوسان روی سطح بدون اصطكاكی صورت می گيرد و مكان جسم را در بازه های متوالی و يكسان ثبت كنيم به نموداری سينوسی می رسيم كه در شكل مقابل آمده است:
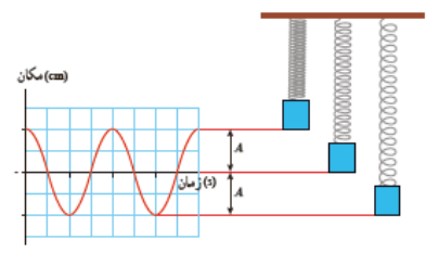
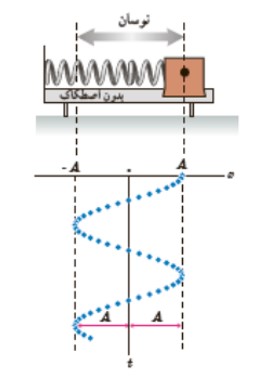
نقطه تعادل (مرکز نوسان)
وسط پاره خط نوسانی مركز نوسان گفته می شود.
دامنه نوسان (A)
بيشترين فاصله ی نوسانگر از نقطه ی تعادل دامنه ناميده می شود.

نقاط بازگشت حركت
وقتی نوسانگر در مكان \(x = \pm A\) است، سرعت آن برابر صفر است. به اين نقطه ها نقاط بازگشت حركت می گوييم.
بسامد زاويه ای
رابطه ای به صورت زير دارد:
\(\omega = \frac{{2\pi }}{T}\)
بسامد زاویه (\(\frac{{rad}}{s}\) )
ويژگی های كلی حركت نوسانی
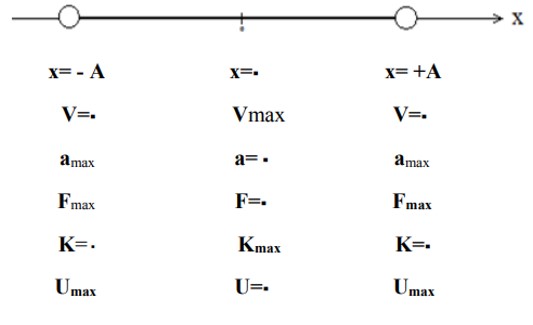
انرژی مكانيكی (E) در كل حركت نوسانی ثابت است.
علامت و جهت سرعت، شتاب و نيرو در حركت نوسانی
1) سرعت (V) همواره در جهت حركت است.
2) شتاب (a) و نیرو (F) همواره به سمت مركز نوسان است.
علامت هر يک از بردارهای فوق كه در جهت محور x باشد، مثبت، و هركدام كه در خلاف جهت محور x، باشد منفی است.
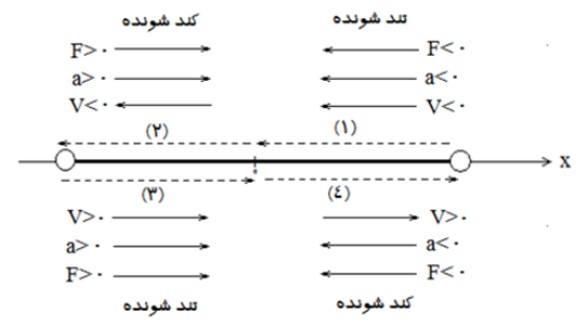
معادله و نمودار مكان-زمان در حركت نوسانی
\(X = A\cos \omega t\)
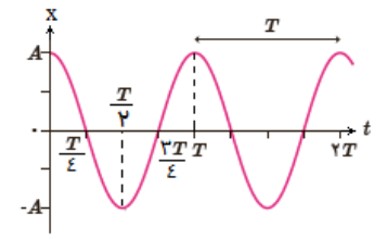
X مکان نوسانگر
A دامنه
\(\omega \) بسامد زاویه ای (\(rad.{s^{ - 1}}\) )
T دوره
بيشينه سرعت نوسانگر
نوسانگر هماهنگ ساده هنگامی كه به نقطه ی تعادل می رسد سرعتش بيشينه می شود كه اين بيشينه ی سرعت با را بطه ی زير قابل محاسبه است:
\({V_m} = A\omega \)
معادله شتاب-مكان در حركت نوسانی
\(a = - {\omega ^2}x\)
با توجه به اينكه يک نوسان كامل 4 قسمت دارد و اين 4 قسمت به اندازه يک دوره (T) زمان نياز دارد، می توان نتيجه گرفت هر يک از 4 قسمت \(\frac{T}{4}\) زمان نیاز دارد:
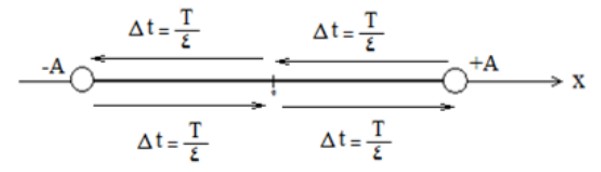
دوره تناوب نوسانگر جرم-فنر
علاوه بر فرمول های قبلی رابطه ی زير برای محاسبه ی دوره تناوب سامانه وزنه-فنر قابل محاسبه است:
\(\begin{array}{l}T = 2\pi \sqrt {\frac{m}{k}} \\k = m{\omega ^2}\end{array}\)
با توجه به رابطه فوق می توان گفت دوره و بسامد نوسانگر وزنه-فنر به دو عامل جرم و ثابت فنر بستگی دارد.
دامنه نوسان یک حرکت هماهنگ ساده \(4cm\) و بسامد آن \(40Hz\) است. معادله حرکت این نوسانگر را بنویسید.
\(\begin{array}{l}\omega = 2\pi f \to \omega = 2\pi \times 40 = 80\pi \frac{{rad}}{s}\\x = A\cos \omega t \to {x_{(cm)}} = 4\cos 80\omega t\end{array}\)
آونگ
فصل 3 : نوسان و موج
آونگ
آونگ ساده شامل وزنه ی كوچكی به جرم m است كه از نخی بدون جرم و كش نيامدنی به طول L كه سر ديگر آن ثابت شده، آويزان است. اگر زاويه ی انحراف آونگ از وضع تعادل كوچک باشد، آونگ حركت هماهنگ ساده خواهد داشت و علاوه بر تمام روابط حركت هماهنگ ساده، رابطه ی زير نيز برای دوره تناوب آن بر قرار است:
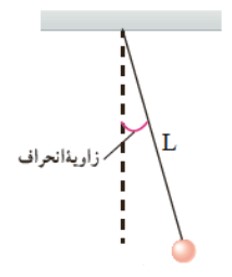
\(T = 2\pi \sqrt {\frac{L}{g}} \)
1 دوره تناوب و بسامد آونگ تنها به طول آن و شتاب گرانش محل نوسان آونگ بستگی دارد (دوره و بسامد آن به جرم وزنه ی متصل به آن بستگی ندارد)
2 وابسته بودن دوره ی آونگ به شتاب گرانش باعث می شود كه با اندازه گيری طول (L) و دوره ی آن (T) بتوان به طور دقيق شتاب گرانش يک محل را به دست آورد.
3 شتاب گرانش در سطح زمين، ارتفاعات زمين و ساير كرات ديگر روابطی در ديناميک دارد كه آنها را برايتان يادآوری می كنيم:
شتاب گرانش در سطح زمین : \(g = \frac{{G{M_e}}}{{R_e^2}}\)
شتاب گرانش در ارتفاعات زمین : \({g_h} = \frac{{G{M_e}}}{{{{({{\mathop{\rm R}\nolimits} _e} + h)}^2}}}\)
شتاب گرانش در کرات و سیارات دیگر : \(g' = \frac{{GM'}}{{{{R'}^2}}}\)
دوره آونگ ساده ای 2 ثانیه است. طول این آونگ چند متر است؟ (\({\pi ^2} = g\) )
\(T = 2\pi \sqrt {\frac{L}{g}} \to 2 = 2\pi \sqrt {\frac{L}{g}} \to 1 = {\pi ^2}(\frac{L}{{10}}) \to L = 1m\)
انرژی در حرکت هماهنگ ساده
فصل 3 : نوسان و موج
انرژی در حرکت هماهنگ ساده
انرژی جنبشی در حركت هماهنگ ساده
با توجه به فيزيک 1 به صورت زير قابل محاسبه است:
\(K = \frac{1}{2}m{V^2}\)
انرژي پتاسيل در حركت هماهنگ ساده
برای اين انرژی رابطه ای در كتاب درسی نيامده است ولی با كمک انرژی جنبشی (K) و انرژی مكانيكی (E) می توان آن را به دست آورد.
انرژی مكانيكی در حركت هماهنگ ساده
انرژی مكانيكی، مجموع انرژی جنبشی و انرژی پتانسيل است و به صورت زير می توان برای آن رابطه نوشت:
\(\begin{array}{l}E = U + K\\E = \frac{1}{2}m{\omega ^2}{A^2}\end{array}\)
1 چون در حركت هماهنگ ساده از اصطكاک صرف نظر می شود انرژی مكانيكی ثابت می ماند، به عبارت ديگر برای يک نوسانگر، مجموع انرژی جنبشی و پتانسيل در تمام نقاط حركت برابر است و اين يعنی در طول حركت هر مقدار انرژی جنبشی كاهش يابد بر انرژی پتانسيل افزوده می شود و برعكس.
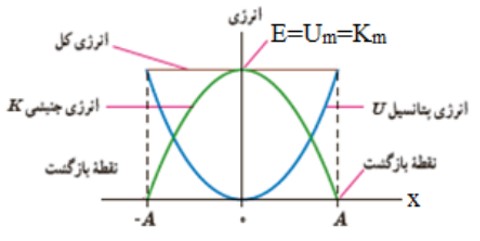
2 هنگامی كه انرژی پتانسيل بيشينه است، انرژی جنبشی صفر است و هنگامی كه انرژی پتانسيل صفر است انرژی جنبشی بيشينه است و اين يعنی بيشينه ی انرژی جنبشی و بيشينه ی انرژی پتانسيل برابر انرژی مكانيكی است، پس:
\({K_m} = {U_m} = \frac{1}{2}m{\omega ^2}{A^2}\)
نمودار انرژی جنبشی و انرژی پتانسيل بر حسب مكان:
- آزمون آنلاین تمامی دروس پایه ریاضی
- گام به گام تمامی دروس پایه ریاضی
- ویدئو های آموزشی تمامی دروس پایه ریاضی
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ریاضی
- فلش کارت های آماده دروس پایه ریاضی
- گنجینه ای جامع از انشاء های آماده پایه ریاضی
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ریاضی
نوسان
فصل 3 : نوسان و موج
نوسان
بسامد طبيعی
هر نوسانگر با انحراف از وضع تعادل با بسامدی معين شروع به نوسان می كند. به اين نوسان ها بسامد طبيعی گفته می شود. (بسامد اين نوسان با \({f_o}\) نمايش داده می شود.)
نوسان واداشته
هر نوسانگری با اعمال نيروی خارجی با بسامد متفاوتی نسبت به بسامد طبيعی شروع به نوسان می كند، به چنين نوسانی، نوسان واداشته گفته می شود. (بسامد اين نوسان با \({f_d}\) نمايش داده می شود.)
نوسان ميرا
اتلاف انرژی و اصطكاک برای هر نوسانگری كه با بسامد طبيعی نوسان می كند سبب می شود كه پس از مدتی نوسان متوقف گردد، به چنين نوسانی ، نوسان ميرا گفته می شود.
1 تاب خوردن يک كودک بدون هل دادن يک نوسان طبيعی است، اگر هل داده شود يک نوسان واداشته است، و اين هل دادن باعث جبران اتلاف انرژی و مقاومت هوا می گردد و مانع از ميرا شدن نوسان تاب می گردد.
2 با توجه به روابط آونگ ساده و نوسان وزنه-فنر می توان گفت بسامد طبيعی آونگ ساده به صورت \({f_o} = \frac{1}{{2\pi }}\sqrt {\frac{g}{L}} \) و بسامد طبیعی وزنه-فنر به صورت \({f_o} = \frac{1}{{2\pi }}\sqrt {\frac{k}{m}} \) است.
تشديد يا رزونانس
اگر به يک نوسانگر به صورت دوره ای نيرو وارد كنيم و بسامد اين نيرو با بسامد طبيعی نوسانگر برابر باشد (\({f_d} = {f_o}\) ) باشد، دامنه ی نوسانگر تا مقدار معينی بزرگ شده و سپس با همين دامنه نوسان خود را ادامه می دهد، به اين پديده تشديد گفته می شود.
اگر بسامد نيروی وارد بر نوسانگر، بيش تر يا كم تر از نوسان طبيعی آن باشد تشديد رخ نمی دهد ودامنه ی نوسان كوچكتر از حالتی خواهد شد كه بسامد نيرو با بسامد طبيعی برابر است.
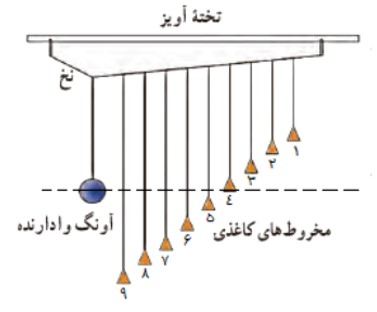
آونگ های بارتون
یک آونگ با وزنه ی سنگين و تعدادی آونگ سبک با طول های متفاوت را مطابق شكل زیر در نظر بگيريد. آونگ ها روی نخی سوار شده اند كه هر دو انتهای آن توسط گيره هايی به تخته آويز متصل شده است. به آونگ سنگين اصطلاحا آونگ وادارنده گفته می شود، زيرا به نوسان در آوردن اين آونگ، موجب تاب خوردن نخ آويز و در نتيجه به نوسان واداشتن ساير آونگ ها می شود. اما از آنجا كه بسامد آونگ مطابق رابطه ی \(f = \frac{1}{{2\pi }}\sqrt {\frac{g}{L}} \) با جذر طول (\(\sqrt L \) ) رابطه مستقيم دارد، بسامد آونگ وادارنده و بسامد آونگ شماره 4 يكسان است (\({f_d} = {f_o}\) ) و در آونگ 4 تشديد رخ می دهد، يعنی دامنه ی نوسان آن بيش از ساير آونگ ها می شود و به مدت طولانی تری نوسان می كند.
موج
فصل 3 : نوسان و موج
موج
هرگاه در ناحيه ای از محيط كشسان ارتعاشی به وجود آيد، موجب پديد آمدن ارتعاش های پی در پی ديگری می شود كه از محل شروع ارتعاش دور و دور ترند و به اين ترتيب موج حاصل می شود.
انواع موج با توجه به محيط انتشار:
1) موج مكانيكی
امواجی كه برای انتشار خود نياز به محيط مادی كشسان دارند موج مكانيكی هستند. ( مانند امواج روی سطح آب و امواج صوتی)
2) موج الكترومغناطيسی
امواجی كه برای انتشار خود نياز به محيط مادی ندارند موج الكترومغناطيسی هستند. (مانند نور مرئی، موج های راديويی و تلويزيونی، ميكروموج ها و پرتوهای X)
تپ موج
تغيير يا آشفتگی ايجاد شده در يک محيط كشسان را تپ موج می گوييم.
موج پيشرونده
موجی است كه از نقطه ای به نقطه ی ديگر حركت كرده و انرژی را با خود منتقل می كنند. (در اين امواج ماده منتقل نمی شود)
انواع موج پيش رونده
1) موج عرضی
موجی است كه راستای جابه جايی هر جزء نوسان كننده (راستای ارتعاش) عمود بر راستای حركت موج (راستای انتشار) است. تصوير زير موج عرضی روی فنر را نشان می دهد.
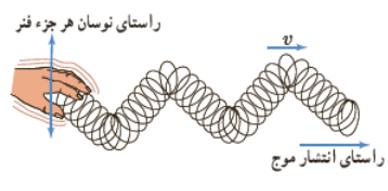
2) موج طولی
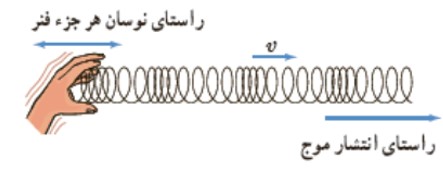
موجی است كه راستای جابه جايی هر جزء نوسان كننده (راستای ارتعاش) منطبق بر راستای حركت موج( راستای انتشار) است. تصوير زير موج طولی روی فنر را نشان می دهد.
چشمه موج
چشمه موج معمولاً يک نوسانگر است كه حركت هماهنگ ساده انجام می دهد و بسامد يک موج همان بسامد چشمه ی موج است.
جبهه موج روی سطح آب
برآمدگی ها يا فرورفتگی های ايجاد شده روی سطح آب، يی جبهه موج ناميده می شود. (به برآمدگی ها قله يا ستيغ و به فرو رفتگی ها دره يا پاستيغ گفته می شود)
دامنه ی موج (A)
بيشينه ی فاصله ی يک ذره از مكان تعادل، دامنه ی موج ناميده می شود. (همان فاصله ی قله يا دره نسبت به سطح آرام يا ساكن است)
دوره تناوب موج (T)
مدت زمانی كه هر ذره ی محيط يک نوسان كامل انجام می دهد دوره تناوب موج ناميده می شود.
بسامد موج (f)
تعداد نوسان های انجام شده توسط هر ذره از محيط در يک ثانيه بسامد موج ناميده می شود.
تندی انتشار موج (V)
مسافت طی شده توسط موج در واحد زمان تندی انتشار ناميده می شود:
\(V = \frac{L}{{\Delta t}}\)
1 بسامد و دوره تناوب موج همان بسامد ودوره ی چشمه ی موج است و به ويژگی های فيزيكی چشمه ی موج بستگی دارند و به ويژگی های محيط انتشار وابسته نيستند.
2 تندی انتشار موج به جنس و ويژگی های محيط انتشار بستگی دارد و به ويژگی های چشمه ی موج وابسته نيست.
3 با افزايش عمق آب، تندی انتشار امواج روی سطح آب نيز بيش تر می شود.
4 اختلاف زمانی دو موج با تندی متفاوت به صورت زير قابل محاسبه است:
\(\Delta {t_T} = \Delta {t_2} - \Delta {t_1} \to \Delta {t_T} = \frac{L}{{{V_2}}} - \frac{L}{{{V_1}}}\)
طول موج (\(\lambda \))
مسافتی است كه موج در مدت دوره تناوب نوسان چشمه طی می كند.
\(\begin{array}{l}\lambda = \frac{V}{f}\\\lambda = VT\end{array}\)
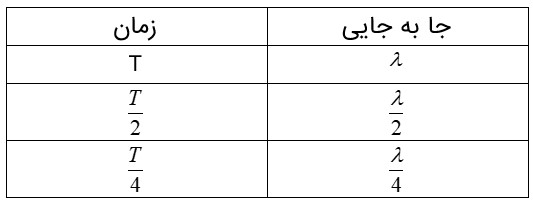
با توجه به مفهوم طول موج می توان گفت در مدت زمان) Tدوره) مسافتی كه موج می پيمايد برابر \(\lambda \) است، همچنين برای مسافتی كه موج می پيمايد و زمان، می توان تناسب هايی به صورت زير نوشت:
مشخصه های موج عرضی
فاصله ی دو قله ی متوالی يا دو دره ی متوالی در امواج عرضی برابر طول موج است، همچنين بيشينه ی فاصله ی هر نقطه از مركز نوسان دامنه است:
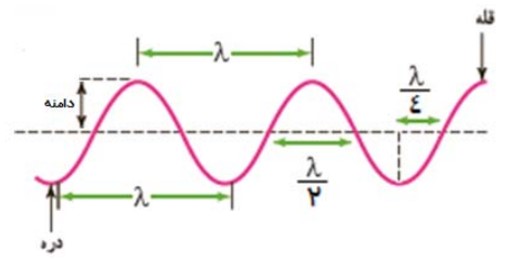
برای تعيين جهت حركت هر ذره روی موج عرضی به وضعيت نقاط قبل تر از آن توجه كنيد. جهت حركت هر نقطه به سمت نقاط قبل تر از خودش است.
مشخصه های موج طولی
فاصله دو انبساط (بازشدگی) متوالی يا دو تراكم (جمع شدگی) متوالی در امواج طوليی برابر طول موج است، همچنين بيشينه ی فاصله ی هر نقطه از مركز نوسان، دامنه است:
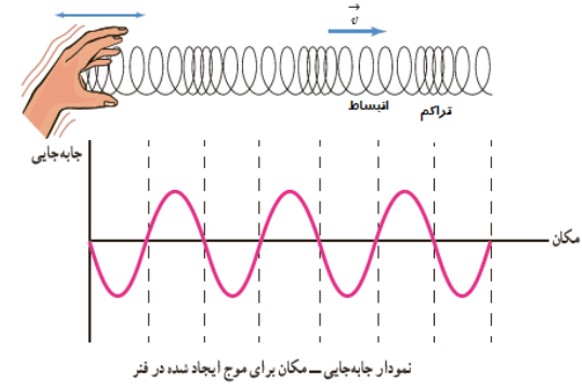
برای امواج مكانيكی، تندی انتشار امواج طولی در يک محيط جامد بيش تر از تندی انتشار امواج عرضی در همان محيط است.
امواج لرزه ای
امواج لرزه ای، موج های مكانيكی هستند كه از لايه های زمين عبور می كنند. يكی از منشأ های مهم امواج لرزه ای، زمين لرزه ها هستند. انواع امواج لرزه ای عبارتند از:
- امواج P يا امواج اوليه كه طولی بوده و سرعت بيش تری داشته و سريع تر به دستگاه لرزه نگار می رسد.
- امواج S يا امواج ثانويه كه عرضی بوده و سرعت كم تری داشته و دير تر به دستگاه لرزه نگار می رسد.
انتقال انرژی در موج عرضی
هر موجی حامل انرژی است. می توان ثابت كرد كه متوسط آهنگ انتقال انرژی (توان متوسط) در يک موج عرضی برای همه ی امواج مكانيكی با دو عامل زير متناسب است:
1) مربع دامنه (\({A^2}\) )
2) مربع بسامد (\({f^2}\) )
محاسبه تندی انتشار موج عرضی در تار (سيم) يا فنر:
\(V = \sqrt {\frac{F}{\mu }} = \sqrt {\frac{{FL}}{m}} = \sqrt {\frac{F}{{\rho A}}} = \frac{1}{r}\sqrt {\frac{F}{{\rho \pi }}} = \frac{2}{D}\sqrt {\frac{F}{{\rho \pi }}} \)
\(\mu \) چگالی خطی (\(Kg.{m^{ - 1}}\) )
M جرم تار
L طول تار
A سطح مقطع تار
R شعاع مقطع تار
D قطر مقطع تار
\(\rho \) چگالی
V تندی انتشار در تار
\(\begin{array}{l}\mu = \frac{m}{L}\\\rho = \frac{m}{V} \to m = \rho V\\V = AL = \pi {r^2}L\end{array}\)
1شکل مقابل نشان دهنده انتشار کدام موج در طول فنر است؟ چرا؟
موج عرضی زیرا، جابجایی هر جزء نوسان کننده از فنر، در راستای عمود بر حرکت موج است.
2یک موج مکانیکی از محیط 1 وارد محیط 2 می شود و تندی انتشار آن افزایش می یابد. طول موج و بسامد موج چگونه تغییر می کنند؟
طول موج افزایش می یابد و بسامد ثابت می ماند.
بسامد از ویژگی های چشمه موج است لذا از محیطی به محیط دیگر، ثابت می ماند ولی طبق رابطه \(V = f\lambda \) ، سرعت و طول موج رابطه مستقیم دارند؛ لذا اگر سرعت افزایش یابد طول موج نیز افزایش می یابد.
موج الکترومغناطیسی
فصل 3 : نوسان و موج
موج الکترومغناطیسی
- بار الكتريكی ، ميدان الكتريكی ايجاد می كند.
- جريان الكتريكی، ميدان مغناطيسی توليد می كند.
- اگر بارهای الكتريكی ساكن باشند، ميدان الكتريكی حاصل از آن ها با زمان تغيير نمی كند.
- اگر جريان الكتريكی ثابت باشد، ميدان مغناطيسی حاصل از آن ثابت و بدون تغيير می شود.
نحوه ايجاد موج الكترومغناطيس
امواج الكترومغناطيسی از رابطه ی متقابل ميدان های الكتريكی و مغناطيسی به وجود می آيند. يعنی هر تغييری در ميدان الكتريكی در هر نقطه از فضا، ميدان مغناطيسی متغيری ايجاد می كند و اين ميدان مغناطيسی متغير، خود ميدان الكتريكی متغيری به وجود می آورد. اين رابطه ی متقابل ميدان ها سبب انتقال نوسان ها ی ميدان های الكتريكی و مغناطيسی از يک نقطه ی فضا به نقاط ديگر و يا همان انتشار موج الكترومغناطيسی می شود.
ايجاد ميدان الكتريكی به علت تغيير ميدان مغناطيسی همان قانون القای الكترومغناطيس است كه توسط مايكل فاراده كشف شد.
نظر ماكسول در مورد موج الكترومغناطيس
عكس قانون فاراده توسط جيمز كلارک ماكسول پيش بيني شد، يعنی او پيش بينی كرد كه همانطور كه طبق قانون فاراده بر اثر تغيير ميدان مغناطيسی می توان ميدان الكتريكی توليد نمود، بر اثر تغيير ميدان الكتريكی نيز می توان ميدان مغناطيسی توليد نمود. ماكسول از اين دو پديده نتيجه گرفت كه امواج الكترومغناطيس بايد لزوماً ناشی از تغييرات هم زمان ميدان های الكتريكی و مغناطيسی (اصطلاحاً ميدان الكترومغناطيسی) باشد.
تصويری از يک موج الكترومغناطيس و نحوه ی انتشار آن:
مهمترين مشخصات موج الكترومغناطيسی
- ميدان الكتريكی (E) همواره عمود بر ميدان مغناطيسی (B) است.
- ميدان الكتریکی و مغناطيس (E) و (B) همواره بر جهت حركت موج عمودند و در نتيجه موج الكترومغناطيسی، يک موج عرضی است.
- ميدان های الكتريكی و مغناطيسی با بسامد يكسان و همگام با يكديگر تغيير می كنند.
نحوه تعيين جهت انتشار موج الكترومغناطيسی
با كمک قاعده ی دست راست تعيين می شود.
تندی انتشار امواج الكترومغناطيس
ماكسول با يک تحليل رياضی نشان داد كه تندی انتشار امواج الكترومغناطيس در هوا يا خلأ از رابطه ی زير به دست می آيد:
\(C = \frac{1}{{\sqrt {{\mu _0}{\varepsilon _0}} }} = 3 \times {10^8}\)
\({\mu _0}\) تراوایی مغناطیسی خلاء (\(4\pi \times {10^{ - 7}}\frac{{T.m}}{A}\) )
\({\varepsilon _0}\) تراوايی الكتريكي خلاء (\(8/85 \times {10^{ - 12}}\frac{{{C^2}}}{{N.{m^2}}}\) )
C تندی انتشار موج الكترومغناطيس در هوا يا خلاء (\(\frac{m}{s}\) )
انرژی امواج الكترو مغناطيس
انرژی اين امواج مانند امواج مكانيكی به صورت انرژی جنبشی و پتانسيل ذرات محيط نيست (زيرا اين امواج برای انتشار نياز به محيط مادی ندارند) بلكه اين امواج انرژی را به صورت انرژی ميدان های الكتريكی و مغناطيسی منتقل می كنند.
طيف امواج الكترومغناطيسی
اين طيف به ترتيب افزايش طول موج به صورت زير است. (هيچ گسستگی در اين طيف وجود ندارد و همگی با تندی نور درخلأ حركت می كنند)
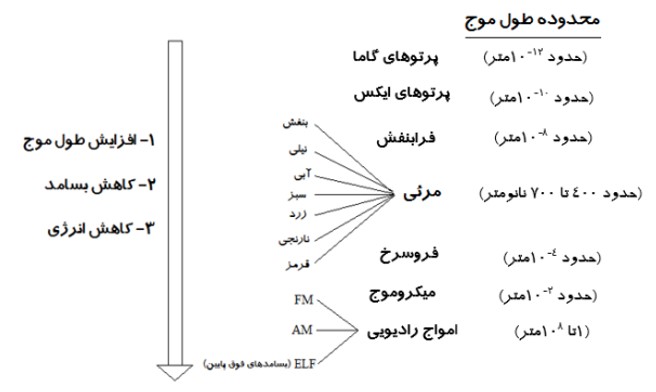
امواج الکترومغناطیسی طولی هستند یا عرضی؟ چرا؟
عرضی ،چون راستای نوسان میدان های الکتریکی و مغناطیسی بر راستای انتشار موج عمود است.
- آزمون آنلاین تمامی دروس پایه ریاضی
- گام به گام تمامی دروس پایه ریاضی
- ویدئو های آموزشی تمامی دروس پایه ریاضی
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ریاضی
- فلش کارت های آماده دروس پایه ریاضی
- گنجینه ای جامع از انشاء های آماده پایه ریاضی
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ریاضی
موج صوتی
فصل 3 : نوسان و موج
موج صوتی
صوت يک موج مكانيكی طولی است كه توسط جسم مرتعش توليد می شود. (به اين جسم مرتعش نيز چشمه ی صوت گفته می شود)
1 انتشار صوت با تندی ثابت و در تمام جهات به صورت سه بعدی صورت می گيرد. (جبهه های موج كروی است)
2 هنگام انتشار صوت هر مولكول هوا، با موج حركت نمی كند، بلكه در مكان ثابتی نوسان می نمايد.
3 هر چه محيطی متراكم تر باشد سرعت انتشار آن نيز بيش تر می شود، به طور مثال سرعت انتشار در جامدها بيش تر از مايعات و در مايعات نيز بيش تر از گازها است. (البته استثناهايی نيز وجود دارد)
4 چشمه ی صوت برای انتقال انرژی، لايه ای از محيط كه در تماس با آن است را به حركت در می آورد و انرژی از اين لايه به لايه ی بعدی در تمام جهات منتشر می شود.
5 با توجه به اينكه صوت حركت يكنواخت انجام می دهد رابطه ی زير برای آن برقرار است:
\(V = \frac{L}{{\Delta t}}\)
عوامل مؤثر بر تندی صوت
- جنس محيط انتشار
- دمای محيط انتشار
شدت صوت (I)
شدت صوت برابر با آهنگ متوسط انرژی ای است كه توسط موج به واحد سطح، عمود بر راستای انتشار صوت می رسد.
\(\begin{array}{l}I = \frac{P}{A}\\I = \frac{P}{{4\pi {r^2}}}\end{array}\)
P متوسط توان چشمه صوتی (W)
I شدت صوت (\(\frac{W}{{{m^2}}}\) )
R فاصله از چشمه صوت (m)
A مساحت جبه های موج صوتی (\({m^2}\) )
عوامل مؤثر بر شدت صوت
1) مجذور دامنه (\({A^2}\) )
2) مجذور بسامد (\({f^2}\) )
3) مجذور فاصله (\({r^2}\))
براساس 3 عامل فوق رابطه ای به صورت زير می توان برای مقايسه ی دو شدت صوت نوشت:
\(\frac{{{I_2}}}{{{I_1}}} = {(\frac{{{A_2}}}{{{A_1}}} \times \frac{{{f_2}}}{{{f_1}}} \times \frac{{{r_1}}}{{{r_2}}})^2}\)
تراز شدت صوت يا تراز صوتی (\(\beta \))
به صورت زير و برای تشخيص مقدار بلندی صوت محاسبه می شود:
(b) بر حسب بل : \(\beta = Lo{g^{\frac{I}{{{I_o}}}}}\)
(db) بر حسب دسی بل : \(\beta = 10Lo{g^{\frac{I}{{{I_o}}}}}\)
\({I_o}\) شدت صوت مرجع يا حد پايين شنوای انسان (\({10^{12}}\frac{W}{{{m^2}}}\) )
I شدت صوت (\(\frac{W}{{{m^2}}}\) )
\(\beta \) تراز شدت صوت
مقايسه دو تراز شدت صوت
هر گاه دو تراز صوتی در سؤالی مطرح شد، به صورت زير رابطه بنويسيد:
بر حسب بل : \({\beta _2} - {\beta _1} = Lo{g^{\frac{{{I_2}}}{{{I_1}}}}}\)
بر حسب دسی بل : \({\beta _2} - {\beta _1} = 10Lo{g^{\frac{{{I_2}}}{{{I_1}}}}}\)
تراز شدت صوتی\(80db\) است. شدت این صوت چند وات بر متر مربع است؟ (\({I_0} = {10^{ - 12}}\frac{W}{{{m^2}}}\) )
\(\beta = 10Lo{g^{\frac{I}{{{I_0}}}}} \to 80 = 10Lo{g^{\frac{I}{{{{10}^{ - 12}}}}}} \to {10^8} = \frac{I}{{{{10}^{ - 12}}}} \to I = {10^{ - 4}}\)
تن موسیقی
فصل 3 : نوسان و موج
تن موسیقی
به صوت حاصل از چشمه ی صوتی كه به دليل ميرايی كم مشابه حركت هماهنگ ساده است، تن گفته می شود. (مانند صوت حاصل از يک دياپازون)
دو ويژگی مهم تن موسيقی
1) ارتفاع تن
ارتفاع، بسامدی است كه گوش انسان درک می كند.
2) بلندی تن
بلندی، شدتی است كه گوش انسان درک می كند.
1 ارتفاع و بلندی تن به ادراک شنوايی انسان مربوط است.
2 اگر به يک دياپازون ضربه هايی با قدرت های متفاوت بزنيم، بسامد صدايی كه می شنويم تغيير نمی كند اما صداهايی با بلندی متفاوت را حس می كنيم كه به شدت اين ضربه ها بستگی دارد.
3 بلندی با شدت متفاوت است. شدت را می توان با يک آشكارساز اندازه گيری كرد، اما بلندی چيزی است كه شما احساس می كنيد.
4 بيش ترين حساسيت انسان به بسامدهايی در گستره ی \(2000Hz\) تا \(5000Hz\) است. درحالی كه گوش انسان قادر به شنيدن تن های صدای \(20Hz\) تا \(20000Hz\) است.
اثر دوپلر
هنگامی كه چشمه ی صوتی و شنونده نسبت به هم دور يا نزديک شوند، بسامد و طول موجی كه شنونده دريافت می كند با بسامد و طول موج واقعی چشمه موج متفاوت است. به اين پديده اثر دوپلر گفته می شود.
بررسی حالت های مختلف اثر دوپلر
1) چشمه ی متحرک و ناظر (شنونده ی ساكن)
در اين حالت با توجه تصوير زير اگر چشمه ی موج به شنونده نزديک شود، طول موج كوتاه تر و اگر از آن دور شود طول موج بيش تر خواهد شد:
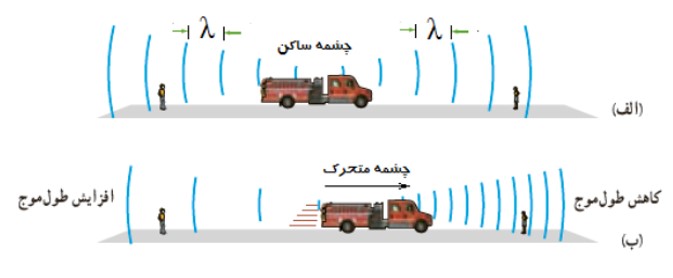
2) چشمه ساكن و ناظر (شنونده ) متحرک
در اين حالت تجمع جبهه های موج در دو سوی چشمه يكسان است. اگر ناظر به طرف چشمه حركت كند، در مقايسه با ناظر ساكن، در مدت زمان يكسان، با جبهه های موج بيش تری مواجه می شود كه اين منجر به افزايش بسامد صوتی می شود كه ناظر می شنود و اگر ناظر از چشمه دور شود، در مقايسه با ناظر ساكن، در مدت زمان يكسان، با جبهه های موج كم تری مواجه می شود كه اين منجر به كاهش بسامد صوتی می شود كه ناظر می شنود :
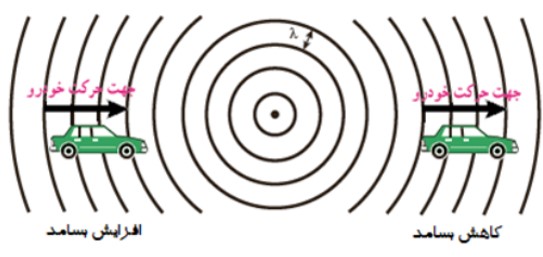
اثر دوپلر برای امواج الكترومغناطيس
بررسی اثر دوپلر در صوت با بررسی اثر دوپلر در امواج الكترومغناطيس متفاوت است. در بررسی اثر دوپلری برای موج الكترومغناطيس دو اصطلاح زير را به كار مي برند:
1) انتقال به سرخ
وقتی چشمه ی نور از ناظر (آشكار ساز) دور می شود، طول موج افزايش می يابد كه به آن انتقال به سرخ گفته می شود.
2) انتقال به آبی
وقتی چشمه ی نور به ناظر (آشكار ساز) نزديک می شود ، طول موج كاهش می يابد كه به آن انتقال به آبی گفته می شود.
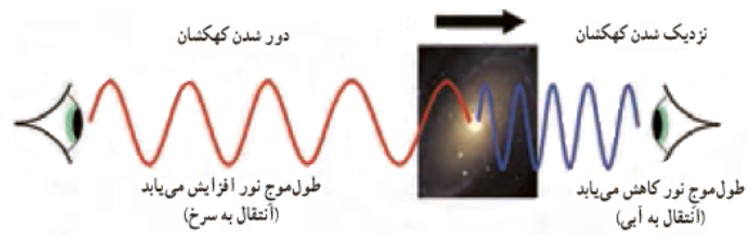
در رصد های نجومی ستارگان، كهكشان ها و ساير چشمه های نوری سماوی، چه هنگامی كه از ما دور می شوند چه هنگامی كه به ما نزديک می شوند، با اندازه گيری جابه جايی دوپلری آن ها می توان اطلاعاتی در مورد تندی و چگونگی حركت آن ها به دست آورد.
برهم کنش موج ها
فصل 4 : برهم کنش های موج
برهم کنش موج ها
مفهوم بر هم كنش موج
پديده هايی مانند بازتاب امواج، شكست موج و تداخل امواج، بر هم كنش امواج ناميده می شود.
بازتاب امواج مكانيكی در يک بعد
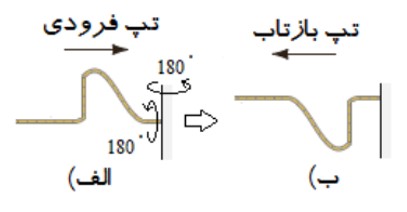
اگر تپی را در يک فنر (يا يک ريسمان) كشيده ی بلند كه يک سر آن بر تكيه گاهی ثابت شده است روانه كنيم، وقتی تپ به تكيه گاه (مرز) می رسد نيرويی به آن وارد می كند و طبق قانون سوم نيوتن، تكيه گاه نيز نيرويی با اندازه ی برابر و در جهت مخالف بر فنر وارد می آورد. اين نيرو در محل تكيه گاه، تپی در فنر ايجاد می كند كه روی فنر در جهت مخالف تپ تابيده حركت می كند. به مثال زير توجه كنيد:
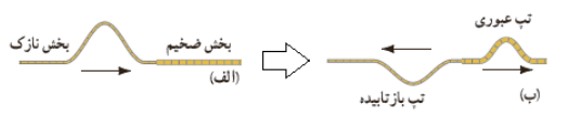
1 وقتی موجی به مرز جدايی دو محيط می رسد، بخشی از آن بازتابيده می شود و بخشی ديگر عبور می كند، به طور مثال تپ عبور در يک طناب را به صورت زير در نظر بگيريد كه از سمت نازک طناب به سمت بخش ضخيم آن در حركت است، بخشی از اين تاب بازتاب می شود و بخش ديگر عبور می كند. براي يک موج سينوسی بسامد اين دو موج همان بسامد فرودی است كه توسط چشمه ی موج تعيين می گردد، اما چون تندی آن در قسمت ضخيم كم تر است، طبق رابطه ی \(\lambda = \frac{V}{f}\) ، طول موج كم تری نسبت به موج فرودی خواهد داشت:
2 توليد صدا در آلات موسيقی، پژواک صداها، ديدن ماه، گرم شدن مواد غذايی در اجاق های خورشيدی، جمع شدن امواج راديويی در كانون آنتن های بشقابی و . . . مثال هايی از كاربرد بازتاب امواج در زندگی هستند.
- آزمون آنلاین تمامی دروس پایه ریاضی
- گام به گام تمامی دروس پایه ریاضی
- ویدئو های آموزشی تمامی دروس پایه ریاضی
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ریاضی
- فلش کارت های آماده دروس پایه ریاضی
- گنجینه ای جامع از انشاء های آماده پایه ریاضی
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ریاضی
امواج مکانیکی
فصل 4 : برهم کنش های موج
امواج مکانیکی
بازتاب امواج مكانيكی در دو بعد
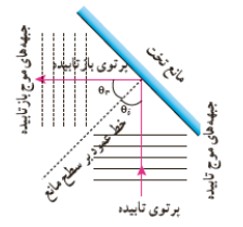
امواج تختی كه بر سطح آب تشكيل می شود پس از برخورد با مانع تخت بازتاب می شوند كه اين امواج بازتابيده مانند تصاوير زير نيز تخت هستند. با استفاده از جبهه های موج می توانيم به طور تجربی به رفتار موج در برخورد با يک مانع پی ببريم:
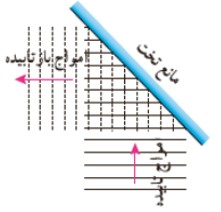
در تصوير فوق موج جبهه های موج تابيده با خطوط توپر و خطوط خط چين جبهه های موج بازتابيده را نشان می دهند.
نمودار پرتويی برای نمايش بازتاب امواج مكانيكی در دو بعد
در اين نمودار يک پرتو، پيكان مستقيمی عمود بر جبهه های موج است كه جهت انتشار موج را نشان می دهد. در اين نمودار به موارد زير توجه كنيد:
1) زاويه ی تابش (\({\theta _i}\))
زاويه يی بين خط عمود بر سطح مانع و پرتوی تابيده (فرودی) زاويه ی تابش ناميده می شود.
2) زاویه بازتابش (\({\theta _r}\))
زاويه ی بين خط عمود بر سطح مانع و پرتوی بازتابيده زاويه ی تابش ناميده می شود.
3) برای امواج دايره ای و كروی همواره زاويه ی تابش و بازتابش برابر است. ( يعنی \({\theta _i} - {\theta _r}\) است كه به آن، قانون بازتاب عمومی گفته می شود(
بازتاب امواج مكانيكی در سه بعد
بازتاب امواج صوتی نمونه ای از بازتاب امواج در سه بعد است. صوت می تواند از يک مانع سخت مانند ديوار بازتاب می شود. بازتاب صوت نيز از قانون بازتاب عمومی پيروی می كند.
كاربرد بازتاب امواج صوتی در پارک های تفريحی
دو سطح كاو مانند شكل زير را در نظر بگيريد كه وقتی شخصی در كانون يكی از اين سطوح صحبت می كند، شخص ديگری در كانون سطح كاو ديگر آن را می شنود.
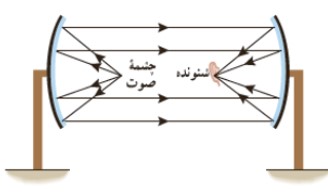
در ساخت ميكروفون سهموی كه برای ثبت صداهای ضعيف استفاده می شود و دستگاه ليتوتريپسی كه از آن برای شكستن سنگ های كليه استفاده می شود از باز تابنده های بيضوی استفاده می شود.
پژواک
اگر صوت پس از بازتاب، با يک تأخير زمانی به گوش شنونده ای برسد كه صوت اوليه را مستقيماً می شنود به چنين بازتابی پژواک می گويند. (اگر تأخير زمانی بين دو صوت كم تر از \(0/1\) ثانيه باشد گوش انسان نمی تواند پژواک صوت را از صوت اصلی تشخيص دهد)
مكان يابی پژواكی
روشی است كه بر اساس امواج بازتابيده از يک جسم، مكان آن جسم را تعيين می كند.
1 برخی جانواران نظير خفاش و دلفين از مكان يابی پژواكی استفاده می كنند.
2 در فناوری هايی نظير اندازه گيری تندی شارش خون در رگ ها، دستگاه سونار كه در كشتی ها برای مكان يابی اجسام زير آب و در سونوگرافی از مكان يابی پژواكی استفاده می شود.
3 از مكان يابی پژواكی به همراه اثر دوپلر در تعيين مكان و تعيين تندی اجسام متحرک به كار می رود.
امواج الکترومغناطیس
فصل 4 : برهم کنش های موج
امواج الکترومغناطیس
اين امواج نيز می توانند از يک سطح بازتابيده شوند و بازتاب آن ها نمونه ديگری از بازتاب در سه بعد است.
امواج الكترومغناطيسی تخت تابيده به يک سطح كاو پس از بازتابش، به يک نقطه ی كانونی می رسند. از اين ساز و كار برای دريافت امواج راديويی توسط آنتن های بشقابی و يا امواج فرو سرخ برای گرم كردن آب يا مواد غذايی در اجاق های خورشيدی استفاده می شود:
رادار دوپلری وسيله ای است كه از امواج الكترومغناطيسی براي مكان يابی پژواكی و تعيين تندی خودروها استفاده می شود.
بازتاب در نور مرئی
از آنجا كه نور مرئی نيز يک موج الكترو مغناطيس است از قانون بازتاب عمومی امواج پيروی می كند. يعنی اولاً زاويه تابش و بازتابشی با هم برابرند و ثانياً پرتوی تابش، پرتوی بازتابش و خط عمود بر سطح بازتابنده، در هر بازتابش در يک صفحه واقع اند.
انواع بازتاب نور مرئی
1) بازتاب آينه ای يا منظم
در مواردی كه سطح بازتابنده ی نور همچون يک آينه، بسيار هموار باشد، بازتاب نور را بازتاب آينه ای يا منظم می گويند.
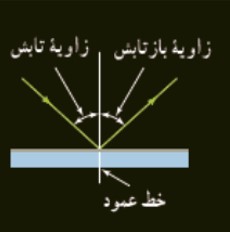
2) بازتاب پخشنده يا نامنظم
اين بازتاب وقتی رخ می دهد كه صيقلی و هموار نباشد. پرتوهای نور به طور كاتوره ای از پستی و بلندی های سطح بازتابيده، و در تمام جهات پراكنده می شود. علت ديدن اجسام رخ دادن اين نوع بازتاب است.

1 در بازتاب آينه ای از يک آينه تخت، دسته پرتوی موازی را تنها در يک جهت می توانيد ببينيد، اما در بازتاب پخشنده، اين دسته پرتو را در جهت های مختلف می توان مشاهده كرد.
2 منظور از سطح ناهموار آن است كه سطح در مقايسه با طول موج نور ناهموار است، مثلاً كاغذ در ظاهر بسيار هموار به نظر می رسد اما از ديد ميكروسكوپی اين سطح از اجزای متمايز و كوچكی تشكيل شده است كه برای يک نور مرئی ناهموار محسوب می شود.
3 برای مسائل محاسباتی مربوط به آينه های تخت به موارد زير توجه كنيد:
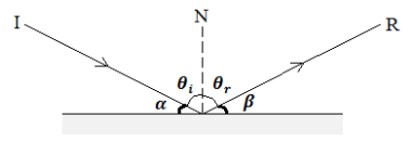
\(\begin{array}{l}{\theta _1} = {\theta _2}\\\alpha = \beta \\{\theta _1} + \alpha = 90\\{\theta _2} + \beta = 90\end{array}\)
شکست موج
فصل 4 : برهم کنش های موج
شکست موج
در امواج دوبعدی (مانند امواج روی آب) و سه بعدی (امواج الكترومغناطيس) با عبور موج از يک مرز و ورود آن به محيط ديگر، تندی موج تغيير می كند و موجب تغيير جهت موج می گردد كه به آن شكست موج گفته می شود.
بررسی علت شكست موج در آب
همان طور كه قبل تر گفته شد تندی موج در سطح آب به عمق آب بستگی دارد. در تشت موج، با ورود موج به بخش كم عمق آب، تندی امواج سطحی كاهش می يابد. در حقيقت آن بخش كه زودتر به ناحيه ی كم عمق می رسد، چون با تندی كم تر حركت می كند از بقيه ی موج كه هنوز وارد اين ناحيه نشده، عقب می افتد و مطابق شكل در مرز دو ناحيه تغيير جهت می دهد. (اين مطلب را می توان در نزديک شدن امواج به يک ساحل شيب دار مشاهده كرد، درست مانند تغيير مسير يک اسباب بازی چرخ دار كه از كف صاف اتاق وارد قاليچه ای می شود(
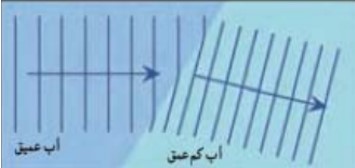
حالت های مختلف شكست با نمودار پرتويی
1) در صورتی كه موجی از محيطی با تندی كم تر به محيطی با تندی بيش تر برود زاويه ی شكست \({\theta _2}\) بزرگ تر از زاويه ی تابش \({\theta _1}\) می شود.
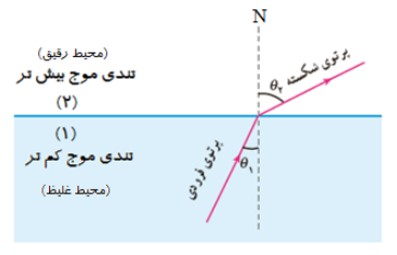
2) در صورتی كه موجی از محيطی با تندی بيش تر به محيطی با تنديی كم تر برود زاويه ی شكست \({\theta _2}\) كوچک تر از زاويه ی تابش \({\theta _1}\) می شود.
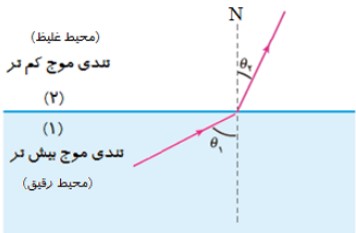
قانون عمومی شكست
نسبت سينوس زاويه شكست در محيط دوم (\({\theta _2}\)) به سينوس زاويه تابش در محيط اول (\({\theta _1}\))، برابر نسبت تندی انتشار در محيط دوم به تندی انتشار در محيط اول است:
\(\frac{{{\mathop{\rm Sin}\nolimits} {\theta _2}}}{{{\mathop{\rm Sin}\nolimits} {\theta _1}}} = \frac{{{V_2}}}{{{V_1}}}\)
ضريب شكست
برای يک پرتوی نور، نسبت تندی نور در خلأ به تندی نور در يک محیط، ضريب شكست آن محيط است:
\(n = \frac{C}{V}\)
C تندی نور در خلا (\(3 \times {10^8}\frac{m}{s}\) )
V تندی نور در يک محيط شفاف (\(\frac{m}{s}\) )
N ضريب شكست محيط شفاف
قانون شكست اسنل
رابطه ی زير كه مربوط به شكست نور و ضريب شكست است، قانون اسنل ناميده می شود:
\({n_1}{\mathop{\rm Sin}\nolimits} {\theta _1} = {n_2}{\mathop{\rm Sin}\nolimits} {\theta _2}\)
1 ضريب شكست خلأ (هوا) برابر 1 است.
2 اگر پرتو نوری به طور عمود به سطح جداكننده ی دو محيط تابش شود شكسته نمی شود.
3 هرچه محيطی متراكم تر باشد ضريب شكست آن محيط نيز بيش تر است.
4 ضريب شكست يک محيط با تندی نور در آن محيط (V) و طول موج (\(\lambda \)) رابطه ی وارونه دارد. (هر چه ضريب شكست بيش تر باشد، تندی نور و طول موج نور در آن كم تر است.)
5 بسامد، دوره تناوب و انرژی موج الكترو مغناطيس تنها به چشمه ی موج وابسته است و به ضريب شكست بستگی ندارد.
بيش تر روابطی كه در رابطه با شكست نور نوشته شده است را می توان در رابطه ی زير خلاصه نمود:
\(\frac{{{\mathop{\rm Sin}\nolimits} {\theta _2}}}{{{\mathop{\rm Sin}\nolimits} {\theta _1}}} = \frac{{{n_1}}}{{{n_2}}} = \frac{{{V_2}}}{{{V_1}}} = \frac{{{\lambda _2}}}{{{\lambda _1}}}\)
عمق ظاهری
هنگامی كه از يک محيط شفاف به محيط شفاف ديگر نگاه می كنيم ، اجسام داخل محيط دوم در عمق بيش تر يا كم تر از مكان واقعی خود مشاهده می شوند كه در دوحالت زير می توان برای آن محاسبه انجام داد:
1) اگر ازمحيط رقيق تر به محيط غليظ تر نگاه كنيم، اجسام را در عمق كمتر از مكان واقعی خود می بينيم:
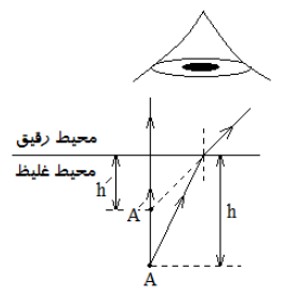
2) اگر از محيط غليظ تر به محيط رقيق تر نگاه كنيم: اجسام را در عمق می بینیم:
سراب
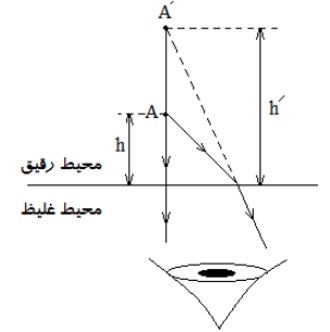
در روز های گرم، سطح زمين داغ است. از طرفی، چگالی هوا با افزايش دما كاهش می يابد كه اين سبب كاهش ضريب شكست نيز می شود. با پايين آمدن هر چه بيش تر پرتوها، آن ها با ضريب شكست كمتر و كمتری مواجه می شوند و در هر مرحله با دور شدن از خط عمود، بيشتر و بيشتر به سمت افق خم می شوند. وقتی پرتوها در نزديكی زمين تقريبا افقی می شوند، به سمت بالا خم بر می دارند زيرا بخش پايينی هر جبهه ی موج در هوای كمی گرم قرار دارد و بنابراين كمی تند تر از بخش بالايی جبهه ی موج حركت می كند و اين تفاوت رفتار دو قسمت جبهه های موج ، موجب خم شدن رو به بالای پرتوهای موج می شود، زيرا پرتوهای موج بايد همواره عمود بر جبهه های موج باشند. وقتی پرتوها رو به بالا می روند به خم شدن رو به بالای خود ادامه می دهند، زيرا اكنون مدام با محيط هايی با ضريب شكست های بزرگ و بزرگ تر مواجه می شوند و در هر مرحله با نزديک شدن به خط عمود، بيش تر و بيش تر رو به بالا خم می شوند. اگر بخشی از اين نور به چشم ما برسد، به نظر می آيد كه منشأ اين نور از امتداد رو به عقب پرتوهايی است كه به چشم ما رسيده اند و اين احساس را ايجاد می كنند كه گويی از سطح زمين آمده اند.
پاشندگی نور
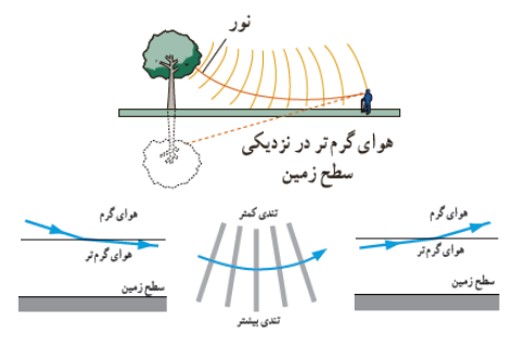
وقتی باريكه ی نوری شامل پرتوهايی با طول موج های مختلف باشد، اين پرتوها هنگام عبور از مرز دو محيط در زاويه های مختلفی شكسته می شوند. به اين پخش شدگی نور، پاشندگی نور می گويند. (دليل اين پديده آن است كه ضريب شكست يک محيط برای طول موج های مختلف، يكسان نيست و هر رنگی كه طول موج كم تری دارد ضريب شكست بيش تری داشته و انحراف بيش تری پيدا می كند.) تصوير زير پاشندگی نور سفيد را در يک منشور نشان می دهد:
پراش موج
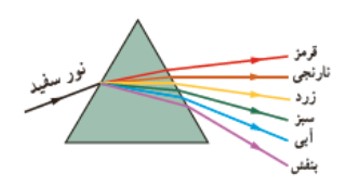
هنگامی كه موج از يک شكاف با پهنايی از مرتبه ی طول موج عبور می كند، به اطراف گسترده می شود، به اين پديده پراش موج گفته می شود.
1 اگر موج تختی از شكافی عبور كند كه پهنای آن خيلی بزرگ تر از طول موج باشد، آن قسمتی كه از شكاف می گذرد تقريباً تخت باقی می ماند، اما اگر موج تختی از شكافی عبور كند كه پهنای آن خيلی بزرگ تر از طول موج نباشد، آن قسمتی كه از شكاف می گذرد كاملاً از حالت موج تخت خارج شده و به مقدار بيش تری به اطراف گسترده می شود. شكل زير پراش در سه شكاف با پهناهای متفاوت را نشان می دهد:
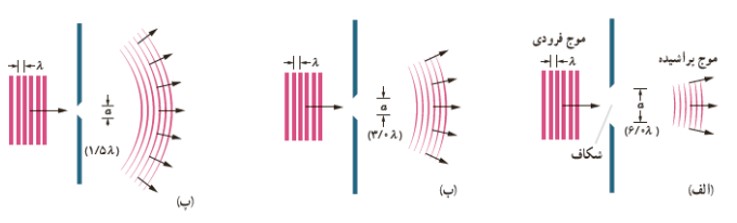
2 پراش فقط به وضعيت عبور موج از يک شكاف باريک (روزنه) محدود نمی شود بلكه هنگام عبور موج از لبه های مانعی كه ابعاد آن در حدود طول موج باشد باشد نيز رخ می دهد.
نقش پراش
اگر پراش نوری تكفام از يک شكاف باريک يا لبه ای تيز را روی يک پرده ملاحظه كنيم، همواره نوارهای تاريک و روشنی مشاهده می كنيم كه به آن نقش پراش گفته می شود. به طور مثال تصوير زير نقش پراش نوری تكفام را نشان می دهد كه از لبه های يک تيغ عبور می كند.

1 سيگنال های فرستنده های راديويی و تلويزيونی هنگام برخورد به يک مانع (مانند ديوار يا يک تپه) به دليل پراش از لبه های مانع دريافت خواهد شد. (ناحيه ای كه سيگنال به آن نمی رسد ناحيه ی سايه ناميده می شود)
2 طول موج سيگنال های فرستنده های تلويزيونی ديجيتالی امروزی كوتاه تر از طول فرستنده های قديمی است، كه اين موضوع سبب می شود پراش سيگنال ها به ناحيه ی سايه كاهش پيدا كند، زيرا همان طور كه گفته شد هرچه شكاف ها و لبه ها ابعاد بزرگتری نسبت به طول موج داشته باشد پراش كم تری رخ می دهد و گستردگی و خميدگی موج كم تر می شود.
علت خطوط تاریک در طیف نور خورشید چیست؟
طول موج مربوط به این خطوط، توسط گازهای جو خورشید و جو زمین جذب شده است.
- آزمون آنلاین تمامی دروس پایه ریاضی
- گام به گام تمامی دروس پایه ریاضی
- ویدئو های آموزشی تمامی دروس پایه ریاضی
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ریاضی
- فلش کارت های آماده دروس پایه ریاضی
- گنجینه ای جامع از انشاء های آماده پایه ریاضی
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ریاضی
تداخل امواج
فصل 4 : برهم کنش های موج
تداخل امواج
به تركيب موج ها با يكديگر تداخل می گويند.
اصل بر هم نهی امواج
وقتی چند موج به طور هم زمان بر ناحيه ای از فضا تأثير بگذارند، اثر خالص آن ها برابر مجموع اثرهای مجزای هر يک از آنها است. (به عبارت ديگر تداخل، تركيب دو يا چند موج است كه به طور هم زمان از يک منطقه عبور می كنند.)
تپ ها يا امواجی كه با يكديگر تداخل دارند به هيچ وجه شكل حركت يكديگر را تغيير نمی دهند و پس از هم پوشانی و تداخل، بدون هرگونه تغيير شكلی به حركت خود ادامه می دهند.
انواع تداخل موج
1) تداخل سازنده
اگر تپ ها در اثر هم پوشانی تپ برگتری را ايجاد كنند به آن تداخل سازنده گفته می شود.

2) تداخل ويرانگر(مخرب)
اگر تپ ها در اثر همپوشانی يكديگر را حذف كنند به آن تداخل ويرانگر گفته می شود.

تداخل امواج سطحی آب
برای مشاهده ی تداخل امواج سطحی بر سطح آب با استفاده از تشت موج، دو گوی كوچک را با بسامد يكسان، به طور هم زمان بر سطح آب به نوسان در می آوريم. دو دسته موج دايره ای ايجاد می شود كه در برخی نقاط برآمدگی ها يا فرورفتگی ها به طور هم زمان در نقطه ای به هم می رسند و همديگر را تقويت می كنند (تداخل سازنده) و اگر برآمدگی يک موج در يک زمان و در يک نقطه به فرورفتگی موج ديگر برسد، دو موج يكديگر را تضعيف می كنند (تداخل مخرب) و بنابراين سطح آب در چنين نقطه ای نوسان چندانی نخواهد داشت.

تداخل امواج صوتی
برای بررسی تداخل امواج صوتی به تصوير مقابل دقت كنيد، در اين آزمايش دو بلندگو كه به يک مولد سيگنال الكتريكی متصل اند امواج سينوسی هم بسامدی در فضا منتشر می كنند. با حركت دادن ميكروفون در امتداد خط فرضی نشان داده شده در شكل كه در فاصله ی مناسبی از بلندگوها قرار دارد در می يابيم كه بلندی صدا به طور متناوب كم يا زياد می شود. در نواحی كاهش صدا تداخل ويرانگر و در نواحی افزايش صدا تداخل سازنده رخ داده است.
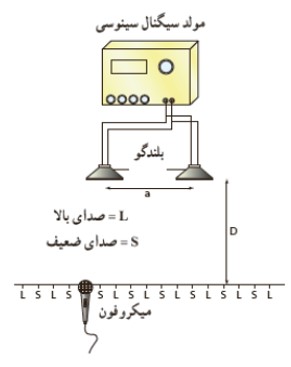
تداخل امواج نوری
شخصی به نام (يانگ) با طراحی آزمايشی ثابت كرد كه بر خلاف نظر بيش تر فيزيكدانان آن زمان، نور يک موج است. شكل زير طرحی از آزمايش يانگ را نشان می دهد. نور حاصل از يک چشمه ی تكفام بر يک شكاف می تابد، سپس نور خروجی بر اثر پراش، گسترده می شود و دو شكاف و
را روشن می كند. موج های حاصل از پراش نور توسط اين دو شكاف با يكديگر تداخل می كنند و نقش حاصل از اين تداخل را می توان روی پرده ای كه در ناحيه ی سمت راست دو شكاف قرار دارد مشاهده كرد.
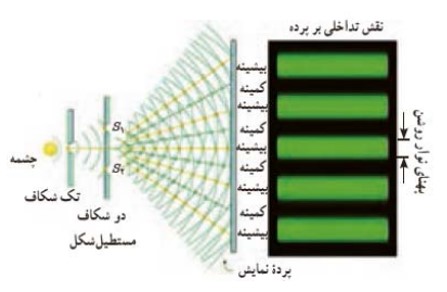
روی پرده، نقطه های با تداخل سازنده، نوارها يا فريزهای روشن را تشكيل می دهند.
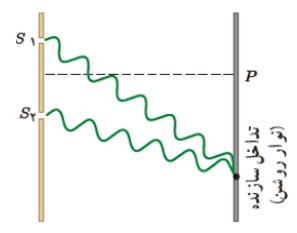
و نقطه های با تداخل ويرانگر نوارها يا فريزهای تاريک را تشكيل می دهند.
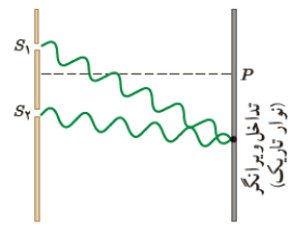
نقش تداخلی
نوارهای روشن و تاريک روی پرده كه ناشی از تداخل های سازنده و ويرانگر هستند، نقش تداخلی ناميده می شوند.
1 در نقش تداخلی پهنای نوارهای روشن و تاريک برابرند.
2 پهنای نوار های روشن و تاريک با طول موج نور به كار رفته در آزمايش رابطه ی مستقيم دارد. (يعنی هر چه طول موج به كار رفته بيش تر باشد پهنای نوارهای روشن و تاريک بيش تر است.)
3 با كمک آزمايش يانگ طول موج نور به كار رفته را می توان محاسبه نمود.
مشاهده ی نقش تداخلی به كمک نور ليزر
اگر از نور ليزر استفاده كنيم، ديگر نيازی به استفاده از يک تک شكاف در آزمايش يانگ نيست. با استفاده از يک ليزر مدادی، می توان صفحه ی دو شكاف يانگ را روشن نمود. (البته ممكن است لازم باشد از يک عدسی واگرا در برابر نور ليزر استفاده شود تا هر دو شكاف روشن گردد.)
موج ایستاده و کشیده
فصل 4 : برهم کنش های موج
موج ایستاده و کشیده
موج ايستاده و تشديد در ريسمان كشيده
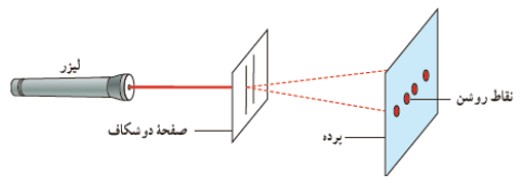
هر گاه دو موج عرضی كاملاً مشابه كه در دو سوی مختلف انتشار پيدا می كنند با يكديگر تداخل نمايند، موج برايند ديگر رونده نيست و به آن موج ساكن يا ايستاده گفته می شود، كه تصوير موج برايند به شكل زير است:
گره
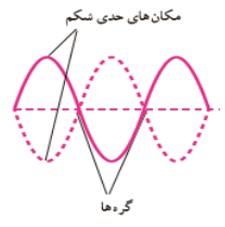
نقاطی روی موج ايستاده كه هرگز نوسان نمی كنند، گره هستند. (دامنه ی نوسان صفر است)
شكم
نقاطی روی موج ايستاده كه دامنه ی موج برايند در آنجا بيشينه است. (دامنه آن ها دو برابر دامنه موج های اوليه است)
1 فاصله ی دو گره ی متوالی يا دو شكم متوالی برابر \(\frac{\lambda }{2}\) است.
2 فاصله ی يک گره از شكم مجاورش برابر \(\frac{\lambda }{4}\) است.
3 موج های تابش و بازتابش در محل گره ها با يكديگر تداخل ويرانگر انجام می دهند و در اصطلاح گفته می شود دو موج در محل گره ها كاملاً ناهمفاز (در فاز مخالف) هستند.
4 موج های تابش و بازتابش در محل شكم ها با يكديگر تداخل سازنده انجام می دهند و در اصطلاح گفته می شود دو موج در محل شكم ها در كاملاً همفاز هستند.
5 از آن جا كه موج ايستاده به چپ يا راست حركت نمی كند محل گره ها يا شكم ها ثابت است.
بسامد های تشديدی
هر گاه يک تار كشيده شده به وسيله ی يک چشمه به نوسان در آيد، به ازای بسامدهای معينی، تداخل موجب ايجاد موج ايستاده ی بارزی (يا اصطلاحاً يک مد نوسان) در تار می شود كه به اين بسامدها، بسامدهای تشديدی گفته می شود. (اگر تار در بسامدهای غير از بسامدهای تشديدی نوسان كند موج ايستاده بارزی ايجاد نمی شود.)
روابط محاسباتی موج ساكن در تار مرتعش تحت كشش
شكل زير تصاوير مربوط به حالت های مختلف موج ايستاده در يک تار است.

\(\begin{array}{l}L = n\frac{{\lambda n}}{2}\\{f_n} = n\frac{V}{{2L}} = n{f_1}\\{f_1} = \frac{V}{{2L}}\end{array}\)
(n) تعداد شكم ها(تعدادگره ها \(n + 1\) است) یا عدد هماهنگ
L طول تار
V تندي انتشار موج در طناب
\({\lambda _n}\) طول موج تشدیدی
\({f_n}\) بسامد تشدیدی
\({f_1}\) بسامد اصلی يا بسامد هماهنگ (مد) اول
1 تندی انتشار در تار مرتعش با رابطه ی \(V = \sqrt {\frac{F}{\mu }} = \sqrt {\frac{{F.L}}{m}} \) بدست می آید.
2 اختلاف بسامد دو هماهنگ متوالی در ريسمان دو انتها ثابت برابر بسامد اصلی (\({f_1}\)) است.
\({f_{n + 1}} - {f_n} = {f_1} = \frac{V}{{2L}}\)
موج ايستاده و تشديد در لوله های صوتی
در لوله های پر شده از هوا نيز می توان موج ايستاده ايجاد كرد كه به آن ها لوله های صوتی گفته می شود و در نوع دو انتها باز و يک انتها باز ساخته می شوند. وقتی موج های صوتی در هوای درون لوله حركت می كنند، از هر دو انتها باز می تابند و به درون لوله باز می گردند، حتی اگر آن انتها باز باشد (البته اگر انتهای لوله باز باشد اين بازتاب به كاملی بازتابی نيست كه از يک انتهای بسته رخ می دهد) بسياری از مشخصه های اين موج ايستاده مشابه موج ايستاده در ريسمان است؛ انتهای بسته ی لوله مانند انتهای ثابت شده ی ريسمان است كه در آنجا بايد يک گره وجود داشته باشد، و در انتهای باز لوله نيز يک شكم وجود دارد. (البته اين شكم كمی بيرون از انتهای باز لوله قرار دارد كه آن را در نظر نمی گيريم) همچنين فاصله ی گره های مجاور از هم برابر \(\frac{\lambda }{2}\) و فاصله ی گره ها از شكم های مجاور \(\frac{\lambda }{4}\) است. تصوير های زير سه مد اول را در هر دو نوع لوله نشان می دهد:
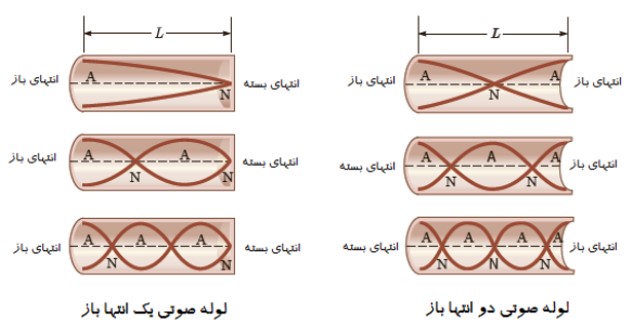
1 هر چه بسامد صوتی بيش تر می شود، آن صوت زير تر شنيده می شود و هرچه بسامد صوتی كم تر می شود آن صوت بم تر شنيده خواهد شد.
2 طول موج صوت حاصل از لوله ی صوتی با طول لوله رابطه ی مستقيم دارد. (يعنی هر چه طول لوله بيشتر باشد طول موج صوت حاصل از آن نيز بيش تر است)
3 صدای حاصل از پر شدن آب داخل يک ليوان گستره وسيعی از بسامدها را دارد كه در هر لحظه، يكی از اين بسامدها با پايين ترين بسامد تشديدی هوای درون ظرف ( بسامد مد اول) منطبق است، به همين دليل با پر شدن ليوان و كوتاه شدن فضای پر از هوای آن (كه يک لوله ی صوتی فرض می شود) طول موج صوت حاصل كاهش و بسامد آن افزايش يافته و صدا زير تر شنيده می شود.
تشديدگر هلمهولتز
كره هايی توخالي با دهانه ای باز به شكل گردن است كه همانند لوله های صوتی بسامدهای تشديدی معينی دارند و هر گاه بسامد يک صوت برابر با يكی از بسامدهای تشديديی آن ها باشد تشديدگر پاسخ قوی تری به اين صوت می دهد. (اين موضوع درست مانند دميدن در يک بطری است، در بطری نيز يكی از بسامدهايی كه هنگام دميدن توليد می شود با يكی از بسامدهای تشديدی منطبق باشد، يک موج صوتی قوی ايجاد می شود)

اجاق های ميكروموج (مايكروفر)
اين اجاق ها بر اساس تداخل امواج الكترومغناطيسی و تشكيل امواج ايستاده كار می كنند. در مورد اين وسيله به نكات زير توجه كنيد:
- ميكرو موج های بازتابيده از ديواره های فلزی اجاق با بر هم نهی با موج های تابيده (با طول موج حدود \(12cm\) ) موج های ايستاده ای را در داخل محفظه ی اجاق ايجاد می كنند كه از گره ها و شكم هايی تشكيل شده اند.
- در محل شكم ها دامنه ی نوسان ميدان الكتريكی بيشينه است. مولكول های آب موجود در مواد غذايی در اين نقاط به شدت به ارتعاش در می آيند و بيش ترين افزايش دما ايجاد می شود. (نقاط گرم)
- در محل گره ها دامنه نوسان صفر است و غذا گرم نمی شود. (نقاط سرد)
فوتو الکتریک
فصل 5 : آشنایی با فیزیک اتمی
فوتو الکتریک
اثر فوتو الكتريک
وقتی نوری با بسامد مناسب مانند نور فرابنفش به سطحی فلزی بتابد الكترون هايی از آن گسيل می شوند. اين پديده را اثر فوتو الكتريک والكترون های جداشده از سطح فلز را فوتو الكترون می نامند.
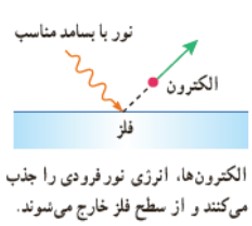
1 برهم كنش نور فرودی فرابنفش با كلاهک برق نما سبب می شود تا ورقه های آن به سرعت به هم نزديک شوند.
2 برهم كنش نور مرئی گسيل شده از يک لامپ رشته ای تغييری در انحراف ورقه های برق نما به وجود نمی آورد.
فوتون
حداقل انرژی موج الكترومغناطيس با يک بسامد معين فوتون ناميده می شود و انرژی آن برابر \(E = h{\textstyle{c \over \lambda }}\) یا \(E = hf\) است.
انرژی امواج الكترومغناطيس
انرژی امواج الكترومغناطيس مضرب صحيحی از انرژی يک فوتون (hf) است:
\(E = nhf\) یا \(E = nh{\textstyle{c \over \lambda }}\)
(n) تعداد فوتون ها
(h) ثابت پلانک (\(6/6 \times {10^{ - 34}}j.s\) )
(c) سرعت امواج الکترومغناطیس (\(3 \times {10^8}\frac{m}{s}\) )
E انرژی امواج الکترومغناطیس
الكترون-ولت
انرژی الكترون تحت ولتاژ يک ولت است و الكترون-ولت يكای غير SI انرژی در فيزيک اتمی و فيزيک هسته ای است. الكترون-ولت به صورت زير به ژول تبديل می شود:
\(1ev = 1/6 \times {10^{ - 19}}j\)
در رابطه های \(E = nhf\) اگر ثابت پلانک (h) بر حسب \(j.s\) باشد E بر حسب ژول (J) به دست می آید و در صورتی که ثابت پلانک (h) بر حسب \(ev.s\) باشد E بر حسب الکترون-ولت (ev) به دست می آیند.
بررسی اثر پديده ی فوتو الكتريک
برای بررسی اثر فوتوالكتريک دستگاهی به صورت زير طراحی می شود:
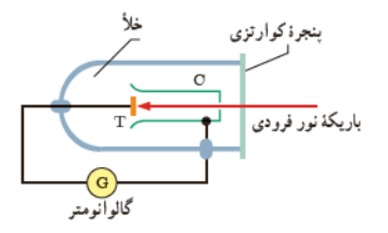
در اين دستگاه صفحه ی فلزی هدف T و جمع كننده ی فلزی C درون يک محفظه شيشه ای خلأ قرار دارند كه از بيرون به يک گالوانومتر (آمپرسنج حساس) متصل شده اند. نور تكفام (تک بسامد) كه بسامد آن به قدر كافی بالا است بر صفحه T فرود می آيد و فوتو الكترون ها را آزاد می كند. اين فوتو الكترون ها به جمع كننده ی C می رسند و در نتيجه گالوانومتر كه در مدار قرار دارد جريانی را آشكار می كند. در اين آزمايش به نكات زير بايد توجه كنيد:
1) با افزايش شدت اين نور چون تعداد فوتوالكترون های جدا شده افزايش می يابد، جريان بيشتر شده و گالوانومتر عدد بزرگتری را نشان می دهد .
2) اگر بسامد نور فرودی از مقدار معينی كم تر باشد، هر چه قدر هم كه شدت نور فرودی افزايش يابد پديده فوتو الكتريک رخ نمی دهد و گالوانومتر عبور جريانی را نشان نمی دهد.
تناقض های فيزيک كلاسيک با نتايج تجربی در پديده ی فوتو الكتريک
1) بر اساس ديدگاه فيزيک كلاسيک هنگام بر هم كنش موج الكترومغناطيسی (نور فرودی) با سطح فلز، ميدان الكتريكی اين موج، نيروی \(f = - eE\) به الكترون های فلز وارد می كند و آن ها را به نوسان در می آورد. به اين ترتيب، وقتی دامنه نوسان برخی از الكترون ها به قدر كافی بزرگ شود انرژی جنبشی لازم را برای جدا شدن از سطح فلز پيدا می كنند. بنابراين پديده ی فوتوالكتريک بايد در هر بسامدی رخ دهد در حالی كه اين نتيجه با تجربه سازگار نيست.
2) براساس نظريه ماكسول شدت نور با مربع دامنه ی ميدان الكتريكی موج الكترومغناطيسی متناسب است (\(I\alpha {E^2}\) )، به اين ترتيب انتظار می رود به ازای يک بسامد معين، اگر شدت نور فرودی بر سطح فلز را افزايش دهيم بايد الكترون ها با سرعت و انرژی جنبشی بيش تری از فلز خارج شوند، اما چنين نتيجه ای در تجربه مشاهده نمی گردد.
نظريه اينشتين در رابطه با پديده ی فوتوالكتريک
1) اينشتين با توجه به نظريه ی پلانک فرض كرد نور با بسامد f را می توان به صورت مجموعه ای از بسته های انرژی در نظر گرفت. هر بسته ی انرژی بعدها فوتون نام گرفت، انرژی هر فوتون از رابطه زير به دست می آيد:
\(\begin{array}{l}E = hf\\E = \frac{{hc}}{\lambda }\end{array}\)
(h) ثابت پلانک (\(6/6 \times {10^{ - 34}}j.s\) )
(f) بسامد (Hz)
(\(\lambda \)) طول موج (m)
(c) سرعت امواج الکترومغناطیس (\(3 \times {10^8}\frac{m}{s}\) )
E انرژی هر فوتون (J)
2) هر فوتون صرفاً با يک الكترون بر هم كنش دارد.
3) بسامدی كه در آن الكترون بدون هيچ انرژی جنبشی ای در آستانه ی ترک فلز است بسامد آستانه ناميده می شود و با \({f_0}\) نمايش داده می شود. (بسامد آستانه حداقل بسامد برای انجام پديده ی فوتوالكتريک است و در كم تر از آن پديده ی فوتوالكتريک انجام نمی شود)
4) طول موجی كه در آن الكترون بدون هيچ انرژی جنبشی ای در آستانه ی ترک فلز است طول موج آستانه ناميده می شود و با \({\lambda _0}\) نمايش داده می شود. (طول موج آستانه حداكثر طول موج برای انجام پديده ی فوتوالكتريک است و در بالاتر از آن پديده ی فوتوالكتريک انجام نمی شود)
5) انرژی لازم برای خارج كردن يک الكترون از سطح يک فلز تابع كار ناميده می شود و با \({W_0}\) نمايش داده می شود.
\(\begin{array}{l}{W_0} = h{f_0}\\{W_0} = \frac{{hc}}{{{\lambda _0}}}\end{array}\)
(h) ثابت پلانک (\(6/6 \times {10^{ - 34}}j.s\) )
(\({f_0}\)) بسامد (Hz)
(\({\lambda _0}\) ) طول موج (m)
(\({W_0}\) ) (J)
6) تابع کار (\({W_0}\) )، بسامد آستانه (\({f_0}\)) و طول موج آستانه (\({\lambda _0}\) ) هر سه به جنس فلز بستگی دارند.
7) اگر فوتون تابشی انرژی كافی داشته باشد، بخشی از انرژی صرف گسيل الكترون از فلز می شود و مابقی آن به انرژی جنبشی الكترون خارج شده تبديل می شود، انرژی جنبشی سريع ترين فوتوالكترون های گسيل شده از رابطه زير به دست می آيد:
\({K_{\max }} = hf - {W_0}\)
8) بيشينه انرژی جنبشی فوتو الكترون ها (\({K_{\max }}\) ) به بسامد نور فرودی و جنس فلز بستگی دارد.
نمودار بيشينه انرژی جنبشی فوتوالكترون ها بر حسب بسامد نور فرودی:
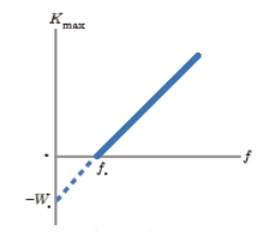
شیب نمودار : \(\tan \alpha = h\)
شرط انجام پديده فوتو الكتريک
اگر يكی از شرط های زير در پديده فوتو الكتريک برقرار باشد پديده فوتو الكتريک رخ می دهد و در غير اينصورت الكترونی از سطح فلز جدا نمی شود.
1) انرژی فوتون تابشی بيش تر از تابع كار باشد. (\(hf\rangle {W_0}\) )
2) بسامد نور فرودی بيش تر از بسامد آستانه باشد. (\(f\rangle {f_0}\) )
3) طول موج نور فرودی كم تر از طول آستانه باشد. (\(\lambda \rangle {\lambda _0}\) )
1 افزايش يا كاهش شدت نور فرودی تنها بر تعداد فوتون های تابشی و تعداد الكترون های جدا شده تأثير می گذارد و بر بيشينه انرژی جنبشی الكترون ها (\({K_{\max }}\) ) و بسامد آستانه (\({f_0}\)) بی تاثیر است.
2 در رابطه با بررسی ويژگی های نور هم مدل موجی و هم مدل ذره ای جايگاه خود را دارد به طور مثال بررسی پديده ی فوتو الكتريک با كمک مدل ذره ای و بررسی آزمايش يانگ با مدل موجی صورت می گيرد.
1شکل (1) بیانگر کدام پدیده در فیزیک جدید است؟
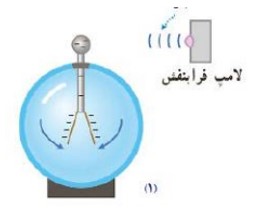
پدیده فوتوالکتریک
2در پدیده فوتوالکتریک، تابع کار یک فلز تحت تابش \(3/8ev\) است.
الف) طول موج آستانه برای گسیل فوتوالکترون ها از سطح این فلز چند نانو متر است؟ (\(hc = 1240ev.nm\) )
\(\frac{{hc}}{{{\lambda _0}}} = {W_0} \to {\lambda _0} = \frac{{hc}}{{{W_0}}} \approx 326/3nm\)
ب) اگر طول موج فرودی بر سطح این فلز \(155nm\) باشد، بیشینه انرژی جنبشی فوتوالکترون ها چقدر است؟
\({K_{\max }} = \frac{{hc}}{\lambda } - {W_0} \to {K_{\max }} = \frac{{1240}}{{155}} - 3/8 = 4/2ev\)
- آزمون آنلاین تمامی دروس پایه ریاضی
- گام به گام تمامی دروس پایه ریاضی
- ویدئو های آموزشی تمامی دروس پایه ریاضی
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ریاضی
- فلش کارت های آماده دروس پایه ریاضی
- گنجینه ای جامع از انشاء های آماده پایه ریاضی
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ریاضی
طیف
فصل 5 : آشنایی با فیزیک اتمی
طیف
انواع طیف
1) طیف پیوسته (مانند طیف تابش گرمایی)
2) طیف گسسته
الف) طیف گسیلی
ب) طیف جذبی
1) طیف پیوسته
طيفی كه در آن بين طول موج های متوالی فاصله ای نباشد طيف پيوسته ناميده می شود.
2) طیف گسسته
طيفی كه در آن تمام طول موج های متوالی وجود نداشته باشد؛ ( بين آن ها فاصله وجود داشته باشد) طيف گسسته ناميده می شود. تصاوير زير مثال هايی از طيف گسسته را نشان می دهد:
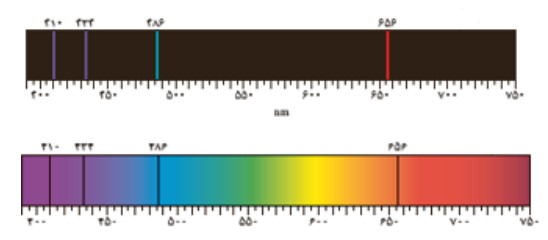
تابش گرمايی
اجسام در هر دمايی موج الكترومغناطيس گسيل (نشر) می كنند كه به آن تابش گرمايی گفته می شود.
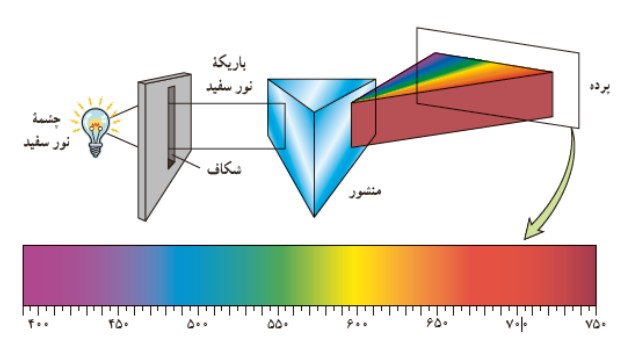
1 تابش گرمايی طيف گسيلی پيوسته محسوب می شود.
2 طول موج تابش گرمايی بستگی به دمای جسم دارد. به طور مثال اجسام در دماهای بالا از سطح خود نور مرئی گسيل می كنند (مانند آهن گداخته) و در دماهای معمولی اجسام در ناحيه ی فروسرخ تابش می كنند (مانند بدن انسان)
3 تشكيل طيف پيوسته توسط جسم جامد، ناشی از برهم كنش قوی بين اتم های سازنده ی آن است.
طيف گسيلی خطی (طيف خطی)
گازهای كم فشار و رقيق كه اتم های منفرد آن ها از برهم كنش های قوی موجود در جسم جامد آزادند به جای طيف پيوسته، طيفی گسسته را گسيل می كنند كه شامل طول موج های معينی است و به آن طيف خطی گفته می شود. (اين طيف زمينه ی تاريک و خطوط رنگی دارد)
نحوه توليد طيف خطی هيدروژن
برای ايجاد اين طيف از يک لامپ باريک و بلند شيشه ای كه حاوی مقداری گاز رقيق و كم فشار است استفاده می شود. دو الكترود به نام های آند و كاتد در دوطرف اين لامپ قرار دارد كه به ترتيب به پايانه های مثبت و منفی که منبع تغذيه با ولتاژ بالا وصل اند. اين ولتاژ بالا، سبب تخليه ی الكتريكی در گاز می شود و اتم های درون گاز درون لامپ شروع به گسيل نور می كنند. طيف خطی ايجاد شده و همچنين رنگ نور گسيل شده، به نوع گاز درون لامپ بستگی دارد. تصوير زير مربوط به توليد طيف خطی اتم هيدروژن است.
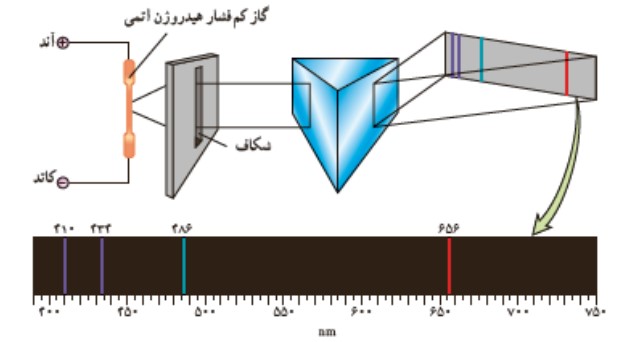
طيف جذبی
اگر نور سفيد از داخل گاز عنصری عبور كند و سپس طيف آن تشكيل شود، درآن طيف خط های تاريكی تشكيل می شود زيرا برخی طول موج های نور سفيد توسط گاز جذب شده و از طيف نور سفيد حذف می گردند. به اين طيف طيف جذبی گفته می شود. (اين طيف زمينه ی رنگی با خطوط تاريک دارد)
نحوه توليد طيف جذبی اتم هيدروژن
برای ايجاد اين طيف باريكه ی نور سفيد ابتدا از گاز كم فشار هيدروژن عبور می كند و سپس از منشور عبور داده می شود. اتم های هيدروژن در اين فرايند برخی طول موج های نور سفيد را جذب می كنند و به جای آن ها روی پرده خطوط تاريک مشاهده می شود.
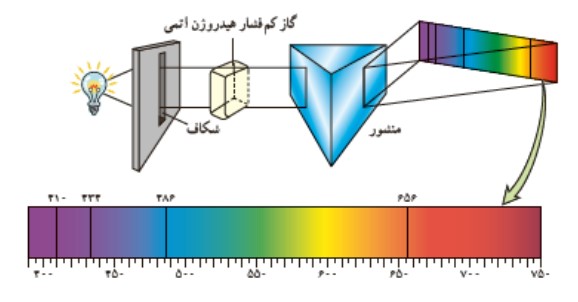
1 طيف خطی برای اتم های هر گاز منحصر به فرد هستند و سرنخ های مهمی را درباره نوع و ساختار اتم های آن گاز می دهند.
2 طول موج های مرئی خاصی كه اتم های نئون و جيوه گسيل می كنند به تابلو های نئونی و لامپ های جيوه ای رنگ های مشخصی می دهند.
دو ويژگی مهم طيف های گسيلی و جذبی
- هم در طيف گسيلی و هم در طيف جذب اتم های گازی هر عنصر، طول موج های معينی وجود دارد كه از مشخصه های آن عنصر است. (يعنی طيف گسيلی و جذبی هيچ دو عنصری همانند يكديگر نيست و از اين ويژگی برای شناسايی عناصر استفاده می شود)
- اتم های هر گاز دقيقاً همان طول موج هايی را از نور سفيد جذب می كنند كه اگر دمای آن ها به اندازه ی كافی بالا رود يا به هر صورت ديگر برانگيخته شوند، آن ها را تابش می كنند.
خطوط فرانهوفر
طيف خورشيد يک طيف جذبی خطی گسسته است كه خط های نازک تاريكی در آن به علت جذب برخی طول موج ها توسط گازهای جو خورشيد و گازهای جو زمين ديده می شود كه به اين خطوط تاريک خطوط فرانهوفر گفته می شود.
معادله ی ريدبرگ-بالمر
يک رابطه رياضی به صورت زير است كه برای محاسبه ی طول موج های طيف خطی هيدروژن از آن استفاده می شود:
\(\frac{1}{\lambda } = R(\frac{1}{{{{n'}^2}}} - \frac{1}{{{n^2}}})\)
R ثابت ریدربرگ (\(n{m^{ - 1}}\) )
مقادیر n و \(n'\) با توجه به جدول رشته ی خط های طيفی گسيل هيدروژن از جدول زير تعيين می شود:
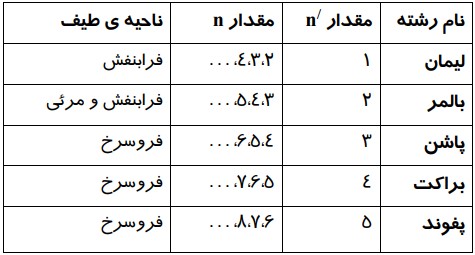
به طور مثال سومين خط رشته ی بالمر دارای \(n' = 2\) و \(n = 5\) است.
1 هرچه اختلاف n و \(n'\) بيش تر باشد، انرژی خط طيفی و بسامد آن بيش تر و طول موج آن كوتاه تر است.
2 با توجه به نكته قبل در يک رشته معين با \(n'\) مشخص، برای بلندترين طول موج كم ترين مقدار n كوتاه ترين طول موج بيش ترين مقدار n (یعنی \(\infty \)) قرار می دهيم. به طور مثال:

3 برای امواج الكترومغناطيس تابش شده توسط اتم هيدروژن، طول موج های 400 تا 700 نانومتر مرئی، كم تر از 400 نانو متر فرابنفش و بالاتر از 700 نانومتر فروسرخ است.
4 برای اتم هيدروژن منظور از حالت پايه وضعيتی است كه الكترون در لايه ی \(n = 1\) قرار دارد و منظور از حالت برانگيخته وضعيتی است كه الكترون در تراز بالاتر قرار گرفته باشد.
5 هنگامی كه اتمی يونش انجام می دهد فرض می شود الكترون به لايه ی \(n = \infty \) می رسد.
گستره طول موج های يک رشته
اختلاف كوتاه ترين و بلندترين طول موج در هر رشته را، گستره ی طول موج های آن رشته می نامند.
شکل زیر، طیف جذبی گازهای هیدروژن و جیوه را نشان می دهند:
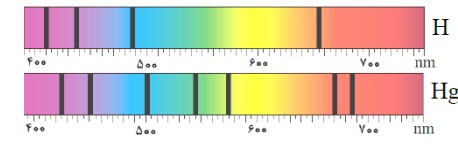
الف خط های تیره در زمینه طیف معرف چیست؟
معرف طول موج های جذب شده توسط اتم های گاز هستند.
ب از مقایسه این دو طیف چه نتیجه مهمی می گیریم؟
طیف گسیلی و جذبی هیچ دو گازی مانند هم نیست.
مدل های اتمی
فصل 5 : آشنایی با فیزیک اتمی
مدل های اتمی
مدل اتمی تامسون
بنابر مدل اتمی تامسون اتم همچون كره ای است كه بار مثبت به طور همگن در سرتاسر آن گسترده شده است و الكترون ها كه سهم ناچيزی در جرم اتم دارند در جاهای مختلف آن پراكنده شده اند. اين مدل را گاهی مدل كيک كشمشی هم می گويند.
ناسازگاری مدل تامسون با نتايج تجربی
مدل تامسون قادر به پيش بينی بسامدهای تابش گسيل شده از اتم نبود.
آزمايش پراكندگی رادرفورد
اين آزمايش باعث شد مدل اتمی تامسون كنار گذاشته شود. اين آزمايش به صورت زير انجام شد.
رادرفورد و همكارانش باريكه ای از ذره های دارای بارمثبت را (از جنس هسته ی هليم كه به آن ذرات آلفا گفته می شود) بر سطح ورقه ای نازک از جنس طلا تاباندند. رادرفورد بنابر مدل تامسون انتظار داشت كه تمامی ذره های آلفا، با انحراف بسيار اندكی از ورقه ی طلا عبور كنند. در عمل نيز بيش تر اين ذره ها بدون انحراف يا انحراف اندكی از ورقه ی طلا می گذشتند و در برخورد با صفحه ی فلوئورسان، در پشت آن، جرقه های نورانی توليد می كردند. با وجود اين، برخی از ذره های آلفا در هنگام خروج از ورقه ی نازک طلا، در زاويه های بزرگ منحرف و پراكنده می شدند و حتی تعدادی به عقب برمی گشتند. رادرفورد پس از انجام اين آزمايش و بر اساس مدل تامسون و شناختی كه از باريكه ی ذرات آلفا داشت، گفت: مثل آن بود كه گلوله ی توپی را به ورقه ی نازكی از كاغذ شليک كنيد و با شگفتی مشاهده كنيد كه پس از برخورد گلوله ی توپ با سطح كاغذ، گلوله بازگردد. اين ذره ها بايد چيز پر جرمی برخورد كرده باشد. رادرفورد استدلال كرد كه ذره های بدون انحراف بايد از قسمت هايی از ورقه گذشته باشند كه تهی بوده باشد، در حالی كه ذره های با انحراف شديد از مركزهايی بسيار چگال و دارای بار مثبت منحرف شده اند. وی سرانجام نتيجه گرفت بايد هسته ای چگال و دارای بار مثبت در مركز هر اتم باشد كه با مدل اتمی تامسون به طور آشكار مغايرت داشت.
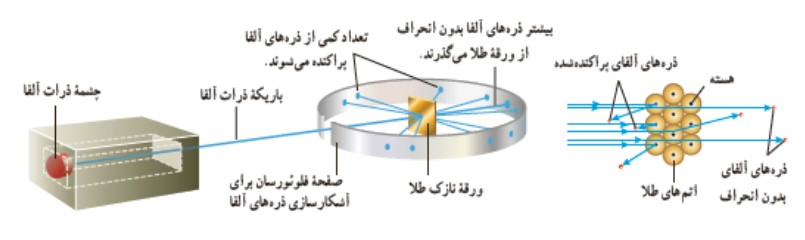
خلاصه مشاهدات و نتايج آزمايش پراكندگی رادفورد
پرتوهای 1و 2 انحرافی ندارند و يا انحراف اندک نشان می دهند اين موضوع نشان می دهد بيش تر فضای اتم خالی است. پرتوهای 3 انحراف بسيار زيادی داشته است كه نشان می دهد كه يک هسته ی كوچک و متراكم و پرجرم در مركز اتم وجود دارد.
مدل اتمی هسته ای رادرفورد
مطابق اين مدل اتم دارای يک هسته ی بسيار چگال و كوچک و با بار مثبت است كه با تعدادی الكترون در فاصله هايی به نسبت دور احاطه شده است.
ناسازگاری های مدل اتمی رادرفورد با نتايج تجربی
1) عدم توجيه پايداری اتم
اگر الكترون ها را نسبت به هسته ساكن فرض كنيم، بايد تحت تأثير نيروی ربايشی الكتريكی بين هسته و الكترون، روی هسته سقوط كنند و در نتيجه اتم ناپايدار باشد، و اين با واقعيت سازگار نيست. همچنين اگر الكترون به دور هسته گردش داشته باشد باز هم اين حركت پايدار نمی ماند، زيرا حركت مداری الكترون به دور هسته، شتابدار است. بنابر فيزيک كلاسيک، اين حركت شتابدار الكترون سبب تابش امواج الكترومغناطيسی می شود. (زيرا در اينجا الكترون يک ذره ی باردار شتابدار است) كه بسامد آن با بسامد حركت مداری (دايره ای) الكترون برابر است. با تابش موج الكترومغناطيسی توسط الكترون، از انرژی آن كاسته می شود اين كاهش انرژی باعث می شود كه شعاع مدار الكترون به دور هسته به تدريج كوچک تر شده و در نهايت روی هسته فرو افتد. و بسامد حركت آن به تدريج بيش تر شود.
2) عدم توجيه طيف گسسته اتمی
با تابش موج الكترومغناطيسی توسط الكترون، از انرژی آن كاسته می شود و اين كاهش انرژی باعث می شود كه شعاع مدار الكترون به دور هسته به تدريج كوچک تر شده و بسامد تابش ها بيش ترگردد. اين افزايش تدريجی بسامد حركت مداری الكترون ها به اين معنی است كه طيف امواج الكترومغناطيسی گسيل شده بايد پيوسته باشد و اين مطلب نيز با واقعيت سازگار نيست.
مدل اتمی بور
بور توانست مسأله ی ناپايداری اتم در مدل رادرفورد را حل كند و توجيهی برای طيف خطی اتم هيدروژن در معادله ی ريدبرگ مطرح نمود. پيشنهاد بور اين بود كه (در مقياس اتمی، قوانين مكانيک كلاسيک و الكترومغناطيس بايد توسط قوانين ديگری جايگزين يا تكميل شود) مهمترين اصول بور برای اتم هيدروژن به شرح زير است:
1) مدارها و انرژی های الكترون در هر اتم كوانتيده اند، يعنی فقط مدارها و انرژی های گسسته ی معينی مجاز هستند. (يعنی الكترون در مدارهايی با شعاع های معين و ثابت در گردش است) شعاع و انرژی مدارهای هيدروژن به صورت زير به دست می آيد:
\(\begin{array}{l}{r_n} = {a_0}{n^2}\\{E_n} = \frac{{ - {E_R}}}{{{n^2}}}\end{array}\)
\({a_0}\) شعاع كوچک ترين مدار در اتم هيدروژن (\(5/29 \times {10^{ - 11}}m\) )
\({E_R}\) انرژی الكترون در اولين مدار (\(13/6ev\) )
(n) شماره ی مدار
\({r_n}\) شعاع مدار nام
\({E_n}\) انرژی مدار n ام (ev)
\({a_0}\) شعاع بور اتم هيدروژن، \({E_R}\) يک ريدبرگ و n عدد كوانتومی نيز ناميده می شود.
2) حالت مانا
وقتی الكترون در يكی از مدارهای مجاز است، هيچ نوع تابش الكترومغناطيسی گسيل نمی كند. از اين رو گفته می شود الكترون در مدار مانا يا حالت مانا قرار دارد. (اين مطلب برخلاف قوانين فيزيک كلاسيک است)
3) توجيه تابش گسسته ی اتم
الكترون می تواند از يک حالت مانا به حالت مانای ديگر برود. هنگام گذار الكترون از يک حالت مانا با انرژی بيش تر (\({E_U}\) ) به يک حالت مانا با انرژی كم تر (\({E_L}\) )، يک فوتون تابش می شود. در اين صورت انرژی فوتون تابش شده برابر اختلاف انرژی بين دو مدار اوليه و نهايی است. يعنی:
\({E_U} - {E_L} = hf\)
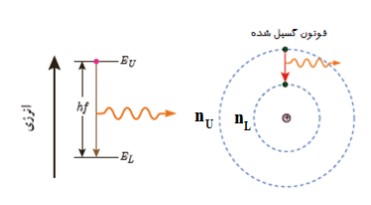
توجيه جذب به وسيله ی الگوی اتمی بور
هنگام گذار الكترون از یک حالت مانا با انرژی كم تر (\({E_L}\) ) به يک حالت مانا با انرژی بيش تر (\({E_U}\) )، يک فوتون تابش می شود. در اين صورت انرژی فوتون تابش شده برابر اختلاف انرژی بين دو مدار اوليه و نهايی است. يعنی:
\({E_U} - {E_L} = hf\)
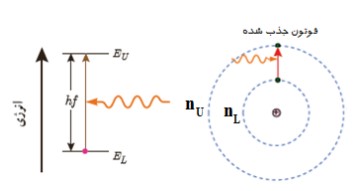
نمودار ترازهای انرژی الكترون برای اتم هيدروژن
1) هرچه از هسته دورتر می شويم انرژی الكترون بيش تر می شود.
2) بالاترين تراز انرژی به \(n = \infty \) مربوط است و در اين لايه، انرژی الكترون ev است. بنابراين انرژی لايه های پايين تر منفی است.
3) پايين ترين تراز انرژی حالت پايه ناميده می شود و انرژی الكترون در ترازهای بالا تر حالت برانگيخته ناميده می شود.
4) هرچه از هسته دورتر می شويم فاصله ی بين لايه های الكترونی كم تر می شود.
5) برای بالا بردن الكترون از حالت پايه (\(n = 1\) ) به بالاترين حالت برانگيخته ممكن (\(n = \infty \)) مقدار \(13/6ev\) انرژی بايد صرف شود. صرف اين مقدار انرژی، الكترون را از اتم خارج می كند. اين كم ترين انرژی لازم برای خارج كردن الكترون از حالت پايه، انرژی يونشالكترون ناميده می شود.
با تلفيق رابطه ی ريدبرگ و رابطه ی بور می توان ثابت كرد:
\(R = \frac{{{E_R}}}{{{h_c}}}\)
اتم هيدروژن گونه
به اتم هايی گفته می شود كه تنها يک الكترون دارند و مدل بور می تواند انرژی يونش و طول موج های طيف خطيی آن ها را با موفقيت پيش بينی كند. (به طور مثال ليتيم سه الكترون دارد و دارای يک الكترون است و اتم هيدروژن گونه محسوب می شود)
نارسايی های مدل اتمی بور
- اين مدل برای وقتی كه بيش از يک الكترون به دور هسته می گردد به كار نمی رود، زيرا در مدل بور، نيروی الكتريكی كه يک الكترون به الكترون ديگر وارد می كند در محاسبات در نظر گرفته نشده است.
- اين مدل نمی تواند متفاوت بودن شدت خط های طيفی گسيلی را توضيح دهد. (برای مثال مدل بور نمی تواند توضيح دهد چرا شدت خط قرمز با شدت خط آبی در طيف گسيلی گاز هيدروژن اتمی با يكديگر متفاوت است)
پديده فلوئورسانی
وقتی نور فرابنفش به بسياری از مواد تابيده شود، تابش مرئی از خود گسيل می كنند. طول موج های گسيل يافته معمولاً برابر همان طول موج نور فرودی يا بزرگ تر از آن است، زيرا الكترون ها با جذب انرژی تابش فرابنفش به لايه های بالاتر می رسند و در بازگشت ممكن است برخی الكترون ها به صورت پلكانی سقوط كنند (يعنی به طور مستقيم به حالت پايه برگشت نمی كنند) و از آنجا كه انرژی فوتون گسيل شده برابر اختلاف انرژی دو لايه ای است كه در آن گذار الكترون رخ داده، فوتون های با انرژی پايين تر و طول موج بلندتر گسيل می شود.
1اتم هیدروژن در حالت برانگیخته \(n = 3\) قرار دارد. کوتاه ترین طول موج تابشی آن چند نانو متر است؟ (\(R = 0/01n{m^{ - 1}}\) )
\(\frac{1}{\lambda } = R(\frac{1}{{{{n'}^2}}} - \frac{1}{{{n^2}}}) \to \frac{1}{\lambda } = \frac{1}{{100}}(\frac{1}{1} - \frac{1}{9}) \to \frac{1}{\lambda } = \frac{1}{{100}}(\frac{8}{9})\)
هر چه اختلاف انرژی دو تراز بیشتر باشد، طول موج گسیلی کوتاه تر است؛ لذا گذار از 3 به 1 است.
2کوتاه ترین طول موج رشته پاشن (\(n' = 3\) ) در اتم هیدروژن را بدست آورید. (\(R = 0/01n{m^{ - 1}}\) )
\(\frac{1}{\lambda } = R(\frac{1}{{{{n'}^2}}} - \frac{1}{{{n^2}}}) \to \frac{1}{\lambda } = \frac{1}{{100}}(\frac{1}{9} - 0) \to \lambda = 900nm\)
گسیل فوتون
فصل 5 : آشنایی با فیزیک اتمی
گسیل فوتون
انواع روش های گسيل فوتون
1) گسيل خود به خود
وقتی الكترونی در تراز برانگيخته قرار داشته باشد با گسيل فوتون كاتوره ای به تراز پايين تر جهش می كند كه به آن گسيل خود به خود گفته می شود.
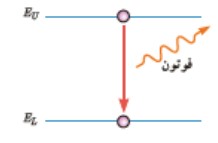
2) گسيل القايی
در اين نوع گسيل، يک فوتون ورودی، الكترون برانگيخته را تحريک يا (القا) می كند تا تراز انرژی خود را تغيير دهد و به تراز پايين تر برود و فوتونی هم سو با فوتون ورودی گسيل می كند.
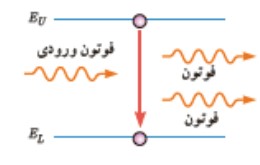
در گسيل خود به خود، گسيل القايی و جذب، انرژی فوتون هايی كه مبادله می شود همواره برابر اختلاف انرژی دو ترازی است كه در آن گذار الكترون اتفاق می افتد.
ويژگی های گسيل القايی
- از آنجا كه يک فوتون وارد و دو فوتون خارج می شود، تعداد فوتون ها را افزايش می دهد و نور را تقويت می كند.
- فوتون گسيل شده در همان جهت فوتون ورودی حركت می كند.
- فوتون گسيل شده با فوتون ورودی همگام يا هم فاز است.
لیزر (Laser): ليزر برگرفته از سرواژه های عبارت زير است:
Light Amplification by Stimulated Emission of Radiation
ليزر، تقويت نور به وسيله ی گسيل القايی تابش است. به عبارت ديگر اگر گسيل القايی را در مجموعه ی زيادی از اتم های برانگيخته انجام دهيم تعداد زيادی فوتون همسو، هم بسامد و هم انرژی ايجاد می شود كه باريكه ای از نور تقويت شده است.
وارونی جمعيت
در گسيل القايی يک چشمه ی خارجی مناسب بايد وجود داشته باشد تا الكترون ها را به ترازهای انرژی بالاتر برانگيخته كند. اين انرژی به روش های متعددی از جمله درخش های شديد نور معمولی يا تخليه های ولتاژ بالا فراهم می شود. اگر انرژی كافی به اتم ها داده شود، الكترون های بيش تری به تراز بالاتر برانگيخته خواهند شد. چنين شرطی وارونی جمعيت ناميده می شود:
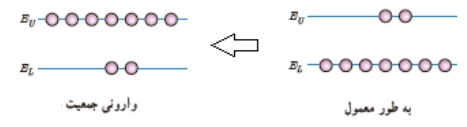
ترازهای شبه پايدار
در وارونی جمعيت الكترون ها در يک محيط ليزری بايد تعداد الكترون ها در ترازهايی موسوم به ترازهای شبه پايدار نسبت به تراز پايين تر بيش تر باشد. در اين ترازها الكترون ها در مدت زمان بسيار طولانی تری (\({10^{ - 3}}s\) ) نسبت به حالت برانگيخته ی معمولی (\({10^{ - 8}}s\) ) باقی می مانند. اين زمان طولانی تر، فرصت بيش تری برای افزايش وارونی جمعيت و در نتيجه تقويت نور ليزر فراهم می كند.
تفاوت های ليزر با نور معمولی
- بسامد و انرژی فوتون های ليزر كاملاً خالص است. يعنی در باريكه ی ليزر فقط يک نوع فوتون مشاهده می شود اما در نور معمولی اغلب طيف وسيعی از بسامدها وجود دارد.
- ليزر به خط راست منتشر می شود اما نور معمولی واگرايی دارد.
به سوالات زیر در مبحث فیزیک اتمی پاسخ دهید.
الف در اتم هیدروژن اگر الکترون از مدار \(n = 4\) به مدار \(n' = 3\) برود، طول موج گسیلی در کدام ناحیه از طیف امواج الکترومغناطیسی قرار دارد؟
فروسرخ
ب فوتون هایی که بر اثر فرآیند گسیل القایی به تراز پایین تر می روند، چه ویژگی های مشترکی دارند؟
هم بسامد، هم جهت و هم فاز
- آزمون آنلاین تمامی دروس پایه ریاضی
- گام به گام تمامی دروس پایه ریاضی
- ویدئو های آموزشی تمامی دروس پایه ریاضی
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ریاضی
- فلش کارت های آماده دروس پایه ریاضی
- گنجینه ای جامع از انشاء های آماده پایه ریاضی
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ریاضی
فیزیک هسته ای
فصل 6 : آشنایی با فیزیک هسته ای
فیزیک هسته ای
شاخه ای از فيزيک است كه در آن با ساختار، بر هم كنش ها و واپاشی هسته های اتمی سرو كار داريم.
نوكلئون
به ذرات تشكيل دهنده ی هسته كه شامل پروتون ها و نوترون ها می باشند نوكلئون گفته می شود.
عدد اتمی (Z)
تعدا پروتون های هسته را عدد اتمی می نامند.
عدد نوترونی (N)
تعداد نوترون های هسته را عدد نوترونی آن می گويند.
عدد جرمی (A)
مجموع تعداد پروتون ها و نوترون های را عدد جرمی ناميده می شود.
\(A = Z + N\)
در يک عنصر خنثی تعداد پروتون ها و الكترون ها برابر است
نماد شيميايی عنصرها
برای يک عنصر با نماد شيميايی X ، نماد هسته به صورت زير نشان داده می شود:
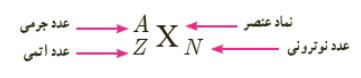
ايزوتوپ ها(هم مكان)
شكل های مختلف يک عنصر كه عدد اتمی يكسان وعدد جرمی متفاوت دارند.
1 ايزوتوپ ها تعداد پروتون های برابر و تعداد نوترون های متفاوت دارند.
2 ايزوتوپ های خواص شيميايی يكسان اما خواص فيزيكی تفاوت دارند.
ايزوتوپ های هيدروژن
هيدروژن دارای سه ايزوتوپ طبيعی است:
هیدروژن \({}_1^1H\) ، \({}_1^2D\) یا دوتریوم و \({}_1^3T\)
ابعاد هسته در مقايسه با ابعاد اتم بسيار كوچک تر است. با اين وجود \(99/9\) درصد جرم اتم در هسته متمركز شده است. (چگالی هسته \({10^{14}}\frac{g}{{c{m^3}}}\) )
نيروی هسته ای
فصل 6 : آشنایی با فیزیک هسته ای
نيروی هسته ای
نيروی جاذبه بين نوكلئون های هسته كه باعث می شود نوكلئون ها به صورت پايدار در كنار هم باقی بمانند نيروی هسته ای ناميده می شود.
1 نيروی هسته ای بسيار قوی تر از نيروی رانش الكتريكی بين دو پروتون است.
2 نيروی هسته ای با نيروی گرانشی بسيار تفاوت دارد زيرا جاذبه نيروی گرانشی بين نوكلئون ها چنان ضعيف است كه نمی تواند بر نيروی دافعه ی الكتروستاتيكی دو پروتون غلبه كند.
3 نيروی هسته ای كوتاه برد است و تنها در فاصله ای كوچک تر از ابعاد هسته اثر می كند.
4 نيروی هسته ای مستقل از بار الكتريكی است، يعنی نيروی ربايشی هسته ای يكسانی بين دو پروتون، دو نوترون، يا يک پروتون و يک نوترون وجود دارد. (به همين دليل از منظر نيروی هسته ای، تفاوتی بين پروتون و نوترون وجود ندارد و دليل نامگذاری آن ها با نام عام نوكلئون نيز همين است)
شرط پايداری هسته
براي پايداری هسته، بايد نيروی دافعه ی الكتروستاتيكی بين پروتون ها با نيروی جاذبه ی بين نوكلئون ها، كه ناشی از نيروی هسته ای است برابر باشد. ولی به دليل بلند برد بودن نيروی الكتروستاتيكی، يک پروتون تمام پروتون های ديگر درون هسته را دفع می كند، در حالی كه يک پروتون يا يک نوترون فقط نزديک ترين نوكلئون های مجاور خود را با نيروی هسته ای جذب می كند. به همين دليل وقتی تعداد پروتون های درون هسته افزايش يابد، اگر هسته بخواهد پايدار بماند، بايد تعداد نوترون های درون هسته نيز افزايش يابد. شكل زير نموداری از Z بر حسب N را برای عنصرهای مختلف نشان می دهد.
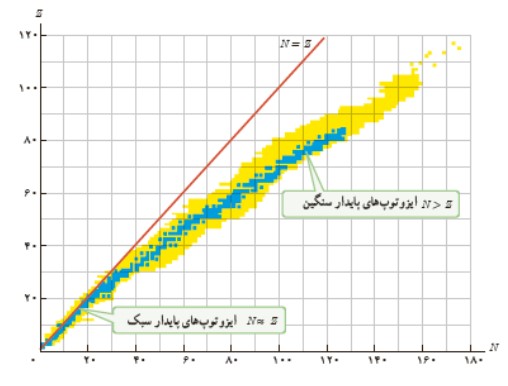
هسته ی پايدار با بيش ترين تعداد پروتون (\(Z = 83\) ) متعلق به بيسوت است. به جز توريم و اورانيوم كه در طبيعت يافت می شوند ساير هسته های سنگين با عدد اتمی بزرگتر از 83 ناپايدارند. اين دو عنصر تنها عنصرهايی اند كه واپاشی آن چنان كند است كه از هنگام تشكيل منظومه ی شمسی، فقط مقدار كمی از آن ها بر اثر واپاشی به عنصرهای سبک تر تبديل شده اند.
برای هسته های پايدار نسبت نوترون به پروتون (\(\frac{N}{Z}\) ) برابر \(1/5\) یا بیش تر است.
انرژی بستگی هسته ای
انرژی لازم برای جدا كردن نوكلئون های هسته انرژی بستگی هسته ای ناميده می شود.
كاستی جرم هسته
جرم هسته از مجموع جرم پروتون ها و نوترون های تشكيل دهنده كم تر است. اين اختلاف جرم كاستی جرم هسته ناميده می شود.
محاسبه ی انرژی بستگی هسته ای
برای به دست آوردن اين انرژی بايد از رابطه معروف اينيشتين در نظريه نسبيت استفاده نمود؛ (البته اين محاسبه خارج از برنامه ی كتاب درسی است)
\(E = m{c^2}\)
ترازهای انرژی هسته
انرژی نوكلئون های وابسته به هسته نيز مانند انرژی الكترون های وابسته به اتم كوانتيده اند و نوكلئون ها درون هسته نمی توانند هر انرژی دلخواهی را اختيار كنند. همچنين همان طور كه الكترون های اتم می توانند با جذب انرژی از تراز پايه به تراز برانگيخته بروند، نوكلئون ها نيز می توانند با جذب انرژی به ترازهای انرژی بالاتر بروند و درنتيجه هسته برانگيخته شود. هسته ی برانگيخته با گسيل فوتون به به تراز پايه بر می گردد. انرژی فوتون گسيل شده، با اختلاف انرژی بين دو تراز برانگيخته و تراز پايه برابر است.
(هسته های برانگيخته را با نماد \({X^ + }\) نمايش می دهند)
تفاوت ترازهای انرژی نوكلئون ها با ترازهای انرژی الكترون
اختلاف بين ترازهای انرژی نوكلئون ها در هسته از مرتبه ی keV تا مرتبه ی MeV است، در حالی كه اختلاف بين ترازهای انرژی الكترون ها در اتم از مرتبه ی ev است. از اين رو، هسته ها در واكنش های شيميايی برانگيخته نمی شود.
1دو ویژگی نیروهای هسته ای را بنویسید.
کوتاه برد، بسیار قوی
2غنی سازی اورانیوم به چه معناست؟
افزایش درصد یا غلظت ایزوتوپ 235 در یک نمونه را می گویند.
پرتوزايی
فصل 6 : آشنایی با فیزیک هسته ای
پرتوزايی
پرتوزايی طبيعی
وقتی يک هسته ی ناپايدار يا پرتوزا به طور طبيعی (خود به خود) واپاشی می كند، نوع معينی از ذرات يا فوتون های پر انرژی آزاد می شوند. اين فرايند واپاشی، پرتوزايی طبيعی ناميده می شود.
انواع پرتوها در پرتوزايی طبيعی و قدرت نفوذ آن ها
در پرتوزايی طبيعی سه نوع پرتو ايجاد می شود:
1) پرتو های آلفا (\(\alpha \))
كم ترين نفوذ را دارند و با ورقه ی نازک سربی با ضخامت ناچيز متوقف می شوند. (حدود \(0/01mm\) در سرب نفوذ دارند)
2) پرتو های بتا (\(\beta \))
اين پرتوها مسافت خيلی بيش تری در سرب نفوذ می كنند. (حدود \(0/1mm\) )
3) پرتو های گاما (\(\gamma \))
اين پرتوها بيش ترين نفوذ را در سرب دارند (حدود \(100mm\) )
تعداد نوكلئون ها در تمام فرايندهای واپاشی هسته ای پايسته است. يعنی تعداد نوكلئون ها، پيش از فرايند با تعداد نوكلئون ها پس از فرآيند مساوی است .
آزمايش مقايسه ی بار و جرم سه نوع ذره ی پرتوزا
برای انجام اين آزمايش نمونه ی ماده ی پرتوزا داخل استوانه ای سربی قرار می گيرد و پرتوهای آن عمود بر يک ميدان مغناطيسی عبور می كنند كه با توجه به قاعده ی دست راست می توان نوع بارالكتريكی هر ذره را تعيين كرد:
- پرتو ی گاما در ميدان مغناطيسی انحراف ندارد كه نشان می دهد بار الكتريكی ندارد.
- پرتو ی بتا به گونه ای در ميدان مغناطيسی انحراف پيدا کرده است كه نشان می دهد دارای بار الكتريكی منفی است و چون بيش ترين انحراف را دارد نشان می دهد كم ترين جرم را در مقايسه با ساير ذرات واپاشی دارد.
- پرتو ی آلفا به گونه ای در ميدان مغناطيسی انحراف پيدا كرده است كه نشان می دهد دارای بار الكتريكی مثبت است و چون كم ترين انحراف را دارد نشان می دهد بيش ترين جرم را در مقايسه با ساير ذرات واپاشی دارد.
واكنش هسته ای مربوط به واپاشی آلفا (\(\alpha \))
اين نوع پرتوها ذرات با بار مثبت از جنس هسته ی هليم (\({}_2^4He\) ) است، يعنی از دو پروتون و دو نوترون تشكيل شده است. معادله ی اين واپاشی به اين صورت زير است:
\({}_Z^AX \to {}_{Z - 2}^{A - 4}Y + {}_4^2He\)
در اين رابطه X هسته ي مادر و Y هسته ی دختر ناميده می شود.
واكنش هسته ای مربوط به واپاشی بتا (\(\beta \)) اين واپاشی به دوشكل صورت می گيرد.
1) بتای منفی
اين پرتوها از نوع الكترون هستند. الكترون واپاشی شده در هسته ی مادر وجود ندارد و همچنين يكی از الكترون های مداری اتم نيست. اين الكترون وقتی به وجود می آيد كه نوترونی درون هسته، به پروتون و الكترون تبديل شود. معادله ی اين واپاشی به صورت زير است.
\({}_Z^AX \to {}_{Z + 1}^AY + {}_{ - 1}^0{e^ - }\)
در اين رابطه X هسته ی مادر و Y هسته ی دختر ناميده می شود.
2) پوزيترون
اين پرتوها جرم يكسان با الكترون دارند اما به جای بار \( - e\) حامل بار \( + e\) هستند. به اين الكترون مثبت پوزيترون گفته می شود. در اين فرايند يكی از پروتون های درون هسته به يک نوترون و پوزيترون تبديل می شود سپس اين پوزيترون از هسته گسيل می شود. معادله ی اين واپاشی به صورت زير است:
\({}_Z^AX \to {}_{Z - 1}^AY + {}_1^0{e^ + }\)
در اين رابطه X هسته ی مادر و Y هسته ی دختر ناميده می شود.
واكنش هسته ای مربوط به واپاشی گاما (\(\gamma \))
پرتوی گاما يک فوتون پر انرژی است. اغلب هسته ها پس از واپاشی آلفا يا بتا، در حالت برانگيخته قرار می گيرند و با گسيل فوتون های پرانرژی گاما به حالت پايه می رسند. در اين فرايند A و Z تغيير نمی كنند. معادله ی اين واپاشی به صورت زير است:
\({}_Z^A{X^ + } \to {}_Z^AX + \gamma \)
در اين رابطه \({X^ + }\) هسته ی مادر و X هسته ی دختر ناميده می شود.
ذره های آلفا سنگين اند و برد كوتاهی دارند. اين ذرات پس از طی مسافت كوتاهی در هوا ( 1 تا 2 سانتی متر) و يا با عبور از لايه ای نازک از مواد جذب می شوند. اگر اين ذره ها از راه تنفس يا دستگاه گوارش وارد بدن شوند، باعث آسيب شديد به بافت های بدن می شوند.
نیمه عمر (\({T_{1/2}}\) )
نيمه عمر مدت زمانی است كه طول می كشد تا تعداد هسته های مادر موجود در يک نمونه به نصف برسند.
محاسبات جرمی ماده ی پرتوزا با توجه به نيمه عمر آن:
\(\begin{array}{l}n = \frac{t}{{{T_{\frac{1}{2}}}}}\\m = \frac{{{m_0}}}{{{2^n}}}\\{m_0} - m = {m_0}(1 - \frac{1}{{{2^n}}})\end{array}\)
\({T_{1/2}}\) نیمه عمر
(t) كل زمان لازم برای واپاشی ( مدت تجزيه)
(n) تعداد نيمه عمرهای سپری شده
\({m_0}\) مقدار اوليه ی ماده ی پرتوزا
(m) مقدار باقی مانده ی ماده ی پرتوزا (مقدار فعال)
\({m_0} - m\) مقدار واپاشی شده يا تجزيه شده (غير فعال)
به جای جرم در كليه ی روابط بالا می توان تعداد هسته های ماده پرتوزا (N) را قرار داد.
1عنصر (\({}_{92}^{238}U\) ) با گسیل دو ذره الکترون واپاشی می کند. معادله این واکنش را بنویسید.
\({}_{92}^{238}U \to {}_{94}^{238}Y + 2({}_{ - 1}^0{e^ - })\)
2از یک ماده رادیواکتیو پس از گذشت 135 روز، \(\frac{7}{8}\) ماده فعال اولیه، واپاشیده شده است. نیمه عمر این ماده چند روز است؟
\(\begin{array}{l}N = \frac{{{N_0}}}{{{2^n}}} \to \frac{1}{8}{N_0} = \frac{1}{{{2^3}}}{N_0} \to n = 3\\n = \frac{t}{T} \to 3 = \frac{{135}}{T} \to T = 45Day\end{array}\)
3نیمه عمر یک ماده رادیو اکتیو 14 ساعت است. پس از گذشت 56 ساعت، چه کسری از هسته های فعال آن، باقی مانده اند؟
\(\begin{array}{l}n = \frac{t}{T} \to n = \frac{{56}}{{14}} \to n = 4\\N = \frac{{{N_0}}}{{{2^n}}} \to N = \frac{{{N_0}}}{{{2^4}}} \to \frac{1}{{16}}{N_0}\end{array}\)
- آزمون آنلاین تمامی دروس پایه ریاضی
- گام به گام تمامی دروس پایه ریاضی
- ویدئو های آموزشی تمامی دروس پایه ریاضی
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ریاضی
- فلش کارت های آماده دروس پایه ریاضی
- گنجینه ای جامع از انشاء های آماده پایه ریاضی
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ریاضی
شکافت هسته ای
فصل 6 : آشنایی با فیزیک هسته ای
شکافت هسته ای
فرايند تقسيم شدن يک هسته ی سنگين به دو هسته با جرم كم تر، شكافت هسته ای ناميده می شود.
شكافت هسته ی اورانيوم
اورانيوم 235 (\({}_{92}^{235}U\) ) پس از جذب نوترون به دو تكه تقسيم می شود و هر تكه، جرم كم تری از هسته ی اوليه دارد. در فرايند شكافت اورانيوم، تركيب های متفاوتی از هسته های كوچک تر همراه با تعدادی نوترون (بین 2 تا 5) به وجود می آید.
وقتی نوترونی با هسته ی اورانيوم 235 برخورد كند و جذب شود، هسته ی اورانيوم شروع به ارتعاش می كند و تغيير شكل می دهد. ارتعاش تا وقتی ادامه می يابد كه تغيير شكل چنان جدی شود كه نيروی جاذبه ی هسته ای ديگر نتواند با نيروی دافعه ی الكتروستاتيكی بين پروتون های هسته متوازن شود. در اين هنگام، هسته به پاره هايی وا می پاشد كه حامل انرژی (به طور عمده انرژی جنبشی) هستند.
واکنش زنجیره ای
فرايند شكافت اورانيوم 235 با جذب يک نوترون كند آغاز می شود. اگر محصولات شكافت Ba و Kr باشند در اين فرايند 3 نوترون به وجود می آيد. چون نوترون ها بار الكتريكی ندارند، هسته های ديگر آن ها را دفع نمی كنند. نوترون ها پس از كند شدن، توسط هسته های ديگر جذب می شوند و باعث شكافت در 3 هسته ی اورانيوم ديگر می شوند و 9 نوترون آزاد می كنند. اگر هر يک از اين نوترون ها نيز موفق به شكافت يک هسته ی اورانيوم شود، 27 نوترون آزاد می شود به همين ترتيب تا آخر؛ اين واكنش را واكنش زنجيری می نامند.
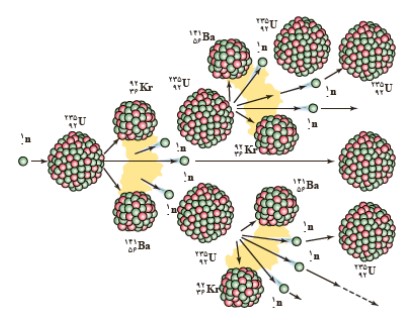
انرژی هسته ای
در واكنش شكافت هسته ای، جرم محصولات شكافت، كم تر از جرم هسته ی مركب است. اين اختلاف جرم بنا به رابطه ی \(E = m{c^2}\) سبب آزاد شدن انرژی گرمايی زيادی می شود. انرژی ای كه توسط محصولات شكافت حمل می شود عمدتاً به شكل انرژی جنبشی است.
علت انجام نشدن واكنش زنجيره ای در معادن
در سنگ معدن اورانيوم، دو ايزوتوپ 235 و 238 وجود دارد، به طوری كه فراوانی ايزوتوپ 235 كه توانايی انجام شكافت را دارد حدود \(0/72\) درصد است (يعنی از هر 140 اتم اورانيوم در سنگ معدن تنها يكی از آن ها ايزوتوپ 235 است) احتمال اينكه اورانيوم 235 نوترونی را گير بيندازد و شكافته شود بسيار كم است و درنتيجه واكنش شكافت را ناممكن می سازد.
غنی سازی اورانيوم
به فرايند افزايش درصد يا غلظت ايزوتوپ 235 در يک نمونه، غنی سازی گفته می شود. (بيش تر راكتورهای تجاری توليد برق تا 3 درصد غنی سازی انجام می دهند(
كندساز نوترون در واكنش شكافت
نوترون هاd آزاد شده در فرايند شكافت اورانيوم 235 (\({}_{92}^{235}U\) )، انرژي 235 جنبشی زيادی دارند. (حدود \(2Mev\) ) و به نوترون های تند معروف اند. اين نوترون ها با احتمال بسيار بيش تری جذب ايزوتوپ اورانيوم 238 (\({}_{92}^{235}U\) ) می شوند. تجربه نشان می دهد اگر بتوان نوترون های تند را به نحوی كند ساخت كه انرژی جنبشی آن ها به حدود \(0/04ev\) برسد، احتمال جذب آن ها توسط ايزوتوپ های اورانيوم 235 افزايش می يابد. اين افزايش احتمال می تواند برای ايجاد واكنش زنجيره ای شكافت كافی باشد. آب معمولی (\({H_2}O\) ) و آب سنگين (\({D_2}O\) ) و گرافيت (اتم های كربن) از جمله موادی هستند كه به عنوان كند ساز نوترون ها در واكنش شكافت هسته ای استفاده می شوند.
راكتور هسته ای
راكتور جايی است كه در آن واكنش زنجيری شكافت به طور كنترل شده رخ می دهد. راكتور ها بيش تر به منظور توليد انرژی الكتريكی در نيروگاه های هسته ای به كار می روند.
ساختمان و نحوه ی كار راكتور هسته ای
راكتور هسته ای افزون بر سوخت هسته ای و ماده ی كند ساز، دارای ميله های كنترل و شاره ای (معمولاً) آب هستند كه گرما را به خارج راكتور انتقال می دهد.
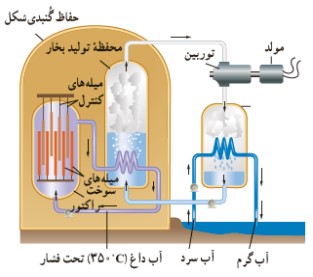
سوخت هسته ای (معمولاً با حدود 3 درصد ايزوتوپ اورانيوم 235) به صورت ميله هايی با قطر حدود \(1cm\) است و هزاران عدد از اين ميله ها در قلب راكتور قرار دارد. با وارد كردن ميله های كنترل به داخل راكتور، آهنگ شكافت، يعنی تعداد نوترون های موجود برای به وجود آوردن شكافت تنظيم می شود. ميله های كنترل معمولاً از مواد جذب كننده ی نوترون مانند كادميم يا بور، ساخته می شوند. در نوعی از رآكتور ها كه به راكتورهای آب تحت فشار (PWR) معروف اند، آبی كه سوخت هسته ای را احاطه كرده است، تحت فشار زياد قرار دارد تا بدون آنكه بجوشد به دماهای بالا برسد. اين آب داغ، به سامانه ی بسته ی ديگری كه محتوی آب كم فشار است، پمپ می شود تا اين آب را گرم كند. گرمای انتقال يافته به سامانه ی دوم، سبب توليد بخار می شود كه توربين و مولد الكتريسيته را به كار می اندازد.
گداخت (همجوشی) هسته ای
يک واكنش هسته ای است كه منشأ توليد انرژی در ستارگان و ازجمله خورشيد است. در اين فرايند دو هسته ی سبک با يكديگر تركيب می شوند و هسته ی سنگين تری به وجود می آورند.
مثالی از واكنش همجوشی هسته ای
واكنش گداخت زير را در نظر بگيريد:
\(D + T \to {}^4He + {}^1n\)
در اين واكنش با همجوشی هسته ای دو ايزوتوپ هيدروژن يعني دوتريم و تريتيم، هسته ی هليم و يک نوترون پر انرژی توليد می شود. در واكنش گداخت، مجموع جرم محصولات فرايند، كم تر از مجموع جرم هسته های اوليه است. در اينجا نيز اين اختلاف جرم با توجه به رابطه ی سبب آزاد شدن مقدار زيادی انرژی می شود.
مشكل ساخت راكتور گداخت
برای انجام واكنش گداخت بايد دو هسته ی كم جرم به حد كافی به هم نزديک شوند تا نيروی كوتاه برد هسته ای بتواند آن ها را كنار هم نگه دارد. ولی هر هسته، بار مثبت دارد و هسته ی ديگر را دفع می كند، برای آنكه هسته ها با وجود اين نيروی رانشی بسيار قوی، بتوانند به هم گداخته شوند، بايد دما بسيار بالا باشد تا هسته ها با انرژی جنبشی زيادی به يكديگر برخورد كنند. به همين دليل، برای انجام اين واكنش بايد مقدار زيادی انرژی صرف كرد. (چنين دمايی در ستارگان و خورشيد وجود دارد)
1کاستی جرم هسته چیست؟
جرم هسته از مجموع جرم پروتون ها و نوترون های تشکیل دهنده اش، اندکی کمتر است. این اختلاف جرم را کاستی جرم هسته گویند.
2چرا واکنش زنجیری به طور طبیعی در معادن اورانیوم رخ نمی دهد؟
چون فراوانی ایزوتوپ 235 حدود \(0/72\) درصد است و احتمال اینکه ایزوتوپ 238 بتواند توسط نوترونی شکافته شود، بسیار کم است.
3شکافت هسته را توضیح دهید.
تقسیم شدن یک هسته سنگین به دو هسته با جرم کمتر
4سه مورد از ویژگی های ایزوتوپ ها را بنویسید.
ایزوتوپ ها هسته هایی هستند که تعداد پروتون های مساوی ولی تعداد نوترون های متفاوت و خواص شیمیایی یکسانی دارند و در یک خانه جدول تناوبی قرار می گیرند.



1736019749.png)