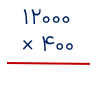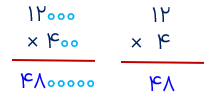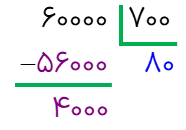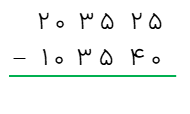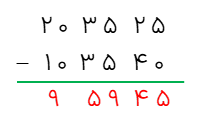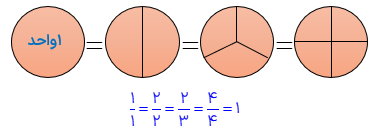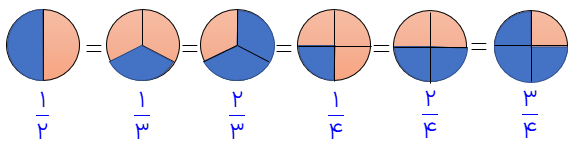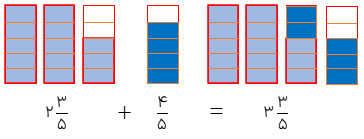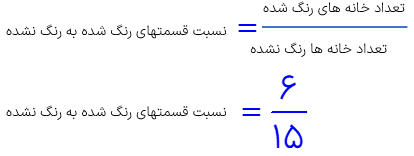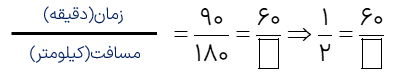درسنامه کامل ریاضی پنجم
تعداد بازدید : 299.61kخلاصه نکات ریاضی پنجم - درسنامه شب امتحان ریاضی پنجم - جزوه شب امتحان ریاضی پنجم نوبت اول
عدد نویسی
فصل 1 : عددنویسی و الگوها
عدد نویسی
در سال گذشته با خواندن و نوشتن اعداد تا طبقه میلیون آشنا شدیم و دانش آموزان اکنون قادر به خواندن و نوشت اعداد 9 رقمی می باشند. دانش آموزان یاد گرفتند که در جدول ارزش مکانی ارزش هر عدد نسبت به عدد سمت راست خود 10 برابر است.
1 ارزش مکانی هر رقم از 2 بخش "مرتبه" و "طبقه" تشکیل شده است.برای مثال: وقتی میگوییم صدگان هزار "صدگان" مرتبه ی آن است و "هزار" طبقه ی آن است.
2 هر گاه عددی در 10، 100، 1000 و...ضرب شود، ارزش آن به تعداد ارقام بیشتر میشود.
مثال
اگر اعداد 751 و 49512 و 85043 را 100 برابر کنیم ارزش عدد 5 در آنها چند خواهد شد؟
ارزش رقم ۵: یکان هزار \(751\,\,\mathop \Rightarrow \limits^{ \times 100} \,75100\)
ارزش رقم ۵: دهگان هزار \(49512\,\mathop \Rightarrow \limits^{ \times 100} \,4951200\)
ارزش رقم ۵: صدگان هزار \(85043\,\mathop { \Rightarrow \,}\limits^{ \times 100} 8504300\)
هرگاه عددی بر 10، 100، 100 و تقسيم شود، ارزش ارقام آن عدد به تعداد صفرها کم تر می شود.
مثال
هرگاه اعداد 72400، 31007000 و 760000 بر 100 تقسیم شوند ارزش مکانی عدد 7 در آنها چند خواهد شد؟
ارزش رقم ۷: صدگان \(72400\,\mathop \Rightarrow \limits^{ \div 100} \,724\)
ارزش رقم ۷: دهگان \(3100700\mathop \Rightarrow \limits^{ \div 100} 310070\)
ارزش رقم ۷: یکان هزار \(760000\mathop \Rightarrow \limits^{ \div 100} 7600\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه پنجم- آزمون آنلاین تمامی دروس پایه پنجم
- گام به گام تمامی دروس پایه پنجم
- ویدئو های آموزشی تمامی دروس پایه پنجم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه پنجم
- فلش کارت های آماده دروس پایه پنجم
- گنجینه ای جامع از انشاء های آماده پایه پنجم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه پنجم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
معرفی میلیارد
فصل 1 : عددنویسی و الگوها
معرفی میلیارد
با قرار دادن 10 تا دسته ی 100 هزارتایی در کنار هم عدد 1،000،000،000 (یک میلیارد) به دست می آید. همچنین با کنار هم قرار دادن 100 تا بسته 10 هزارتایی نیز عدد یک میلیارد به دست می آید. بنابراین یک طبقه جدید به نام میلیارد به جدول ارزش مکانی اضافه خواهد شد.
مثال
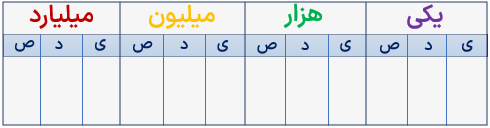
عدد مربوط به جدول ارزش مکانی زیر را به حروف بنویسید.
سیصد و هفت میلیارد و چهارصد و سی میلیون و سه هزار و هشتصد و پنجاه و نه
جزوات جامع پایه پنجم
جزوه جامع ریاضی پنجم
جزوه جامع علوم تجربی پنجم
جزوه جامع مطالعات اجتماعی پنجم
جزوه جامع فارسی پنجم
جزوه جامع نگارش پنجم
جزوه جامع هدیه های آسمانی پنجم
جزوه جامع آموزش قرآن پنجم
مقایسه اعداد
فصل 1 : عددنویسی و الگوها
مقایسه اعداد
هدف از مقایسه دو عدد این است که ببینیم دوم عدد مساوی هستند یا خیر و اگر مساوی نیستند کدام یک بزرگتر است و کدام یک کوچکتر است.
برای مقایسه دو عدد به روش زیر عمل میکنیم.
1 تعداد ارقام دو عدد را می شماریم هر کدام ارقام بیشتری داشت بزرگتر است.
2 اگر تعداد ارقام برابر بود ارقام با ارزش تر را بررسی کرده و مرتبه آنها را با هم مقایسه می کنیم اگر باز هم برابر بود به سراغ مقایسه ارقام مرتبه بعدی می رویم.
مثال
اعداد زیر را با هم مقایسه کنید.
الف \(111142305\,\,\left\lceil {\,\,} \right\rceil \,\,9998756\)
الف در مثال اول عدد سمت چپ 8 رقمی و عدد سمت راست 7 رقمی .است پس عدد سمت چپ بزرگتر است و نیازی به مقایسه مرتبه اعداد نیست.
\(111142305\,\,\left\lceil > \right\rceil \,\,9998756\)
ب \(57619874\,\,\left\lceil {\,\,\,} \right\rceil \,\,57620018\)
ب ولی در مثال دوم هر دو 8 رقمی هستند . پس مرتبه آنها را از با ارزش ترین سمت چپ شروع به مقایسه میکنیم.
\(57619874\,\,\left\lceil < \right\rceil \,\,57620018\)
مقدار تقریبی اعداد روی محور
فصل 1 : عددنویسی و الگوها
مقدار تقریبی اعداد روی محور
برای نشان دادن محل تقریبی یک عدد روی محور به صورت زیر عمی میکنیم:
الف) مشخص کردند اندازه های هر واحد (با توجه به تقریب خواسته شده ) روی محور مثلا اگر با تقریب صدهزار خواست واحدهای محور را باید صدهزارتایی مشخص کنیم
ب) یافتن دو عدد متوالی که عدد داده شده بین آن دو قرار داشته باشد.
ج) با مقایسه عدد داده شده با این دو عدد متوالی، تعیین میکنیم به کنام یک نزدیک تر است.
مثال
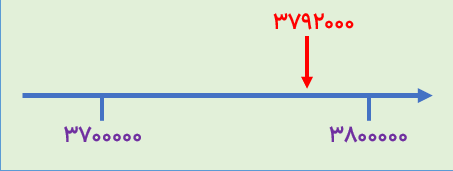
مقدار تقريب عدد 3792000 با تقریب صدهزار چند است؟
چون تقریب صدهزار خواسته شده است، پس واحدهای محور را باید صدهزارتایی مشخص کنیم.(یعنی چون صدهزار 5 تا صفر دارد دو عدد متوالی باید آخرشان 5 تا صفر باشد و با هم 100 هزار تا فاصله داشته باشند).
با توجه به محور رسم شده میبینیم عدد داده شده بین دو عدد 3700000 و 3800000 قرار دارد. حالا بررسی میکنیم ببینیم به کدام یک از دو عدد نزدیک تر است که مشخص میشود به عدد 3800000 نزدیک تر است.
تقریب بدون رسم محور
در تقریب با هر رقمی بدون نیاز به رسم محور به صورت زیر عمل میکنیم :
باید به تعداد صفرهای مقداری که قرار است با آن تقریب بزنیم از سمت یکان عدد که کم ارزش ترین مرتبه است سمت راست عدد شمارش کرده و به جای آنها صفر قرار دهیم.
با ارزش ترین رقمی که صفر شده سمت چپ ا ترین عددی که صفر (شده را بررسی میکنیم اگر مقدار آن 5 یا بیشتر از 5 ،بود، به رقم سمت چپ آن یک واحد اضافه میکنیم ولی اگر کمتر از 5 بود در رقم سمت چپ آن هیچ تغییری ایجاد نمی شود.
مثال
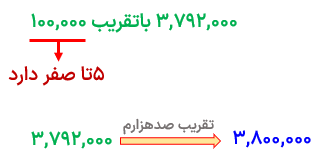
مقدار تقريب عدد 3792000 با تقریب صدهزار چند است؟ (بدون رسم محور)
به تعداد ۵ تا صفر ۱۰۰۰۰۰،صفر گذاشتیم
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه پنجم- آزمون آنلاین تمامی دروس پایه پنجم
- گام به گام تمامی دروس پایه پنجم
- ویدئو های آموزشی تمامی دروس پایه پنجم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه پنجم
- فلش کارت های آماده دروس پایه پنجم
- گنجینه ای جامع از انشاء های آماده پایه پنجم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه پنجم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
جمع و تفریق
فصل 1 : عددنویسی و الگوها
جمع و تفریق
جمع و تفریق اعداد به 2 صورت زیر انجام می شود.
الف- جمع و تفریق اعداد با طبقه یکسان:
در این روش ابتدا اعداد را هم طبقه کرده و سپس عملیات جمع و تفریق را انجام میدهیم.
ب- جمع و تفریق با زیر هم نویسی:
برای جمع در این روش با ارزش ترین رقم عدد دوم را به عدد اول اضافه می کنیم و سپس رقم های بعدی را به ترتیب به حاصل هر مرحله اضافه می کنیم.
برای تفریق در این روش با ارزش ترین رقم عدد دوم را از عدد اول کم میکنیم و سپس رقم های بعدی را به همین ترتیب از حاصل مرحله قبل كم می کنیم
مثال
جمع زیر را به روش هم طبقه کردن محاسبه کنید.
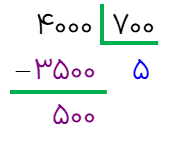
= ۲۵ ده هزار - ۳۲ صدهزار
عدد اول طبقه صدهزارتایی است و عدد دوم طبقه ده هزارتایی ابتدا باید آنها را هم طبقه کنیم و برای هم طبقه کردند به طبقه کمتر تبدیل می کنیم .
پس 32 تا صدهزارتا می شود 320 تا ده هزارتایی ؛ حالا که هم طبقه شدند عملیات جمع را انجام داده و در نهایت عدد واقعی را می نویسیم
۲۵ ده هزار - ۳۲ صدهزار=۲۵ ده هزار - ۳۲۰ده هزار
۲۹۵ ده هزار =
۲ میلیون و ۹۵۰ هزار=
مثال
تفریق زیر را با زیر هم نویسی حل کنید.
جزوات جامع پایه پنجم
جزوه جامع ریاضی پنجم
جزوه جامع علوم تجربی پنجم
جزوه جامع مطالعات اجتماعی پنجم
جزوه جامع فارسی پنجم
جزوه جامع نگارش پنجم
جزوه جامع هدیه های آسمانی پنجم
جزوه جامع آموزش قرآن پنجم
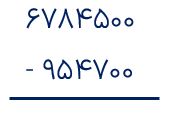
ضرب و تقسیم
فصل 1 : عددنویسی و الگوها
ضرب
برای ضرب اعدادی که سمت راست آنها صفر وجود دارد، کافیست ابتدا اعداد را بدون در نظر گرفتن صفرهای جلوی آنها در همدیگر ضرب کنیم ونهایت بعد از به دست آمدن حاصل ضرب صفرهایی که کنار گذاشته ایم را در سمت راست جواب قرار دهیم.
مثال
ضرب زیر را انجام دهید.
تقسیم اعداد بخش پذیر
در این نوع تقسیم به صورت زیر عمل می کنی:
1) عدد دوم را به صورت حاصل ضرب دو عدد می نویسیم.
2) عدد اول را به یکی از دو عدد به دست آمده تبدیل عدد دوم به دو قسمت تقسیم می کنیم. (بهتر است به عدد بزرگتر تقسیم کنیم).
3) حالا جواب به دست آمده را بر عدد دیگر نیز تقسیم می کنیم
مثال
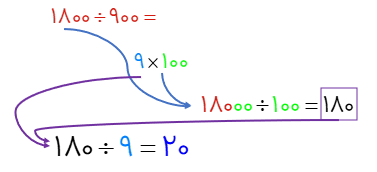
حاصل تقسیم 18000 بر 900 را به دست آورید.
\(18000 \div 900 = \)
میتوانیم تعداد صفرهای مشترک را در نظر نگیریم و تقسیم را انجام دهیم حاصل این تقسیم با تقسیم اول برابر خواهد بود
\(\begin{array}{l}18000 \div 900\\\,\,\,\,\,\,\,\,\,\,\, \Downarrow \\\,180 \div 9 = 20\end{array}\)
تقسیم اعداد بخش ناپذیر
در تقسیم دو عدد که بر هم بخش پذیر نیستند(باقی مانده صفر ندارند) ابتدا بررسی می کنیم با توجه به تعداد مقسوم به هر مقسوم چند بسته 10 تایی می.رسد آن را در خارج قسمت نوشته و با ضرب آن عدد در مقسوم علیه جوابی به دست میآید که از مقسوم کم میکنیم و هرچی باقی ماند دوباره به مقسوم عليه تقسيم میکنیم ببینیم به هر مقسوم چند تا می رسد. حالا تعداد بسته های ده تایی خارج قسمت را با این عدد به دست آمده جدید در خارج قسمت با هم جمع میکنیم تا جواب اصلی خارج قسمت مشخص شود.
مثال
تقسیم زیر را حل کنید.
به ۷۰۰ تا ۸۰ بسته ۱۰ تایی میرسد .
در ۴۰۰۰ تا ۵ تا ۷۰۰ تا وجود دارد
خارج قسمت: 80+5=85
باقی مانده: 500
عدد مرکب
فصل 1 : عددنویسی و الگوها
عدد مرکب
هر عددی که دارای دو یا چند جزء باشد، عدد مرکب است. مانند مثال های زیر:
عدد مرکب با 2 جزء کیلوگرم و گرم
عدد مرکب با 3 جزء ساعت، دقیقه و ثانیه
عدد مركب با 4 جزء ،سال ماه روز و ساعت
عدد مركب تشکیل شده از ساعت، دقیقه و ثانیه به صورت زیر نمایش داده میشود:
“ثانیه : ‘دقیقه : ساعت
با داشتن یک زمان و یک فاصله ،زمانی میتوان یک الگوی زمانی ایجاد کرد
مثال
الگوهای زیر را کامل کنید.
الف)\(5:45\,,5:40,\,\,\,\,\,,\,\,\,\,\,,\)
در این الگو هر زمان نسبت به زمان قبلی 5 دقیقه کاهش داشته .است در نتیجه جواب به صورت زیر خواهد بود.
۵:۲۵ ، ۵:۳۰ ، ۵:۳۵ ، ۵:۴۰ ، ۵:۴۵ : الف
جمع زمان ها
برای انجام عملیات جمع، باید اعداد مربوط به ثانیه و دقیقه و ساعت را زیر هم نوشته و جمع می کنیم.
اگر حاصل جمع ثانيه ها از 60 بیشتر شد، باید 60 واحد از آن کم کرده و یک واحد به دقیقه ها اضافه کنیم.
اگر حاصل جمع دقیقه ها از 60 بیشتر شد باید 60 واحد از آن کم کرده و یک واحد به ساعت ها اضافه کنیم.
تفریق زمان ها
برای انجام تفریق زمان ها باید زمان بزرگتر بالا نوشته شده و زمان کوچکتر زیر آن نوشته شود .اعداد مربوط به ساعت دقیقه و ثانیه را زیر هم نوشته و تفریق کنیم.
اگر در تفریق ثانیه ی عدد اول از ثانیه ی عدد دوم کوچکتر بود باید از دقیقه ی عدد اول یک واحد کم کرده و 60 واحد به ثانیه ی عدد اول اضافه کنیم و بعد تفریق را انجام دهیم.
اگر در تفریق دقیقه ی عدد اول از دقیقه ی عدد دوم کوچکتر بود باید از ساعت عدد اول یک واحد کم کرده و 60 واحد به دقیقه ی عدد اول اضافه کنیم و بعد تفریق را انجام دهیم.
هر 60 ثانیه بربر با 1 دقیقه است.
هر 60 دقیقه برابر با 1 ساعت است.
مثال
حاصل تفریق زیر را به دست آورید.
عدد مركب شامل گرم و کیلوگرم
برای جمع و تفریق دو یا چند عدد مرکب شامل گرم و کیلوگرم باید گرمها را با هم جمع و تفریق کنیم و کیلوگرم ها را با هم جمع و تفریق کنیم.
هر 1000 گرم 1 کیلوگرم است.
مثال
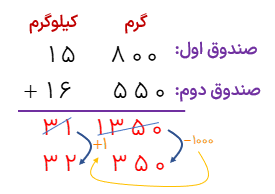
دو صندوق سیب داریم. صندوق اول 15 کیلو و 800 گرم و صندوق دوم 16 کیلو و 550 گرم می باشد. هر دو صندوق روی هم چند کیلو میباشند؟
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه پنجم- آزمون آنلاین تمامی دروس پایه پنجم
- گام به گام تمامی دروس پایه پنجم
- ویدئو های آموزشی تمامی دروس پایه پنجم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه پنجم
- فلش کارت های آماده دروس پایه پنجم
- گنجینه ای جامع از انشاء های آماده پایه پنجم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه پنجم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
الگویابی
فصل 1 : عددنویسی و الگوها
الگویابی
الگویابی روشی برای راحت تر نمودن حل مسئله می باشد. مهمترین چیزی که در الگویابی مطرح است موضوع پیدا کردن رابطه منطقی و درست بین عددها و شکلها است. به طوری که بتوان اعداد یا شکل های بعدی را پیش بینی کرد.
الگویابی ها به شرح زیر می باشند.
الگویابی عددی
در این نوع الگویابی به دنبال کشف رابطه بین عددها هستیم.
در برخی الگوهای عددی بهتر است یک جدول نظام دار رسم کنیم و اطلاعات عددی مربوط به مسئله را در آن بنویسیم.
مثال
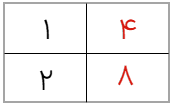
جدول زیر را کامل کنید.
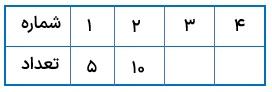
\(\begin{array}{l}3 \times 5 = 15\\4 \times 5 = 20\end{array}\)
در جدول فوق، مقدار عددی تعداد پنج برابر مقدار عددی شماره است.
در برخی الگوهای عددی که فاصله ها یکسان است تنها با عمل جمع میتوان به اعداد بعدی دست یافت و عمل ضرب در این الگوها به تنهایی برای یافتن اعداد بعدی کاربرد ندارد
مثال
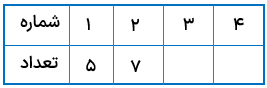
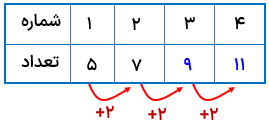
جدول ریر را کامل کنید.
اگر به ردیف تعداد نگاه کنید مقدار عددی نسبت به عدد قبل 2 تا اضافه شده است.
جزوات جامع پایه پنجم
جزوه جامع ریاضی پنجم
جزوه جامع علوم تجربی پنجم
جزوه جامع مطالعات اجتماعی پنجم
جزوه جامع فارسی پنجم
جزوه جامع نگارش پنجم
جزوه جامع هدیه های آسمانی پنجم
جزوه جامع آموزش قرآن پنجم
الگویابی هندسی
فصل 1 : عددنویسی و الگوها
الگویابی هندسی
در این نوع الگویابی به دنبال کشف رابطه بین شکل ها بوده و بهتر است از دسته بندی استفاده کنیم.
مثال
الگوی بعدی را رسم کنید.
در هر شکل تعداد مثلث ها نسبت به شکل قبل 2 عدد اضافه شده است.
عددهای مثلثی
فصل 1 : عددنویسی و الگوها
عددهای مثلثی
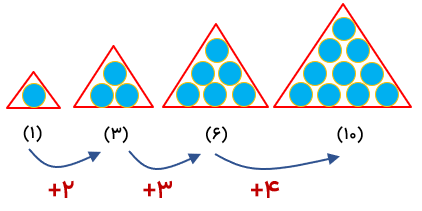
عددهای مثلثی همواره از 1 شروع شده و در مرحله اول 2 واحد به عدد اول اضافه میشود تا عدد دوم به دست آید و در مرحله بعدی 3 واحد به عدد بلی اضافه میشود و به همین ترتیب الگوی عددی شکل گرفته و اگر آن را به الگوی هندسی تبدیل کنیم شکل هر مرحله به صورت یک مثلث خواهد بود.
در عددهای مثلثی با فرمول زیر تعداد دایره های هر مرحله به دست می آید.
۲÷ [(۱+ شماره مرحله) ×( شماره مرحله(] = تعداد دایره هر مرحله
مثال
در الگوی عددهای مثلثی شکل هشتم چند تا دایره دارد؟
\((8) \times (8 + 1) \div 2 = 72 \div 2 = 36\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه پنجم- آزمون آنلاین تمامی دروس پایه پنجم
- گام به گام تمامی دروس پایه پنجم
- ویدئو های آموزشی تمامی دروس پایه پنجم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه پنجم
- فلش کارت های آماده دروس پایه پنجم
- گنجینه ای جامع از انشاء های آماده پایه پنجم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه پنجم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
مفهوم کسرها
فصل 2 : کسر
مفهوم کسرها
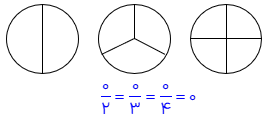
وقتی یک شکل واحد را به قسمت های مساوی تقسیم کنیم و تعدادی از این قسمت ها را رنگ کنیم قسمت رنگ شده کسری از واحد را نشان می دهد. در نمایش ،کسرها مخرج کسر نشان دهنده تعداد كل قسمتهای مساوی شکل واحد میباشد و صورت کسر نیز نشان دهنده تعداد قسمت های رنگ شده می باشد.
مثال
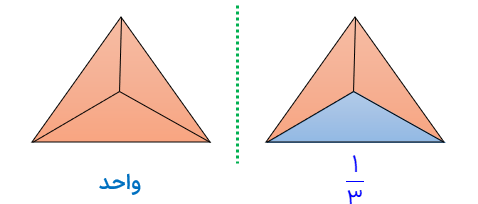
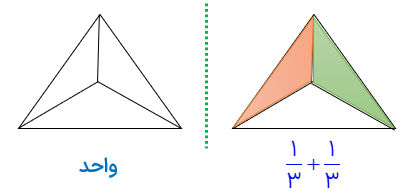
در مثال زیر شکل واحد یک مثلث است که به 3 قسمت مساوی تقسیم شده است. لذا مخرج کسر 3 می باشد ، تعداد خانه های رنگ ،شده یعنی صورت کسر نیز 1 می باشد.
مثال
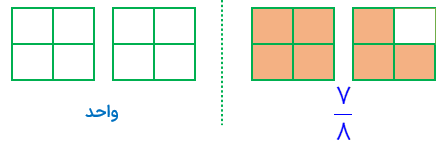
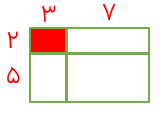
در مثال زیر دو تا مربع یک واحد را تشکیل می دهند که در سمت چپ خط چنین نشان داده شده است.
چون كل واحد (دو مربع) جمعا 8 قسمت مساوی ،دارند لذا مخرج کسر 8 می باشد. تعداد قسمت رنگی 7 قسمت است، لذا صورت کسر 7 می باشد.
جزوات جامع پایه پنجم
جزوه جامع ریاضی پنجم
جزوه جامع علوم تجربی پنجم
جزوه جامع مطالعات اجتماعی پنجم
جزوه جامع فارسی پنجم
جزوه جامع نگارش پنجم
جزوه جامع هدیه های آسمانی پنجم
جزوه جامع آموزش قرآن پنجم
دسته بندی کسرها
فصل 2 : کسر
دسته بندی کسرها
کسرها به دسته های زیر تقسیم میشوند:
الف) كسرهای برابر واحد:
کسری است که صورت و مخرج آن برابر واحد است. یعنی تمام قسمت های یک واحد کامل رنگ شده اند لذا یک واحد کامل بوده و برابر با 1 می باشد.
به این نکته توجه کنید که ما نمی توانیم شکلی رسم کنیم که آن را به صفر قسمت تقسیم کنیم تا عدد صفر در مخرج کسر قرار گیرد. لذا هیچگاه مخرج یک کسر صفر نخواهد بود.
ب) کسر کوچکتر از واحد:
در این نوع ،کسرها صورت از مخرج کوچکتر است. یعنی تعداد قسمت های رنگ شده از تعداد کل قسمت های شکل واحد کمتر است.
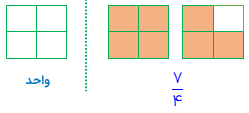
ج) کسر بزرگتر از واحد
کسر بزرگتر از ،واحد کسری است که صورت کسر از مخرج آن بزرگتر باشد برای رسم شکل مربوط به کسر بزرگتر از واحد یک یا چند شکل واحد کامل به همراه یک کسر کوچکتر از واحد رسم میشود. مثال زیر نمونه ای از کسر کوچکتر از واحد هستند.
د) کسر مساوی صفر
کسری که فقط صورت آن صفر باشد کسری مساوی صفر است. در رسم این نوع ،کسرها هیچ یک از قسمتهای کسر رنگ نمیشود و کل شکل بی رنگ باقی می ماند. زیرا تعداد واحدهای رنگ آمیزی صورت کسر صفر تعیین شده است.
مقدار رنگ شده در تمام شکل ها صفر است
نمایش کسر روی محور
فصل 2 : کسر
نمایش کسر روی محور
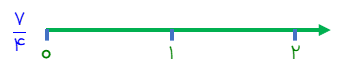
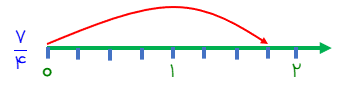
برای نمایش کسر بر روی محور ابتدا می بایست هر واحد روی محور را به تعداد عدد مخرج كسر تقسیم کنیم سپس به تعداد صورت کسر از این واحدها شمارش میکنیم و از صفر محور به این نقطه وصل میکنیم
مثال
کسر زیر را روی محور نشان دهید.
مخرج كسر عدد 4 است پس باید بین واحدها را به چهار قسمت تقسیم .کنیم بعد به تعداد عدد صورت یعنی هفت شمارش کرده و از نقطه صفر به آن رسم میکنیم.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه پنجم- آزمون آنلاین تمامی دروس پایه پنجم
- گام به گام تمامی دروس پایه پنجم
- ویدئو های آموزشی تمامی دروس پایه پنجم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه پنجم
- فلش کارت های آماده دروس پایه پنجم
- گنجینه ای جامع از انشاء های آماده پایه پنجم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه پنجم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
عدد مخلوط
فصل 2 : کسر
عدد مخلوط
عدد مخلوط روش دیگری برای نمایش کسرهای بزرگتر از واحد است.
وقتی کسری بزرگتر از واحد بود باید تا آنجا که ممکن است واحدهای کامل را از آن بیرون بکشیم و به صورت عدد صحیح در کنار آنچه باقی مانده و کسر کوچکتر از واحد است قرار دهیم در این صورت عدد مخلوط را به دست آورده ایم. برای این کار باید صورت کسر را به مخرج تقسیم کنیم. بعد خارج قسمت تقسیم را به عنوان عدد صحیح در نظر میگیریم و باقیمانده تقسیم را به عنوان صورت بخش کسری نوشته و مقسوم عليه تقسيم را نیز به عنوان مخرج بخش کسری می نویسیم .
مثال
کسر زیر را با تقسیم کردن به عدد مخلوط تبدیل کنید. سپس با رسم شکل و محور آن را نمایش دهید.
\(\frac{{23}}{7}\)
\(\frac{{23}}{7} \Rightarrow 3\frac{2}{7}\)
تبدیل عدد مخلوط به کسر بزرگتر از واحد
برای تبدیل یک عدد مخلوط به کسر بزرگتر از واحد می بایست قسمت صحیح عدد سمت چپ کسر را در مخرج ضرب کرده و جواب هر چه به دست آمد با صورت کسر جمع کنیم و به عنوان صورت کسر جدید قرار میدهیم. مخرج کسر نیز بدون تغییر باقی می ماند.
مثال
عدد مخلوط زیر را به کسر تبدیل کنید
\(6\frac{2}{7}\)
\(\begin{array}{l}6\frac{2}{7} = \frac{{44}}{7}\\\\(7 \times 6 + 2 = 44)\end{array}\)
در اعداد مخلوط بين عدد صحیح و قسمت کسری علامتی قرار ندارد ولی در واقعیت بین آنها علامت جمع وجود دارد ولی نوشته نمی شود.
جزوات جامع پایه پنجم
جزوه جامع ریاضی پنجم
جزوه جامع علوم تجربی پنجم
جزوه جامع مطالعات اجتماعی پنجم
جزوه جامع فارسی پنجم
جزوه جامع نگارش پنجم
جزوه جامع هدیه های آسمانی پنجم
جزوه جامع آموزش قرآن پنجم
مقایسه عدد مخلوط
فصل 2 : کسر
مقایسه عدد مخلوط
برای مقایسه دو عدد ،مخلوط از روشهای زیر استفاده میکنیم.
الف) قسمت های صحیح دو عدد را با هم مقایسه می کنیم:
هر کدام عدد صحیح بزرگتری داشت آن عدد مخلوط، بزرگتر است.
عدد مخلوط باید استاندارد باشد یعنی کسری عدد مخلوط باید خودش کوچکتر از واحد باشد و در غیر اینصورت می بایست قسمت کسری خوبه عدد مخلوط دیگری تبدیل شده و با عدد صحیح اولیه جمع شود آنگاه مقایسه صورت پذیرد.
مثال
دو عدد مخلوط زیر را مقایسه کنید.( به نکته بالا دقت کنید)
\(3\frac{4}{5}\left\lfloor {} \right\rfloor 2\frac{7}{2}\)
\(\begin{array}{l}3\frac{4}{5}\left\lfloor < \right\rfloor 2\frac{7}{2}\\\\\frac{7}{2} = 3\frac{1}{2}\\\\3\frac{4}{5}\left\lfloor < \right\rfloor 2 + 3\frac{7}{2}\end{array}\)
بخش کسری بزرگتر از واحد است. باید خودش به عدد مخلوط تبدیل شود.
ب) مقایسه دو عدد مخلوط دارای اعداد صحیح برابر:
هر گاه در مقایسه دو عدد مخلوط قسمت عدد صحیح هر دو با همدیگر برابر بود، سراغ قسمت کسری رفته و آنها را مقایسه میکنیم و هر کدام قسمت کسری بزرگتری ،داشت آن عدد مخلوط بزرگتر است. در مقایسه کسرها یکی از حالات زیر مشاهده میشود:
حالت اول:
در اعداد مخلوط با عدد صحیح برابر اگر مخرج دو کسر برابر ،باشد کسری بزرگتر است که صورت بزرگتری داشته باشد.
مثال
\(\begin{array}{l}\,\,\,\,\,\,\,2 < 4\\\\3\frac{2}{5}\,\,\left\lfloor < \right\rfloor \,\,3\frac{4}{5}\end{array}\)
حالت دوم:
در اعداد مخلوط با عدد صحیح برابر اگر صورت دو کسر برابر ،باشد کسری بزرگتر است که مخرج کوچکتری داشته باشد.
مثال
\(\begin{array}{l}3\frac{4}{7}\left\lfloor < \right\rfloor 3\frac{4}{5}\\\\\,\,\,\,\,\,\,\,7 > 5\end{array}\)
حالت سوم :
در اعداد مخلوط با عدد صحیح برابر اگر مخرج دو کسر برابر باشد و صورت دو کسر نیز برابر باشد آن دو کسر با هم برابرند.
مثال
\(3\frac{4}{5}\left\lfloor = \right\rfloor 3\frac{4}{5}\)
حالت چهارم :
در اعداد مخلوط با عدد صحیح برابر اگر مخرج دو کسر برابر نباشد و صورت نیز برابر نباشد با نوشتن کسرهای مساوی با هر کدام صورت ها یا مخرج ها را برابر کرده و سپس با یکی از 3 حالت بالا آنها را با هم مقایسه می کنیم.
جمع و تفریق عددهای مخلوط
فصل 2 : کسر
جمع و تفریق عددهای مخلوط
در جمع و تفریق اعداد مهمترین کار یکسان نمودن مخرج کسرها می باشد. در زیر نمونه هایی از روشهای جمع و تفریق اعداد مخلوط را مشاهده میکنید
استفاده از شکل
برای جمع دو عدد مخلوط به روش رسم شکل ابتدا اگر مخرج یکسان ، نداشتند، آنها را هم مخرج کرده و بعد شکل مربوطه را رسم کرده و عملیات جمع یا تفریق را انجام میدهیم.
در جمع برای هر کسر یک شکل رسم میکنیم و بعد شکلها را کنار هم گذاشته و جمع می کنیم. دقت کنید گاهی از جمع دوتا ،کسر کسری بزرگتر از واحد درست میشه که میتوان واحد کامل را از داخل آن بیرون کشید و با عدد صحیح جمع
کرد. در تفریق کسر مربوط به عدد مخلوط اول را رسم کرده و به اندازه کسر یا عدد مخلوط دوم از آن خط می زنیم اگر بخش کسری کسر دوم کوچکتر از بخش کسری کسر اول بود میبایست از بخش عدد صحیح کسر اول نیز خط بزنیم
مثال
\(2\frac{2}{3} + \frac{5}{6} \Rightarrow 2\frac{4}{6} + \frac{5}{6}\)
با رسم محور
در این روش ابتدا کسرها را هم مخرج می کنیم بعد اندازه بین واحدها را به اندازه مخرج به قسمت های مساوی تقسیم میکنیم.
عدد مخلوط اول را با فلشی که شروع آن از صفر میباشد روی محور نمایش میدهیم و عدد مخلوط دوم را از انتهای فلش دوم رسم میکنیم اگر جمع بود به سمت راست و اگر تفریق بود به سمت چپ رسم میکنیم جهت راحتی کار میتوان عدد مخلوط دوم را به کسر بزرگتر از واحد تبدیل کرد و بعد فلش آن را رسم کرد.
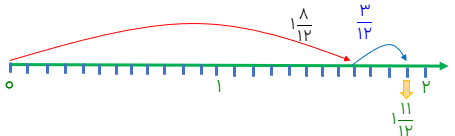
مثال
\(1\frac{2}{3} + \frac{1}{4} \Rightarrow 1\frac{8}{{12}} + \frac{3}{{12}}\)
محاسبه ریاضی
ابتدا اعداد صحیح را با هم جمع میکنیم و بعد کسرها را اگر مخرج برابر نداشتند، هم مخرج نموده و با هم جمع میکنیم. در انتها اگر بخش کسری جواب بزرگتر از واحد بود، آن را به عدد مخلوط تبدیل کرده و با عدد صحيح جمع میکنیم.
مثال
جمع دو عدد مخلوط زیر ،را با روش محاسبه ریاضی به دست آورید.
\(1\frac{2}{3} + 2\frac{1}{4}\)
\(1\frac{2}{3} + 2\frac{1}{4} \Rightarrow 1\frac{8}{{12}} + 2\frac{3}{{12}} = 3\frac{{11}}{{12}}\)
انجام عملیات تفریق
ابتدا كسرها را اگر دارای مخرج برابر نیستند هم مخرج می.کنیم بعد مقایسه می کنیم آیا بخش کسری عدد مخلوط اول از بخش کسری عدد مخلوط دوم بزرگتر هست که قابل تفریق باشد یا خیر؟
اگر بخش کسری عدد مخلوط اول از بخش کسری عدد مخلوط دوم بزرگتر بود اعداد صحیح دوم را از عدد صحیح اولی کم میکنیم و بعد کسر دوم را نیز از کسر اول کم میکنیم.
مثال
تفریق عدد مخلوط زیر را انجام دهید.
\(4\frac{3}{4} - 1\frac{2}{3}\)
\(4\frac{3}{4} - 1\frac{2}{3} = 4\frac{9}{{12}} - 1\frac{8}{{12}} = 3\frac{1}{{12}}\)
اگر در جمع یا تفریق اعداد مخلوط یکی از اعداد نداشت و تنها دارای قسمت کسری صحيح بود به این معنی است که عدد صحیح آن صفر می باشد.
اگر در تفریق اعداد مخلوط قسمت کسری عدد مخلوط اولی از قسمت کسری عدد مخلوط دوم کوچکتر باشد امکان تفریق عدد بزرگ از یک عدد کوچک وجود ندارد بنابراین به کمک قسمت عدد صحیح عدد مخلوط نیز نیاز داریم لذا به یکی از دو روش زیر اقدام میکنیم:
روش اول:
در روش اول هر دو عدد مخلوط را به کسر بزرگتر از واحد تبدیل میکنیم تا عدد صحیح به کمک بخش کسری آمده و کسر اول به کمک یک واحد عدد صحیح بزرگتر شده و امکان تفریق وجود داشته باشد و سپس تفریق را انجام می دهیم. در نهایت اگر جواب تفریق کسر بزرگتر از واحد ه بود آن را مجددا به عدد مخلوط تبدیل میکنیم
مثال
تفریق دو عدد مخلوط زیر را به دست آورید.
\(4\frac{1}{3} - 2\frac{2}{3}\)
\(4\frac{1}{3} - 2\frac{2}{3} = \frac{{13}}{3} - \frac{8}{3} = \frac{5}{3} = 1\frac{2}{3}\)
روش دوم:
در روش دوم یک واحد از عدد صحیح مربوط به عدد مخلوط اول کم کرده و به کسر آن اضافه میکنیم حالا قسمت کسری آن به کمک این یک واحد بزرگتر شده و امکان تفريق وجود دارد، لذا عملیات تفریق را انجام میدهیم.
مثال
تفریق دو عدد مخلوط زیر را به دست آورید.
\(4\frac{1}{3} - 2\frac{2}{3}\)
کسر اول از کسر دوم کوچکتر است و تفریق نمی شود.
\(\begin{array}{l}4\frac{1}{3} - 2\frac{2}{3} = 3 + 1\frac{1}{3} - 2\frac{2}{3}\\ = 3 + \frac{4}{3} - 2\frac{2}{3}\\ = 3\frac{4}{3} - 2\frac{2}{3}\\ = (3 - 2) + (\frac{4}{3} - \frac{2}{3})\\ = 1 + \frac{2}{3}\end{array}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه پنجم- آزمون آنلاین تمامی دروس پایه پنجم
- گام به گام تمامی دروس پایه پنجم
- ویدئو های آموزشی تمامی دروس پایه پنجم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه پنجم
- فلش کارت های آماده دروس پایه پنجم
- گنجینه ای جامع از انشاء های آماده پایه پنجم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه پنجم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
ضرب عدد در کسر
فصل 2 : کسر
ضرب عدد در کسر
برای به دست آوردن حاصل ضرب یک عدد در یک کسر سه روش زیر وجود دارد:
استفاده از شکل
در این روش ابتدا باید شکل واحد را انتخاب کنیم تا بدانید یک واحد کامل به چند قسمت تقسیم شده .است زیرا شکل به هر چند قسمت مساوی که تقسیم شود این تعداد قسمتها نشان دهنده مخرج کسر است.
بعد از اینکه شکل واحد و تعداد قسمتها مشخص شد به تعداد عدد داده شده که قرار است در کسر ضرب ،شود با رنگهای مختلف کسر مورد نظر را نشان می دهیم.
مثال
حاصل ضرب زیر را با رسم شکل به دست آورید.
\(2 \times \frac{1}{3}\)
با توجه به شکل ،واحد مخرج کسر 3 بوده و تا انتهای محاسبات تغییر نمی کند صورت کسر 1 است و عددی که ضرب شده 2 است. پس 2 نوع رنگ لازم داریم که از هر رنگ تعداد 1 خانه باید رنگ شود. (اگر لازم بود می توانستم تعداد مثلث ها را بیشتر کنیم تا بتوانیم به تعداد مورد نیاز خانه رنگ کنیم).
واحد به ۳ قسمت مساوی تقسیم شده، پس مخرج ۳ می باشد.
\(\frac{1}{3} + \frac{1}{3} = 2 \times \frac{1}{3} = \frac{2}{3}\)
با رسم محور:
در این روش ابتدا به اندازه کسر داده شده از صفر محور یک فلش می کشیم و بعد این فلش را تعداد عددی که در کسر ضرب شده است تکرار می کنیم
مثال
حاصل ضرب زیر را با رسم محور به دست آورید .
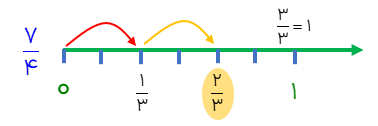
\(2 \times \frac{1}{3}\)
\(2 \times \frac{1}{3} = \frac{2}{3}\)
محاسبه ریاضی:
در این روش عدد ضرب شده در کسر را فقط در صورت کسر ضرب میکنیم و مخرج بدون تغییر ماند. باقی می ماند.
مثال
حاصل ضرب زیر را با محاسبه ریاضی به دست آورید.
\(7 \times \frac{3}{4}\)
عدد 7 فقط در صورت کسر یعنی 3 ضرب می شود و مخرج کسر بدون تغییر باقی می ماند.
\(7 \times \frac{3}{4} = \frac{{7 \times 3}}{4} = \frac{{21}}{4}\)
جزوات جامع پایه پنجم
جزوه جامع ریاضی پنجم
جزوه جامع علوم تجربی پنجم
جزوه جامع مطالعات اجتماعی پنجم
جزوه جامع فارسی پنجم
جزوه جامع نگارش پنجم
جزوه جامع هدیه های آسمانی پنجم
جزوه جامع آموزش قرآن پنجم
ضرب کسر در کسر
فصل 2 : کسر
ضرب کسر در کسر
برای به دست آوردن حاصل ضرب دو ،کسر یکی از سه روش زیر را به کار می بریم.
استفاده از شکل:
در این روش طبق مراحل زیر اقدام میکنیم شکل واحد را انتخاب می کنیم:
1 شكل واحد را انتخاب می کنیم.
2 شكل واحد را به تعداد مخرج کسر دوم تقسیم بندی می کنیم .
3 به اندازه صورت کسر ،دوم، از قسمتهای شکل رنگ می کنیم.
4 حالا سراغ کسر دوم می رویم.
5 قسمت رنگ شده کسر را در نظر میگیریم و به قسمت رنگ نشده کار نداریم.
6 این قسمت رنگ شده کسر را به اندازه مخرج كسر اول جداگانه تقسیم بندی می کنیم.
7 حالا از این تقسیم بندی جدید که انجام داده ایم به اندازه صورت کسر اول با رنگی دیگر رنگ آمیزی می کنیم
8 حالا کسر جواب را می نویسیم که در آن قسمت رنگ شدهی ،جدید صورت کسر بوده وتعداد كل تقسیم بندی شکل چه رنگ شده و چه رنگ نشده مخرج کسر می باشد.
مثال
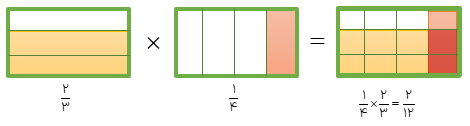
حاصل ضرب دو کسر زیر را با استفاده از رسم شكل به دست آورید.
\(\frac{1}{4} \times \frac{2}{3}\)
با رسم محور:
در این روش به اندازه کسر دوم از صفر محور یک فلش رسم می کنیم.
حالا قسمتی که جدا کرده ایم و با فلش نشان داده ایم را به اندازه مخرج کسر اول تقسیم بندی کرده و به اندازه صورت کسر اول از آن انتخاب می کنیم و بعد یک فلش دیگر (با شروع از نقطه صفر محور) رسم می کنیم.
محل فلش دوم جواب ضرب می باشد.
مثال
حاصل دو کسر زیر را با رسم نمودار به دست آورید.
\(\frac{1}{2} \times \frac{3}{5}\)
ابتدا کسر دوم را با فلش نمایش میدهیم و محدوده بالا را به اندازه مخرج کسر اول به دو قسمت تقسیم کرده و به اندازه صورت آن را انتخاب میکنیم
محل فلش دوم (زرد رنگ) جواب است
محاسبه ریاضی:
در ضرب دو کسر در ،همدیگر صورت کسر اول در صورت کسر دوم ضرب میشود و مخرج کسر اول نیز در مخرج کسر دوم ضرب می شود.
در ضرب کسرها اصلا نیازی به هم مخرج کردن کسرها نیست.
مثال
حاصل ضرب زیر را از طریق محاسبه ریاضی به دست آورید.
\(\frac{1}{2} \times \frac{3}{5}\)
\(\frac{1}{2} \times \frac{3}{5} = \frac{{1 \times 3}}{{2 \times 5}} = \frac{3}{{15}}\)
ضرب عددهای مخلوط
فصل 2 : کسر
ضرب عددهای مخلوط
عددهای مخلوط را میتوان به دو روش در هم ضرب کرد:
استفاده از شکل:
در این ،روش برای ضرب دو عدد مخلوط مستطیلی رسم می کنیم و عدد کوچکتر را به عنوان عرض مستطیل و عدد بزرگ تر را به عنوان طول مستطیل در نظر می گیریم.
در مرحله بعد قسمت های صحیح و کسری اعداد مخلوط طول و عرض را با پاره خط جدا می کنیم با این کار مستطیل بزرگ به چند مستطیل کوچکتر تقسیم میشود و با به دست آوردن مساحت این مستطیلها و جمع آنها با همدیگر مساحت مستطیل بزرگتر و در نتیجه ضرب دو عدد مخلوط به دست می آید.
روش حل ضرب اعداد مخلوط با رسم شکل را می توانیم بدون اینکه خود شکل را رسم کنیم ولی از فرمول رسم استفاده کنیم نیز حل کنیم برای حل باید مراحل زیر را انجام دهیم
الف عدد صحیح مربوط به عدد مخلوط اول را در عدد صحیح مربوط به عدد مخلوط دوم ضرب می کنیم
ب عدد صحیح مربوط به عدد مخلوط اول را در کسر مربوط به عدد مخلوط دوم ضرب می کنیم.
ج عدد کسری مربوط به عدد مخلوط اول را در عدد صحیح مربوط به عدد مخلوط دوم ضرب می کنیم
د عدد کسری مربوط به عدد مخلوط اول را در کسر مربوط به عدد مخلوط دوم ضرب می کنیم
در مرحله آخر جوابهای "الف" ، "ب" ، "ج" ، "د" را با هم جمع می کنیم.
محاسبه ریاضی:
در این روش ابتدا هر دو عدد مخلوط را به کسر بزرگتر از واحد تبدیل کرده و سپس عددهای مخلوط را در هم ضرب می کنیم. در نهایت جواب را مجددا به عدد مخلوط تبدیل می کنیم
مثال
حاصل همان مثال قبلی را با روش محاسبه ریاضی به دست آورید
\(1\frac{1}{2} \times 2\frac{1}{3}\)
\(1\frac{1}{2} \times 2\frac{1}{3} = \frac{3}{2} \times \frac{7}{3} = \frac{{21}}{6} = 3\frac{3}{6} = 3\frac{1}{2}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه پنجم- آزمون آنلاین تمامی دروس پایه پنجم
- گام به گام تمامی دروس پایه پنجم
- ویدئو های آموزشی تمامی دروس پایه پنجم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه پنجم
- فلش کارت های آماده دروس پایه پنجم
- گنجینه ای جامع از انشاء های آماده پایه پنجم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه پنجم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
ساده کردن در ضرب کسرها
فصل 2 : کسر
ساده کردن در ضرب کسرها
در ضرب کسرها عملیات ساده کردن به دو روش قابل انجام است.
الف ابتدا کسرها را ساده کنیم و بعد عملیات ضرب را انجام دهیم .
ب عملیات ضرب کسرها را انجام دهیم و بعد جواب به دست آمده را ساده کنیم.
مثال
حاصل ضرب های زیر را به دست آورده و در آخر جواب را ساده کنید
\(\frac{7}{4} \times \frac{2}{5}\)
\(\frac{7}{4} \times \frac{2}{5} = \frac{{7 \times 2}}{{4 \times 5}} = \frac{{14 \div 2}}{{20 \div 2}} = \frac{7}{{10}}\)
اگر در صورت و مخرج کسر فقط از عملیات ضرب استفاده شده ،باشد میتوانیم اعداد صورت و مخرج را بر عددی مشترک تقسیم کنیم و عدد قبلی را خط بزنیم و حاصل تقسیم را به جای آن قرار دهیم.
جزوات جامع پایه پنجم
جزوه جامع ریاضی پنجم
جزوه جامع علوم تجربی پنجم
جزوه جامع مطالعات اجتماعی پنجم
جزوه جامع فارسی پنجم
جزوه جامع نگارش پنجم
جزوه جامع هدیه های آسمانی پنجم
جزوه جامع آموزش قرآن پنجم
تقسیم کسرها
فصل 2 : کسر
تقسیم عدد بر عدد
برای تقسیم دو عدد بر همدیگر میتوانیم از روش های زیر استفاده کنیم.
الف) استفاده از شکل:
در این روش اگر اگر عدد اول صورت کسر کوچکتر از عدد دوم مخرج کسر بود، شکل واحدی را در نظر گرفته و به اندازه مخرج به قسمت های مساوی تقسیم نموده و به اندازه صورت کسر از این قسمتها رنگ میکنیم.
مثال
تقسیم دو عدد زیر را با رسم شکل نشان دهید.
\(3 \div 5 = \frac{3}{5}\)
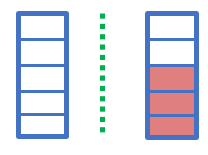
ولی اگر عدد اول صورت کسر بزرگتر از عدد دوم مخرج کسر بود آن را به عدد مخلوط تبدیل میکنیم و به تعداد عدد صحيح واحد کامل رسم میکنیم و به اندازه عدد کسری که کوچکتر از واحد است نیز شکلی مانند روشی که در بالا گفتیم رسم میکنیم.
ب)با رسم محور:
در این نوع نمایش روی محور اگر عدد اولی صورت کسر از عدد دوم مخرج کسر کوچکتر بود، یعنی کسر کوچکتر از واحد بود، بین سفر تا یک را به اندازه مخرج کسر به اندازه های مساوی تقسیم کرده و بعد به اندازه صورت از این قسمتها انتخاب میکنیم ولی اگر کسر بزرگتر از واحد بود باید ابتدا آن را به عدد مخلوط تبدیل کرده و بعد روی محور نمایش دهیم. که در این صورت باید به اندازه عدد صحیح از روی محور انتخاب کرده و فاصله بین عدد صحیح و عدد بعدی را اندازه مخرج کسر تقسیم بندی کرده و بعد به اندازه صورت از آن انتخاب کنیم.
ج)محاسبه ریاضی :
برای تقسیم دو عدد بر یکدیگر می بایست عدد اول را در صورت کسر نوشته و عدد دوم را در مخرج بنویسیم. اگر قابل ساده کردن بود ساده میکنیم و اگر بزرگتر از واحد بود به عدد مخلوط تبدیل می کنیم.
تقسیم کسر بر عدد
برای تقسیم کسر بر عدد به روشهای زیر عمل می کنیم.
الف) استفاده از شکل:
ابتدا شکل را به اندازه کسر اول رسم کرده و بعد دوباره همان شکل را به اندازه عدد مجددا تقسیم بندی میکنیم بخش رنگی مشخص شده در یکی از قسمتها جواب تقسیم است.
مثال
حاصل تقسیم کسر بر عدد زیر را با رسم شکل نشان دهید.
\(\frac{2}{5} \div 3\)
ب) با رسم محور :
در این روش ابتدا کسر را با فلش نمایش می دهیم. سپس قسمت مشخص شده با فلش را به تعداد عدد دوم به قسمتهای مساوی تقسیم می کنیم یکی از قسمتهای جدید جواب تقسیم می باشد.
ج)محاسبه ریاضی:
در این روش کسر اول را می نویسیم و بعد علامت تقسیم را به ضرب تقسیم کرده و به عدد دوم مخرج 1 میدهیم و جای صورت و مخرج را عوض می کنیم کسری می نویسیم که صورت آن 1 بوده و مخرجش این عدد میباشد حالا عمل ضرب را انجام میدهیم.
مثال
حاصل تقسیم کسر بر عدد زیر را با محاسبه ریاضی به دست آورید
\(\frac{1}{5} \div 3\)
\(\frac{1}{5} \div 3 = \frac{1}{5} \times \frac{1}{3} = \frac{1}{{15}}\)
تقسیم عدد بر کسر
الف) استفاده از شکل :
در این روش ابتدا به تعداد عدد داده شده، شکل واحد رسم میکنیم، بعد به اندازه مخرج کسر هر شکل را تقسیم بندی می کنیم تعداد قسمتهای بدست آمده در شکل جواب نهایی تقسیم می باشد.
مثال
حاصل تقسیم عدد بر کسر زیر را با استفاده از رسم شکل محاسبه کنید.
\(3 \div \frac{1}{5}\)
عدد ما ۳ است، پس ۳ واحد رسم میکنیم و مخرج کسر ۵ است پس هر واحد را به ۵ قسمت تقسیم میکنیم.
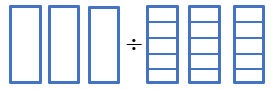
تعداد کل قسمت ها 15 شده است. جواب = 15
ب) با رسم محور :
در این روش به تعداد عدد داده شده باید روی محور واحد در نظر بگیریم و بعد این واحدها را به اندازه ی مخرج کسر تقسیم میکنیم تعداد قسمتهای کوچک به دست آمده جواب تقسیم می باشد.
مثال
حاصل تقسیم بر کسر زیر را با استفاده از رسم محور به دست آورید.
\(3 \div \frac{1}{5}\)
عدد ما ۳ است. روی محور ۳ واحد در نظر میگیریم.مخرج کسر ۵ است. هر واحد به ۵ قسمت تقسیم میشود
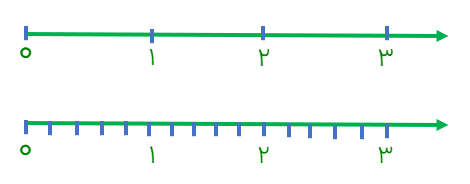
تعداد کل قسمتهای جدید ۱۵ تا میباشد = جواب15
ج) محاسبه ریاضی :
در این روش عدد را مینویسیم. بعد علامت تقسیم را به ضرب تبدیل می کنیم در انتها جای صورت و مخرج کسر را با هم عوض میکنیم و عمل ضرب را انجام میدهیم.
مثال
حاصل تقسیم عدد بر کسر زیر را با استفاده از محاسبه ریاضی به دست آورید.
\(3 \div \frac{1}{5}\)
\(3 \div \frac{1}{5} = 3 \times \frac{5}{1} = \frac{{15}}{1} = 15\)
نکات مهم زیر را به خاطر بسپارید
نیم یعنی:\(\frac{1}{2}\) ثلث یعنی:\(\frac{1}{3}\)
ربع یعنی:\(\frac{1}{4}\)
خمس یعنی:\(\frac{1}{5}\)
نسبت
فصل 3 : نسبت، تناسب و درصد
نسبت
برای مقایسه دو مقدار از مفهوم نسبت استفاده می کنیم. برای مثال در یک کتابخانه 20 عدد كتاب داريم،که 6 تا از آنها کتاب داستان است ؛ نسبت کتاب های داستان به کل کتاب ها 6 به 20 می باشد.
همچنین می توانیم این نسبت را به صورت کسری زیر نمایش دهیم:
\(\frac{6}{{20}}\)
نسبت جزء به کل
در این خصوص تعداد کل را در مخرج نوشته و تعدادی که مربوط به یک مورد خاصی است را در صورت کسر می نویسیم.
مثال
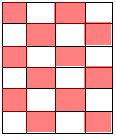
در شکل زیر نسبت قسمت های رنگ شده به کل قسمت ها را بنویسید.
نسبت جزء به جزء
در این حالت نسبت دو ویژگی خاص را با نوشتن آنها به ترتیب در صورت و مخرج کسر مشخص میکنیم.
مثال
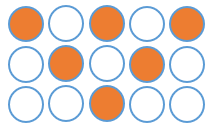
در شکل زیر تعداد خانه های رنگ شده به رنگ نشده را بنویسید.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه پنجم- آزمون آنلاین تمامی دروس پایه پنجم
- گام به گام تمامی دروس پایه پنجم
- ویدئو های آموزشی تمامی دروس پایه پنجم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه پنجم
- فلش کارت های آماده دروس پایه پنجم
- گنجینه ای جامع از انشاء های آماده پایه پنجم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه پنجم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
نسبت در مساحت
فصل 3 : نسبت، تناسب و درصد
نسبت در مساحت
نسبت مساحت ها را میتوان به 2 صورت زیر تعیین کرد:
الف) میتوان با تقسیم بندی شکل به واحدهای مساوی این نسبت ها را تعیین کرد.
مثال
مساحت قسمت رنگی به مساحت کل شکل چه قدر است؟
\(\frac{{12}}{{24}}\)
ب) در شکل هایی که محاسبه مساحت طبق رابطه های مربوطه به راحتی امکان پذیر است با داشتن اندازه های لازم و بدون تقسیم بندی شکل میتوان نسبت مساحتها را محاسبه کرد و بعد نسبت ها را نوشت.
مثال
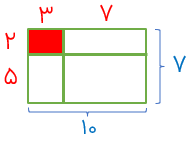
در شکل زیر مساحت قسمت رنگی به مساحت کل را بنویسید.
برای مساحت مستطیل بزرگ ، باید طول عرض مستطیل بزرگ را در نظر داشته باشیم.
۶ = ۳×۲ = مساحت قسمت رنگی
۷۰ = ۱۰×۷ = مساحت کل
مساحت قسمت رنگی به مساحت کل \( = \frac{6}{{70}}\)
جزوات جامع پایه پنجم
جزوه جامع ریاضی پنجم
جزوه جامع علوم تجربی پنجم
جزوه جامع مطالعات اجتماعی پنجم
جزوه جامع فارسی پنجم
جزوه جامع نگارش پنجم
جزوه جامع هدیه های آسمانی پنجم
جزوه جامع آموزش قرآن پنجم
مقایسه نسبت ها
فصل 3 : نسبت، تناسب و درصد
مقایسه نسبت ها
برای مقایسه عملکرد دو نفر یا دو چیز از نسبت ها استفاده می کنیم.
مثال
مقایسه سرعت دو خودرو در اصل مقایسه نسبت میزان حرکت در واحد زمان آن دو خودرو می باشد.
مقایسه پیشرفت کار دو نقاش مقایسه نسبت میزان رنگ کاری در مدت زمان معین آنها می باشد.
نسبت را با خط کسری نشان می دهیم پس تمام خواص یک کسر را دارا بوده و میتوان مانند کسرها آن را ساده کرد پس در مقایسه نسبت،ها جهت سهولت در کار می توانیم ابتدا آنها را ساده کنیم و بعد ساده شده با هم مقایسه کنیم
مثال
على 540 متر مربع زمین را در 6 روز چمن کاری می کند و رضا 400 متر مربع زمین را در در 5 روز چمن کاری می کند نسبت زمین چمن کاری شده به روز را برای هر دو نفر حساب کنید و عملکرد آنها را با هم مقایسه کنید.
\(\frac{{540}}{6}\left\lfloor > \right\rfloor \frac{{400}}{5}\)
نسبت های مساوی
فصل 3 : نسبت، تناسب و درصد
نسبت های مساوی
همان طور که پیش از این گفته شد، نسبت ها تمامی خواص کسرها را دارند.
مثلا میتوانی هر دو جز نسبت را بر عددی یکسان ضرب یا تقسیم کنیم . در این صورت نسبت جدیدی که با این ضرب یا تقسیم به دست می آید با نسبت اولیه برابر است.
مثال
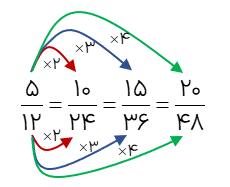
برای نسبت زیر 3 نسبت دیگر بنویسید.
\(\frac{5}{{12}}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه پنجم- آزمون آنلاین تمامی دروس پایه پنجم
- گام به گام تمامی دروس پایه پنجم
- ویدئو های آموزشی تمامی دروس پایه پنجم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه پنجم
- فلش کارت های آماده دروس پایه پنجم
- گنجینه ای جامع از انشاء های آماده پایه پنجم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه پنجم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
تناسب
فصل 3 : نسبت، تناسب و درصد
تناسب
دو نسبت ،مساوی با یکدیگر تناسب تشکیل می دهند. مانند:
\(\frac{1}{2} = \frac{4}{8}\)
معمولا تناسب را با جدول نشان می دهیم برای مثال تناسب بالا را در جدول به صورت زیر میتوان نشان داد:
در حل مسائل مربوط به نسبت ها می توانیم هم از روش تساوی کسرها و هم از جدول تناسب استفاده کنیم.
مثال
نقاشی در دو ساعت 7 متر مربع را نقاشی می و در چهار روز 16 متر مربع را نقاشی می نسبت تعداد روز به میزان نقاشی شده را در هر دو حالت به دست آورید و بررسی کنید آیا این نسبتها با هم متناسب هستند؟
بعد از ساده کردن، نسبتها با هم برابر نمیشوند لذا تشکیل تناسب نمی دهند و با هم متناسب نیستند.
\(\frac{4}{{16}} = \frac{2}{8},\,\frac{2}{7}\)
جزوات جامع پایه پنجم
جزوه جامع ریاضی پنجم
جزوه جامع علوم تجربی پنجم
جزوه جامع مطالعات اجتماعی پنجم
جزوه جامع فارسی پنجم
جزوه جامع نگارش پنجم
جزوه جامع هدیه های آسمانی پنجم
جزوه جامع آموزش قرآن پنجم
حل مسئله به کمک تناسب
فصل 3 : نسبت، تناسب و درصد
حل مسئله به کمک تناسب
منظور از حل تناسب اینست که مقدار خواسته شده را در دو نسبت مساوی به دست بیاوریم.
باید توجه کرد هر کدام از اجزای تناسب اول در چه عدد ضرب یا بر چه عددی تقسیم شده است تا جزء مقابل آنها در تناسب دوم به دست آمده است. البته باید دقت کنیم واحدها در دو تناسب یکسان باشد.
مثال
اتومبیلی 180 کیلومتر را در 1 ساعت و نیم کند این اتومبیل در هر ساعت چند طی می کیلومتر طی می کند؟
۹۰ دقیقه = ۱ ساعت و نیم
۶۰ دقیقه = ۱ ساعت
\(\ 2 \times 60 = 120\)
جدول تناسب
برای حل مسائلی که در آن دو مقدار داده شده باشد از جدول تناسب استفاده میکنیم حالا اگر غیر از خود ،نسبت ها مجموع یا تفاضل نسبت ها هم داده شده باشد میتوانیم یک ردیف به جدول تناسب اضافه کرده و جدول سه طبقه تشکیل دهیم و باز با همان روش تناسب مقادیر خواسته شده را به دست آوریم.
به بیان دیگر در حل مسائل نسبت می توانیم هر ترکیبی از نسبتهای داده شده را به عنوان ردیفی در جدول تناسب اضافه کنیم.
مثال
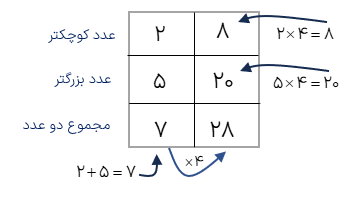
مجموع دو عدد که نسبت آنها 2 به 5 است برابر 28 میباشد این دو عدد را بیابید.
مثال
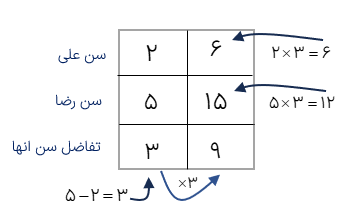
نسبت سن على به رضا مثل 2 به 5 است. اگر اختلاف سن آنها 9 سال باشد سن هر کدام چقدر است؟
در مسائلی که اختلاف یا مجموع دو مقدار داده شده است ولی در نهایت فقط یکی از مقدارها خواسته می،شود نیازی نیست جدول 3 طبقه درست کنیم و با دست کردن یک جدول 2 طبقه تنها مقادير مجموع یا تفاضل و مقدار خواسته شده را در جدول قرار میدهیم
در برخی موارد نسبت دو مقدار داده میشود و مقدار مجموع یا تفاضل آنها خواسته می شود. در این موارد نیز باید از جدول دو طبقه استفاده کنیم و یک طبقه را به مجموع یا تفاضل نسبت ها اختصاص دهیم.
مثال
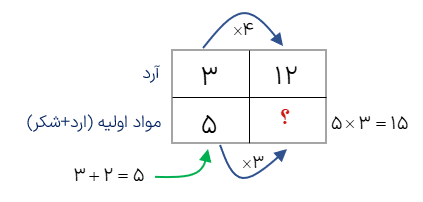
برای تهیه مواد اولیه ،شیرینی به ازای هر 3 پیمانه آرد 2 پیمانه شکر نیاز داریم با 12 پیمانه آرد در کل چند پیمانه مواد اولیه شیرینی تشکیل می شود؟
درصد
فصل 3 : نسبت، تناسب و درصد
مفهوم درصد
از نظر معنا و مفهوم درصد به معنای کسری از عدد 100 می.باشد یعنی کسری که مخرج آن صد می باشد.
وقتی میخواهیم کسری را که مخرج آن 100 نیست به صورت کسری از صد نشان دهیم می بایست کسر مساوی با آن را طوری بنویسیم مخرج 100 داشته باشد.
مثال
وقتی میگوییم 2 درصد جمعیت یک شهر دانش آموز کلاس پنجم ،هستند یعنی از هر 100 نفر که در این شهر زندگی میکنند 2 نفر در کلاس پنجم درس می خوانند.
میزان 25 درصد تخفیف یعنی از هر 100 تومان 25 تومان گرفته نمی شود و فقط 75 تومان گرفته میشود.
هر نسبتی که مخرج آن 100 باشد را میتوان به صورت درصد بیان کرد، نماد درصد به صورت % می باشد.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه پنجم- آزمون آنلاین تمامی دروس پایه پنجم
- گام به گام تمامی دروس پایه پنجم
- ویدئو های آموزشی تمامی دروس پایه پنجم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه پنجم
- فلش کارت های آماده دروس پایه پنجم
- گنجینه ای جامع از انشاء های آماده پایه پنجم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه پنجم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
محاسبه ی درصد
فصل 3 : نسبت، تناسب و درصد
محاسبه ی درصد
می توانیم برخی از نسبت ها را میتوان به صورت درصد بنویسیم.روش کار به این صورت است که کسری با مخرج 100 را مساوی نسبت مورد نظر قرار داده و بعد صورت آن را با روش حل تناسب به دست می آوریم به این ترتیب کسری داریم که از نظر مقدار با نسبت ما مساوی است و مخرج آن صد می باشد.
به طورکلی برای این که یک نسبت را به صورت درصد بنویسیم باید در صورت و مخرج آن نسبت عدد را ضرب کنیم که مخرجش 100 شود.
مثال
در یک مدرسه تعداد دانش آموزان کلاس پنجم به کل دانش آموزان 2 به 5 است. اگر این مدرسه 100 نفر دانش آموز داشته باشد تعداد دانش آموزان کلاس پنجم چند نفر است؟ آن را به صورت درصد بیان کنید.
از هر ۱۰۰ نفر ۴۰ نفر کلاس پنجم هستند ، یعنی ۴۰ دانش آموزان کلاس پنجم هستند.
گاهی اوقات برای اینکه بتوانیم کسر مساوی با مخرج صد را برای کسر موجود بنویسیم، می بایست ابتدا کسر موجود را ساده کنیم و بعد صورت و مخرج آن را در عددی ضرب کنیم که مخرجش 100 شود.
مثال
یک راننده اتوبوس 6 ساعت از شبانه روز را رانندگی میکند او چند درصد از شبانه روز را مشغول رانندگی است؟
هر شبانه روز ۲۴ ساعت می باشد.
\(\left\lfloor {} \right\rfloor = 1 \times 25 = 25\)
برای محاسبه میزان درصد قسمت رنگ شده شکل داده شده می بایست ابتدا نسبت مساحت قسمت رنگی به کل شکل را بنویسیم و بعد با مساوی قرار دادن آن با کسری که مخرج صد دارد به صورت درصد تبدیل کنیم.
مثال
چند درصد شکل زیر رنگ شده است؟
\(\frac{3}{4} = \frac{{\left\lceil {} \right\rceil }}{{100}} \Rightarrow \left\lfloor {\,\,\,} \right\rfloor = 3 \times 25 = 75\)
گاهی درصدی از چیزی داده میشود و بعد مقدار را میخواهند در این صورت باید ابتدا درصد داده شده را به صورت کسری که دارای مخرج 100 میباشد بنویسیم و بعد مقدار را به دست آوریم.
على 3000 تومان پول دارد او 20% از پولش را به برادرش می.دهد حالا او چند تومان پول دارد؟
\(\% 12\) یعنی\(\frac{{12}}{{100}}\)
\(\frac{{12}}{{100}} = \frac{{\left\lceil {} \right\rceil }}{{3000}} \Rightarrow \left\lfloor {\,\,} \right\rfloor = 12 \times 30 = 360\)
۳۶۰ تومان از کل پول (۳۰۰۰ تومان) داده شده است\(3000 - 360 = 2640\)
۲۶۴۰ تومان از پول باقی مانده است.
در مسائل مربوط به "تخفيف" مثل بقيه سوالات ، میتوان با نوشتن نسبتهای متناسب مقادیر مورد نظر را به دست آورد. نکته مهم این که مقدار ،تخفیف، مبلغی است که پرداخت نمی شود.
قیمت یک کتاب 2500 تومان میباشد آن را با %20 تخفیف خریده ایم بدون اینکه مبلغ تخفیف را حساب کنید حساب کنید چقدر باید بپردازیم؟
وقتی %20 تخفیف گرفته ایم یعنی ۸۰%باید پرداخت شود
\(\frac{{80}}{{100}} = \frac{{\left\lceil {} \right\rceil }}{{3000}} \Rightarrow \left\lfloor {} \right\rfloor = 80 \times 30 = 24000\)
۲۴۰۰۰ تومان باید پرداخت شود
جزوات جامع پایه پنجم
جزوه جامع ریاضی پنجم
جزوه جامع علوم تجربی پنجم
جزوه جامع مطالعات اجتماعی پنجم
جزوه جامع فارسی پنجم
جزوه جامع نگارش پنجم
جزوه جامع هدیه های آسمانی پنجم
جزوه جامع آموزش قرآن پنجم
تعريف خط تقارن
فصل 4 : تقارن و چندضلعی ها
تعريف خط تقارن
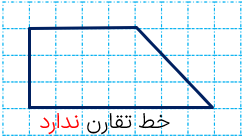
خط تقارن خطی است که شکل را به دو قسمت مساوی تقسیم می کند. به طوری که اگر شکل را از روی آن خط تا کنیم آن دو قسمت کاملا بر هم منطبق میشوند. مانند شکل زیر:
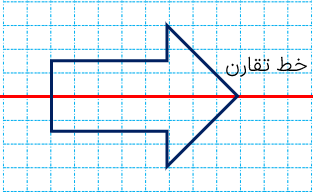
1 بعضی از شکل ها خط تقارن ندارند.
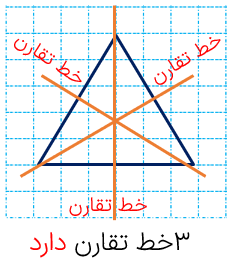
2 برخی شكل ها بیشتر از یک خط تقارن دارند.
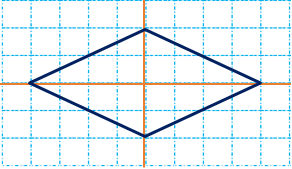
3 در برخی شکل ها قطرها خط تقارن نیز .هستند. مانند: مربع لوزی و دایره.
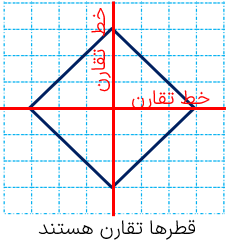
4 با رسم خط های تقارن یک شکل، می توان آن رسم را به چند قسمت مساوی با مساحت های برابر تقسیم کرد. به عنوان نمونه با رسم خط های تقارن لوزی زیر به 4 مثلث مساوی کوچک تقسیم میشود که مساحت همه ی آنها با هم برابر است و مجموع مساحتهای آنها مساحت کل شکل را تشکیل میدهد.
قرینه یک نقطه نسبت به خط
فصل 4 : تقارن و چندضلعی ها
قرینه یک نقطه نسبت به خط
برای یافتن قرینه یک نقطه نسبت به یک خط ابتدا به وسیله گونیا از آن نقطه خط عمودی بر خط داده شده رسم کرده و بعد به اندازه خودش ادامه می دهیم و در انتهای خط نقطه مذکور را می گذاریم.
مثال
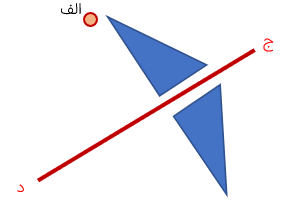
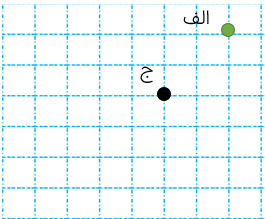
قرینه نقطه ی "الف" را نسبت به خط (ج د) رسم کنید.
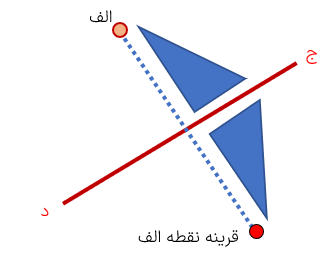
1 قرینه هر نقطه روی خط تقارن، همان نقطه باشد زیرا فاصله آن از خط تقارن صفر میباشد و قابل ادامه دادن نیست تا از خط تقارن خارج شود.
2 در شکل زیر، قرینه ی نقطه ی "الف" که روی روی خط ج د قرار دارد همان نقطه ی "الف" می باشد.
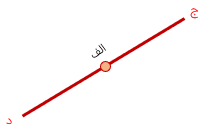
3 برای پیداکردن قرینه ی یک پاره خط نسبت به یک خط ،کافیست قرینه نقاط ابتدا و انتهای پاره خط مذکور را، نسبت به خط تقارن پیدا کنیم و بعد آن دو نقطه را به همدیگر وصل کنیم.پاره خط به دست آمده ی جدید ،قرینه پاره خط اولیه است.
مثال
تقاورن شکل زیر را رسم کنید.
برای رسم قرینه ی یک نقطه نسبت به یک خط باید ابتدا قرینه مرکز دایره را نسبت به خط قرینه داده شده رسم .کنیم بعد به اندازه شعاع دایره اولیه از نقطه قرینه ای که پیدا کرده ایم دایره ای رسم کنیم.
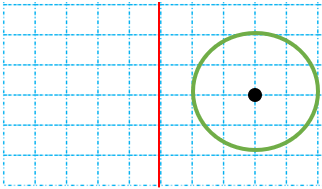
مثال
قرینه دایره زیر را نسبت به خط تقارن رسم کنید.
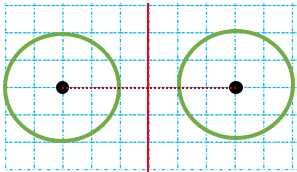
اگر نیمی از یک شکل را در یک طرف خط تقارن داشته باشیم با رسم قرینه شکل نسبت به خط تقارن شکل تکمیل میشود.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه پنجم- آزمون آنلاین تمامی دروس پایه پنجم
- گام به گام تمامی دروس پایه پنجم
- ویدئو های آموزشی تمامی دروس پایه پنجم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه پنجم
- فلش کارت های آماده دروس پایه پنجم
- گنجینه ای جامع از انشاء های آماده پایه پنجم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه پنجم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
مرکز تقارن
فصل 4 : تقارن و چندضلعی ها
مرکز تقارن
مرکز شکل نقطه ای است که اگر هر نقطه از محیط شکل را به آن وصل کنیم و به اندازه خودش ادامه دهیم،دوباره به نقطه ای روی محیط شکل برسیم.
مثال
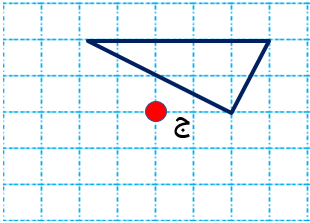
مرکز تقارن شکل زیر را پیدا کنید.
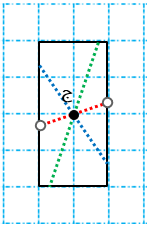
برای پیدا کردن قرینه هرنقطه نسبت به نقطه دیگر، نقطه اول را به نقطه دوم وصل می کنیم و پاره خطی تشکیل می شود که آن را به اندازه خودش در طرف دیگر نقطه دوم ادامه می دهیم.
مثال
قرینه نقطه الف نسبت به نقطه ج را رسم کنید.
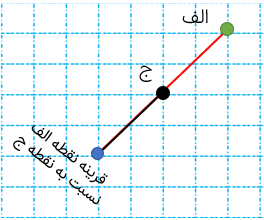
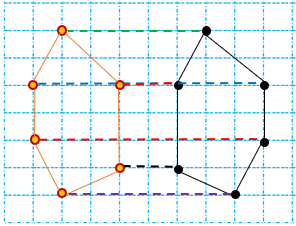
برای رسم قرینه یک شکل نسبت به یک نقطه ابتدا قرینه راس های آن را نسبت به نقطه داده شده به دست می آوریم و سپس آن ها را به هم وصل میکنیم تا قرینه شکل نسبت به نقطه به دست آید.
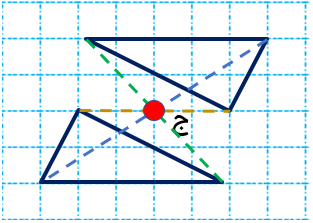
مثال
در مثال زیر قرینه شکل ،را نسبت به نقطه "ج" رسم کنید.
همه شکل ها دارای مرکز تقارن نیستند. مانند: انواع مثلث و ذوزنقه.
جزوات جامع پایه پنجم
جزوه جامع ریاضی پنجم
جزوه جامع علوم تجربی پنجم
جزوه جامع مطالعات اجتماعی پنجم
جزوه جامع فارسی پنجم
جزوه جامع نگارش پنجم
جزوه جامع هدیه های آسمانی پنجم
جزوه جامع آموزش قرآن پنجم
چند ضلعی ها
فصل 4 : تقارن و چندضلعی ها
چند ضلعی ها
در سال ،گذشته با چند ضلعی ها آشنا شدیم. اکنون به آشنایی بیشتر و ارائه نکاتی می پردازیم.
مجموع زاویه های داخلی هر مثلث 180 درجه می باشد. در این خصوص نوع مثلث مهم نیست.
مثال
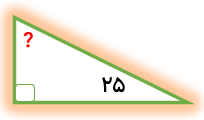
اندازه زاویه خواسته شده را پیدا کنید.
مثلث قائم الزاویه است. پس زاویه دیگر 90 درجه است.
در هر مثلث متساوى الساقين اندازه دو ضلع با هم برابر است و همچنین اندازه دو زاویه کنار قاعده با هم برابر است.
مثال
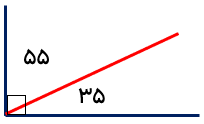
اندازه زاویه خواسته شده را حساب کنید.
چون مثلث متساوی الساقین است دو زاویه کنار قاعده با هم برابرند جمع دو زاویه با هم ۸۰ میباشد
۱۸۰-۱۰۰ = ۸۰
پس اندازه هر زاویه ۴۰ میشود:
۲÷80=۴۰
1 در هر مثلث متساوی الاضلاع، اندازه همه اضلاع برابر است و همچنین اندازه همه زاویه ها . با هم برابر است و هر کدام 60 درجه می باشد.
2 در هر مثلث قائم الزاویه اندازه یک ،زاویه همواره 90 دذرجه است بنابراین مجموع دو زاویه دیگر ، برابر با 90 درجه می باشد.
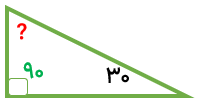
مثال
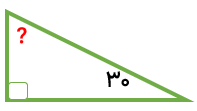
مثلث زیر قائم الزاویه است. اندازه زاویه خواسته شده را به دست آورید.
در مثلث قائم الزاویه، مجموع دو زاویه دیگر غیر از زاویه قائمه ۹۰ درجه است.
90=25=؟
65=25-90=؟
1 دو زاویه که مجموع آنها با هم 90 درجه باشد را متمم .گویند برای مثال دو زاویه زیر متمم هستند.
2 اگر دو زاویه با همدیگر تشکیل زاویه نیم صفحه دهند (یعنی مکمل یکدیگر باشند) در این صورت برای به دست آوردن زاویه نامشخص باید اندازه زاویه دیگر که) مشخص شده است را از 180 درجه کم کنیم.
نیمساز
فصل 4 : تقارن و چندضلعی ها
نیمساز
نیمساز زاویه نیم خطی است که زاویه را به دو قسمت مساوی تقسیم می کند.جهت رسم نیمساز ابتدا به کمک نقاله زاویه را اندازه میگیریم و نصف اندازه آن را مشخص کرده و علامت می.گذاریم اگر از نقطه علامت گذاری شده به راس ،زاویه یک خط راست رسم کنیم نیمساز زاویه رسم می شود.
مثال
در شکل زیر ابتدا زوايه (ب ج س) را اندازه می گیریم که 80 درجه میباشد. نصف آن می شود 40 درجه حالا زاویه 40 درجه را علامت زده و از راس ،زاویه به آن خطی وصل میکنیم. این خط نیمساز زاویه است.
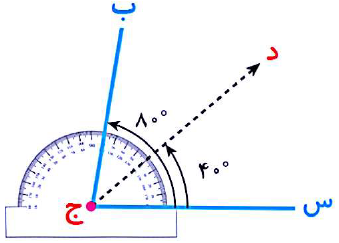
برای محاسبه اندازه دو زاویه ای که از نیمساز به دست می آیند کافیست اندازه زاویه را بر 2 تقسیم کنیم
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه پنجم- آزمون آنلاین تمامی دروس پایه پنجم
- گام به گام تمامی دروس پایه پنجم
- ویدئو های آموزشی تمامی دروس پایه پنجم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه پنجم
- فلش کارت های آماده دروس پایه پنجم
- گنجینه ای جامع از انشاء های آماده پایه پنجم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه پنجم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
مجموع زاویه های چند ضلعی ها
فصل 4 : تقارن و چندضلعی ها
مجموع زاویه های چند ضلعی ها
می دانیم مجموع زاویه های داخلی هر مثلث از هر نوعی که باشند برابر با 180 درجه می باشد. حالا با استفاده از ،این می توانیم زاویه های داخلی چند ضلعی ها را حساب کنیم فقط کافیست چند ضلعی ها را به چند مثلث تبدیل کنیم.
مثال
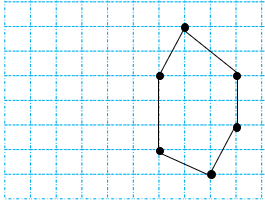
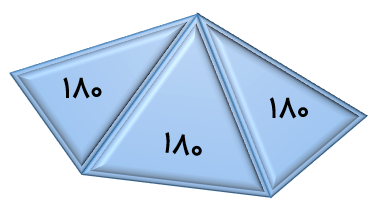
جمع زاویه های داخلی شکل زیر را حساب کنید.
با توجه به اینکه شکل 5 ضلعی می باشد و می توان 3 مثلث در آن درست ،کرد جواب به صورت زیر حساب میشود.
۵۴۰ = ۱۸۰× ۳ = مجموع زاویه های پنج ضلعی
مجموع زاویه های هر چهار ضلعی برابر با 360 درجه است.
مثال
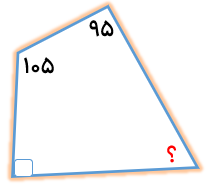
مقدار زاویه خواسته شده را حساب کنید.
شکل داده شده چهار ضلعی می باشد. لذا مجموع زاویه های داخلی 360 درجه می باشد. چون میتواند شامل دو تا مثلث شود زاوییه های داخلی هر مثلث هم 180 در جه است).
360=؟+95+105+90=مجموع زاویه های چهار ضلعی
1 در مربع مستطیل متوازی الاضلاع و لوزی مجموع دو زاویه کنار هم همواره 180 درجه است.
2 در لوزی و ،مربع قطرها نیمساز و بر هم عمود هستند.
3 در مربع و لوزی چهارضلع با هم برابرند ولی در متوازی الاضلاع و مستطیل فقط ضلع های روبرو برابرند.
4 در مربع لوزی متوازی الاضلاع و مستطیل قطرها همدیگر را نصف می کنند.
5 برای رسم انواع متوازی الاضلاع، با توجه به ویژگی آنها با داشتن اندازه قطرها، تنها کافیست به این نکته توجه کنیم که قطرها طوری رسم شوند که یکدیگر را نصف کنند.
جزوات جامع پایه پنجم
جزوه جامع ریاضی پنجم
جزوه جامع علوم تجربی پنجم
جزوه جامع مطالعات اجتماعی پنجم
جزوه جامع فارسی پنجم
جزوه جامع نگارش پنجم
جزوه جامع هدیه های آسمانی پنجم
جزوه جامع آموزش قرآن پنجم
اعداد اعشاری
فصل 5 : عددهای اعشاری
اعداد اعشاری
کسرهایی که مخرج آنها برابر با 10، 100 باشد را می توانیم به صورت . 1000اعشاری نمایش دهیم.
اعداد اعشاری دارای دو قسمت می باشد
الف قسمت اعشاری که در سمت راست خط اعشار (ممیز) قرار می گیرد.
مانند:
35/72 و 890/015 و 300/001
ب قسمت صحیح که در سمت چپ که در سمت چپ خط اعشار (ممیز) قرار می گیرد.
مانند:
\(430/002\,\,,\,\,30/25\,\,,\,\,24/129\)
اعداد اعشاری با یک رقم اعشار
فصل 5 : عددهای اعشاری
اعداد اعشاری با یک رقم اعشار
کسرهایی که مخرج آنها 10 می باشد را می توانیم به صورت عدد اعشاری با یک رقم اعشار نمایش دهیم.
\(\frac{7}{{10}} = 0/7\)
1 برای تبدیل عدد مخلوط که بخش کسری آن مخرج 10 دارد به عدد اعشاری باید قسمت صحیح را قبل از ممیز نوشته و قسمت کسری را به صورت اعشاری نمایش دهیم.
\(5\frac{8}{{10}} = 5 + \frac{8}{{10}} = 5 + 0/8 = 5/8\)
2 برای تبدیل عدد اعشاری با یک رقم اعشار به عدد مخلوط عدد قبل از ممیز همان قسمت صحیح و عدد بعد از ممیز نشان دهنده صورت کسر با مخرج 10 می باشد.
\(3/8 = 3 + 0/8 = 3 + \frac{8}{{10}} = 3\frac{8}{{10}}\)
3 اگر ۱۰ تا را با هم جمع کنیم برابر با ا می شود و برای اینکه بدانیم هر عدد از چند تا 0/1 یا \(\frac{1}{{10}}\) تشکیل شده، باید آن عدد را بر \(\frac{1}{{10}}\) تقسیم کنیم
مثال
8/4 از چند تا0/1 یا\(\frac{1}{{10}}\) تشکیل شده است؟
\(8/4 = \frac{{84}}{{10}} \Rightarrow \frac{{84}}{{10}} \div \frac{1}{{10}} = \frac{{84}}{{10}} \times \frac{{10}}{1} = 84\)
یعنی8/4 از ۸۴ تا\(\frac{1}{{10}}\) درست شده است
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه پنجم- آزمون آنلاین تمامی دروس پایه پنجم
- گام به گام تمامی دروس پایه پنجم
- ویدئو های آموزشی تمامی دروس پایه پنجم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه پنجم
- فلش کارت های آماده دروس پایه پنجم
- گنجینه ای جامع از انشاء های آماده پایه پنجم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه پنجم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
نمایش اعداد اعشاری با یک رقم اعشار
فصل 5 : عددهای اعشاری
نمایش به کمک شکل
در نمایش یک عدد اعشاری با یک رقم اعشار. بايد شكل واحد را به 10 قسمت مساوی تقسیم کنیم سپس به تعداد (0/1)های عدد از شکل رنگ کنیم.
به بیان دیگر باید به میزان عدد صحيح شكل واحد رسم کرده و به اندازه مقدار اعشاری بخشی از واحد ده قسمتی را رنگ کنیم.
مثال
عدد2/7 را بر روی شکل نشان دهید.
به کمک محور
در نمایش عدد اعشاری با یک رقم اعشار روی محور باید هر واحد را به 10 قسمت مساوی تقسیم کنیم و بعد به تعداد 0/1 های عدد روی محور جلو برویم.
به بیان دیگر به تعداد عدد صحیح از اعداد محور که ده تا یک دهم است انتخاب میکنیم و به تعداد اعشار از واحدهای کوچک یک دهمی انتخاب میکنیم.
مثال
عدد1/5 را روی محور نشان دهید.
هر عدد اعشاری بین دو عدد صحیح متوالی قرار دارد که آن دو عدد عبارتند از قسمت صحیح آن عدد اعشاری و عدد صحیح بعدی
مثال
عدد اعشاری3/6 بین کدام دو عدد صحیح قرار دارد؟
\(3 < 3/6 < 4\)
جزوات جامع پایه پنجم
جزوه جامع ریاضی پنجم
جزوه جامع علوم تجربی پنجم
جزوه جامع مطالعات اجتماعی پنجم
جزوه جامع فارسی پنجم
جزوه جامع نگارش پنجم
جزوه جامع هدیه های آسمانی پنجم
جزوه جامع آموزش قرآن پنجم
اعداد اعشاری با دو رقم اعشار
فصل 5 : عددهای اعشاری
اعداد اعشاری با دو رقم اعشار
کسرهایی که مخرج آنها برابر با 100 میباشد را می توان به صورت اعداد اعشاری با دو رقم اعشار نمایش داد.
\(\frac{{45}}{{100}} = 0/45\)
1 وقتی مخرج کسری 100 باشد و آن را به عدد اعشاری تبدیل ،کنیم در سمت راست ممیز دو رقم قرار می دهیم
2 اگر ۱۰۰ تا \(\frac{1}{{100}}\) را با هم جمع کنیم برابر با ۱ میشود پس برای اینکه بدانیم هر عدد از چند تا 0/01 یا\(\frac{1}{{100}}\) تشکیل شده، باید آن عدد را بر\(\frac{1}{{100}}\) تقسیم کنیم.
مثال
3/82 از چند تا 0/01 یا \(\frac{1}{{100}}\) تشکیل شده است؟
\(3/82 = \frac{{382}}{{100}} \Rightarrow \frac{{382}}{{100}} \div \frac{1}{{100}} = \frac{{382}}{{100}} \times \frac{{100}}{1} = 382\)
یعنی 3/82 از ۳۸۲ تا\(\frac{1}{{100}}\) درست شده است.
نمایش اعداد اعشاری با دو رقم اعشار
فصل 5 : عددهای اعشاری
نمایش به کمک شکل
در نمایش اعداد اعشاری با دو رقم اعشار باید شكل واحد را به 100 قسمت مساوی تقسیم کنیم. بعد به تعداد (0/10)های عدد از شکل رنگ کنیم.
مثال
عدد2/48 را با رسم شکل نشان دهید.
نمایش به کمک محور
در نمایش اعداد اعشاری با دو رقم اعشار روی محور، باید هر واحد را به 100 قسمت مساوی تقسیم کنیم و بعد به تعداد (0/10) های عدد، روی محور جلو می رویم.
مثال
عدد 2/37 را روی محور اعداد نمایش دهید.
عدد 2/37 بین ۲ و ۳ قرار دارد. عدد اعشاری فوق ۲ رقم اعشار دارد پس باید هر واحد به ۱۰۰ قسمت مساوی تقسیم شود. جهت سهولت در مرحله اول هر واحد را به ۱۰ قسمت کوچکتر تقسیم میکنیم. در مرحله دوم دوباره واحد کوچکتر که عدد ما در محدوده است را به ۱۰ قسمت تقسیم میکنیم.
هر عدد اعشاری با دو رقم اعشار، بین دو عدد با مرتبه های دهم متوالی قرار دارد.
مثال
عدد4/38 بين کدام دو عدد متوالی با مرتبه های دهم قرار دارد؟
\(4/3 < 4/38 < 4/4\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه پنجم- آزمون آنلاین تمامی دروس پایه پنجم
- گام به گام تمامی دروس پایه پنجم
- ویدئو های آموزشی تمامی دروس پایه پنجم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه پنجم
- فلش کارت های آماده دروس پایه پنجم
- گنجینه ای جامع از انشاء های آماده پایه پنجم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه پنجم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
اعداد اعشاری با سه رقم اعشار
فصل 5 : عددهای اعشاری
اعداد اعشاری با سه رقم اعشار
کسرهایی که مخرج آنها برابر با 1000 است را می توانیم به صورت عدد اعشاری با سه رقم اعشار نمایش دهیم.
\(\frac{{45862}}{{1000}} = 45/862\)
اگر ۱۰۰۰ تا\(\frac{1}{{1000}}\) را با هم جمع کنیم، برابر با ا می شود و برای اینکه بدانیم هر عدد از چند تا0/001 یا\(\frac{1}{{1000}}\) تشکیل شده، باید آن عدد را بر\(\frac{1}{{1000}}\) تقسیم کنیم.
مثال
4/739 از چند تا 0/001 یا\(\frac{1}{{1000}}\) تشکیل شده است؟
\(4/739 = \frac{{4739}}{{1000}} \Rightarrow \frac{{4739}}{{1000}} \div \frac{1}{{1000}} = \frac{{4739}}{{1000}} \times \frac{{1000}}{1} = 4739\)
یعنی 4/739 از 4739 تا\(\frac{1}{{1000}}\) درست شده است.
جزوات جامع پایه پنجم
جزوه جامع ریاضی پنجم
جزوه جامع علوم تجربی پنجم
جزوه جامع مطالعات اجتماعی پنجم
جزوه جامع فارسی پنجم
جزوه جامع نگارش پنجم
جزوه جامع هدیه های آسمانی پنجم
جزوه جامع آموزش قرآن پنجم
نمایش اعداد اعشاری با سه رقم اعشار
فصل 5 : عددهای اعشاری
به کمک محور
برای نمایش اعداد اعشاری با سه رقم اعشار باید هر واحد را به 1000 قسمت مساوی تقسیم کنیم. جهت سهولت این کار را در 3 مرحله انجام می دهیم. در مرحله اول واحد را به 10 قسمت تقسیم میکنیم هر قسمت یک دهم میباشد در حرحله دوم هر یک دهم را مجددا به 10 قسمت تقسیم میکنیم و در این صورت هر کدام از قسمت های جدید یک صدم می باشد. در مرحله سوم هر کدام از این قسمتها را مجددا به 10 قسمت تقسیم میکنیم که قسمت های یک صدم به دست می آید.
مثال
عدد1/247 را روی محور نشان دهید.
عدد مورد نظر بین ۱ و ۲ قرار دارد. عدد اعشاری فوق ۳ رقم اعشار دارد پس باید هر واحد به ۱۰۰۰ قسمت مساوی تقسیم شود.جهت سهولت در ۳ مرحله هر واحد را به ۱۰ قسمت کوچکتر تقسیم میکنیم.
جدول ارزش مکانی
در این جدول رقم های قبل از ممیز را به ترتیب یکان ،دهگان ،صدگان و ... نام گذاری می کنیم و رقم های بعد از ممیز (سمت راست ممیز ) را به ترتیب ،دهم صدم و هزارم نام گذاری می کنیم، جدول آن به صورت زیر می باشد:
مثال
عدد "بیست و سه و پانصد و چهار هزارم" را در جدول ارزش مکانی قرار دهید.
مقایسه اعداد اعشاری
فصل 5 : عددهای اعشاری
مقایسه اعداد اعشاری
در مقایسه دو عدد اعشاری عددی بزرگتر است که قسمت صحیح آن بزرگتر باشد
\(13/802\left\lfloor {} \right\rfloor 14/024\)
حالا اگر قسمت صحیح هر دو عدد اعشاری با هم برابر بود عددی بزرگتر است که رقم دهم آن بزرگتر باشد. اگر عدد صحیح و رقم دهم دو عدد نیز برابر بود عددی بزرگتر است که رقم صدم آن بزرگتر باشد. اگر عدد صحیح و رقم های دهم و صدم نیز با هم برابر بود، عددی بزرگتر است که هزارم آن بزرگتر باشد.
مثال
دو عدد زیر را با هم مقایسه کنید.
\(12/749\left\lfloor {} \right\rfloor 12/753\)
\(12/749\left\lfloor < \right\rfloor 12/753\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه پنجم- آزمون آنلاین تمامی دروس پایه پنجم
- گام به گام تمامی دروس پایه پنجم
- ویدئو های آموزشی تمامی دروس پایه پنجم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه پنجم
- فلش کارت های آماده دروس پایه پنجم
- گنجینه ای جامع از انشاء های آماده پایه پنجم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه پنجم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
گسترده نویسی
فصل 5 : عددهای اعشاری
گسترده نویسی
در کلاس چهارم گسترده نویسی اعداد را یاد گرفتیم. اکنون گسترده نویسی اعداد اعشاری تا سه رقم اعشار را یاد خواهیم گرفت.
بخش اعداد صحیح را مانند سال گذشته نوشته و بخش اعشاری را به تفکیک ، دهم صدم و هزارم جداگانه می نویسیم و بین همه آنها علامت جمع می گذاریم.
مثال
گسترده عدد 245/719 را بنویسید.
\(245/719 = 200 + 405 + 0/7 + 0/7 + 0/01 + 0/009\)
1 هر متر 100 سانتی متر و هر سانتی متر 10 میلی متر است لذا هر متر 1000 میلی متر است.
2 برای تبدیل واحدهای بزرگتر به واحدهای کوچکتر باید آنها را در عددی مطابق شکل زیر ضرب کنیم ولی برای تبدیل واحد کوچکتر به واحد بزرگتر باید آنها را مطابق شکل زیر به عددی تقسیم کنیم.
مثال
به سوالات زیر پاسخ دهید
الف 3/5 متر چند سانتی متر است؟
\(3/5 \times 100 = \frac{{35}}{{10}} \times 100\frac{{3500}}{{10}} = 350\)
ب 437 سانتی متر چند متر است؟
\(437 \div 100 = 437 \times \frac{1}{{100}} = \frac{{437}}{{100}} = 4/37\)
جزوات جامع پایه پنجم
جزوه جامع ریاضی پنجم
جزوه جامع علوم تجربی پنجم
جزوه جامع مطالعات اجتماعی پنجم
جزوه جامع فارسی پنجم
جزوه جامع نگارش پنجم
جزوه جامع هدیه های آسمانی پنجم
جزوه جامع آموزش قرآن پنجم
جمع اعداد اعشاری
فصل 5 : عددهای اعشاری
جمع اعداد اعشاری
اعداد اعشاری به یکی از روش های زیرین برای جمع اقدام میکنیم.
الف) به کمک شکل :
در این روش با انتخاب شکل واحد مناسب شكل هر یک از اعداد داده شده را رسم میکنیم و در نهایت شکل حاصل جمع را به دست می آوریم.
ب)به کمک محور:
در این روش با رسم یک فلش به اندازه عدد اول به جلو میرویم و در ادامه آن با رسم یک فلش دیگر به اندازه عدد دوم نیز به جلو می رویم. عددی که انتهای فلش دوم نشان می دهد جواب است.
مثال
جمع دو عدد اعشاری 3/3 و 2/5 را با کمک محور نمایش دهید.
ج) با هم مرتبه سازی :
در این روش ابتدا با اضافه کردن صفر های بی تاثیر تعداد ارقام اعشار هر دو عدد را یکسان کرده و سپس بدون در نظر گرفتن ممیز دو عدد را با هم جمع میکنیم و در نهایت همان ممیز را برای حاصل جمع در نظر میگیریم
مثال
جمع دو عدد اعشاری 12/47 و 3/8 را به روش هم مرتبه سازی به دست آورید.
\(\begin{array}{l}\,\,\,\,\,\,12/47 + 8/3 = 12/47 + 8/30\\ \Rightarrow 1247 + 830 = 2077\\ \Rightarrow 20/77\end{array}\)
د) روش تبدیل به کسر
در این روش ابتدا اعداد اعشاری را به کسر تبدیل می کنیم و کسرها را با هم جمع میکنیم بعد جواب به دست آمده را دوباره به عدد اعشاری تبدیل میکنیم.
هـ) جدول ارزش مکانی
این روش خود دارای 2 نوع میباشد نوع اول جمع مرحله ای است و ارقام یکی از ا اعداد را در جدول ارزش مکانی قرار می دهیم و عدد دیگر را از سمت چپ با عدد اول جمع می کنیم.
نوع دوم جمع در یک مرحله میباشد در این نوع باید ممیز را زیر ممیز نوشته و بقسه اعداد را با توجه به ارزش ،مکانی زیر هم بنویسیم و جمع کنیم.
اگر بخواهیم بدون اینکه جدو ارزش مکانی را رسم کنیم عملیات جمع زیر هم نویسی یک مرحله ای را انجام دهیم کافیست ممیزها را زیر هم بنویسیم و بعد مثل روش جدول ارزش مکانی عمليات جمع را انجام دهیم.
مقدار تقریبی اعداد اعشاری
فصل 5 : عددهای اعشاری
مقدار تقریبی اعداد اعشاری
مقدار تقریبی اعداد اعشاری را به دو روش زیر توان به دست آورد.
الف) حذف رقم های اعشاری :
در این روش بدون توجه به قسمت اعشاری عدد آن را حذف کرده و فقط قسمت صحيح عدد را به عنوان تقریب آن عدد در نظر میگیریم.
مثال
حاصل مقدار تقریبی اعشاری زیر را با روش حذف رقم های اعشاری به دست می آوریم.
\(\begin{array}{l}3/14 = 3\\27/39 = 27\\21/5 = 21\end{array}\)
ب) نزدیک ترین :
در این روش بررسی میکنیم ببینیم عدد اعشاری به کدام یک از دو عدد صحیح متوالی قبلی یا بعدی نزدیک تر است، آن را به عنوان مقدار تقریبی در نظر میگیریم.
اگر عدد اعشاری دقیقا وسط دو عدد صحیح متوالی قرار داشت عدد صحیح بزرگ تر را به عنوان مقدار تقریبی در نظر میگیریم.
مثال
حاصل مقدار تقریبی اعداد اعشاری زیر را با روش نزدیکی به یکان پیدا میکنیم.
\(\begin{array}{l}11/79 = 12\\25/169 = 2\\6/5 = 7\end{array}\)
1 اگر بخواهیم کسری را به عدد اعشاری تبدیل کنیم مخرج آن باید همواری یکی از اعداد 10 100، 100 و ... باشد ولی اگر مخرج کسر یکی از این اعداد ،نباشد باید صورت و مخرج آن را در عددی مناسب ضرب یا تقسیم کنیم تا مخرج به یکی از اعداد 10، 100، 1000 و ... تبدیل شود.
\(\frac{{{3_{ \times 2}}}}{{{5_{ \times 2}}}} = \frac{6}{{10}}\,\,\,\,\,\,\,\,\,\,\,\,,\,\,\,\,\,\,\,\,\,\,\,\frac{{{8_{ \div 2}}}}{{{{20}_{ \div 2}}}} = \frac{4}{{10}}\)
2 البته همه اعداد کسری را نمی توان به کسر با مخرج 10، 100، 1000 و ... تبدیل کرد و لذا همه اعداد کسری را نمیتوان به عدد اعشاری تبدیل کرد.
\(\frac{{11}}{{23}}\,\,,\,\,\frac{2}{7}\,\,,\,\,\frac{1}{3}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه پنجم- آزمون آنلاین تمامی دروس پایه پنجم
- گام به گام تمامی دروس پایه پنجم
- ویدئو های آموزشی تمامی دروس پایه پنجم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه پنجم
- فلش کارت های آماده دروس پایه پنجم
- گنجینه ای جامع از انشاء های آماده پایه پنجم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه پنجم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
تفریق اعداد اعشاری
فصل 5 : عددهای اعشاری
تفریق اعداد اعشاری
برای تفریق اعداد اعشاری از یکی از روشهای زیر می توانیم استفاده کنیم
الف) به کمک شکل :
در این روش با انتخاب یک شکل مناسب به عنوان شكل واحد شكل مربوط به عدد اعشاری اول را رسم میکنیم و به اندازه عدد اعشاری دوم از آن خط میزنیم و عدد مربوط به قسمت باقی مانده را می نویسیم.
ب) به کمک محور :
در این روش با رسم یک فلش از صفر به اندازه عدد اول به جلو میرویم و از آن جا به اندازه عدد دوم با رسم یک فلش ،دیگر قسمت ها را می شماریم و به عقب بر میگردیم. هر عددی که انتهای فلش دوم بود همان جواب ما می باشد.
مثال
حاصل تفریق زیر را با رسم محور به دست آورید.
\(2/35 - 1/04\)
می دانیم 1/7 یعنی 17 تا 0/1 می باشد. پس جهت تفریق باید 17 تا قسمت به سمت عقب برگردیم.
ج) روش تبدیل به کسر
در این روش اعداد اعشاری را به کسر تبدیل کرده و عملیات تفریق را انجام میدهیم در نهایت جواب را دوباره به عدد اعشاری تبدیل می می کنیم.
مثال
حاصل تفریق زیر را از طریق تبدیل به کسر انجام دهید.
\(43/7 - 15/21\)
\(\begin{array}{l}43/7 - 15/21 = 43\frac{7}{{10}} - 15\frac{{21}}{{100}}\\\\ = 43\frac{{70}}{{100}} - 15\frac{{21}}{{100}}\\\\28\frac{{49}}{{100}} = 28/49\end{array}\)
د) روش ارزش مکانی
نوع اول: انجام عملیات تفریق به صورت مرحله ای ؛ بدین صورت که ارقام بزرگتر را در جدول ارزش مکانی قرار داده و عدد کوچکتر را از سمت چپ از عدد اول کم میکنیم.
مثال
تفریق زیر را به روش زیر هم نویسی در جدول مکانی حل کنید.
\(5/127 - 2/481\)
جزوات جامع پایه پنجم
جزوه جامع ریاضی پنجم
جزوه جامع علوم تجربی پنجم
جزوه جامع مطالعات اجتماعی پنجم
جزوه جامع فارسی پنجم
جزوه جامع نگارش پنجم
جزوه جامع هدیه های آسمانی پنجم
جزوه جامع آموزش قرآن پنجم
ضرب اعداد اعشاری
فصل 5 : عددهای اعشاری
ضرب اعداد اعشاری
برای ضرب عدد صحیح در عدد اعشاری یا ضرب دو عدد اعشاری در یک دیگر از چند روش زیر استفاده می کنیم. به عددهایی که در هم ضرب می کنیم عامل ضرب میگویند و به جواب عملیات ضرب حاصل ضرب میگویند.
الف) به کمک شکل :
1_ ضرب عدد صحیح در عدد اعشاری: در این روش شکلی را به عنوان شکل واحد انتخاب میکنیم و بعد به اندازه عدد اعشاری رنگ می.کنیم حالا این کار را به تعداد عدد صحيح تکرار میکنیم.
2_ ضرب عدد اعشاری در عدد اعشاری: در این روش یک مستطیل در نظر میگیریم که عدد اعشاری بزرگتر مربوط به طول مستطیل و عدد اعشاری کوچکتر مربوط به عرض مستطیل می باشد.
حالا مساحت مستطیل را محاسبه میکنیم در نتیجه ضرب دو عدد اعشاری به دست می آید.
ب) به کمک محور :
برای ضرب یک عدد صحیح در یک عدد اعشاری یه کمک رسم محور به اندازه عدد اعشاری از صفر محور با رسم یک فلش جلو می رویم این کار را به تعداد عدد صحیح تکرار میکنیم. انتهای فلش آخر جواب حاصل ضرب می باشد
مثال
ج) روش تبدیل به کسر :
در این روش ابتدا اعداد اعشاری را به کسر ا تبدیل می.کنیم بعد کسرها را در هم ضرب می کنیم صورتها در هم ضرب میشوند و مخرج ها نیز در هم ضرب می شوند در انتها جواب به دست آمده را مجددا به عدد اعشاری تبدیل میکنیم.
مثال
\(2/3 \times 5/07 = \frac{{23}}{{10}} \times \frac{{507}}{{100}} = \frac{{11661}}{{1000}} = 11/661\)
چهار ضلعی ها
فصل 6 : اندازه گیری
چهار ضلعی ها
هر چهار ضلعی از برخورد چهار پاره خط تشکیل می شود.
متوازی الاضلاع
هر چهار ضلعی که در آن ضلع های رو به رو با هم موازی ،باشند متوازی الاضلاع نام دارد. مانند شکل های زیر:
خواص متوازی الاضلاع
ضلع های رو به رو با هم برابرند.
ضلعهای رو به رو با هم موازی اند.
زاویه های رو به رو با هم برابرند
قطرها همیشه یک دیگر را نصف می کنند
هر قطر، شکل را به دو مثلث مساوی تقسیم می کند.
مجموع زاویه های کنار هم 180 درجه است.
مساحت متوازی الاضلاع
با داشتن اندازه قاعده و ارتفاع نظیر آن با استفاده از فرمول ،زیر میتوانیم مساحت متوازی الاضلاع را به دست آوریم
ارتفاع × قاعده = مساحت متوازی الاضلاع
ارتفاع در متوازی الاضلاع میتواند در داخل یا خارج از شکل باشد
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه پنجم- آزمون آنلاین تمامی دروس پایه پنجم
- گام به گام تمامی دروس پایه پنجم
- ویدئو های آموزشی تمامی دروس پایه پنجم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه پنجم
- فلش کارت های آماده دروس پایه پنجم
- گنجینه ای جامع از انشاء های آماده پایه پنجم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه پنجم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
مستطيل و مربع
فصل 6 : اندازه گیری
مستطيل و مربع
مستطیل چهار ضلعی ای است که دارای چهار زاویه ی 90 درجه باشد همچنین میتوان گفت مستطيل نوعى متوازی الاضلاع می باشد.
خواص مستطيل
ضلع های رو به رو با هم برابرند.
ضلع های رو به رو با هم موازی اند.
همه زاویه ها با هم برابرند.
قطرها با هم برابرند
قطرها یک دیگر را نصف می کنند.
قطرها شکل را به دو مثلث مساوی تقسیم می کنند.
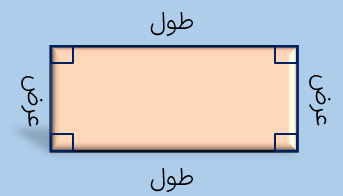
محیط و مساحت مستطیل
با داشتن طول و عرض یک مستطیل می توان محیط و مساحت آن را مطابق فرمول زیر حساب کرد.
عرض × طول = مساحت مستطیل
۲ ×(عرض + طول) = محیط مستطیل
مربع
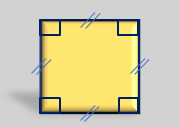
مربع چهار ضلعی ای است که دارای چهار ضلع برابر و چهار زاویه 90 درجه است همچنین میتوان گفت ؛ مربع نوعی مستطیل میباشد که دارای اضلاع برابر می باشد.
خواص مربع
ضلع های رو به رو موازی اند.
قطرها با هم برابرند
قطرها همدیگر را نصف می کنند
قطرها بر هم عمود هستند.
محیط و مساحت مربع
با داشتن اندازه ضلع ،مربع میتوان از طریق فرمول زیر محیط و مساحت آن را حساب کرد.
خودش× یک ضلع = مساحت مربع
۴ × یک ضلع = محیط مربع
جزوات جامع پایه پنجم
جزوه جامع ریاضی پنجم
جزوه جامع علوم تجربی پنجم
جزوه جامع مطالعات اجتماعی پنجم
جزوه جامع فارسی پنجم
جزوه جامع نگارش پنجم
جزوه جامع هدیه های آسمانی پنجم
جزوه جامع آموزش قرآن پنجم
لوزی
فصل 6 : اندازه گیری
لوزی
چهار ضلعی ای که دارای چهار ضلع مساوی است را لوزی می نامیم. همچنین میتوان گفت لوزی، نوعی متوازی الاضلاع است که ضلع های آن با هم برابر است.
خواص لوزی
اضلاع رو به رو با هم موازی اند.
زاویه های رو به رو با هم برابرند.
قطرها همدیگر را نصف می کنند.
قطرها بر هم عمودند.
مجموع زوایای کنار هم 180 درجه است.
مساحت لوزی
با داشتن اندازه دو قطر لوزی مساحت آن را طبق فرمول زیر محاسبه میکنیم:
۲ ×حاصل ضرب دو قطر = مساحت لوزی
مثال
قطر بزرگ یک لوزی 6 و قطر کوچک آن 4 می باشد. مساحت لوزی را حساب کنید.
۲ ÷حاصل ضرب دو قطر = مساحت لوزی
\((6 \times 4) \div 2 = 24 \div 2 = 12\) = مساحت لوزی
مربع، نوعی لوزی است که زاویه ها یا قطرهای آن با هم برابرند لذا مساحت مربع را میتوان از رابطه ی گفته شده برای مساحت لوزی به صورت فرمول زیر نیز محاسبه کرد.
۲ ÷خودش × قطر = مساحت مربع
مثال
در شکل زیر قطر مربع را داریم. حالا مساحت مربع زیر را به دست می آوریم.
۲ ÷خودش × قطر = مساحت مربع
\(\left( {6 \times 6} \right) \div 2 = 36 \div 2 = 18\)
اگر قطرهای یک لوزی را رسم کنیم به 4 مثلث قائم الزاویه با مساحت های برابر تقسیم میشود.
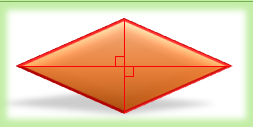
محیط لوزی
با داشتن اندازه یک ضلع لوزی میتوان فرمول را به صورت زیر به دست آورد:
۴ × یک ضلع = محیط لوزی
رسم لوزی
برای رسم ،لوزی کافیست اندازه دو قطر را داشته باشیم این دو قطر را طوری رسم می که دو قطر همدیگر را قطع کرده بر هم عمود باشند و همدیگر را نصف کرده باشند.
ذوزنقه
فصل 6 : اندازه گیری
ذوزنقه
هر چهار ضلعی ای که فقط دارای دو ضلع موازی باشد ذوزنقه نام دارد.
انواع ذوزنقه
ذوزنقه متساوى الساقين: ذوزنقه ای است که در آن دو ضلع غیر موازی با هم برابر هستند.
ذوزنقه قائم الزاويه: ذوزنقه ای است که دارای دو زاویه ی قائمه می باشد.
فقط در یک ذوزنقه ی متساوی الساقین است که قطرها با هم برابرند.
مساحت ذوزنقه
مساحت ذوزنقه از طریق فرمول زیر به دست می آید:
۲ ÷(ارتفاع ×مجموع دو قاعده)= مساحت ذوزنقه
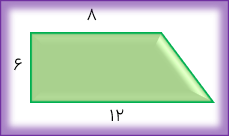
مثال
مساحت ذوزنقه زیر را حساب کنید.
۲ ÷(ارتفاع ×مجموع دو قاعده)= مساحت ذوزنقه
.\((8 + 12 \times 6) \div 2 = 120 \div 2 = 60\) =مساحت ذوزنقه
مساحت شکل های ترکیبی
گاهی اوقات با تقسیم بندی های مناسب می توانیم شکلها را به چند شکل شناخته شده که برای محاسبه مساحت آنها فرمول ارائه شده است تبدیل کنیم و مساحت آنها را یک به یک محاسبه کرده و در نهایت با هم جمع میکنیم تا مساحت کل شکل به دست آید.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه پنجم- آزمون آنلاین تمامی دروس پایه پنجم
- گام به گام تمامی دروس پایه پنجم
- ویدئو های آموزشی تمامی دروس پایه پنجم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه پنجم
- فلش کارت های آماده دروس پایه پنجم
- گنجینه ای جامع از انشاء های آماده پایه پنجم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه پنجم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
دایره
فصل 6 : اندازه گیری
دایره
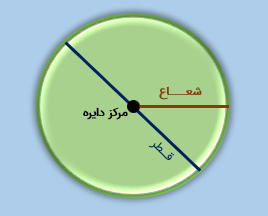
هر دایره شامل اجزای زیر می باشد:
مرکز : نقطه ای در وسط دایره که از تمام قسمت های آن به یک فاصله است.
شعاع: پاره خطی که مرکز را به محیط دایره وصل می کند.( شعاع نصف قطر است).
قطر: پاره خطی که دو نقطه از محیط دایره را به هم وصل میکند و از مرکز هم عبور می کند.(قطر دو برابر شعاع است).
هر دایره بی نهایت شعاع و قطر دارد.
محیط دایره
جهت محاسبه محیط دایره از فرمول زیر استفاده می کنیم:
۳/۱۴ × قطر = محیط دایره
به عدد3/14 که نسبت محیط دایره به قطر آن می باشد عدد پی نیز گفته می شود.
مثال
محیط دایره ای با شعاع 3 سانتی متر را حساب کنید.
۶ = ۲×۳ = ۲× شعاع = قطر
3/14 × قطر = محیط دایره
18/84=محیط دایره
1 هرگاه شعاع یا قطر یک دایره در عددی ضرب شود، محیط آن نیز در همان عدد ضرب می شود. به عنوان مثال اگر قطر یک دایره دو برابر شود محید آن نیز دو برابر میشود و یا اگر قطر یک دایره نصف شود محیط آن نیز نصف می شود.
2 برای تبدیل دقیقه به ساعت باید نسبت زیر را تشکیل دهیم.
مثال
یک ربع چه کسری از ساعت است؟
\(\frac{{{{15}_{ \div 3}}}}{{{{60}_{ \div 3}}}} = \frac{{{5_{ \div 5}}}}{{{{20}_{ \div 5}}}} = \frac{1}{4}\)
مقدار حرکت نوک عقربه دقیقه شمار در ساعت
اگر شعاع یا قطر صفحه ی ساعتی را داشته باشیم از رابطهی رو به رو میتوانیم میزان جا به جایی نوک عقربه ی دقیقه شمار را به دست آوریم.
مثال
اگر شعاع یک ساعت 10 سانتی متر باشد میزان جابجایی نوک عقربه ی دقیقه شمار از ساعت 2:45 به ساعت 3:00 چند سانتی متر است؟
میزان جابجایی 7/15 سانتی متر می باشد.
۲۰ = ۲×۱۰ = ۲ × شعاع = قطر
8/62=14/3×۲۰=14/3× قطر = محیط دایره
میزان جابجایی \(\frac{{15}}{{60}} \times 62/8 = \frac{1}{4} \times \frac{{628}}{{10}} = \frac{{157}}{{10}} = 15/7\)
اگر یک استوانه داشته باشیم، طول خط یا برچسب دور آن برابر با محیط دایره ی سقف یا کف آن می باشد.
محیط نیم دایره
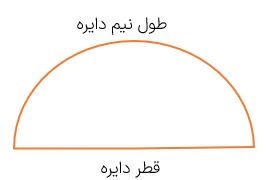
محیط یک نیم دایره از دو بخش تشکیل شده است:
الف) طول نیم دایره (نصف محیط دایره)
ب) قطر دایره
قطر دایره + طول نیم دایره = محیط شکل
جزوات جامع پایه پنجم
جزوه جامع ریاضی پنجم
جزوه جامع علوم تجربی پنجم
جزوه جامع مطالعات اجتماعی پنجم
جزوه جامع فارسی پنجم
جزوه جامع نگارش پنجم
جزوه جامع هدیه های آسمانی پنجم
جزوه جامع آموزش قرآن پنجم
حجم
فصل 6 : اندازه گیری
حجم
مقدار فضایی که یک جسم اشغال میکند را حجم آن جسم می گویند.
مكعب
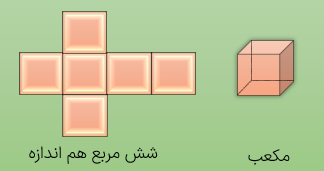
به جسم حاصل از تا کردن و به هم چسباندن شش مربع هم اندازهی مانند شکل زیر مکعب می گوییم.
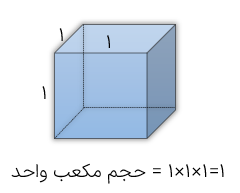
مكعب واحد
مكعب واحد مکعبی است که از شش مربع با اندازه 1 واحد درست شده باشد. اگر واحد اندازه گیری سانتی متر باشد حجم مكعب واحد که از شش مربع با اندازه هر ضلع 1 سانتی متر درست شده برابر با یک سانتی متر “مکعب" است.
واحد اندازه گیری حجم
برای اندازه گیری حجم یک جسم از مکعب واحد استفاده میکنیم
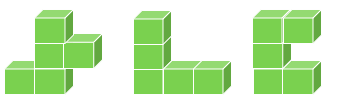
حجم یک جسم با تغییر شکل ظاهری آن تغییر نمی کند.
هر سه تا شکل از ۷ مکعب درست شده اند پس حجم همه ی آنها با هم برابر است
مكعب مستطيل
فصل 6 : اندازه گیری
مكعب مستطيل
دو نوع مكعب مستطیل داریم:
نوع اول: مستطیلی که از تا کردن و چسباندن 6 مستطیل که دو به دو با هم برابر هستند درست می شود.
نوع دوم: از تا کردن و جسباندن 2 مربع و 4 مستطیل هم اندازه درست میشود.
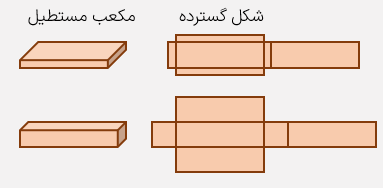
هر مکعب مستطیل دارای "طول" ، "عرض" و عدد"ارتفاع" است.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه پنجم- آزمون آنلاین تمامی دروس پایه پنجم
- گام به گام تمامی دروس پایه پنجم
- ویدئو های آموزشی تمامی دروس پایه پنجم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه پنجم
- فلش کارت های آماده دروس پایه پنجم
- گنجینه ای جامع از انشاء های آماده پایه پنجم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه پنجم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
حجم مكعب مستطيل
فصل 6 : اندازه گیری
حجم مكعب مستطيل
برای محاسبه حجم مكعب مستطیل از فرمول زیر استفاده می کنیم:
ارتفاع ×عرض×طول = حجم مکعب مستطیل
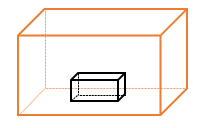
اگر مکعبی داخل مکعب دیگر باشد برای محاسبهی فضای بین آن دو مکعب باید ابتدا حجم مكعب بیرونی را حساب کنیم در مرحله دوم حجم مکعب داخلی را حساب میکنیم در نهایت حجم مکعب داخلی را از حجم مكعب بیرونی کم میکنیم:
حجم مکعب داخلی - حجم مکعب بیرونی = حجم فضای بین دو مکعب
مثال
در یک جعبه به شکل مکعب و با ابعاد 20 سانتی متر جعبه کوچکتری با ابعاد ،5، 20 و 30 سانتی متر قرار داده ایم فضای خالی بین جعبه و کارتن چند یانتی متر مکعب است؟
۸۰۰۰ = ۲۰×۲۰×۲۰ = حجم مکعب بزرگتر
۳۰۰۰ ۳۰×۲۰×۵ = حجم مکعب مستطیل کوچک
۵۰۰۰ = ۸۰۰۰-۳۰۰۰ = حجم فضای بین مکعب و مکعب مستطیل
اگر بخواهیم مکعب مستطیل بزرگی را با تعدادی مكعب مستطیل کوچک تر پر کنیم برای اینکه بدانیم چند تا مکعب مستطیل کوچک برای این کار نیاز داریم باید حم مكعب مستطیل بزرگتر را به حجم مکعب مستطیل کوچکتر تقسیم کنیم تا مشخص شود چند برابر آن است.
مثال
در یک کارخانه کبریت سازی هر 12 تا کبریت با ابعاد 1، 4 و 5 سانتی متر در یک جعبه قرار می گیرد. حجم جعبه چند سانتی متر مکعب است؟
سانتی متر مکعب ۲۰ = ۵×۴×۱ = حجم هر کبریت
سانتی متر مکعب ۲۴۰ = ۲۰×۱۲= حجم جعبه
برخی اجسام شکل مشخصی ندارند و به دست آوردن حجم آنها به سادگی امکان پذیر نیست. برای این کار ابتدا حجم مشخصی از آب را درون یک ظرف درجه بندی شده میریزیم و بعد جسم مورد نظر را داخل ظرف آب قرار میدهیم. تا آب روی جسم را بگیرد. حالا بررسی میکنیم سطح آب چقدر بالاتر ر آمده است.
مثال
ظرف به شکل مكعب مستطيل داریم که طول و عرض آن به ترتیب 2 و 10 می باشد ابتدا ارتفاع آب 5 بوده است وقتی سنگی را داخل آن می اندازیم، ارتفاع آب به 7 می رسد. حجم سنگ را حساب کنید.
سانتی متر ۲ = 7-5= تغییر ارتفاع آب
سانتی متر مکعب ۴۰=۲×۱۰×۲ = حجم
جزوات جامع پایه پنجم
جزوه جامع ریاضی پنجم
جزوه جامع علوم تجربی پنجم
جزوه جامع مطالعات اجتماعی پنجم
جزوه جامع فارسی پنجم
جزوه جامع نگارش پنجم
جزوه جامع هدیه های آسمانی پنجم
جزوه جامع آموزش قرآن پنجم
گنجایش
فصل 6 : اندازه گیری
گنجایش
مقدار مایعی که درون یک ظرف قرار میگیرد را گنجایش آن ظرف می نامند. برای مثال اگر یک ظرف برای پر شدن از آب برای مثال اگر یک ظرف برای پر شدن از آب نیاز به 5 لیتر آب داشته باشد، می گوییم گنجایش این ظرف 5 لیتر میباشد.
شباهت و تفاوت حجم و گنجایش
شباهت: روش محاسبه حجم و گنجایش از نظر فرمول یکسان میباشد
تفاوت: حجم جسم مقدار فضایی است که جسم اشغال کرده است ولی گنجایش یک جسم مقدار فضای خالی درون یک جسم است.
مثال
فرض کنیم یک ظرف تواند حداكثر 5 لیتر آب را در خود جای دهد و اکنون 3 لیتر آب در آن باشد یعنی هنوز امکان اضافه کردن 2 لیتر دیگر آب جهت پر شدن داشته باشد. در این صورت میگوییم حجم ظرف 5 لیتر است و گجایش آن 2 لیتر می باشد.
واحدهای اندازه گیری مایعات
جهت اندازه گیری مایعات از واحدهای زیر استفاده می شود.
الف) متر مكعب
اگر ظرفی به شکل مکعب که هر ضلع آن 1 متر باشد را در نظر بگیریم گنجایش آن یک متر مکعب خواهد بود.
ب) ليتر
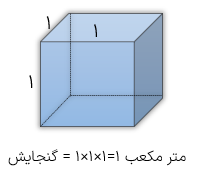
اگر ظرفی به شکل مکعب که هر ضلع آن 10 سانتی متر باشد را در نظر بگیریم، گنجایش آن یک لیتر خواهد بود.
اگر ظرفی به شکل مکعب که هر ضلع آن 10 سانتی متر باشد را در نظر بگیریم، گنجایش آن یک لیتر خواهد بود.
سانتی متر مکعب ۱۰۰۰=۱۰×۱۰×۱۰ = گنجایش
سانتی متر مکعب ۱۰۰۰=۱ لیتر
ج) سی سی (میلی لیتر)
اگر ظرفی به شکل مکعب که هر ضلع آن 1 سانتی متر باشد را در نظر بگیریم، گنجایش آن یک سی خواهد بود.
سانتی متر مکعب ۱ = 1×1×1= گنجایش
سانتی متر مکعب ۱ = ۱ سی سی (میلی لیتر)
مثال
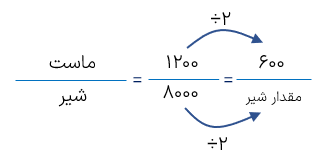
اگر از هر 8 لیتر شیر بتوانیم 1/2 لیتر ماست تهیه کنیم برای تهیه 600 سی سی ماست لیتر شیر نیاز داریم؟
۸۰۰۰ سیسی = ۸ لیتر
۱۲۰۰ سی سی =1/2 لیتر
مقدار شیر \( = 8000 \div 2 = 4000\,cc\,\, = 4L\)
امار
فصل 7 : آمار و احتمال
آمار
علم آمار علم جمع آوری اطلاعات سازماندهی و بررسی آنها میباشد این اطلاعات را داده های آماری می.نامیم هدف علم آمار این است که از این داده،ها نتیجه گیری قابل فهمی ارائه دهند.
جدول داده ها
برای آن که دادههای عددی جمع آوری شده به راحتی مورد استفاده قرار ،گیرند، آنها را در یک جدول نظام دار قرار میدهیم که به این جدول جدول داده ها می گویند.
نمودار اطلاعات
برای بررسی بهتر داده های عددی می توان نمودار آنها را رسم کرد. ویژگی نمودار این است که اطلاعات را به صورتی خلاصه بیان می کند و با یک نگاه کلی می توان خلاصه ای از وضعیت اطلاعات را درک کرد ولی با نگاه کلی به جدول داده ها نمی توان این اطلاعات را درک کرد.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه پنجم- آزمون آنلاین تمامی دروس پایه پنجم
- گام به گام تمامی دروس پایه پنجم
- ویدئو های آموزشی تمامی دروس پایه پنجم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه پنجم
- فلش کارت های آماده دروس پایه پنجم
- گنجینه ای جامع از انشاء های آماده پایه پنجم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه پنجم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
نمودار ستونی
فصل 7 : آمار و احتمال
نحوه ی رسم نمودار ستونی
نحوه ی رسم به شرح زیر است:
1 دو محور عمود بر هم رسم میکنیم .
2 روی محور افقی موضوع داده ها و روی محور اطلاعات عددی را می نویسیم
3 حالا ستون هایی را با ارتفاع هایی متناسب با مقدار عددی داده های محور عمودی رسم می کنیم.
کاربرد نمودار ستونی
این نمودا برای مقلیسه مقدار واقعی داده ها استفاده می شود.
بیشترین و کمترین دادهها نیز با توجه به ارتفاع ستون ها با یک نگاه کلی تشخیص داده می شود.
مثال
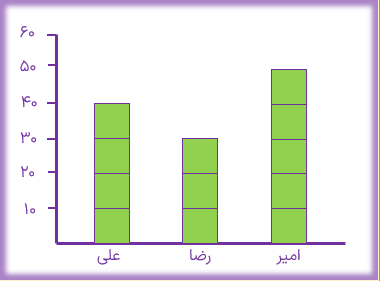
تعداد صفحات خوانده شده توسط امیر رضا و علی به ترتيب 50، 30 و 40 صفحه می باشد. نمودار ستونی را رسم کنید.
در نمودار ستونی اعداد روی محور عمودی لازم نیست حتما از صفر شروع و یک واحد اضافه شوند بلکه با توجه به اطلاعات عددی داده شده میتوان اعداد را از عددی غیر از صفر شروع و با فاصله های مناسب انتخاب کرد.
انجام مقایسه در نمودار ستونی
برای بررسی اطلاعات مربوط به چند موضوع مختلف در یک نمودار ستونی می توان ستون های مربوط به هر موضوع را در کنار هم و با رنگ های متفاوت نمایش داد.
مثال
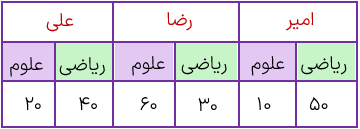
نمرات علوم و ریاضی 3 نفر از دانش آموزان به صورت زیر می.باشد نمودار مقایسه ای آن را رسم کنید.
جزوات جامع پایه پنجم
جزوه جامع ریاضی پنجم
جزوه جامع علوم تجربی پنجم
جزوه جامع مطالعات اجتماعی پنجم
جزوه جامع فارسی پنجم
جزوه جامع نگارش پنجم
جزوه جامع هدیه های آسمانی پنجم
جزوه جامع آموزش قرآن پنجم
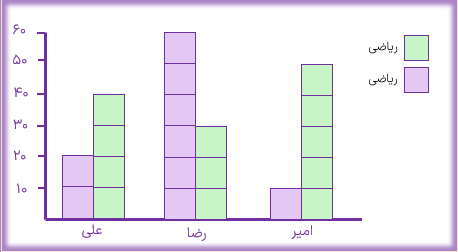
نمودار دایره ای
فصل 7 : آمار و احتمال
نحوه رسم نمودار دایره ای
1 دایره ای رسم کرده و با توجه به مجموع تعداد اطلاعات ،عددی آن را به قسمت های مساوی تقسیم میکنیم
2 با نوشتن رابطهی نسبت تعداد هر داده به تعداد کل داده ها درصد مربوط به هر مجموع داده را محاسبه میکنیم .
3 به کمک نسبت هر داده به کل داده ها، بخشی از دایره که مربوط به آن داده است را رنگ می کنیم و سپس آن را بر حسب درصد بیان میکنیم.
کاربرد نمودار دایره ای
بعضی اطلاعات مشخص می کنند که چگونه ا یک مقدار مشخص به بخشهای کوچک تر تقسیم می شود در این موارد میتوان از نمودار دایره ای استفاده کرد و سهم هر بخش را نشان داد. نمودار دایره ای برای نشان دادن تعداد داده ها نسبت به کل داده ها استفاده می شود.
روش های جمع آوری داده
فصل 7 : آمار و احتمال
روش های جمع آوری داده
الف) مشاهده کردن
مثل داده های مربوط به دانش آموزانی که لباس ورزشی پوشیده اند
ب) پرسیدن
مثلا دادههای مربوط به افرادی که حافظ قرآن هستند.
ج) استفاده از پرسش نامه
مثل داده های مربوط به اعلام نظر افراد در علاقه به سریالهای تلویزیونی با پرکردن فرم های نظرسنجی
د) مراجعه به کتاب ها یا سایت ها
مثل اطلاعات مربوط به جمعیت کشورها که با مراجعه به سایتهای اینترنتی و کتاب ها قابل دستیابی هستند.
هـ) اندازه گیری
مثل داده های مربوط به اطلاعات دمای هوای یک شهر در ساعتهای مختلف که با اندازه گیری قابل دستیابی است.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه پنجم- آزمون آنلاین تمامی دروس پایه پنجم
- گام به گام تمامی دروس پایه پنجم
- ویدئو های آموزشی تمامی دروس پایه پنجم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه پنجم
- فلش کارت های آماده دروس پایه پنجم
- گنجینه ای جامع از انشاء های آماده پایه پنجم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه پنجم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
میانگین
فصل 7 : آمار و احتمال
میانگین
به میانگین تعدادی ،داده مقدار "متوسط" یا "معدل" نیز گفته می شود.
محاسبه ی میانگین
برای به دست آوردن میانگین داده های عددی باید ابتدا تمام دادههای عددی را با هم جمع بعد این مقدار را بر تعداد دادههای عددی تقسیم می کنیم
مثال
فرض میکنیم چهار ظرف داریم که آن ها به ترتیب 1 و 2 و 5 و 8 لیتر آب دارند اگر آب ها را به طور مساوي بين ظرف ها تقسیم کنیم به طور متوسط میانگین در هر ظرف چند لیتر آب خواهد بود.
براي محاسبه میانگین میتوان حجم آب ظرف ها را با هم جمع و بر تعداد ظرف ها تقسیم کرد.
1+2+5+8=16
4=4÷16
ما اگر تعداد و میانگین یکسری از اعداد را داشته باشیم با توجه به تعداد و با محاسبه ی مجموع اعداد میتوانیم مقدارهای ممکن برای آن اعداد را حدس بزنیم.
مثال
در سه حالت مختلف 4 عدد بنویسید که میانگین آنها 7 شود.
۲۸ = ۷×۴ = میانگین× تعداد = مجموع
در ۴ حالت مختلف، جمع ۴ عدد باید ۲۸ شود
۵ و ۶ و ۷ و ۱۰
۵ و ۶ و ۸ و ۹
۴ و ۵ و ۱۳۹۶
۴ و ۵ و ۷ و ۱۲
1 اگر چند عدد متوالی داشته باشیم که تعداد آنها فرد باشد عدد ،وسطی میانگین آنها می باشد
2 اگر چند عدد متوالی داشته باشیم که تعداد آنها زوج باشد، دو عددی که وسط قرار می گیرند را انتخاب میکنیم و میانگین آن دو را حساب می کنیم جواب هر چه شد با میانگین کل اعداد برابر است.
جزوات جامع پایه پنجم
جزوه جامع ریاضی پنجم
جزوه جامع علوم تجربی پنجم
جزوه جامع مطالعات اجتماعی پنجم
جزوه جامع فارسی پنجم
جزوه جامع نگارش پنجم
جزوه جامع هدیه های آسمانی پنجم
جزوه جامع آموزش قرآن پنجم
احتمال
فصل 7 : آمار و احتمال
احتمال
برای رخ دادن یک موضوع حالتهای مختلفی را می توان پیش بینی ،نمود به این پیش بینی ها احتمال رخ دادن آن موضوع میگویند برخی از این احتمال ها به شرح زیر است:
به طور حتم اتفاق می افتد.
به احتمال بیش تر
به احتمال برابر
به احتمال کمتر
به طور حتم اتفاق نمی افتد
مثال
احتمال آمادن عدد 9 در پرتاب تاس:
به طور حتم اتفاق نمی افتد
احتمال خط آمدن در صورت پرتاب سکه:
به احتمال برابر اتفاق می افتد.
انسان بیش تر از 90 سال عمر کند:
احتمال کمتر اتفاق می افتد.
مثال
فرض کنیم کیسه هایی با مهره هایی مطابق شکل های زیر داریم. حالا احتمالات مختلف را مطابق تصاویر زیر بررسی میکنیم.
احتمال اینکه از کیسه مهره قرمز بیرون بیاید؟
به طور حتم اتفاق نمی افتد؛ زیرا مهره قرمز در کیسه وجود ندارد
احتمال اینکه از کیسه مهره قرمز بیرون بیاید؟
به احتمال بیشتر اتفاق می افتد؛زیرا مهره قرمز در کیسه بیشتر است
احتمال اینکه از کیسه مهره قرمز بیرون بیاید؟
به طور حتم اتفاق می افتد؛ زیرا همه مهره ها قرمز هستند.
احتمال اینکه از کیسه مهره قرمز بیرون بیاید؟
به احتمال کمتر اتفاق می افتد؛ زیرا از سه مهره فقط یکی قرمز است.
احتمال اینکه از کیسه مهره قرمز بیرون بیاید؟
به احتمال برابر اتفاق می افتد؛ زیرا نیمی از مهره ها قرمز است
بازی شانسی
فصل 7 : آمار و احتمال
بازی شانسی
بازی ای که نتیجه برد یا باخت در آن، بر اساس شانس و اتفاق ،باشد بازی شانسی است.
بازی شانسی عادلانه
اگر در یک بازی شانسی احتمال برنده شدن بازیکنان مساوی باشد بازی را عادلانه می نامیم
مثال
برای مثال اگر تاسی را پرتاب کنیم و اعلام کنیم اگر عدد زوج آمد نفر اول برنده است و اگر عدد فرد آمد نفر دوم برنده ،است این بازی را عادلانه می نامیم ؛ زیرا از 6 تا حالت تاس 3 تا زوج است و 3 تا فرد است و احتمال زوج و فرد برابر است.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه پنجم- آزمون آنلاین تمامی دروس پایه پنجم
- گام به گام تمامی دروس پایه پنجم
- ویدئو های آموزشی تمامی دروس پایه پنجم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه پنجم
- فلش کارت های آماده دروس پایه پنجم
- گنجینه ای جامع از انشاء های آماده پایه پنجم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه پنجم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
نمودار خط شکسته
فصل 7 : آمار و احتمال
نحوه ی رسم نمودار خط شکسته
1 دو محور عمود بر هم رسم میکنیم.
2 روی محور افقی نام داده ها را می نویسیم و روی محور عمودی اطلاعات عددی داده ها را می نویسیم.
3 از روی نام داده،ها یک خط عمودی و از روی مقدار عددی دادهها یک خط تفقی رسم میکنیم محل برخورد این دو خط را با یک نقطه نشان می دهیم.
4 نقاط نشان داده شده را به ترتیب با اره خط های کوچک به هم وصل میکنیم.
کاربرد نمودار خط شکسته
نمودار خط شکسته برای تمایش میزان تغییرات چیزی در مدت زمانی مشخص استفاده میشود برای مثال میزان تغییرات قیمت یک جنس در چند روز متوالی را میتوان با نمودار خط شکسته نشان داد.
در نمودار خط ،شکسته به نکات زیر دقت کنید.
مثال
دمای هوای یک شهر در ساعت های مختلف در جدول دادههای زیر آمده است. نمودار خط شکسته آن را رسم کنید.
