درسنامه کامل ریاضی دهم
تعداد بازدید : 496.9kخلاصه نکات ریاضی دهم - درسنامه شب امتحان ریاضی دهم - جزوه شب امتحان ریاضی دهم نوبت اول
مجموعه های اعداد
فصل 1 : مجموعه، الگو و دنباله
مجموعه های اعداد
ابتدایی ترین مجموعه مورد استفاده بشر همان طور که می دانید مجموعه اعداد طبیعی بوده است. مجموعه اعداد طبیعی بصورت زیر است:
\(\mathbb{N} = \{ 1,2,3,...\} \)
لازم است خاصیتی جالب را در مورد مجموعه \(\mathbb{N}\) معرفی کنیم. چنانچه دو عدد دلخواه از اعداد طبیعی را باهم جمع کنیم حاصل باز هم عدد طبیعی است بعنوان مثال :
\(1 + 3 = 4 \in \mathbb{N}\)
در حالت کلی اگر a، b دو عدد طبیعی باشند واضح است که \(a + b\) نیز عددی طبیعی است. این خاصیت را اصطلاحا بسته بودن \(\mathbb{N}\) نسبت به عمل + می نامیم.
خاصیت بسته بودن برای اعداد طبیعی در اعمال ضرب، تقسیم و توان نیز صادق است ولی در عمل تفریق صادق نیست.
مثال
1 مجموعه \(A = \{ {2^n}|n \in \mathbb{N}\} \) را در نظر بگیرید. نشان دهید این مجموعه نسبت به عمل توان بسته است.
\(\begin{array}{l}n \in \mathbb{N} \to n = \{ 1,2,3,...\} \\ \to {2^n} \in \mathbb{N}\end{array}\)
عدد 2 به هر تعداد در خودش ضرب شود همچنان جزو اعداد طبیعی خواهد ماند.
2 آیا مجموعه \(A = \{ {a^2} - b|a,b \in \mathbb{N}\} \) نسبت به اعداد طبیعی بسته است؟ در صورت منفی بودن جواب مثال نقضی ارائه دهید.
خیر زیرا؛
\(\begin{array}{l}a,b \in \mathbb{N} \to a,b = \{ 1,2,3,...\} \\a = 2,b = 5 \to {a^2} - b = {2^2} - 5 = 4 - 5 = - 1\\ \to {a^2} - b = - 1 \to - 1 \notin \mathbb{N}\end{array}\)
حال با توجه به مثال بالا می توان متوجه ضعف مجموعه اعداد طبیعی شد. \(\mathbb{N}\) نسبت به تفریق بسته نیست. این بزرگترین ضعف \(\mathbb{N}\) است. زمانی که بشر برای معاملات خود متوجه شد که مقروض بودن را نمی توان با اعداد طبیعی نمایش داد خلاء اعداد صحیح را حس کرد و مجبور شد اعداد صحیح را بکار بگیرد.
مجموعه اعداد صحیح را که با نماد \(\mathbb{Z}\) نشان می دهیم عبارت است از :
\(\mathbb{Z} = \{ ..., - 2, - 1,0,1,2,...\} \)
اینکه اعداد صحیح را با حرف \(\mathbb{Z}\) نمایش می دهند به خاطر کلمه Zahlen می باشد که لغتی آلمانی است. اعداد صحیح نیز به نوبه ی خود دارای ضعف بسته نبودن نسبت به عمل تقسیم بود به عنوان مثال دقت کنید که :
\(\frac{2}{4} = \frac{1}{2} = 0/5 \notin \mathbb{Z}\)
برای برطرف کردن این ضعف \(\mathbb{Z}\) مجموعه ای مورد نیاز بود که شامل تمام کسرهای ممکن که می توان به کمک اعداد صحیح ساخت باشد. این مجموعه را اعداد گویا می نامیم و بصورت زیر تعریف می کنیم:
مجموعه اعداد گویا را که با نماد \(\mathbb{Q}\) نشان می دهیم (\(\mathbb{Q}\) حرف اول کلمه Quotient به معنای خارج قست) بصورت زیر تعریف می کنیم:
\(\mathbb{Q} = \left\{ {\frac{a}{b}|a,b \in \mathbb{Z},b \ne 0} \right\}\)
مجموعه اعداد گویا کوچکترین مجموعه ای است که نسبت به هر چهار عمل اصلی بسته است، با این حال همین مجموعه هم بی نقص نیست.
می دانیم که قطر مربعی به ضلع یک عددی غیر گویا یا اصم است. این عدد عددی نیست جز \(\sqrt 2 \).
می توان ثابت کرد که \(\sqrt 2 \) را نمی توان بصورت یک کسر نوشت به عبارت بهتر به ازای هر دو عدد صحیح دلخواه a و b همواره داریم: \(a,b \ne \sqrt 2 \)
مجموعه اعداد گنگ را با نماد \(\mathbb{Q}'\) نشان می دهیم. یکی دیگر از اعداد گنگی، که قدمت زیادی دارد عدد  است. نسبت محیط دایره به قطر آن عدد \(\pi \) است. (داستان پیدایش عدد پی با مسأله تربیع دایره در ارتباط تنگاتنگ است.)
است. نسبت محیط دایره به قطر آن عدد \(\pi \) است. (داستان پیدایش عدد پی با مسأله تربیع دایره در ارتباط تنگاتنگ است.)
تاکنون با مجموعه های \(\mathbb{Q}',\mathbb{Q},\mathbb{Z},\mathbb{N}\) آشنا شده اید. رابطه بین سه مجموعه اول به صورت زیر است:
\(\mathbb{N} \subseteq \mathbb{Z} \subseteq \mathbb{Q}\)
در این رابطه مجموعه \(\mathbb{Q}'\) چه جایگاهی دارد؟ حال می توان مجموعه اعداد حقیقی را هم تعریف کرد.
مجموعه اعداد حقیقی را که با نماد \(\mathbb{R}\) نشان می دهیم برابر است با :
\(\mathbb{R} = \mathbb{Q} \cup \mathbb{Q}'\)
(علامت \( \cup \) به معنای اجتماع است.)
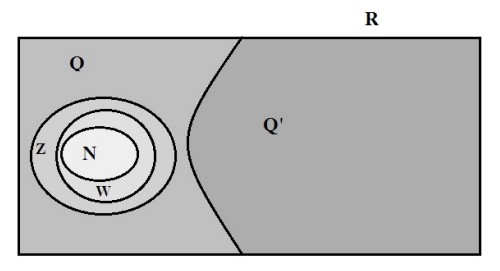
رابطه ی بین مجموعه اعداد
متناظر به هر عدد حقیقی نقطه ای روی محور اعداد حقیقی وجود دارد. در اشکال زیر موقعیت برخی از اعداد روی محور نشان داده شده است.
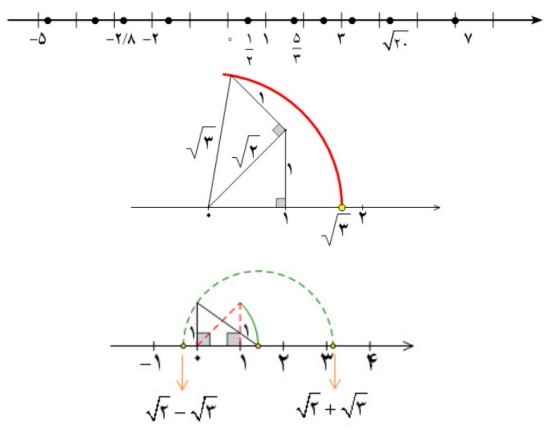
نمایش اعداد گویا و گنگ روی محور اعداد
اگر به شکل با دقت نگاه کنید متوجه خواهید شد که این شکل راه حل بسیار زیبایی را به شما معرفی کرده است و ارزش آن بیش از یک شکل ساده است. سرانجام آخرین مجموعه از اعداد را که بزرگتر از \(\mathbb{N}\) و کوچکتر از \(\mathbb{Z}\) است را معرفی می کنیم. مجموعه اعداد حسابی که با نماد W نشان می دهیم عبارتست از:
\(W = \{ 0,2,3,...\} \)
جاهای خالی را با مجموعه مناسب کامل کنید.
الف \(\mathbb{R} - \mathbb{Q} = \)
\(\mathbb{R} - \mathbb{Q} = \mathbb{Q}'\)
ب \(\mathbb{Z} - W = \)
\(\mathbb{Z} - W = \{ ..., - 2, - 1\} \)
پ \(\mathbb{N} - W = \)
\(\mathbb{N} - W = \emptyset \)
ت \(\mathbb{Q}' - \mathbb{Q} = \)
\(\mathbb{Q}' - \mathbb{Q} = \mathbb{Q}'\)
تهیه کننده: فرهاد صمدی
- آزمون آنلاین تمامی دروس پایه دهم
- گام به گام تمامی دروس پایه دهم
- ویدئو های آموزشی تمامی دروس پایه دهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه دهم
- فلش کارت های آماده دروس پایه دهم
- گنجینه ای جامع از انشاء های آماده پایه دهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه دهم
بازه های اعداد حقیقی
فصل 1 : مجموعه، الگو و دنباله
بازه های اعداد حقیقی
برای ورود به مطلب و آشنایی با بازه ها دو نامعادله زیر را در نظر بگیرید:
1)
\(x = {-b \pm \sqrt{b^2-4ac} \over 2a} - 1 \le \frac{{2x + 1}}{3}\langle 3\)
2)
\(3x + 1\langle 7\)
با حل این دو نامعادله مجموعه جواب معادله شماره ١ عبارتست از \(\{ x \in \mathbb{R}| - 2 \le x\langle 4\} \) و مجموعه جواب معادله شماره ٢ عبارت است از \(\{ x \in \mathbb{R}|x\langle 2\} \).
آیا می توان مجموعه جواب را با نمادی ساده تر از مجموعه های فوق نوشت؟ جواب مثبت است. بازه ها جواب گوی ما برای این ساده نویسی هستند. مجموعه جواب نامعادله ١ بازه ی \([ - 2,4)\) است و مجموعه جواب نامعادله شماره ٢ بازه ی بی کران \(\left( { - \infty ,2} \right)\) است. حال به سراغ تعریف بازه ها می رویم.
یک بازه، زیر مجموعه ای از اعداد حقیقی است که بصورت های زیر تعریف می شود:
بازه ی باز:
\(\left( {a,b} \right) = \{ x \in \mathbb{R}|a\langle x\langle b\} \)
بازه ی نیم باز:
\(\left[ {a,b} \right) = \{ x \in \mathbb{R}|a \le x\langle b\} \)
بازه ی بسته:
\(\left[ {a,b} \right] = \{ x \in \mathbb{R}|a \le x \le b\} \)
بازه ی باز بی کران:
\(\left( {a, + \infty } \right) = \{ x \in \mathbb{R}|a\rangle x\} \)
بازه ی نیم باز بی کران:
\(\left[ {a, + \infty } \right) = \{ x \in \mathbb{R}|a\rangle x\} \)
بازه ی باز بی کران:
\(\left( { - \infty ,a} \right) = \{ x \in \mathbb{R}|a\langle x\} \)
بازه ی نیم باز بی کران:
\(\left( { - \infty ,a} \right] = \{ x \in \mathbb{R}|a\langle x\} \)
اغلب بجای اصطلاح نیم باز از اصطلاح نیم بسته هم استفاده می شود. نماد ∞ که بی نهایت خوانده می شود (مثبت بی نهایت یا منفی بی نهایت) یک عدد حقیقی نیست فقط نمادی است برای اینکه نشان دهیم بازه بی کران است. یعنی هر عددی خواه بسیار بزرگ یا خواه بسیار کوچک در این بازه ها می تواند وجود داشته باشد.
در اشکال زیر چند بازه را بعنوان مثال روی محور اعداد حقیقی نمایش داده ایم.

درست و نادرست را بررسی کنید و جاهای خالی را با عبارت مناسب پر کنید.
الف \(3 \in \left[ { - 1,\sqrt {10} } \right)\)
درست زیرا؛
\(\sqrt {10} = 3/16 \to 3 \in \left[ { - 1,\sqrt {10} } \right)\)
ب \(\frac{1}{{\sqrt 2 }} \in \left( {0,1} \right]\)
درست زیرا؛
\(\begin{array}{l}\sqrt 2 = 1/41 \to \frac{1}{{\sqrt 2 }} = \frac{1}{{1/41}} = 0/7\\0/7 \in \left( {0,1} \right] \to \frac{1}{{\sqrt 2 }} \in \left( {0,1} \right]\end{array}\)
پ \(\mathbb{Z} - \mathbb{N} = W\)
درست است.
ت \(\sqrt {841} \in \mathbb{Q}\)
درست زیرا؛
\(\begin{array}{l}\sqrt {841} = 29 \to 29 \in \mathbb{N}\\\mathbb{N} \subseteq \mathbb{Z} \subseteq \mathbb{Q} \to \sqrt {841} \in \mathbb{Q}\end{array}\)
تهیه کننده: فرهاد صمدی
مجموعه های متناهی و نامتناهی
فصل 1 : مجموعه، الگو و دنباله
مجموعه های متناهی و نامتناهی
در این بخش می خواهیم در مورد تعداد اعضای یک مجموعه صحبت کنیم.
مجموعه ای چون A را یک مجموعه متناهی (باپایان) گوییم هرگاه تعداد اعضای آن را بتوان با یک عدد حسابی نمایش داد. اگر تعداد اعضای یک مجموعه را با نماد \(\left| A \right|\) |نمایش دهیم متناهی بودن یک مجموعه چون A به معنای آن است که به ازای یک عدد حسابی مثل k داریم \(\left| A \right| = k\)، در غیر اینصورت مجموعه را نامتناهی (بی پایان) گوییم.
مثال
مجموعه های زیر را بررسی کنید و متناهی یا نامتناهی بودن آنها را معین کنید.
الف مجموعه دانش آموزان سال دهم رشته ریاضی در کشور.
متناهی
ب تعداد اعداد ٣ رقمی و بزرگتر از ۵00.
متناهی (\(\{ x \in \mathbb{N}|500\langle x\langle 1000\} \))
پ تعداد اعداد اول.
نامتناهی
ج مجموعه اعداد طبیعی فرد.
نامتناهی
اگر مجموعه ای چون A دارای زیرمجموعه ای چون B باشد (\(B \subseteq A\)) به طوری که B نامتناهی باشد آنگاه بناچار خود A نیز نامتناهی است. در نتیجه چون اعداد گویای واقع در بازه ی (\(0,1\)) نامتناهی هستند پس \(\mathbb{Q}\) هم نامتناهی است و به همین ترتیب \(\mathbb{R}\) نیز نامتناهی است زیرا، (\(\mathbb{Q} \subseteq \mathbb{R}\)).
متناهی یا نامتناهی بودن مجموعه های زیر را بررسی کنید.
الف مجموعه کلمات بکار رفته در کتاب ریاضی دهم.
متناهی
ب مجموعه مضارب مثبت عدد ۵.
نامتناهی
پ مجموعه پلنگ های زنده در قاره آفریقا.
متناهی
ج مجموعه تمام زیر مجموعه های \(\mathbb{N}\).
نامتناهی
د مجموعه تمام موبایل های تولید شده در ٢٠ سال گذشته.
متناهی
و مجموعه تمام اعدادی که در تقسیم بر ۵ باقیمانده ١ دارند.
نامتناهی
تهیه کننده: فرهاد صمدی
متمم یک مجموعه
فصل 1 : مجموعه، الگو و دنباله
متمم یک مجموعه
مجموعه مرجع
در هر مبحث مجموعه ای که همه مجموعه های مورد بحث زیر مجموعه آن باشند را مجموعه مرجع یا مجموعه جهانی می نامند و با حرف U نشان می دهند. در این حالت اگر \(A \subseteq U\) مجموعه ای دلخواه باشد، \(U - A\) را با نماد \(A'\) نشان می دهیم و آن را متمم A می نامیم. به عبارت بهتر \(A'\) شامل اعضایی از U است که در A نیستند.
در شکل زیر رابطه بین مجموعه های \(A,A',U\) دیده می شود.
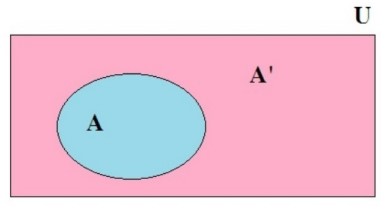
بطور معمول در هر بحثی مجموعه مرجع را معرفی می کنند. چنانچه در بحثی مجموعه مرجع را معرفی نکردیم شما می توانید بزرگترین مجموعه موجود را به عنوان مجموعه مرجع در نظر بگیرید. وقتی صحبت از اعداد باشد بزرگترین مجموعه ممکن همان \(\mathbb{R}\) است.
مثال
1 متمم هر یک از مجموعه های زیر را بنویسید.
الف \(A = \{ 1,3,5,...\} ,U = \mathbb{N}\)
\(A' = \{ 2,4,6,...\} \)
ب \(B = \mathbb{N},U = \mathbb{Z}\)
\(B' = \{ ..., - 2, - 1,0\} \)
2 اگر U مجموعه مرجع دلخواهی باشد و \(A \subseteq U\) باشند طرف دوم تساوی های زیر را بنویسید.
الف \(A \cup A' = \)
\(A \cup A' = U\)
ب \(A \cap A' = \)
\(A \cap A' = \emptyset \)
تعداد اعضای اجتماع دو مجموعه
فرض کنید تعداد اعضای مجموعه های A ,B معلوم باشد. می خواهیم تعداد اعضای مجموعه \(A \cup B\) را بر حسب \(n(A)\) و \(n\left( B \right)\) بیابیم. (تعداد اعضای یک مجموعه را هم با نماد \(\left| A \right|\) و هم با نماد \(n(A)\)نشان می دهند) ممکن است تصور کنید که جواب واضح است و برابر است با عدد \(n\left( A \right) + n\left( B \right)\) اما این نادرست است، چرا که اگر \(U = \mathbb{N},A = \{ 1,2,3\} ,B = \{ 2,3,4\} \) آنگاه:
\(4 = n\left( {A \cup B} \right) \ne n\left( A \right) + n\left( B \right) = 3 + 3 = 6\)
دلیل آن ها ساده است. هنگامی که می نویسیم \(n\left( A \right) + n\left( B \right)\) در واقع اعضای مشترک دوبار شمارش شده اند. یعنی \(n\left( {A \cap B} \right)\) یکبار در هنگام شمارش اعضای A و یک بار در شمارش اعضای B حساب شده است. لذا برای یافتن تعداد درست باید یکبار \(n(A \cap B)\) را از \(n\left( A \right) + n\left( B \right)\) کم کنیم. پس جواب درست بصورت زیر است:
\(n\left( {A \cup B} \right) = n\left( A \right) + n\left( B \right) - n\left( {A \cap B} \right)\)
به شکل زیر دقت کنید. می توان درستی رابطه فوق را از روی نمودار ون زیر تحقیق کرد.
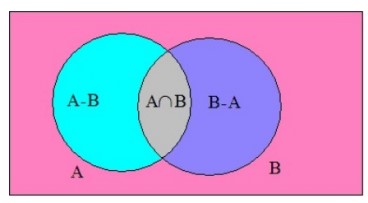
از روی شکل فوق روابط جالب دیگری بین اعضای مجموعه های \(A - B\) و \(A \cap B\) به دست می آید. این روابط به صورت زیر هستند:
\(\begin{array}{l}n\left( {A - B} \right) + n\left( {A \cap B} \right) + n\left( {B - A} \right) = n\left( {A \cup B} \right)\\n\left( {A - B} \right) = n\left( A \right) - n\left( {A \cap B} \right)\\n\left( {B - A} \right) = n\left( B \right) - n\left( {A \cap B} \right)\end{array}\)
1 در یک کلاس مدرسه ٣٠ دانش آموز وجود دارد. ٢٢ نفر از آنها فوتبال بازی می کنند و ١٨ نفر هم والیبال بازی می کنند. چند نفر هم فوتبال بازی می کنند و هم والیبال؟
\(\begin{array}{l}n\left( F \right) = 22\\n\left( V \right) = 18\\n\left( {F \cup V} \right) = 30\\n\left( {F \cap V} \right) = ?\\n\left( {F \cup V} \right) = n\left( F \right) + n\left( V \right) - n\left( {F \cap V} \right)\\30 = 22 + 18 - n\left( {F \cap V} \right) \to n\left( {F \cap V} \right) = 10\end{array}\)
2 از بین اعداد ١ تا ٢٠٠ چند عدد وجود دارد که بر ۵ یا ٧ بخش پذیر باشد؟
\(\begin{array}{l}n\left( 5 \right) = 40\\n\left( 7 \right) = 28\\n\left( {35} \right) = 5\\n\left( {A \cup B} \right) = n\left( A \right) + n\left( B \right) - n\left( {A \cap B} \right)\\ \to n\left( {A \cup B} \right) = 40 + 28 - 5 = 63\\ \to n\left( {A \cup B} \right) = 63\end{array}\)
الف چند عدد بر ۵ بخش پذیر است اما بر ٧ بخش پذیر نیست؟
\(\begin{array}{l}n\left( {A - B} \right) = n\left( A \right) - n\left( {A \cap B} \right)\\ \to n\left( {5 - 7} \right) = 40 - 5 = 35 \to n\left( {5 - 7} \right) = 35\end{array}\)
3 در يک کلاس ٣٠ نفری، ٢١ نفر به زبان انگليسی، ١٧ نفر به زبان فرانسه و ١٠ نفر به هـر دو زبان می توانند صحبت کنند. در اين کلاس چند نفر هستند که به هيچ يک از ايـن دو زبـان صـحبت نمی کنند؟
\(\begin{array}{l}n\left( U \right) = 30\\n\left( E \right) = 21\\n\left( F \right) = 17\\n\left( {E \cap F} \right) = 10\\n\left( {E \cup F} \right) = n\left( E \right) + n\left( F \right) - n\left( {E \cap F} \right)\\n\left( {E \cup F} \right) = 21 + 17 - 10 = 28 \to n\left( {E \cup F} \right) = 28\\n\left( U \right) - n\left( {E \cup F} \right) \to 30 - 28 = 2\end{array}\)
4 در یک نظرسنجی از ١١٠ مشتری یک فروشگاه زنجیره ای مشخص شد که ٧٠ نفر آنها در یک ماه گذشته از محصولات شرکت A و ۵٧ نفرشان از محصولات شرکت B خرید کرده اند. همچنین ٣٢ نفر از آنان نیز اعلام کردند که در این مدت از هر دو شرکت خرید داشته اند. چه تعداد از این ١١٠ نفر در یک ماه گذشته :
الف دست کم از یکی از این دو شرکت خرید داشته باشند؟
\(\begin{array}{l}n\left( A \right) = 70\\n\left( B \right) = 57\\n\left( {A \cap B} \right) = 32\\n\left( {A \cup B} \right) = n\left( A \right) + n\left( B \right) - n\left( {A \cap B} \right)\\n\left( {A \cup B} \right) = 70 + 57 - 32 \to n\left( {A \cup B} \right) = 95\end{array}\)
ب فقط از شرکت A خرید داشته اند.
\(\begin{array}{l}n\left( {A - B} \right) = n\left( A \right) - n\left( {A \cap B} \right)\\n\left( {A - B} \right) = 70 - 32 \to n\left( {A - B} \right) = 38\end{array}\)
پ دقیقاً از یکی از این دو شرکت خرید داشته اند.
\(\begin{array}{l}n\left( {B - A} \right) = n\left( B \right) - n\left( {A \cap B} \right)\\n\left( {B - A} \right) = 57 - 32\\n\left( {B - A} \right) = 25\\n\left( {A - B} \right) = 38\\25 + 38 = 63\end{array}\)
تهیه کننده: فرهاد صمدی
- آزمون آنلاین تمامی دروس پایه دهم
- گام به گام تمامی دروس پایه دهم
- ویدئو های آموزشی تمامی دروس پایه دهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه دهم
- فلش کارت های آماده دروس پایه دهم
- گنجینه ای جامع از انشاء های آماده پایه دهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه دهم
الگو ها
فصل 1 : مجموعه، الگو و دنباله
الگو
دنیای اطراف ما سرشار از الگوهای مختلفی است. به عنوان نمونه، پیدایش شبانه روز و تغییر فصول مختلف سال جلوه ای از الگوی حاکم بر طبیعت است. از سوی دیگر نظم و قانونمندی های موجود در یک الگو به خودی خود برای ما جذاب است. چه بسا ممکن است طرح های روی یک گل آفتابگردان، شکل های هندسی روی یک سطح کاشی کاری شده و یا مارپیچ های روی میوه آناناس توجه شما را به خود جلب کرده باشند. به طور کلی می توان گفت الگو یک ساختار منظم از اشکال، تصاویر، صداها، نمادها، وقایع و یا اعداد می باشد که ممکن است تکرار شونده یا رشد کننده و یا ترکیبی از این دو باشد. ریاضیات به عنوان ملکه علوم، یکی از رسالت های مهم خود را مدل سازی کردن پدیده های طبیعی و پی بردن به الگوهای نهفته در آنها می داند. اهمیت این موضوع به قدری است که برخی از ریاضیدانان معتقدند که ریاضی عبارتست از علم مطالعه الگوها. در این بخش برخی الگوهای هندسی و نیز الگوهای عددی متناظر با آنها مورد بررسی قرار می گیرند.
به شکل زیر دقت کنید در هر مورد ارتباطی بین a و b و c وجود دارد:

همانطور که در شکل بالا دیده شد اختلاف هر جمله از جمله قبلی مقدار ثابتی است. این نوع الگو ها را الگوی خطی می نامیم چرا که به شکل معادله درجه اول \({t_n} = an + b\) در اینجا \({t_n}\) جمله nام الگو است.
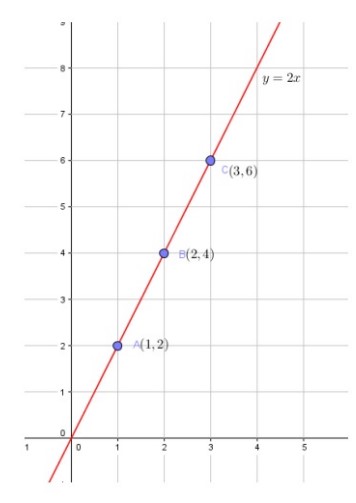
نمودار یک الگوی خطی
همانطور که در شکل بالا مشاهده می کنید اعضای دنباله ی \(2,4,6,...\) در واقع عرض نقاط \(A,B,C,...\) روی خط \(y = 2x\) هستند. به همین علت هم به این الگوها خطی گویند. اگر خوب به معادله آن که بر حسب متغبر n نوشته شده است دقت کنید بلافاصله به یاد معادله خط ار کلاس نهم خواهید افتاد یعنی عبارت \(y = ax + b\) اما همه ی الگوها لزوما خطی نیستند.
الف جمله ی عمومی الگوی زیر را با توجه به تعداد مربع ها به دست آورید.
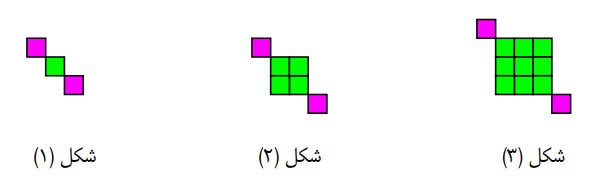
\(\begin{array}{l}{a_1} = {\left( 1 \right)^2} + 2\\{a_2} = {\left( 2 \right)^2} + 2\\{a_n} = {n^2} + 2\end{array}\)
ب آیا این یک الگوی خطی است؟
چون جمله ی عمومی اين الگو به صورت \(y = ax + b\) نیست، پس این الگو خطی نمی باشد.
تهیه کننده: فرهاد صمدی
دنباله ها
فصل 1 : مجموعه، الگو و دنباله
دنباله
به هر تعداد از اعداد که آنها را پشت سر هم نوشته باشیم یک دنباله گوییم. هر عدد که در دنباله قرار دارد را یک عضو دنباله گوییم و جمله n ام یا جمله عمومی دنباله را با نماد \({a_n}\) نمایش می دهیم. نماد رایج برای نوشتن جمله عمومی یک دنباله نماد \(\{ \} \) است. مثلا می نویسیم \({a_n} = \frac{{{n^2} + 1}}{{5n}}\) یا معادلا عبارت \(\{ \frac{{{n^2} + 1}}{{5n}}\} \) .
مثال
پنج جمله اول دنباله های زیر را بنویسید.
الف \({a_n} = {\left( { - 1} \right)^n}{2^n}\)
\(\begin{array}{l}n = 1\\{a_1} = {\left( { - 1} \right)^1}{2^1} \to {a_1} = - 2\\n = 2\\{a_2} = {\left( { - 1} \right)^2}{2^2} \to {a_2} = 4\\n = 3\\{a_3} = {\left( { - 1} \right)^3}{2^3} \to {a_3} = - 8\\n = 4\\{a_4} = {\left( { - 1} \right)^4}{2^4} \to {a_4} = 16\\n = 5\\{a_5} = {\left( { - 1} \right)^5}{2^5} \to {a_5} = - 32\end{array}\)
ب \({b_n} = {\left( {\frac{1}{3}} \right)^n}\)
\(\begin{array}{l}n = 1\\{b_1} = {\left( {\frac{1}{3}} \right)^1} \to {b_1} = \frac{1}{3}\\n = 2\\{b_2} = {\left( {\frac{1}{3}} \right)^2} \to {b_2} = \frac{1}{9}\\n = 3\\{b_3} = {\left( {\frac{1}{3}} \right)^3} \to {b_3} = \frac{1}{{27}}\\n = 4\\{b_4} = {\left( {\frac{1}{3}} \right)^4} \to {b_4} = \frac{1}{{81}}\\n = 5\\{b_5} = {\left( {\frac{1}{3}} \right)^5} \to {b_5} = \frac{1}{{243}}\end{array}\)
دنباله حسابی
دنباله ای که در آن هر جمله (به جز جمله اول) با اضافه شدن عددی ثابت به جمله قبل از خودش به دست می آید، یک دنباله حسابی نامیده می شود و به آن عدد ثابت، قدر نسبت دنباله می گویند. فرض کنید جمله اول دنباله a و قدر نسبت عدد d باشد در این صورت جملات ابتدایی دنباله بصورت زیر است:
\(a,a + d,a + 2d,a + 3d,...,a + \left( {n - 1} \right)d\)
به این ترتیب جمله عمومی دنباله حسابی بصورت زیر حاصل می شود:
\({a_n} = {a_1} + \left( {n - 1} \right)d\)
مثال
در یک دنباله حسابی داریم \({a_{11}} = 48\) و \({a_5} = 24\) مطلوبست محاسبه \({a_{20}}\) .
\(\begin{array}{l}{a_n} = {a_1} + \left( {n - 1} \right)d\\{a_{11}} = {a_1} + 10d \to {a_1} + 10d = 48\\{a_5} = {a_1} + 4d \to {a_1} + 4d = 28\\d = \frac{{10}}{3},{a_1} = \frac{{44}}{3}\\{a_{20}} = \frac{{44}}{3} + \left( {19} \right)\frac{{10}}{3} \to {a_{20}} = 78\end{array}\)
برای پیدا کردن مجموع n جمله اول یک دنباله حسابی را به دست آوریم از فرمول زیر استفاده می کنیم:
\({S_n} = \frac{n}{2}\left[ {2a + \left( {n - 1} \right)d} \right]\)
دنباله هندسی
دنباله هندسی، دنباله ای است که در آن هر جمله (به جز جمله اول) از ضرب جمله قبل از خودش در عددی ثابت به دست می آید. این عدد ثابت را قدرنسبت دنباله می نامیم. جمله اول دنباله هندسی \(a \ne 0\) است. قدر نسبت را با q نشان می دهیم. در حالت های خاص اگر \(q = 0\) یا \(q = 1\) باشد، دنباله های خاصی پدید می آیند.
اگر \(q = 0\) باشد دنباله به صورت \(a,0,0,0,...\) و اگر \(q = 1\) دنباله ثابت \(a,a,a,...\) حاصل می شوند.
برای یافتن جمله عمومی یک دنباله هندسی فرض می کنیم جمله اول آن a و قدرنسبت q باشد در این صورت ترتیب جملات بصورت زیر است:
\(a,aq,a{q^2},...,a{q^{n - 1}}\)
بنابراین جمله n ام یا جمله عمومی دنباله هندسی بصورت زیر حاصل می شود:
\({a_n} = {a_1}{q^{n - 1}}\)
در یک دنباله هندسی که جمله اول آن مثبت است چنانچه \(q\rangle 1\) باشد دنباله افزایشی است و اگر \(0\langle q\langle 1\) باشد دنباله کاهشی است. اگر \(q = - 1\) باشد دنباله متناوب است و اگر \(q\langle 0\) باشد، دنباله نوسانی است.
1 اگر تعداد زیر مجموعه های یک مجموعه \(k + 1\) عضوی 24 واحد کم تر از تعداد زیر مجموعه های یک مجموعه \(k + 3\) عضوی باشد، آنگاه k را بیابید.
\(\begin{array}{l}{2^{k + 1}} = {2^{k + 3}} - 24 \to {2^{k + 3}} - {2^{k + 1}} = 24 \to {2^k}\left( {8 - 2} \right) = 24\\{2^k} = 4 \to k = 2\end{array}\)
2 اگر جمله چهارم یک دنباله هندسی 1 و جمله ی هفتم آن 8 باشد، آنگاه جمله عمومی این دنباله را بیابید.
\(\begin{array}{l}{a_n} = {a_1}{q^{n - 1}}\\{a_1}{q^3} = 1\\{a_1}{q^6} = 8\\ \to \frac{{{a_1}{q^6}}}{{{a_1}{q^3}}} = \frac{8}{1} \to {q^3} = 8 \to q = 2\\{a_1}{q^3} = 1 \to {a_1}{2^3} = 1 \to {a_1} = \frac{1}{8}\\{a_n} = {a_1}{q^{n - 1}} = \left( {\frac{1}{8}} \right)\left( {{2^{n - 1}}} \right) = \frac{1}{{{2^3}}} \times {2^{n - 1}} \to {a_n} = {2^{n - 4}}\end{array}\)
3 اگر در یک دنباله ی حسابی جمله ی چهارم برابر \(-8\) باشد، مجموع جملات اول، سوم، پنجم و هفتم چیست؟
\(\begin{array}{l}{a_1} + 3d = - 8\\{a_1} + {a_1} + 2d + {a_1} + 4d + {a_1} + 6d = 4{a_1} + 12d = 4\left( {{a_1} + 3d} \right) = 4 \times \left( { - 8} \right) = - 32\end{array}\)
تهیه کننده: فرهاد صمدی
نسبت های مثلثاتی
فصل 2 : مثلثات
نسبت های مثلثاتی
از کلاس نهم می دانید چنانچه دو زاویه از مثلثی با دو زاویه از مثلث دیگر برابر باشند دو مثلث متشابه اند. در شکل زیر دو مثلث \(ABC,A'B'C'\) متشابه اند.
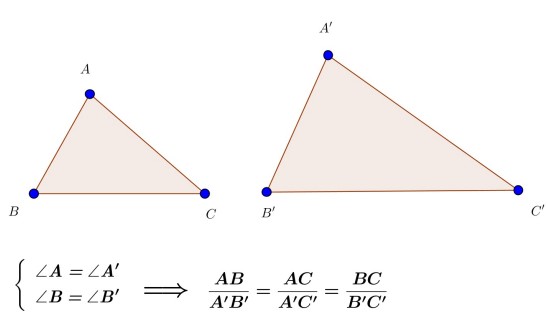
حال در دو مثلث قائم الزاویه برابری تنها یک زاویه حاده از مثلث اولی با یک زاویه حاده از مثلث دومی برای تشابه دو مثلث کفایت می کند.
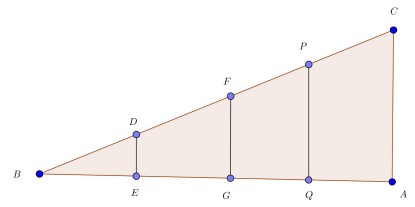
در شکل بالا داریم \(A = E = G = Q = {90^0}\) ولذا مثلث های قائم الزاویه ای که در راس B مشترک اند متشابه هستند. حال اگر نسبت تشابه را در این مثلث ها بنویسیم خواهیم داشت:
\(\frac{{DE}}{{BE}} = \frac{{FG}}{{BG}} = \frac{{PQ}}{{BQ}} = \frac{{GA}}{{BA}}\)
پس برای زاویه B همه این نسبت ها مقداری ثابت است . برای این نسبت ثابت نامی انتخاب می کنیم. این نام تانژانت زاویه B است. پس داریم:
\(\tan B = \frac{{AC}}{{AB}}\)
در مثلث، تانژانت هر زاویه ای از ضلع مقابل بر ضلع مجاور به دست می آید.
عکس نسبت تانژانت را کتانژانت می نامیم. پس داریم:
\(\cot B = \frac{{AB}}{{AC}}\)
در مثلث، کتانژانت هر زاویه ای از ضلع مجاور بر ضلع مقابل به دست می آید.
به همین ترتیب در این مثلث های متشابه نسبت های زیر نیز ثابت اند و باید نامی برای آنها انتخاب کرد.
\(\begin{array}{l}1)\frac{{DE}}{{BD}} = \frac{{FG}}{{BF}} = \frac{{PQ}}{{BP}} = \frac{{AC}}{{BA}}\\2)\frac{{BD}}{{DE}} = \frac{{BF}}{{FG}} = \frac{{BP}}{{PQ}} = \frac{{BA}}{{AC}}\end{array}\)
اولی را سینوس و دومی را کسینوس می نامند. پس داریم:
\(\sin B = \frac{{AC}}{{BC}}\)
\(\cos B = \frac{{AB}}{{AC}}\)
در مثلث، سینوس و کسینوس هر زاویه ای از ضلع مقابل بر وتر و ضلع مجاور بر وتر به دست می آید.
در یک مثلث قائم الزاویه نسبت های ، سینوس، کسینوس، تانژانت، کتانژانت را نسبت های مثلثاتی می نامیم.
مقدار نسبت های مثلثاتی در درجاتی که نیاز خواهید داشت به صورت زیر است:
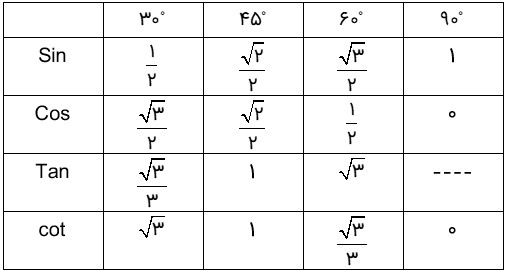
1 مقدار عددی عبارات زیر را بدست آورید.
الف \({{\mathop{\rm Sin}\nolimits} ^2}{45^0} + {{\mathop{\rm Cos}\nolimits} ^2}{45^0} = \)
\(\begin{array}{l}{\left( {\frac{{\sqrt 2 }}{2}} \right)^2} + {\left( {\frac{{\sqrt 2 }}{2}} \right)^2} = \frac{1}{2} + \frac{1}{2} = 1\\{{\mathop{\rm Sin}\nolimits} ^2}{45^0} + {{\mathop{\rm Cos}\nolimits} ^2}{45^0} = 1\end{array}\)
ب \(\frac{{\tan {{45}^0} - \tan {{60}^0}}}{{1 + \tan {{45}^0} \times \tan {{60}^0}}} = \)
\(\begin{array}{l}\frac{{1 - \sqrt 3 }}{{1 + \sqrt 3 }} = \frac{1}{1} = 1\\\frac{{\tan {{45}^0} - \tan {{60}^0}}}{{1 + \tan {{45}^0} \times \tan {{60}^0}}} = 1\end{array}\)
2 در شکل زیر طول نردبان را بیابید. (\({\mathop{\rm Cos}\nolimits} {36^0} \approx 0/8\))
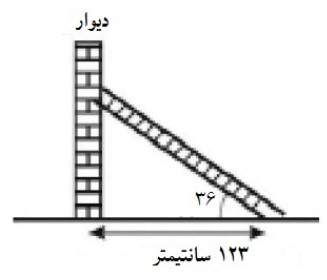
\({\mathop{\rm Cos}\nolimits} A = \frac{{AB}}{{AC}} \to 0/8 = \frac{{1/23}}{{AC}} \to AC = \frac{{1/23}}{{0/8}} \to AC = 1/5375\)
تهیه کننده: فرهاد صمدی
- آزمون آنلاین تمامی دروس پایه دهم
- گام به گام تمامی دروس پایه دهم
- ویدئو های آموزشی تمامی دروس پایه دهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه دهم
- فلش کارت های آماده دروس پایه دهم
- گنجینه ای جامع از انشاء های آماده پایه دهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه دهم
مساحت مثلث بر حسب نسبت های مثلثاتی
فصل 2 : مثلثات
مساحت مثلث بر حسب نسبت های مثلثاتی
از گذشته می دانیم مساحت یک مثلث برابر است با نصف حاصل ضرب ارتفاع در قاعده ی نظیر به آن ارتفاع؛ حال در شکل زیر می خواهیم مساحت مثلث ABC را محاسبه کنیم. برای این منظور می نویسیم:
\({S_{ABC}} = \frac{{AH \times BC}}{2} = \frac{{AB \times {\mathop{\rm Sin}\nolimits} \alpha \times BC}}{2} = \frac{1}{2}AB \times BC \times {\mathop{\rm Sin}\nolimits} \alpha \)
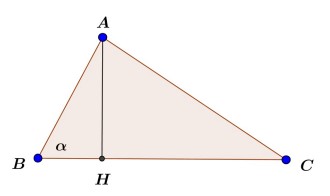
\(AH = AB \times {\mathop{\rm Sin}\nolimits} \beta = AB \times {\mathop{\rm Sin}\nolimits} \alpha \)
1 مساحت مثلث ABC را بیابید. (\(BC = 5\sqrt 3 ,\hat C = {30^0}\))
\(\begin{array}{l}AB = h \to \tan {30^0} = \frac{h}{{5\sqrt 3 }} \to h = 5\sqrt 3 \times \frac{{\sqrt 3 }}{3} \to h = 5\\{S_{ABC}} = \frac{1}{2}h \times BC = \frac{1}{2} \times 5 \times 5\sqrt 3 = \frac{{25}}{2}\sqrt 3 \end{array}\)
2 مساحت مثلث متساوی الساقین ABC برابر 9 است. اندازه x را بیابید. (\({\mathop{\rm Sin}\nolimits} A = {30^0}\) و طول ساق را x بگیرید.)
\({S_{ABC}} = \frac{1}{2}AB{\mathop{\rm Sin}\nolimits} \alpha \to {S_{ABC}} = \frac{1}{2}{x^2}{\mathop{\rm Sin}\nolimits} {30^0} = \frac{1}{2}{x^2} \times \frac{1}{2} = \frac{1}{4}{x^2} = 9 \to {x^2} = 36 \to x = 6\)
تهیه کننده: فرهاد صمدی
دایره مثلثاتی
فصل 2 : مثلثات
دایره مثلثاتی
پرسشی که بطور طبیعی به ذهن می رسد این است که نسبت های مثلثاتی در مورد زوایای غیرحاده تعریف می شود؟ مثلا برای زاویه ١۵٠ درجه می توان سینوس تعریف کرد و چگونه؟ جواب مثبت است. اما مثلث قائم الزاویه دیگر جوابگوی این تعریف نیست. دایره مثلثاتی را برای این منظور معرفی می کنیم.دایره ای به شعاع یک و مرکز مبداء مختصات. اگر از نقطه \(A\left( {1,0} \right)\) و در خلاف جهت حرکت عقربه های ساعت سروع به حرکت کنیم زاویه ای مثبت تولید خواهد شد. در صورت چرخش در جهت عقربه های ساعت زاویه ی منفی حاصل می شود.
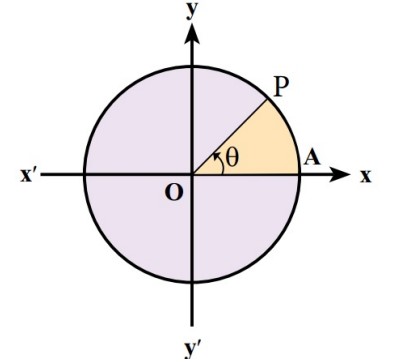
در شکل زیر چند زاویه مثبت و منفی در دایره مثلثاتی دیده می شود.
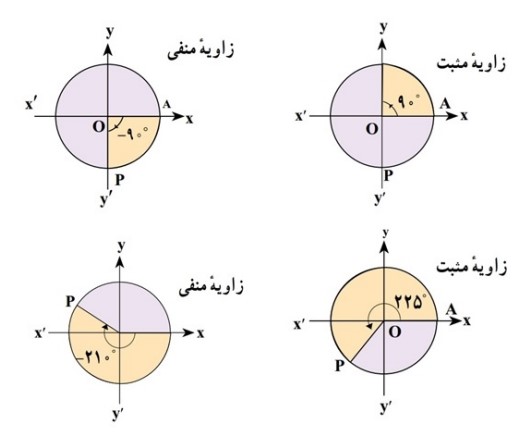
حال نقطه \(P\left( {x,y} \right)\) را در نظر بگیرید. از نقطه p عمودی بر محور طول ها رسم می کنیم. در مثلث قائم الزاویه ی حاصل نسبت های مثلثاتی زاویه \(\theta \) را محاسبه می کنیم.
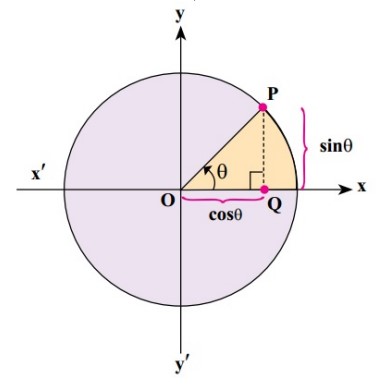
\(\begin{array}{l}{\mathop{\rm Sin}\nolimits} \theta = \frac{{PQ}}{{OP}} = y\\{\mathop{\rm Cos}\nolimits} \theta = \frac{{OQ}}{{OP}} = x\\{\mathop{\rm Tan}\nolimits} \theta = \frac{{PQ}}{{OQ}} = \frac{y}{x}\\Cot\theta = \frac{{OQ}}{{PQ}} = \frac{x}{y}\end{array}\)
علامت نسبت های مثلثاتی با توجه به هر ناحیه در جدول زیر گردآوری شده است.
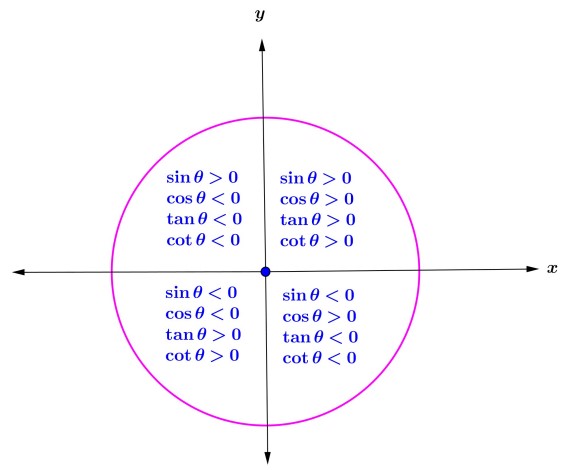
با توجه به دایره مثلثاتی و تعریف نسبت های مثلثاتی متوجه می شویم که همواره \( - 1 \le {\mathop{\rm Sin}\nolimits} \theta \le 1\) و همین طور \( - 1 \le {\mathop{\rm Cos}\nolimits} \theta \le 1\). اما در مورد دو نسبت دیگر یعنی \(\tan \theta ,\cot \theta \) این گونه نیست. در واقع این دو نسبت هر مقداری می توانند باشند، چه مثبت و چه منفی. به زبان ریاضی:
\({\mathop{\rm Sin}\nolimits} \theta \in \left[ { - 1,1} \right],{\mathop{\rm Cos}\nolimits} \theta \in \left[ { - 1,1} \right],\tan \theta ,\cot \theta \in \left( { - \infty , + \infty } \right)\)
شکلی دیگری از دایره مثلثاتی نیز مرسوم است که در آن چهار محور به نام نسبت های مثلثاتی بصورت زیر وجود دارد.
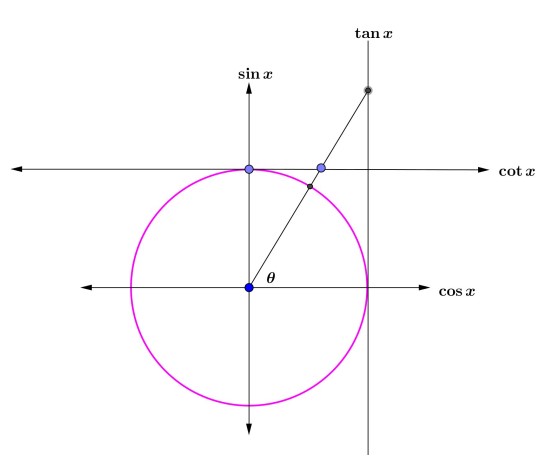
از روی شکل فوق بهتر متوجه خواهید شد که چرا مثلا \(\tan \theta \) می تواند هر مقداری را اختیار کند.
در کلاس نهم معادله خط و مفهوم شیب را خوانده اید. برای یک خط که از نقاط \(B\left( {{x_2},{y_2}} \right),A\left( {{x_1},{y_1}} \right)\) می گذرد شیب چنین تعریف می شود:
\(m = \frac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}\)
M شیب خط است.
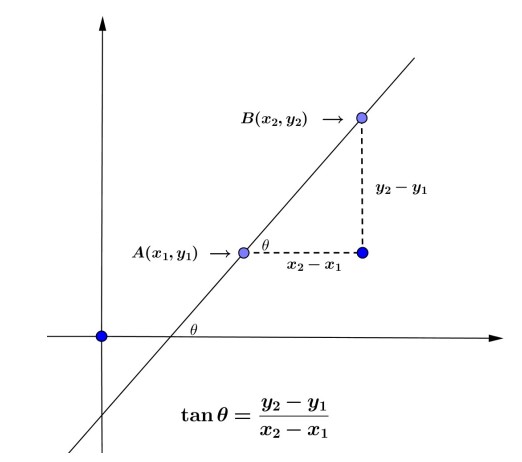
همان طور که در شکل بالا می بینید تانژانت زاویه ای که خط با جهت مثبت محور طول ها می سازد برابر شیب خط است.از این نکته می توان در نوشتن معادله خط استفاده کرد.
روابط بین نسبت های مثلثاتی
شاید تا الان متوجه شده باشید که چهار نسبت مثلثاتی علیرغم نام های متفاوت با هم ارتباط نزدیکی دارند. این روابط را در زیر فهرست کرده ایم.
\(\begin{array}{l}1)\tan x = \frac{{\sin x}}{{\cos x}}\\2)\cot x = \frac{{\cos x}}{{\sin x}}\\3){\sin ^2}x + {\cos ^2}x = 1\\{\sin ^2}x = 1 - {\cos ^2}x\\{\cos ^2}x = 1 - {\sin ^2}x\\4)1 + {\tan ^2}x = \frac{1}{{{{\cos }^2}x}}\\5)1 + {\cot ^2}x = \frac{1}{{{{\sin }^2}x}}\end{array}\)
1 \(\alpha \) زاویه ای در ربع دوم دایره مثلثاتی و \(\tan \alpha = - \frac{{12}}{5}\) است. با استفاده از روابط بین نسبت های مثلثاتی، مقدار \(\cos \alpha \) را به دست آورید.
\({\cos ^2}\alpha = \frac{1}{{1 + {{\tan }^2}\alpha }} = \frac{1}{{1 + \frac{{144}}{{25}}}} = \frac{{25}}{{169}} \to \cos \alpha = - \frac{5}{{13}}\)
2 با فرض با معنی بودن کسرها ، درستی تساوی مقابل را ثابت کنید.
\(\frac{1}{{\cos x}} - \tan x = \frac{{\cos x}}{{1 + sinx}}\)
\(\frac{1}{{\cos x}} - \tan x = \frac{1}{{\cos x}} - \frac{{sinx}}{{\cos x}} = \frac{{1 - \sin x}}{{\cos x}} \times \frac{{1 + \sin x}}{{1 + \sin x}} = \frac{{1 - {{\sin }^2}x}}{{\cos x\left( {1 + \sin x} \right)}} = \frac{{{{\cos }^2}x}}{{\cos x\left( {1 + \sin x} \right)}} = \frac{{\cos x}}{{1 + \sin x}}\)
3
الف معادله خط شکل زیر را بنویسید.
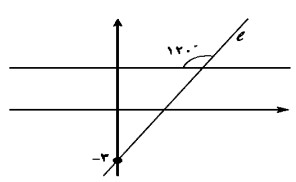
\(y = \sqrt 3 x - 3\)
ب اگر \(\tan \beta \) و \(\sin \beta \) هم علامت باشند، آنگاه \(\beta \) در کدام ربع مثلثاتی قرار دارد؟
\(\beta \) در ربع اول قرار دارد.
تهیه کننده: فرهاد صمدی
ریشه و توان اعداد حقیقی
فصل 3 : توان های گویا و عبارت های جبری
ریشه و توان اعداد حقیقی
فرض کنیم \(n \ge 2\) عددی طبیعی باشد.دراین صورت عدد حقیقی b را یک ریشه n ام عدد حقیقی a گوییم هرگاه \({b^n} = a\) باشد.
اگر n زوج باشد عدد حقیقی و مثبت a دارای دو ریشه n ام می باشد که قرینه یکدیگرند. در این حالت ریشه n ام مثبت را ریشه n ام اصلی می نامیم و با نماد \(\sqrt[n]{a}\) نشان می دهیم. اعداد منفی دارای ریشه n ام زوج نیستند ولی ریشه n ام فرد دارند.
مثال
کامل کنید.
الف \(\sqrt[3]{{64}} = \)
\(\sqrt[3]{{64}} = 4\)
ب \(\sqrt[4]{{0/0625}} = \)
\(\sqrt[4]{{0/0625}} = 0/5\)
مهمترین خواص رادیکال ها در زیر فهرست کرده ایم.
1) \(\sqrt[n]{{{a^n}}} = a\)
در 1 اگر n زوج باشد قدر مطلق a را می نویسیم.
2) \(\sqrt[n]{a}\sqrt[n]{b} = \sqrt[n]{{ab}},a,b \in \mathbb{N}\)
3) \(\frac{{\sqrt[n]{a}}}{{\sqrt[n]{b}}} = \sqrt[n]{{\frac{a}{b}}}\)
4) \({\left( {\sqrt[n]{a}} \right)^m} = \sqrt[n]{{{a^m}}} \to m,n \in \mathbb{N},a \ge 0\)
5) \(\sqrt[n]{{\sqrt[m]{a}}} = \sqrt[{mn}]{a} \to m,n \in \mathbb{N},a \ge 0\)
6) \(a\sqrt[n]{b} = \sqrt[n]{{{a^n}b}}, - \sqrt[n]{{{a^n}b}}\)
7) \(\sqrt[{mn}]{{{a^m}}} = \sqrt[n]{a} \to a\rangle 0,m,n \in \mathbb{N}\)
بدون استفاده از ماشین حساب می توان مقدار تقریبی (اما با دقت بالا) رادیکال ها را بدست آورد.
\(\sqrt[n]{x} = \sqrt[n]{{{a^n} \pm b}} \approx a \pm \frac{b}{{n{a^{n - 1}}}}\)
1 برای هر عدد رادیکالی زیر، اگر حاصل آن یک عدد صحیح است، جواب را بنویسید و در غیر اینصورت دو عدد صحیح متوالی بنویسید که عدد رادیکالی مورد نظر بین آنها باشد.
الف \(\sqrt[4]{{400}} = \)
\(\sqrt[4]{{400}} \to \sqrt[4]{{256}}\langle \sqrt[4]{{400}}\langle \sqrt[4]{{625}} = 4\langle \sqrt[4]{{400}}\langle 5\)
ب \(\sqrt {75} = \)
\(\sqrt {75} \to \sqrt {64} \langle \sqrt {75} \langle \sqrt {81} = 8\langle \sqrt {75} \langle 9\)
پ \(\sqrt[3]{{250}} = \)
\(\sqrt[3]{{250}} \to \sqrt[3]{{216}}\langle \sqrt[3]{{250}}\langle \sqrt[3]{{343}} = 6\langle \sqrt[3]{{250}}\langle 7\)
2 اگر \(\sqrt[4]{{625}} = a\) باشد، در این صورت حاصل عبارت \({a^3} + 5a - 6\) را بیابید.
\(\begin{array}{l}\sqrt[4]{{625}} = a \to a = 5\\ \to {5^3} + 5\left( 5 \right) - 6 \to 125 + 25 - 6 = 144\end{array}\)
3 مقدار تقریبی هر کدام از اعداد رادیکالی زیر را با یک رقم اعشار مشخص کنید.
الف \(\sqrt {10} \)
\(\sqrt {10} = 3/1\)
ب \(\sqrt[3]{{7/25}}\)
\(\sqrt[3]{{7/25}} = 1/8\)
پ \(\sqrt[5]{{16}}\)
\(\sqrt[5]{{16}} = 1/7\)
4 مثالی ارائه دهید که نشان دهد تساوی زیر همیشه درست نیست.
\(\sqrt[n]{{{a^n}}} = {\left( {\sqrt[n]{a}} \right)^n}\)
\(\begin{array}{l}\sqrt[n]{{{a^n}}} = {\left( {\sqrt[n]{a}} \right)^n}\\\sqrt[4]{{{{\left( { - 2} \right)}^4}}} = {\left( {\sqrt[4]{{ - 2}}} \right)^4}\end{array}\)
تهیه کننده: فرهاد صمدی
- آزمون آنلاین تمامی دروس پایه دهم
- گام به گام تمامی دروس پایه دهم
- ویدئو های آموزشی تمامی دروس پایه دهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه دهم
- فلش کارت های آماده دروس پایه دهم
- گنجینه ای جامع از انشاء های آماده پایه دهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه دهم
توان های گویا
فصل 3 : توان های گویا و عبارت های جبری
توان های گویا
فرض کنید \(x = {-b \pm \sqrt{b^2-4ac} \over 2a}n \in \mathbb{N}\) باشد و \(a \in \mathbb{R}\) عددی دلخواه. عدد \({a^n}\) را بصورت:
\({a^n} = a \times a \times a \times ... \times a\)
تعریف می کنیم. برای اعداد صحیح منفی نیز این تعریف قابل تعمیم است. \({a^{ - n}}\) را بصورت زیر تعریف می کنیم:
\({a^{ - n}} = \frac{1}{{{a^n}}}\)
در نهایت \({a^0} = 1\) تعریف می شود و حال \({a^n}\) را برای تمام اعداد صحیح تعریف کرده ایم.
مهم ترین خواص توان عبارتند از:
\(\begin{array}{l}1){a^n} \times {a^m} = {a^{m + n}}\\2)\frac{{{a^m}}}{{{a^n}}} = {a^{m - n}}\\3){\left( {{a^m}} \right)^n} = {a^{mn}}\end{array}\)
می توان در حالت کلی توان گویای یک عدد حقیقی را تعریف کرد.
فرض کنید a عددی حقیقی باشد. اگر \(m,n \in \mathbb{N}\) باشند تعریف می کنیم:
\({a^{\frac{m}{n}}} = \sqrt[n]{{{a^m}}}\)
1 حاصل عبارات زیر را بدست آورید.
الف \({8^{\frac{2}{3}}} = \)
\({8^{\frac{2}{3}}} = \sqrt[3]{{{8^2}}} = \sqrt[3]{{64}} = 4\)
ب \({\left( {0/25} \right)^{\frac{3}{2}}} = \)
\({\left( {0/25} \right)^{\frac{3}{2}}} = \sqrt[2]{{{{0/25}^3}}} = \sqrt[2]{{0/015625}} = 0/125\)
2 تساوی های زیر را مانند نمونه به صورت رادیکالی بنویسید.
الف \({2^{\frac{2}{3}}} \times {2^{\frac{3}{2}}} = \)
\({2^{\frac{2}{3}}} \times {2^{\frac{3}{2}}} = {2^{\frac{2}{3} + \frac{3}{2}}} = {2^{\frac{{13}}{6}}} = {2^{2 + \frac{1}{6}}} = {2^2} \times {2^{\frac{1}{6}}} = 4\sqrt[6]{2}\)
ب \({\left( {{{16}^{\frac{1}{3}}}} \right)^{\frac{3}{4}}} = \)
\({\left( {{{16}^{\frac{1}{3}}}} \right)^{\frac{3}{4}}} = {16^{\frac{1}{3} \times \frac{3}{4}}} = {16^{\frac{1}{4}}} = \sqrt[4]{{16}} = 2\)
تهیه کننده: فرهاد صمدی
عبارت های جبری
فصل 3 : توان های گویا و عبارت های جبری
عبارت های جبری
یک تساوی که به ازای تمامی مقادیر متغیر موجود در آن تساوی درست باشد را یک اتحاد گوییم. به تساوی زیر دقت کنید.
\({\left( {x + y} \right)^2} = {x^2} + 2xy + {y^2}\)
در تساوی بالا به ازای تمامی مقادیر x ,y درست است و لذا به آن اتحاد گوییم . از کلاس نهم با برخی اتحادها آشنا شده اید. در اینجا آن اتحادها را بازنویسی می کنیم.
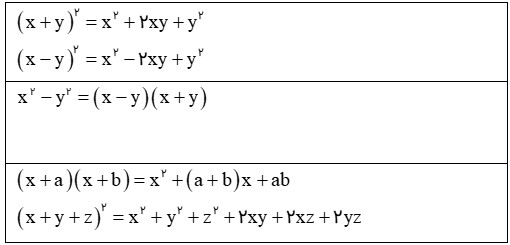
حال آماده هستیم تا چند اتحاد جدید معرفی کنیم. اولین اتحاد ، اتحاد مربع سه جمله ای است. یعنی هدف یافتن حاصل\({\left( {x + y} \right)^3}\) است. به کمک اتحادهای بالا عبارت فوق را تا سرحد امکان ساده می کنیم.
\(\begin{array}{l}{\left( {x + y} \right)^3} = {\left( {x + y} \right)^2} \times \left( {x + y} \right)\\ = \left( {{x^2} + 2xy + {y^2}} \right) \times \left( {x + y} \right)\\ = {x^3} + {x^2}y + 2{x^2}y + 2x{y^2} + {y^2}x + {y^3}\\ = {x^3} + 3{x^2}y + 3x{y^2} + {y^3}\end{array}\)
بنابراین نتیجه حاصل بصورت زیر بدست می آید:
\({\left( {x + y} \right)^3} = {x^3} + 3{x^2}y + 3x{y^2} + {y^3}\)
اگر در رابطه فوق \({\left( {x - y} \right)^3}\) رابطه زیر حاصل می شود:
\({\left( {x - y} \right)^3} = {x^3} - 3{x^2}y + 3x{y^2} - {y^3}\)
در نهایت اگر از xy در جملات دوم و سوم فاکتور بگیریم خواهیم داشت:
\(\begin{array}{l}{x^3} + {y^3} = {\left( {x + y} \right)^3} - 3xy\left( {x + y} \right)\\{x^3} - {y^3} = {\left( {x - y} \right)^3} + 3xy\left( {x - y} \right)\end{array}\)
اتحاد مجموع و تفاضل مکعبات نیز به صورت زیر حاصل می شود:
\(\begin{array}{l}{x^3} + {y^3} = \left( {x + y} \right)\left( {{x^2} - xy + {y^2}} \right)\\{x^3} - {y^3} = \left( {x - y} \right)\left( {{x^2} + xy + {y^2}} \right)\\\end{array}\)
کاربرد تجزیه در یافتن ب م م و ک م م چندجمله ای ها
یک چندجمله ای مثل \(a + b\) را در نظر بگیرید. اگر این دو جمله ای را در اعداد صحیح یا هر چندجمله ای دیگری ضرب کنیم ، حاصل را مضربی از \(a + b\) گوییم. پس عبارات زیر همگی مضارب \(a + b\) هستند.
\(2\left( {a + b} \right),\left( {{a^2} - {b^2}} \right),\left( {{a^3} - {b^3}} \right),...\)
همچنین عبارت \(a + b\) مقسوم علیه مشترک هر سه عبارت فوق است. بطور کلی برای یافتن بزرگترین مقسوم علیه مشترک و کوچکترین مضرب مشترک دو عبارت جبری ابتدا آنها راتجزیه کرده و سپس برای ب م م عوامل مشترک با کمترین توان در تجزیه را منظور می کنیم و برای ک م م هم عوامل مشترک را با بزرگترین توان در عوامل غیر مشترک ضرب می کنیم. به عنوان یک مثال ساده فرض کنید هدف یافتن ب م م و ک م م دو عبارت جبری \({a^2} - {b^2},{a^3} - {b^3}\) است. با تجزیه کردن آنها داریم:
\(\begin{array}{l}{a^2} - {b^2} = \left( {a - b} \right)\left( {a + b} \right)\\{a^3} - {b^3} = \left( {a - b} \right)\left( {{a^2} + ab + {b^2}} \right)\end{array}\)
پس با این حساب ب م م برابر \(a - b\) است و ک م م برابر \(\left( {a - b} \right)\left( {a + b} \right)\left( {{a^2} + ab + {b^2}} \right)\). یکی از فواید محاسبه ک م م در مخرج مشترک گرفتن برای جمع و تفریق عبارات گویاست.
1 عبارت زیر را تا حد ممکن (به عبارت های گویا) تجزیه کنید.
\({x^6} - {y^6} = \)
\({x^6} - {y^6} = \left( {{x^3} - {y^3}} \right)\left( {{x^3} + {y^3}} \right) = \left( {x - y} \right)\left( {{x^2} + xy + {y^2}} \right)\left( {x + y} \right)\left( {{x^2} - xy + {y^2}} \right)\)
2 عبارت زیر را تجزیه کنید.
\({x^6} - 1 = \)
\({x^6} - 1 = \left( {{x^3} - 1} \right)\left( {{x^3} + 1} \right) = \left( {x - 1} \right)\left( {{x^2} + x + 1} \right)\left( {x + 1} \right)\left( {{x^2} - x + 1} \right)\)
تهیه کننده: فرهاد صمدی
عبارات گویا
فصل 3 : توان های گویا و عبارت های جبری
عبارات گویا
منظور از یک عبارت گویا عبارتی است که صورت و مخرج آن چندجمله ای باشند. اگر \(q\left( x \right),p\left( x \right)\) دو چند جمله ای باشند عبارت \(\frac{{p\left( x \right)}}{{q\left( x \right)}}\) را یک عبارت گویا گوییم. شرط تعریف چنین عبارتی آن است که \(q\left( x \right) \ne 0\) باشد.
حذف رادیکال از عبارات جبری
در اتحاد \({a^3} - {b^3} = \left( {a - b} \right)\left( {{a^2} + ab + {b^2}} \right)\) اگر قرار دهیم \(a = \sqrt[3]{x},b = 1\) آنگاه:
\({\left( {\sqrt[3]{x}} \right)^3} - 1 = \left( {x - 1} \right) = \left( {\sqrt[3]{x} - 1} \right)\left( {\sqrt[3]{{{x^2}}} + \sqrt[3]{x} - 1} \right)\)
همان طور که مشاهده می کنید با ضرب دو عبارت در هم حاصل یک عبارت فارغ از رادیکال است. این کار اغلب به گویا کردن معروف است و یک دلیل ساده این کار این است که کلا کار با چندجمله ایها و عملیات بر آنها بسیار ساده تر از کار با عبارات رادیکالی است. بویژه زمانی که عبارت رادیکالی در مخرج باشد ، از بین بردن رادیکال آن امری مستحب است. به عنوان مثال ساده مخرج عبارت \(\frac{1}{{\sqrt x - \sqrt y }}\) را گویا می کنیم.
\(\frac{1}{{\sqrt x - \sqrt y }} = \frac{1}{{\sqrt x - \sqrt y }} \times \frac{{\sqrt x + \sqrt y }}{{\sqrt x + \sqrt y }} = \frac{{\sqrt x + \sqrt y }}{{\left( {\sqrt x - \sqrt y } \right)\left( {\sqrt x + \sqrt y } \right)}} = \frac{{\sqrt x + \sqrt y }}{{x - y}}\)
مخرج کسر های زیر را گویا کنید.
الف \(\frac{1}{{\sqrt[3]{x} - \sqrt[3]{y}}} = \)
\(\frac{1}{{\sqrt[3]{x} - \sqrt[3]{y}}} = \frac{1}{{\sqrt[3]{x} - \sqrt[3]{y}}} \times \frac{{\sqrt[3]{{{x^2}}} + \sqrt[3]{{xy}} + \sqrt[3]{{{y^2}}}}}{{\sqrt[3]{{{x^2}}} + \sqrt[3]{{xy}} + \sqrt[3]{{{y^2}}}}} = \frac{{\sqrt[3]{{{x^2}}} + \sqrt[3]{{xy}} + \sqrt[3]{{{y^2}}}}}{{x - y}}\)
ب \(\frac{1}{{\sqrt x - 1}} + \frac{2}{{\sqrt x + 1}} - \frac{{5x}}{{x - 1}} = \)
\(\frac{1}{{\sqrt x - 1}} + \frac{2}{{\sqrt x + 1}} - \frac{{5x}}{{x - 1}} = \frac{{\sqrt x + 1}}{{x - 1}} + \frac{{2\left( {\sqrt x - 1} \right)}}{{x - 1}} - \frac{{5x}}{{x - 1}} = \frac{{\sqrt x + 1 + 2\sqrt x - 2 - 5x}}{{x - 1}} = \frac{{3\sqrt x - 5x - 1}}{{x - 1}}\)
تهیه کننده: فرهاد صمدی
- آزمون آنلاین تمامی دروس پایه دهم
- گام به گام تمامی دروس پایه دهم
- ویدئو های آموزشی تمامی دروس پایه دهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه دهم
- فلش کارت های آماده دروس پایه دهم
- گنجینه ای جامع از انشاء های آماده پایه دهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه دهم
معادله درجه دوم و روش های حل آن
فصل 4 : معادله ها و نامعادله ها
معادله درجه دوم و روش های حل آن
به معادله ی \(a{x^2} + bx + c = 0\) یک معادله درجه دوم گوییم به شرطی که \(a \ne 0\) باشد. اعداد \(a,b,c \in \mathbb{R}\) را ضرائب معادله می نامیم. X مجهول معادله است و منظور از حل معادله فوق یعنی یافتن تمام اعداد حقیقی چون x که در معادله صدق کنند.
حال به معرفی روش های حل این معادله می پردازیم. برای این منظور با توجه به وضعیت ضرایب معادله روش هایی ارائه می شود.
روش ریشه گیری
اگر در معادله درجه دوم \(a{x^2} + bx + c = 0\) داشته باشیم \(b = 0\& c \le 0\) آنگاه با یک ریشه گیری جواب معادله بدست می آید.
مثال
معادله \(4{x^2} - 16 = 0\) را به روش ریشه گیری حل کنید.
\(4{x^2} - 16 = 0 \to 4{x^2} = 16 \to {x^2} = 4 \to x = \pm 2\)
روش فاکتورگیری
اگر در معادله درجه دوم داشته باشیم \(b = 0\) با یک فاکتورگیری ساده معادله حل می شود.
مثال
معادله \(3{x^2} + 12x = 0\) را به روش فاکتور گیری حل کنید.
\(3{x^2} + 12x = 0 \to 3x\left( {x + 4} \right) = 0 \to x = 0\& x = - 4\)
روش تجزیه
چنانچه هیچ یک از ضرائب صفر نباشد به کمک تجزیه کردن سه جمله ای می توان معادله را حل کرد. در این مورد توجه داریم که ازیکی از خواص اعداد حقیقی استفاده می کنیم که قبلا به آن اشاره کرده ایم :
\(ab = 0 \to a = 0 \vee b = 0\)
مثال
معادله \({x^2} - x - 12 = 0\) را به روش تجزیه حل کنید.
\(\begin{array}{l}{x^2} - x - 12 = \left( {x - 4} \right)\left( {x + 3} \right) = 0\\ \to x - 4 = 0 \to x = 4\\ \to x + 3 = 0 \to x = - 3\end{array}\)
روش مربع کامل کردن
تصور کنید می خواهید جواب معادله \({x^2} + 2x - 1 = 0\) را بدست آورید. هرچه تلاش کنید ، معادله به روش های معمول اشاره شده در بالا حل نخواهد شد. پس باید راهکار تازه ای بکار برد. بدین منظور می توان نوشت:
\(\begin{array}{l}{x^2} + 2x - 1 = 0 \to {x^2} + 2x = 1 \to {x^2} + 2x + 1 = 1 + 1\\ \to {\left( {x + 1} \right)^2} = 2 \to x + 1 = \pm \sqrt 2 \to x = \pm \sqrt 2 - 1\end{array}\)
اگر خوب به محاسبات نگاه کنید هدف از اضافه کردن عدد ١ به طرفین تساوی این بوده است که یک طرف معادله مربع کامل شود تا بتوان از طرفین جذر گرفت و جواب را یافت. چرا عدد ١؟ جواب در محاسبه زیر نهفته است. در حالت کلی برای اینکه عبارت \({x^2} + bx\) را به عبارتی تبدیل کنیم که شامل مربع کامل باشد به شکل زیر عمل می کنیم:
\({x^2} + bx = {x^2} + bx + \frac{{{b^2}}}{4} - \frac{{{b^2}}}{4} = {\left( {x + \frac{b}{2}} \right)^2} - \frac{{{b^2}}}{4}\)
مثال
جواب های معادله \(3{x^2} - 9x + 3 = 0\) را به روش مربع کامل پیدا کنید.
\(\begin{array}{l}3{x^2} - 9x + 3 = 0 \to {x^2} - 3x + 1 = 0 \to {x^2} - 3x + \frac{9}{4} - \frac{9}{4} + 1 = 0\\ \to {\left( {x - \frac{3}{2}} \right)^2} = \frac{9}{4} - 1 \to x - \frac{3}{2} = \pm \frac{{\sqrt 5 }}{2}\\ \to x = \pm \frac{{\sqrt 5 }}{2} + \frac{3}{2}\end{array}\)
روش کلی حل معادله درجه دوم
همان طور که مثال های حل شده بالا ملاحضه کردید،روش مربع کامل کردن کمی وقت گیر و پرمحاسبه است. به همین دلیل یکبار روش مربع کامل را روی فرم کلی معادله درجه دوم \(a{x^2} + bx + c = 0\) بکار می بریم تا دستوری کلی بر حسب رادیکال ها بیابیم و بعد از آن برای حل از دستور یافت شده استفاده کنیم. قبل از شروع محاسبات مبین معادله درجه دوم را بصورت \(\Delta = {b^2} - 4ac\) تعریف می کنیم. \(\Delta \) یک عدد حقیقی است و لذا هر سه حالت \(\Delta \langle 0,\Delta \rangle 0,\Delta = 0\) ممکن است اتفاق بیافتد.
\(\begin{array}{l}a{x^2} + bx + c = 0 \to {x^2} + \frac{b}{a}x + \frac{c}{a} = 0\\ \to {x^2} + \frac{b}{a}x + \frac{{{b^2}}}{{4{a^2}}} - \frac{{{b^2}}}{{4{a^2}}} + \frac{c}{a} = 0\\ \to {\left( {x + \frac{b}{{2a}}} \right)^2} = \frac{{{b^2}}}{{4{a^2}}} - \frac{c}{a} \to {\left( {x + \frac{b}{{2a}}} \right)^2} = \frac{{{b^2} - 4ac}}{{4{a^2}}}\\ \to x + \frac{b}{{2a}} = \pm \frac{{\sqrt \Delta }}{{2a}} \to x = \frac{{ - b \pm \sqrt \Delta }}{{2a}}\end{array}\)
به این ترتیب با فرض اینکه \(\Delta \rangle 0\) باشد معادله دارای دو جواب \({x_2} = \frac{{ - b - \sqrt \Delta }}{{2a}}\) و \({x_1} = \frac{{ - b + \sqrt \Delta }}{{2a}}\) می باشد. اگر \(\Delta = 0\) باشد هر دو جواب برابرند و داریم: \({x_1} = {x_2} = \frac{{ - b}}{{2a}}\) و سرانجام اگر \(\Delta \langle 0\) باشد، گوییم معادله جواب حقیقی ندارد.
1 معادله های زیر را به روش مربع کامل حل کنید.
الف \({x^2} - 6x = 7\)
\(\begin{array}{l}{x^2} - 6x = 7 \to {x^2} - 6x + 9 = 7 + 9 \to {\left( {x - 3} \right)^2} = 16 \to x - 3 = \pm 4\\x - 3 = 4 \to {x_1} = 7\\x - 3 = - 4 \to {x_2} = - 1\end{array}\)
ب \({r^2} + 4r + 4 = 0\)
\({r^2} + 4r + 4 = 0 \to {\left( {r + 2} \right)^2} = 0 \to r + 2 = 0 \to r = - 2\)
2 هر یک از معادله های زیر را به روش دلخواه حل کنید.
الف \(2{x^2} = 250\)
\(2{x^2} = 250 \to \div 2 \to {x^2} = 125 \to x = \pm \sqrt {125} \to x = \pm 5\sqrt 5 \)
ب \(4{x^2} - 13x + 3 = 0\)
\(\begin{array}{l}4{x^2} - 13x + 3 = 0 \to \Delta = {b^2} - 4ac \to \Delta = 169 - 48 \to \Delta = 121\\x = \frac{{ - b \pm \sqrt \Delta }}{{2a}}\\ \to {x_1} = \frac{{13 + 11}}{8} = 3\\ \to {x_2} = \frac{{13 - 11}}{8} = \frac{1}{4}\end{array}\)
3 طول یک مستطیل 3 سانتی متر بیشتر از 4 برابر عرض آن است. اگر مساحت این مستطیل 45 سانتی متر مربع باشد، ابعاد این مستطیل را مشخص کنید.
\(\begin{array}{l}S = a\left( {4a + 3} \right) \to 45 = a\left( {4a + 3} \right) \to 4{a^2} + 3a - 45 = 0 \to \Delta = {b^2} - 4ac \to \Delta = 729\\x = \frac{{ - b \pm \sqrt \Delta }}{{2a}}\\{x_1} = \frac{{ - 3 + 27}}{8} \to {x_1} = 3\\{x_2} = \frac{{ - 3 - 27}}{8} \to {x_2} = - \frac{{15}}{4}\end{array}\)
عرض مستطیل 3 و طول مستطیل 15 است.
تهیه کننده: فرهاد صمدی
سهمی ها
فصل 4 : معادله ها و نامعادله ها
سهمی ها
ساده ترین سهمی دارای معادله ی \(y = {x^2}\) است. اگر به متغیر x مقدار دهیم می توانیم نمودار آن را رسم کنیم. مثلا با فرض \(x = 0, \pm 1, \pm 2, \pm 3\) مقادیر حاصل عبارتند از \(y = 0,1,4,9\) اگر این نقاط را روی محورهای مختصات مشخص کنیم و نقاط حاصل را به هم وصل کنیم شکل زیر حاصل می شود.
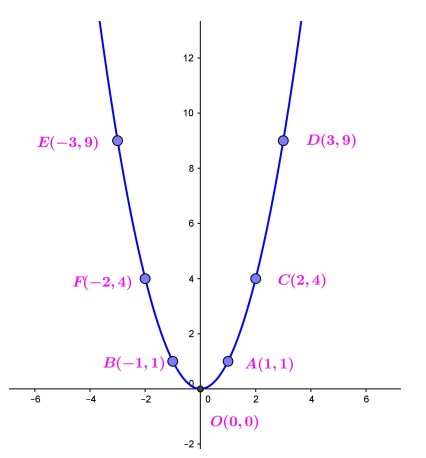
پایین ترین نقطه سهمی در شکل فوق مبداء مختصات است.
نقطه \(O\left( {0,0} \right)\) را مینیمم(کمینه) سهمی گوییم.
محور عرض ها سهمی را به دو قسمت یکسان تقسیم کرده است. محور عرض ها \(x = 0\) را محور تقارن سهمی گوییم.
منظور از یک سهمی معادله ای بصورت \(y = a{x^2} + bx + c\) است که \(a \ne 0\& a,b,c \in \mathbb{R}\) با مربع کامل کردن این عبارت بصورت:
\(y = a{\left( {x - h} \right)^2} + k\)
درمی آید که در این حالت راس سهمی یا مینیمم سهمی نقطه \(M\left( {h,k} \right)\) است و خط \(x = h\) را محور تقارن سهمی گوییم. اگر \(a\rangle 0\) باشد دهانه ی سهمی رو به بالا باز می شود و اگر \(a\langle 0\) باشد دهانه سهمی رو به پایین باز می شود.
رسم سهمی ساده تر می شود اگر بتوانیم دستوری صریح از راس سهمی بدست آوریم. برای این منظور داریم :
\(\begin{array}{l}y = a{x^2} + bx + c \to y = a\left( {{x^2} + \frac{b}{a}x + \frac{c}{a}} \right)\\ \to y = a\left( {{x^2} + \frac{b}{a}x + \frac{{{b^2}}}{{4{a^2}}} - \frac{{{b^2}}}{{4{a^2}}} + \frac{c}{a}} \right)\\ \to y = a{\left( {x + \frac{b}{{2a}}} \right)^2} - \frac{{{b^2}}}{{4a}} + c\\ \to y = a{\left( {x + \frac{b}{{2a}}} \right)^2} + \frac{{4ac - {b^2}}}{{4a}}\end{array}\)
با این حساب راس سهمی بصورت زیر بدست می آید:
\(M\left( { - \frac{b}{{2a}},\frac{{4ac - {b^2}}}{{4a}}} \right)\)
به این ترتیب با داشتن راس سهمی کافیست یک یا دو نقطه قبل و بعد از آن را در معادله منحنی جایگذاری کنیم تا عرض آن نقاط حاصل شده و سپس سهمی را رسم کنیم. همچنین توجه کنید که اگر \(a\rangle 0\) باشد سهمی مینیمم دارد و اگر \(a\langle 0\) باشد سهمی ماکزیمم (بیشینه) دارد.
1 اگر \(\left( { - 2,5} \right)\) و \(\left( {0,5} \right)\) دو نقطه از یک سهمی باشند، خط تقارن این سهمی را به دست آورید.
با توجه به اینکه عرض نقاط یکسان است، این دو نقطه نسبت به محور تقارن سهمی قرینه ی یکدیگرند، به عبارت دیگر محور تقارن از وسط طول های این دو نقطه می گذرد.
\(x = \frac{{ - 2 + 0}}{2} \to x = - 1\)
2 دو پرتابگر وزنه در یک مسابقه ورزشی، وزنه های خود را با زاویه های متفاوت \(\alpha \) و \(\beta \) که \(\alpha \langle \beta \) است، پرتاب کرده اند. پرتابگر A، زاویه \(\alpha \) را انتخاب می کند و مسیر طی شده از رابطه ی \(y = - \frac{{{x^2}}}{2} + \frac{3}{2}x + 2\) به دست می آید. پرتابگر B نیز زاویه \(\beta \) را انتخاب می کند و مسیر طی شده از رابطه ی \(y = - 2{x^2} + 3x + 2\) به دست می آید. در هر دو معادله، y ارتفاع وزنه از سطح زمین و x مسافت افقی طی شده، بر حسب متر است. کدام یک از وزنه ها ارتفاع بیشتری از سطح زمین پیدا کرده است؟ اندازه آنها را مشخص کنید.
\(\begin{array}{l}A)y = - \frac{{{x^2}}}{2} + \frac{3}{2}x + 2 = 0 \to \times 2 \to - {x^2} + 3x + 4 = 0 \to \Delta = 25\\{x_1} = - 1\& {x_2} = 4\end{array}\)
مسافتی که وزنه A طی کرده است 5 متر است.
\(\begin{array}{l}B)y = - 2{x^2} + 3x + 2 = 0 \to \Delta = 25\\{x_1} = - \frac{1}{2}\& {x_2} = 2\end{array}\)
مسافتی که وزنه B طی کرده است \(\frac{5}{2}\) متر است.
بنابراین وزنه پرتابگر A مسافت بیشتری پیموده است.
میزان ارتفاع هر دو وزنه یکی است که هر دو \(\frac{{25}}{8}\) را نشان می دهد.
تهیه کننده: فرهاد صمدی
تعیین علامت چندجمله ای ها
فصل 4 : معادله ها و نامعادله ها
تعیین علامت چندجمله ای ها
به دقت به شکل زیر نگاه کنید. نمودار یک منحنی در دستگاه مختصات ترسیم شده است. نام منحنی \(p\left( x \right)\) است و در برخی بازه ها بالای محور x هاست و لذا مثبت است و در برخی بازه ها زیر محور x هاست و لذا منفی است. اگر دقت کنید نقاطی که منحنی محور طولها را در آن ها قطع کرده است نقشی اساسی در تعیین اینکه p مثبت است یا منفی بازی می کند. چنین نقاطی را ریشه های p گوییم. در حالت کلی نقاط حاصل از حل معادله \(p\left( x \right) = 0\) را ریشه های p گوییم.
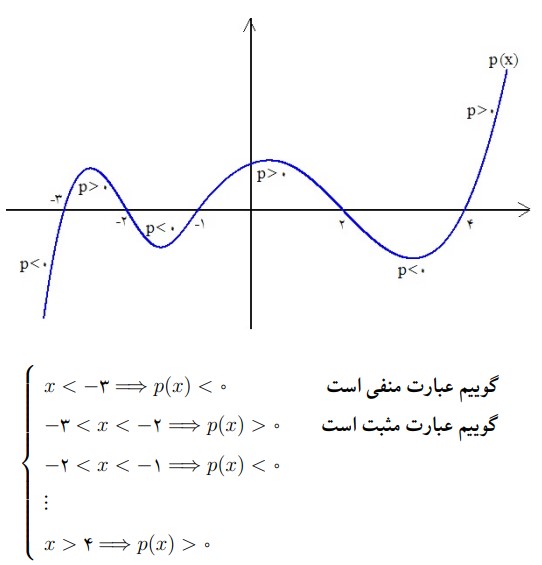
تعیین علامت دوجمله ای درجه اول
می خواهیم عبارت \(p\left( x \right) = ax + b\) را تعیین علامت کنیم. ابتدا ریشه یا ریشه های آن را بدست می آوریم:
\(p\left( x \right) = 0 \to ax + b = 0 \to x = - \frac{b}{a}\)
در حالت کلی نمودار \(p\left( x \right) = y = ax + b\) یکی از دو حالت زیر را دارد:
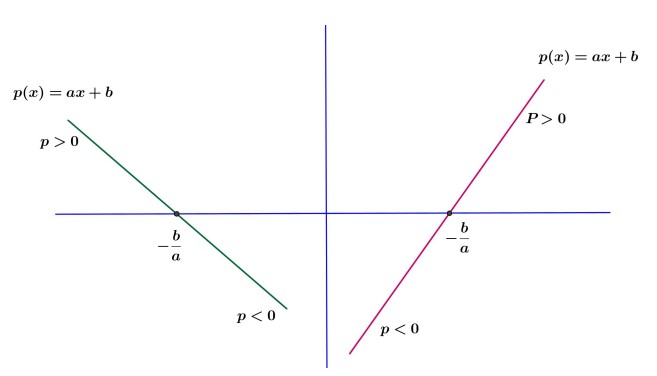
ازنمودار فوق می توان نتیجه گرفت:
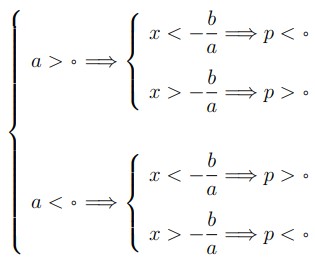
خلاصه بحث فوق در جدول زیر که آن را جدول تعیین علامت می نامیم آمده است.

چنانچه بخواهیم علامت یک عبارت جبری را که شامل چند دوجمله ای درجه اول است را تعیین کنیم، می توانیم در یک جدول همه ی دوجمله ایها را نوشته و ریشه تک تک آنها را یافته و هر کدام را تعیین علامت کنیم و دست آخر با ضرب علامت ها درهم علامت کل عبارت را بیابیم.
مثال
عبارت \(y = 5x - 2\) را تعیین علامت کنید.
ریشه عبارت \(5x - 2\) از معادله \(5x + 2 = 0\) به دست می آید که برابر \(x = \frac{2}{5}\) است.
با توجه به اینکه علامت ضریب x ؛ یعنی \(a = 5\) مثبت است، طبق جدول بالا، جدول تعیین علامت به صورت زیر است:
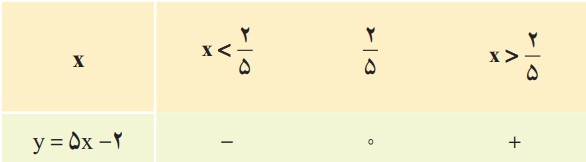
مقدار y را برای \(x = 3\) و \(x = - 1\) به دست آورید و صحت علامت اعداد به دست آمده را با جدول بالا بررسی کنید.
\(\begin{array}{l}x = 3 \to y = 5\left( 3 \right) - 2 = 13\\x = - 1 \to y = 5\left( { - 1} \right) - 2 = - 7\end{array}\)
تعیین علامت سه جمله ای درجه دوم
همان طور که تا الان متوجه شدید یک سه جمله ای درجه دوم را می توان با تجزیه به عامل های درجه اول تعیین علامت کرد. اما این زمانی شدنی است که عبارت تجزیه شود . در صورتیکه عبارت تجزیه نشود راه حل چیست؟ راه حل یافتن روشی است که به کمک آن بتوان سه جمله ای ها را مستقیما تعیین علامت کرد. در حالت کلی یک سه جمله ای درجه دوم یا همان سهمی به یکی از صورت های زیر است:
الف: اگر \(\Delta \rangle 0\)
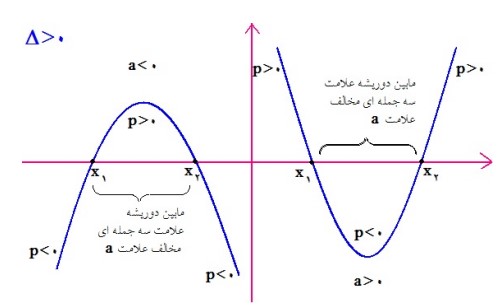
ب: اگر \(\Delta = 0\)
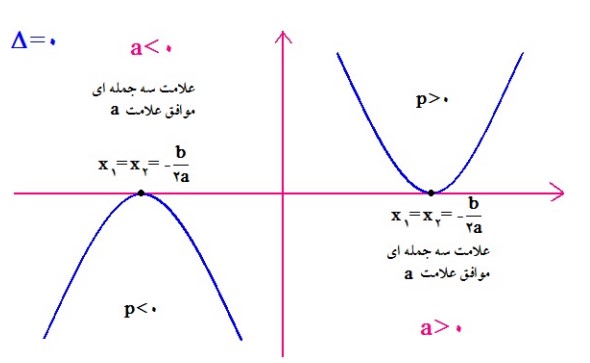
ج: اگر \(\Delta \langle 0\)
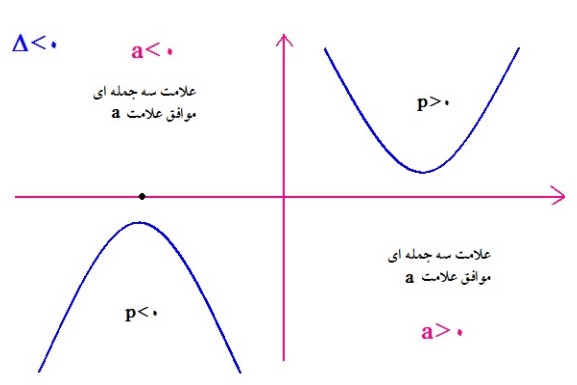
پس برای تعیین علامت سه جمله ای \(p\left( x \right)\) ابتدا باید \(p\left( x \right) = 0\) را حل کنیم. پس اولین گام یافتن مبین معادله درجه دوم است یعنی \(\Delta = {b^2} - 4ac\) است که بسته به علامت \(\Delta \) یکی از جداول زیر را تشکیل می دهیم.
اگر \(\Delta \rangle 0\) باشد:
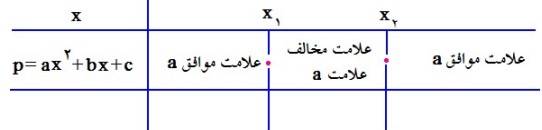
اگر \(\Delta = 0\) باشد:

اگر \(\Delta \langle 0\) باشد:

نتایج حاصل از بررسی نمودارهای یک سه جمله ای درجه دوم را می توان از روی معادله سه جمله ای درجه دوم \(p\left( x \right) = a{x^2} + bx + c\) نیز بدست آورد. برای این منظور فرم تبدیل شده ی عبارت p را که قبلا محاسبه کرده ایم بصورت زیر می نویسیم:
\(\begin{array}{l}p\left( x \right) = a{x^2} + bx + c = a\left( {{{\left( {x + \frac{b}{{2a}}} \right)}^2} - \frac{{{b^2} - 4ac}}{{4{a^2}}}} \right) = a\left( {{{\left( {x + \frac{b}{{2a}}} \right)}^2} - \frac{\Delta }{{4{a^2}}}} \right) \to \frac{{p\left( x \right)}}{a} = \left( {{{\left( {x + \frac{b}{{2a}}} \right)}^2} - \frac{\Delta }{{4{a^2}}}} \right)\\\end{array}\)
حال اگر \(\Delta \langle 0\) باشد عبارت \({\left( {x + \frac{b}{{2a}}} \right)^2} - \frac{\Delta }{{4{a^2}}}\) همواره مثبت است پس \(\frac{{p\left( x \right)}}{a}\) هم مثبت است و این یعنی اگر a مثبت باشد آنگاه \(p\left( x \right)\) هم مثبت است.و اگر a منفی باشد آنگاه \(p\left( x \right)\) هم منفی است.
حال اگر \(\Delta = 0\) باشد عبارت حاصل بصورت \({\left( {x + \frac{b}{{2a}}} \right)^2}\) درمی آید و باز \(\frac{{p\left( x \right)}}{a}\) مثبت است و مانند حالت قبل نتیجه حاصل می شود.
سرانجام اگر \(\Delta \rangle 0\) باشد، پس \(\sqrt \Delta \) با معنی است و داریم:
\(\begin{array}{l}1)\frac{{p\left( x \right)}}{a} = \left( {{{\left( {x + \frac{b}{{2a}}} \right)}^2} - \frac{\Delta }{{4{a^2}}}} \right)\\\frac{{p\left( x \right)}}{a} = \left( {x + \frac{b}{{2a}} - \frac{{\sqrt \Delta }}{{2a}}} \right)\left( {x + \frac{b}{{2a}} + \frac{{\sqrt \Delta }}{{2a}}} \right)\end{array}\)
عبارت های داخل پرانتز که بلافاصله بعد از x آمده اند همان ریشه های معادله \(p\left( x \right) = 0\) هستند. اگر قرار دهیم: \({x_2} = \frac{{ - b - \sqrt \Delta }}{{2a}}\) و \({x_1} = \frac{{ - b + \sqrt \Delta }}{{2a}}\)
آنگاه معادله (1) بصورت زیر تبدیل می شود:
\(\frac{{p\left( x \right)}}{a} = \left( {x - {x_1}} \right)\left( {x - {x_2}} \right)\)
بدون آنکه استدلال دچار نقصان شود می توان فرض کرد \({x_1}\langle {x_2}\) است. حال برای بررسی علامت \(\frac{{p\left( x \right)}}{a}\) باید حالات زیر را بررسی کرد.
1) اگر \({x_1}\langle x\langle {x_2}\) باشد عبارت \(\left( {x - {x_1}} \right)\left( {x - {x_2}} \right)\) منفی است و لذا \(\frac{{p\left( x \right)}}{a}\) منفی است و این یعنی \(p\left( x \right)\) و a از نظر علامت مخالف هم هستند.
2) اگر \({x_1}\langle x\langle {x_2}\) باشد و یا \({x_1}\langle {x_2}\langle x\) باشد عبارت \(\left( {x - {x_1}} \right)\left( {x - {x_2}} \right)\) مثبت است و لذا \(\frac{{p\left( x \right)}}{a}\) هم مثبت است و این یعنی \(p\left( x \right)\) و a هم علامت هستند.
همان طور که مشاهده کردید نتایج بدست آمده در این حالت منطبق بر نتایج بدست آمده از نمودارهای هندسی است.
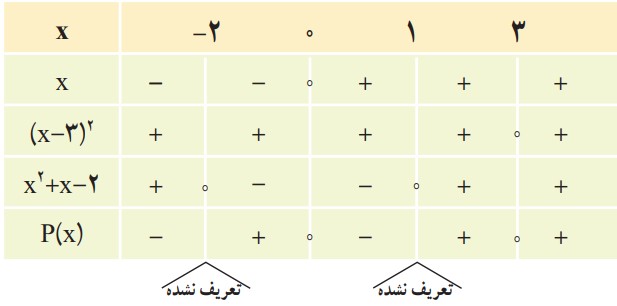
عبارت \(p\left( x \right) = \frac{{x{{\left( {x - 3} \right)}^2}}}{{{x^2} + x - 2}}\) را تعیین علامت کنید.
هریک از عبارت های موجود در صورت و مخرج را تعیین علامت می کنیم و نتایج را در یک جدول می نویسیم.
\(\begin{array}{l}x = 0\\{\left( {x - 3} \right)^2} = 0 \to x - 3 = 0 \to x = 3\\{x^2} + x - 2 = 0 \to \left( {x + 2} \right)\left( {x - 1} \right) = 0 \to x = - 2 \vee x = 1\end{array}\)
تهیه کننده: فرهاد صمدی
- آزمون آنلاین تمامی دروس پایه دهم
- گام به گام تمامی دروس پایه دهم
- ویدئو های آموزشی تمامی دروس پایه دهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه دهم
- فلش کارت های آماده دروس پایه دهم
- گنجینه ای جامع از انشاء های آماده پایه دهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه دهم
نا معادله
فصل 4 : معادله ها و نامعادله ها
نا معادله
یکی از مهم ترین کاربردهای تعیین علامت حل نامعادلات جبری است. برای یافتن مقادیری از x که در شرط \(p\left( x \right)\rangle 0\) صدق می کند تنها راه تعیین علامت p است . حتی ممکن است p لزوما چندجمله ای نباشد. قبل از هر چیز خواص مقدماتی نامساوی ها را بیان می کنیم.
خواص اصلی نامساوی ها
\(\begin{array}{l}1)a \le b \to a + c \le b + c\\2)a \le b\\ \to c\rangle 0 \to ac \le bc\\ \to c\langle 0 \to ac \ge bc\\3)a \le b\& b \le c \to a \le c\\4)0\langle a \le b \to \frac{1}{a} \ge \frac{1}{b}\rangle 0\\5)a \le b\langle 0 \to \frac{1}{b} \le \frac{1}{a}\langle 0\\6)a\langle 0\langle b \to \frac{1}{a}\langle 0\langle \frac{1}{b}\end{array}\)
قدرمطلق و معادلات و نامعادلات قدرمطلقی
قدر مطلق x را که با نماد \(\left| x \right|\) نشان داده می شود بصورت زیر تعریف می کنیم:
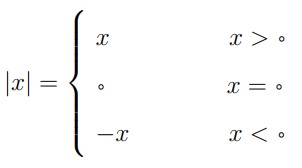
مثال
قدرمطلق عبارت های زیر را حساب کنید.
الف \(\left| {1 + \sqrt 2 } \right| = \)
\(\left| {1 + \sqrt 2 } \right| = 1 + \sqrt 2 \)
ب \(\left| {1 + {t^2}} \right| = \)
\(\begin{array}{l}\left| {1 + {t^2}} \right| = 1 + {t^2}\\\end{array}\)
پ \(\left| {1 - \sqrt 2 } \right| = \)
\(\left| {1 - \sqrt 2 } \right| = \sqrt 2 - 1\)
ج \(\left| {1 - \frac{\pi }{3}} \right| = \)
\(\left| {1 - \frac{\pi }{3}} \right| = \frac{\pi }{3} - 1\)
مهم ترین خواص قدرمطلق ها
\(\begin{array}{l}1)\left| u \right| = 0 \to u = 0\\2)\left| u \right| = a \to u = \pm a,a\rangle 0\\3)\left| u \right| \le a \to - a \le u \le a,a\rangle 0\\4)\left| u \right| \ge a \to u \ge a \vee u \le - a,a\rangle 0\\5){u^2} \le {a^2} \leftrightarrow \left| u \right| \le a \leftrightarrow - a \le u \le a,a\rangle 0\\6){u^2} \ge {a^2} \leftrightarrow \left| u \right| \ge a \leftrightarrow u \ge a \vee u \le - a,a\rangle 0\\7)\left| u \right| = u \leftrightarrow u \ge 0\& \left| u \right| = - u \leftrightarrow u \le 0\\8)\left| {\left| a \right| - \left| b \right|} \right| \le \left| {a \pm b} \right| \le \left| a \right| + \left| b \right|\\9)\left| {ab} \right| = \left| a \right|\left| b \right|\& \frac{{\left| a \right|}}{{\left| b \right|}} = \left| {\frac{a}{b}} \right|\end{array}\)
به خاصیت 8ام نامساوی مثلثی نیز می گویند.
1 تعداد ضربان قلب، پس از X دقیقه کار سنگین بدنی، طبق رابطه ی \(y = \frac{{15}}{8}{x^2} - 30x + 200\) به دست می آید. در چه زمان هایی پس از یک کار سنگین بدنی، تعداد ضربان قلب بیشتر است؟ آیا تمام جواب های به دست آمده قابل قبول اند؟
\(\begin{array}{l}\frac{{15}}{8}{x^2} - 30x + 200\rangle 110 \to y = \frac{{15}}{8}{x^2} - 30x + 90\rangle 0 \to \times 8 \to 15{x^2} - 240x + 720\rangle 0\\15{x^2} - 240x + 720 = 0 \to \Delta = 14400 \to {x_1} = 12\& {x_2} = 4\\ \to x\langle 4 \vee x\rangle 12\end{array}\)
2 معادلات و نامعادلات زیر را حل کنید.
الف \(\left| {{x^3} - 9x} \right| = 0\)
\(\begin{array}{l}\left| {{x^3} - 9x} \right| = 0 \to {x^3} - 9x = 0 \to x\left( {{x^2} - 9} \right) = 0\\{x_1} = 0 \vee {x_2} = 3\end{array}\)
ب \(\left| {3x - 5} \right| = 4\)
\(\left| {3x - 5} \right| = 4 \to 3x - 5 = 4 \to 3x = 9 \to x = \pm 3\)
ج \(\left| {2x - 1} \right|\langle 1\)
\(\left| {2x - 1} \right|\langle 1 \to - 1\langle 2x - 1\langle 1 \to 0\langle 2x\langle 2 \to 0\langle x\langle 1\)
3 یک نا معادله قدر مطلقی بنویسید که مجموعه جواب آن \(\left( { - \infty ,6} \right] \cup \left[ {6, + \infty } \right)\) باشد.
با توجه به اینکه \(\frac{9}{2}\) وسط فاصله \(\left[ {3,6} \right]\) است. شکل مجموعه نقاطی است که فاصله شان از \(\frac{9}{2}\) بیشتر از \(\frac{3}{2}\) می باشد بنابراین \(\left| {x - \frac{9}{2}} \right| \ge \frac{3}{2}\) جواب است.
تهیه کننده: فرهاد صمدی
مفهوم تابع و روش های نمایش آن
فصل 5 : تابع
مفهوم تابع و روش های نمایش آن
یک تابع بین دو مجموعه A و B رابطه ای است که به هر عضو از A دقیقا یک عضو از B نسبت داده شود.
مثال
از نمودارهای ون زیر کدام تابع است و کدام نیست؟

از نمودار های ون بالا A و C تابع نیستند و مابقی تابع هستند.
1 در نمودار های ون توابع فقط باید یک پیکان از مولفه اول خارج شود و هیچگاه نباید در مولفه اول تابعی تنها باشد.
2 یک مجموعه شامل زوج های مرتب زمانی تابع است که در آن هیچ دو زوج مرتبی با مولفه اول یکسان وجود نداشته باشد و چنانچه دو مولفه اول یکسان باشند به ناچار (برای تابع بودن) مولفه های دوم آن ها نیز یکسان باشند.
تشخیص تابع بودن یک رابطه از روی نمودار مختصاتی آن
تاکنون متوجه شده اید یک نمودار پیکانی ون زمانی معرف تابع است که از هر عضو مجموعه اول یک و تنها یک پیکان به مجموعه دوم خارج شده باشد. در مورد روابطی که بصورت زوج مرتب بیان می شوند نیز متوجه شده اید که شرط تابع بودن، نبودن دو زوج مرتب متفاوت با مولفه های اول یکسان است. همچنین متوجه شده اید که روابطی که بصورت زوج های مرتب بیان می شوند و مولفه های آن اعداد حقیقی اند دارای نموداری در دستگاه مختصات هستند. حال پرسش اینجاست که اگر تنها یک نمودار به ما داده باشند چگونه از روی نمودار تشخیص دهیم که آن نمودار معرف تابع است یا خیر؟
یک نمودار در دستگاه مختصات معرف تابع است هرگاه هر خطی که به موازات محور عرض ها رسم شود نمودار را حداکثر در یک نقطه قطع کند.
مثال
کدام یک از روابط زیر یک تابع را معلوم می کند؟ توضیح دهید.
الف) رابطه ای که به ضلع یک مربع، محیط مربع را نسبت می دهد.
تابع است، زیرا به ضلع یک مربع فقط یک محیط را می توان نسبت داد.
ب) رابطه ای که به هر عدد، ریشه های دوم آن عدد را نسبت می دهد.
تابع نیست، اعداد مثبت دارای دو ریشه هستند.
دامنه و برد توابع
دامنه و برد یک تابع را در مثال های بالا دیده و بکاربرده ایم ، بدون اینکه متوجه شده باشید. در واقع مولفه های اول زوج های مرتب در هر تابع را دامنه تابع و مولفه های دوم زوج های مرتب را برد تابع می نامند. دامنه ی تابعی چون f را با \({D_f}\) و برد آن را با \({R_f}\) نشان می دهیم. در اینجا برای سادگی قراردادی را معرفی می کنیم. اگر f تابعی از مجموعه A به مجموعه B باشد و عضو \(a \in A\) به عضو \(b \in B\) نسبت داده شده باشد یعنی \(a \to b\) اغلب این عبارت را با نماد \({f_{\left( a \right)}} = b\) خلاصه نویسی می کنیم. گاهی اوقات هم گوییم تصویر a تحت f برابر b است. مثلا در تابع :
\(f = \left\{ {\left( {2, - 1} \right),\left( {\sqrt 2 ,1 - \sqrt 2 } \right),\left( {\pi ,\frac{1}{\pi }} \right),\left( {\frac{1}{3},\frac{2}{5}} \right)} \right\}\)
می نویسیم:
\({f_{\left( 2 \right)}} = - 1,{f_{\left( {\sqrt 2 } \right)}} = 1 - \sqrt 2 ,{f_{\left( \pi \right)}} = \frac{1}{\pi },{f_{\left( {\frac{1}{3}} \right)}} = \frac{2}{5}\)
واضح است که در اینجا :
\(\begin{array}{l}{D_f} = \left\{ {2,\sqrt 2 ,\pi ,\frac{1}{3}} \right\}\\{R_f} = \left\{ { - 1,1 - \sqrt 2 ,\frac{1}{\pi },\frac{2}{5}} \right\}\end{array}\)
در شکل زیر شناسنامه ی یک تابع را نوشته ایم.
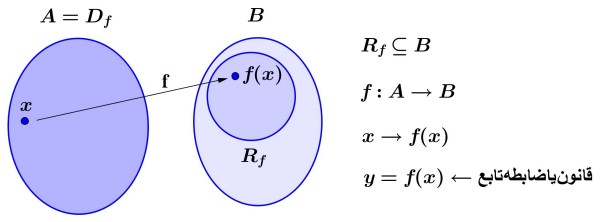
وقتی مینویسیم \(f:A \to B\) منظور از A دامنه تابع است. اما B لزوما برد f نیست و همان طور که از شکل مشخص است همواره \({R_f} \subseteq B\) است. به \(y = {f_{\left( x \right)}}\) ضابطه یا قانون تابع گویند. مجموعه B را اغلب هم دامنه تابع f می نامیم.
در تابع خطی لزومی ندارد که دامنه تمام اعداد حقیقی باشد. ممکن است دامنه ی یک تابع خطی یک مجموعه متناهی، یا مجموعه اعداد طبیعی ویا مجموعه اعداد صحیح باشد.
1 تابعی مثال بزنید که:
الف دامنه آنها تنها شامل دو عضو باشد.
\(\left\{ {\left( {2,1} \right),\left( {3,4} \right)} \right\}\)
ب برد آن تنها از یک عضو تشکیل شده باشد.
\(\left\{ {\left( {1,1} \right),\left( {2,1} \right)} \right\}\)
ج دامنه و برد آن نامتناهی باشند.
\(\left\{ {\left( {1,1} \right),\left( {2,2} \right),\left( {3,3} \right),...} \right\}\)
2 نمایش جبری سه تابع خطی را بنویسید که دامنه آن بازه \(\left[ { - 3,5} \right]\) باشد.
\(\begin{array}{l}{f_{\left( x \right)}} = 2x + 4\& {D_f} = \left[ { - 3,5} \right]\\{g_{\left( x \right)}} = x - 3\& {D_f} = \left[ { - 3,5} \right]\\{h_{\left( x \right)}} = - 3x + 2\& {D_f} = \left[ { - 3,5} \right]\end{array}\)
3 جدول زیر دمای سنگ ها در عمق های متفاوت زیر سطح زمین را نشان می دهد.

الف معادله ای برای این تابع به دست آورید.
\({f_{\left( x \right)}} = 35x + 20\)
ب دمای یک سنگ را که در عمق 10 کیلومتری زیر زمین است، بیابید.
\({f_{\left( {10} \right)}} = 35 \times 10 + 20 = 370\)
تهیه کننده: فرهاد صمدی
انواع تابع
فصل 5 : تابع
تابع ثابت
تابع ثابت تابعی است که تمام اعضای دامنه را به یک و فقط یک عضو از برد نظیر کند. تابع ذکر شده در زیر تابع ثابت است.
\(f = \left\{ {\left( {a,a} \right),\left( {b,a} \right),\left( {c,a} \right),\left( {d,a} \right)} \right\}\)
نمودار چنین توابعی وقتی دامنه بصورت بازه باشد خطی موازی محور طول هاست و اگر دامنه زیرمجموعه ای از اعداد صحیح باشد بصورت نقاطی در دستگاه مختصات است که همگی روی خطی موازی محور طول ها قرار دارند.
تابع همانی
تابع \(i:A \to A\) را تابع همانی گوییم هرگاه برای هر \(x \in A\) داشته باشیم: \({i_{\left( x \right)}} = x\) به عبارت بهتر هر عضو از دامنه به خودش نظیر می شود. در حالتی که دامنه \(\mathbb{R}\) باشد ، تابع همانی همان خط \(y = x\)، نیم ساز ناحیه اول و سوم است.
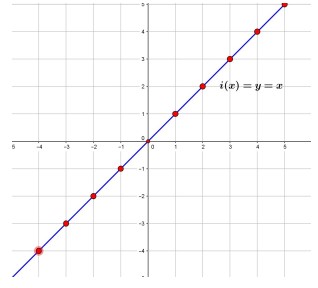
توابع چندجمله ای
فرض کنید مربعی به ضلع x دارید. مساحت این مربع بر حسب ضلع آن برابر است با: \({S_{\left( x \right)}} = {x^2}\) همچنین مساحت دایره ای به شعاع r برابر است با \({S_{\left( r \right)}} = \pi {r^2}\) حجم مکعبی به ضلع x برابر است با \({V_{\left( x \right)}} = {x^3}\) و حجم کره ای به شعاع r برابر \({V_{\left( r \right)}}\frac{4}{3}\pi {r^3}\) اینها همه نمونه هایی از توابع چندجمله ای هستند. در حالت کلی توابعی که ضابطه ی جبری آن ها یک چندجمله ای از یک متغیر باشد را تابع چندجمله ای گوییم. شکل کلی یک تابع چندجمله ای بصورت زیر است:
\({p_{\left( x \right)}} = {a_n}{x^n} + {a_{n - 1}}{x^{n - 1}} + ... + {a_1}x + {a_0}\)
آشناترین توابع چندجمله ای تابع دوجمله ای درجه اول \({f_{\left( x \right)}} = ax + b\) یا همان تابع خطی است و تابع سه جمله ای درجه دوم \({f_{\left( x \right)}} = a{x^2} + bx + c\) است که همان سهمی است. از این توابع در ضابطه های توابع چندضابطه ای زیاد استفاده می کنیم. برای نمونه در تابع سه ضابطه ای زیر هر ضابطه به تنهایی یک تابع چندجمله ای است.
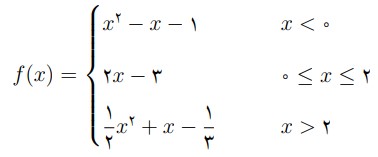
در حالت کلی در معرفی یک تابع باید دامنه آن مشخص شده باشد.درغیراین صورت بزرگترین مجموعه ممکن را به عنوان دامنه تابع اختیار می کنیم.توابع چندجمله ای چنانچه دامنه مشخصی نداشته باشند دامنه آن ها را برابر \(\mathbb{R}\) در نظر می گیریم.
تابع قدرمطلق
در فصل قبل با قدرمطلق و خواص آن آشنا شدید. در حالت کلی تابع قدرمطلق بصورت زیر تعریف می شود:
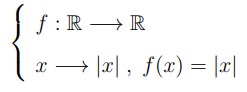
یادآوری می کنیم که:
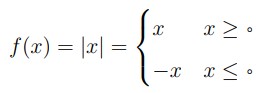
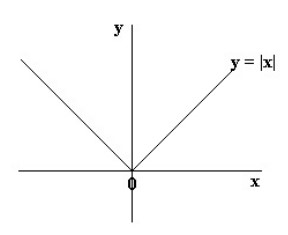
نمودار تابع \({f_{\left( x \right)}} = \left| x \right|\) یکی از مهمترین نمودارهاست و بصورت زیر است:
معرفی دو تابع رادیکالی مهم
اولین تابع رادیکالی که می خواهیم بررسی کنیم تابع:
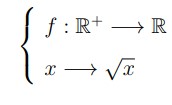
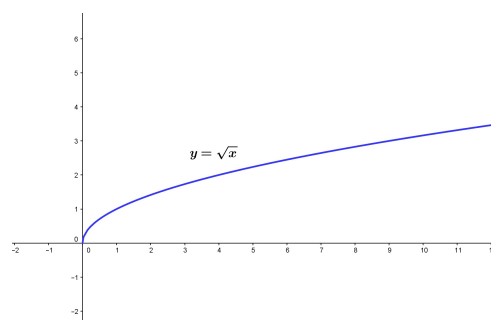
با ضابطه ی \({f_{\left( x \right)}} = \sqrt x \) است. این تابع داری دامنه ای بصورت \({D_f} = \left[ {0, + \infty } \right)\) است و برد آن نیز \({R_f} = \left[ {0, + \infty } \right)\) است. نمودار این تابع را در شکل زیر می بینید.
تابع رادیکالی دیگری که قصد معرفی آن را داریم تابع ریشه سوم است:
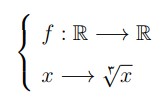
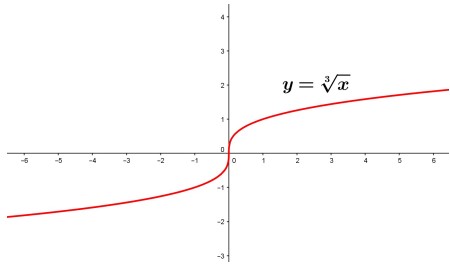
ضابطه ی این تابع \({f_{\left( x \right)}} = \sqrt[3]{x}\) است. نمودار آن را در زیر می بینید:
نمودار تابع قطعه ای f داده شده است. ضابطه ی آن را بدست آورید. دامنه و برد این تابع را به دست آورید.
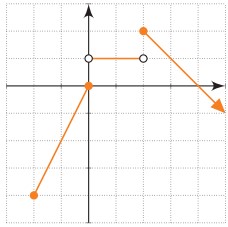
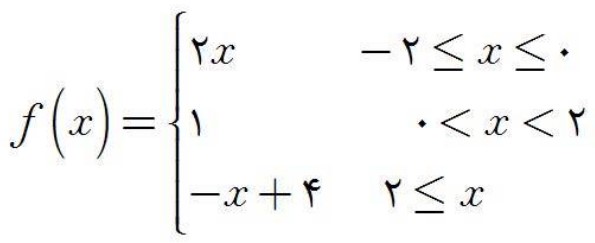
\(\begin{array}{l}{D_f} = \left[ { - 2, + \infty } \right)\\{R_f} = \left[ { - 4,2} \right]\end{array}\)
تهیه کننده: فرهاد صمدی
- آزمون آنلاین تمامی دروس پایه دهم
- گام به گام تمامی دروس پایه دهم
- ویدئو های آموزشی تمامی دروس پایه دهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه دهم
- فلش کارت های آماده دروس پایه دهم
- گنجینه ای جامع از انشاء های آماده پایه دهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه دهم
ترسیم با انتقال
فصل 5 : تابع
ترسیم با انتقال
در این قسمت می خواهیم به کمک انتقال نمودارهای جدیدی را به کمک نمودارهای قبلی رسم کنیم. به دقت به شکل های زیر نگاه کنید.
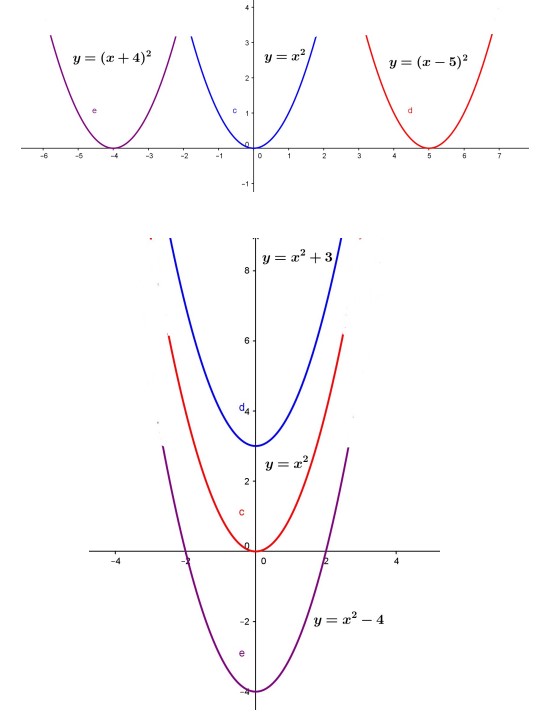
همان طور که دیده می شود با تبدیل شدن \(x \to x - 5\) نمودار \(y = {x^2}\) به اندازه ۵ واحد در جهت مثبت روی محور طول ها جابجا شده است و با تبدیل \(x \to x + 4\) نمودار \(y = {x^2}\) به اندازه چهار واحد در جهت منفی روی محور طول ها جابجا شده است.
همچنین با تبدیل \({f_{\left( x \right)}} \to {f_{\left( x \right)}} + 3\) نمودار \(y = {x^2}\) به اندازه ٣ واحد در جهت مثبت محور عرض ها به بالا حرکت کرده و با تبدیل \({f_{\left( x \right)}} \to {f_{\left( x \right)}} - 4\) به اندازه ی ۴ واحد روی محور عرض ها به پایین حرکت کرده است.
در حالت کلی همین روابط درست است. نمودار \(y = {f_{\left( {x - a} \right)}},a\rangle 0\) نسبت به \(y = {f_{\left( x \right)}}\) به اندازه a واحد در جهت مثبت محور طول ها حرکت کرده است و \({f_{\left( {x + a} \right)}}\) همان تغییر منتها در جهت منفی. به همین ترتیب \({f_{\left( x \right)}} \pm a,a\rangle 0\) هم تغییرات روی محور عرض هاست.
بررسی تابع بودن یک رابطه ی جبری
در این قسمت این موضوع مهم را بررسی می کنیم که یک ضابطه ی جبری به تنهایی چه زمانی معرف تابع است. به عنوان یک مثال ساده فرض کنید هدف بررسی عبارت \(\left| y \right| = x\) است. آیا این ضابطه می تواند معرف یک تابع باشد. یعنی به ازای هر مقدار x دقیقا یک مقدار y بدست می آید؟ با قرار دادن \(x = 1\) نتیجه می شود \(\left| y \right| = 1\) و لذا \(y = \pm 1\) و این یعنی هم \(1 \to 1\) و هم \(1 \to - 1\) و این یعنی این رابطه نمی تواند یک تابع باشد.
1 درستی یا نادرستی گزاره های زیر را بررسی کنید.
الف دامنه تابع \(f\left( x \right) = {x^2} - 1\) برابر \(\left( {0, + \infty } \right)\) و برد آن نیز \(\left( {0, + \infty } \right)\) است.
نادرست
ب دامنه تابع ثابت \({f_{\left( x \right)}} = 2\) برابر \(\left( { - \infty , + \infty } \right)\) است.
درست
2 یک تانکر گاز از یک استوانه و دو نیم کره به شعاع r در دو انتهای استوانه، تشکیل شده است. اگر ارتفاع استوانه 30 متر باشد، حجم تانکر را بر حسب تابعی از r بنویسید.
\(V = \frac{4}{3}\pi {r^3} + 30\pi {r^2}\)
تهیه کننده: فرهاد صمدی
اصل ضرب و جمع
فصل 6 : شمارش، بدون شمردن
اصل ضرب
فرض کنید کاری به دو جزء تقسیم شده است،چنانکه جز اول به m طریق انجام شدنی است و جزء دوم مستقل از اولی به n طریق انجام شدنی است. در این صورت این کار به mn طریق انجام شدنی است. البته این اصل قابل تعمیم است. اگر کاری به k طریق مجزا تقسیم شده باشد بطوریکه اولی به \({m_1}\) طریق انجام شدنی باشد، دومی به \({m_2}\) طریق انجام شدنی باشدو ... و k امی به \({m_k}\) طریق انجام شدنی باشد آنگاه کل کار به \({m_1} \times {m_2} \times ... \times {m_k}\) طریق شدنی است.
مثال
از شهر A به شهر B سه راه و از شهر B به شهر C چهار راه وجود دارد.
الف به چند طریق می توان از شهر A به شهر B رفت؟
به 3 طریق می توان رفت.
ب به چند طریق می توان از شهر A به شهر C رفت و به شهر A برگشت،بطوری که هر جاده حداکثر یک بار طی شود؟
به 6 طریق می توان رفت.
اصل جمع
فرض کنید کاری را بتوان به دو روش انجام داد طوری که در روش اول m انتخاب و در روش دوم n انتخاب موجود باشد. در این صورت برای انجام این کار \(m + n\) روش وجود دارد.مثل اصل ضرب این اصل نیز قابل تعمیم است.
مثال
بین شهرهای A و B سه جاده ،بین A و C ٢ جاده و بین B و C سه جاده احداث شده است.به چند طریق می توان با طی حداکثر دو جاده از A به B رفت؟
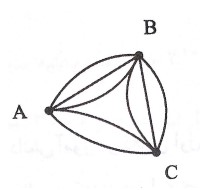
به 6 طریق می توان از A به B با طی حداکثر دو جاده رفت.
تکنیک به کار رفته در حل مسئله فوق ، استفاده از اصل متمم است. گاهی اوقات شمارش خاصیت ذکر شده در مسئله ای به مراتب مشکل تر از شمارش اعضایی است که خاصیت ذکرشده را ندارند. در این حالت بهتر است آنهایی که آن ویژگی معین را ندارند (متمم) شمارش شده و از کل اعضای مجموعه اصلی کم شوند.
\(\left| S \right| = \left| A \right| + \left| {A'} \right|\)
1 به چند طریق می توان یک نفر را از بین ۶ زن و ٨ مرد انتخاب کرد؟
\(6 + 8 = 14\)
به 14 روش میتوان فرد را انتخاب کرد.
2 در یک شهرک صنعتی 5 بلوار اصلی و در هر بلوار، بین 8 تا 10 خیابان، و در هر خیابان بین 10 تا 12 کوچه و در هر کوچه بین 20 تا 30 کارخانه وجود دارد. حداقل و حداکثر تعداد کارخانه هایی که ممکن است در این شهرک وجود داشته باشد، چند تاست؟
\(\begin{array}{l}\max = 5 \times 10 \times 12 \times 30 = 18000\\\min = 5 \times 8 \times 10 \times 20 = 8000\end{array}\)
تهیه کننده: فرهاد صمدی
جایگشت
فصل 6 : شمارش، بدون شمردن
جایگشت
سه نفر به چند صورت متفاوت می توانند در یک ردیف کنار هم ایستاده و عکس بگیرند؟ اگر این سه شخص را با حروف لاتین a و b و c نمایش دهیم، تمام حالات ممکنه در زیر آمده است:
abc, acb, bca, bac, cab, aba
هر یک از این ۶ حالت را یک جایگشت از سه حرف \(\left\{ {a,b,c} \right\}\) گوییم. حال اگر ۴ نفر بخواهند در یک ردیف و کنار هم عکس بگیرند چند حالت متفاوت پدید می آید؟
abcd , abdc , acbd , acdb , adcb , adbc
bacd , badc , bcad , bcda , bdac , bdca
cabd , cadb , cbad , cbda , cdab , cdba
dabc , dacb , dbac , dbca , dcab , dcba
به کمک اصل ضرب می توان تعداد جایگشت ها را بدون رسم کردن بدست آورد. تعداد جایگشت های ۴ شیء برابر است با \(4 \times 3 \times 2 \times 1 = 24\) و تعداد جایگشت های ٣ شیء برابر است با \(3 \times 2 \times 1 = 6\) در حالت کلی اگر n شیء متمایز داشته باشیم در این صورت تعداد جایگشت های این n شیء برابر است با: \(n \times \left( {n - 1} \right) \times \left( {n - 2} \right) \times ... \times 3 \times 2 \times 1\)
معرفی یک نماد: حاصل ضرب \(n \times \left( {n - 1} \right) \times \left( {n - 2} \right) \times ... \times 3 \times 2 \times 1\) را با نماد \(n!\) نشان می دهیم و n فاکتوریل خوانده می شود.
مثال
حاصل عبارت زیر را بدست آورید.
\(\frac{{8!}}{{5!}} = \)
\(\frac{{8!}}{{5!}} = \frac{{8 \times 7 \times 6 \times 5 \times 4}}{{5 \times 4 \times 3 \times 2 \times 1}} = \frac{{56}}{1} = 56\)
حال تصور کنید هفت شیء متمایز \({a_7},{a_6},{a_5},...,{a_1}\) داشته باشیم. می خواهیم تعداد جایگشت های بطول ٣ ( یعنی با سه شیء) را که می توان از ٧ شیء فوق ساخت محاسبه کنیم. یک جایگشت بطول ٣ را بصورت زیر در نظر می گیریم:
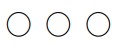
اولین خانه به هفت طریق ، دومین خانه به ۶ طریق و سومین خانه به ۵ طریق پر می شود. پس طبق اصل ضرب تعداد چنین جایگشت هایی برابر \(7 \times 6 \times 5\) است. می توان این عبارت را طور دیگری هم نوشت:
\(7 \times 6 \times 5 = 7 \times 6 \times 5 \times \frac{{4!}}{{4!}} = \frac{{7!}}{{7!}} = \frac{{7!}}{{\left( {7 - 3} \right)!}}\)
عدد ٣ و ٧ که نقشی اصلی در مسئله داشتند را در آخرین کسر می بینیم. در حالت کلی اگر باشد و بخواهیم تعداد جایگشت های r شیء را از n شیء بیابیم همانند مثال بالا عمل می کنیم:
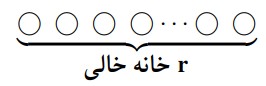
اولین خانه دارای n انتخاب،دومین خانه \(\left( {n - 1} \right)\) انتخاب، سومین خانه \(\left( {n - 2} \right)\) انتخاب .... و r امین خانه دارای \(\left( {n - r + 1} \right)\) نتخاب است. حال حاصلضرب این اعداد برابر است با:
\(n\left( {n - 1} \right)\left( {n - 2} \right)...\left( {n - r + 1} \right) = \frac{{n!}}{{\left( {n - r} \right)!}} = p\left( {n,r} \right)\)
عبارت \(p\left( {n,r} \right)\) را برای تعداد جایگشت های r شیء از n شیء انتخاب کرده ایم. پس تعداد جایگشت های rشیء از n شیء یا \(p\left( {n,r} \right)\) برابر است با :
\(p\left( {n,r} \right) = \frac{{n!}}{{\left( {n - r} \right)!}}\)
مثال
با حروف کلمه جهانگردی و بدون تکرار حروف:
الف) چند کلمه ٨ حرفی می توان نوشت؟ چند تا از آن ها به «ی» ختم می شود؟
\(8!,\frac{{8!}}{{7!}}\)
ب) چند کلمه ٨ حرفی می توان نوشت که در آن ها حروف «د» و «ی» کنار هم قرار گرفته باشند؟
\(\frac{{8!}}{{6!}}\)
پ) چند کلمه ۶ حرفی می توان نوشت؟ چند تا از آنها به «گردی» ختم می شوند؟
\(\frac{{6!}}{{4!}}\)
جایگشت های دوری
به هر روش قرار گرفتن n شیء دور یک دایره یک جایگشت دوری آن n شیء گوییم،با این ویژگی که اگر یک آرایش از دوران یک آرایش دیگر بدست آید این دو آرایش را هم ارز گوییم. در شکل زیر آرایش های ١ و ٢ از جایگشت های دوری \(E,D,E,B,A\) هم ارزند اما این دو با ٣ هم ارز نیست.
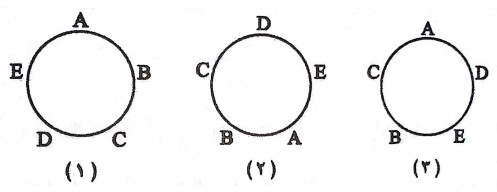
قضیه: تعداد جایگشت های دوری n شیء برابر است با \(\left( {n - 1} \right)!\) .
1 در یک لیگ فوتبال 18 تیم قرار دارند. در پایان این لیگ تیم های اول تا سوم به چند حالت مختلف می توانند مشخص شوند؟
\(\begin{array}{l}P\left( {18,3} \right)\\\frac{{n!}}{{\left( {n - r} \right)!}} = \frac{{18!}}{{15!}} = \frac{{18 \times 17 \times 16 \times 15!}}{{15!}} = 4896\end{array}\)
2 از بین تعدادی کتاب مختلف می خواهیم سه کتاب را انتخاب کنیم و در قفسه ای بچینیم. اگر تعداد حالت های مختلف برای این کار 210 تا باشد، تعداد کتاب ها چند تاست؟
\(\begin{array}{l}P\left( {n,3} \right)\\\frac{{n!}}{{\left( {n - r} \right)!}} = \frac{{n!}}{{\left( {n - 3} \right)!}} = n\left( {n - 1} \right)\left( {n - 2} \right) = 7 \times 6 \times 5 = 210 \to n = 7\end{array}\)
3 در یک نوع ماشین حساب کوچک که دارای 20 کلید است، برای انجام یک دستور خاص باید سه کلید مشخص با ترتیبی مشخص فشار داده شوند. اگر فردی نداند سه کلید مورد نظر کدام اند و بخواهد به طور تصادفی این کار را انجام دهد و فشردن هر سه کلید 2 ثانیه زمان بخواهد، این فرد حداکثر (در بدترین حالت) در چه زمانی می تواند دستور مورد نظر را اجرا کند؟
\(2 \times P\left( {20,3} \right) = 13680s\)
تهیه کننده: فرهاد صمدی
- آزمون آنلاین تمامی دروس پایه دهم
- گام به گام تمامی دروس پایه دهم
- ویدئو های آموزشی تمامی دروس پایه دهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه دهم
- فلش کارت های آماده دروس پایه دهم
- گنجینه ای جامع از انشاء های آماده پایه دهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه دهم
ترکیب
فصل 6 : شمارش، بدون شمردن
ترکیب
اگر در انتخاب r شیء از میان n شیء \(r \le n\) ترتیب انتخاب مهم نباشد با مسئله ترکیب روبرو هستیم. تعداد راه های انتخاب r شیء بدون اهمیت ترتیب آنها را ترکیب r شیء از n شیء گوییم و با نماد \(\left( {\begin{array}{*{20}{c}}n\\r\end{array}} \right)\) نشان می دهیم و برابر است با:
\(\left( {\begin{array}{*{20}{c}}n\\r\end{array}} \right) = C\left( {n,r} \right) = \frac{{n!}}{{r!\left( {n - r} \right)!}}\)
مثال
به چندطریق می توان از بین ده عضو شورای شهر دو نفر را به عنوان رئیس و معاون انتخاب کرد؟
\(\left( {\begin{array}{*{20}{c}}{10}\\2\end{array}} \right) = \frac{{10!}}{{2!\left( {8!} \right)}}\)
جایگشت با تکرار
فرض کنید \({m_1}\) شیء از نوع \({a_1}\) و \({m_2}\) شیء از نوع \({a_2}\) و ... و \({m_k}\) شیء از نوع \({a_k}\) داریم که \({m_1} + {m_2} + ... + {m_k} = n\) در اینصورت هر چیدن این n شیء را یک جایگشت با تکرار می نامیم. تعداد این جایگشت ها برابر است با :
\(\frac{{n!}}{{{m_1}!{m_2}!...{m_k}!}}\)
1 تعداد کلماتی یازده حرفی که با حروف کلمه ی Mississippi می توان نوشت را بیابید؟
\(\frac{{11!}}{{1!4!4!2!}}\)
2 چند عدد ده رقمی با استفاده از سه رقم ۴ و دو رقم ٢ و پنج رقم ٨ می توان نوشت؟
\(\frac{{10!}}{{3!2!5!}}\)
تهیه کننده: فرهاد صمدی
احتمال و عملیات بر پیشامدها
فصل 7 : آمار و احتمال
احتمال و عملیات بر پیشامدها
تنها یک مسئله است که آن را ریشه ی شاخه ی احتمالات می دانند و به مسئله امتیازها معروف است. در این مسئله چگونگی تقسیم جایزه ی بازی شانسی نیمه تمام بین دو بازیکن فرضی هم قدرت ، با داشتن امتیازهای دو بازیکن در موقع قطع بازی و تعداد امتیازهای لازم برای بردن بازی خواسته شده است.این مسئله را کاردانو و تارتاگلیا نیز مورد بررسی قرار داده بودند،اما پیشرفت واقعی در سال ١٩۵۴ رخ داد. یک قمارباز حرفه ای زیرک طی نامه ای به بلز پاسکال علت عدم تطبیق تجربه شخصی با واقعیت تئوری این مسئله را جویا شده بود. پاسکال به مسئله علاقمند شد و طی نامه ای آن را به اطلاع پی یر فرما رساند.از اینجا به بعد مکاتبات زیادی بین این دو بزرگ مرد تاریخ ریاضیات شکل گرفت که شالوده ی احتمالات را تشکیل دادند. فرما و پاسکال مسئله را جداگانه حل کردند با این تفاوت که پاسکال مسئله را در حالت کلی حل کرد. پدیده های پیرامون ما در حالت کلی به دو دسته تقسیم می شوند:

در بحث احتمال پدیده های تصادفی بررسی می شوند و با پدیده های قطعی کاری نخواهیم داشت. منظور از یک آزمایشی تصادفی در تمام این فصل آزمایشی است که نتیجه ی آن از قبل قابل پیش بینی نباشد. در هر آزمایش تصادفی مجموعه ای وجود دارد که شامل تمام نتایج ممکنه در آن آزمایش تصادفی است. به چنین مجموعه ای فضای نمونه گوییم.
در هر آزمایش تصادفی به مجموعه ای که شامل تمام حالات ممکنه از آن آزمایش تصادفی باشد فضای نمونه گوییم و آن را با حرف S نشان می دهیم. همچنین به هر زیرمجموعه دلخواه از S یک پیشامد یا رخداد گوییم. پس A یک پیشامد است هرگاه: \(A \subseteq S\) باشد.
مثال
جاهای خالی را پر کنید.
الف) در پرتاب یک سکه فضای نمونه ای برابر است با ..........
\(S = \left\{ {P,R} \right\}\)
ب) در پرتاب یک تاس فضای نمونه ای برابر است با ..........
\(S = \left\{ {1,2,3,4,5,6} \right\}\)
عملیات بر پیشامدها
چون پیشامدها زیرمجموعه های فضای نمونه هستند ، امکان ترکیب کردن آنها و ساختن پیشامدهای جدید وجود دارد.
اشتراک دو پیشامد: اگر \(A,B \subseteq S\) دو پیشامد دلخواه باشند \(A \cap B\) پشامد وقوع هردوی A و B بطور همزمان است. مثلا در پرتاب یک تاس اگر A پیشامد آمدن عدد زوج و B پیشامد اینکه عدد اول بیاید باشد آنگاه \(A \cap B\) به معنای زوج و اول آمدن است. و لذا:
\(A \cap B = \left\{ 2 \right\}\)
اجتماع دو پیشامد: پیشامد \(A \cup B\) به معنای وقوع A یا B یا هردوی آنها است. مانند حالت قبل داریم:
\(A \cup B = \left\{ {2,3,4,5,6} \right\}\)
تفاضل دو پیشامد: پیشامد \(A - B\) به معنای رخ دادن A و رخ ندادن B است.مانند حالت قبل داریم:
\(A - B = \left\{ {4,6} \right\}\)
متمم یک پیشامد: پیشامد \(A'\) به معنای رخ ندادن A است. مانند حالت قبل داریم:
\(A' = \left\{ {1,3,5} \right\}\)
تفاضل متقارن دو پیشامد: می دانیم \(A\Delta B = \left( {A - B} \right) \cup \left( {B - A} \right)\) . پس پیشامد \(A\Delta B\) به معنای رخ دادن A و رخ ندادن B یا رخ دادنB و رخ ندادن A است. بعبارت دیگر فقط یکی از A یا B رخ دهد. مانند حالت قبل:
\(A\Delta B = \left\{ {3,4,5,6} \right\}\)
یشامدهای ناسازگار: دو پیشامد A و B را ناسازگار گوییم هرگاه: \(A \cap B = \emptyset \)
سکه ای را به هوا می اندازیم. اگر پشت بیاید، یک تاس می اندازیم و اگر رو بیاید دو سکه دیگر می اندازیم:
الف فضای نمونه ای این آزمایش تصادفی را مشخص کنید.
\(S = \left\{ {\left( {1,P} \right),\left( {2,P} \right),\left( {3,P} \right),\left( {4,P} \right),\left( {5,P} \right),\left( {6,P} \right),\left( {P,P} \right),\left( {P,R} \right)} \right\}\)
ب پیشامد آن که تاس زوج بیاید را مشخص کنید.
\(A = \left\{ {\left( {2,P} \right),\left( {4,P} \right),\left( {6,P} \right)} \right\}\)
تهیه کننده: فرهاد صمدی
مقدمه ای بر آمار، جامعه و نمونه
فصل 7 : آمار و احتمال
مقدمه ای بر آمار، جامعه و نمونه
در زندگی روزمره انسان ها به کرات و بدون آنکه متوجه باشند از جملات آماری استفاده می کنند. مثلا در محاوره و درباره ی این پرسش که در شبانه روز چندساعت می خوابید و پاسخ « بنده در هر شبانه روز و بطور میانگین حدود ٨ ساعت می خوابم» و یا این جمله ی « اگر مدت زمان مطالعه را دوبرابر کنی شانس قبولی در امتحان پایانی شما ۵٠ درصد افزایش می یابد» همگی جملاتی هستند که مبین مفاهیم آماری و یا روش آماری هستند. بطورکلی می توان علم آمار را مبتنی بر ۴ مرحله زیر در نظر گرفت:
- طرح و انجام آزمایش برای دستیابی به اطلاعات عددی و یا هر روشی که منجر به گردآوری داده ها شود.
- جمع بندی و سازماندهی اطلاعات عددی بدست آمده برای درک و فهم بهتر موضوع.
- تحلیل و تفسیر و آنالیز دقیق اطلاعات عددی بدست آمده.
- نتیجه گیری براساس اطلاعات بدست آمده از قسمت های فوق و پیش بینی آینده ی موضوع مورد بحث.
آمار و علم آمار
آمار، مجموعه ای از اعداد، ارقام و اطلاعات است. علم آمار مجموعه روش هایی است که شامل جمع آوری اعداد و ارقام، سازماندهی و نمایش، تحلیل و تفسیر داده ها و در نهایت نتیجه گیری، قضاوت و پیش بینی مناسب در مورد پدیده ها و آزمایش های تصادفی می شود.
منظور از پیش بینی آینده ، پیشگوئی هایی به سبک نوستراداموس نیست. در اینجا براساس یک الگوی بدست آمده از اطلاعات عددی بطور تصادفی و نه لزوما قطعی می توان آینده ی موضوعی را بررسی کرد. به عنوان مثال نظرسنجی برای تعیین نتیجه ی انتخابات در یک کشور، چنانچه بر اساس موازین علمی و درست انجام شود می تواند قبل از روز رای گیری نتیجه را مشخص کند و در این مورد نمونه های بسیار زیادی در دنیا و در کشور خودمان وجود دارد که نتیجه نظرسنجی و رای گیری واقعی تقریبا تا ٩۵ درصد و گاهی ١٠٠ درصد منطبق بوده اند.
جامعه یا جمعیت
مجموعه تمام افراد یا اشیایی که دربارۀ یک یا چند ویژگی آنها تحقیق صورت گیرد، جامعه یا جمعیت نامیده می شود و هریک از این افراد یا اشیا را عضو جامعه می نامند.
اندازه یا حجم جامعه
تعداد اعضای جامعه را اندازه جامعه یا حجم جامعه گویند. به عنوان مثال، دانش آموزان یک مدرسه می توانند یک جامعه باشند و هریک از دانش آموزان مدرسه عضو این جامعه هستند.
تعریف نمونه
بخشی از جامعه را که برای مطالعه انتخاب شود، نمونه گویند و هریک از افراد یا اشیای انتخاب شده را عضو نمونه گویند.
اندازه یا حجم نمونه
تعداد اعضای نمونه را اندازه نمونه یا حجم نمونه گویند. به عنوان مثال دانش آموزان یک کلاس به عنوان یک نمونه از دانش آموزان مدرسه هستند و هر یک از دانش آموزان کلاس، عضو نمونه محسوب می شوند.
نمونه باید اولا تصادفی انتخاب شود به این معنی که هر عضو جامعه شانس حضور در نمونه را داشته باشد و تعداد اعضای نمونه هم باید به درستی انتخاب شود تا بیانگر ویژگی های جامعه باشد. مثلا در یک کلاس ٣٠ نفری می توان یک نمونه ٨ نفری انتخاب کرد ولی نمونه ٨ نفری برای یک مدرسه ۵٠٠ نفری نمونه ی خوبی به حساب نمی آید.
1 تفاوت آمار و علم آمار در چیست؟
آمار، مجموعه ای از اعداد، ارقام و اطلاعات است. علم آمار مجموعه روش هایی است که شامل جمع آوری اعداد و ارقام، سازماندهی و نمایش، تحلیل و تفسیر داده ها و در نهایت نتیجه گیری، قضاوت و پیش بینی مناسب در مورد پدیده ها و آزمایش های تصادفی می شود.
2 کدام جمله درست و کدام جمله نادرست است:
الف اولین قدم در استفاده از )علم آمار(، جمع آوری داده ها است.
درست
ب پیشبینی و تصمیم گیری برای آینده، نتیجه استفاده از (علم آمار) است.
درست
پ (علم آمار)، همان اعداد و ارقام است.
نادرست
تهیه کننده: فرهاد صمدی
- آزمون آنلاین تمامی دروس پایه دهم
- گام به گام تمامی دروس پایه دهم
- ویدئو های آموزشی تمامی دروس پایه دهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه دهم
- فلش کارت های آماده دروس پایه دهم
- گنجینه ای جامع از انشاء های آماده پایه دهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه دهم
متغیر و انواع آن
فصل 7 : آمار و احتمال
متغیر و انواع آن
متغیر، ویژگی از اعضای یک جامعه است که بررسی و مطالعه می شود و معمولا از یک عضو به عضو دیگر تغییر می کند. عددی را که به ویژگی یک عضو نسبت داده می شود، مقدار متغیر می گویند. برخی متغیرها قابل اندازه گیری اند مثل قد و وزن و ... و برخی غیر قابل اندازه گیری مثل رنگ ماشین، کیفیت یک میوه، گروه خونی و .... . بر این اساس باید متغیرها را طبقه بندی کنیم. جدول زیر انواع متغیرها را نشان می دهد.

متغیرهای کمی
متغیرهایی را که قابل اندازه گیری اند، (متغیرهای کمی) گویند. به عنوان مثال تعداد فرزندان خانواده و وزن افراد متغیرهای کمی اند.
متغیرهای کیفی
متغیر هایی را که قابل اندازه گیری نیستند، (متغیرهای کیفی) گویند. به عنوان مثال گروه خونی افراد و پاسخ سؤال (میزان لذت بردن از آشپزی) متغیرهای کیفی اند.
متغیر پیوسته
متغیری است که اگر دو مقدار a و b را بتواند اختیار کند، هر مقدار بین آنها را نیز بتواند اختیار کند. به عنوان مثال وزن یک دانش آموز میتواند ۴۶ کیلوگرم، ۴٧ کیلوگرم یا هر عددی بین این دو رقم باشد.
متغیر گسسته
متغیر گسسته، متغیری است که پیوسته نباشد. به عنوان مثال تعداد فرزندان یک خانواده متغیر گسسته است.
1 انواع متغیر های زیر را مشخص کنید:
الف تعداد ماهی های دریا
گسسته
ب مدت زمانی که طول می کشد از خانه به مدرسه برسید.
پیوسته
پ وزن افراد
پیوسته
ج تعداد دانش آموزان یک مدرسه
گسسته
2 جامعه و نمونه را تعریف کنید.
جامعه: مجموعه تمام افراد یا اشیایی که دربارۀ یک یا چند ویژگی آنها تحقیق صورت گیرد، جامعه یا جمعیت نامیده می شود و هریک از این افراد یا اشیا را عضو جامعه می نامند.
نمونه: بخشی از جامعه را که برای مطالعه انتخاب شود، نمونه گویند و هریک از افراد یا اشیای انتخاب شده را عضو نمونه گویند.
تهیه کننده فرهاد صمدی
اندازه گیری احتمال
فصل 7 : آمار و احتمال
اندازه گیری احتمال
برای اندازه گیری شانس در آزمایش تصادفی روش های متعددی وجود دارد. یکی از این روش ها روش آماری است. به این معنی که آزمایش را به دفعات زیاد انجام می دهیم و نتیجه های مشاهده شده و مطلوب را بر تعداد کل دفعات آزمایش تقسیم می کنیم و عدد حاصل را شانس آن پیشامد در نظر می گیریم. یکی دیگر از روش ها، روش ذهنی است. کارشناس فوتبال بر اساس تجربیات خود حدس میزند که تیم A به احتمال مثلا ۶٠٪ برنده خواهد شد. روش دیگر استفاده از اصول موضوعه احتمال و استخراج مابقی قوانین آن از همان چند اصل ابتدایی است که برای اولین آشنایی در احتمال چندان مناسب نیست. اما یکی از مفیدترین و ساده ترین روش ها محاسبه احتمال از طریق شمارش تعداد اعضای پیشامد و فضای نمونه و تقسیم آنها بر یک دیگر است.
فرض کنید S یک فضای نمونه و \(A \subset S\) یک پیشامد دلخواه باشد. شانس وقوع پیشامد A را که با نماد \(P\left( A \right)\) نشان می دهیم بصورت زیر تعریف می کنیم:
\(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( S \right)}} = \frac{{\left| A \right|}}{{\left| S \right|}}\)
یا به فارسی می توان گفت تعداد حالات مساعد یا مطلوب بر تعداد کل حالات ممکن
مثال
یک تاس را پرتاب می کنیم. مطلوب است احتمال آن که:
الف عدد رو شده زوج باشد.
\(\begin{array}{l}S = \left\{ {1,2,3,4,5,6} \right\}\\A = \left\{ {2,4,6} \right\}\\P\left( A \right) = \frac{3}{6} = \frac{1}{2}\end{array}\)
ب عدد رو شده مضرب 3 باشد.
\(\begin{array}{l}S = \left\{ {1,2,3,4,5,6} \right\}\\B = \left\{ {3,6} \right\}\\P\left( B \right) = \frac{2}{6} = \frac{1}{3}\end{array}\)
پ عدد رو شده کمتر از 7 باشد.
\(\begin{array}{l}S = \left\{ {1,2,3,4,5,6} \right\}\\C = \left\{ {1,2,3,4,5,6} \right\}\\P\left( C \right) = \frac{6}{6} = 1\end{array}\)
طبق اصل کولموگروف:
برای هر دو پیشامـد A و B از فضـای نمونه ای S، همـواره تسـاوی زیر برقرار است:
\(P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) - P\left( {A \cap B} \right)\)
اگر A و B دو پیشامد ناسازگار باشند، این تساوی به صورت زیر نوشته می شود:
\(P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right)\)
\(0/3\) احتمال دارد فرزندی در یک خانواده با گروه خونی A متولد شود و احتمال آن که رنگ چشم فرزند میشی باشد، \(0/4\) است. اگر احتمال متولد شده فرزندی با گروه خونی A و رنگ چشم میشی \(0/15\) باشد؛ مطلوب است احتمال آن که:
الف حداقل یکی از آن ها گروه خونی A یا رنگ چشم میشی داشته باشد.
\(0/55\)
ب فقط گروه خونی A داشته باشد.
\(0/15\)
تهیه کننده: فرهاد صمدی



1736019749.png)















