جواب تمرین صفحه 40 درس 2 ریاضی یازدهم تجربی (هندسه)
تعداد بازدید : 80.87Mپاسخ تمرین صفحه 40 ریاضی یازدهم تجربی
-گام به گام تمرین صفحه 40 درس هندسه
-تمرین صفحه 40 درس 2
-شما در حال مشاهده جواب تمرین صفحه 40 ریاضی یازدهم تجربی هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
1 در شکل مقابل مساحت مثلث قائم الزاویهٔ ABC را به دو روش محاسبه کنید و از تساوی دو عبارت به دست آمده برای مساحت مثلث، یک تناسب به دست آورید.
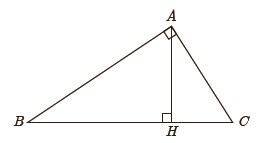
\(\begin{array}{l}\left\{ \begin{array}{l}{S_{ABC}} = \frac{1}{2} \times AH \cdot BC\\\\{S_{ABC}} = \frac{1}{2} \times AB \cdot AC\end{array} \right.\\\\ \Rightarrow \frac{1}{2} \times AH \cdot BC = \frac{1}{2} \times AB \cdot AC\\\\ \Rightarrow AH \cdot BC = AB \cdot AC \Rightarrow \frac{{AH}}{{AB}} = \frac{{AC}}{{BC}}\end{array}\)
2 در هر مورد، مقدار عددی نسبت \(\frac{a}{b}\) را به دست آورید.
الف \(\frac{a}{{10 + a}} = \frac{b}{{8 + b}}\)
ب \(\frac{{3a + 10}}{{10 + 2a}} = \frac{{3b + 7}}{{7 + 2b}}\)
الف
\(\begin{array}{l}\frac{a}{{10 + a}} = \frac{b}{{8 + b}}\\\\ \Rightarrow \frac{a}{{10 + a - a}} = \frac{b}{{8 + b - b}}\\\\ \Rightarrow \frac{a}{{10}} = \frac{b}{8} \Rightarrow \frac{a}{b} = \frac{{10}}{8}\end{array}\)
ب
\(\begin{array}{l}\frac{{3a + 10}}{{10 + 2a}} = \frac{{3b + 7}}{{7 + 2b}}\\\\ \Rightarrow \frac{{3a + 10 - \left( {10 + 2a} \right)}}{{10 + 2a}} = \frac{{3b + 7 - \left( {7 + 2b} \right)}}{{7 + 2b}}\\\\ \Rightarrow \frac{a}{{10 + 2a}} = \frac{b}{{7 + 2b}}\\\\ \Rightarrow \frac{a}{{10 + 2a - 2a}} = \frac{b}{{7 + 2b - 2b}}\\\\ \Rightarrow \frac{a}{{10}} = \frac{b}{7} \Rightarrow \frac{a}{b} = \frac{{10}}{7}\end{array}\)
3 ثابت کنید در هر مثلث، پاره خطی که وسط های دو ضلع مثلث را به هم وصل کند، با ضلع سوم موازی و مساوی نصف آن است.
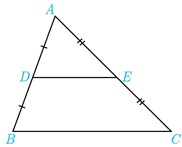
عکس قضیه تالس
\(\begin{array}{l}\left\{ {\begin{array}{*{20}{l}}\begin{array}{l}AD = DB \Rightarrow \frac{{AD}}{{DB}} = 1\\\end{array}\\{AE = EC \Rightarrow \frac{{AE}}{{EC}} = 1}\end{array}} \right.\\\\ \Rightarrow \frac{{AD}}{{DB}} = \frac{{AE}}{{EC}} \Rightarrow DE\parallel BC\end{array}\)
تعمیم قضیه تالس
\(\begin{array}{l}DE\parallel BC\quad \Rightarrow \quad \frac{{AD}}{{AB}} = \frac{{AE}}{{AC}} = \frac{{DE}}{{BC}}\\\\{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \mathop \Rightarrow \limits_{AC = 2AE}^{AB = 2AD} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \frac{{DE}}{{BC}} = \frac{1}{2} \Rightarrow DE = \frac{1}{2}BC\end{array}\)
4 در شکل مقابل EQ||BC است. طول پاره خط های AP و PQ را به دست آورید.
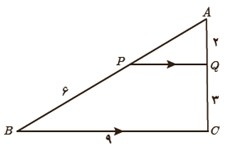
\(\begin{array}{l}PQ\parallel BC:\\\\\frac{{AP}}{{PB}} = \frac{{AQ}}{{QC}} \Rightarrow \frac{{AP}}{6} = \frac{2}{3} \Rightarrow AP = 4\\\\\frac{{AP}}{{AB}} = \frac{{AQ}}{{AC}} = \frac{{PQ}}{{BC}} \Rightarrow \frac{{PQ}}{9} = \frac{2}{5} \Rightarrow PQ = \frac{{18}}{5}\end{array}\)
5 در شکل مقابل BT||BC است. مقادیر x و y را به دست آورید.
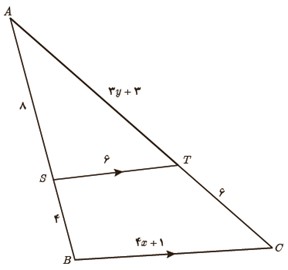
\(\begin{array}{l}ST\parallel BC:\\\\\frac{{AS}}{{SB}} = \frac{{AT}}{{TC}} \Rightarrow \frac{8}{4} = \frac{{3y + 3}}{6}\\\\ \Rightarrow 2 = \frac{{y + 1}}{2} \Rightarrow y + 1 = 4 \Rightarrow y = 3\\\\\frac{{AS}}{{AB}} = \frac{{ST}}{{BC}} \Rightarrow \frac{8}{{12}} = \frac{6}{{4x + 1}}\\\\ \Rightarrow \frac{2}{3} = \frac{6}{{4x + 1}} \Rightarrow 8x + 2 = 18 \Rightarrow x = 2\end{array}\)
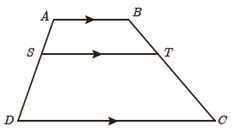
6 در ذوزنقه مقابل AB||ST||DC است. ثابت کنید: \(\frac{{AB}}{{SD}} = \frac{{BT}}{{TC}}\)
(راهنمایی: یکی از قطرها را رسم کنید.)
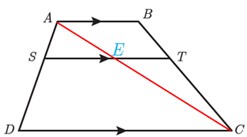
\(\begin{array}{l}\left\{ \begin{array}{l}A\mathop C\limits^\Delta D:\quad SE\parallel DC \Rightarrow \frac{{AS}}{{SD}} = \frac{{AE}}{{EC}}\\\\A\mathop B\limits^\Delta C:\quad TE\parallel AB \Rightarrow \frac{{BT}}{{TC}} = \frac{{AE}}{{EC}}\end{array} \right.\\\\ \Rightarrow \frac{{AS}}{{SD}} = \frac{{BT}}{{TC}}\end{array}\)
7 در هر مورد با عوض کردن جای فرض و حکم عکس آنچه را داده شده است، بنویسید.
الف اگر در مثلثی سه ضلع برابر باشند، آنگاه سه زاویه نیز برابر خواهند بود.
ب اگر در یک چهارضلعی اضلاع روبه رو موازی باشند، در این صورت زوایای مقابل با هم برابرند.
پ اگر رأس های یک چهارضلعی روی یک دایره قرار داشته باشند، در این صورت زوایای مقابل آن چهارضلعی مکمل اند.
ت یک مثلث اگر دو ارتفاع نابرابر باشند. «ضلع متناظر به ارتفاع بزرگ تر» کوچک تر است از «ضلع مقابل به ارتفاع کوچک تر».
(راهنمایی: شکل بکشید و به زبان ریاضی بنویسید)
الف
اگر در مثلثی سه زاویه مساوی باشند، آنگاه سه ضلع نیز با هم برابر خواهند بود.
ب
اگر در یک چهار ضلعی زوایای مقابل با هم برابر باشند، در این صورت اضلاع مقابل موازی هستند.
پ
اگر زوایای مقابل یک چهار ضلعی مکمل یکدیگر باشند، در این صورت رأس های چهارضلعی روی یک دایره قرار دارند.
ت
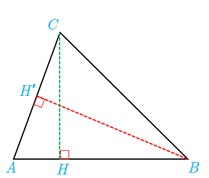
در مثلث ABC ، اگر AB>AC آنگاه CH<CH’
به عبارتی: AB>AC
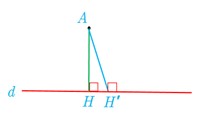
8 با برهان خلف ثابت کنید نمی توان از یک نقطهٔ غیر واقع بر یک خط، دو عمود بر آن خط رسم کرد.
خط d و نقطه A خارج آن را در نظر می گیریم. از نقطه A، عمود AH را رسم می کنیم. با استفاده از برهان خلف فرض می کنیم که از نقطه A می توانیم خط دیگری مانند AH’ را بر خط d عمود کنیم (فرض خلف). بنابراین در مثلث AHH’ ، \(\hat H = \hat H' = {90^ \circ }\) ؛ ولی با توجه به اینکه مجموع زوایای داخلی هر مثلث 180 درجه است، به تناقض می رسیم. پس از ابتدا فرض غلط بودن حکم نادرست بوده است و حکم نمی تواند غلط باشد. به عبارت دیگر فرض خلف باطل است و حکم مسئله اثبات می شود.
٩ هر یک از حکم های کلی زیر را با یک مثال نقض رد کنید.
الف هیچ عدد اولِ بزرگ تر از 127 وجود ندارد.
ب مساحت هر مثلث از مساحت هر مربع بیشتر است.
پ در هر مثلث اندازهٔ هر ضلع از اندازهٔ هر ارتفاع بزرگ تر است.
ت در هر مثلث میانه و عمودمنصف متناظر به هر ضلع برهم منطبق اند.
الف
عدد 131 اول است و بزرگتر از 127 می باشد. پس این حکم کلی با این مثال نقض، رد می شود.
ب
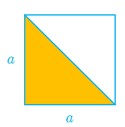
مساحت مربع شکل مقابل، \({a^2}\) می باشد، اما مساحت مثلث قائم الزاویه رنگی \(\frac{{{a^2}}}{2}\) است.
\(\frac{{{a^2}}}{2} < {a^2}\)، پس با این مثال نقض، حکم کلی رد می شود.
پ
در مثلث قائم الزاویه، ارتفاع با طول ضلع مثلث برابر است. با این مثال نقض، این حکم کلی رد می شود.
ت
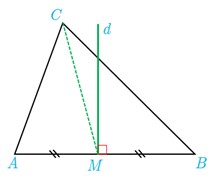
در مثلث ABC شکل مقابل خط AB و CM میانه ضلع AB است ولی بر هم منطبق نیستند.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















