آیا تمام سوالات سوال صفحه 118 ریاضی دهم، مطابق با آخرین تغییرات کتب درسی پاسخ داده شده است ؟

بله، تمام جواب ها به سوال صفحه 118 ریاضی دهم مطابق با آخرین تغییرات کتب درسی 1402 - 1401 است.

آیا جواب ها به صورت آموزش محور و کامل بیان شده اند ؟

بله، جواب سوالات به صورت کاملا تشریحی و با هدف یادگیری و تسلط به مبحث بیان شده اند.

گام به گام سوال صفحه 118 درس 6 ریاضی دهم (شمارش، بدون شمردن)

تعداد بازدید : 61.12M

پاسخ سوال صفحه 118 ریاضی دهم

گام به گام سوال صفحه 118 درس شمارش، بدون شمردن

سوال صفحه 118 درس 6

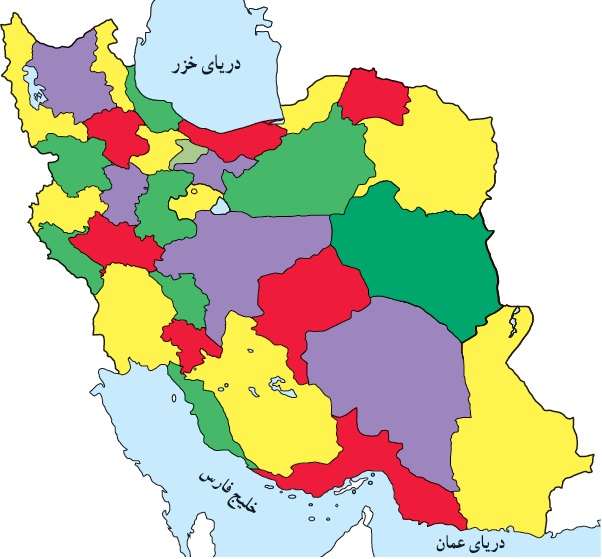
سوال صفحه 118 ریاضی دهم

داشتن حداقل چند رنگ کافی است تا هر نقشه ای را بتوان به گونه ای رنگ آمیزی کرد که هیچ دو ناحیهٔ هم مرزی هم رنگ نباشند؟

برای رنگ‌آمیزی هر نقشه‌ای به گونه‌ای که هیچ دو ناحیهٔ هم‌مرز رنگ مشابه نداشته باشند، به حداقل چهار رنگ نیاز است. این ایده تحت عنوان قضیه چهار رنگ شناخته می‌شود و یکی از مسائل معروف در ریاضیات و نظریه گراف است.

این قضیه می‌گوید: «برای هر نقشه‌ای که روی صفحه مسطح یا روی کره رسم شده باشد، کافی است که از چهار رنگ استفاده کنید تا بتوانید نواحی را طوری رنگ‌آمیزی کنید که هیچ دو ناحیهٔ هم‌مرز هم‌رنگ نباشند.»

این مسئله به صورت دقیق در قرن نوزدهم مطرح شد و پس از سال‌ها تلاش، در سال ۱۹۷۶ توسط کامپیوتر اثبات شد. یکی از نکات جالب این قضیه این است که بسیار ساده به نظر می‌رسد، اما اثبات آن پیچیدگی زیادی دارد!