جواب کاردرکلاس صفحه 159 درس 7 ریاضی یازدهم تجربی (آمار و احتمال)
تعداد بازدید : 80.73Mپاسخ کاردرکلاس صفحه 159 ریاضی یازدهم تجربی
-گام به گام کاردرکلاس صفحه 159 درس آمار و احتمال
-کاردرکلاس صفحه 159 درس 7
-شما در حال مشاهده جواب کاردرکلاس صفحه 159 ریاضی یازدهم تجربی هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
واریانس تعداد کتاب های غیردرسی مطالعه شده در «کار در کلاس» قبل، توسط 7 و 9 دانش آموز را محاسبه کنید.
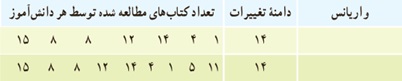
مقدار واریانس برای 7 دانش آموز:
\(\begin{array}{l}\bar x = \frac{{15 + 8 + 8 + 12 + 14 + 4 + 1}}{7} = \\\\8/85 \simeq 9\\\\{\sigma ^2} = \frac{\begin{array}{l}{\left( {15 - 9} \right)^2} + {\left( {8 - 9} \right)^2} + \\{\left( {8 - 9} \right)^2} + {\left( {12 - 9} \right)^2} + \\{\left( {14 - 9} \right)^2} + {\left( {4 - 9} \right)^2} + \\{\left( {1 - 9} \right)^2}\end{array}}{7} = \\\\\frac{\begin{array}{l}{6^2} + {\left( { - 1} \right)^2} + {\left( { - 1} \right)^2} + {3^2} + \\{5^2} + {\left( { - 5} \right)^2} + {\left( { - 8} \right)^2}\end{array}}{7} = \\\\\frac{{36 + 1 + 1 + 9 + 25 + 25 + 64}}{7} = \\\\\frac{{161}}{7} = 23\end{array}\)
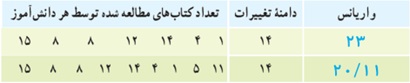
مقدار واریانس برای 9 دانش آموز:
\(\begin{array}{l}\bar x = \frac{\begin{array}{l}15 + 8 + 8 + 12 + \\14 + 4 + 1 + 5 + 11\end{array}}{9} = 8/67 \simeq 9\\\\{\sigma ^2} = \frac{\begin{array}{l}{\left( {15 - 9} \right)^2} + {\left( {8 - 9} \right)^2} + \\{\left( {8 - 9} \right)^2} + {\left( {12 - 9} \right)^2} + \\{\left( {14 - 9} \right)^2} + {\left( {4 - 9} \right)^2} + \\{\left( {1 - 9} \right)^2} + {\left( {5 - 9} \right)^2} + {\left( {11 - 9} \right)^2}\end{array}}{9} = \\\\ = \frac{\begin{array}{l}{6^2} + {\left( { - 1} \right)^2} + {\left( { - 1} \right)^2} + {3^2} + \\{5^2} + {\left( { - 5} \right)^2} + {\left( { - 8} \right)^2} + {\left( { - 4} \right)^2} + {2^2}\end{array}}{9} = \\\\\frac{{181}}{9} \simeq 20/11\end{array}\)
!!!(توجه: این قسمت پایین بایستی خارج از قالب جواب بیاید و داخل قالب سوال باشد)
همان طور که در این «کار در کلاس» دیده می شود، واریانس برخلاف دامنهٔ تغییرات، با تغییر تعداد و مقادیر داده ها تغییر می کند.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















