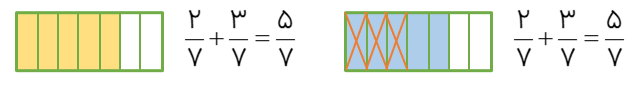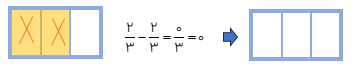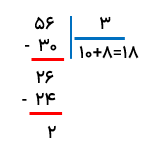درسنامه کامل ریاضی چهارم
تعداد بازدید : 299.57kخلاصه نکات ریاضی چهارم - درسنامه شب امتحان ریاضی چهارم - جزوه شب امتحان ریاضی چهارم نوبت اول
حل مساله - الگوهای - رسم شکل
فصل 1 : اعداد و الگوها
الگویابی
یکی از روش های حل مساله، روش الگو یابی یا کشف رابطه ها است. الگو ها دو دسته هستند :
الگوهای عددی - الگوهای هندسی
الگوهای عددی
در الگوهای عددی رابطه ای افزایشی یا کاهشی بین اعداد پیدا می کنیم.
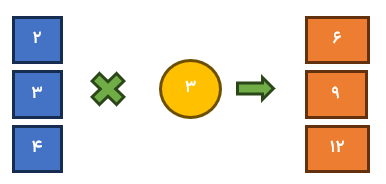
در این الگوی عددی هر عدد ۳ واحد بیشتر از عدد قبلی است.
\(6\mathop \to \limits^{ + 3} 9\mathop \to \limits^{ + 3} 12\mathop \to \limits^{ + 3} 15\)
در این الگو عددی هر عدد ۲ برابر عدد قبلی است.
\(10\mathop \to \limits^{ \times 2} 20\mathop \to \limits^{ \times 2} 40\mathop \to \limits^{ \times 2} 80\)
در این الگو بر هر درد ۲۵ واحد از عدد قبلی کمتر است.
\(175\mathop \to \limits^{ - 25} 150\mathop \to \limits^{ - 25} 125\mathop \to \limits^{ - 25} 100\)
الگوی هندسی
در الگوهای هندسی رابطه ای بین اشکال پیدا می کنیم.
در این الگوی هندسی هر شکل ۲ واحد از شکل قبلی بیشتر است.
\(2\mathop \to \limits^{ + 2} 4\mathop \to \limits^{ + 2} 6\mathop \to \limits^{ + 2} 8\)
در این الگو ار هندسی هر شکل 3 چوب کبریت از شکل قبلی بیشتر دارد.
الگوهای عددی زیر را ادامه دهید.
\(1)130 - 260 - 390 - ....... - ....... - ....... - ....... - \)
\(130\mathop \to \limits^{ + 130} 260\mathop \to \limits^{ + 130} 390\mathop \to \limits^{ + 130} 520\mathop \to \limits^{ + 130} 650\mathop \to \limits^{ + 130} 780\mathop \to \limits^{ + 130} 910\)
\(2)120 - 340 - 560 - ...... - ...... - ...... - ...... - \)
\(120\mathop \to \limits^{ + 220} 340\mathop \to \limits^{ + 220} 560\mathop \to \limits^{ + 220} 780\mathop \to \limits^{ + 220} 1000\mathop \to \limits^{ + 220} 1220\mathop \to \limits^{ + 220} 1440\)
\(3)\,10 - 30 - 70 - ........ - ........ - ........ - ........ - \)
\(10\mathop \to \limits^{ + 20} 30\mathop \to \limits^{ + 40} 70\mathop \to \limits^{ + 60} 130\mathop \to \limits^{ + 80} 210\mathop \to \limits^{ + 100} 310\mathop \to \limits^{ + 120} 430\)
به الگوی زیر توجه کنید.
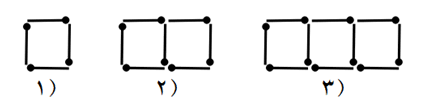
الف چه الگویی در کشیدن شکل ها وجود دارد؟
تعداد مربع ها در هر مرحله نسبت به مرحله قبل یک واحد بیشتر است (در هر مرحله 3 چوب کبریت اضافه می شود)
ب اگر الگوی هندسی به الگوی عددی تبدیل شود شکل ششم از چند چوب کبریت ساخته می شود؟
\(4\mathop \to \limits^{ + 3} 7\mathop \to \limits^{ + 3} 10\mathop \to \limits^{ + 3} 13\mathop \to \limits^{ + 3} 16\mathop \to \limits^{ + 3} 19\)
تهیه کننده : عزیزی و حیدرزاده
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم- آزمون آنلاین تمامی دروس پایه چهارم
- گام به گام تمامی دروس پایه چهارم
- ویدئو های آموزشی تمامی دروس پایه چهارم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه چهارم
- فلش کارت های آماده دروس پایه چهارم
- گنجینه ای جامع از انشاء های آماده پایه چهارم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه چهارم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
عدد نویسی
فصل 1 : اعداد و الگوها
عدد نویسی
هر عدد از یک، دو یا چند رقم ساخته می شود و ارزش هر رقم در یک عدد بستگی به ارزش مکانی دارد که رقم در آن قرار گرفته است که به آن ارزش مکانی میگویم.
در جدول ارزش مکانی به ترتیب از سمت راست به چپ ،طبقه یکی، هزارها ، میلیون ها، میلیاردها قرار دارند.
هر طبقه دارای سه مرتبه یکان - دهگان - صدگان می باشد که این مرتبه ها در تمام طبقات تکرار می شوند.
در سال قبل با طبقه هزار آشنا شدیم. با گذاشتن 10 بسته ی ۱۰۰ تایی عدد هزار ساخته می شود.
10بسته هزارتایی = عدد ده هزار((10,000
10بسته ده هزارتایی = عدد صد هزار (100,000)
مثال
عدد زیر را با توجه ارزش مکانی ارقام بنویسید
782236
۲۳۶, ۷۸۲ = ۷ تا صد هزارتایی + ۸ تا ده هزارتایی+ 2 تا هزارتایی +2 تا صدتایی+3تا دهه تایی+6 تا یکی
برای گسترده کردن عدد با توجه به ارزش مکان آن رقم آن را گسترده می کنیم در جدول ارزش مکانی به جای ارقامی که نداریم صفر می گذاریم
هرچه از سمت راست به چپ حرکت کنیم ارزش رقم ها بیشتری میشود.
مثال
در عدد ۲۱۳۰۵
الف کدام رقم ارزش بیشتری دارد؟
۲ در مرتبه ده گان هزار
ب بزرگترین رقم در چه مرتبه ای قرار دارد ؟
بزرگترین رقم ۵ است در مرتبه یکان
برای خواندن اعداد از است راست سه رقم سه رقم جدا کرده و از سمت چپ سه رقم جدا شده را با عنوان طبقه می خوانیم: 526,152
پانصد و بیست و شش هزار و صد و پنجاه و دو
در نوشتن اعداد با رفتم های خواسته شده به ارزش ارقام ترجمه شود مثلاً برای نوشتن بزرگترین عدد باید بزرگترین ارقام در ارزش مکانی بیشتر یعنی از چپ به راست قرار گیرد
باید توجه داشته باشیم که صفر می تواند اولین رقم از است چپ قرار گیرد چون کمتر در سمت چپ عدد خوانده می شود.
مثال
با رقم های 4-0-5-7-2 کوچکترین و بزرگترین عدد 5 رقمی را بنویسید.
بزرگترین:
75420
کوچک ترین:
75420
یک دو چرخه سوار فاصله ی دو شهر را طی میکند. اگر او با طی کردن هر ۱۰,۰۰۰ متر در یک ایستگاه استراحت کنه با ادامه ی الگوی زیر حساب کنید پس از رسیدن به ایستگاه نهم چه مسافتی را طی کرده است؟
\(10000 - 20000 - 30000 - ...... - ........ - \)
\(10000 - 20000 - 30000 - 40000 - 50000 - 60000 - 70000 - 80000 - 90000\)
تا ایستگاه نهم 90000 متر را طی می کند.
عدد ۶۸۵ ۴۳۹ را در نظر بگیرید.
الف عدد را به حروف بنویسید.
چهارصد و سی و نه هزار و ششصد و هشتاد و پنج
ب بزرگترین رقم کدام است و چه ارزشی دارد؟
رقم 9 در جایگاه یکان هزار
ج کدام رقم بیشترین ارزش مکانی را دارد؟
رقم چهار
د کدام رقم کمترین ارزش مکانی را دارد؟
رقم 5
تهیه کننده : عزیزی و حیدرزاده
جزوات جامع پایه چهارم
جزوه جامع ریاضی چهارم
جزوه جامع فارسی چهارم
جزوه جامع نگارش چهارم
جزوه جامع هدیه های آسمانی چهارم
جزوه جامع علوم تجربی چهارم
جزوه جامع مطالعات اجتماعی چهارم
جزوه جامع آموزش قرآن چهارم
الگو ها
فصل 1 : اعداد و الگوها
الـگـو ها
در یک الگوی عددی با هندسی گاهی با توجه به شماره شکل و تعداد می توانیم رابطه ای کشف کرده و الگو را ادامه دهیم.
مثال
الگوها را ادامه دهید و مقدار افزایش یا کاهش الگوها را بنویسید
\(1)5 - 30 - 180 - ........ - ........ - ........ - ........ - \)
\(5\mathop \to \limits^{ \times 6} 30\mathop \to \limits^{ \times 6} 180\mathop \to \limits^{ \times 6} 1080\mathop \to \limits^{ \times 6} 6480\mathop \to \limits^{ \times 6} 38880\)
\(2)7 - 14 - 28 - ....... - ....... - ....... - ....... - \)
\(7\mathop \to \limits^{ \times 2} 14\mathop \to \limits^{ \times 2} 28\mathop \to \limits^{ \times 2} 56\mathop \to \limits^{ \times 2} 112\mathop \to \limits^{ \times 2} 224\)
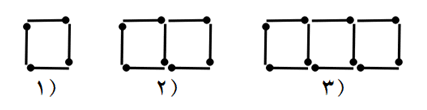
الگوی هندسی زیر را در نظر بگیرید.
الف چه رابطه ای بین شماره شکل و تعداد مربع ها وجود دارد؟
2+(3×شماره شکل)
\(5\mathop \to \limits^{ + 3} 8\mathop \to \limits^{ + 3} 11\)
ب با توجه به رابطه کشف شده حساب کنید در کدام شکل 62 مربع خواهیم داشت؟
شماره شکل: 62
188=2+(3×62)
تهیه کننده : عزیزی و حیدرزاده
ماشین ورودی خروجی
فصل 1 : اعداد و الگوها
ماشین ورودی خروجی
در این ماشین ها اعداد با توجه به نوع کاری که انجام می شود تغییر کرده و از آن خارج می شوند.
مثال
محیط مثلث متساوی الاضلاع : ۳×یک ضلع
ماشین محیط یابی:
مثال
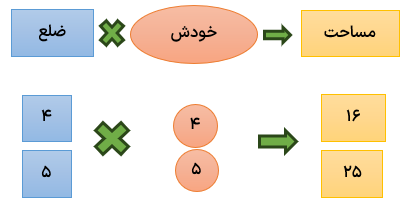
مساحت مربع : (خودش × یک ضلع)
گاهی اوقات عدد خروجی داده شده است که در این صورت باید عملیات را بر عکس انجام داده و عدد ورودی را حساب کنیم..
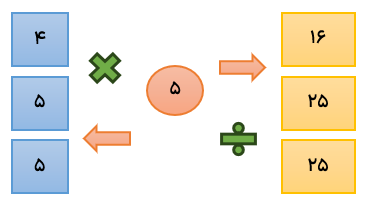
ممکن اسمت چندین عملیات وجود داشته باشد که باید در عدد ورودی به ترتیب هر مرحله را انجام دادند و با حاصل به دست آمده مرحله بعدی را انجام دهیم.
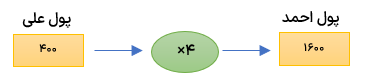
الف احمد 4 برابر علی پول دارد. اگر علی ۴۰۰ تومان داشته باشد احمد چند تومان پول دارد؟
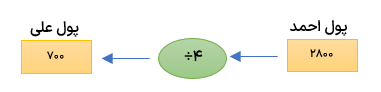
ب اگر احمد ۲۸۰۰ تومان پول داشته باشه علی چند تومان پول دارد؟
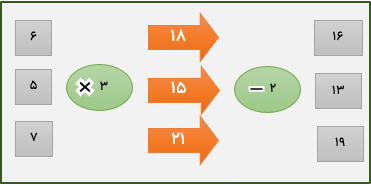
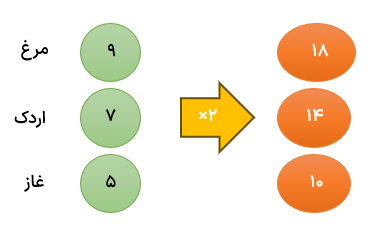
در حیاط یک خانه روستایی 9 مرغ و 7 اردک و 5 غاز وجود دارد با قرار دادن اعداد در ماشین ورودی و خروجی تعداد پاها را حساب کنید.
تهیه کننده : عزیزی و حیدرزاده
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم- آزمون آنلاین تمامی دروس پایه چهارم
- گام به گام تمامی دروس پایه چهارم
- ویدئو های آموزشی تمامی دروس پایه چهارم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه چهارم
- فلش کارت های آماده دروس پایه چهارم
- گنجینه ای جامع از انشاء های آماده پایه چهارم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه چهارم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
معرفی میلیون
فصل 1 : اعداد و الگوها
معرفی میلیون
هر طبقه دارای ۳ مرتبه یکی _ ده تایی _ صدتایی است _ در ادامه عدد نویسی با عدد صد هزار آشنا شدیم. اگر 10 دسته ی هزار تایی در کنار هم قرار گرد عدد یک میلیون به دست می آید و یک طبقه میلیون ها به جدول ارزش مکانی اضافه می شود.
سیصد و یک میلیون و شش هزار و ده
1 هنگام قرار دادن اعداد در جدول ارزش مکانی رقم ها را با توجه به ارزش و مرتبه در جدول قرار داده و بقیه ارقامی را که نداریم صفر قرار می دهیم
2 اگر 1 واحد به بزرگترین عدد شش رقمی اضافه شود کوچکترین عدد هفت وقتی یعنی یک میلیون ساخته می شود
999999+1=1,000,000
عدد یک میلیون برابر است با 10 تا صد هزار تایی:1,000,000
عدد ده میلیون برابر است با ۱۰ تا یک میلیون تایی:10,000,000
عدد صد میلیون برابر است با 10 تا ده میلیون تایی: 100,000,000
مقایسه اعداد
مثال
الف اگر تعداد و رقم ها برابر نباشد عددی بزرگ تر است که تعداد رقم های آن بیشتر است.
\(31752\left[ > \right]5791\)
ب اگر تعداد رقم ها برابر نباشد از بزرگ ترین مرتبه یعنی از دست چپ در هر دو عدد مقایسه می شود.
3492و6578 هر دو چهار رقمی هستند ولی رقم مرتبه یکان هزار در عدد ۶۵۷۸ عدد 6 است و از رقم مرتبه کیان هزار در عدد 3۴۹۲ یعنی ۳ بزرگ تر است پس :
\(3492\left[ < \right]6578\)
مثال
الگوهای عددی زیر را ادامه دهید.
600,000 - 700,000 - ……. الف
600,000 - 700,000 – 800,000 – 900,000 – 1,000,000
10,700,000 - 10,800,000 - ……. ب
10,700,000 - 10,800,000 – 10,900,000 – 11,000,000
995,000 - 996,0000 - ……… ج
995,000 - 996,0000 – 997,000 – 998,000 – 999,000 – 1,000,000
با توجه به درد ۵۰۷۹۴۰۰۲۸ به سوالات پاسخ دهید.
الف رقم های طبقه میلیون را بنویسید.
507
ب بزرگ ترین رقم در کدام مرتبه قرار دارد؟
صدگان هزار
ج ارزش مکانی رقم 4 چیست؟
دهگان هزار
د عدد را به حروف بنویسید.
پانصد و هفت میلیون و نهصد و چهل هزار و بیست و هشت.
تفریق زیر را انجام دهید.
\(\begin{array}{l}\,\,\,\,\,8447321\\ - \,\,\,\,\,\,1\,\,2\,\,0\,0\,0\,0\\ - - - - - - - - \end{array}\)
\(\begin{array}{l}\,\,\,\,\,8447321\\ - \,\,\,\,\,\,1\,\,2\,\,0\,0\,0\,0\\ - - - - - - - - \\\,\,\,\,\,8\,5\,67321\end{array}\)
تهیه کننده : عزیزی و حیدرزاده
جزوات جامع پایه چهارم
جزوه جامع ریاضی چهارم
جزوه جامع فارسی چهارم
جزوه جامع نگارش چهارم
جزوه جامع هدیه های آسمانی چهارم
جزوه جامع علوم تجربی چهارم
جزوه جامع مطالعات اجتماعی چهارم
جزوه جامع آموزش قرآن چهارم
شناخت کسر ها
فصل 2 : کسر
شناخت کسر ها
کسر به معنای بخشی از یک کل (واحد کامل) است وقتی یک واحد کامل را به قسمت های مساوی تقسیم می کنیم و فقط قسمت هایی از آن واحد مورد نظر ماست می توانم به صورت کسری مقدار مورد نظر را بیان کنیم.
یک کسر به این صورت نمایش داده می شود:
مثال
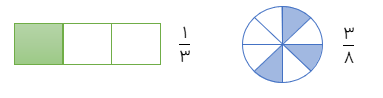
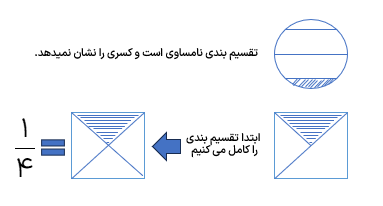
در خواندن کسر ها از روی شکل واحد تقسیم شده باید به قسمتهای مساوی تقسیم شود در غیر این صورت ابتدا باید تقسیم بندی کامل شود و بعد کسر کامل شود.
مثال
در نوشتن عدد مخلوط دارای واحد کامل و واحد کسری هستیم. برای رسم شکل با توجه به واحد عدد صحیح واحد کامل را رسم کرده و با توجه به مخرج واحد کسری شکل را تقسیم بندی می کنیم و با در نظر گرفتن صورت مقدار کسری را نمایش می دهیم.
مثال
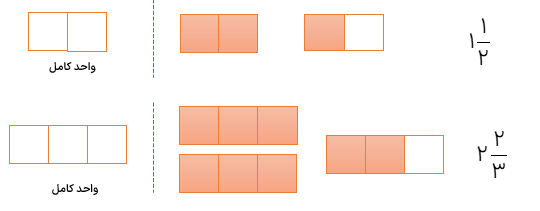
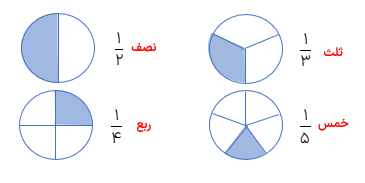
کسر های خاص
در صورت تقسیم عددی بر ۲ و ۳ و ۴ و ۵ کسر هایی به شکل زیر به وجود می آید.
کسر هایی که صورت آنها صفر باشد برابر صفر است و کسر هایی که صورت و مخرج برابر است 1 واحد کامل اند.
مقدار خواسته شده را به صورت کسری بنویسید و روی شکل نشان دهید.
جاهای خالی را کامل کنید
الف نصف ۶۰ تا می شود .................. تا
نصف ۶۰ تا می شود 30تا
ب ثلث ۱۵ تا می شود.............. تا
ثلث ۱۵ تا می شود 5 تا
ج ربع ۲۰ تا می شود ................. تا
ربع ۲۰ تا می شود5 تا
د خمس ۵۰ تا می شود................... تا
خمس ۵۰ تا می شود 10 تا
تهیه کننده : عزیزی و حیدرزاده
جمع و تفریق کسر ها
فصل 2 : کسر
جمع و تفریق کسر ها
در جمع کسر که مخرج های آن برابر است کافی است یکی از مخرج ها را در مخرج کسر حاصل نوشته و سپس صورت ها را با هم جمع کرده و حاصل جمع را در صورت کسر حاصل مینویسم و در تفریق حاصل تفریق صورت در کسر را در کسر حاصل می نویسیم.
مثال
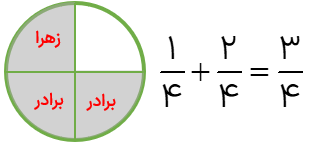
\(\frac{1}{4}\) از یک سیب را از زهرا و \(\frac{2}{4}\) دیگر آن را برادرش خورد چه کسری از سیب خورده شده است؟
رسم شکل
شکل واحد به اندازه مخرج تقسیم می شود. در جمع به اندازه صورت اول شکل را رنگ کرده و به اندازه کسر دوم از قسمت های باقی مانده شکل رنگ دیگر می کنیم.
در تفریق به اندازه صورت اول شکل رنگ کرده و به اندازه کسر دوم از قسمت های رنگ شده حذف می کنیم.
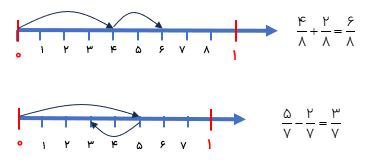
رسم محور
با توجه به مخرج واحدهای محور را به قسمت های مساوی تقسیم می کنیم.
از روی صفر به اندازه صورت کسر اول حرکت می کنیم
در جمع از انتهای فلش کسر اول به اندازه صورت کسر دوم شمرده و جلو رویم.
در تفریق از انتهای فلش کسر اول به اندازه صورت کسر دوم قسمت ها را شمرده و به عقب بر میگردیم.
1 در بعضی جمع های کسری صورت و مخرج کر حامل با هم برابری شود بعضی که حاصل برابر یک واحد است.
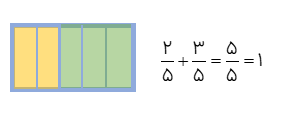
2 هر گاه در تفریق کسر حاصل برابر صفر شود حاصل صفر است.
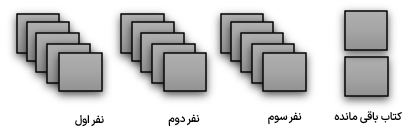
\(\frac{4}{8}\) از کتاب های کتابخانه ای در نوبت اول و \(\frac{4}{9}\) آن ها در نوبت دوم مطالعه شده است چه کسری از کتاب ها خوانده شده است؟
\(\frac{4}{8} + \frac{3}{8} = \frac{7}{8} \Rightarrow \frac{8}{8} - \frac{7}{8} = \frac{1}{8}\) کتاب ها خوانده نشده
\(\frac{6}{9}\)و از محصول سب باید به تهران حمل شود. \(\frac{4}{9}\) آن دیروز حمل شده است. چه کسری باید امروز حمل شود؟
\(\frac{6}{9} - \frac{4}{9} = \frac{2}{9}\) باید امروز حمل شود
تهیه کننده : عزیزی و حیدرزاده
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم- آزمون آنلاین تمامی دروس پایه چهارم
- گام به گام تمامی دروس پایه چهارم
- ویدئو های آموزشی تمامی دروس پایه چهارم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه چهارم
- فلش کارت های آماده دروس پایه چهارم
- گنجینه ای جامع از انشاء های آماده پایه چهارم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه چهارم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
تساوی کسر ها
فصل 2 : کسر
تساوی کسر ها
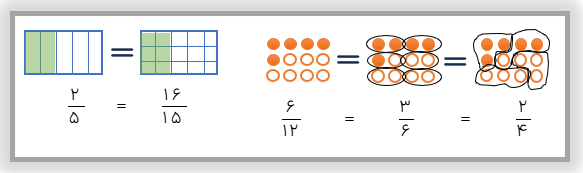
اگر بخواهم برای کسری که داریم کسر های مساوی بنویسیم به صورت های زیر عمل می کنیم:
رسم شکل
برای نوشتن کسر مساوی با کمک شکل باید توجه کرد که تغییری در شکل و قسمت های رنگی آن به وجود نمی آید و فقط با ایجاد تقسیم بندی ها مختلف روی شکل کسر مساوی با یک کسر را می نویسم.
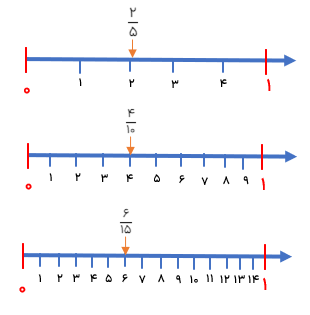
رسم محور
با تقسیم بندی های مختلف روی محور کسر های مساوی را می نویسیم.
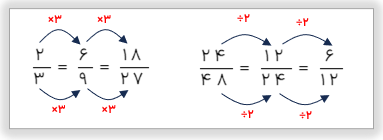
ضرب و تقسیم
برای نوشتن کسر مساوی با نیم یک کسر صورت و مخرج را در یک عدد مساوی ضرب و یا بر یک عدد مساوی تقسیم می کنیم.
جمع و تفریق کسر ها با استفاده از کسر های مساوی
در جمع و تفریق کسر هایی که مخرج برابر ندارند. ابتدا با نوشتن کسر های مساوی آن ها را به کسر هایی با مخرج یکسان تبدیل می کیم سپس جمع و تفریق را انجام می دهیم.
\(\frac{{{1_{ \times 2}}}}{{{6_{ \times 2}}}} - \frac{1}{{12}} = \frac{2}{{12}} - \frac{1}{{12}} = \frac{3}{{12}}\)
می توانیم مخرج کوچکتر را به مخرج بزرگتر برسانیم.
مقایسه کسر با استفاده از کسر های مساوی
برای مقایسه کسر ها باید کسر ها صورت یا مخرج مساوی داشته باشند.
\(\frac{2}{{10}}\left[ {\,\,\,} \right]\frac{{{1_{ \times 2}}}}{{{7_{ \times 2}}}} \Rightarrow \frac{2}{{10}} > \frac{2}{{14}}\) تساوی صورت
\(\frac{{{3_{ \times 2}}}}{{{4_{ \times 2}}}}\left[ {\,\,\,} \right]\frac{5}{8} \Rightarrow \frac{6}{8} > \frac{5}{8}\) تساوی مخرج
در صورتی که چندین کسر و عدد مخلوط داشته باشیم عدد مخلوطی که واحد عدد صحیح آن بزرگتر است از سایر کسرها بزرگتر می باشد و نیازی به یکسان کردن مخرج ندارد.
\(3\frac{1}{2} - \frac{9}{{10}} - \frac{{{3_{ \times 2}}}}{{{5_{ \times 2}}}} - 5\frac{1}{3}\,\,\,\,\,\,\,\,\,\,\,\,\,\, \to \,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{3}{5}\left( {\frac{6}{9}} \right) < \frac{9}{{10}} < 3\frac{1}{2} < 5\frac{1}{3}\)
کسری بنویسید که از \(\frac{5}{9}\) کوچکتر بوده و مخرج ان 45 باشد.
\(\frac{{{5_{ \times 5}}}}{{{9_{ \times 5}}}} = \frac{{25}}{{45}} \Rightarrow \frac{{24}}{{45}} < \frac{{25}}{{45}}\)
در صورت کسر از هر عددی که کوچک تر از 25 است می توانیم استفاده کنیم.
کسر های زیر و عدد مخلوط را از کوچک به بزرگ مرتب کنید.
\(\frac{1}{2},5\frac{1}{2},\frac{7}{{12}},\frac{1}{3},4\frac{1}{3},\frac{4}{6}\)
\(\frac{{{1_{ \times 4}}}}{{{3_{ \times 4}}}} = \frac{4}{{12}} < \frac{{{1_{ \times 6}}}}{{{2_{ \times 6}}}} = \frac{6}{{12}} < \frac{7}{{12}} < \frac{{{4_{ \times 2}}}}{{{6_{ \times 2}}}} = \frac{8}{{12}} < 4\frac{1}{3} < 5\frac{1}{2}\)
تهیه کننده : عزیزی و حیدرزاده
جزوات جامع پایه چهارم
جزوه جامع ریاضی چهارم
جزوه جامع فارسی چهارم
جزوه جامع نگارش چهارم
جزوه جامع هدیه های آسمانی چهارم
جزوه جامع علوم تجربی چهارم
جزوه جامع مطالعات اجتماعی چهارم
جزوه جامع آموزش قرآن چهارم
ضرب کسر ها
فصل 2 : کسر
ضرب کسر ها
برای رسم شکل\(2 \times \frac{3}{7}\) باید:
1 یک شکل رسم کرده و با توجه به مخرج آن را 7 قسمت می کنیم.
2 با توجه به صورت ۳ قسمت آن را رنگ می کنیم
3 با توجه به عدد ضرب شده در کسر ۲ تا \(\frac{3}{7}\) داریم پس \(\frac{3}{7}\) دیگر را رنگ متفاوت می زنیم الان \(\frac{6}{7}\) با شکل رنگی است.
برای رسم محور\(3 \times \frac{2}{{10}}\) باید:
فاصله بین صفر و یک را به اندازه مخرج کسر تقسیم می کنیم.
با توجه به صورت به تعداد عددی که در کسر ضرب شده است از نقطه صفر به جلوی رویم.
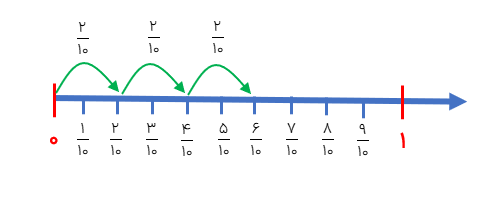
\(3 \times \frac{2}{{10}} = \frac{6}{{10}}\)
برای ضرب زیر شکل متناسب کشیده و حاصل را بدست آورید
\(4 \times \frac{1}{5}\)
علی ۷ سال دارد. سن او خمس سن پدرش در ربع سن مادرش است.
الف سن پدر را حساب کنید.
5×7=35
ب سن مادر علی را حساب کنید.
4×7=28
ج مجموع سن این سه نفر را حساب کنید.
35+28+7=70
تهیه کننده : عزیزی و حیدرزاده
حل مسئله
فصل 3 : ضرب و تقسیم
الگوسازی و حذف حالت های نامطلوب
در حل بعضی مساله ها باید تمام حالت های ممکن برای جواب مساله را بنویسیم.
مثال
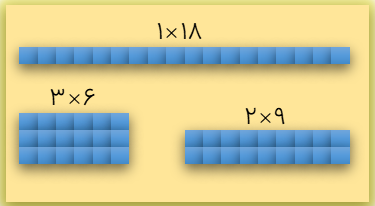
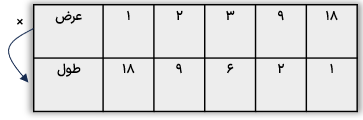
میخواهیم با ۱۸ کاشی مربع شکل یک مستطیل بسازیم:
روش اول: رسم شکل
روش دوم: الگویابی
مثال
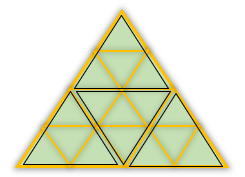
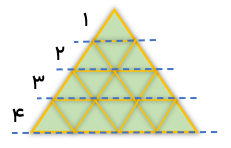
شکل رو برو چند مثلث کوچک دارد؟
اگر شکل را به صورت زیر تقسیم کنیم ۴ تا از این تقسیم بندی داریم . از طرفی درون هر کدام ۴ ملت است بنابراین 4×4=16 می شود تعداد مثلث های این شکل.
می توانیم الگوی برای این شکل به دست آوریم:
\(\begin{array}{l}1 = 1\,\,\,\,\,\,\,,\,\,\,\,\,\,\,2 = 3\,\,\,\,\,\,\,\,,\,\,\,\,\,3 = 5\,\,\,\,\,\,\,,\,\,\,\,\,\,4 = 7\,\,\,\,\,,\,\,\,\,\,5 = 9\\\\1 + 3 + 5 + 7 = 16\end{array}\)
حذف حالت های نامطلوب
برای حل بعضی مساله های توانیم همه حالت های مسکن را نوشته و از میان آن ها حالت های تا نا مطلوب را حذف کنیم.
مثال
بزرگترین عددی را که می توان در جای خالی نوشت تا الگو یابی مساوی برقرار باشد بنویسید.
\(\left[ {\,\,\,} \right] \times 8 < 7 \times 9\)
8 پاسخ مختلف (0-1-2-3-4-5-6-7) را می توان در جای خالی قرار داد ولی چون بزرگترین را خواسته با حذف پاسخ های دیگر عدد 7 را در جای خالی می نویسم.
7×8<7×9
مثال
در این جمع چه رقم قرار گیرد تا حاصل مقابل درست باشد؟
\(\begin{array}{l}\,\,\,\,\,\,1\,\,\,\,\left[ {\,\,\,} \right]\\ + \left[ {\,\,\,} \right]\,\,\,9\\ - - - - - - \\\,\,\,\,\,\,7\,\,\,\,4\end{array}\)
تمام اعداد را امتحان کرده و حالت های نا مطلوب را حذف میکنیم.
\(11 + 19 = 30\,\,\,\,,\,\,\,\,\,\,\,\,12 + 29 = 41\,\,\,\,\,\,\,\,\,,\,\,\,\,\,\,\,\,\,\,13 + 39 = 52\,\,\,\,\,\,\,\,,\,\,\,\,\,\,\,\,14 + 49 = 63\,\,\,\,\,\,\,\,,\,\,\,\,\,\,\,\,15 + 59 = 74\)
\(\begin{array}{l}\,\,\,\,\,\,1\,\,\,5\\ + \,\,\,5\,\,9\\ - - - - \\\,\,\,\,\,7\,\,4\end{array}\)
برای عبارت \(\left[ {\,\,\,} \right] \times 9 < 65\) تمام جواب های ممکن را پیدا کنید.
0-1-2-3-4-5-6-7
چه عددی را در جای خالی قرار دهیم تا حاصل آن نزدیک ترین عدد به ۶۵ باشد؟
وقتی عدد 7 در جای خالی قرار می گیرد ، حاصل نزدیک ترین عدد به 65 است.
تمام عدد هایی را پیدا کنید که حاصل ضرب آن ها ۲۴ و حاصل تفریق آنها زوج باشد پیدا کنید.
\(\begin{array}{l}24 \times 1 = 24\,\,\,\,\,\,\,\,,\,\,\,\,\,\,\,\,12 \times 2 = 24\,\,\,\,\,\,\,\,,\,\,\,\,\,\,\,\,8 \times 3 = 24\,\,\,\,\,\,\,\,,\,\,\,\,\,\,\,\,6 \times 4 = 24\\\\24 - 1 = 23\,\,\,\,\,\,\,\,,\,\,\,\,\,\,\,\,12 - 2 = 10\,\,\,\,\,\,\,\,\,\,,\,\,\,\,\,\,\,\,\,\,8 - 3 = 5\,\,\,\,\,\,\,\,,\,\,\,\,\,\,\,\,\,\,6 - 4 = 2\end{array}\)
تهیه کننده : عزیزی و حیدرزاده
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم- آزمون آنلاین تمامی دروس پایه چهارم
- گام به گام تمامی دروس پایه چهارم
- ویدئو های آموزشی تمامی دروس پایه چهارم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه چهارم
- فلش کارت های آماده دروس پایه چهارم
- گنجینه ای جامع از انشاء های آماده پایه چهارم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه چهارم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
ضرب عدد دو رقمی
فصل 3 : ضرب و تقسیم
ضرب عدد دو رقمی در یک رقمی
سال قبل با ضرب عدد های یک رقمی و چند رقمی آشنا شدید میتوانید به دو صورت عمل کنید:
مثال
رسم شکل:
میخواهیم برای ضرب عدد های یک رقمی در یکی ها ، ده تایی ها ، صدتایی ها ،.... شکل رسم می کنیم.
\(\begin{array}{l}\,\,\,\,\,\,241\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(200 + 40 + 1)\\ \times \,\,\,\,\,\,\,\,\,4\\ - - - - - \\\,\,\,\,\,8\,0\,0\\ + \,\,\,1\,6\,\,0\\ + \,\,\,\,\,\,\,\,\,4\\ - - - - - \\\,\,\,\,\,\,9\,6\,4\\\,\,\,\,\,\end{array}\)
گسترده کردن عدد:
\(\begin{array}{l}\,\,\,\,\,\,241\,\,\,\,\,\,\,\,\,\,\,\,\,(200 + 40 + 1)\\ \times \,\,\,\,\,\,\,\,\,4\\ - - - - - \\\,\,\,\,\,8\,0\,0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(4 \times 200)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,241\\ + \,\,\,1\,6\,\,0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(4 \times 40)\,\,\,\,\, \Rightarrow \,\,\,\,\,\, \times \,\,\,\,\,\,\,4\\ + \,\,\,\,\,\,\,\,\,4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(4 \times 1)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - - - - - \\ - - - - - \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,964\\\,\,\,\,\,\,9\,6\,4\\\,\,\,\,\,\end{array}\)
ضرب عدد دورقمی در دو رقمی
مثال
در یک مدرسه هر دانش آموز ۱۵ کتاب به کتابخانه اهدا کرد. اگر تعداد بچه ها ۲3 تر باشد میکند کتاب به کتابخانه اهدا شده است؟
روش اول : تجزیه عامل اول
\(23 \times 15 = (20 + 3) \times 15 \Rightarrow \,\left\{ \begin{array}{l}20 \times 15 = 300\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,300\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \,\,\,\,45\,\,\,\,\,\,\,\,\,\,\,\,\\3 \times 15 = 45\,\,\,\,\,\,\,\,\,\,\,\,\,\, - - - - - \\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,345\end{array} \right.\)
روش دوم : تجزیه عامل دوم
\(23 \times 15 = 23 \times (10 + 5) \Rightarrow \,\left\{ \begin{array}{l}23 \times 10 = 230\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,230\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \,\,115\,\,\,\,\,\,\,\,\,\,\,\,\\23 \times 5 = 115\,\,\,\,\,\,\,\,\,\,\,\,\,\, - - - - - \\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,345\end{array} \right.\)
ضرب دو عدد دو رقمی بصورت خلاصه
ابتدا قم یکان عدد دوم را در عدد اول ضرب می کنیم سپس ده گان عدد دوم را در عدد اول ضرب می کنیم در پایان عدد های بدست آمده را ما هم جمع می کنیم.
\(\begin{array}{l}\,\,\,\,\,15\\ \times \,\,\,\,11\\ - - - - \\\,\,\,\,\,\,15\,\,\,\,\,\,(1 \times 15)\\ + 150\,\,\,\,\,\,\,(10 \times 15)\\ - - - - \\\,\,\,165\end{array}\)
بار کامیونی را ۸۳ عدد کیسه ۴۵ کیلویی آرد تشکیل می دهند بار این کامیون چند کیلو گرم است؟
\(\begin{array}{l}\,\,\,\,\,83\\ \times \,\,\,45\,\,\,\,\,\,\,\,\,\,(40 + 5)\\ - - - - \\\,\,3320\,\,\,\,\,\,\,(40 \times 83)\\\,\,\,\,\,415\,\,\,\,\,\,\,(5 \times 83)\\ - - - - \\\,\,3735\end{array}\)
قیمت هر نان سنگک ۶۰۰ تومان است یک نانوایی امروز ۸۰۰ نان فروخته است در آمد امروز او چقدر است؟
800×600=480000
تهیه کننده : عزیزی و حیدرزاده
جزوات جامع پایه چهارم
جزوه جامع ریاضی چهارم
جزوه جامع فارسی چهارم
جزوه جامع نگارش چهارم
جزوه جامع هدیه های آسمانی چهارم
جزوه جامع علوم تجربی چهارم
جزوه جامع مطالعات اجتماعی چهارم
جزوه جامع آموزش قرآن چهارم
محاسبه ی حاصل ضرب
فصل 3 : ضرب و تقسیم
محاسبه ی حاصل ضرب
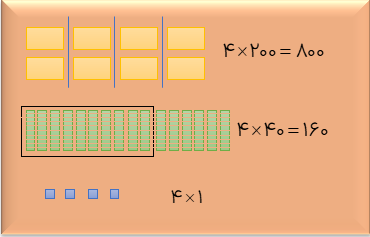
در محاسبه حاصل ضرب دو عدد که جلوی آن صفر قرار دارد ، ابتدا صفر های جلوی عددها را در نظر نمی گیریم و عمل ضرب را انجام می دهیم. سپس به تعداد صفر هایی که در نظر نگرفتیم جلوی حاصل رقم صفر قرار می دهیم.
\(45 \times 20 = 900\)
ضرب عدد سه رقمی در سه رقمی
ابتدا رقم یکان عدد دوم را در عدد اول، سپس رقم ده گان عدد دوم را در عدد اول در انتها رقم صد گان عدد دوم را در عدد اول ضرب کرده و حاصل ضرب حاصل ضرب ها را با هم جمع می کنیم.
\(\begin{array}{l}\,\,\,\,\,\,\,204\,\,\,\,\,\,\,\,(200 \times 4)\\ \times \,\,\,\,603\\\_\_\_\_\_\_\_\_\\\,\,\,\,\,\,\,120600\,\,\,\,\,\,\,\,(200 \times 603)\\ + \,\,\,\,\,\,\,2\,4\,1\,2\,\,\,\,\,\,\,\,(4 \times 63)\\\_\_\_\_\_\_\_\_\_\\\,\,\,\,\,\,\,123012\end{array}\)
در عدد دوم عدد صد گان وجود ندارد و ضرب ردیف ده گان صفر می شود
حاصل ضرب تقریبی
برای بدست آوردن حاصل ضرب تقریبی اعداد را به نزدیک ترین ده تایی، صد تایی و هزار تایی تقریب می زنیم سپس حاصل را بدست می آوریم.
\(\begin{array}{l}\,\,\,\,\,\,448\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,400\\ \times \,\,\,728\,\,\,\,\,\,\,\,\, \to \,\,\, \times \,\,700\\\_\_\_\_\_\_\_\_\_\,\,\,\,\,\,\, - - - - \\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,280000\end{array}\)
عدد ردیف اول از بین ۵۰۰ و ۴۰۰ به 400 نزدیک تر است.
عدد ردیف دوم از بین 700 و 800 به 700 نزدیک تر است.
\(\begin{array}{l}\,\,\,\,\,\,453\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,500\\ \times \,\,\,\,342\,\,\,\,\,\,\,\,\, \to \,\,\, \times \,\,300\\\_\_\_\_\_\_\_\_\_\,\,\,\,\,\,\, - - - - \\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,15\,00\,00\end{array}\)
عدد ردیف اول از بین 400 و 500 به 500 نزدیک تر است.
عدد ردیف دوم از بین 300 و 400 به 300 نزدیک تر است.
در جای خالی عدد مناسب بنویسید.
الف 2×10×6=…….
2×10×6=120
ب 5×4×…….=2000
5×4×100=2000
ج 81×10×300=…..
81×10×300=243000
یک ماشین چاپ در هر ساعت 800 ورق بزرگ را که هر ورق تبدیل به 16 صفحه کتاب می شود چاپ می کند ، این ماشین چاپ در هر ساعت چند صفحه چاپ می کند؟
\(\begin{array}{l}\,\,\,\,\,\,800\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,12800\\ \times \,\,\,\,\,\,\,\,16\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times \,\,\,\,\,\,\,100\\\_\_\_\_\_\_\_\_ \to - - - - - \\\,\,\,\,12800\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,128000\end{array}\)
در هر ساعت 128000 صفحه کتاب را چاپ می کند.
تهیه کننده : عزیزی و حیدرزاده
محاسبه های تقریبی
فصل 3 : ضرب و تقسیم
محاسبه های تقریبی
برای نوشتن عددها به صورت تقریبی با توجه به مرتبه ی تقریب، عددها را به نزدیک ترین ده تایی ، صد تایی با هزار تایی تقریب می زنیم.
تقریب ده گان
ده تایی قبل و بعد عدد را بنویسید. سپس از بین دو عدد نزدیک ترین را به عدد مورد نظر انتخاب می کنیم.
\(53 \to \left( {50} \right)\,,\,\,52\,\,,\,\,60\)
اگر رقم یکان 1 تا 4 بود رقم جلوی ده گان صفر می شود یعنی به ده تایی کمتر نزدیک تر می شود
\(266 \to 260\,\,\,\,,\,\,\,\,222\,\,\,,\,\,\,\,\left( {270} \right)\)
اگر رقم ده گان ۵ تا ۹ بود رقم یکان را صفر کرده و رقم ده گان را با 1 جمع می کنیم یعنی به ده تایی ها نزدیک تر می شود.
تقریب با صدگان
صد تایی قبل و بعد از عدد را بنویسید سپس از بین این دو عدد نزدیکترین را به عدد مورد نظر انتخاب کنید.
\(\begin{array}{l}486 \to 400\,\,\,\,\,,\,\,\,\,\,486\,\,\,\,,\,\,\,\,\left( {500} \right)\\\\1576 \to 1500\,\,\,\,,\,\,\,\,1576\,\,\,\,,\,\,\,\,\left( {1600} \right)\end{array}\)
تقریب هزارگان
هزار تایی قبل و بعد عدد را بنویسید پس از بین این دو عدد نزدیکترین را به عدد مورد نظر انتخاب کنید.
\(\begin{array}{l}1280 \to \left( {1000\,} \right)\,\,\,,\,\,\,\,1280\,\,\,\,,\,\,\,\,2000\\\\1580 \to 1000\,\,\,\,,\,\,\,\,1580\,\,\,\,,\,\,\,\,\left( {2000} \right)\end{array}\)
کاربرد تقریب
مثال
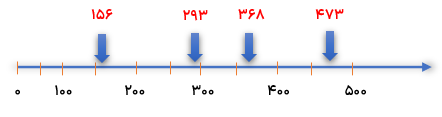
عدد های تقابل را به صورت تقریبی روی محور نشان دهید.
156-293-473-358
نقطه وسط در دو عدد مورد نظر را پیدا می کنیم و با و با توجه به آن اعداد تقریبی را نشان می دهیم
مثال
برای این که تشخیص دهیم ۴۷۵۲ کیلوگرم چند تن است. ابتدا عدد را با رقم هزارگان تقریب می زنیم بعد آن را به تن تبدیل می کنیم هر (۱۰۰۰ کیلوگرم 1 تن است).
کیلوگرم:\(6327 \to \left( {6000} \right)\,\,\,\,,\,\,\,\,\,6237\,\,\,,\,\,\,\,\,7000 \Rightarrow 6000 = 6\) تن
کیلوگرم:\(2828 \to \,2000\,\,\,,\,\,\,\,\,2828\,\,\,,\,\,\,\,\,\left( {3000} \right) \Rightarrow 3000 = 3\) تن
در محاسبه حاصل یک عبارت ریاضی به صورت تقریبی دو راه داریم:
الف ابتدا عددها را تقریب بزنیم و سپس حاصل عبارت را بنویسیم.
\(43 \times 19 \Rightarrow 40 \times 20 = 800\)
ب حاصل را بدست آوریم بعد تقریب بزنیم.
\(48 + 63 - 24 = 86 \Rightarrow 90\)
1 در ضرب دو عدد اگر یکان یکی از عدد های ضرب ۵ بود اگر عدد دیگر به سمت بالا تقریب مورد نظر به سمت پایین تقریب می خورد.
\(\begin{array}{l}35 \times 47 \Rightarrow 30 \times 50\\\\59 \times 25 \Rightarrow 60 \times 20\end{array}\)
2 اگر عدد دیگر به سمت پایین تقریب خورده باشد عددی که رقم یکان اش ۵ باشد به سمت بالا تر تقریب زده می شود.
\(\begin{array}{l}23 \times 45 \Rightarrow 30 \times 50\\\\55 \times 72 \Rightarrow 60 \times 70\end{array}\)
تقریب در تقسیم
برای به دست آوردن حاصل تقریبی تقسیم عدد مقسوم را به صورت تقریبی می نویسیم و حاصل تقسیم را به دست می آوریم. با این روش می توان خارج قسمت تقریبی اعداد سه رقمی را نیز به دست آورند
\(936 \div 3 \Rightarrow 900 \div 3 = 3000\)
عدد های زیر با چه تقریبی نوشته شده است؟
الف 245=200
تقریب صدگان
ب 16345=16300
تقریب صدگان
ج 1282=1000
تقریب هزارگان
د 2722=2730
تقریب ده گان
برای تماشای مسابقه والیبال ۱۲۸۳۹ نفر به ورزشگاه رفتند . این عدد با تقریب رقم هزارگان به کدام عدد نزدیک تر است؟
1300
مدیر کارخانه ای برای پاداش 835000 را به طور مساوی بین 8 نفر تقسیم کرده است. به طور تقریبی به هر نفر چند تومان پاداش می رسد؟
\(800000 \div 8 = 100000\)
تهیه کننده : عزیزی و حیدرزاده
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم- آزمون آنلاین تمامی دروس پایه چهارم
- گام به گام تمامی دروس پایه چهارم
- ویدئو های آموزشی تمامی دروس پایه چهارم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه چهارم
- فلش کارت های آماده دروس پایه چهارم
- گنجینه ای جامع از انشاء های آماده پایه چهارم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه چهارم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
تقسیم و بخش پذیری
فصل 3 : ضرب و تقسیم
تقسیم و بخش پذیری
تقسیم به معنای قسمت کردن به طور مساوی است. در یک تقسیم :
1 - عددی که تقسیم می شود مقسوم است.
2 - به عددی که مقسوم بر آن تقسیم می شود مقسوم علیه میگویم.
3 - به جواب تقسیم خارج قسمت می گوییم.
4 - پس از عمل تقسیم ممکن است باقی مانده داشته باشیم یا باقی مانده صفر شود
مفهوم تقسیم
عدد را به چند قسمت مساوی تقسیم می کنیم تا ببینیم در هر قسمت چه مقداری قرار می گیرد.
مثال
آموزگار ۱۷ کتاب دارد. او می خواهد به هر دانش آموز ۵ کتاب هدیه بدهد این کتابها به چند دانش آموز می رسد؟
با کمک شکل:
17کتاب را به دسته های ۵ تایی تقسیم کردیم 3 دسته درست می شود 2کتاب باقی مانده می شود و این تعداد را دیگر نمی توان تقسیم کرد چون ۲<۵ است.
با کمک محور:
عدد مقسوم را روی محور پیدا کرده از آن به اندازه مقسوم علیه به سمت چپ تا جایی که امکان دارد به عقب بر می گردیم.
محاسبه بدون شکل و محور :
ضرب های مختلف را امتحان کرده و بزرگترین ضرب را که نزدیک ترین حاصل ضرب را به مقسوم دارد انتخاب می کنیم.
5×2=10 , 5×3=15 (درست) , 5×4=20(غلط)
رابطه ی تقسیم
منظور از رابطه ی تقسیم احتمال درستی تقسیم است که در پایان تقسیم بررسی می شود.
مقسوم = باقی مانده + ( مقسوم علیه x خارج قسمت )
مقسوم علیه > باقی مانده
(6×8)+6=54
6<8
بخش پذیری
به تقسیم مقابل دقت کنید.
5×2=10
5×3=15
5×4=20
5×5=25
5×6=30
وقتی در تقسیم باقی مانده صفر شود می گوییم مقسوم بر مقسوم علیه بخش پذیر است.
1 باقی مانده تقسیم هر عدد بر خودش صفر می باشد.
2 اعدادی بر ۲ بخش پذیر هستند که یکان آنها (۰-۲- ۴-۶-۸) باشد.
3 اعدادی بر 3 بخش پذیر هستند که مجموع ارقام آنها بر ۳ بخش پذیر باشد
4 اعدادی بر 5 بخش پذیر هستند که یکان آن 0 یا ۵ باشد.
5 اعدادی بر ۹ بخش پذیر هستند که مجموع ارقام آن ها بر 9بخش پذیر باشد.
6 اعدادی به ۱۰ بخش پذیر هستند که یکان آن ها صفر باشد.
جاهای خال را تکمیل کنید.
الف عدد دو رقمی که بر 4 بخش پذیر باشد و رقم ده گان 3 است و رقم یکان از رقم ده گان کوچکتر باشد.................. است
32
ب عدد دو رقمی که رقم یکان و ده گان یکسان است و بر 9 بخش پذیر باشد .................. است
99
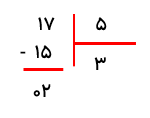
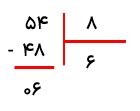
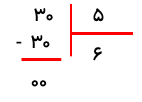
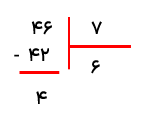
می خواهیم یک تخته چوب به طول 46 سانتی متر را به قطعات 7 سانتی متری تقسیم کنیم چند قطعه چوب 7 سانتی متری به دست می آید؟ و چند سانتی متر باقی می ماند؟
6 قطعه چوب به دست می آید و 4 سانتی متر باقی می ماند.
تهیه کننده : عزیزی و حیدرزاده
جزوات جامع پایه چهارم
جزوه جامع ریاضی چهارم
جزوه جامع فارسی چهارم
جزوه جامع نگارش چهارم
جزوه جامع هدیه های آسمانی چهارم
جزوه جامع علوم تجربی چهارم
جزوه جامع مطالعات اجتماعی چهارم
جزوه جامع آموزش قرآن چهارم
تقسیم دو رقمی
فصل 3 : ضرب و تقسیم
تقسیم تقریبی
برای به دست آوردن خارج قسمت تقریبی یک تقسیم مقسوم و مقسوم علیه را به صورت تقریبی نوشته و تقسیم را انجام می دهیم.
تقسیم بر عدد دو رقمی
ابتدا خارج قسمت را تقریبی محاسبه می کنیم. سپس خارج قسمت تقریبی را در تقسیم اصل قرار می دهیم.
مثال
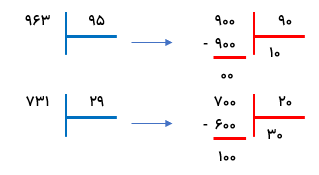
تقسیم 528 بر 24 را انجام دهید.
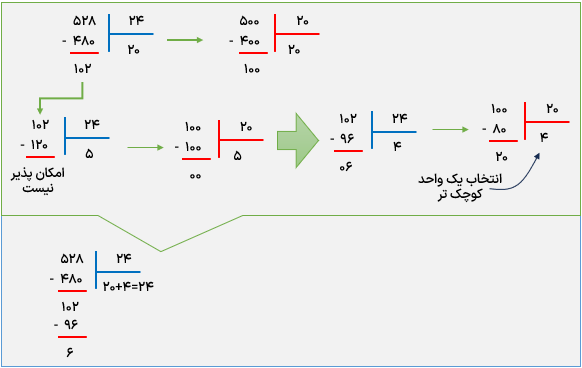
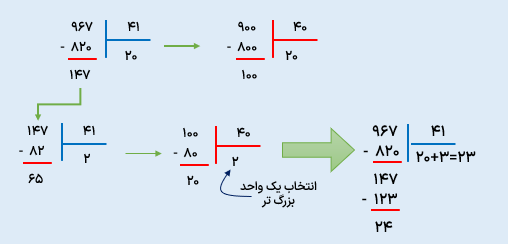
تقسیم 967 بر 41 را انجام دهید.
برای دوختن یک مانتو 30 متر پارچه نیاز است با یک توپ پارچه که 56 متر است حداکثر چند مانتو می توان دوخت؟
تهیه کننده : عزیزی و حیدرزاده
زاویه
فصل 4 : اندازه گیری
زاویه
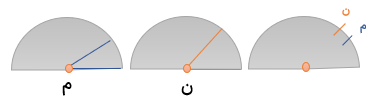
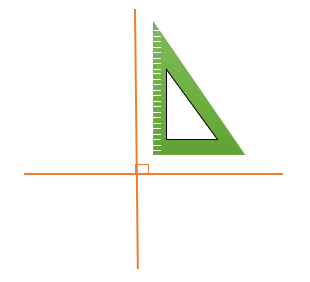
اگر به محیط اطراف خود نگاه کنیم بسیاری از زاویه ها راست هستند به برای تشخیص زاویه های راست از گونیا استفاده می کنیم.
راس زاویه راست گونیا را روی راس زاویه گذاشته و یک ضلع گونیا روی یک ضلع زاویه قرار می گیرد.
اگر ضلع دوم زاویه نیز روی ضلع دوم گونیا قرار گیرد می گوییم زاویه راست است.
زاویه تند
به زاویه ای که از زاویه راست کوچک تر باشد می گوییم (حاده)
زاویه باز
زاویه ای که از زاده راست بزرگتر باشد ( منفرجه)
مقایسه زاویه ها
روش اول:
می توانیم برای مقایسه هر زاویه از کاغذ شفاف نیز استفاده کنیم. یکی از دو زاویه را روی کاغذ شفاف رسم می کنیم سپس کاغذ را روی زاویه دیگر قرار می دهیم تا تشخیص دهیم کدام بزرگتر است و اگر کامل دو ضلع روی هم قرار گیرد دو زاویه باهم برابرند.
روش دوم:
یک نیم دایره را با کاغذ شفاف درست می کنیم مرکز نیم دایره را روی راس زاویه ها می گذاریم و اندازه آن را روی نیم دایره علامت می زنیم.
1 به دو نوع از گونیا برای زوایای مختلف استفاده می کنیم.
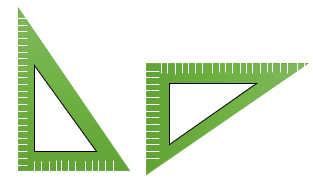
2 دو نوع گونیا داریم:
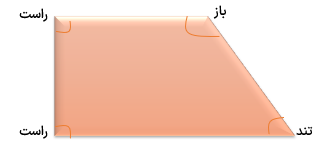
شکلی رسم کنید که هر سه زاویه تند باز و راست را داشته باشد.
جاهای خالی را کامل کنید.
الف زاویه راست از زاویه باز...................... است.
کوچکتر
ب اندازه هر زاویه با دور و نزدیک شدن ضلع از هم تغییر ........................
می کند
ج زاویه کوچکتر از زاویه راست..................... نامیده می شود.
تند
تهیه کننده : عزیزی و حیدرزاده
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم- آزمون آنلاین تمامی دروس پایه چهارم
- گام به گام تمامی دروس پایه چهارم
- ویدئو های آموزشی تمامی دروس پایه چهارم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه چهارم
- فلش کارت های آماده دروس پایه چهارم
- گنجینه ای جامع از انشاء های آماده پایه چهارم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه چهارم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
اندازه گیری زاویه
فصل 4 : اندازه گیری
اندازه گیری زاویه
برای اندازه گیری زاویه های مختلف نیاز به یک واحد مشخص و استاندارد است، برای این کار یک نیم دایره به ۱۸۰ قسمت مساوی تقسیم شده که هر کدام از این قسمتهای کوچک یک درجه نام دارد هر درجه \(\frac{1}{{180}}\) یک نیم دایره است و به این صورت نمایش داده می شود:\(1^\circ \) (یک درجه)
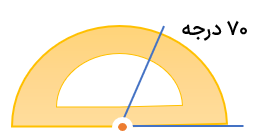
نقاله
وسیله ای برای اندازه گیری و مقایسه داده ها می باشد.
الف نقطه وسط نقاله (مرکز نیم دایره) را بر روی راس زاویه قراری می دهیم.
ب شعاع نقاله (نیم دایره) برابر روی یکی از دو ضلع زاویه قرار می دهیم.
ج توجه می کنیم ضلع دیگر زاویه برروی کدام درجه ی نقاله (از 0 تا ۱۸۰) قرار دارد.
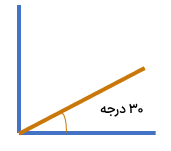
در نقاله بالا اندازه زاویه ما 70 درجه است.
زاویه راست : 90 درجه و زاویه نیم صفحه : ۱۸۰ درجه است
در دو گونیا (45-45 و 30-60) اندازه ها به صورتی میباشد که می توانیم زاویه های مختلفی بسازیم ، برای مثال:
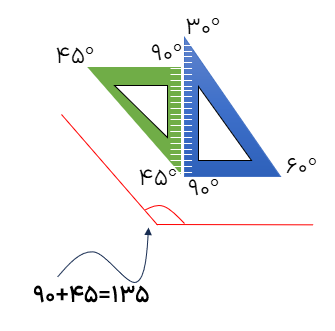
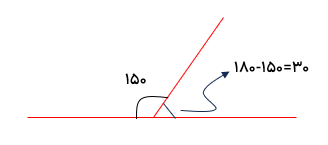
زمانی که از کنار هم قرار گرفتن دو زاویه، یک زاویه ۱۸۰ درجه (نیم صفحه) تشکیل شود. کافی است زاویه مشخص شده را از 180 کم کنیم تا اندازه زاویه خواسته شده بدست آید.
۱۸۰ - ۱۵۰ = ۳۰
زمانی که از کنار هم قرار گرفتن دو زاویه یک زاویه قائمه یا راست ( ۹۰ درجه) تشکیل شود کافی است زاویه مشخص شده را از ۹۰ درجه کم کنیم تا اندازه زاویه خواسته شده بدست آید.
۶۰ =90-3۰
1 اگر دو زاویه راست کنار هم قرار گیرد زاویه ۱۸۰ درجه به وجود می آید.
2 اگر دو زاویه نیم صفحه کنار هم قرار گیرد تشکیل یک دایره کامل می دهد که اندازه این زاویه ۳۶۰ درجه است.
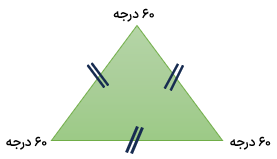
3 در مثلث متساوی الاضلاع هر سه ضلع، با هم برابر است هر سه زاویه برابر و مساوی ۶۰ است.
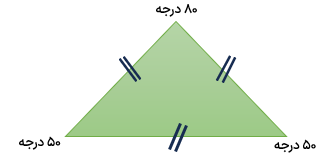
4 در مثلث ستادی الساقین دو ضلع باهم برابر است و دو زاویه مثلث با هم برابر هستند.
5 در مثلث قائم الزاویه حتما یکی از زاویه ها ۹۰ درجه است.
6 مجموع زاویه های داخلی هر چهار ضلعی ۳۶۰ درجه است.
جمله های زیر را کامل کنید
الف اندازه زاویه راست..............................است
90 درجه
ب دو زاویه راست تشکیل یک زاویه.................. می دهند
180 درجه یا نیم صفحه
ج واحد اندازه گیری زاویه...................... است
درجه
اگر مثلثی یک زاویه 110 درجه داشته باشد و دو زاویه دیگر ان مساوی باشد هر کدام چند درجه است؟
مثلث مورد نظر متساوی الساقین است و مجموع زوایای ان 180 درجه می باشد بنابراین داریم:
180-110=70 مجموع دو ضلع
70÷2=35
تهیه کننده : عزیزی و حیدرزاده
جزوات جامع پایه چهارم
جزوه جامع ریاضی چهارم
جزوه جامع فارسی چهارم
جزوه جامع نگارش چهارم
جزوه جامع هدیه های آسمانی چهارم
جزوه جامع علوم تجربی چهارم
جزوه جامع مطالعات اجتماعی چهارم
جزوه جامع آموزش قرآن چهارم
اندازه گیری زمان
فصل 4 : اندازه گیری
اندازه گیری زمان
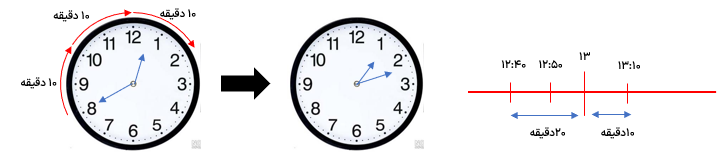
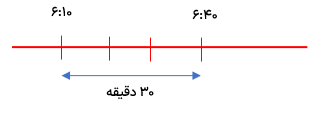
یکی از راه های اندازه گیری زبان نمودار است اگر بر روی نمودار زمان هر واحد (یک ساعت) را 6 قسمت کنیم که هر قسمت به معنای ۱۰ دقیقه می باشد با شمردن فاصله ها زمانی را که لازم داریم پیدا می کنیم.
مثال
رضا در ساعت ۱۲:۴۰ به منزل آمد و تا آماده شدن ناهار ۳۰ دقیقه استراحت کرد. چه ساعتی از خواب بیدار شد؟
پس هر کاری در زمان مشخصی شروع و در یک زمان مشخص پایان می یابد. از )زمان پایان کار) = (مدت زمان ) + ( زمان شروع)
ثانیه
یکی از واحدهای اندازه گیری زمان است برای اندازه گیری زمانهای کمتر از یک دقیقه استفاده می شود.
هر ساعت 60 دقیقه است و هر 60 دقیقه یک ساعت
هر دقیقه 60 ثانیه است و هر 60 ثانیه یک دقیقه
هر ساعت 3600 ثانیه است و هر 3600 ثانیه یک ساعت است.
1 ثانیه در ساعت های عقربه ای عقربه نازک است و در ساعت های دیجیتال در سمت راست نوشته می شود.
2 برای بیان تقریبی زمان عدد دقیقه یا عدد ساعت را به نزدیک ترین دقیقه یا ساعت تقریب می زنیم.
مثال
الف 8 ساعت و ۱۲ دقیقه
تقریبا ۸ ساعت
ب ساعت ۱۸ و ۴۹ دقیقه
تقریبا ساعت ۱۹
ج ۸ دقیقه و ۹ ثانیه
تقریبا ۸ دقیقه
د 4ا دقیقه و ۵۸ ثانیه
تقریبا ۱۵ دقیقه
جاهای خالی را تکمیل کنید
الف برای اندازه گیری زمانهای کمتر از یک دقیقه از واحد .................... استفاده می شود.
ثانیه
ب مدت زمان حضور شما در مدرسه 6 ...................... است.
ساعت
ج مدت زمان آگهی بازرگانی......................... است
دقیقه
مریم ساعت 6:10 از خواب بیدار می شود ، او برای رفتن به مدرسه 30 دقیقه طول میکشد تا آماده شود ، او چه ساعتی از خانه خارج می شود؟
تهیه کننده : عزیزی و حیدرزاده
اندازه گیری طول
فصل 4 : اندازه گیری
اندازه گیری طول
هر متر ۱۰۰ سانتی متر و هر سانتی متر ۱۰ میلی متر است.
برای اندازه گیری طول از واحد متر استفاده می شود. متر از قسمت های کوچکی که به نام سانتی متر و دسی متر و میلی متر تشکیل شده .
مثال
علی و رضا می خواهند طول تخت خود را حساب کنند. آنها در خط کش 1 متری با خود آورده و کنار هم می گذارند ولی تخت کوچکتر از ۲ متر است به گونه ای که 10 سانتی متر از خط کش ها بر روی یک دیگر می افتد. آن ها چگونه میتوانند اندازه تخت را حساب کنند؟
راه اول
۲ متر برابر است ۲۰۰ سانتی متر بعد مقدار 10 سانتی متر را که روی هم قرار گرفته را کم می کنند.
۱۰۰ + ۱۰۰ =200
۲۰۰ - ۱۰ =190
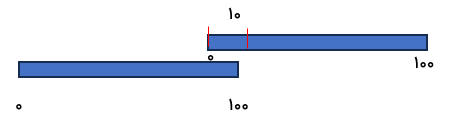
راه دوم
۱۰ سانتی متر را از یک متر که همان ۱۰۰ سانتی متر است کم می کنیم: 100-10=90
بعد با ا متر دیگر که همان ۱۰۰ سانتی متر است جمع می کنید. 100+90=190
بیان کسری طول
اگر 1 یک نوار کاغذی به طول یک متر را یک واحد کامل در نظر بگیریم و به ۴ قسمت تقسیم شود و یک قسمت را برش بزنیم طول 1 قسمت از ۴ قسمت . \(\frac{1}{4}\) متر می شود یعنی25 سانتی متر.
کسر شکل مقابل را بنویسید.
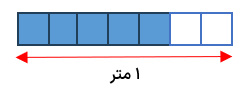
\(\frac{5}{7}\)
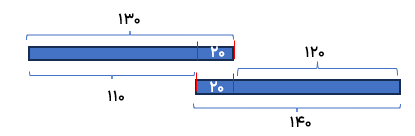
می خواهیم دو پارچه به طول 140 سانتی متر و 130 سانتی متر داشته باشیم . چند سانتی متر از این پارچه ها باید روی هم قرار بگیرد؟
140+130=270
270-250=20
110+20+120=250
تهیه کننده : عزیزی و حیدرزاده
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم- آزمون آنلاین تمامی دروس پایه چهارم
- گام به گام تمامی دروس پایه چهارم
- ویدئو های آموزشی تمامی دروس پایه چهارم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه چهارم
- فلش کارت های آماده دروس پایه چهارم
- گنجینه ای جامع از انشاء های آماده پایه چهارم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه چهارم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
عدد مخلوط
فصل 5 : عدد مخلوط و عدد اعشاری
عدد مخلوط
برای حل بعضی از مسائل به ظاهر سخت می توانیم او را به مساله های ساده تر تبدیل کنید و یا شکل رسم کنیم.
مثال
بین دو عدد ۸ و ۹ چطور می توانیم اعداد بیشتری پیدا کنیم؟
بین دو عدد ۸ و ۹ نمیتوان عدد کامل پیدا کرد پس بین دو عدد را تقسیم می کنیم به دو قسمت اگر تقسیم بندی بیشتر شود اعداد بیشتری پیدا می کنیم.
مثال
عدد\(3\frac{3}{4}\) بین کدام دو عدد کامل قرار دارد و به کدام عدد نزدیک تر است؟
ابتدا شکل رسم کنید. در شکل پاسخ معلوم است که به ۴ نزدیک تر است.
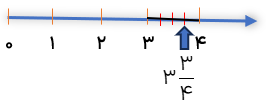
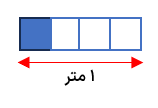
1 به شکل تقابل دقت کنید سپس ۵ تا \(\frac{1}{5}\) متر برابر است با 1 متر.
2 اگر 2 متر را تقسیم بندی کنیم ۱۰ تا \(\frac{1}{5}\) می شود ۲ متر.
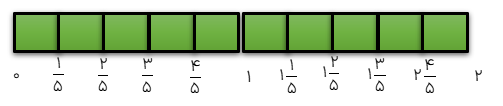
عدد مخلوط
عدد مخلوط از ۲ قسمت تشکیل شده است:
۱ عدد صحیح
۲ عدد کسری
برای نمایش عدد مخلوط از شکل و محور می توان استفاده کرد:
مقایسه اعداد مخلوط
رسم شکل
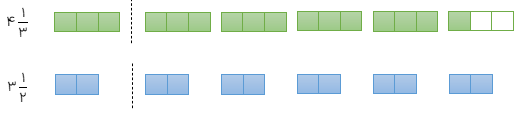
نمایش روی محور
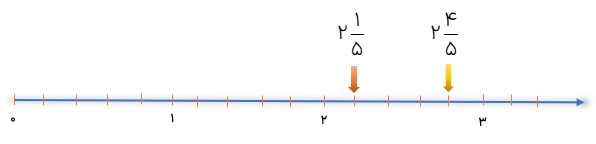
برای مقایسه دو عدد مخلوط ابتدا به واحدهای عدد صحیح نگاه می کنیم اگر برابر بودند کسرها با هم مقایسه می شود.
\(3\frac{2}{3}\left[ {\,\, < \,} \right]4\frac{1}{3}\,\,\,\,\,\,\,\,\,\,\,\,,\,\,\,\,\,\,\,\,\,\,\,\,\,\,2\frac{2}{3}\left[ {\, > \,} \right]2\frac{1}{3}\,\,\,\,\,\,\,\,\,\,\,,\,\,\,\,\,\,\,\,\,\,\,6\frac{1}{2}\left[ {\, > } \right]6\frac{1}{4}\)
در نمایش اعداد مخلوط با شکل اول واحد معلوم می شود - در اندازه گیری های مختلف می توانیم از عدد مخلوط استفاده کنیم.
۳۴ میلی متر ۳ سانتی متر \(3\frac{4}{{10}} \Leftarrow \) سانتی متر
کدام یک از عدد های زیر بین 2 و3 قرار دارند؟
\(2\frac{3}{5}\,\,\,,\,\,\,\frac{7}{8}\,\,\,,\,\,\,3\frac{1}{{10}}\,\,\,,\,\,\,2\frac{1}{8}\,\,\,,\,\,\,\frac{{58}}{{60}}\,\,\,,\,\,\,3\frac{1}{5}\,\,\,,\,\,\,1\frac{2}{3}\,\,\,,\,\,\,2\frac{5}{6}\)
\(2\frac{3}{5}\,\,\,,\,\,\,2\frac{1}{8}\,\,\,,\,\,\,2\frac{5}{6}\)
یک پارچ را در 8 لیوان ریختیم و لیوان ها پر و پارچ خالی شده:
الف گنجایش پارچ چند برابر لیوان است ؟
8 برابر
ب گنجایش لیوان چه کسری از پارچ است؟
یک هشتم\(\frac{1}{8}\)
تهیه کننده : عزیزی و حیدرزاده
جزوات جامع پایه چهارم
جزوه جامع ریاضی چهارم
جزوه جامع فارسی چهارم
جزوه جامع نگارش چهارم
جزوه جامع هدیه های آسمانی چهارم
جزوه جامع علوم تجربی چهارم
جزوه جامع مطالعات اجتماعی چهارم
جزوه جامع آموزش قرآن چهارم
عدد اعشاری
فصل 5 : عدد مخلوط و عدد اعشاری
عدد اعشاری
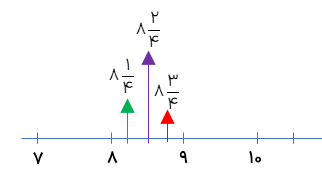
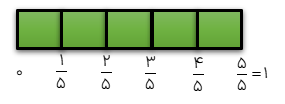
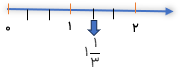
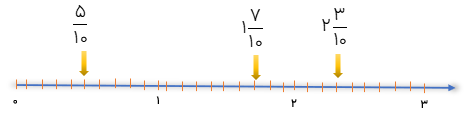
به محور زیر توجه کنید.
کسرهایی با مخرج 10 را می توان به این صورت هم نوشت:
\(\frac{5}{{10}} = 0/5\,\,\,\,\,\,\,\,\,\,\,\,\,,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,1\frac{7}{{10}} = 1/7\,\,\,\,\,\,\,\,\,\,\,,\,\,\,\,\,\,\,\,\,\,\,2\frac{3}{{10}} = 2/3\)
به این شکل نوشتن کسرها و عدد های مخلوط عدد اعشاری گویند. با عدد های اعشاری می توان عدد های کسری و عدد مخلوط را نشان داد.
هر عدد اعشاری ۲ قسمت دارد واحد کامل و اعشاری.2/4 عدد 2 واحد کامل و 4 قسمت اعشاری است.
1 برای این که یک عدد کسری را به صورت اعشاری بنویسم باید مخرج کسر 10 باشد می توانیم صورت و مخرج را در عددی ضرب کنیم یا صورت و مخرج را ساده کنیم تا مخرج 10 شود.
\(\begin{array}{l}\frac{{{4_{ \div 2}}}}{{{{20}_{ \div 2}}}} \Rightarrow \frac{2}{{10}} = 0/2\\\\1\frac{{{3_{ \times 2}}}}{{{5_{ \times 2}}}} = 1\frac{6}{{10}} = 1/6\end{array}\)
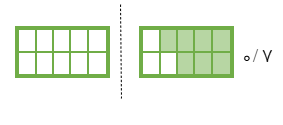
2 برای نوشتن اعداد اعشاری روی شکل ، شکل واحد را به 10 قسمت تقسیم می کنیم.
در یک خط کش هر سک سانتی متر به 10 قسمت به نام میلی متر تقسیم می شود. پس 1 سانتی متر = ۱۰ میلی متر و هر ا میلی متر 0/1 سانتی متر است.
برای نوشتن اعداد اعشاری روی محور یک محور رسم کرده و با توجه به عدد صحیح روی محور جلو رفته و قسمت بعدی را تا 10 قسمت می کنیم.
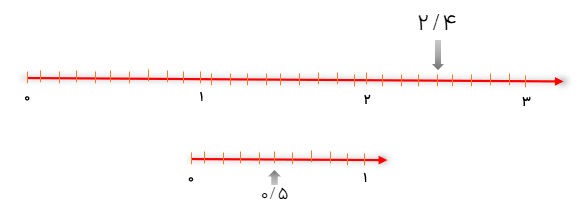
هر عدد اعشاری را می توانیم به صورت جمع قسمت صحیح و قسمت اعشاری بنویسیم:
\(3/1 = 3 + 0/1\)
هر کدام از عدد های کسری زیر را به صورت عدد اعشاری نمایش دهید.
الف \(\frac{3}{{10}}\)
0/3
ب \(\frac{9}{{10}}\)
0/9
هر عدد بین کدام دو عدد کامل قرار دارد؟
الف \(.....\,\, < \,\,3/9\,\, < ......\)
\(3\, < \,3/9\,\, < 4\)
ب \(.....\,\, < \,\,\frac{7}{{10}}\,\, < ......\)
\(0\,\, < \,\,\frac{7}{{10}}\, < 1\)
تهیه کننده : عزیزی و حیدرزاده
جمع و تفریق اعداد اعشاری
فصل 5 : عدد مخلوط و عدد اعشاری
جمع و تفریق اعداد اعشاری
روش اول : استفاده از محور
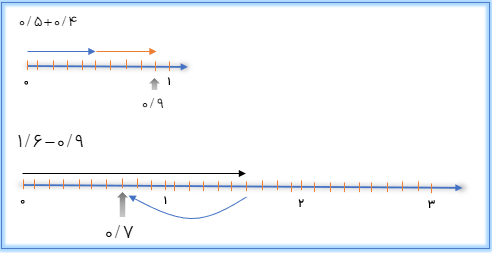
روش دوم:
0/5+0/4=5 تا یک دهم +4 تا یک دهم =9 تا یک دهم = 0/9
1/6-0/9=16 تا یک دهم - 9 تا یک دهم = 7تا یک دهم =0/7
روش سوم: شکل
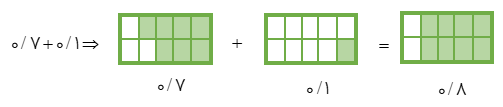
1 گاهی اوقات در جمع و تفریق کسرها با تبدیل آنها به اعشار می توانیم آن را انجام دهیم.
\(\frac{1}{2} + \frac{7}{{10}} = \frac{5}{{10}} + \frac{7}{{10}} = 0/5 + 0/7 = 1/2\)
2 در مقایسه اعداد اعشاری ابتدا قسمت عدد صحیح را مقایسه می کنیم اگر برابر باشد قسمت اعشاری را مقایسه می کنیم.
\(3/2\,\left[ > \right]2/9\,\,\,\,\,\,\,\,\,\,\,,\,\,\,\,\,\,\,\,\,\,0/4\left[ < \right]0/6\,\,\,\,\,\,\,\,\,\,,\,\,\,\,\,\,\,\,\,\,7/9\left[ > \right]7/6\)
3 زمانی که قسمت اعشاری وجود ندارد آن را صفر در نظر می گیریم :7=7/0
حاصل جمع یا تفریق های زیر را بدست آورید.
الف \(2\frac{2}{5} + \frac{1}{2}\)
22/8
ب \(2\frac{2}{5} + \frac{1}{2}\)
0/2
از کوچک به بزرگ مرتب کنید.
\(1/3 - 0/7 - 0/4 - 2/3 - 1/8 - 0/2\)
\(0/2 - 0/4 - 0/7 - 1/3 - 1/7 - 2/3\)
تهیه کننده : عزیزی و حیدرزاده
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم- آزمون آنلاین تمامی دروس پایه چهارم
- گام به گام تمامی دروس پایه چهارم
- ویدئو های آموزشی تمامی دروس پایه چهارم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه چهارم
- فلش کارت های آماده دروس پایه چهارم
- گنجینه ای جامع از انشاء های آماده پایه چهارم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه چهارم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
ارزش مکانی عدد های اعشاری
فصل 5 : عدد مخلوط و عدد اعشاری
ارزش مکانی عدد های اعشاری
اعداد اعشاری از قسمت صحیح و اعشاری تشکیل شده که به وسیله ممیز از هم جدا شده انده به جدول ارزش مکانی زیر دقت کنید.
مرتبه دهم کمترین ارزش مکانی را در این جدول های ارزش مکانی دارد.
1 برای جمع و تفریق اعداد اعشاری بدون استفاده از جدول ارزش مکانی ابتدا آنها را زیر هم می نویسم به طوری که ممیز ها زیر یکدیگر قرار گیرد و سپس جمع یا تفریق را انجام می دهیم.
\(\begin{array}{l}\,\,\,\,\,\,\,1/2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,6/3\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,8/6\,\,\,\\ + \,\,4/7\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \,\,5/2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - \,\,3/7\\ - - - - - \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - - - - - - \,\,\,\,\,\,\,\,\,\,\, - - - - - - \\\,\,\,\,5/2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,11/5\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,5/6\\\,\,\,\,0/7\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - \,\,0/7\\ - - - - - \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - - - - - - \\\,\,\,5/9\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,4/9\end{array}\)
2 برای محاسبه تقریبی جمع یا تفریق می توانیم ابتدا جمع یا تفریق را انجام داده و حاصل را تقریبی بنویسیم یا از ابتدا دو عدد را به صورت تقریبی بنویسیم و جمع و یا تفریق را انجام دهیم.
\(\begin{array}{l}3/8 + 10/1 = 13/9 \Rightarrow 14\\\\3/8 + 10/1 \Rightarrow 4 + 10 \Rightarrow 14\end{array}\)
کیف سارا 3/5 کیلوگرم و کیف مریم 2/9 کیلوگرم است کدام یک سنگین تر است؟
\(\begin{array}{l}\,\,\,\,\,3/5\\ - \,\,2/9\\ - - - - - \\\,\,\,\,0/6\end{array}\)
کیف سارا سنگین تر است. چرا که وزن کیف مریم را از وزن کیف سارا کم کرده ایم.
حاصل عبارت زیر را بدست آورید.
الف \(4/5 + 3/8 - 4/7\)
3/6
ب \(9/6 - 3/8 + 2/4\)
8/2
تهیه کننده : عزیزی و حیدرزاده
جزوات جامع پایه چهارم
جزوه جامع ریاضی چهارم
جزوه جامع فارسی چهارم
جزوه جامع نگارش چهارم
جزوه جامع هدیه های آسمانی چهارم
جزوه جامع علوم تجربی چهارم
جزوه جامع مطالعات اجتماعی چهارم
جزوه جامع آموزش قرآن چهارم
حدس و آزمایش (عمود و موازی)
فصل 6 : شکل های هندسی
حدس و آزمایش (عمود و موازی)
وقتی که دو خط با هم برخورد کنند و بین آن ها زاویه ی راست به وجود بیاید، می گوییم دو خط بر هم عمود هستند.
برای رسم دو خود عبود بر هم یا برای تشخیص از گونیا استفاده می شود.
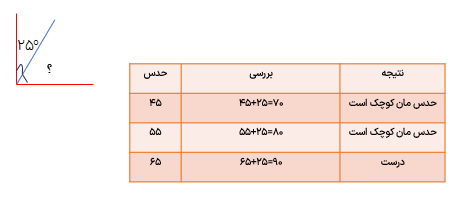
برای پیدا کردن اندازه یک زاویه می توان از حدس و آزمایش استفاده کرد.
مثال
1 از هر نقطه روی خط و یا خارج از یک خطه فقط یک خط می توان بر آن عمود کرد.
2 اگر خطی دو خط موازی را قطع کند زاویه هایی که مشخص شده با هم برابر خواهند بود.
3 کوتاه ترین فاصله یک نقطه تا خط برابر طول پاره خط عمودی است که از آن فقط بر این خط رسم می شود وقتی دو خط همزمان بر یک خط عود شوند آن در خط با هم موازی هستند.
با کمک گوشه گونیا نیز می توان دو خط موازی رسم کرد.
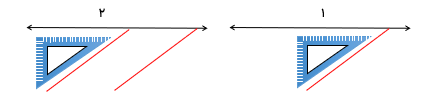
زاویه ای را 5 برابر کردیم و از ان 20 درجه کم کردیم حاصل برابر با 130 شد با استفاده از حدس و آزمایش آن زاویه را پیدا کنید.
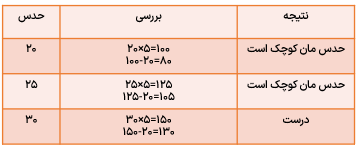
جای خالی را پر کنید
الف دو خطی که بر یک خط عمود هستند باهم......................... هستند.
موازی
ب فاصله دو خط موازی از هم در همه نقاط ..................... است.
یکسان
تهیه کننده : عزیزی و حیدرزاده
چهار ضلعی ها
فصل 6 : شکل های هندسی
چهار ضلعی ها
چهار ضلعی که فقط دو ضلع موازی دارد ذوزنقه نام دارد.
چهار ضلعی هایی که در آن ضلع های روبرو دو به دو باهم موازی باشند متوازی الاضلاع نام دارند.
در متوازی الاضلاع ضلع های روبرو با هم و زاویه های روبرو با هم برابرند.
مستطیل نوعی متوازی الاضلاع است که علاوه بر ویژگی های متوازی الاضلاع، ویژگی دیگری دارد، زاویه های مستطیل راست است.
لوزی نوعی متوازی الاضلاع است که علاوه بر ویژگی متوازی الاضلاع تمام ضلع های آن نیز برابر است.
مربع نوعی متوازی الاضلاع است که علاوه بر در ب ویژگی متوازی الاضلاع تمام خصوصیات مستطیل و لوزی را نیز دارد.
یک متوازی الاضلاع را با برش از روی یکی از قطرها می توان به دو مثلث تبدیل کرد.
با دو مثلث متشابه از مثلث های نام برده شده زیر کدام چهار ضلعی ها را می توان ساخت؟
الف 2مثلث متساوی الساقین
لوزی
ب دو مثلث قائم
مستطیل
جای خالی را پر کنید
الف به چهار ضلعی که فقط دو ضلع موازی دارد................... می گویند.
ذوزنقه
ب متوازی الاضلاع چهار ضلعی است که ضلع های روبرو باهم ...................... و.................... هستند.
موازی و مساوی
تهیه کننده : عزیزی و حیدرزاده
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم- آزمون آنلاین تمامی دروس پایه چهارم
- گام به گام تمامی دروس پایه چهارم
- ویدئو های آموزشی تمامی دروس پایه چهارم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه چهارم
- فلش کارت های آماده دروس پایه چهارم
- گنجینه ای جامع از انشاء های آماده پایه چهارم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه چهارم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
مساحت متوازی الاضلاع
فصل 6 : شکل های هندسی
مساحت متوازی الاضلاع
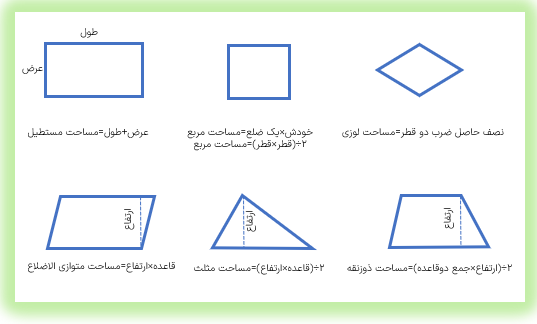
ارتفاع پاره خطی است که از راس به ضلع مقابل عمود شده است. ضلعی که ارتفاع بر آن عمود می شود قاعده نام دارد.
هر مثلث سه ارتفاع دارد.
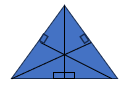
هر متوازی الاضلاع 8 ارتفاع دارد
که با بریدن قسمتی از متوازی الاضلاع از روی ارتفاع و انتقال به طرف دیگر متوازی الاضلاع به یک مستطیل تبدیل می شود که طول آن برابر با قاعده و عرض آن برابر با ارتفاع متوازی الاضلاع خواهد بود در نتیجه
مساحت مستطیل=طول × عرض
مساحت متوازی الاضلاع= قاعده × ارتفاع
هر متوازی الاضلاع از دو مثلث برابر تشکیل شده است پس مساحت هر مثلث نصف مساحت یک متوازی الاضلاع مساحت مثلث=قاعده × ارتفاع) ) ÷ 2
تهیه کننده : عزیزی و حیدرزاده
جزوات جامع پایه چهارم
جزوه جامع ریاضی چهارم
جزوه جامع فارسی چهارم
جزوه جامع نگارش چهارم
جزوه جامع هدیه های آسمانی چهارم
جزوه جامع علوم تجربی چهارم
جزوه جامع مطالعات اجتماعی چهارم
جزوه جامع آموزش قرآن چهارم
محیط و مساحت
فصل 6 : شکل های هندسی
محیط
به اندازه دور تا دور هر شکل کل محیط آن شکل گفته می شود و احد اندازه گیری محیط کیلومتر ، متر ، سانتی متر و میلی متر است.
برای محاسبه ی محیط یک تشکل باید اندازه های داده شده ، واحد یکان داشته باشند اگر این طور نبود ابتدا باید اندازه ی ضلع ها را بر حسب واحدهای یکسان بنویسیم بعد محیط را محاسبه کنیم.
1000میلی متر=100سانتی متر=1 متر
مساحت
به اندازه سطح یک شکل مساحت آن شکل گفته می شود واحد اندازه گیری مساحت کیلومتر مربع ، متر مربع ، سانتی متر مربع و میلی متر مربع می باشد.
ا متر مربع = ۱۰۰۰۰ سانتی مترمربع
مثال
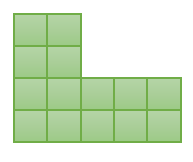
مساحت شکل رو برو چند است؟ (مساحت هر مربع 1 سانتی متر مربع می باشد)
سطح دارای ۱۴ مربع که مساحت هر کدام یک سانتی متر مربع می باشد ؛ بنابراین مساحت 14 سانتی متر مربع می باشد.
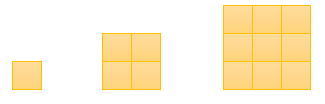
به الگوی مقابل دقت کنید.
الف ششمین شکل دارای چند مربع است؟
6×6=36
ب مساحت شکل ششم چند برابر مساحت شکل سوم است؟
36÷9=4 برابر
درستی یا نادرستی جملات را مشخص کنید.
الف به سطح هر شکل مساحت آن گفته می شود.
درست
ب یکی از واحد های اندازه گیری مساحت ؛ متر است
نادرست
تهیه کننده : عزیزی و حیدرزاده
نمودار خط شکسته
فصل 7 : آمار و احتمال
نمودار خط شکسته
داشتن اطلاعات کافی درباره مساله و دانستن روابط و قواعد ریاضی به ما کمک می کند حدسی که می زنیم نزدیک به راه اصلی باشد
مثال
مجموع دو عدد 36 است. اگر یکی از عددها ۸ تا بیشتر از دیگری باشد هر یک از عددها را پیدا کنید.
از یک عدد حدسی مثل 10 شروع می کنیم . چون اختلاف ۸ است. پس عدد دوم ۱۸ از خواهد شد ولی جواب مورد نظر نیست.
چون 10+18=28 و به پاسخ 36 نرسیدیم پس عدد اول را بیشتر می کنیم.
نمودار
برای مقایسه و بررسی بهتر بسیاری از اطلاعات و آمارهای آنها را بر روی نمودار نشان می دهند.
انواع نمودار
1 نمودار ستونی
2 نمودار خط شکسته
3 نمودار دایره ای
4 نمودار تصویری
که بنا به موضوع مورد مطالعه از یکی از انواع نمودار استفاده می کنند با داشتن اطلاعاتی میتوان نمودار رسم کرد.
مثال
در یک بوستان تعداد درختان بر اساس جدول روبرو است. نمودار آن را رسم کنید.
نمودار ستونی
برای مقایسه تعداد و یا پیدا کردن بیشترین و کمترین داده ها در یک موضوع از این نمودار استفاده می کنیم.
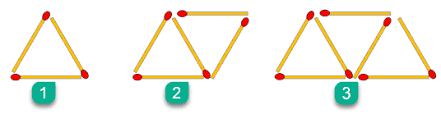
نمودار خط شکسته
وقتی بخواهیم در یک موضوع تغییرات و نوسانات را در یک دوره ی زمانی بررسی کنیم نمود در خط شکسته استفاده می کنیم تا تغیرات و کم و زیاد شدن ها را نشان دهد.
اندازه قد حامد و ناصر و بهزاد به ترتیب 154-161-159 سانتی متر است ، قد کدام یک بلندتر است؟
با کمک نمودار ستونی حل میکنیم:
ناصر<بهزاد<حامد
فروش یک کارگاه جوراب بافی در ماه اول 10 جفت جوراب در ماه دوم 30 جفت جوراب در ماه سوم 50 جفت جوراب و در ماه چهارم 40 جفت بوده ، نمودار خط شکسته فروش این کارگاه را رسم کنید.
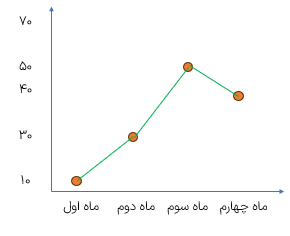
تهیه کننده : عزیزی و حیدرزاده
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم- آزمون آنلاین تمامی دروس پایه چهارم
- گام به گام تمامی دروس پایه چهارم
- ویدئو های آموزشی تمامی دروس پایه چهارم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه چهارم
- فلش کارت های آماده دروس پایه چهارم
- گنجینه ای جامع از انشاء های آماده پایه چهارم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه چهارم
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
احتمال
فصل 7 : آمار و احتمال
احتمال
برخی از اتفاقات در زندگی به طور حتم اتفاق می افتد. مثلاً به طور حتم بعد از فصل بهار تابستان است.
اما بعضی اتفاق ها به طور حتم روی نمی دهند مثلاً در پرتاب یک تاس در بازی مار و پله امکان ندارد عدد 8 در بیاید.
احتمال اتفاق افتادن برخی اتفاق ها نسبت به بقیه کمتر یا بیشتر است.
مثال : در یک کیسه سه مهره آبی و سه مهره زرد و یک مهره قرمز است
احتمال بیرون آمدن آبی و زرد برابر است اما احتمال بیرون آمدن قرمز کمتر از دو مهره دیگر است.
در بیان احتمال انفاق های مختلف از عبارت هایی مانند:
به طور حتم اتفاق نمی افتاد - به احتمال بیشتر اتفاق می افتد - به احتمال برابر اتفاق می افتد - به احتمال کمتر اتفاق می افتد و به طور حتم اتفاق نمی افتد، استفاده می کنیم.
پرتاب تاس
فرزانه یکی از عددهای سه رقمی را در ذهن خود انتخاب کرده است. احتمال این که این عدد بیشتر از ۲۷۹ باشد را با عبارت مناسب بیان کنید و دلیل خود در بنویسید.
به احتمال بیشتر اتفاق می افتد چون تعداد اعداد سه رقمی بزرگتر از 279 بیشتر است.
در یک بازی فوتبال برای تعیین زمین سکه انداختند. احتمال این که تیم آبی تعیین کننده زمین باشد را با یک عبارت مناسب نوشته و دلیل خود را بیان کنید.
به احتمال برابر ؛ چون سکه یا پشت می آید یا رو.
تهیه کننده : عزیزی و حیدرزاده