درسنامه کامل فیزیک یازدهم ریاضی فصل 4 القای الکترومغناطیسی و جریان متناوب
تعداد بازدید : 7.26Mخلاصه نکات فیزیک یازدهم ریاضی فصل 4 القای الکترومغناطیسی و جریان متناوب - درسنامه شب امتحان فیزیک یازدهم ریاضی فصل 4 القای الکترومغناطیسی و جریان متناوب - جزوه شب امتحان فیزیک یازدهم ریاضی نوبت اول فصل 4 القای الکترومغناطیسی و جریان متناوب
شار مغناطیسی
شار مغناطیسی
پدیده القای الکترو مغناطیسی
هرگاه جریان الکتریکی در یک رسانا القا گردد، به این پدیده (القای الکترو مغناطیسی) می گویند.
جریان القایی
حرکت آهنربا به سمت پیچه (دور و نزدیک شدن آهنربا از پیچه) باعث القای جریانی در پیچه می گردد، که به آن جریان القایی می گویند.
عوامل موثر در ایجاد جریان القایی
- با دور و نزدیک کردن آهنربا به پیچه، میدان در محل پیچه تغییر کرده و جریان القایی در مدار ایجاد می گردد. (تغییر در اندازه میدان مغناطیسی، در محل پیچه مدار بسته)
- اگر پیچه (انعطاف پذیر) در یک میدان مغناطیسی قرار دهید و از دو نقطه گرفته و بکشید، بطوری که شکل آن عوض شود، در اثر تغییر شکل، مساحت پیچه تغییر کرده و جریان در مدار به وجود می آید. (تغییر مساحت مدار بسته در میدان مغناطیسی)
- تغییر زاویه ین حلقه و راستای میدان مغناطیسی نیز می تواند عامل برقراری جریان الکتریکی القایی شود. (تغییر زاویه بین حلقه و راستای میدان مغناطیسی)
علت ایجاد جریان القایی در مدار
در اثر تغییر میدان مغناطیسی، یک میدان الکتریکی القایی در فضا ایجاد می شود و از آنجایی که مدار در این میدان الکتریکی قرار دارد بر الکترون های آزاد داخل آن نیرو وارد می شود و حرکت الکترون ها باعث ایجاد نیروی محرکه و جریان القایی، می شود.
تعریف شار مغناطیسی \(\Phi \)
معرف تعداد خطوط مغناطیسی که به طور عمود از یک سطح بسته می گذرند، شار مغناطیسی می گویند.
شار کمیتی نرده ای است.
بردار سطح
برای نمایش یک سطح، نیم خطی بر سطح پیچه عمود می کنیم. جهت این نیم خط همان جهت برداری سطح خواهد بود.
اگر یک سطح بچرخد، نیم خط عمود بر سطح N نیز با همان اندازه می چرخد.
فرمول شار مغناطیسی
\(\Phi = B \times A \times \cos \theta \)
در این فرمول
\(\Phi \) شار مغناطیسی و بر حسب وبر (wb)
B میدان مغناطیسی
A مساحت پیچه
\(\theta \) زاویه بین نیم خط عمود بر سطح پیچه و راستای میدان
1 بردار N را بر هر طرف سطح حلقه عمود کنیم، اهمیت ندارد. البته با تعویض جهت N، علامت \(\Phi \) تغییر خواهد کرد، ولی اندازه آن تغییر نمی کند.
2 در مسائل شار، اگر زاویه بین سطح قاب با سوی مثبت میدان مغناطیسی (\(\alpha \)) را داده باشند آنگاه:
3 زاویه بین نیم خط عمود بر سطح و سوی مثبت میدان مغناطیسی یعنی \(\alpha \) از رابطه ی زیر پیدا می شود.
\(\theta = \left| {90 - \alpha } \right|\)
تغییر شار مغناطیسی عبوری از یک حلقه
همواره دو جهت برای رسم نیم خط عمود بر یک سطح معین وجود دارد. علامت شار مغناطیسی عبوری از این سطح نیز به انتخاب این جهت بستگی دارد. در حل یک مسئله، همواره باید یک جهت را انتخاب کنیم و تا پایان آن را تغییر ندهیم، بنابراین ممکن است شار مثبت، منفی یا صفر شود.
\(\Delta \Phi = {\Phi _2} - {\Phi _1} \to \Delta \Phi = AB(\cos {\theta _2} - \cos {\theta _1})\)
یکای شار مغناطیسی
اگر قابی به مساحت \(1m{}^2\) عمود بر میدان مغناطیسی یکنواختی به بزرگی \(1T\) قرار گیرد، شار مغناطیسی گذرنده از آن برابر یک وبر (\(1wb\)) خواهد شد.
\(\Phi = BA\cos \theta \to 1wb = 1T \times 1{m^2} \times \cos 0\)
1 هرگاه سطح قاب عمود بر میدان مغناطیسی باشد، آنگاه \(\alpha = {90^0}\) بوده یعنی؛ شار عبوری از قاب ماکزیمم می شود.
\(\begin{array}{l}\theta = \left| {90 - \alpha } \right|\\\theta = \left| {90 - 90} \right| = {0^0} \to {\Phi _{\max }} = BA\\\cos {0^0} = 1\end{array}\)
2 هرگاه سطح قاب موازی میدان مغناطیسی باشد، آنگاه \(\alpha = 0\) بوده یعنی؛ شار عبوری از قاب صفر می شود.
\(\begin{array}{l}\theta = \left| {90 - \alpha } \right|\\\theta = \left| {90 - 0} \right| = {90^0} \to {\Phi _{\min }} = 0\\\cos {90^0} = 0\end{array}\)
تغییر شار مغناطیسی
هنگامی رخ می دهد که میدان مغناطیسی یا مساحت سطح و یا زاویه نیم خط عمود بر سطح رسانا با میدان، تغییر کند.
مثال
صفحه ای مربع شکل به ضلع \(20cm\) در یک میدان مغناطیسی یکنواخت به بزرگی \(3\mu T\) قرار دارد؛ به طوری که خط های میدان با سطح صفحه زاویه \({37^0}\) می سازند. شار مغناطیسی گذرنده از صفحه چند وبر است؟ (\(\cos 53 = 0/6\))
\(\begin{array}{l}a = 20cm = 0/2m \to A = {a^2} \to A = 4 \times {10^{ - 2}}{m^2}\\\alpha = {37^0} \to \theta = \left| {90 - \alpha } \right| \to \theta = \left| {90 - 37} \right| = {53^0}\\B = 3\mu T = 3 \times {10^{ - 6}}T\\\Phi = ?\\\Phi = BA\cos \theta \to \Phi = 3 \times {10^{ - 6}} \times 4 \times {10^{ - 2}} \times 0/6\\\Phi = 7/2 \times {10^{ - 8}}Wb\end{array}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه ریاضی- آزمون آنلاین تمامی دروس پایه ریاضی
- گام به گام تمامی دروس پایه ریاضی
- ویدئو های آموزشی تمامی دروس پایه ریاضی
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ریاضی
- فلش کارت های آماده دروس پایه ریاضی
- گنجینه ای جامع از انشاء های آماده پایه ریاضی
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ریاضی
قانون فارادی
قانون فارادی
هرگاه شار مغناطیسی ای که بسته ای می گذرد تغییر کند، نیروی محرکه ای در آن القا می شود که بزرگی نیروی محرکه القایی با آهنگ تغییر شار مغناطیسی متناسب است.
\(\varepsilon = - N\frac{{\Delta \Phi }}{{\Delta t}}\)
1 علامت منفی در رابطه به خاطر رعایت قانون لنز می باشد.
2 هنگامی که آهنگ تغییر شار مغناطیسی ثابت بماند، نیروی محرکه القایی متوسط \(\varepsilon \) برابر نیروی محرکه ای لحظه ای بوده و با نماد \(\varepsilon \) نمایش می دهیم.
مقدار شدت جریان القا شده از رابطه زیر بدست می آید:
\(I = \frac{\varepsilon }{R} \to I = - \frac{N}{R}\frac{{\Delta \Phi }}{{\Delta t}}\)
هر چه آهنگ تغییر شار مغناطیسی بیشتر باشد، نیروی محرکه القایی و در نتیجه جریان القایی تولید شده در مدار بیشتر خواهد بود.
هرگاه حلقه ای به هر وضعیتی که در یک میدان مغناطیسی قرار داشته باشد و شار عبوری از آن \(\Phi \) باشد، اگر حلقه حول خطی که در سطح حلقه است \({180^0}\) دوران نماید، شار عبوری از آن \( - \Phi \) می شود.
مثال
سیملوله ای با 500 دور در یک میدان مغناطیسی متغیر با زمان قرار گرفته است. مساحت مقطع سیملوله \(25c{m^2}\) و آهنگ تغییر میدان \(8 \times {10^{ - 3}}\frac{T}{s}\) است. بیشینه نیروی محرکه القایی متوسط در سیملوله را محاسبه کنید.
\(\begin{array}{l}N = 500\\A = 25 \times {10^{ - 4}}{m^2}\\\frac{{\Delta B}}{{\Delta t}} = 8 \times {10^{ - 3}}{m^2}\\\theta = 0\\\varepsilon = ?\\\varepsilon = - NA\frac{{\Delta B}}{{\Delta t}}\cos \theta \to \varepsilon = - 500 \times 25 \times {10^{ - 4}} \times 8 \times {10^{ - 3}} \times \cos 0 \to \varepsilon = - 0/01v = - {10^{ - 2}}v\end{array}\)
جزوات جامع پایه ریاضی
جزوه جامع فیزیک یازدهم ریاضی فصل 1 الکتریسیتۀ ساکن
جزوه جامع فیزیک یازدهم ریاضی فصل 2 جریان الکتریکی و مدارهای جریان مستقیم
جزوه جامع فیزیک یازدهم ریاضی فصل 3 مغناطیس
جزوه جامع فیزیک یازدهم ریاضی فصل 4 القای الکترومغناطیسی و جریان متناوب
قانون لنز
قانون لنز
جریان حاصل از نیروی محرکه القایی در یک مدار در جهتی است که آثار مغناطیسی ناشی از آن، با عامل به وجود آورنده جریان القایی، یعنی تغییر شار مغناطیسی، مخالفت می کند.
علامت منفی در رابطه فارادی نشان دهنده همین مخالفت است.
به قوانین فارادی و لنز، قانون های القای الکترومغناطیسی می گویند.
1 جهت جریان القایی ایجاد شده در حلقه هم با افزایش شار و هم با کاهش شار عبوری از حلقه، مخالفت می کند.
2 هنگامی که شار گذرنده از حلقه در حال افزایش می باشد، میدان مغناطیسی القایی در خلاف جهت میدان اصلی به وجود می آید تا اثر تضعیف کننده آن با افزایش شار مخالفت کند.
3 هنگامی که شار گذرنده از حلقه در حال کم شدن باشد، میدان مغناطیسی القایی در جهت میدان مغناطیسی اصلی به وجود می آید تا اثر تقویت کننده آن با کاهش شار مخالف کند.
مثال
در شکل رو به رو با توجه به جهت جریان القایی در حلقه توضیح دهید، جریان در سیم راست در حال افزایش است یا کاهش؟
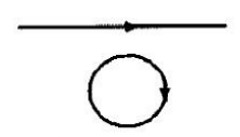
در حال کاهش، چون میدان مغناطیسی سیم راست هم جهت با میدان مغناطیسی حلقه است، طبق قانون لنز باید شار مغناطیسی در حال کاهش باشد یعنی جریان در حال کاهش است.
خود-القاوری
خود-القاوری
القاگر وسیله ای الکتریکی شبیه سیم پیچ با دو سر اتصال است که برای تولید میدان مغناطیسی و ذخیره انرژی مغناطیسی استفاده می شود.
القاگر می توانند میدان های مغناطیسی را در حجم های کوچک نگه دارند؛ همچنین می توان از آنه برای ذخیره کردن انرژی استفاده کرد.
خود-القاوری
در مدار شامل القاگری (پیچه یا سیملوله) باتری و رئوستا، آمپرسنج و القاگری است که به طور متوالی به یکدیگر بسته شده اند.
با تغییر مقاومت رئوستا، جریان در مدار تغییر می کند. تغییر جریان در مدار، سبب تغییر میدان مغناطیسی القاگر شده و در نتیجه شار مغناطیسی عبوری از آن نیز تغییر می کند. این فرایند سبب القای نیروی محرکه ای در القاگر می شود که بنابر قانون لنز با تغییر جریان عبوری از آن مخالفت می کند. این پدیده را اثر خود-القاوری نامیده می شود.
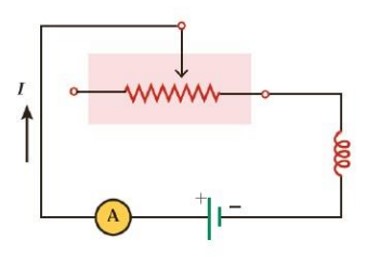
تغییر جریان در یک مدار باعث ایجاد نیروی محرکه ای القایی در همان مدار می شود، این پدیده را خود-القاوری می نامند.
نیروی محرکه ی خود القاوری \({\varepsilon _L}\)
اگر جریان گذرنده از سیملوله تغییر کند، به علت تغییر شار مغناطیسی گذرنده از آن، نیروی محرکه ای در خود مدار القا می شود که با عامل تغییر شار مغناطیسی که در اینجا تغییر جریان است مخالفت کند.
1 هرگاه جریان در مدار اصلی رو به افزایش باشد، جهت جریان خود- القاوری خلاف جهت جریان در مدار اصلی است.
2 هرگاه جریان در مدار اصلی رو به کاهش باشد، جهت جریان خود-القاوری هم جهت با جهت جریان در مدار اصلی است.
3 به هر قسمتی از یک مدار که خاصیت خود القاوری داشته باشد، القاگر می گویند.
4 پیچه و سیملوله در مداری با جریان متغیر القاگرند.
5 اثر خود-القاوری مخصوص جریان های متغیر است و در مدار های جریان پیوسته تنها به هنگام قطع و وصل کلید در مدار ایجاد می گردد.
ضریب القاوری (با نماد l نمایش می دهند.)
این پارامتر، ویژگی های فیزیکی القاگر را نشان می دهد و به عواملی همچون تعداد دور، طول و سطح مقطع القاگر و جنس هسته ای که داخل آن قرار می گیرد بستگی دارد.
یکای ضریب القاوری در SI، اهم در ثانیه (\(\Omega \times S\)) است که هانری نامیده و با H نشان داده می شود.
ضریب القاوری فقط به مشخصات ساختمانی سیم لوله بستگی دارد.
فرمول ضریب القاوری سیملوله
\(L = \frac{{AK{\mu _0}{N_2}}}{I}\)
در این فرمول
L ضریب القاوری
A مساحت هر حلقه ی سیملوله
K ضریب تراوایی نسبی هسته
\({\mu _0}\) ضریب تراوایی مغناطیسی خلاء
N تعداد دور های سیملوله
مثال
تعداد حلقه های سیملوله ای بدون هسته، به طول \(2/8cm\) و سطح \(10c{m^2}\) چه تعداد باشد تا ضریب القاوری آن \(1H\) شود؟
\(\begin{array}{l}K = 1\\I = 2/8 \times {10^{ - 2}}m\\A = 10 \times {10^{ - 4}}{m^2}\\N = ?\\L = 1H\\{\mu _0} = 4\pi \times {10^{ - 7}}\frac{{Tm}}{A}\\L = \frac{{AK{\mu _0}{N^2}}}{I} \to {N^2} = \frac{{IL}}{{AK{\mu _0}}}\\{N^2} = \frac{{2/8 \times 10 - 2 \times 1}}{{{{10}^{ - 3}} \times 1 \times 4 \times 3/14 \times {{10}^{ - 7}}}} \to {N^2} = 22 \times {10^6} \to N = 4/7 \times {10^3}\end{array}\)
القای متقابل
تغییر جریان در یک مدار باعث تغییر شار مغناطیسی در مدار دیگر و ایجاد نیروی محرکه القایی می شود.
با تغییر مقاومت رئوستا و تغییر جریان عبوری از پیچه 1 شار عبوری از پیچه 2 نیز تغییر می کند. این تغییر شار، سبب ایجاد نیروی محرکه القایی در پیچه 2 می شود. هم زمان تغییر جریان در پیچه 2، سبب ایجاد نیروی محرکه القایی در پیچه 1 می گردد.
انرژی ذخیره شده در القاگر
هنگامی که به دو سر القاگری اختلاف پتانسیل وصل کنیم، از طرف مولد به القاگر انرژی داده می شود. بخشی از این انرژی در مقاومت R تلف شده و بقیه آن در میدان مغناطیسی سیملوله ذخیره می شود. این انرژی از رابطه زیر بدست می آید:
\({U_L} = \frac{1}{2}L{I^2}\)
در این فرمول
\({U_L}\) انرژی ذخیره شده در القاگر
L ضریب القاوری
I شدت جریان در القاگر
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه ریاضی- آزمون آنلاین تمامی دروس پایه ریاضی
- گام به گام تمامی دروس پایه ریاضی
- ویدئو های آموزشی تمامی دروس پایه ریاضی
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ریاضی
- فلش کارت های آماده دروس پایه ریاضی
- گنجینه ای جامع از انشاء های آماده پایه ریاضی
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ریاضی
جریان متناوب
جریان متناوب
تولید جریان متناوب
ساده ترین راه برای تغییر شار مغناطیسی و ایجاد جریان، تغییر زاویه است.
بنابراین معادله شار به صورت زیر می باشد:
\(\Phi = BA\cos \theta \)
که در آن \(\theta \) در حال تغییر است.
اجزای یک مولد (ژنراتور) جریان متناوب
حرکت یک میله گردان، باعث چرخش پیچه در فضای میدان مغناطیسی ناشی از یک آن ربا می شود. با گردش پیچه، زاویه آن با خطوط میدان و در نتیجه شار گذرنده از پیچه تغییر و نیروی محرکه و جریان الکتریکی در آن القا می شود.
دوره یا زمان تناوب T
زمانی که طول می کشد تا پیچه یک دور کامل بچرخد را دوره می نامند. یکای آن در SI ثانیه است.
\(T = \frac{t}{N}\)
بسامد یا فرکانس f
تعداد چرخش های کامل در مدت یک ثانیه را بسامد می نامند.
یکای بسامد (\({S^{ - 1}}\)) است که معادل هرتز HZ است.
\(f = \frac{1}{T}\)
مثال
قابی در دقیقه، 300 بار دور خود می چرخد. زمان تناوب و بسامد قاب را به دست آورید؟
\(\begin{array}{l}t = 1\min = 60s\\N = 300\\T = ?\\f = ?\\T = \frac{t}{N} \to T = \frac{{60}}{{300}} = 0/2s\\f = \frac{1}{T} \to f = \frac{1}{{0/2}} = 5HZ\end{array}\)
معادله نیروی محرکه متناوب
اگر هر دور کامل برابر \(2\pi \) و زمان یک دور چرخش کامل پیچه T باشد، \(\theta \) زاویه پیچه در مدت زمان t ثانیه چرخیدن از رابطه ی زیر پیدا می شود.
\(\varepsilon = {\varepsilon _m}\sin \frac{{2\pi }}{T}t\)
جریان متناوب
اگر جریان الکتریکی تولید شده در مدار، به طور سینوسی تغییر کند به چنین جریانی جریان متناوب می گویند.
\(I = {{\mathop{\rm I}\nolimits} _M}\sin \frac{{2\pi }}{T}t\)
انواع جریان
جریان مستقیم D.C
اگر مقدار و جهت شدت جریان متوسط در تمام بازه های زمانی ثابت بماند.
جریان متناوب A.C
اگر جهت جریان در زمان های مساوی به طور متناوب عوض می شود.
جزوات جامع پایه ریاضی
جزوه جامع فیزیک یازدهم ریاضی فصل 1 الکتریسیتۀ ساکن
جزوه جامع فیزیک یازدهم ریاضی فصل 2 جریان الکتریکی و مدارهای جریان مستقیم
جزوه جامع فیزیک یازدهم ریاضی فصل 3 مغناطیس
جزوه جامع فیزیک یازدهم ریاضی فصل 4 القای الکترومغناطیسی و جریان متناوب
مبدل ها
مبدل ها
مزایای مولد های AC نسبت به DC
1) در انتقال توان در فاصله های دور، از ولتاژ هرچه بالاتر و جریان هر چه متری استفاده کنیم، باعث کاهش اتلاف \(R{I^2}\) در خط های انتقال می شود.
2) در افزایش انرژی الکتریکی از نیروگاه به محل مصرف کننده توسط یک مبدل ولتاژ را افزایش و جریان را کاهش می دهند (طبق رابطه \(P = VI\) اگر توان تولیدی را ثابت فرض کنیم افزایش ولتاژ توسط یک مبدل با کاهش جریان همراه است) تا توان تلف شده در سیم ها انتقال (\(R{I^2}\)) به کمترین مقدار برسد.
نحوه کارکرد مبدل
مبدل شامل دو پیچه با روکش عایق که روی یک هسته آهنی پیچیده شده اند. اگر پیچه اولیه را به یک مولد جریان متناوب وصل کنیم، شار عبوری از آن نیز تغییر می کند، این شار متغییر از راه هسته از پیچه ثانویه عبور می کند و در اثر پدیده القای متقابل باعث القای نیروی محرکه الکتریکی در پیچه ثانویه می شود.
رابطه تعداد دور ها با ولتاژ در مبدل ها
میدان و شار مغناطیسی در داخل هسته آهنی بسیار بیشتر از خارج هسته است و می توان فرض کرد تمام شار تولید شده در پیچه اولیه از پیچه ثانویه عبور می کند.
\(\frac{{\Delta {\Phi _1}}}{{\Delta t}} = \frac{{\Delta {\Phi _2}}}{{\Delta t}} \to \frac{{{\varepsilon _2}}}{{{\varepsilon _1}}} = \frac{{ - {N_2}\frac{{\Delta {\Phi _2}}}{{\Delta t}}}}{{ - {N_1}\frac{{\Delta {\Phi _1}}}{{\Delta t}}}} \to \varepsilon = V \to \frac{{{V_2}}}{{{V_1}}} = \frac{{{N_2}}}{{{N_1}}}\)
رابطه تعداد دور ها با شدت جریان در مبدل های ایده آل (آرمانی)
مبدلی را ایده آل گویند که هیچگونه اتلاف انرژی در آن وجود نداشته باشد. در نتیجه توان ورودی به مبدل آرمانی برابر توان خروجی از آن است.
\(P{}_{_1} = {P_2} \to {V_1}{I_1} = {V_2}I{}_2 \to \frac{{{I_2}}}{{{I_1}}} = \frac{{{V_1}}}{{{V_2}}} \to \frac{{{I_2}}}{{{I_1}}} = \frac{{{N_1}}}{{{N_2}}}\)
فرمول مبدل ها (ترانسفورماتور ها)
\(\frac{{{V_2}}}{{{V_1}}} = \frac{{{N_2}}}{{{N_1}}} = \frac{{{I_1}}}{{{I_2}}}\)
استفاده از مبدل برای کاهش اتلاف انرژی الکتریکی
در انتقال انرژی الکتریکی از نیروگاه به محل مصرف کنندخ توسط یک مبدل، ولتاژ را تا حد امکان افزایش و جریان را تا حد امکان کاهش می دهند تا توان تلف شده در سیم های انتقال برق (\(R{I^2}\)) به حداقل برسد.
توان تلف شده در خط انتقال
اگر توان تولیدی نیروگاه P ولتاژ بین خط های انتقال V باشد، شدت جریان در خط های فشار قوی \(I = \frac{P}{V}\) می شود. فرض می کنیم که مقاومت خط های انتقال برابر R باشد. در این صورت توان تلف شده \(P'\) در خط انتقال برابر می شود با:
\(P' = R\frac{{{P^2}}}{{{V^2}}}\)
رابطه ی مقایسه ای توان تلف شده در دو خط انتقال
خط انتقال توان، توان الکتریکی ثابت P را تحویل می گیرد. اگر انشعابی در مسیر نیروگاه تا مقصد وجود نداشته باشد، نسبت توان تلف شده در دو خط انتقال به صورت رابطه زیر است.
\(P' = R{I^2} \to P' = R\frac{{{P^2}}}{{{V^2}}} \to \frac{{{{P'}_1}}}{{{{P'}_2}}} = (\frac{{{R_1}}}{{{R_2}}}){(\frac{{{V_2}}}{{{V_1}}})^2}\)
مثال
توان تولیدی نیروگاهی \(2MW\) است. می خواهیم این انرژی را با کابل های مسی به طول \(20Km\) و سطح مقطع \(2c{m^2}\) انتقال دهیم. اگر ولتاژ خط های انتقال \(400kv\) باشد، توان تلف شده در خط های انتقال، چند ولت می شود؟
\(\begin{array}{l}P = 2 \times {10^6}W\\L = 20 \times {10^3}m\\A = 2 \times {10^{ - 4}}{m^2}\\V = 400 \times {10^3}kv\\P' = ?\\\rho = 1/8 \times {10^{ - 8}}\Omega m\\R = \rho \frac{L}{A} \to R = 1/8 \times {10^{ - 8}} \times \frac{{2 \times {{10}^4}}}{{2 \times {{10}^{ - 4}}}} \to R = 1/8\Omega \\P' = R\frac{{{P^2}}}{{{V^2}}} \to P' = 1/8 \times \frac{{{{(2 \times {{10}^6})}^2}}}{{{{(400 \times {{10}^3})}^2}}} \to P' = 45W\end{array}\)



1736019749.png)















