جواب سؤال متن صفحه 62 درس 3 هندسه دهم (چند ضلعی ها)
تعداد بازدید : 81.04Mپاسخ سؤال متن صفحه 62 هندسه دهم
-گام به گام سؤال متن صفحه 62 درس چند ضلعی ها
-سؤال متن صفحه 62 درس 3
-شما در حال مشاهده جواب سؤال متن صفحه 62 هندسه دهم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
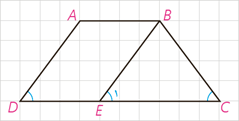
الف آیا عکس این ویژگی نیز درست است؟
ب فرض کنید در ذوزنقه ABCD، دو زاویه \(\angle C\) و \(\angle D\) هم اندازه اند. از B خطی موازی ساق AD رسم می کنیم تا قاعده CD را در E قطع کند. از اینکه \(\angle D\) و \(\angle {E_1}\) نیز __________ هم اندازه اند، پس دو زاویهٔ هم اندازه اند و در نتیجه BC = BE.
چون ABCD متوازی الاضلاع است، پس AD = BE. در نتیجه، AD = BC است: بنابراین:
اگر در یک ذوزنقه دو زاویۀ مجاور به یک قاعده هم اندازه باشند، ذوزنقه متساوی الساقین است.
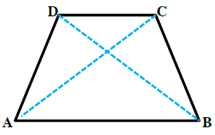
پ به کمک ویژگی ذوزنقهٔ متساوی الساقین، ویژگی زیر به سادگی ثابت می شود. آن را ثابت کنید.
در هر ذوزنقۀ متساوی الساقین، قطرها اندازه های مساوی دارند و بر عکس.
الف بله؛ عکس این ویژگی درست می باشد.
ب \({\hat E_1}\,,\,\hat C\)
پ برهان:
در دو مثلث ABC و ACD داریم:
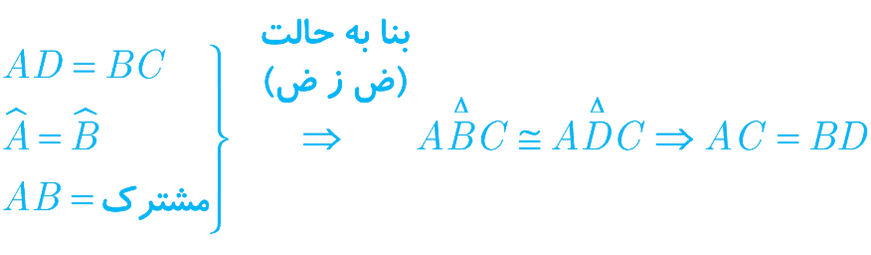
و برعکس آن :
برهان :
عمودهای CF و DE را بر AB وارد می کنیم . چهار ضلعی CDEF مستطیل است. پس: DE=CF
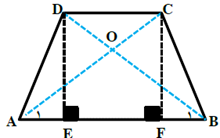
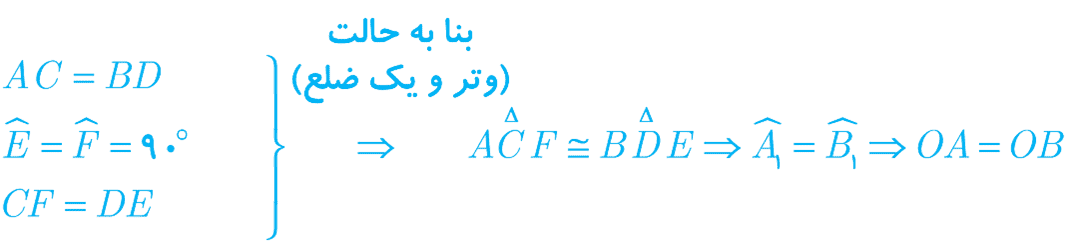
\(\left. {\begin{array}{*{20}{l}}{OA = OB}\\{AC = BD}\end{array}} \right\} \Rightarrow OC = OD\)
پس دو مثلث OBC و OAD بنا به حالت (ض ز ض) همنهشت اند. در نتیجه : AD=BC
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















