جواب فعالیت صفحه 34 درس 3 ریاضی هشتم (چندضلعی ها)
تعداد بازدید : 80.84Mپاسخ فعالیت صفحه 34 ریاضی هشتم
-گام به گام فعالیت صفحه 34 درس چندضلعی ها
-فعالیت صفحه 34 درس 3
-شما در حال مشاهده جواب فعالیت صفحه 34 ریاضی هشتم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
اگر خطی مانند \({d_1}\) ، خطوط a و b را مانند شکل با زاویه های مساوی قطع کرده باشد، خط های a و b با هم موازیند.
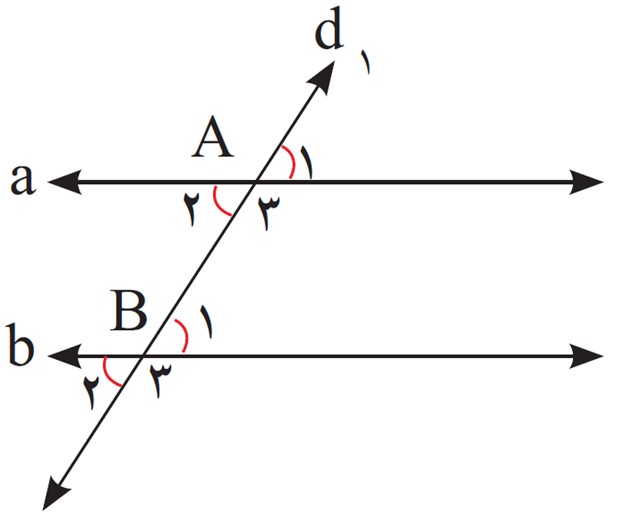
به خط \({d_1}\) ، خط مورب می گویند.
موازی بودن خط های a و b را به صورت a||b نمایش می دهند. هر خطی که دو خط موازی را قطع کند با آنها زاویه های مساوی می سازد.
1 اگر \({\hat A_1} = {60^ \circ }\) باشد، زاویه های خواسته شده را پیدا کنید و راه حل خود را توضیح دهید.
\({\hat A_3} = \)
چون مکمل زاویۀ \({A_1}\) است.
\({\hat B_1} = \)
\({\hat B_2} = \)
چون با زاویۀ \({B_1}\) متقابل به رأس است.
\({\hat B_3} = \)
\({\hat A_3} = {120^ \circ }\)
چون مکمل زاویۀ \({A_1}\) است.
\({\hat B_1} = {\hat A_1} = {60^ \circ }\)
d1 خطوط a و b را با زاویه های مساوی قطع کرده است.
\({\hat B_2} = {\hat B_1} = {60^ \circ }\)
چون با زاویۀ \({B_1}\) متقابل به رأس است.
\({\hat B_3} = {120^ \circ }\)
d1 خطوط a و b را با زاویه های مساوی قطع کرده است.
2 خط \({d_2}\) را بر a عمود کنید و ادامه دهید تا خط d را قطع کند. چرا \({d_2}\) بر b هم عمود است؟
هر خطی که دو خط موازی را قطع کند، با آنها زاویه های مساوی می سازد.
3 خط \({d_3}\) با خط b زاویۀ \({70^ \circ }\) ساخته است. خط \({d_3}\) با خط a چه زاویه ای می سازد؟
مساوی با \({70^ \circ }\) است.
4 دو خط a و b با هم موازی اند و خط \({d_1}\) مورب است؛ پس زاویه های \({A_1}\) و \({B_1}\) با هم مساوی اند. این مطلب را به صورت زیر نشان می دهیم.
\((a\parallel b\) مورب و \({d_1}) \Rightarrow {\hat A_1} = {\hat B_1}\)
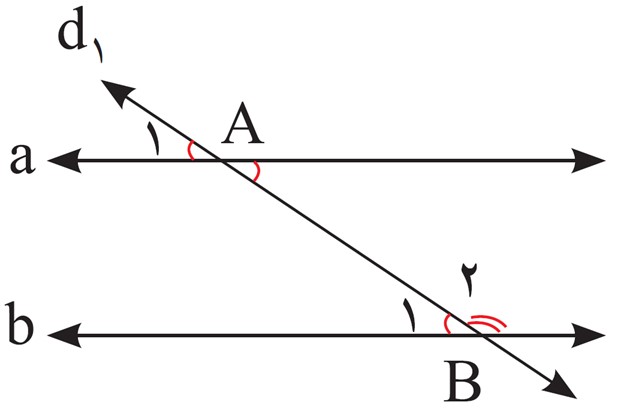
الف چرا A1 و B1 مکمل اند؟
ب اگر خط a را روی صفحه انتقال دهیم تا روی خط b قرار گیرد و نقطهٔ A روی B بیفتد، زاویۀ A1 روی کدام زاویه قرار می گیرد؟
پ چگونه از این طریق می توان توجیه کرد که زاویهٔ A1 و زاویۀ B1 مکمل یکدیگرند؟ توضیح دهید.
الف
چون \({\hat A_1} = {\hat B_1}\) و \({\hat B_1}\) با \({\hat B_2}\) مکمل است.
ب
روی زاویۀ \({\hat B_1}\) قرار می گیرد.
پ
از آنجا که \({\hat A_1}\) بر \({\hat B_1}\) منطبق می شود (یعنی مساوی یکدیگر هستند) و \({\hat B_1}\) و \({\hat B_2}\) مکمل یکدیگر هستند، پس \({\hat A_1}\) و \({\hat B_1}\) مکمل یکدیگرند.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















