جواب فعالیت صفحه 137 درس 6 ریاضی دهم (شمارش، بدون شمردن)
تعداد بازدید : 80.73Mپاسخ فعالیت صفحه 137 ریاضی دهم
-گام به گام فعالیت صفحه 137 درس شمارش، بدون شمردن
-فعالیت صفحه 137 درس 6
-شما در حال مشاهده جواب فعالیت صفحه 137 ریاضی دهم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
1 می دانیم که همان تعداد زیر مجموعه های rتایی از یک مجموعه n عضوی است. حال
و
را یک بار با توجه به این تعبیر از
و یک بار با فرمول، به دست آورید.
هر مجموعه n عضوی دارای یک زیرمجموعه هیچ عضوی به نام تهی است؛ بنابراین: \(\left( \begin{array}{l}n\\0\end{array} \right) = 1\)
\(\left( {\begin{array}{*{20}{l}}n\\0\end{array}} \right) = \frac{{n!}}{{0! \times \left( {n - 0} \right)!}} = \frac{{n!}}{{1 \times n!}} = 1\)
هر مجموعه n عضوی دارای n زیرمجموعه یک است؛ بنابراین: \(\left( {\begin{array}{*{20}{l}}n\\1\end{array}} \right) = n\)
\(\left( {\begin{array}{*{20}{l}}n\\1\end{array}} \right) = \frac{{n!}}{{1! \times \left( {n - 1} \right)!}} = \frac{{n!}}{{1 \times \left( {n - 1} \right)!}} = n\)
2
الف یک مربی قصددارد از بین بازیکنان شماره های 5 و 4 و 3 و 2 و 1، سه نفر را برای رفتن به زمین بازی انتخاب کند. چند حالت برای این کار امکان دارد؟
با پرکردن جدول مقابل تمام حالات را نمایش دهید.
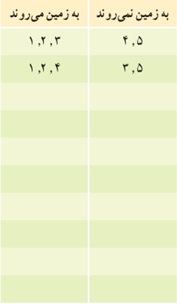
ب این بار این مربی قصد دارد از بین همان بازیکنان دو بازیکن انتخاب کند که روی نیمکت بنشینند. چه انتخاب هایی دارد؟
پ بین تعداد انتخاب های و
چه رابطه ای هست؟ چگونه این رابطه را توجیه می کنید؟
ث درستی تساوی را یک بار با استفاده از توجیه بالا و یک بار با استفاده از فرمول بررسی کنید.
الف 10 حالت امکان پذیر است.
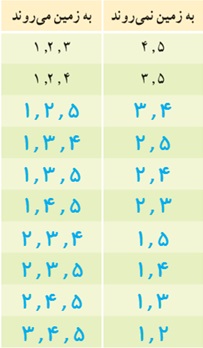
ب جواب، برعکس حالت (الف)، ستون سمت راست می باشد. بنابراین در این مورد نیز 10 انتخاب دارد.
پ این دو انتخاب با هم برابرند؛ زیرا تعداد حالات انتخاب 3 نفر از 5 نفر به این معناست که 2 نفر از 5 نفر انتخاب نشوند.
ت تعداد انتخاب r نفر از n نفر به این معناست که بقیه افراد (یعنی r-n نفر) را انتخاب نکنیم؛ بنابراین: \(\left( \begin{array}{l}n\\r\end{array} \right) = \left( \begin{array}{l}\;\;n\\n - r\end{array} \right)\)
اثبات به کمک فرمول :
\(\left( {\begin{array}{*{20}{l}}{\;\;n}\\{n - r}\end{array}} \right) = \frac{{n!}}{{\left( {n - r} \right)!\left( {n - \left( {n - r} \right)} \right)!}} = \frac{{n!}}{{\left( {n - r} \right)!r!}} = \left( {\begin{array}{*{20}{c}}n\\r\end{array}} \right)\)
3 جاهای خالی را پر کنید.
الف تعداد زیرمجموعه های 5 عضوی از مجموعه حروف انگلیسی برابر است با: \(\left( \begin{array}{l}\\\end{array} \right)\)
ب تعداد زیرمجموعه های 5 عضوی از مجموعه حروف انگلیسی که حرف a در آنها هست برابر است با: \(\left( \begin{array}{l}\\\end{array} \right)\)
پ تعداد زیرمجموعه های 5 عضوی از مجموعه حروف انگلیسی که حرف a در آنها هست برابر است با: \(\left( \begin{array}{l}\\\end{array} \right)\)
ت بنابراین: \(\left( \begin{array}{l}\\\end{array} \right) = \left( \begin{array}{l}\\\end{array} \right) + \left( \begin{array}{l}\\\end{array} \right)\)
الف \(\left( \begin{array}{l}26\\\,5\end{array} \right)\)
ب \(\left( \begin{array}{l}25\\\,4\end{array} \right)\)
پ \(\left( \begin{array}{l}25\\\,5\end{array} \right)\)
ت \(\left( \begin{array}{l}26\\\,5\end{array} \right) = \left( \begin{array}{l}25\\\,4\end{array} \right) + \left( \begin{array}{l}25\\\,5\end{array} \right)\)
4 فرض کنیم A یک مجموعۀ n عضوی و a یکی ازاعضای آن باشد. \(\left( {n \in A} \right)\)
الف تعداد زیرمجموعه های r عضوی مجموعۀ A برابر است با: \(\left( \begin{array}{l}\\\end{array} \right)\)
ب تعداد زیرمجموعه های r عضوی A که a در آنها هست، برابر است با: \(\left( \begin{array}{l}\\\end{array} \right)\)
پ تعداد زیرمجموعه های r عضوی A که a در آنها نیست، برابر است با: \(\left( \begin{array}{l}\\\end{array} \right)\)
ت بنابراین: \(\left( \begin{array}{l}\\\end{array} \right) = \left( \begin{array}{l}\\\end{array} \right) + \left( \begin{array}{l}\\\end{array} \right)\)
الف \(\left( \begin{array}{l}n\\r\end{array} \right)\)
ب \(\left( \begin{array}{l}n - 1\\r - 1\end{array} \right)\)
پ \(\left( \begin{array}{l}n - 1\\\;\;r\end{array} \right)\)
ت \(\left( \begin{array}{l}n\\r\end{array} \right) = \left( \begin{array}{l}n - 1\\r - 1\end{array} \right) + \left( \begin{array}{l}n - 1\\\;\;r\end{array} \right)\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















