درسنامه کامل حسابان یازدهم
تعداد بازدید : 497.72kخلاصه نکات حسابان یازدهم - درسنامه شب امتحان حسابان یازدهم - جزوه شب امتحان حسابان یازدهم نوبت اول
دنباله حسابی
فصل 1 : جبر و معادله
دنباله حسابي (عددي)
دنباله اي است كه به جز جمله اول آن، هر جمله اش برابر است با جمله قبلي آن به اضافه يك مقدار ثابت . اين مقدار ثابت را قدر نسبت دنباله ناميده با d نشان ميدهيم به عبارت ديگر دنباله ي حسابي دنبالهاي است كه تفاضل هر دو جمله متوالي آن مقدار ثابتي است.
مثال
\({a_n} = 3n - 2\) جمله عمومي يك دنباله حسابي است، زيرا:
\({a_{n + 1}} - {a_n} = (3(n + 1) - 2) - (3n - 2) = 3\)
مثال
\({b_n} = {n^2}\)جمله عمومي يك دنباله حسابي نيست، زيرا:
\({b_{n + 1}} - {b_n} = {(n + 1)^2} - {n^2} = 2n + 1\)
به n وابسته است
جمله عمومي دنباله حسابي كه قدر نسبت آن d و جمله اول آن a باشد برابر است با:
\({a_n} = a + (n - 1)d\)
مثال
جمله چندم دنباله ....1،4،7 برابر با 100 است؟
چون\(a = 1\) و \(d = 3\) و\({a_n} = 100\) بنابراين:
\(100 = 1 + (n - 1)(3) \to 100 = 1 + 3n - 3 \to 3n = 102 \to n = 34\)
بنابراين جمله سي و چهارم برابر با 100 ميباشد.
مثال
در يك دنباله حسابي داريم\({a_4} - {a_2} = 10\)\({a_5} + {a_7} = 54\)\({a_{81}}\)را بيابيد.
\(\begin{array}{l}\left\{ \begin{array}{l}{a_4} - {a_2} = 10\\{a_4} + {a_7} = 54\end{array} \right. \Rightarrow \left\{ \begin{array}{l}(a + 3d) - (a + d) = 10\\(a + 4d) + (a + 6d) = 54\end{array} \right. \Rightarrow \left\{ \begin{array}{l}2d = 10\\2a + 10d = 54\end{array} \right. \Rightarrow d = 5,a = 2\\\\ \Rightarrow {a_{81}} = a + 80d \Rightarrow {a_{81}} = 2 + 80 \times 5 = 402\end{array}\)
مجموعn جمله اول دنباله حسابي برابر است با :
\({s_n} = \frac{n}{2}(2a + (n - 1)d)\)
مجموع n جمله اول دنباله حسابي كه جمله اول آن \({a_1}\) و جمله nام آن \({a_n}\) باشد برابر است با:
\({s_n} = \frac{n}{2}({a_1} + {a_n})\)
مثال
در يك دنباله حسابي داريم\({s_n} = 4{n^2} - n\) جمله هفتم اين دنباله را بيابيد.
با كمي دقت متوجه ميشويم كه\({a_7} = {s_7} - {s_6}\) پس :
\({a_7} = (4({7^2}) - 7) - (4({6^2}) - 6) = 51\)
اگر\({a_n} \) و\({a_m}\)دو جمله از يك دنباله حسابي باشد آنگاه\(d = \frac{{{a_m} - {a_n}}}{{m - n}}\).
اگر\({a_l}\)\({a_p}\)\({a_n}\)\({a_m}\) چهار جمله از يك دنباله حسابي و\(m + n = p + l\)آنگاه\({a_m} + {a_n} = {a_p} + {a_l}\).
در هر دنباله حسابي متناهي مجموع هر دو جمله متساوي الفاصله از طرفين باهم برابر است.
اگر در يك دنباله حسابي متناهي تعداد جملات فرد باشد مجموع هر دو جمله متساوي الفاصله از طرفين مساوي دو برابر جمله وسط آن است و مجموع همه جملات آن برابر است با:
مقدار جمله وسط ضربدر تعداد آنها
مثال
در يك دنباله حسابي داريم\({a_3} + {a_7} + {a_{11}} + {a_{15}} = 20\)را بيابيد.
\(\begin{array}{l}{a_3} + {a_7} + {a_{11}} + {a_{15}} = 20 \Rightarrow ({a_3} + {a_{15}}) + ({a_7} + {a_{11}}) = 20\\\\ \to 2({a_1} + {a_{17}}) = 20 \to {a_1} + {a_{17}} = 10\\\\{s_{17}} = \frac{{17}}{2}({a_1} + {a_{17}}) \Rightarrow {s_{17}} = \frac{{17}}{2} \times 10 = 85\end{array}\)
\(\)
مثال
در دنباله حسابي...7 ،3 ، 1-مجموع جملات بيست و يكم تا سي ام را بيابيد.
روش اول: چون\(d = 4\)\(a = - 1\)پس:
مجموع جملات بيست ويكم تا سي ام \( = {S_{30}} - {S_{20}} = \frac{{30}}{2}( - 2 + 29 \times 4) - \frac{{20}}{2}( - 2 + 20 \times 4) = 970\)
روش دوم : چون\({a_{21}} = - 1 + 20 \times 4 = 79\)پس مجموع خواسته شده برابراست بامجموع ده جمله اول دنباله حسابي كه جمله اول آن 79 و قدر نسبت آن 4 ميباشد، بنابراين:
\({S_{10}} = \frac{{10}}{2}(158 + 36) = 970\)
تهیه کننده: حامد دلیجه
- آزمون آنلاین تمامی دروس پایه یازدهم
- گام به گام تمامی دروس پایه یازدهم
- ویدئو های آموزشی تمامی دروس پایه یازدهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه یازدهم
- فلش کارت های آماده دروس پایه یازدهم
- گنجینه ای جامع از انشاء های آماده پایه یازدهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه یازدهم
دنباله ي هندسي
فصل 1 : جبر و معادله
دنباله ي هندسي
دنباله هندسي: دنباله اي است كه به جز جمله اول آن، هر جمله اش برابر است با جمله قبلي آن ضربدر يك مقدار ثابت. اين مقدار ثابت را قدر نسبت دنباله ناميده با q نشان ميدهيم
اگر جمله اول و قدر نسبت آن مخالف صفر باشد ميتوان گفت دنباله هندسي دنبالهاي است كه خارج قسمت هر دو جمله متوالي آن مقدار ثابتي است.
مثال
دنباله هندسي...و 8- ،4 ،2-،1 است ولي دنباله...،16 ،8 ،4-،2-،1 هندسي نيست
جمله عمومي دنباله هندسي كه جمله اول آن a و قدر نسبت آن q باشد برابر است با:
\({a_n} = a{q^{n - 1}}\)
مثال
دنباله... ،\(\frac{1}{2}\),2, 1چند جمله بزرگتر از\({10^{ - 3}}\) دارد؟
چون\(a = 2\) و\(q = \frac{1}{2}\) پس\({a_n} = 2{\left( {\frac{1}{2}} \right)^{n - 1}}\)كه طبق فرض بايد\(2{\left( {\frac{1}{2}} \right)^{n - 1}} > {10^{ - 3}}\)باشد بنابراين:
\(\begin{array}{l}2 \times {\left( {\frac{1}{2}} \right)^n}{\left( {\frac{1}{2}} \right)^{ - 1}} > \frac{1}{{1000}} \Rightarrow {\left( {\frac{1}{2}} \right)^n} > \frac{1}{{4000}} \Rightarrow {2^n} < 4000 \Rightarrow n < 12\\\end{array}\)
درنتيجه يازده جمله بزرگتر از\(\frac{1}{{1000}}\)دارد.
اگر\({a_n}\)و \({a_m}\)دو جمله غير صفر از يك دنباله هندسي باشد آنگاه\(\frac{{{a_m}}}{{{a_n}}} = {q^{m - n}}\).
اگر\({a_l}\),\({a_p}\),\({a_n}\),\({a_m}\) چهار جمله از يك دنباله هندسي و\(m + n = p + l\)آنگاه \({a_m}{a_n} = {a_p}{a_l}\)
در هر دنباله هندسي متناهي حاصل ضرب هر دو جمله متساوي الفاصله از طرفين باهم برابر است.
اگر در يك دنباله هندسي متناهي تعداد جملات فرد باشد حاصل ضرب همه جملات آن برابر است با مقدار جمله وسط به توان تعداد آنها.
مثال
اگر در يك دنباله هندسي\({a_n} = 12\) و\({a_5} = 96\)باشد\({a_7}\)را بيابيد.
\(\begin{array}{l}\frac{{{a_5}}}{{{a_3}}} = {q^3} \Rightarrow \frac{{96}}{{12}} = {q^3} \Rightarrow q = 2\\\\\frac{{{a_7}}}{{{a_5}}} = {q^3} \Rightarrow {a_7} = 96 \times 4 \Rightarrow {a_7} = 384\end{array}\)
مثال
در يك دنباله هندسي داريم \({a_5} = 1\) حاصل ضرب جملات اول تا نهم آن را بيابيد.
\({a_1}{a_2}....{a_9} = {({a_5})^9} = {1^9} = 1\)
مجموعn جمله اول دنباله هندسي برابر است با:
\(\begin{array}{l}{s_n} = \frac{{a(1 - {q^n})}}{{1 - q}}\,\,\,\,(q \ne 1)\\\\{s_n} = \frac{{a - q\, \times \,{a_n}}}{{1 - q}}\,\,\,(q \ne 1)\\\\{s_n} = \frac{{a - {a_{n + 1}}}}{{1 - q}}\,\,\,(q \ne 1)\\\\{s_n} = n \times a\,\,\,(q = 1)\end{array}\)
مثال
در يك دنباله هندسي داريم\({s_3} = 7\) ,\({s_6} = 63\)جمله ششم چند برابر جمله دوم است.
\(\begin{array}{l}\frac{{{s_6}}}{{{s_3}}} = \frac{{63}}{7}\\\\ \Rightarrow \frac{{\frac{{a(1 - {q^6})}}{{1 - q}}}}{{\frac{{a(1 - {q^3})}}{{1 - q}}}} = 9 = \frac{{1 - {q^6}}}{{1 - {q^3}}} = 9\\\\ \Rightarrow 1 + {q^3} = 9 \Rightarrow {q^3} = 8 \Rightarrow q = 2\\\\ \Rightarrow \frac{{{a_6}}}{{{a_3}}} = {q^4} \Rightarrow \frac{{{a_6}}}{{{a_2}}} = 16\end{array}\)
مثال
حداكثر چند جمله ابتداي دنباله ....،\(\frac{1}{9}\), \(\frac{1}{3}\),1را جمع كنيم تا حاصل كمتر از\(1/497\)شود.
چون \(a = 1\) و \(q = \frac{1}{3}\)و ميخواهيم\({s_n} < 1/497\)باشد پس داريم:
\(\begin{array}{l}\frac{{1\left( {1 - {{(\frac{1}{3})}^n}} \right)}}{{1 - \frac{1}{3}}} < 1/497 \Rightarrow \frac{3}{2}\left( {1 - {{\left( {\frac{1}{3}} \right)}^n}} \right) < \frac{{1497}}{{1000}} \Rightarrow 1 - {\left( {\frac{1}{3}} \right)^n} < \frac{{499}}{{500}} \Rightarrow {\left( {\frac{1}{3}} \right)^n} > \frac{1}{{500}} \Rightarrow \\\\{3^n} < 500 \Rightarrow n < 6\end{array}\)
پس مي توان حداكثر 5 جمله آن را باهم جمع نمود.
اگر در يك دنباله هندسي نامتناهي،\(\left| q \right| < 1\)باشد مجموع همه جملات آن برابر است با:
\(s = \frac{a}{{1 - q}}\)
مثال
مجموع همه جملات دنباله... ،\( - \frac{1}{{64}}\),\(\frac{1}{{16}}\),\( - \frac{1}{4}\),1 رابیابید.
\(a = 1\)
\(\left| q \right| < 1 \Rightarrow s = \frac{1}{{1 - ( - \frac{1}{4})}} = \frac{1}{{\frac{5}{4}}} = \frac{4}{5}\)
مثال
در يك دنباله هندسي نامتناهي جمله اول برابر با مجموع ساير جملات آن ميباشد نسبت جمله پنجم به جمله اول اين دنباله را بيابيد.
اگر جمله اول a و قدر نسبت q باشد داريم:
\(a = \frac{{aq}}{{1 - q}} \Rightarrow 1 = \frac{1}{2} \Rightarrow \frac{{{a_5}}}{{{a_1}}} = {q^4} = \frac{1}{{16}}\)
تهیه کننده: حامد دلیجه
تقسيم چند جمله اي ها و بخش پذيري
فصل 1 : جبر و معادله
تقسيم چند جمله اي ها و بخش پذيري
اگر چند جمله اي درجه n ام\(p(x)\) را بر چند جمله اي درجه mام\(k(x)\)که\(m \le n\)تقسيم كنيم؛ خارج قسمت تقسيم، چند جمله اي است مانند\(Q(x)\) از درجه\(n - m\)و باقي مانده صفر و يا چند جمله اي مانند \(R(x)\)ميباشد كه درجه آن از m كمتر است وميتوان نوشت :
\(P(x) = K(x)Q(x) + R(x)\)
كه آن را تساوي تقسيم ميناميم.
مثال
اگر چند جمله اي درجه هفتم را بريك چند جمله اي درجه پنجم تقسيم كنيم خارج قسمت چند جمله اي از درجه 2 و باقي مانده صفر و يا چند جمله اي است كه درجة آن حداكثر 4 ميباشد.
مثال
در تقسيم چند جمله اي \(P(x)\) بر \({x^2} - 3x + 2\) باقی مانده برابر با \(3x + 1\) می باشد \(P(2)\) رابیابید.
بنا به تساوي تقسيم داريم
\(P(x) = ({x^2} - 3x + 2)Q(x)(3x - 1)\)
و در نتيجه
P(2) = (4 - 6 + 2)Q(2) + (6 - 1)
بنابراین
\(P(2) = 5\)
اگر \(P(x)\) و \(q(x)\)دو چند جمله اي باشند براي اينكه تساوي \(P(x) = q(x)\)به ازاي هر مقدار x برقرار باشد، بايد P و q هم درجه باشند و ضرايب هم درجه P و q با هم برابر باشند و براي اينكه تساوي \(P(x) = 0\) به ازاي هر مقدار x برقرار باشد بايد ضرايب كليه جملات P صفر باشد.
مثال
a و b راچنان بيابيد تا تساوي \(\frac{a}{{3x - 1}} + \frac{b}{{3x + 1}} = \frac{1}{{9{x^2} - 1}}\)به ازاي هر مقدار \((x \ne \pm \frac{1}{3})\)برقرار باشد.
\(\begin{array}{l}\frac{a}{{3x - 1}} + \frac{b}{{3x + 1}} = \frac{1}{{9{x^2} - 1}} \Rightarrow \frac{{a(3x + 1) + b(3x - 1)}}{{(3x - 1)(3x + 1)}} = \frac{1}{{9{x^2} - 1}} \Rightarrow a(3x + 1) + b(3x - 1) = 1 \Rightarrow \\\\3(a + b)x + a - b = 0\\\\a - B = 1 \Rightarrow a = \frac{1}{2}\\\\b = - \frac{1}{2}\end{array}\)
مثال
a و b را چنان بيابيد تا تساوي \(({a^2} - 4){x^2} + (a - b)x + b = 0\)به ازاي هر مقدارx برقرار باشد.
بايد \({a^2} - 4 = 0\) و \(a - b = 0\)باشد كه از اينجا داريم \(a = b = 2\).
مثال
بدون انجام عمل تقسيم، باقي مانده و خارج قسمت تقسيم \({x^2} - 2{x^2} + 5x - 1\) را بر \({x^2} + 1\) بيابيد
ميدانيم خارج قسمت و باقي مانده به ترتيب به صورت \(Q(x) = ax + b\)و\(R(x) = cx + d\) ميباشند بنابراين داريم:
\({x^2} - 2{x^2} + 5x - 1 = ({x^2} + 1)(ax + b) + (cx + d)\)
درنتيجه:
\({x^2} - 2{x^2} + 5x - 1 = a{x^3} + b{x^2} + (a + c)x + b + d\)
بنابراين:
\(\begin{array}{l}a = 1,b = - 2,a + c = 5,b + d = - 1 \Rightarrow a = 1,b = - 2,c = 4,d = 1\\\\Q(x) = x - 2,R(x)=4x + 1\end{array}\)
اگر در تقسيم P بر K باقيمانده صفر شود گوئيم P بر K بخشپذير است و K را يك مقسوم عليه ( يك عامل يا يك فاكتور) Q گوييم.
مثال
\(x - 2\) يك فاكتور \({x^2} - 5x + 6\) ميباشد زيرا \({x^2} - 5x + 6 = (x - 2)(x - 3)\)
در تقسيم چند جمله اي \(P(x)\) بر \(x - a\) داريم:
\(P(x) = (x - a)Q(x) + R\)
باقيمانده تقسيم چندجمله اي \(P(x)\) بر \(x - a\) می شود\(P(a)\).
چند جمله اي \(P(x)\) بر \(x - a\) بخش پذير است اگر و تنها اگر \(P(a) = 0\).
مثال
باقيمانده تقسيم \({x^7} - 3{x^2} + 4x - 5\) را بر \(x + 1\)بدست آوريد.
\(\begin{array}{l}R = P( - 1) \Rightarrow R = {( - 1)^7} - 3{( - 1)^2} + 4( - 1) - 5 \Rightarrow R = - 12\\\\P(x) = {x^7} - 3{x^2} + 4x - 5\end{array}\)
مثال
aوb را طوري بيابيد تا \({x^3} - 2{x^2} + ax + b\) بر \({x^2} + x - 2\)بخش پذير باشد.
چون \({x^2} + x - 2 = (x + 2)(x - 1)\) و \(P(x) = {x^3} - 2{x^2} + ax + b\) ميباشد، بايد \(P( - 2) = 0\) ,\(P(1) = 0\)در نتيجه:
\(( - 2) - 2{( - 2)^2} + a( - 2) + b = .\)
\(\begin{array}{l}{(1)^2} - 2{(1)^2} + a(1) + b = 0 \Rightarrow - 2a + b = 16\\\\a + b = 1 \Rightarrow a = - 5,b = 6\end{array}\)
مثال
اگر باقيمانده تقسيم چند جمله اي \(P(x)\) بر \(x - 2\) به ترتيب 2 و 7 باشد، باقي مانده \(P(x)\) را بر \({x^2} - 5x + 6\)بیابید.
باتوجه به فرض داريم \(P(2) = 2\) و \(P(3) = 7\) و طبق تساوي تقسيم \(P(x) = ({x^2} - 5x + 6)Q(x) + (ax + b)\) بنابراین \(P(2) = 2a + b\) و \(P(3) = 3a + b\) در نتیجه
\(\left\{ \begin{array}{l}2a + b = 2\\3a + b = 7\end{array} \right. \Rightarrow a = 5,b = - 8,R = 5x - 8\)
باقيمانده تقسيم چند جمله اي \(P(x)\) بر \(ax + b\left( {a \ne 0} \right)\)برابر است با \(P\left( { - \frac{b}{a}} \right)\).
مثال
نشان دهيد \(2x + 3\) يك فاكتور ميباشد سپس نشان دهيد دوفاكتور درجه اول ديگر نيز دارد..
بايد نشان دهيم عبارت \(g(x) = 2{x^3} + 3{x^2} - 8x - 12\) به ازای \(x = - \frac{3}{2}\)
صفر است.
براي بدست آوردن فاكتورهاي ديگر \(g(x)\)را بر \(2x + 3\)تقسيم ميكنيم.
\(\begin{array}{l}2{x^3} + 3{x^2} - 8x - 12\\\\2{x^3} + 3{x^2}\end{array}\)
بنابراين:
\(\begin{array}{l}2{x^3} - 3{x^2} - 8x - 12 = (2x + 3)({x^2} - 4) \Rightarrow \\\\2{x^3} + 3{x^2} - 8x - 12 = (2x + 3)(x - 2)(x + 2)\end{array}\)
در نتيجه فاكتورهاي مورد نظر \(x = 2,x - 2\) ميباشد.
براي بدست آوردن باقيمانده تقسيم چند جمله اي \(P(x)\) بر\((a \ne 0,n \in N)\) \(a{x^{^n}} + b\) مي توان در عبارت \(P(x)\) به جاي همه \({x^n}\) ها عدد \( - \frac{b}{a}\) را قرار داد و حاصل را ساده نمود.
مثال
باقيمانده تقسيم \({x^{1389}} + 3{x^7} - 4x + 1\) را بر \({x^3} + 1\) بيابيد.
چون \( - \frac{b}{a} = - 1\)
و\({x^{1389}} + 3{x^7} - 4x + 1 = {({x^3})^{463}} + 3(x)x - 4x + 1\) ميباشد پس:
\(R(x) = {( - 1)^{463}} + 3{( - 1)^2}x - 4x + 1 \Rightarrow R = - x\)
بسط دو جمله اي غياث الدين جمشيد كاشاني و مثلث خيام – پاسكال
اگر \(n \in R\) باشد \({(a + b)^n}\) به دو جمله اي كاشاني معروف ميباشد كه بسط آن به صورت زير است:
\({(a + b)^n} = {a^n} + n{a^{n - 1}}b + \frac{{n(n - 1)}}{2}{a^{n - 2}}{b^2} + ... + {b^n}\)
اين بسط:
داراي \(n + 1\) جمله است
مجموع توان هايa,b در هر جمله n است.
اگر آن را بر حسب توان هاي نزولي n مرتب كنيم ضـريب اولـين جملـه 1 و ضريب جملات بعدي برابر است با ضريب جمله قبلي ضربدر توان a تقسـيم بر تعداد جملات قبل از آن.
ضريب جملات در جدول زير موسوم به مثلث خيام پاسكال آمده است
\(\begin{array}{*{20}{c}}{}&{}&{}&{}&{}&1&{}&{}&{}&{}&{}\\{}&{}&{}&{}&{}&{}&{}&{}&{}&{}&{}\\{}&{}&{}&1&{}&2&{}&1&{}&{}&{}\\{}&{}&{}&{}&{}&{}&{}&{}&{}&{}&{}\\{}&{}&1&{}&3&{}&3&{}&1&{}&{}\\{}&{}&{}&{}&{}&{}&{}&{}&{}&{}&{}\\{}&1&{}&4&{}&6&{}&4&{}&1&{}\\{}&{}&{}&{}&{}&{}&{}&{}&{}&{}&{}\\1&{}&5&{}&{10}&{}&{10}&{}&5&{}&1\end{array}\)
مثال
بسط \({(x + y)^3}\) را بنويسيد.
\({(x + y)^3} = {x^3} + 3{x^2}y + 3x{y^3} + {y^3}\)
مثال
بسط \({(2x - 3)^4}\)را بنويسيد.
\(\begin{array}{l}{(2x - 3)^4} = {(2x)^4} + 4{(2x)^3}( - 3) + 6{(2x)^2}{( - 3)^2} + 4(2x){( - 3)^3} + {( - 3)^4}\\\\ = 16{x^4} - 96{x^3} + 216{x^2} - 216x + 81\end{array}\)
براي بدست آوردن مجموع ضرايب يك چند جمله اي كافي است به جاي متغيرها عدد يك قرار داده و حاصل را بدست آوريم.
مثال
مجموع ضرايب \(3{x^4} - 2{x^3} + x{y^2} + 7y - 2\) را بيابيد.
حاصل عبارت را به ازاي \(x = 1,y = 1\) بدست مي آوريم در نتيجه داريم :
یب\(\)\( = 3 - 2 + 1 + 7 - 2 = - 1\)مجموع ضرا
مثال
مجموع ضرايب بسط \({(2{x^3} + 3{x^2} - 6)^{71}}\) را بيابيد.
مجموع ضرایب\( = {(2 + 3 - 6)^{71}} = {( - 1)^{71}} = - 1\)
بسط دو جمله اي كاشاني را ميتوان به صورت زير نيز نوشت:
\({(a + b)^n} = \left( \begin{array}{l}n\\0\end{array} \right){a^n} + \left( \begin{array}{l}n\\1\end{array} \right){a^{n - }}^1b + \left( \begin{array}{l}n\\2\end{array} \right){a^{n - 2}}{b^2} + ... + \left( \begin{array}{l}n\\n\end{array} \right){b^n}\)
كه جمله \((k + 1)\) ام آن به صورت \(\left( \begin{array}{l}n\\k\end{array} \right){a^{n - k}}{b^k}\) ميباشد.
مثال
جمله سوم بسط \({(2X - y)^7}\) را بيابيد.
\(\left( \begin{array}{l}7\\2\end{array} \right){(2x)^2}{( - y)^5} = \frac{{7!}}{{2! \times 5!}}(4{x^2})( - {y^5}) = - 60{x^2}{y^5}\)
تهیه کننده: حامد دلیجه
تابع
فصل 2 : تابع
تابع
يك تابع از مجموعه A به مجموعه B رابطهاي بين دو مجموعه است كه به هر عضو A دقيقاً يك عضو از B را نسبت ميدهد. اعضاي A و B هر شيء ميتوانند باشند اما اگر \(A \subseteq R\) و\(B \subseteq R\) تابع f را تابع حقيقي ميناميم
A را دامنه تابع ، B را هم دامنه آن و مجموعه\(\left\{ {f\left. {\left( x \right)} \right|} \right.x \in \left. A \right\}\) را برد تابع f گوييم.
مثال
تابع حقيقي\(A \to B\) :را كه در آن \(A = \left\{ {1,2,3,4,\left. 5 \right\}} \right.\)و هر عضواز f به صورت \((t,2t)\) ميباشد را در نظر بگيريد
الف) مجموعه B را توصيف كنيد.
ب) تابع f را با اعضايش مشخص كنيد.
ج) ضابطه تابع f را مشخص كنيد؟
د) اگر N) \(B = N\) مجموعه اعداد طبيعي است)، معرفي كاملي از تابع f را بنويسيد.
الف) مجموعه B هر زير مجموعه اي از اعداد حقيقي شامل مجموعه \(\left\{ {2,4,6,8,\left. {10} \right\}} \right.\) ميتواند باشد
ب) اعضاي تابع f به صورت\(f = \left\{ {\left( {1,2} \right)} \right.,\left( {2,4} \right),\left( {3,6} \right),\left( {4,8} \right),\left. {\left( {5,10} \right)} \right\}\) ميباشد.
ج) ضابطه تابع f را ميتوان به صورت \(f(x) = 2x\) نوشت.
د) تابعfراميتوان به صورتهاي\(\left\{ \begin{array}{l}f:A \to N\\f(x) = 2x\end{array} \right.\) يا\(\left\{ \begin{array}{l}\left\{ {f:\left\{ {1,2,3,4,\left. 5 \right\}} \right.} \right. \to \left\{ {1,2,3,4,5,\left. {...} \right\}} \right.\\f(x) = 2x\end{array} \right.\) نوشت كه به طوركامل تابع فوق را معرفي ميكنند توجه كنيد كه مجموعه A دامنه تابع f و مجموعه N ، هم دامنه تابع و همچنين برد تابع مجموعه \(\left\{ {2,4,6,8\left. {,10} \right\}} \right.\) ميباشد.
مثال
مجموعه A داراي m عضو و مجموعه B داراي n عضو ميباشد و تابع g از A به B تعريف شده است.
الف) در نمودار ون مربوط به تابع g چند پيكان بايد وجود داشته باشد.
ب) نمودار ون تابع g را طوري رسم كنيد كه.\(m < n\)
ج) نمودار ون تابع g را طوري رسم كنيد كه \(m = n\)
د) نمودار ون تابع g را طوري رسم كنيد كه \(m > n\)
الف) با توجه به اينكه از هر عضو A دقيقاً يك پيكان بايد خارج شده باشد بنابراين دقيقاً بايد m پيكان از A به B كشيده شود.
ب) بيشمار تابع براي g ميتوان در نظر گرفت.به عنوان مثال ميتوان g را چنين در نظر گرفت:
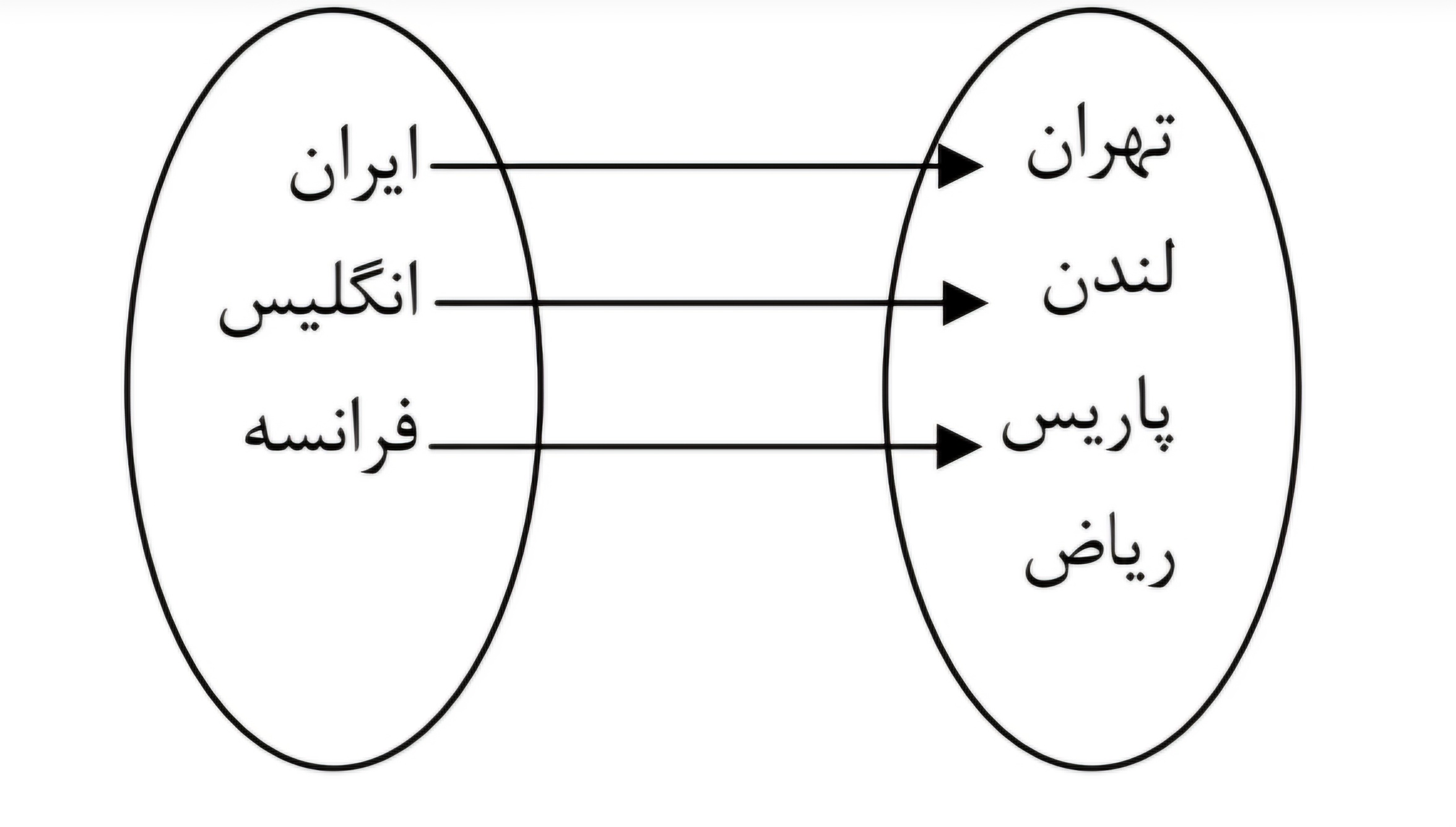
مجموعه {فرانسه، انگليس، ايران} دامنه تابع و مجموعه { رياض، پاريس، لندن، تهران} هم دامنه تابع و مجموعه {پاريس، لندن، تهران} باشندبرد تابع مي باشند.
ج) ميتوان g را چنين در نظر گرفت.
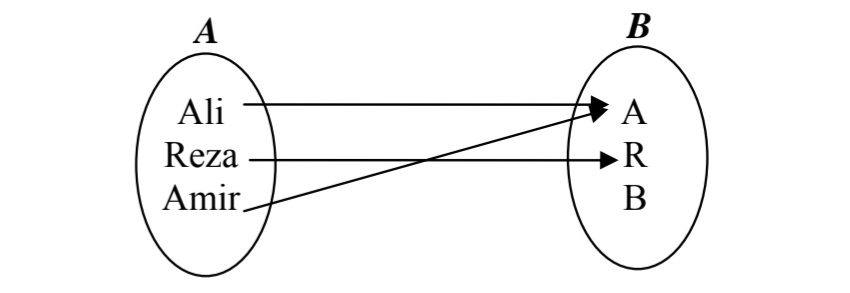
مجموعه \(\left\{ {ali,reza,ami} \right.\left. r \right\}\) دامنه تابع و\(\left\{ {A,R,\left. B \right\}} \right.\) هم دامنه تابع و مجموعه \(\left\{ {A,\left. R \right\}} \right.\) برد تابع ميباشند.
د) تابع g را ميتوان چنين در نظر گرفت
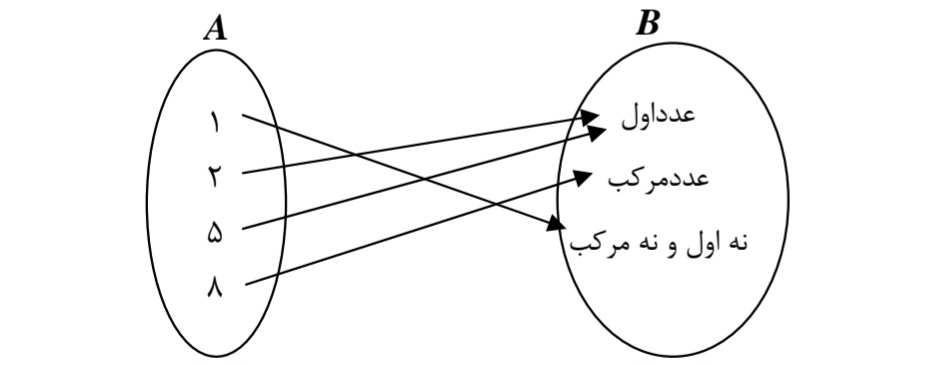
مجموعه \(\left\{ {1,2,5,\left. 8 \right\}} \right.\) دامنه تابع و مجموعه {نه اول و نه مركب، عدد مركب، عدد اول} هم دامنه و برد تابع هستند.
مثال
تابع:\(A \to B\) را طوري مشخص كنيد كه:
الفA (متناهي و B نامتناهي باشد.
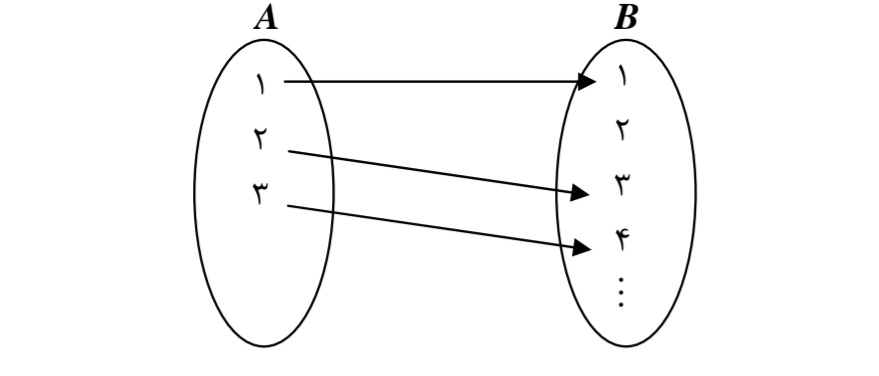
ب A (نامتناهي و B متناهي باشد.
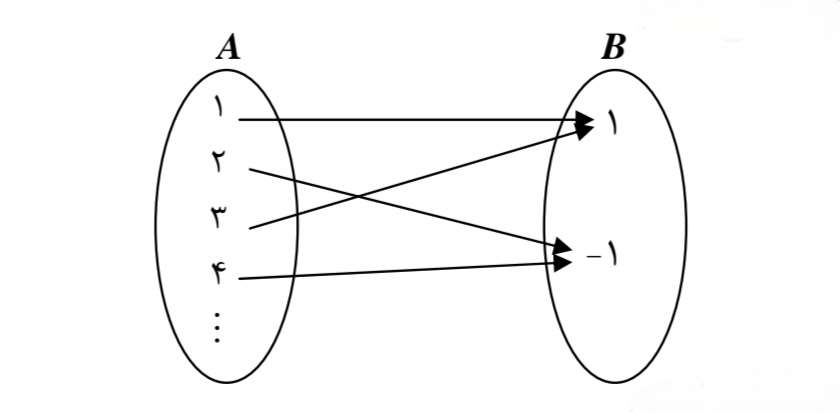
جA ( و B هر دو نامتناهي باشند.
مثال
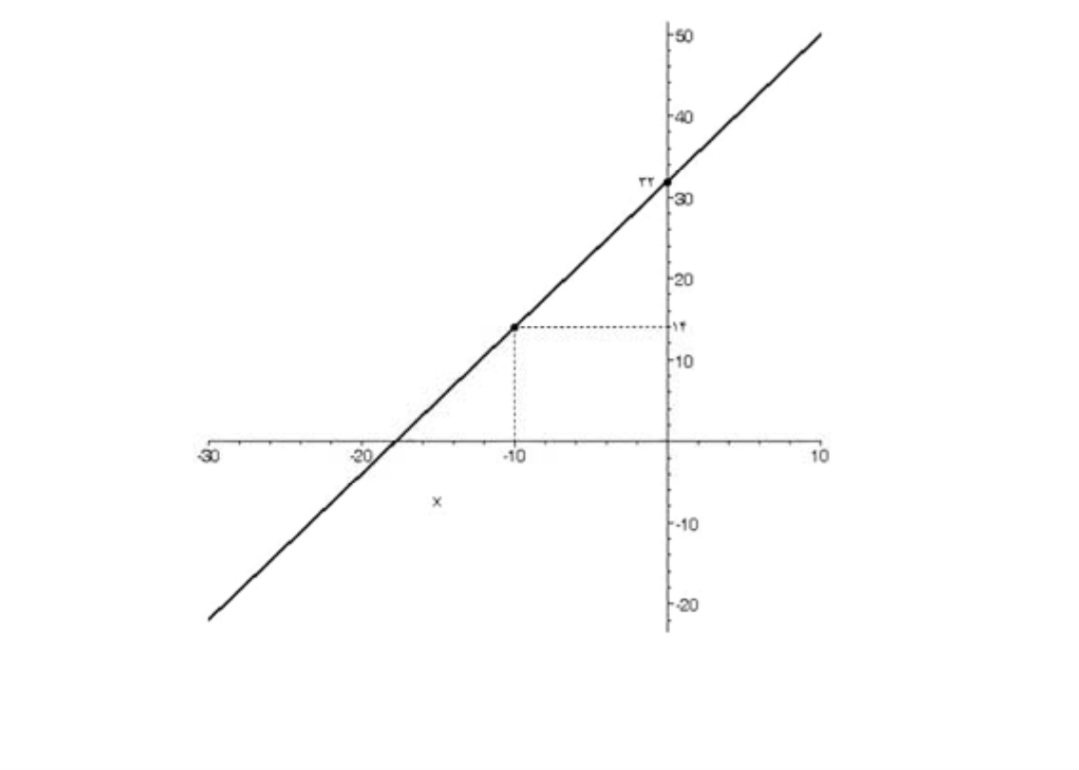
الف) تابع f با ضابطه \(y = \frac{9}{5}x + 32\) را رسم كنيد.
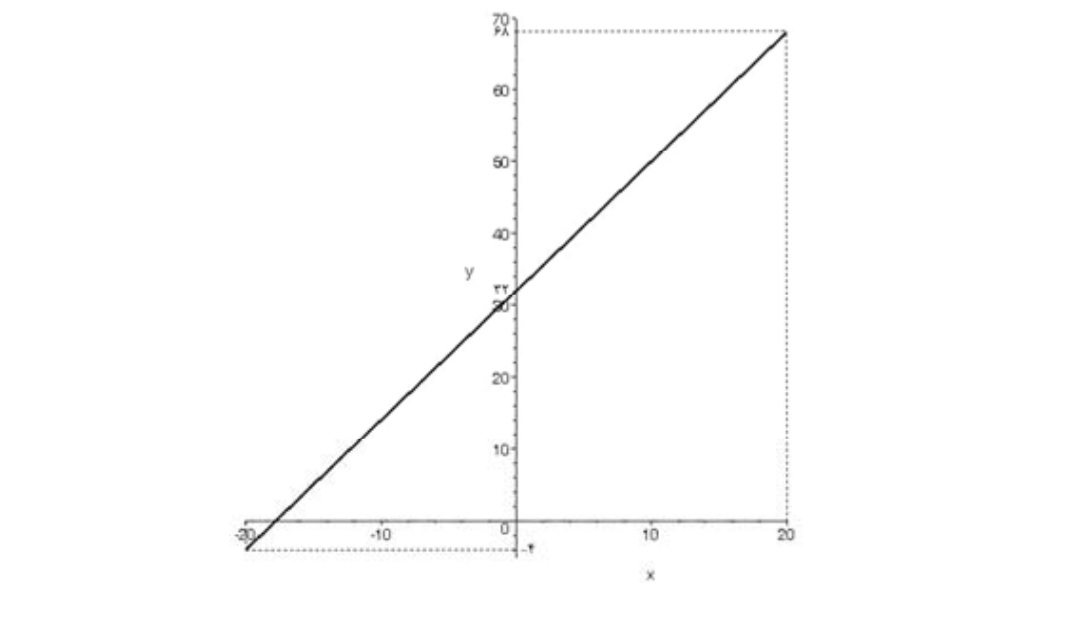
ب) تابع \(g:\left[ { - 20,20} \right] \to R\) با ضابطه \(g(x) = \frac{9}{5}x + 32\) را رسم كنيد.
ج) آيا تابع h را ميتوان به قسمي در نظر گرفت كه دامنه و ضابطه آن با تابع g يكي باشد اما هم دامنه آن مجموعه Z باشد.
الف) با توجه به اينكه نمودار ضابطه داده شده يك خط است و هر خط با 2 نقطه مشخص ميشود كافي است 2 نقطه از اين خط را يافته و خط را رسم كرد.
به عنوان مثال:
\(x = 0 \Rightarrow y = 32 \Rightarrow (0,32) \in f,x = - 10 \Rightarrow y = 14 \Rightarrow ( - 10,14) \in f\)
لذا شكل آن به صورت زير خواهد بود.
ب) نموار اين تابع قسمتي از تابع f است كه در آن \( - 20 \le x \le 20\) در واقع تابع g را تحديد تابع f ميناميم و نمودار آن چنين است:
ج) با توجه به اينكه\(g\left( 1 \right) = \frac{9}{5} + 32 = \frac{{169}}{5}\) لذا چنين تابعي نميتوان يافت.
مثال
از بين مستطيل هاي قابل محاط شدن در مثلث متساوي الاضلاع به ضلع 1 كدام مستطيل بيشترين مساحت را دارد؟
طبق شكل اگر DC را برابر x بگيريم، داريم\(DFC = 30\) (چرا) و از آنجا\(F{C^2} = 2x\) با توجه به رابطه ي فيثاغورس داريم:
\(F{C^2} = D{C^2} + F{D^2} \Rightarrow {(2x)^2} = {x^2} + F{D^2} = FD = \sqrt 3 x\)
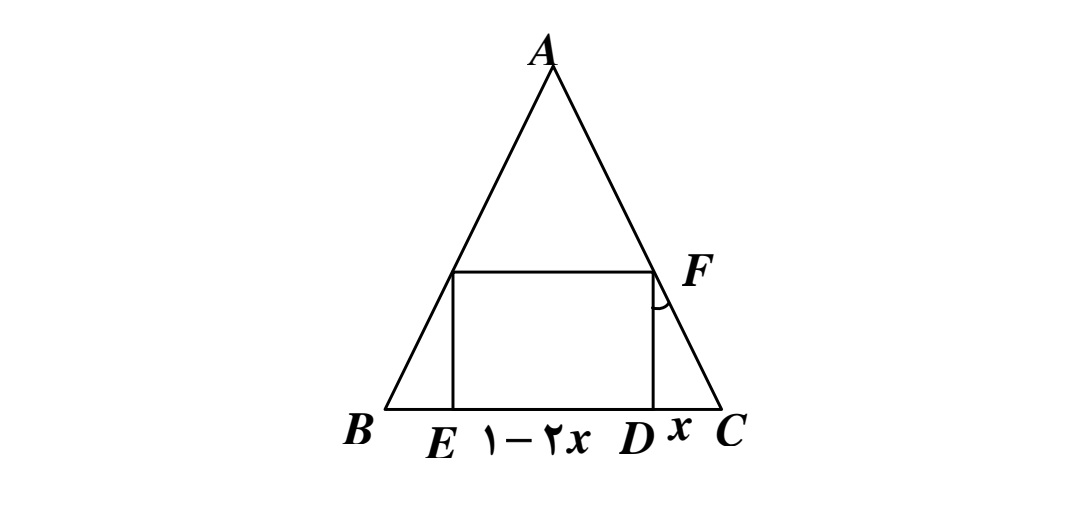
لذا مساحت مستطيل فوق از رابطه\(S = (1 - 2x)x\sqrt 3 \) دست مي آيد و داريم:
\(s = - 2\sqrt 3 ({x^2} - \frac{1}{2}x) = - 2\sqrt 3 \left[ {{{(x - \frac{1}{4})}^2} - \frac{1}{{16}}} \right] = - 2\sqrt 3 {(x - \frac{1}{4})^2} + \frac{{\sqrt 3 }}{8}\)
اما بيشترين مقدار عبارت \( - 2\sqrt 3 {(x - \frac{1}{4})^2}\) صفر است كه به ازاي\(x = \frac{1}{4}\) به دست مي آيد و لذا ماكزيمم S برابر \(\frac{{\sqrt 3 }}{8}\) است و طول و عرض اين مستطيل برابر است با\(x\sqrt 3 = \frac{1}{4}\sqrt 3 \) و
\(1 - 2x = 1 - 2(\frac{1}{4}) = \frac{1}{2}\)
دوتابع f و g در صورتي مساويند كه هردو شرط زير برقرار باشد:
الف) دامنه دو تابع با هم برابر باشند.
ب) به ازاي هر عضو از دامنه آنها داشته باشيم\(f(x) = g(x)\).
مثال
توابع \(g = \left\{ {\left( {3,4} \right)} \right.,(7,5),(9, - 1\left. ) \right\}\) و \(f = \left\{ {(3,4)(7, - 1),(9,5\left. ) \right\}} \right.\) را در نظر بگيريد. آيا اين دو تابع با هم مساويند.
دامنه اين دو تابع مجموعه \(\left\{ {3,7,\left. 9 \right\}} \right.\) است كه با هم مساوي است . \(f(7) = - 1\) ولي \(g(7) = 5\) پس دو تابع با هم مساوي نيستند .
مثال
توابع \(\left\{ \begin{array}{l}f:A \to R\\f(x) = 3{x^3} + 1\end{array} \right.\) و \(\left\{ \begin{array}{l}g:A \to R\\g = \left\{ {(1,a),(b,2),(a,c\left. ) \right\}} \right.\end{array} \right.\) را در نظر بگيريد a ، b وc را طوري بيابيد كه دو تابع با هم مساوي باشند.
چون\(1 \in {D_g}\) لذا بايد \(1 \in {D_f}\) و \(f(1) = 4\) پس بايد \(g(1) = 4\) يعني \(a = 4\) همچنين \(g(b) = 2\) و از حل معادله\(f(x) = 2\) نتيجه ميشود كه \(x = \frac{1}{{^3\sqrt 3 }}\)لذا \(b = \frac{1}{{^3\sqrt 3 }}\) با استدلال هاي مشابه \(4 \in {D_g}\)و در نتیجه باید\(4 \in {D_f}\) و چون \(f(4) = 193\) لذا \(g(4) = 193\) يعني \(c = 193\)
پس تابع gبه صورت \(g(x) = \left\{ {(1,4),(\frac{1}{{^3\sqrt 3 }}} \right.),(4,193\left. ) \right\}\) بوده و A نيز چنين است \(A = \left\{ {(1,4),(\frac{1}{{^3\sqrt 3 }}} \right.),\left. 4 \right\}\)
توابع \(f(x) = {\sin ^2}x + {\cos ^2}x\) و\(g(x) = 1\) با هم برابرند دقت كنيد كه دامنه هر دو تابع مجموعه R است.
مثال
آیا توابع \(f(x) = \sqrt {{x^2}} \) و\(g(x) = x\) با هم مساويند؟
دامنه هر دو تابع مجموعه اعداد حقیقی است اما به ازای هر \(x < 1\) مقادیر هر دو تابع برابر نیست مثلا\(f( - 5) = \sqrt {(5} {)^2} = 25 = 5\) ولی \(g( - 5) = - 5\)
مثال
آيا توابع \(f(x) = \tan x\) و \(g(x) = \frac{1}{{\cot x}}\) باهم برابرند؟
ميدانيد كه \(\tan x\) به ازاي هر\(x = k\pi + \frac{\pi }{2}\) , \(K \in Z\) تعريف نشده است يعني اين نقاط در دامنه تابع f قرار ندارند.
اما \(\cot x\) به ازاي هر \(x = k\pi \) ,\(K \in Z\) تعريف نشده و به ازاي هر\(x = k\pi + \frac{\pi }{2}\) , \(K \in Z\) صفر 2 ميشود لذا مجموعه اين نقاط يعني نقاط به طول\(x = k\frac{\pi }{2}\) \(K \in Z\) , عضو دامنه تابع g نميباشد.
بنابراين دامنه اين دو تابع برابر نيست . به عنوان مثال \(f(0)\) تعريف شده و برابر صفر است اما تابع g به ازاي \(x = 0\) تعريف نشده است
مثال
به طور مشابه با مثال قبل توابع\(f(x) = \log {x^2}\) و \(g(x) = 2\log x\) باهم برابر نیستند زیرا دامنه تابع f مجموعه \(R - \left\{ {\left. 0 \right\}} \right.\) است ولي دامنه تابع g مجموعه \(\left\{ {\left. x \right|} \right.x > \left. 0 \right\}\) مي باشد كه برابر نيستند.
مثال
M و L را طوري بيابيد كه توابع f و g باهم برابر باشند.
\(f(x) = \left\{ {\begin{array}{*{20}{l}}{\frac{{x + 2}}{{{x^2} - 4}},x \ne - 2,2}\\{L,x = - 2}\\{5,x = 2}\end{array}} \right.\,\,\,,\,\,\,g(x) = \left\{ {\begin{array}{*{20}{l}}{\frac{1}{{x - 2}},x \ne 2}\\{}\\{M,x = 2}\end{array}} \right.\)
اولاً دامنه هر دو تابع مجموعه اعداد حقيقي است و \(g(2) = M\) و \(M = 5\) بنابراين 5 همچنين \(f( - 2) = L\) و \(g( - 2) = \frac{1}{{ - 4}}\) لذا.\(L = - \frac{1}{4}\) توجه كنيد كه اگر \(x \ne 2\), \(x \ne - 2\) آنگاه:
\(f(x) = \frac{{x + 2}}{{x - 2}} = \frac{{x + 2}}{{(x - 2)(x + 2)}} = \frac{1}{{x - 2}}\)
تهیه کننده: حامد دلیجه
- آزمون آنلاین تمامی دروس پایه یازدهم
- گام به گام تمامی دروس پایه یازدهم
- ویدئو های آموزشی تمامی دروس پایه یازدهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه یازدهم
- فلش کارت های آماده دروس پایه یازدهم
- گنجینه ای جامع از انشاء های آماده پایه یازدهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه یازدهم
توابع چند ضابطه اي
فصل 2 : تابع
توابع چند ضابطه اي
توابعي كه در بخش هاي مختلف دامنه آن با ضابطه هاي مختلف تعريف مي شوند توابع چند ضابطه اي مينامند.
امروزه توابعي كه در سازمانها جهت محاسبه ي هزينه ي آب، برق، گاز، تلفن و ... مشتركين مورد محاسبه قرار مي گيرد به صورت توابع چند ضابطه اي ميباشد.
مثال
يك مغازه زنجيرهاي جهت جذب مشتري اعلام كرده است كه به مشترياني كه مبلغ خريدشان حداقل 20000 تومان باشد %5 و مشترياني كه مبلغ خريدشان حداقل 100000 تومان باشد %10 تخفيف ميدهد تابع فوق را مشخص كنيد.
x را مبلغ خريد مشتري و \(y = f\left( x \right)\) را مبلغي كه مشتري بايد بپردازد در نظر بگيريد خواهيم داشت.
\(f\left( x \right) = \left\{ \begin{array}{l}x,0 < x < 20000\\\\0/95,200000 \le x < 100000\\\\0/9,x \ge 100000\end{array} \right.\)
مثال
مدرسي تصميم ميگيرد جهت ارفاق به دانشجويان خود، نمره دانشجوياني كه كمتر از 8 است را از فرمول \(6 + \frac{x}{2}\) ودانشجوياني كه نمره 8 تا 20 گرفته اند را از فرمول\(\frac{5}{6}x + \frac{{10}}{3}\) محاسبه كند.
الف) تابع را مشخص كنيد و دامنه و برد آن را بيابيد .
ب)اگر دانشجويي در امتحان نمره 11 گرفته باشد نمره نهايي او چقدر است؟
x را نمره برگه دانشجو و \(y = f(x)\) را نمره نهايي او در نظر بگيريد خواهيم داشت:
\(f(x) = \left\{ \begin{array}{l}6 + \frac{x}{2},0 \le x < 8\\\\\frac{5}{6}x + \frac{{10}}{3},8 \le x \le 20\end{array} \right.\)
بدیهی است دامنه تابع یعن نمراتی که دانشجو گرفته از صفر تا 20 یعنی \(\left[ {0,20} \right]\) می باشد
اما برد آن یعنی نمراتی که مدرس ثبت خواهد کرد چنین به دست می آید:
\(\begin{array}{l}0 \le x \le 8 \Rightarrow 0 \le \frac{x}{2} < 4 \to 6 \le 6 + \frac{x}{2} < 10\\\\8 \le x \le 20 \Rightarrow \frac{{40}}{6} \le \frac{5}{6}x \le \frac{{100}}{6} \to 10 \le \frac{5}{6}x + \frac{{10}}{3} \le 20\end{array}\)
يعني برد تابع يا نمرات نهايي مجموعه [20 , 6] ميباشد.
ب) براي محاسبه نمره نهايي دانشجويي كه نمره 11 گرفته است بايد از ضابطه دوم استفاده كرد، يعني:
\( = \frac{5}{6} \times 11 + \frac{{10}}{3} = \frac{{95}}{6} = 12/5\)
مثال
تابع چند ضابطه اي زير را در نظر بگيريد
\(g(x) = \left\{ \begin{array}{l}{x^2},x < - 2\\\\5, - 2 \le x \le 2\\\\4 - 2x,x > 2\end{array} \right.\)
الف) دامنه و برد تابع را مشخص كنيد.
ب) مقدار \(g(g( - 3))\) را بيابيد..
الف)دامنه به وضوح مجموعه اعداد حقيقي است.
براي محاسبه برد آن ملاحظه ميكنيم كه
\(\left. \begin{array}{l}x < - 2 \Rightarrow {x^2} > 4 \Rightarrow g(x0 > 4\\\\ - 2 \le x \le 2 \Rightarrow g(x) = 5\\\\x > 2 \Rightarrow - 2x < - 4 \Rightarrow 4 - 2x < 0 \Rightarrow g(x) < 0\end{array} \right\} \Rightarrow {R_g} = ( - \infty ,0) \cup (4, + \infty )\)
ب(
\(g( - 3) = {( - 3)^2} = 9 \Rightarrow g(g( - 3)) = g(9) = 4 - 2 \times 9 = - 14\)
مثال
نمودار تابع f به شكل زير است ضابطه آن را مشخص كنيد.
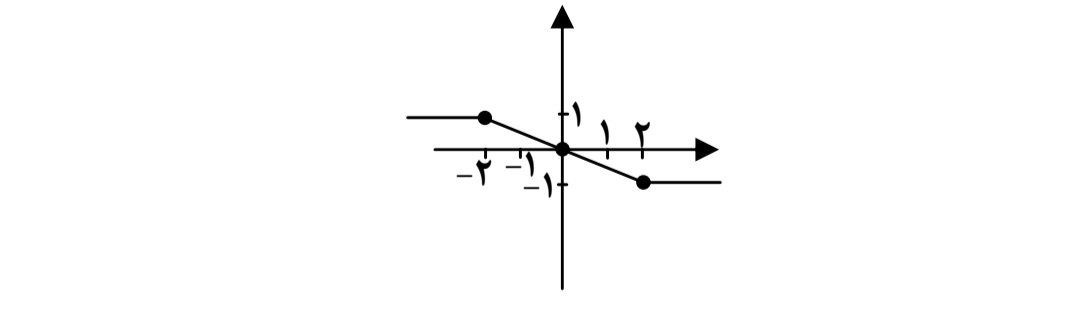
واضح است كه اگر \(x \le - 2\) آن گاه \(f(x) = - 1\) و اگر \(x \ge 2\) آن گاه \(f(x) = - 1\) اما به ازاي \( - 1 \le x \le 1\) نمودار تابع خطي است لذا با داشتن دو نقطه از آن مثلاً نقاط \(( - 2,1)\) و \((0,0)\) ميتوان معادله آن را به دست آورد. شيب خط برابر است با \(\frac{{1 - 0}}{{ - 2 - 0}} = - \frac{1}{2}\) و معادله آن به صورت \(y - 0 = - \frac{1}{2}(x - 1)\) يا \(y - 0 = - \frac{1}{2}x\) است لذا ضابطه تابع f به صورت
\(f(x) = \left\{ \begin{array}{l}1,x < - 2\\\\ - \frac{1}{2}x, - 2 \le x \le 2\\\\ - 1,x > 2\end{array} \right.\)
ميباشد توجه كنيد كه اين تابع را توان به صورت \(f(x) = \frac{1}{4}(\left| {x - 2} \right| - \left| {x + 2} \right|)\) نيز نوشت .
تهیه کننده: حامد دلیجه
معادلات و توابع
فصل 2 : تابع
معادلات و توابع
در رابطه هايي كه شامل x و y هستند اگر به ازاي هر x تنها يك y داشته باشيم اين رابطه نسبت به متغير مستقل x تابعي را مشخص ميكند بهويژه اگر بتوان y را بر حسب x محاسبه كرد اگر به رابطه اي به فرم \(y = \pm f(x)\) كه y همواره صفر نباشد، برسيم؛ رابطه فوق تابعي را مشخص نميكند به عبارت ديگر f تابع است اگر و تنها اگر بتوان نشان داد:
\(f({x_1}) = f({x_2}) \Rightarrow {x_1} = {x_2}\)
يا به طور معادل
\(f({x_1}) \ne f({x_2}) \Rightarrow {x_1} \ne {x_2}\)
مثال
بررسي كنيد روابط زير تابعاند يا خير؟
الف)\({y^2} - {x^2} = 1\) ب)\({y^2} - {x^2}2y = - 1\)
ج)\({y^3} - {x^2} = 2\) د)\(x + \left| y \right| = 0\)
الف) داريم:
يعني به ازاي هر \(x > - 1\) بيش از يك y داريم . مثلاً اگر \(x = 0\) داريم \(y = \pm 1\) .
لذا اين رابطه مشخص كننده ي يك تابع نيست . البته تنها ذكر اين مطلب كه هر دو نقطه \((0,1)\) و \((0, - 1)\) روي نمودار اين رابطه قرار دارد نشان دهنده ي اين است كه رابطه ي فوق تابع نميباشد.
ب) داريم:
\(\begin{array}{l}{x^2} - {y^2} - 2y = - 1 \Rightarrow {x^2} + {(y - 1)^2} = 0 \Rightarrow {(y - 1)^2} = - {x^2}\\\\ \Rightarrow y - 1 = \pm \sqrt { - {x^2}} \Rightarrow y = 1 \pm \sqrt { - {x^2}} \end{array}\)
ما x تنها مقدار صفر را ميتواند اختيار كند كه خروجي آن تنها يك ميباشد يعني در اين رابطه تنها زوج مرتب ( 10 , 0) صدق ميكند لذا y تابعي از x است.
ج) داريم:
\({y^3} + {x^2} = 2 \Rightarrow {y^3} = 2 - {x^2}{ \Rightarrow ^3}\sqrt {2 - {x^2}} \)
يعني به ازاي هر x ، y منحصر به فردي وجود دارد يعني y تابعي از x است براي اثبات اين مطلب ميتوان نوشت:
\({x_1} = {x_2} \Rightarrow x_1^2 = x_2^2 \Rightarrow 2 - x_1^2 = 2 - x_2^2{ \Rightarrow ^3}\sqrt {2 - x_1^2} { = ^3}\sqrt {2 - x_2^2} \Rightarrow {y_1} = {y_2}\)
د) داريم:
\(x + \left| y \right| = 0 \Rightarrow \left| y \right| = - x \Rightarrow y = 9 \pm ( - x),x \le 0\)
يعني اگر\(x > 0\) هيچ نقطه اي در رابطه صدق نميكند . اگر \(x = 0\) ، تنها نقطه ي\((0,0)\) را مشخص ميكند اما اگر \(x < 0\) ، به ازاي هر x ، دو y نظير ميشود؛ لذا y تابعي از x نيست . مثلاً اگر −\(x = - 1\) داريم \(y = \pm 1\) يعني دو نقطه \(( - 1,1)\) و \(( - 1, - 1)\) را مشخص ميكند لذا اين رابطه تابعي را نسبت به x مشخص نميكند . اما اين رابطه يك تابع x بر حسب y را مشخص مي كند .
تهیه کننده: حامد دلیجه
رسم نمودار توابع وابسته به f با استفاده از نمودار تابع f
فصل 2 : تابع
رسم نمودار توابع وابسته به f با استفاده از نمودار تابع f
(1)نمودار تابع \(g(x) = f(x) + a\) همان نمودار تابع \(f(x)\) است كه a واحد در امتداد محور y ها منتقل شده است ( اگر \(a > 0\) انتقال در جهت مثبت محور y و اگر \(a < 0\) انتقال در جهت منفي ميباشد (
توجه كنيد اگر,\(({x_0},{y_0}) \in f\) يعني \({y_0} = f({x_0})\) آن گاه \(g({x_0}) + a = {y_0} + a\) یا \(({x_0},{y_0} + a) \in g\) یعنی نقطه به اندازه a واحد به موازات محور y ها منتقل شده است.
(2) نمودار تابع \(h(x) = f(x + a)\) همان نمودار تابع f است كه a واحد در امتداد محور x ها منتقل شده است (اگر \(a > 0\) انتقال در جهت منفي محور و اگر \(a > 0\) انتقال در جهت مثبت ميباشد (
توجه كنيد كه اگر \(({x_0},{y_0}) \in f\) يعني \({y_0} = f({x_0})\) انگاه:
\(h({x_0} - 0) = f({x_0} - a + a) = f({x_0}) = {y_0}\)
یا \(({x_0} - a,{y_0})\) یعنی نقطه به اندازه a واحد به موازات محور x ها منتقل شده است
(3 )نمودار تابع \(k(x) = a = af(x)\) با كشيدن نمودار تابع \(y = f(x)\) در امتداد محور y ها به دست ميآيد (اگر \(a > 1\) ، انبساط در امتداد محور y ها و با ضريب a رخ ميدهد و اگر 10, \(0 < a < 1\) ، انقباض و در امتداد محور y ها و با ضريب a رخ ميدهد و اگر براي بدست آوردن نمودار تابع \(y = k(x)\) ابتدا قرينه نمودار f نسبت به محور x ها يعني نموار تابع
\(y = - f(x)\) را رسم ميكنيم سپس نمودار جديد را با ضريب -aمنبسط يا منقبض (بسته به اينكه \( - a > 1\) یا \(0 < - a < 1\) ميكنيم.
.
توجه كنيد اگر \(({x_0},{y_0}) \in f\) یعنی \(({x_0} = f({x_0})\) ان گاه \(k({x_0}) = a,f({x_0}) = a{y_0}\) یعنی \(({x_0},a{y_0}) \in k\) كه مويد نكته گفته شده است
(4 ) نمودار تابع \(t(x) = f(ax)\) \(a > 0\)با كشيدن نمودار تابع \(y = f(x)\) در امتداد محور x ها به دست ميآيد. (اگر \(a > 1\) نمودار f با ضريب \(\frac{1}{a}\) ، منقبض شده و اگر \(0 < a < 1\) نمودار f با ضريب منبسط خواهد شد )
توجه كنيد كه اگر \(({x_0},{y_0}) \in f\) يعني \({y_0} = f({x_0})\) ان گاه \(t(\frac{{{x_0}}}{a}) = f(a \times \frac{{{x_0}}}{a}) = f\left( {{x_0}} \right) = y\) یعنی \((\frac{{{x_0}}}{a},{y_0})\) كه نكات گفته شده را تاييد ميكند
( 5 ) براي رسم نمودار تابع \(M(x) = f(ax)\) كه در آن \(a < 0\) با توجه به آنكه نمودار تابع \(l(x) = f( - x)\) قرينه نمودار تابع \(y = f(x)\) نسبت به محور y ها است براي رسم تابع \(a < 0\) \(M(x) = f(ax)\) , ابتدا ميتوان نمودار تابع \(N(x) = f( - ax)\) را مانند آنچه در ((4 بيان شد، رسم نمود سپس نمودار تابع M كه \(M(x) = N( - x)\) ميباشد را با رسم قرينه نمودار تابع N نسبت به محور y ها رسم كرد.
توجه كنيد كه اگر \(\left( {{x_0},{y_0}} \right) \in f\) یعنی \({y_0} = f\left( {{x_0}} \right)\) ان گاه
\(l( - {x_0}) = f( - ( - {x_0})) = f({x_0}) = {y_0}\)
يعني \(( - {x_0},{y_0}) \in l\) که قرینه نقطه \(({x_0},{y_0})\) نسبت به محورy ها است
(6)براي رسم نمودار تابع \(p(x) = af(bx + c) + d\) مراحل زير را انجام ميدهيم:
الف) اگر \(b > 0\) مطابق مرحله )4(نمودار f را با ضريب \(\frac{1}{b}\)در امتداد محور ط انقباض 1 يا انبساط ميدهيم و اگر \(b < 0\)
مطابق مرحله) 5) عمل ميكنيم)در اين حالت نمودار \(f(x)\) حاصل ميشود (
ب) با توجه به مرحله 2 نموار بدست آمده در مرحله قبل را به اندازه \(\frac{c}{b}\)در راستاي محور x ها و در جهت مخالف علامت \(\frac{c}{b}\)انتقال دارد (در اين حالت نمودار تابع \(y = f(bx + c)\) حاصل ميشود.
ج) با توجه به مرحل 3 نمودار به دست آمده در مرحله قبل را انبساط يا انقباض داد . (با ضريب \(\left| a \right|\) در اين مرحله نمودار تابع\(y = af(bx + c)\) بدست می آيد ).
د) با توجه به مرحله 1 نمودار به دست آمده در مرحله قبل را به اندازه d واحد در جهت محور y ها انتقال ميدهيم (در اين مرحله نموار تابع \(y = (bx + c) + d\) كه همان \(y = p(x)\) است به دست مي آيد(
قابل ذكر است كه در اين مرحله اگر \(a = 1\) يا \(b = 1\) يا \(c = 0\) يا \(d = 0\) مرحله نظير داده شده قابل حذف است.
توجه كنيد كه اگر \(( - {x_0},{y_0}) \in f\) یعنی \(y = f\left( {{x_0}} \right)\) آنگاه:
\((\frac{{ - {x_0} - c}}{b}) = af(b(\frac{{ - {x_0} - c}}{b}) + c) + d = af({x_0}) + d = a{y_0} + d\)
لذا
\(yy = f(2x)\)
كه مويد مطالب فوق است.
مثال
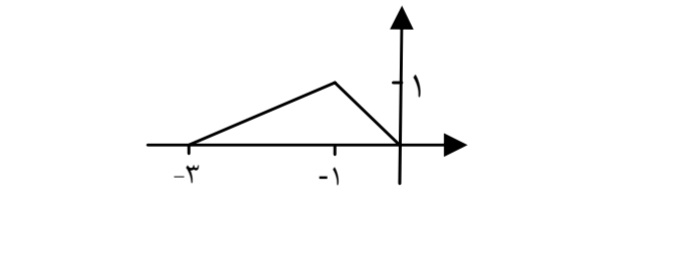
فرض كنيد نمودار تابع \(y = f(x)\) زيربه صورت باشد . مطلوب است رسم نمودار توابع g ،h ، k ، t ، l و p كه در مثال قبل معرفي شدند.
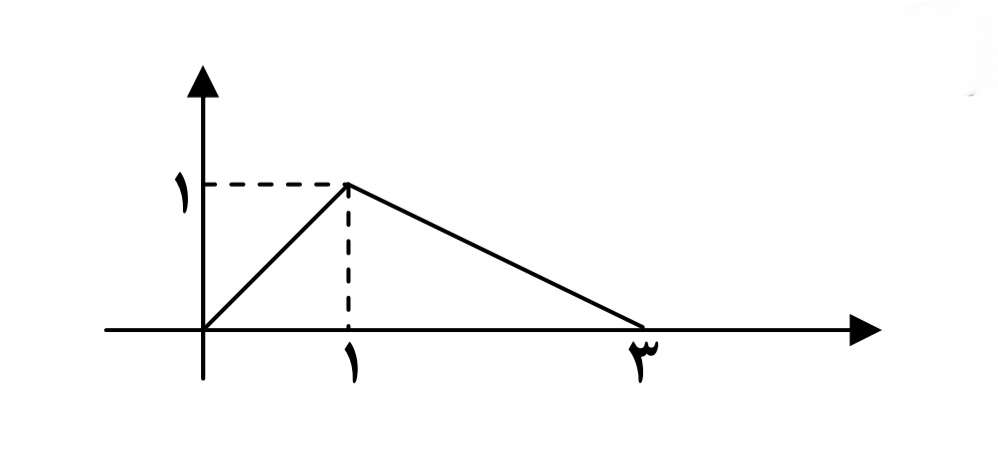
داريم:
الف)
ب)
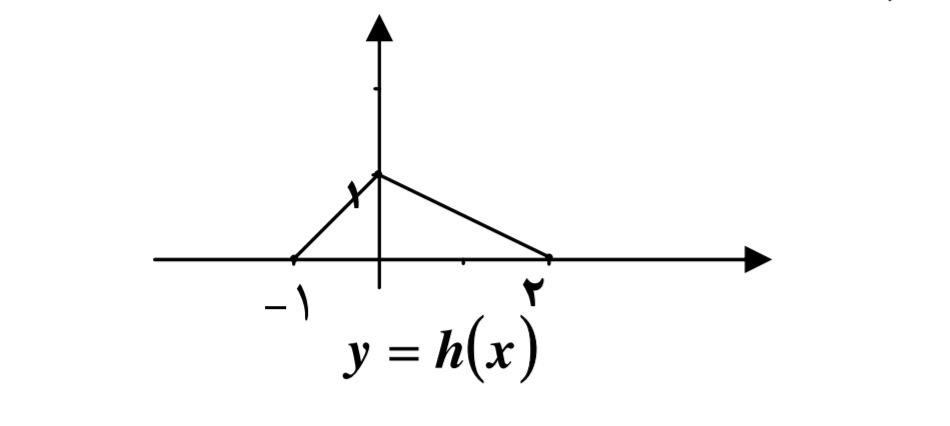
ج)
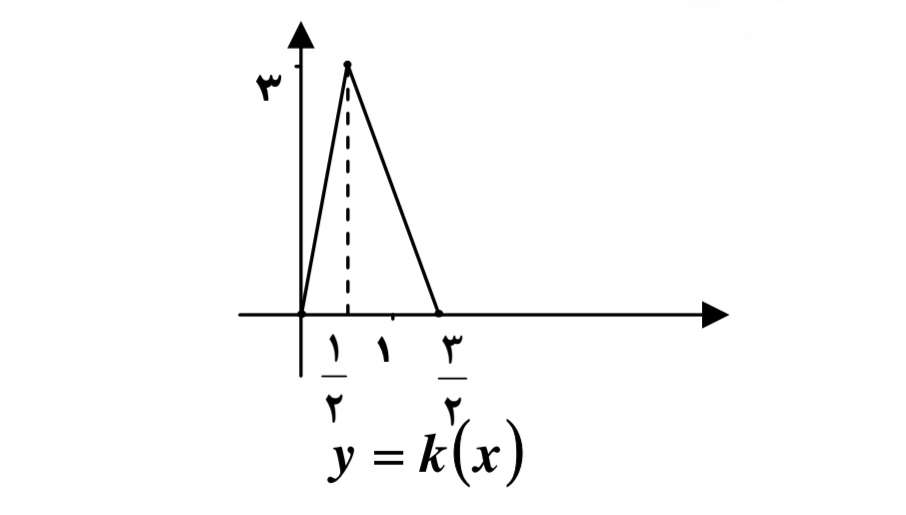
د)
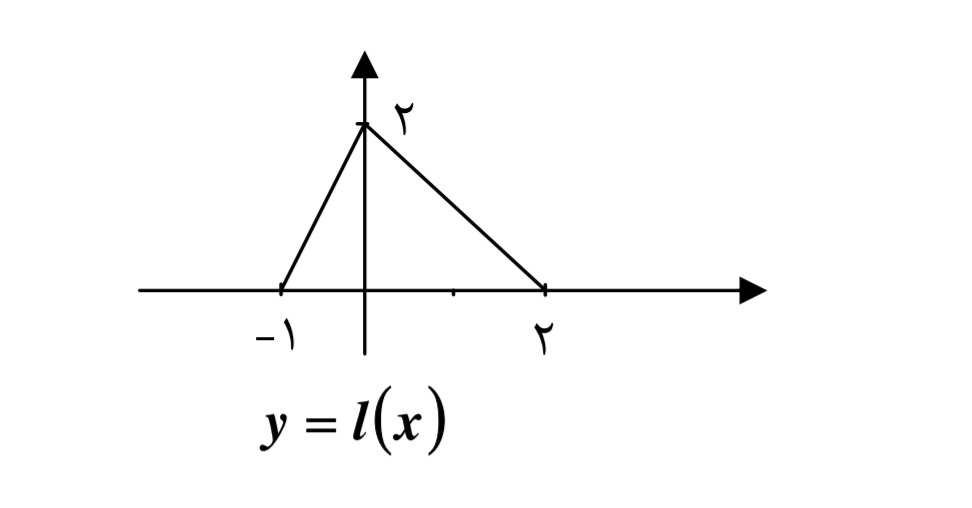
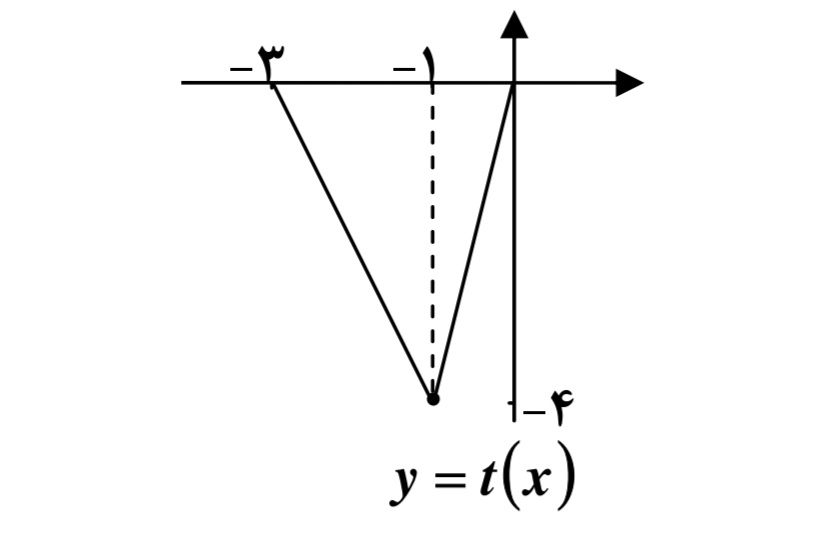
هـ ) توجه كنيد كه نمودار تابع \(y = f( - x)\) به صورت زير است:
و با توجه به آن نمودار \(y = t(x)\) به صورت زير است:
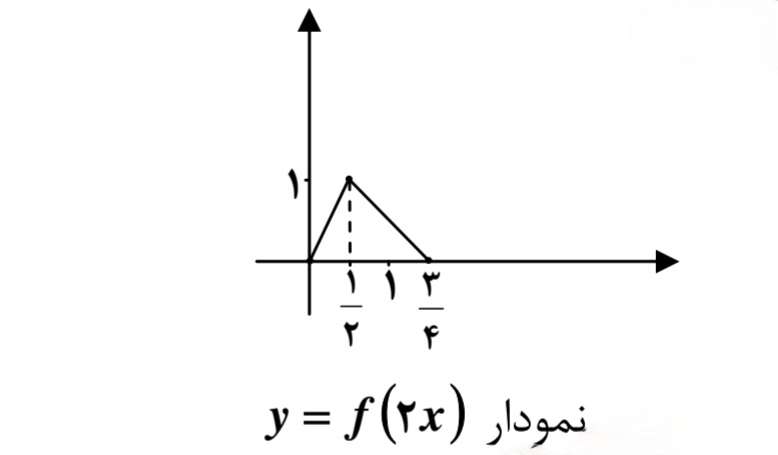
و) براي رسم نمودار تابع p مطابق دستورالعمل 6 به صورت زير عمل ميكنيم: مرحله ي الف) نمودار \(y = f(2x)\)
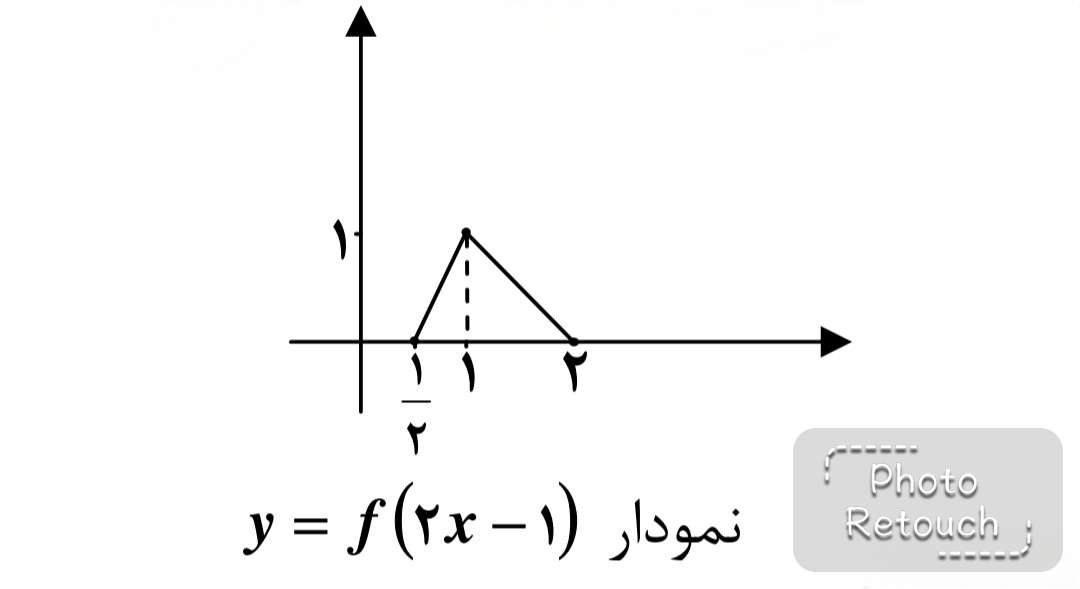
مرحله ي ب) انتقال \(y = f(2x)\) به اندازه\(\frac{1}{2}\) + در جهت محور x ها.
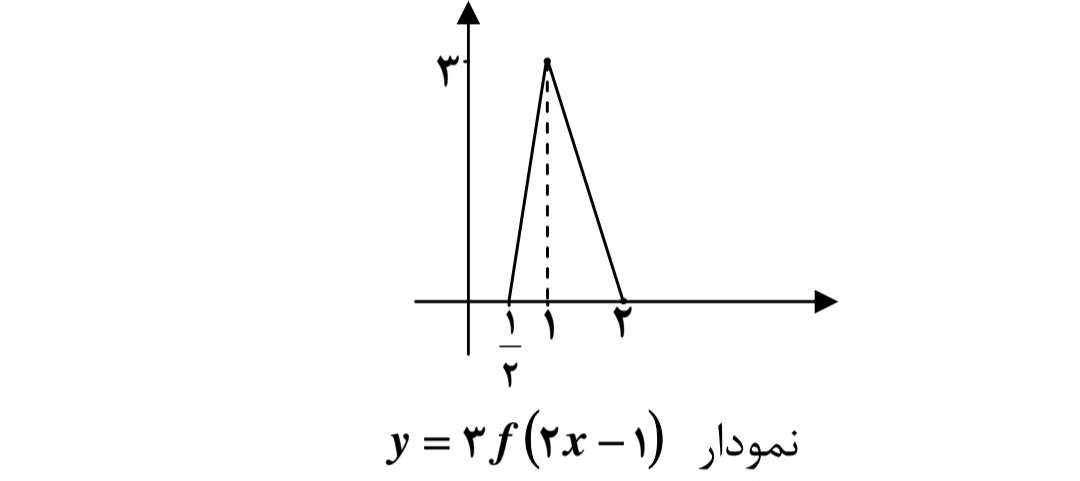
مرحله ي ج) انبساط نمودار \(y = f(2x)\) با ضريب 3 در امتداد محور y ها.
مرحله ی(د) انتقال \(y = 3f(2x - 1)\) به اندازه يك واحد در جهت محور y ها.
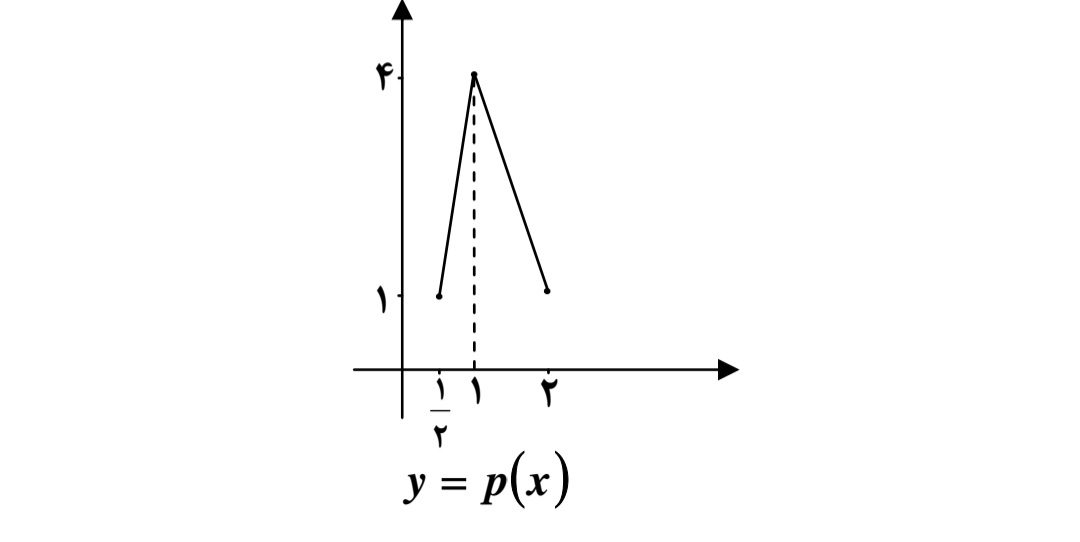
مثال
اگر نمودار تابع \(y = f(x)\) به شكل زير باشد.
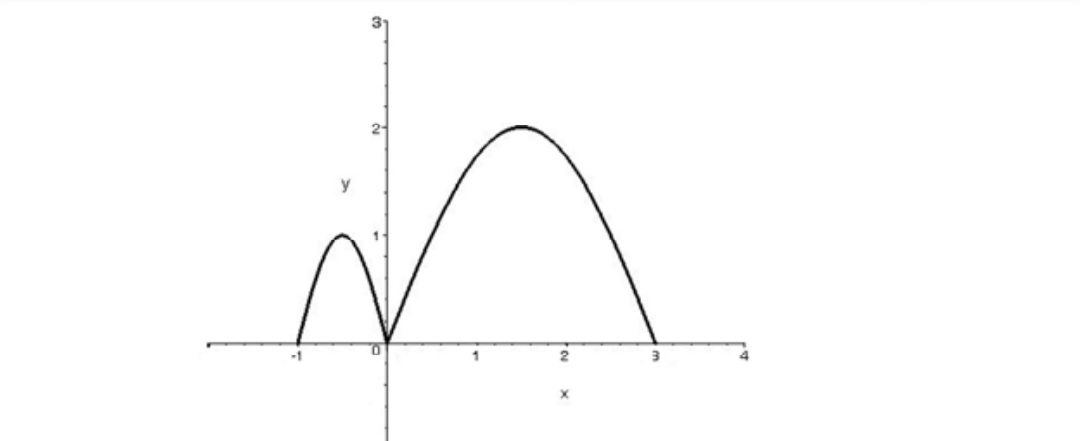
نمودار تابع \(y = f( - 2x)\) را رسم کنید مطابق دستورالعمل 5 و سپس 4 ابتدا نمودار تابع \(y = f(2x)\) را رسم می کنیم .
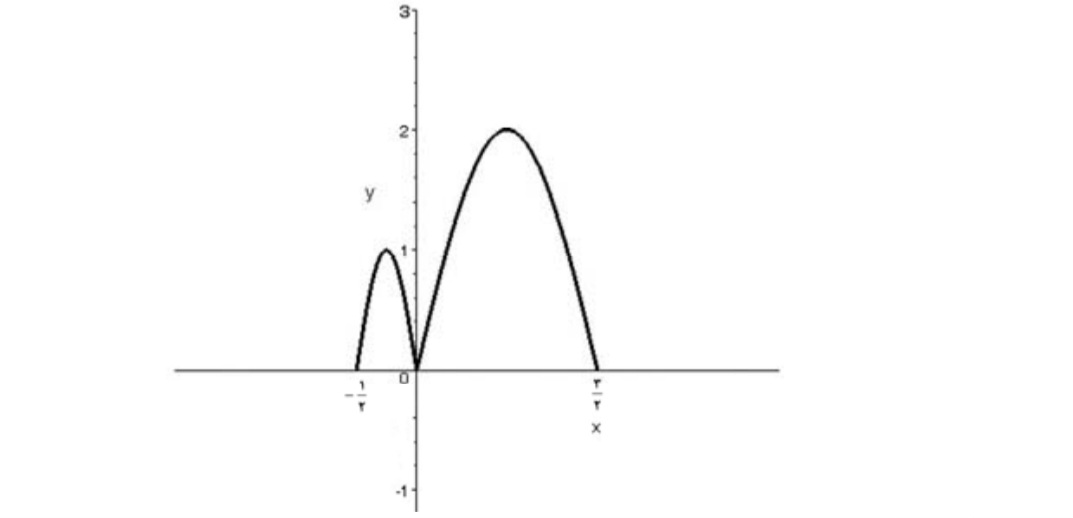
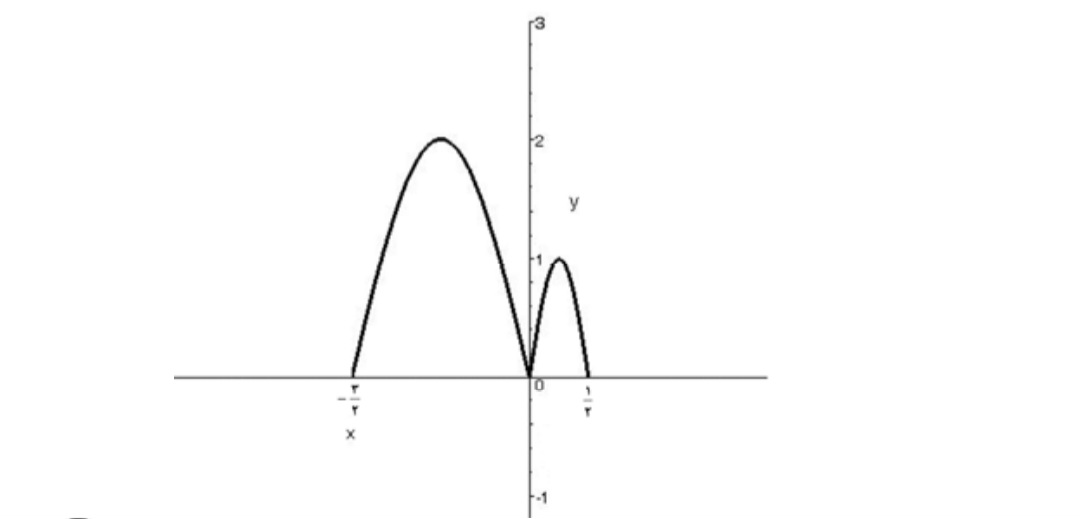
بنابراين نمودار \(y = f( - 2x)\) به صورت ميباشد:
مثال
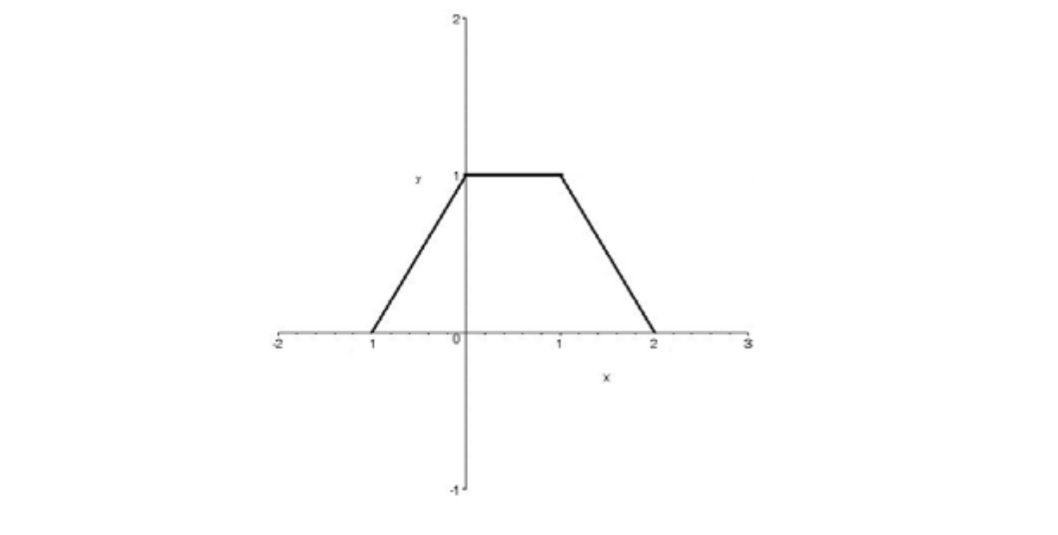
اگر نمودار تابع \(y = f(x)\) به صورت زير باشد نمودار توابع زير را رسم كنيد و دامنه ي آنها را مشخص كنيد.
الف) \(y = f(3x)\) ب) \(y = f( - 3x)\)
ج) \(y = f( - 3x + 1)\)
با توجه به دستورالعمل هاي گفته شده مراحل زير را خواهيم داشت.
الف)نمودار \(y = f(3x)\)
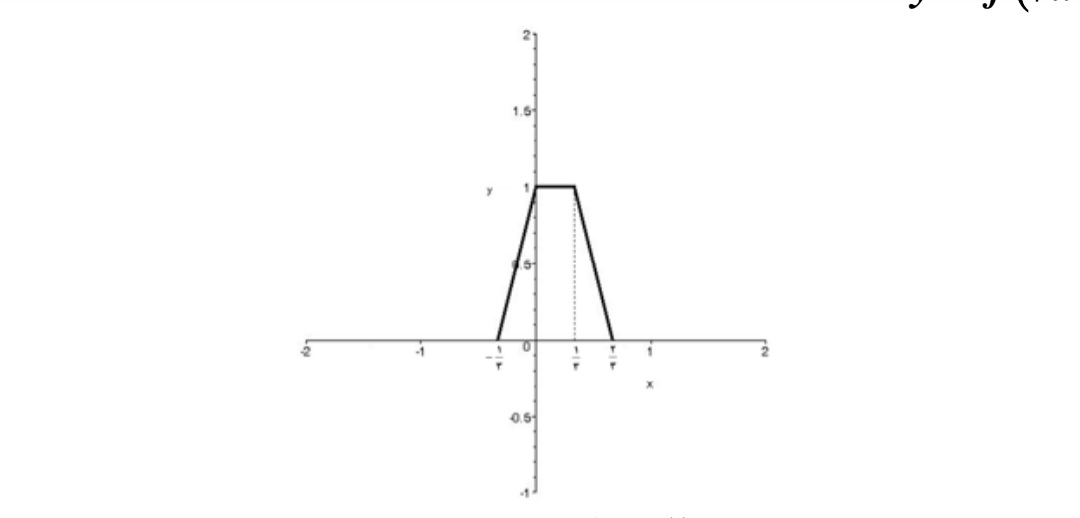
ب)نمودار \(y = f( - 3x)\)
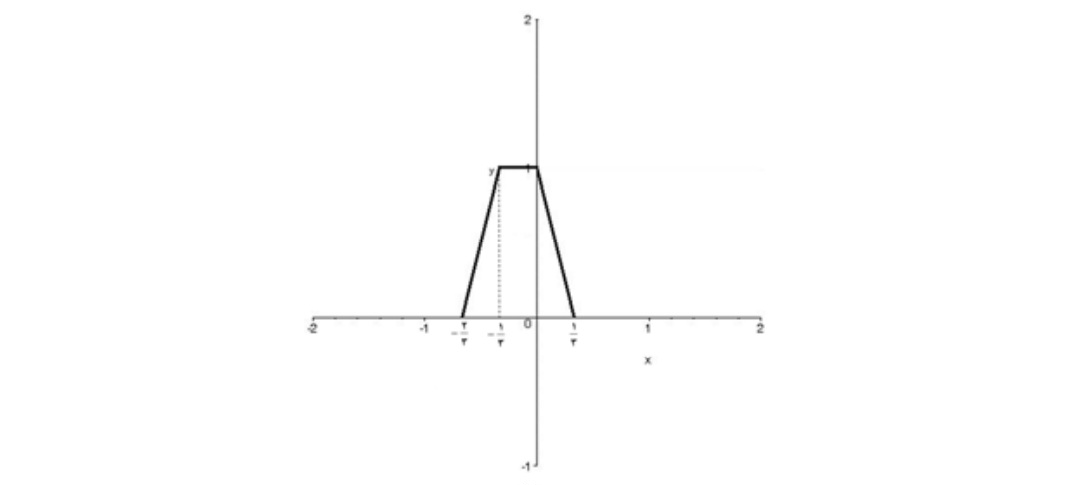
ج)نمودار \(y = f( - 3x + 1)\)
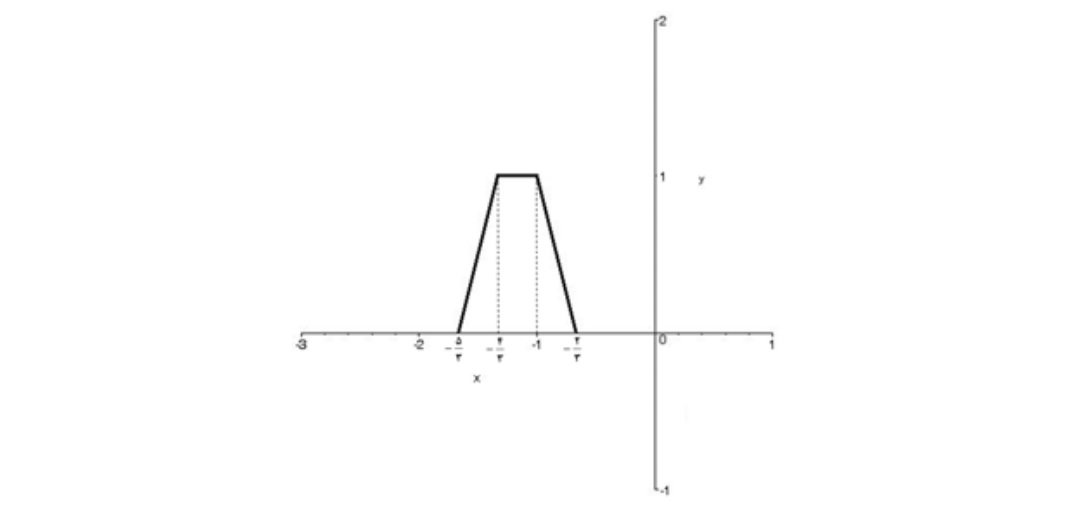
دامنه ي اين تابع با توجه به شكل بازه \(\left[ { - \frac{5}{3}, - \frac{2}{3}} \right]\) است.
تهیه کننده: حامد دلیجه
- آزمون آنلاین تمامی دروس پایه یازدهم
- گام به گام تمامی دروس پایه یازدهم
- ویدئو های آموزشی تمامی دروس پایه یازدهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه یازدهم
- فلش کارت های آماده دروس پایه یازدهم
- گنجینه ای جامع از انشاء های آماده پایه یازدهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه یازدهم
اعمال جبري روي توابع
فصل 2 : تابع
اعمال جبري روي توابع
برای دو تابع \(g,f\) تابع روی \(f + g\) تعریف میشود و براي هر مقدار x در \({D_f} \cap {D_g}\) داریم \((f + g)(x) = f(x) + g(x)\) به طور مشابه توابع \(f - g\) و \(f.g\) نيز روي داريم :\({D_f} \cap {D_g}\) داريم تعريف ميشود و به ازای هر \(x \in {D_f} \cap {D_g}\) داریم :
\(\begin{array}{l}(f - g)(x) = f(x) - g(x)\\\\(f.g)(x) = f(x).g(x)\end{array}\)
و تابع \(\frac{f}{g}\) نیز به ازاي \(x \in {D_f} \cap {D_g} - \left\{ {\left. x \right|} \right.g(x) = \left. 0 \right\}\) تعريف مي شود و به ازاي هرعددx در این مجموعه داريم:
\((\frac{f}{g})(x) = \frac{{f(x)}}{{g(x)}}\)
مثال
مدرسه علي تاكنون از دانش آموزان 2 مرحله آزمون گرفته است . در مرحله اول دروس مورد آزمون عبارتند از : حسابان، هندسه، فيزيك، شيمي، ادبيات و دروس آزمون مرحله دوم عبارتند از: حسابان، جبر و احتمال، فيزيك، ادبيات و زبان انگليسي . نمرات علي بر حسب درصد چنين است:
,85 )ادبيات) ,(79 ,شيمي) ,(68 , فيزيك) ,(56 , هندسه) ,(70 , حسابان )f= مرحله اول
,85)زبان انگليسي ) ,(79 ,ادبيات ) ,(68 ,فيزيك) ,(56 ,جبرواحتمال ) ,(74 ,حسابان)g =مرحله دوم
اگر تابع مربوط به اختلاف نمرات مرحله دوم از مرحله اول را بنويسيم اين تابع تنها براي دروسي با معني است كه در هر دو آزمون مورد سنجش واقع شده اند، يعني
(6-,ادبيات ) (0 , فيزيك ) ,( 4 , حسابان)=G-f
و با مشاهده اين تابع مشخص است كه وي در درس حسابان پيشرفت، در فيزيك بدون تغيير و در ادبيات دچار افت شده است.
مثال
فرض كنيد \(f(x) = 2x + 5\) و \(g = ( - 1,3),(0, - 5),(4,0),( - 2/5),(3,2)\) توابع \(\frac{g}{f},\frac{f}{g},f.g,g - f,f - g,f + g\) را مشخص كنيد. G
دامنه تابع f ، مجموعه ℜ و دامنه تابع g مجموعه \(\left\{ { - 1,0,4, - 2/5} \right.,\left. 3 \right\}\) است . لذا دامنه توابع \(f.g,g - f,f - g,f + g\) مجموعه حاصل از اشتراك اين دو مجموعه يعني مجموعه \(\left\{ { - 1,0,4, - 2/5} \right.,\left. 3 \right\}\) است همچنین \(f(0) = 5,f(4) = 13,f( - 2/5) = 0,f(3) = 11\) و بنابراين:
\(\begin{array}{l}f + g = ( - 1,6)\left( {0,0} \right)\left( {4,13} \right)\left( { - 2/5,1} \right)\left( {3,13} \right)\\\\f + g = ( - 1,0)\left( {0,10} \right)\left( {4,13} \right)\left( { - 2/5, - 1} \right)\left( {3,9} \right)\\\\f + g = ( - 1,0)\left( {0, - 10} \right)\left( {4, - 13} \right)\left( { - 2/5, - 1} \right)\left( {3, - 9} \right)\\\\f.g = ( - 1,0)\left( {0, - 25} \right)\left( {4,0} \right)\left( { - 2/5,0} \right)\left( {3,22} \right)\end{array}\)
همچنين دامنه تابع \(\frac{f}{g}\) مجموعه \(\left\{ { - 1,0,4, - 2/5,\left. 3 \right\}} \right.\) به جز اعضايي كه خروجي g به ازاي آنها صفر است؛ يعني عضو ،4 چون \(g(4) = 0\) لذا دامنه آن، مجموعه \(\left\{ { - 1,0, - 2/5,\left. 3 \right\}} \right.\)ميباشد. بنابراين:
\(\frac{f}{g} = \left\{ {( - 1,1)(0, - 1),( - 2/5,\left. {0)(3,\frac{{11}}{2})} \right\}} \right.\)
دامنه تابع \(\frac{g}{f}\) مجموعه \(\left\{ { - 1,0, - 2/5,\left. 3 \right\}} \right.\) به جز اعضايي كه خروجي f به ازاي آنها صفر است؛ يعني عضو \( - \frac{5}{2}\) ، چون \(f( - \frac{5}{2}) = 0\) لذا دامنه آن مجموعه \(\left\{ { - 1,0,4,\left. 3 \right\}} \right.\) بنابراين:
\(\frac{g}{f} = \left\{ ( \right. - 1,1)(0, - 1),( - 2/5,\left. {0)(3,\frac{{11}}{2})} \right\}\)
مثال
فرض كنيد \(f(x) = \sqrt {{x^2} - 4} \) و \(g(x) = \sqrt {\frac{{{x^2} + 2x}}{{2 - x}}} \) ضابطه و دامنه توابع \(\frac{g}{f},\frac{f}{g},f.g,g - f,f - g,f + g\) و را مشخص كنيد.
دامنه تابع f مجموعه \({d_f} = ( - \infty , - \left. 2 \right] \cup \left[ {2, + \infty )} \right.\) است و دامنه تابع g مجموعه \(dg = ( - \infty , - \left. 2 \right] \cup \left[ {0,2)} \right.\) است . بنابراين:
\(\begin{array}{l}(f + g)(x) = f(x) + g(x) = \sqrt {{x^2} - 4} + \sqrt {\frac{{{x^2} + 2x}}{{2 - x}},} {D_{f + g}} = ( - \infty ,2)\\\\(f - g)(x) = f(x) - g(x) = \sqrt {{x^2} - 4} + \sqrt {\frac{{{x^2} + 2x}}{{2 - x}},} {D_{f - g}} = ( - \infty ,2)\\\\(f.g)(x) = f(x).g(x) = \sqrt {{x^2} - 4} .\sqrt {\frac{{{x^2} + 2x}}{{2 - x}},} {D_{f.g}} = ( - \infty ,2)\end{array}\)
اين تابع با تابع \(h(x) = \left| {x + 2} \right|\sqrt { - x} \) كه به دامنه [2 − , ∞ −) تحديد (محدود) شده باشد برابر است ( . واضح است بدون تحديد دو تابع برابر نيستند ).
تابع g به ازاي \(x = 0\) و \(x = - 2\) صفر خواهد شد لذا تابع \(\frac{f}{g}\) عبارتست از :
\(\left( {\frac{f}{g}} \right)(x) = \frac{{f(x)}}{{g(x)}} = \frac{{\sqrt {{x^2} - 4} }}{{\frac{{\sqrt {{x^2} + 2x} }}{{2 - x}}}},{D_{\frac{f}{g}}} = ( - \infty , - 2)\)
اين تابع با تابع \(h(x) = \frac{{\left| {x - 2} \right|}}{{\sqrt { - x} }}\) وقتي كه دامنه آن به مجموعه \(( - \infty , - 2)\) تحديد شده باشد برابر است.
همچنين تابع g به ازاي \(x = 2\) و \(x = - 2\) صفر خواهد شد لذا
\(\left( {\frac{g}{f}} \right)(x) = \frac{{g(x)}}{{f(x)}} = \frac{{\frac{{\sqrt {{x^2} + 2x} }}{{2 - x}}}}{{\sqrt {x - 4} }},{D_{\frac{g}{f}}} = ( - \infty , - 2)\)
و اين تابع با تابع \(m(x) = \frac{{\sqrt { - x} }}{{\left| {x - 2} \right|}}\) ، وقتي دامنه آن به مجموعه \(( - \infty , - 2)\) تحديد شده باشد برابر x است.
مثال
اگر نمودار توابع f و g به صورت زير باشد، نمودار توابع \(f + g\) و \(f - g\) و \(f.g\) را رسم كنيد.
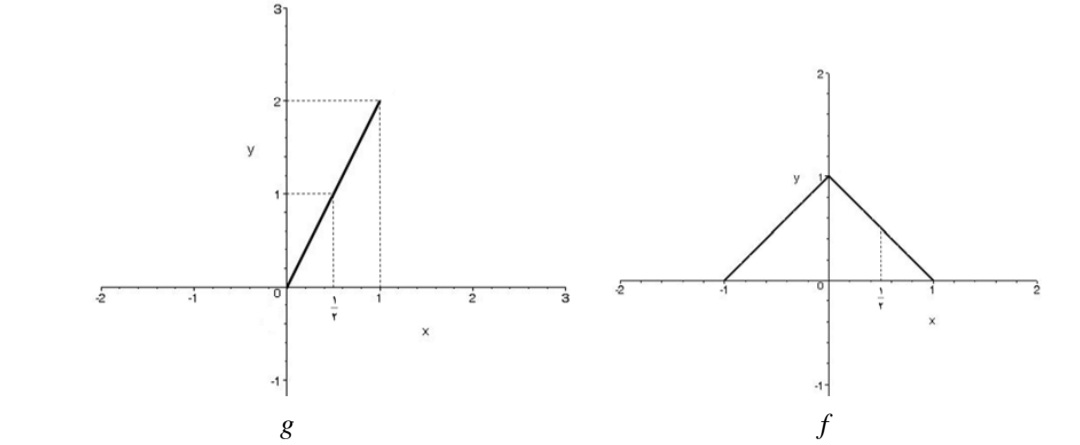
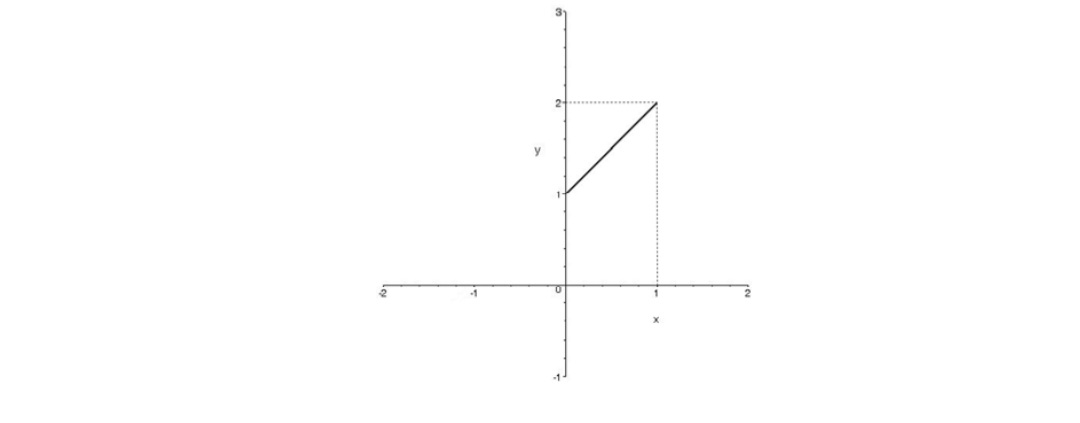
با توجه به شكل تابع f در فاصله [ 11 , 1−] تعريف شده است و تابع g در \(\left[ {0,\infty } \right]\) . لذا توابع \(f + g\) و \(f - g\) و \(f.g\) در فاصله [ 10 ,0 ] تعريف شده اند.
براي رسم \(f + g\) كافي است \((f + g)(x)\) را به ازاي هر مقدار \(0 \le x \le 1\) را محاسبه كنيم يعني مقادير f و g را در هر يك محاسبه نمود و با هم جمع كرد . مثلا:
\(\begin{array}{l}(f + g)(0) = f(0) + g(0) = 1 + 0 = 1\\\\(f + g)(1) = f(1) + g(1) = 0 + 2 = 2\\\\(f + g)(\frac{1}{2}) = f(\frac{1}{2}) + g(\frac{1}{2}) = \frac{1}{2} + 1 = \frac{3}{2}\end{array}\)
لذا شكل \(g + f\) به طور تقريبي چنين خواهد بود.
به طور مشابه مقادير \(f - g\) را به ازاي هر \(0 \le x \le 1\) از تفاضل مقدار تابع g از f وf.g را به ازاي هر \(0 \le x \le 1\) از ضرب مقادير توابع f و g به دست ميآوريم . نمودارهاي تقريبي به صورت زير است:
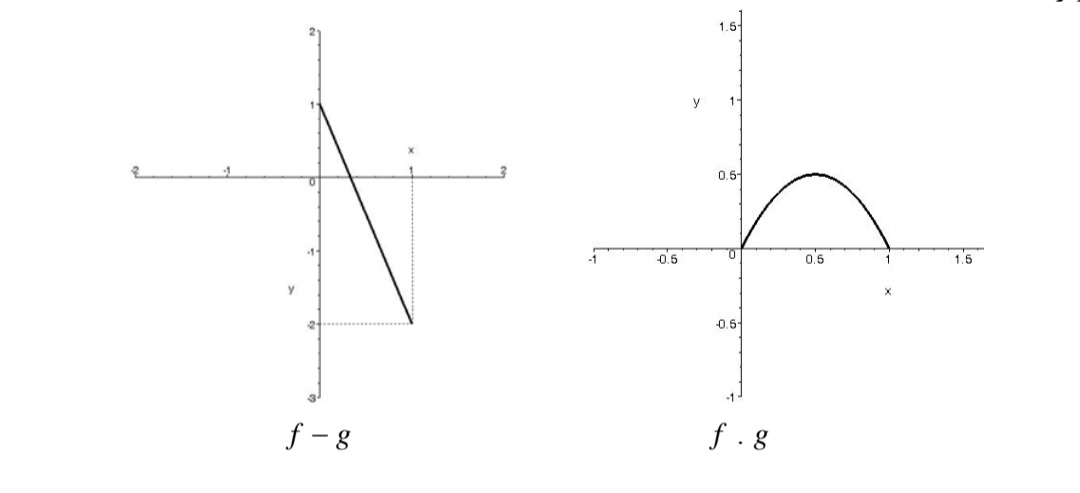
تهیه کننده: حامد دلیجه
ترکیب توابع
فصل 2 : تابع
تركيب توابع
اگر f و g دو تابع باشند، تابع fog تابعي است كه از تركيب دو تابع بوجود ميآيد كه اعضاي آن زوج مرتب هايي از \((x,y)\) هستند كه x در دامنه g قرار دارد و \(g(x)\) هم در دامنه f ميباشد و y مقدار تابع f به ازاي \(g(x)\) ميباشد . يعني:

به عبارت ديگر
مثال
توابع f و g به صورت :\(\begin{array}{l}g = \left\{ {(1,3),(3,5),(5,7),(7,1\left. ) \right\}} \right.\\\\f = \left\{ {(1,2)(2,3)(3,4)(4,5)(6,7\left. ) \right\}} \right.\end{array}\)تعريف شده اند. مطلوب است تعيين توابع fog و gof
براي تعيين تابع fog دقت ميكنيم كه اعضاي دامنه تابع fog اعضايي از دامنه تابع g ميباشد كه در دامنه f قرار داشته باشد . داريم:
\(\left. \begin{array}{l}1 \in {D_f},f(1) = 2,2 \notin {D_g} \to 1 \notin {D_{fog}}\\\\2 \in {D_f},f(2) = 3,3 \notin {D_g} \to 2 \notin {D_{fog}}\\\\3 \in {D_f},f(3) = 4,4 \notin {D_g} \to 3 \notin {D_{fog}}\\\\4 \in {D_f},f(4) = 5,5 \notin {D_g} \to 4 \notin {D_{fog}}\\\\6 \in {D_f},f(6) = 7,7 \notin {D_g} \to 6 \notin {D_{fog}}\end{array} \right\} \Rightarrow {D_{fog}} = \left\{ {2,4,\left. 6 \right\}} \right.\)
و لذا
\(\left. \begin{array}{l}gof(2) = g(f(2)) = g(3) = 5\\\\gof(4) = g(f(4)) = g(5) = 7\\\\gof(6) = g(f(6)) = g(7) = 1\end{array} \right\} \Rightarrow gof = \left\{ {\left( {2,5} \right)} \right.,(4,7),(6,1\left. ) \right\}\)
مثال
فرض كنيد \(g(x) = \sqrt x + 1\) و \(f = \left\{ {\left( { - 2,0} \right)} \right.,(0,1),(1,4\left. {),\left( {2. - 5} \right)} \right\}\)مطلوب است توابع fogو gof
تعيين تابع :fog
دامنه آن اعضايي از دامنه \(\left\{ {\left. x \right|} \right.x \ge \left. 0 \right\}\),g ميباشد كه:
\(\begin{array}{l}g(x) \in {D_f} = \left\{ { - 2} \right.,0,1,\left. 2 \right\}\\\\g(x) = - 2 = \sqrt x + 1 \Rightarrow \sqrt x = - 3\\\\g(x) = 0 \Rightarrow \sqrt x + 1 = 0 \Rightarrow \sqrt x = - 1\\\\g(x) = 1 \Rightarrow \sqrt x + 1 = 1 \Rightarrow \sqrt x = 0 \Rightarrow x = 0\\\\g(x) = 2 \Rightarrow \sqrt x + 1 = 2 \Rightarrow \sqrt x = 1 \Rightarrow x = 1\end{array}\)
دومی غیر ممکن
سومی ممکن
پس از اعضاي دامنه تابع g تنها دو عضو 0 و 1 در دامنه تابع fog وجود دارند و داريم.
\(\begin{array}{l}fog(0) = (f(0)) = f(1) = 4\\\\fog(1) = (f(1)) = f(2) = - 5\end{array}\)
يعني:
\(fog(1) = \left\{ {(0,4),(1, - \left. {5)} \right\}} \right.\)
تعيين تابع: gof
دامنه آن اعضايي از دامنه تابع f ، \(\left\{ { - 2,0,1,\left. 2 \right\}} \right.\) هستند كه \(f(x) \in {D_g} = \left\{ {\left. x \right|} \right.x \ge \left. 0 \right\}\) اما:
\(\begin{array}{l}gof( - 2) = 0,0 \in {D_g} \Rightarrow - 2 \in {D_{fog}}\\\\gof(0) = 1,1 \in {D_g} \Rightarrow 0 \in {D_{fog}}\\\\gof(1) = 4,4 \in {D_g} \Rightarrow 1 \in {D_{fog}}\\\\gof( - 5) = 0, - 5 \in {D_g} \Rightarrow 2 \notin {D_{fog}}\end{array}\)
پس از اعضاي دامنه تابع f تنها سه عضو 2- ، 0 و 1 در دامنه تابع gof حضور دارند و داريم.
\(\begin{array}{l}g( - 2) = 0,0 \in {D_g} \Rightarrow - 2 \in {D_{fog}}\\\\g(0) = g(f(0)) = g(1) = 2\\\\g( - 5) = g(f(1)) = g(1) = 3\end{array}\)
يعني
\(gof = \left\{ {\left( { - 2,1} \right)} \right.,(0,2),(1,3\left. ) \right\}\)
مثال
فرض كنيد \(f(x) = \frac{1}{x}\) و \(g(x) = \sqrt {1 - {x^2}} \) مطلوب است تعيين دامنه و برد توابع fog و . gof
تعيين تابع :fog
دامنه تابع g مجموعه \({D_g} = \left\{ {\left. x \right|} \right. - 1 \le x \le \left. 1 \right\}\) است اماg(x) باید در دامنه تابعf باشدو \({D_f} = \left\{ {\left. x \right|} \right.x \ne \left. 0 \right\}\) پسg(x) نبايد صفر شود. اما g(x)در 1- و 1 صفر ميشود . پس \({D_{fog}} = \left\{ {\left. x \right|} \right. - 1 < x < \left. 1 \right\}\) و به ازای این xها داريم \(fog(x) = f(g(x)) = f(\sqrt {1 - {x^2}} ) = \frac{1}{{\sqrt {1 - {x^2}} }}\) تعيين تابع
دامنه تابع gof عضوهايي از مجموعه \(\left\{ {\left. x \right|} \right.x \ne \left. 1 \right\}\) ميباشد كه \(f(x) \in {D_g}\) باشد يعني \( - 1 \le f(x) \le 1\) یا \( - 1 \le \frac{1}{x} \le 1\) یعنی .\({D_{fog}} = ( - \infty , - \left. 1 \right] \cup \left[ {1, + \infty )} \right.\) پس با در نظر گرفتن هر دو شرط، دامنه gof مجموعه \({D_{fog}} = ( - \infty , - \left. 1 \right] \cup \left[ {1, + \infty )} \right.\) ميباشد و به ازاي اين x ها داريم:
\({D_{fog}} = g(f(x)) = g(\frac{1}{x}) = \sqrt {1 - {{(\frac{1}{x})}^2}} \)
مثال
فرض كنيد \(f(x) = \frac{x}{{2 - x}}\) مطلوب است تعيين دامنه و برد تابع fof
دامنه تابع f مجموعه \(R - \left\{ 2 \right\}\) است . بنابراين
\({D_{fof}} = \left\{ {\left. {x \in {D_f}} \right|} \right.f(x) \in \left. {{D_f}} \right\} = \left\{ {\left. {x \ne 2} \right|} \right.\frac{x}{{2 - x}} \ne \left. 2 \right\}\)
اما
\(\frac{x}{{2 - x}} = 2 \Rightarrow x = 4 - 2x \Rightarrow x = \frac{4}{3}\)
لذا
\({D_{fof}} = \left\{ {x \ne 2,x \ne \left. {\frac{4}{3}} \right\} = ( - \infty ,\frac{4}{3}) \cup } \right.(\frac{4}{3},2) \cup (2, + \infty )\)
همچنين
\(fof(x) = f(f(x)) = f\left( {\frac{x}{{2 - x}}} \right) = \frac{{\frac{x}{{2 - x}}}}{{2 - \frac{x}{{2 - x}}}}\)
توجه كنيد كه اگر اين ضابطه را ساده كنيم حتماً بايد شرط دامنه را قيد كنيم در غير اين صورت تابع حاصل با تابع fof برابر نخواهد بود.
\(fof(x) = \frac{x}{{4 - 3x}},x \ne \frac{4}{3},2\)
البته شرط \(x \ne \frac{4}{3}\) از ضابطه واضح است اما شرط \(x \ne 2\) حتماً بايد قيد شود.
مثال
در پرتاب جسم با سرعت اوليه \({v_0}\) در راستای قائم جسم بر حسب زمان از رابطه ی \(h(t) = \frac{1}{2}g{t^2} + {v_0}t\)\(\) به دست ميآيد كه در آن g ثابت و شتاب ثقل ميباشد . همچنين سرعت جسم بر حسب t از رابطه \(v(t) = {v_0} + gt\) به دست ميآيد. تابع ارتفاع جسم را برحسب متغير v (سرعت جسم) بيابيد.
داريم
\(v = {v_0} + gt \Rightarrow t = \frac{{v - {v_0}}}{g} = t(v) = \frac{{v - {v_0}}}{g}\)
حال از تركيب توابع \(h(t)\) و \(t(v)\) به تابع \(h(t(v))\) ميرسيم . بنابراين:
\(h(t(v)) = \frac{1}{2}g{(\frac{{v - {v_0}}}{g})^2} + {v_0}(\frac{{v - {v_0}}}{g}) \Rightarrow h(t(v)) = \frac{{{v^2} - {v_0}^2}}{{2g}}\)
\(\)
مثال
دامنه تابع \(h(x) = \sqrt {\sqrt {3x - 4} - 6x + 8} \) را بيابيد.
اگر قرار دهيم \(g(x) = 3x - 4\) و \(f(x) = \sqrt {\sqrt x - 2x} \) آنگاه \(h = fog\) و داريم \({D_f} = \left[ {0,\frac{1}{4}} \right]\)
پس
\(\begin{array}{l}{D_h} = {D_{fog}}\left\{ {x\left. { \in {D_g}} \right\}f(x) \in D\left. {_f} \right\}} \right. = \left\{ {x\left. { \in R} \right\}0 \le x \le \left. {\frac{1}{4}} \right\} = \left[ {0,\frac{1}{4}} \right]} \right.\\\end{array}\)
مثال
اگر\(f(x) = \left\{ \begin{array}{l}{x^2},x < 1\\x + 1,x \ge 1\end{array} \right.\) و \(g(x) = \left\{ \begin{array}{l} - 5x,x \le 0\\1,x > 0\end{array} \right.\) ضابطه تابع fog را بيابيد.
توجه كنيد كه x ابتدا به تابع g رفته و خروجي آن وارد تابع f ميشود . حال اگر \(x > 0\) را بعنوان ورودي تابع g در نظر بگيريم خروجي آن عدد 1 ميباشد حال 1 ورودي f را تشكيل ميدهد كه خروجي f به ازاي \(x = 1\) برابر \(1 + 1 = 2\)ميباشد . اين مطلب را چنين نمايش ميدهيم:
\(x > 0 \to 11 + 1 = 2\)
حال اگر \(x \le 0\) ورودي تابع g باشد خروجي آن-5x است . اگر \( - 5x < 1\) باشد، خروجي تابع f ، \(( - 5{x^2}) = 25{x^2}\) است و اگر \( - 5x \ge 1\) باشد خروجي تابع f ، \( - 5x + 1\) است يعني
\(\begin{array}{l}x \le 0 \to - \frac{1}{5} < x \le 0 - 5x{( - 5x)^2} = 25{x^2}\\\\x \le 0 \to x \le - \frac{1}{5} - 5x - 5x + 1\\\\ \Rightarrow fog(x) = \left\{ \begin{array}{l} - 5x + 1,x \le - \frac{1}{5}\\\\25{x^2}, - \frac{1}{5} < x \le 0\\\\2,x > 0\end{array} \right.\\\end{array}\)
مثال
اگر ، تابع \(f(x) = \sqrt x + 1\) و \(fog(x) = \sqrt {{x^2} - 1} + 1\) تابع \(g(x)\) را بيابيد.
داريم
\(\begin{array}{l}f(x) = \sqrt x + 1 \Rightarrow f(g(x)) = \sqrt {g\left( x \right)} + 1\\\\fog(x) = f(g(x)) = \sqrt {{x^2} - 1} + 1\end{array}\)
لذا
\(\sqrt {g\left( x \right)} + 1 = \sqrt {{x^2} - 1} + 1\)
و در نتيجه
\(\sqrt {g\left( x \right)} = \sqrt {{x^2} - 1} \)
يا
\(g(x) = {x^2} - 1\)
اگر
\(\begin{array}{l}fog(x) = f(g(x)) = \sqrt {{{\sin }^4}x + 2{{\sin }^2}x + 2} = \\\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\sqrt {\left( {{{\sin }^2}x + 1} \right)} = \sqrt {{g^2}(x) + 1} \end{array}\)
حالا با قرار دادن x به جاي g(x)در تساوي ها داريم
\(f(x) = \sqrt {{x^2} + 1} \)
تهیه کننده: حامد دلیجه
مجموعه های متقارن
فصل 2 : تابع
مجموعه هاي متقارن
مجموعه ي \(A \subseteq R\) را متقارن گوييم هر گاه به ازاي هر \(x \in A\) داشته باشيم \( - x \in A\)
مثال
مجموعه ي \(A = \left\{ { - 3, - 2, - 1,0,1,\left. 2 \right\}} \right.\) متقارن نيست، زيرا \( - 3 \in A\) ولي \(3 \notin A\)
مثال
مجموعه ي \(A = \left\{ { - 1,\left. 2 \right\}} \right.\) متقارن نيست، زيرا\(2 \in A\) ولي \( - 2 \notin A\)
مثال
مجموعه ي مثال:مجموعه ی \(A = \left\{ { - 2,\left. 2 \right\}} \right.\) متقارن است زيرا هر عضوي از A انتخاب كنيم قرينه ي آن عضو نيز در A وجود دارد.
مثال
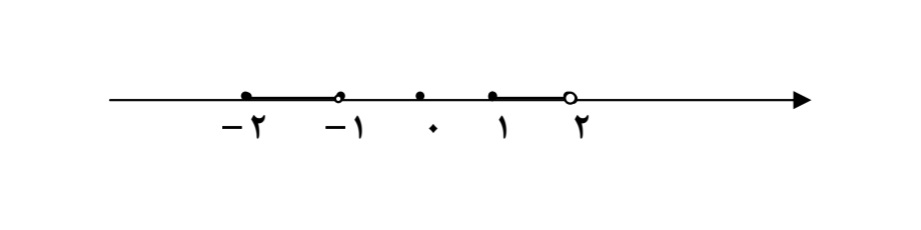
مجموعه ي A كه به صورت زير، روي محور نمايش داده شده، متقارن نيست، زيرا\( - 2 \in A\) و \(2 \notin A\)
توابع زوج و فرد
تابع f با دامنه يي متقارن را زوج گو يم، هر گاه به ازاي هر \(x \in {D_f}\) ، تساوي \(f( - x) = - f(x)\) برقرار باشد.
تابع f با دامنه يي متقارن را فرد گو يم، هر گاه به ازاي هر
\(x \in {D_f}\) تساوي \(f( - x) = - f(x)\) برقرار باشد.
مثال
زوج يا فرد بودن تابع \(f = \left\{ {\left( { - 3, - 1} \right)} \right.,(2,3),( - 2,3\left. {),\left( {3,1} \right)} \right\}\) را بررسي كنيد.
چون \({D_f} = \left\{ { - 3, - 3,2,\left. 3 \right\}} \right.\) ، لذا دامنه f متقارن است \(f( - 3) = - f(3)\) ولي \(f( - 2) = f(2)\) بنابراين تابع f نه زوج است و نه فرد.
مثال
زوج يا فرد بودن تابع \(f(x) = \frac{{x + 1}}{{x - 3}}\) را بررسي كنيد.
داريم \({D_f} = R - 3\) و \( - 3 \in {D_f}\) ولي \(3 \notin {D_f}\) ، پس دامنه تابع f متقارن نيست. بنابراين تابع f نه زوج است نه فرد.
مثال
زوج يا فرد بودن تابع \(f(x) = \frac{{{x^2} - \left| x \right|}}{{{x^2} + 1}}\) را بررسي كنيد.
داريم \({D_f} = R\) و لذا دامنه f متقارن است و
\(f( - x) = \frac{{( - {x^2}) - \left| x \right|}}{{({x^2}) + 1}} = \frac{{{x^2} - \left| x \right|}}{{{x^2} + 1}} = f(x)\)
بنابراين f تابعي زوج است.
مثال
زوج يا فرد بودن تابع \(f(x) = \log (x + \sqrt {{x^2} + 1} )\) رابررسی کنید
باتوجه به \({x^2} + 1 \ge 1\) و اين كه \(x + \sqrt {{x^2} + 1} > 0 \Rightarrow \sqrt {{x^2} + 1} \ge - x\) همواره برقرار است
11 دامنه ي f برابر ℜ است و لذا متقارن است و
\(\begin{array}{l}f( - x) = \log ( - x + \sqrt {({x^2}) + 1} = \log (\frac{{(\sqrt {{x^2} + 1} - x)(\sqrt {{x^2} + 1} + x)}}{{\sqrt {{x^2} + 1} + x}}\\\\ = \log \frac{1}{{\sqrt {{x^2} + 1} - x}} = \log 1 - \log (\sqrt {{x^2} + 1} + x) = - f(x)\end{array}\)
بنابراين f تابعي فرد است.
مثال
زوج يا فرد بودن تابع \(f(x) = \left\{ \begin{array}{l}{x^4} - 2x,x \ge 0\\\\{x^4} + 2x,x < 0\end{array} \right.\) را بررسي كنيد.
\({D_f} = R\) و لذا دامنه f متقارن است.
حالت اول: \(x = 0 \to f(0) = 0\)
حالت دوم: اگر x<0آنگاه –x>0 و داريم:
\(f( - x) = \left( { - {x^4}} \right) + 2\left( { - x} \right) = {x^4} - 2x = f(x)\)
بنابراين f تابعي زوج است.
مثال
زوج يا فرد بودن تابع \(f(x) = \sin x + \cos x\) را بررسي كنيد.
:\({D_f} = R\) و لذا دامنه f متقارن است و
\(f( - x) = \sin ( - x) + \cos ( - x) = - \sin x + \cos x\)
واضح است که \(f( - x) \ne f(x)\) و \(f( - x) \ne - f(x)\) پس تابع نه زوج است نه فرد.
مثال
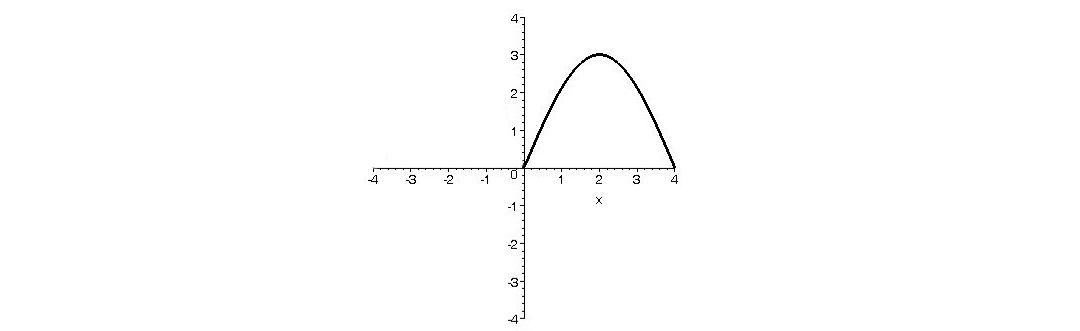
قسمتي از نمودار تابع f با دامنه ي \(\left[ { - 4,4} \right]\) به صورت
رسم شده است، نمودار تابع را طوري كامل كنيد تا:
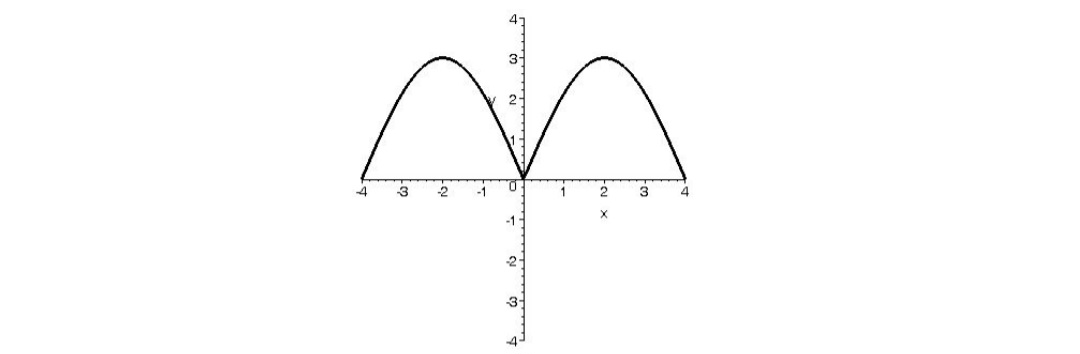
الف) f تابعي زوج را نمايش دهد.
ب) f تابعي فرد را نمايش دهد.
الف) ميدانيم نمودار تابع زوج نسبت به محور y ها متقارن است. پس لازم است نمودار f به صورت مقابل باشد.
ب) ميدانيم نمودار تابع فرد نسبت به مبدأ مختصات متقارن است. پس لازم است نمودار f به صورت مقابل باشد.
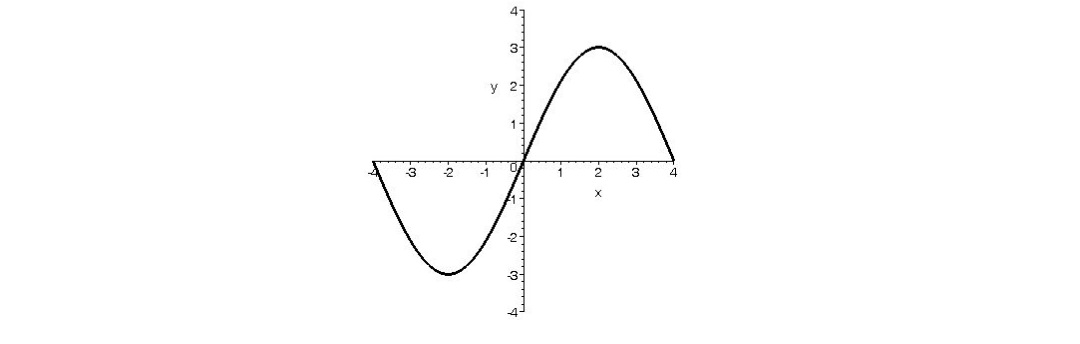
مثال
ثابت كنيد تنها تابعي كه هم زوج است و هم فرد، تابع ثابت صفر با دامنه ي متقارن است.
فرض كنيم f تابعي با دامنهي متقارن باشد، آنگاه به ازاي هر \(x \in {D_f}\) داريم:
تابعی زوج است
\(\left. \begin{array}{l}f \Rightarrow f( - x) = f(x)\\f \Rightarrow f( - x) = - f(x)\end{array} \right\} \Rightarrow f(x) = - f(x) \Rightarrow f(x) = 0\)
تابعی فرد است
مثال
تابع f با ضابطه ي \(f(x) = c{x^3} + {(a - 3)^2} - 2bx + b + 4\) داده شده است.
الف) به ازاي چه مقاديري از a و b تابع f زوج است.
ب) به ازاي چه مقاديري از a و b تابع f فرد است.
واضح است كه \({D_f} = R\)
الف)
\(\begin{array}{l}f( - x) = f(x) \Rightarrow - c{x^3} + (a\_3){x^2} + bx + b + 4 = cx + (a\_3) - 2bx + b + 4\\\\ \Rightarrow \left\{ \begin{array}{l}c = - c\\\\2b = - 2b\\\\a - 3 = a - 3\end{array} \right. \Rightarrow \left\{ \begin{array}{l}c = 0\\\\b = 0\\\\a \in R\end{array} \right.\end{array}\)
براي زوج بودن تابع چند جملهاي f لازم است تنها جملات با درجه ي زوج وجود داشته باشند.
ب(
\(\begin{array}{l}f( - x) = - f(x) \Rightarrow - c{x^3} + (a\_3){x^2} + 2bx + b + 4 = cx - (a\_3){x^2} + 2bx - b - 4\\\\ \Rightarrow \left\{ \begin{array}{l}a - 3 = - (a - 3)\\\\b + 4 = - b + 4\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a = 3\\\\b = - 4\end{array} \right.\end{array}\)
براي فرد بودن تابع چند جمله ای f ، لازم است در ضابطه ی آن تنها جملات با درجه ی فرد وجود داشته باشند.
مثال
اگر f و g هر دو فرد باشند، زوج يا فرد بودن تابع \(\frac{f}{g}\) را بررسي كنيد.
\(\begin{array}{l}x \in {D_{\frac{f}{g}}} \Rightarrow x \in {D_f} \cap {D_g}:g(x) \in {D_{\frac{f}{g}}}\\\left. \begin{array}{l}x \in {D_f} \Rightarrow - x \in {D_f}\\\\x \in {D_g} \Rightarrow - x \in {D_g}\end{array} \right\} \Rightarrow - x \in {D_f} \cap {D_g},g( - x) = - g(x) \ne 0 \Rightarrow - x \in {D_{\frac{f}{g}}}\\\end{array}\)
بنابراين دامنه تابع \(\frac{f}{g}\) متقارن است و داريم:
\(\frac{f}{g}( - x) = \frac{{f( - x)}}{{g( - x)}} = \frac{{ - f( - x)}}{{ - g( - x)}} = \frac{f}{g}(x)\)
پس تابع \(\frac{f}{g}\) تابع زوج است.
- آزمون آنلاین تمامی دروس پایه یازدهم
- گام به گام تمامی دروس پایه یازدهم
- ویدئو های آموزشی تمامی دروس پایه یازدهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه یازدهم
- فلش کارت های آماده دروس پایه یازدهم
- گنجینه ای جامع از انشاء های آماده پایه یازدهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه یازدهم
توابع صعودی و نزولی
فصل 2 : تابع
توابع صعودي و توابع نزولي
اگر براي هر \({x_2} \in {D_f}\) , كه \({x_1} < {x_2}\) بتوان نتيجه گرفت \(f({x_1}) \le f({x_2})\) ، آنگاه تابع f را صعودي گوييم
اگر براي هر \({x_2} \in {D_f}\) , كه \({x_1} < {x_2}\) بتوان نتيجه گرفت
\(f({x_1}) < f({x_2})\)
و بالعكس، آنگاه تابع f را صعودي اكيد گوييم.
اگر براي هر \({x_2} \in {D_f}\) , كه \({x_1} < {x_2}\) بتوان نتيجه گرفت \(f({x_1}) \ge f({x_2})\) ، آنگاه تابع f را نزولي گوييم
اگر براي هر \({x_2} \in {D_f}\) , كه \({x_1} < {x_2}\) بتوان نتيجه گرفت \(f({x_1}) > f({x_2})\) ، آنگاه تابع f را نزولي اكيد گوييم.
مثال
صعودي يا نزولي بودن هر يك از توابع زير را روي دامنه تعريفشان بررسي كنيد.
الف)
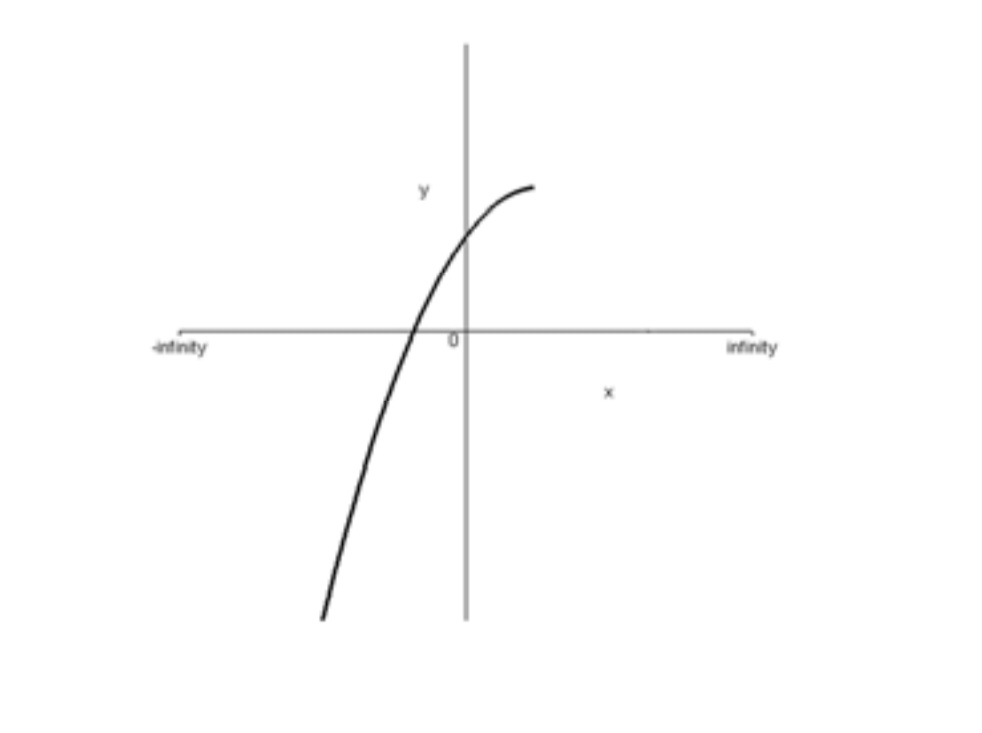
الف) به ازاي هر \({x_2}\) و\({x_1}\) که \({x_1} < {x_2}\) داریم \(f({x_1}) < f({x_2})\) یعنی در واقع با زیاد شدن مقادير x ، مقادير y نيز زياد ميشود. پس تابع صعودي اكيد است.
ب)
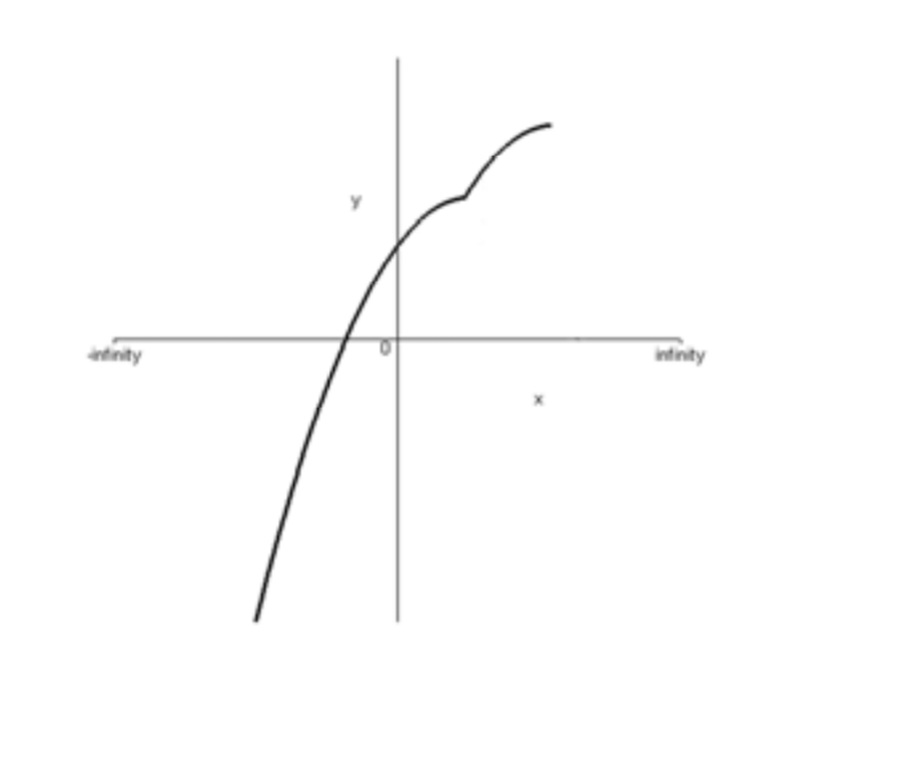
ب) به ازاي هر\({x_2}\) و \({x_1}\) كه \({x_1} < {x_2}\) داريم.\(f({x_1}) \le f({x_2})\) يعني در واقع با زياد شدن مقادير x ، مقادير y زياد ميشود يا ثابت ميماند. پس تابع صعودي است.
ج)
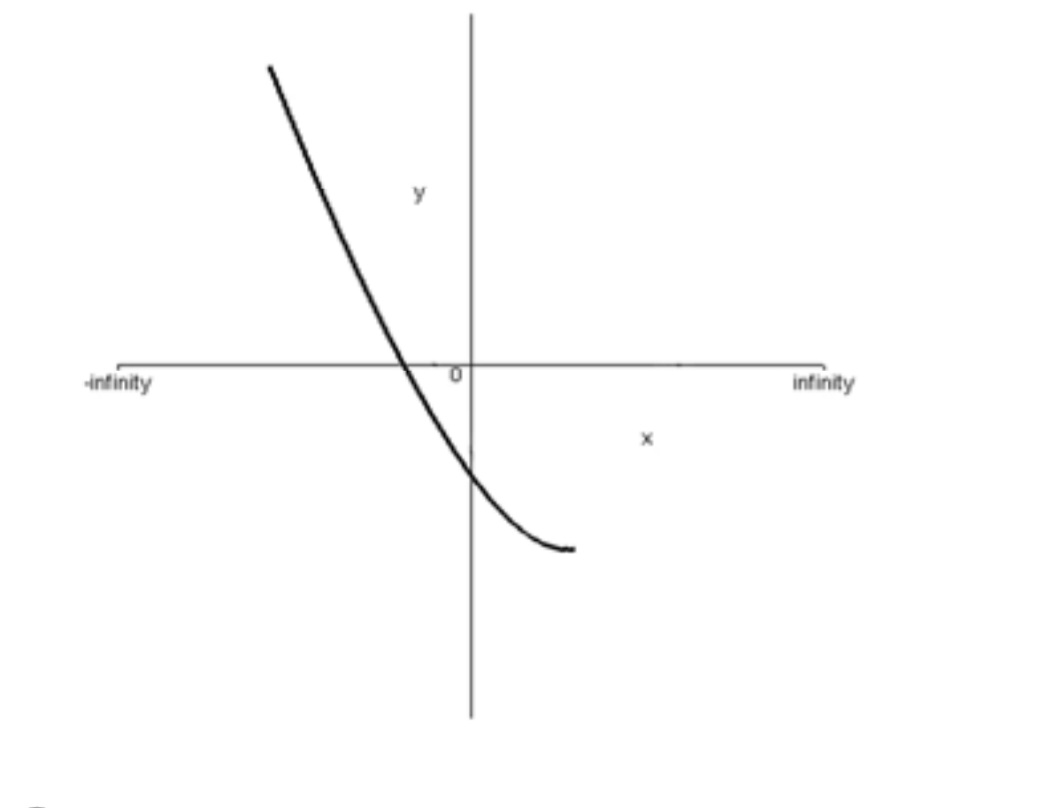
ج) به ازاي هر \({x_2}\) و \({x_1}\) كه \({x_1} < {x_2}\) داريم \(f({x_1}) > f({x_2})\) يعني در واقع با زياد شدن مقادير x ، مقادير y كم ميشود. پس تابع نزولي اكيد است.
د)
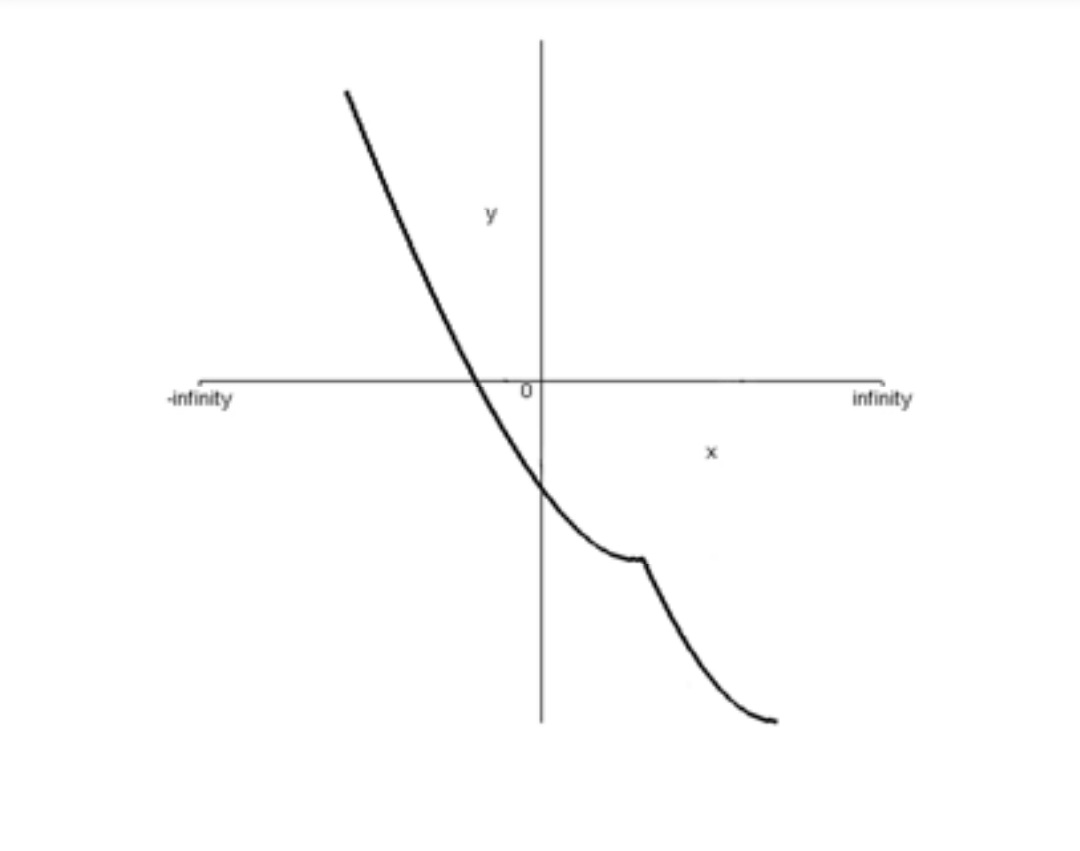
د)به ازای هر \({x_2}\) و\({x_1}\) که داریم \(f({x_1}) \ge f({x_2})\) يعني در واقع با زياد شدن مقاديرداريم كهx و مقادير y كم ميشود يا ثابت ميماند. پس تابع نزولي است.
ه)
ه) اگر \({x_2} \le 0\) و \({x_1}\) و\({x_1} < {x_2}\) آنگاه \(f({x_1}) > f({x_2})\) اين نشان ميدهد تابع f صعودي نيست واز طرف دیگر اگر \({x_2} \ge 0\) و \({x_2} < {x_1}\) آنگاه \(f({x_1}) < f({x_2})\) اين نشان ميدهد تابع f از طرف ديگر، اگر 0 نزولي نيست، بنابراين تابع f نه صعودي است و نه نزولي
و)
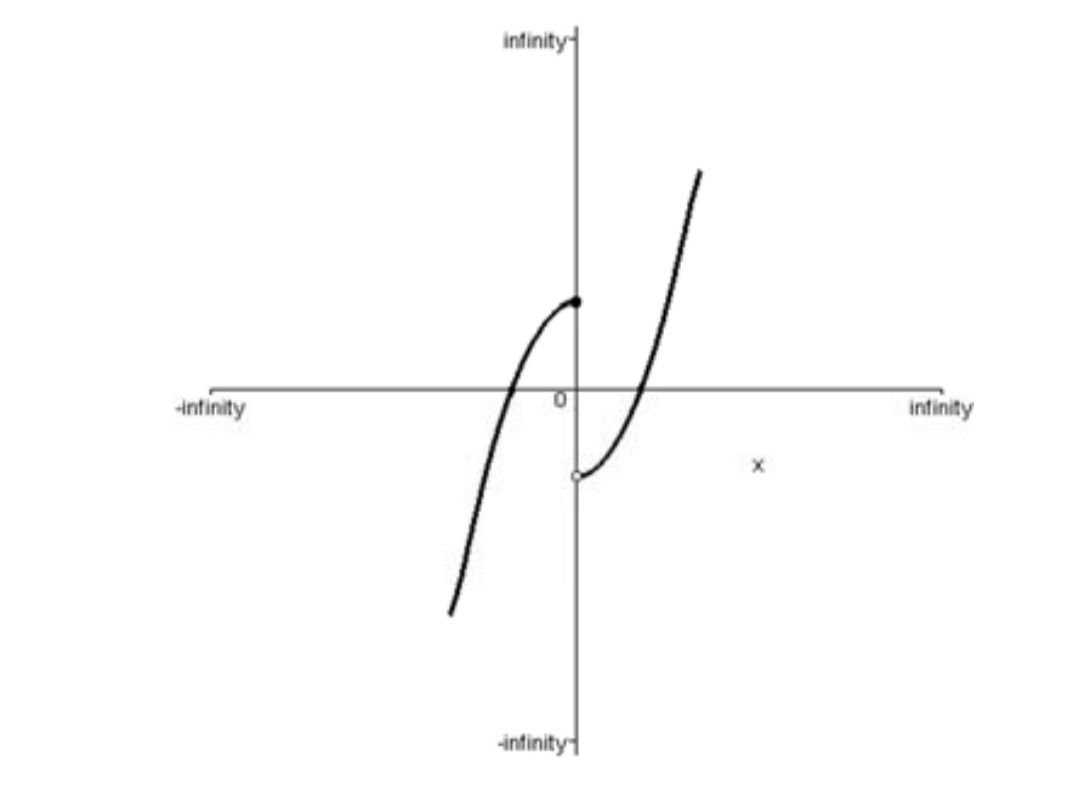
و) تابع در هر يك از بازه هاي [0 , ∞ −) و [∞ + , 0) صعودي اكيد است، ولي مقادير تابع در مجاورت چپ صفر از مقادير تابع در مجاورت راست صفر بيشتر است. بنابراين تابع روي دامنهي تعريف خود يعني بازهي (∞ + , ∞ −) نه صعودي است و نه نزولي.
ز)
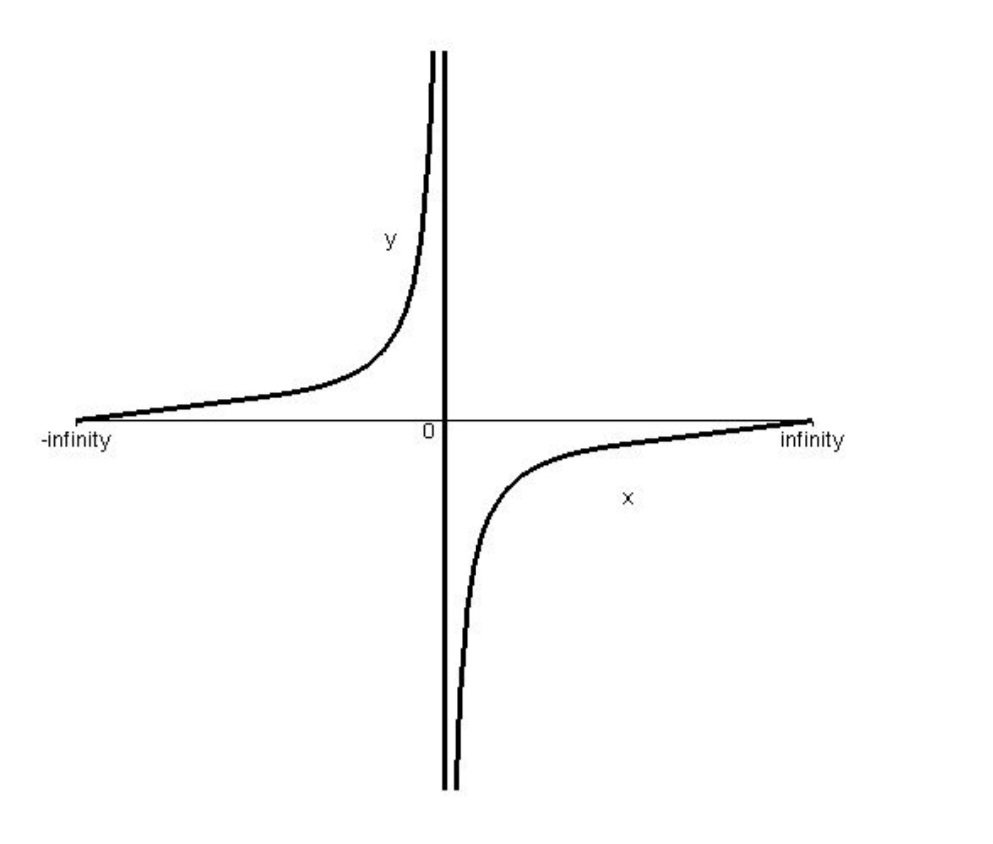
ز) تابع در بازه ي (0 , ∞ −) و (∞ ,+ 0) صعودي اكيد است ولي مقادير تابع در مجاورت چپ صفر از مقادير تابع در مجاورت راست صفر بيشتر است. پس تابع در دامنه ي تعريف خوديعني بازه ي \(( - \infty ,0) \cup (0, + \infty )\) نه صعودي است و نه نزولي.
ح)
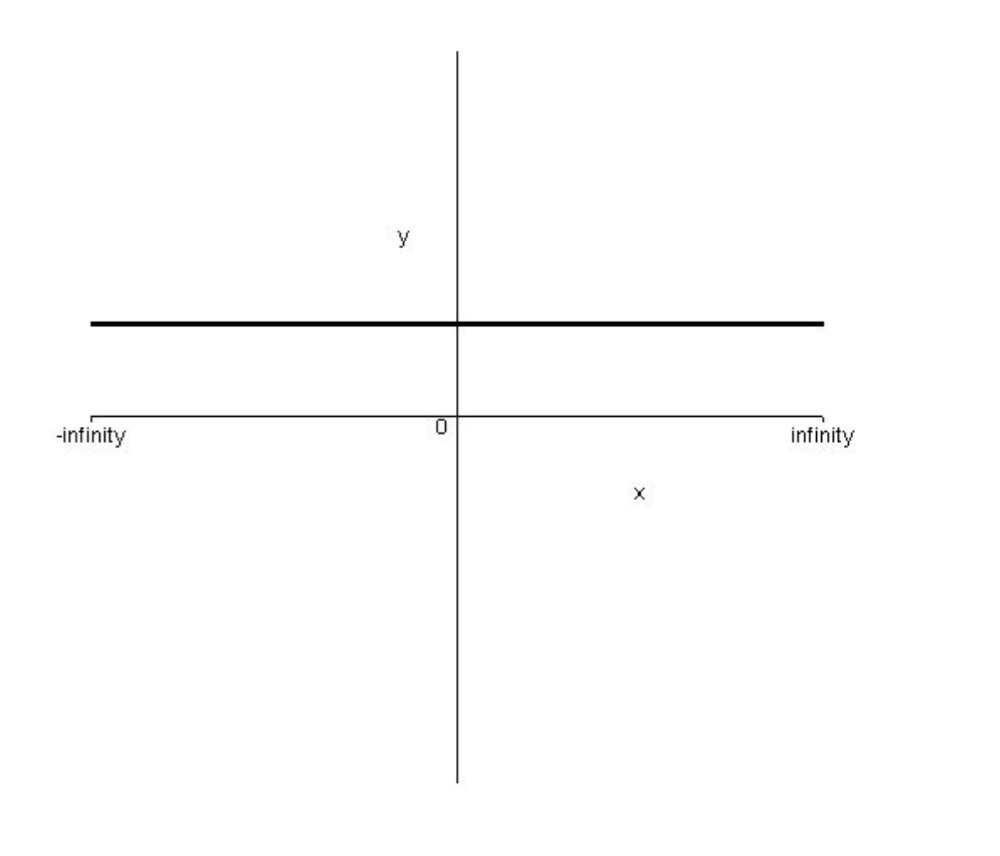
ح) با زياد شدن مقادير x ، مقادير y كم نميشود. پس تابع صعودي است و همچنين با زياد شدن مقادير x ، مقادير y زياد نميشود. پس تابع نزولي است ولي صعودي اكيد يا نزولي اكيد نيست.
مثال
حدود k را طوري به دست آوريد تا تابع \(f = \left\{ {(2,7),( - 1,2),(0,k),( - 2,1\left. ) \right\}} \right.\) صعودي اكيد شود.
چون تابع صعودي اكيد است بايد با زياد شدن مؤلفه هاي اول، مؤلفه هاي دوم نيز زياد شوند. بنابر اين لازم است \(k \in (2,7)\) باشد.
مثال
در تابع f كه نمودار آن به صورت زير رسم شده، مقادير \(f(0)\) در چه بازهاي ميتواند تغيير كند تا تابع f نزولي اكيد باشد.
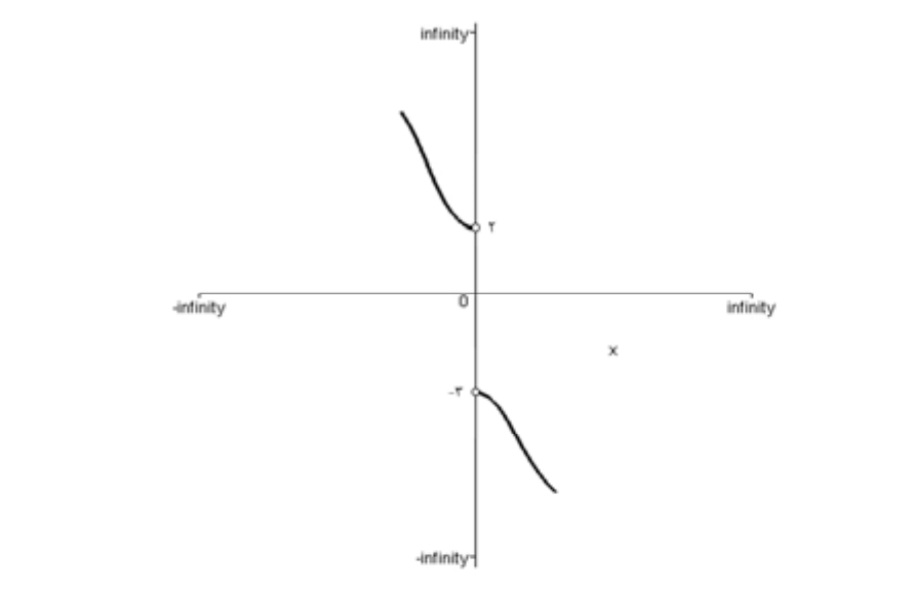
با توجه به اينكه با زياد شدن مقادير x ، مقادير y بايد كم شود. لذا لازم است \(f(0)\) عددي در فاصله ي \(\left[ { - 2,3} \right]\) باشد.
مثال
صعودي يا نزولي بودن هر يك از توابع زير را روي دامنه ي تعريفشان بررسي كنيد.
الف ) \(f(x) = - {x^3}\) ب) \(f(x) = 2{x^3} + 4x - 1\)
ج)\(f(x) = \log _a^x\) د )\(f(x) = \sqrt {3 - 2x} \)
ه) \(f(x) = \left\{ \begin{array}{l}x + 1,x < 0\\\\2 - x,x \ge 0\end{array} \right.\) و) \(f(x) = \left| {x - 1} \right| + 3\)
الف) روش اول نمودار تابع f به صورت زیر است.
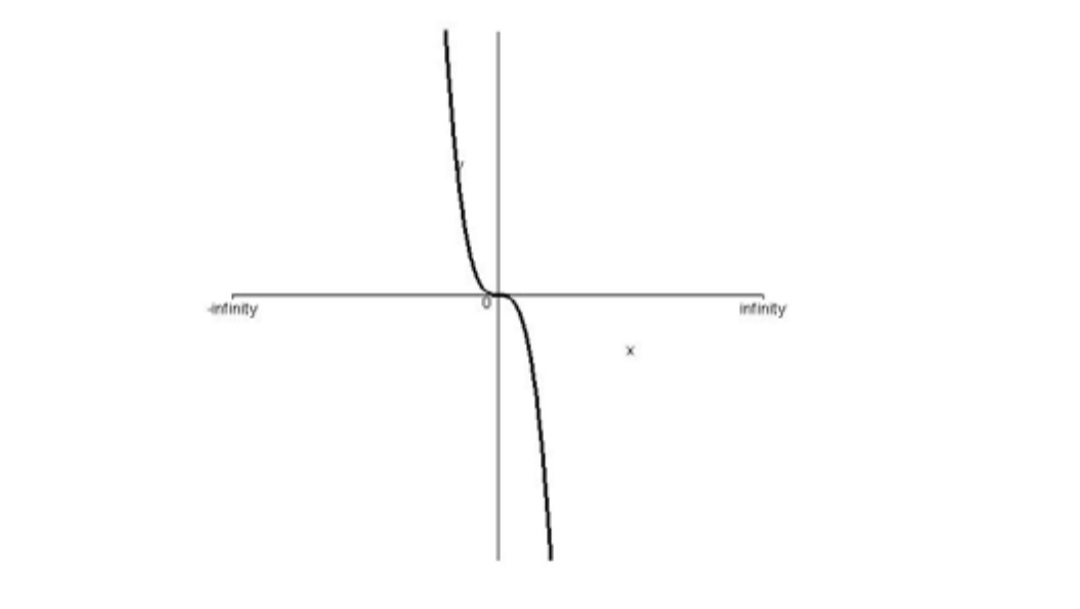
باتوجه به نمودار واضح است كه تابع نزولي اكيد ميباشد. :
ب ) روش اول: نمودار تابع به صورت زير است
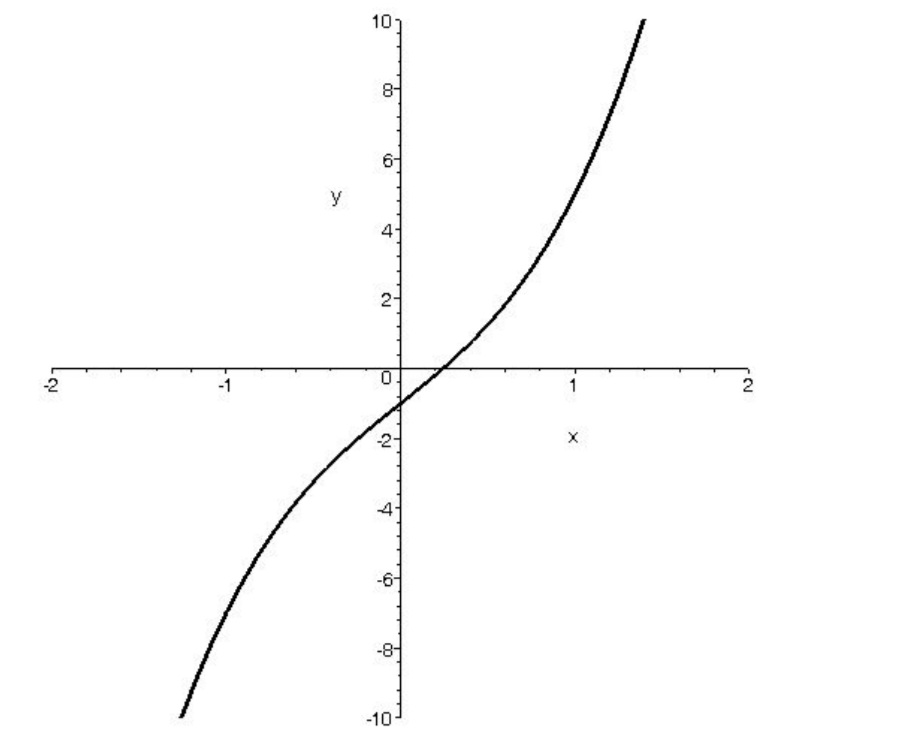
همانگونه که از روی نمودار مشخص است تابع صعودی اکید است.
ج) روش اول: نمودار تابع شبيه يكي از دو نمودار زير است.
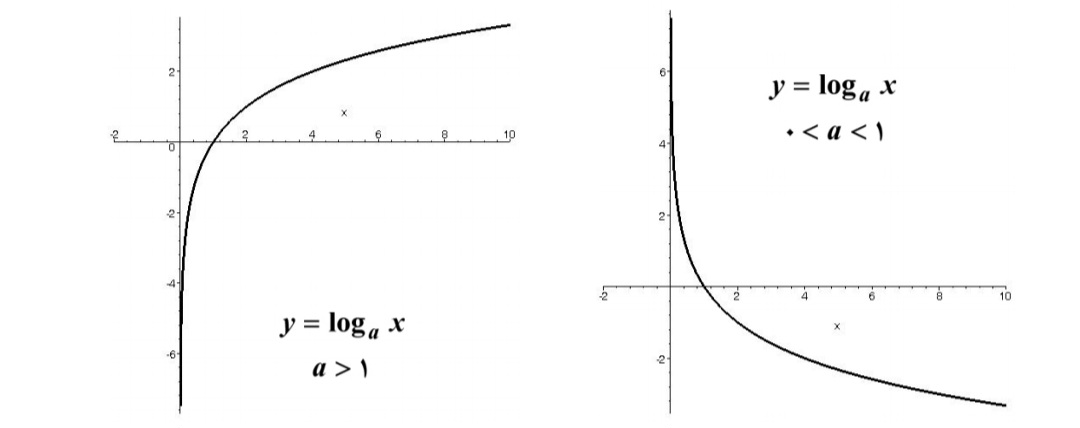
بنابراين اگر a>1باشد تابع صعودي اكيد است و اگر0، تابع نزولي اكيد ميباشد
روش دوم :رابطه های
\({x_1} < {x_2} \Rightarrow \log {x_1} < \log {x_2},\log _a^x = \frac{{\log x}}{{\log a}}\)
را در نظر گرفته دو عضو \({x_1},{x_2} \in {D_f} = \left( {0, + \infty } \right)\) را به دلخواه طوری انتخاب می کنیم که \({x_1} < {x_2}\) سپس دو حالت زیر را در نظر می گیریم
حالت اول :\(\left( {a > 1} \right)\)
\(\begin{array}{l}{x_1} < {x_2} \Rightarrow \log {x_1} < \log {x_2}\frac{{\log {x_1}}}{a} > \frac{{\log {x_2}}}{a} \Rightarrow \log x_a^{{x_1}} > \log x_a^{{x_2}}\\\\ \Rightarrow f({x_1}) > f({x_2})\end{array}\)
در نتيجه fصعودی اكيد است.
حالت دوم: \(\left( {0 < a < 1} \right)\)
در نتيجه f نزولي اكيد است.
د ) روش اول: نمودار تابع به صورت زير است.
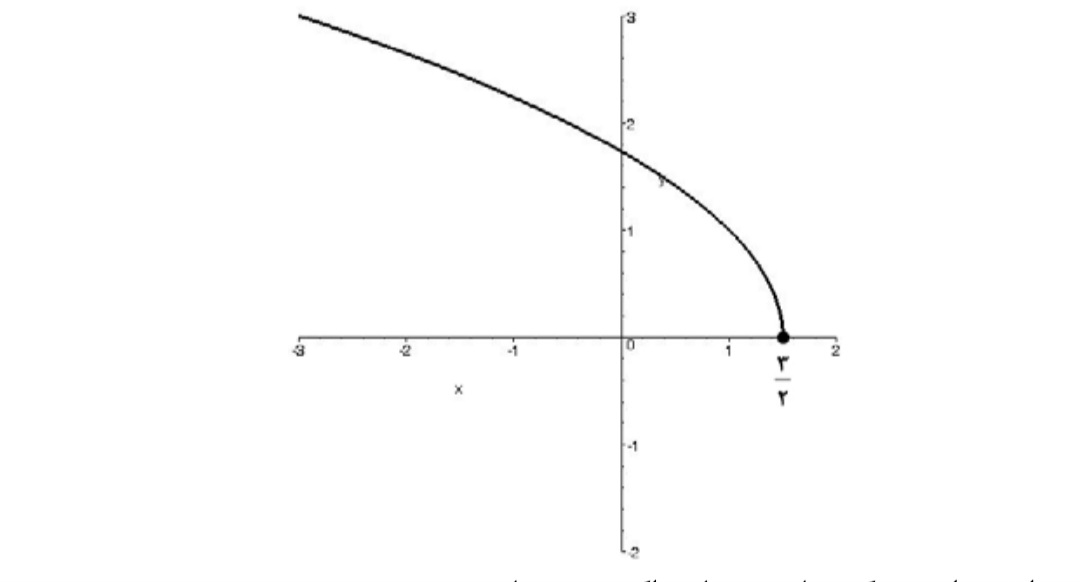
با توجه به نمودار واضح است كه تابع نزولي اكيد ميباشد
روش دوم \({x_1},{x_2} \in {D_f} = ( - \infty ,\left. {\frac{2}{3}} \right]\) را به دلخواه طوري انتخاب ميكنيم كه \({x_1} < {x_2}\) لذا داريم:
\(\begin{array}{l}{x_1} < {x_2} \Rightarrow 3 - 2{x_1} \Rightarrow \sqrt {3 - 2{x_1}} > \sqrt {3 - 2{x_2}} \Rightarrow \\\\f({x_1}) > f({x_2})\end{array}\)
در نتيجه f نزولي اكيد است.
هـ) روش اول: نمودار تابع به صورت زير است.
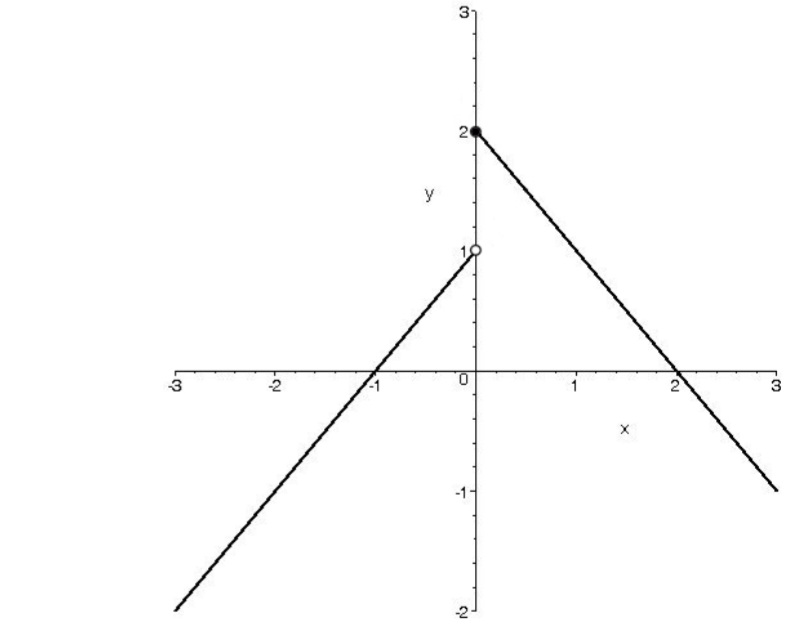
همانگونه كه از نمودار مشخص است تابع f در دامنه ي تعريف خود نه صعودي است نه نزولي .
توجه : تابع روي (0 , ∞ −) صعودي اكيد و روي (∞ + , 0] نزولي اكيد است.
روش دوم: \({x_1}\) و \({x_2}\) را به دلخواه به صورت هاي زير انتخاب ميكنيم . ضابطه قسمت اول تابع صعودي اكيد است.
\(\begin{array}{l}\left\{ \begin{array}{l}{x_1},{x_2} < 0\\\\{x_1} < {x_2}\end{array} \right. \Rightarrow {x_1} + 1 < {x_2} + 1 \Rightarrow f({x_1}) < f({x_2})\\\\\left\{ \begin{array}{l}{x_1},{x_2} > 0\\\\{x_1} < {x_2}\end{array} \right. \Rightarrow - {x_1} < - {x_2} \Rightarrow 2 - {x_1} > 2{x_2} \Rightarrow f({x_1}) > f({x_2})\end{array}\)
ضابطه قسمت دوم، تابع نزولي اكيد است . بنابراين تابع روي دامنهي تعريف خود نه صعودي است و نه نزولي.
و ) روش اول: نمودار تابع به صورت زير است و با توجه به نمودار واضح است كه تابع f روي دامنه ي تعريف خود نه صعودي است نه نزولي
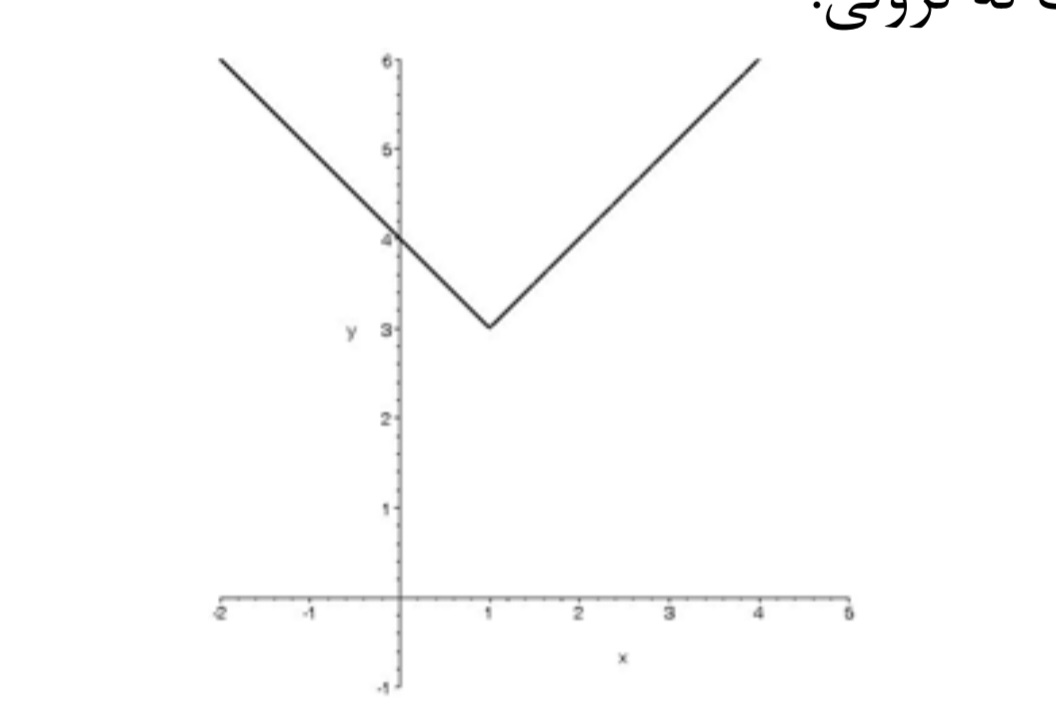
روش دوم : دو عضو دلخواه از \({D_f} = R\) را به هاي زير انتخاب ميكنيم.
\(\begin{array}{l}\\\left\{ \begin{array}{l}{x_1},{x_2} \le 1\\\\{x_1} < x2\end{array} \right. \Rightarrow {x_1} - 1 < {x_2} - 1 \Rightarrow \left| {{x_1} - 1} \right| > \left| {{x_2} - 1} \right| \Rightarrow \left| {{x_1} - 1} \right| + 3 > \left| {{x_2} - 1} \right| + 3 \Rightarrow \\\\f({x_1}) > f({x_2})\end{array}\)
پس تابع f در فاصله ي [,1 ∞ −) نزولي اكيد است.
\(\begin{array}{l}\\\left\{ \begin{array}{l}{x_1},{x_2} \ge 1\\\\{x_1} < {x_2}\end{array} \right. \Rightarrow {x_1} - 1 < {x_2} - 1 \Rightarrow \left| {{x_1} - 1} \right| < \left| {{x_2} - 1} \right| \Rightarrow \left| {{x_1} - 1} \right| + 3 < \left| {{x_2} - 1} \right| + 3 \Rightarrow \\\\f({x_1}) < f({x_2})\end{array}\)
پس تابع f در فاصلهي (∞ + , 1] صعودي اكيد است . اما تابع روي دامنه ي تعريف خود نه صعودي است و نه نزولي.
مثال
اگر f تابعي صعودي با دامنه ي ℜ باشد، دامنه ي تعريف تابع \(g(x) = \sqrt {f\left( {\left| {x - 2} \right|} \right)f\left( {\left| {2x - 1} \right|} \right)} \)را به دست آوريد.
داريم
\(f\left( {\left| {x - 2} \right|} \right) - f\left( {\left| {2x - 1} \right|} \right) \ge 0 \Rightarrow f\left( {\left| {x - 2} \right|} \right) \ge f\left( {\left| {fx - 1} \right|} \right)\)
چون f تابعي صعودي است داريم:
\(\begin{array}{l}\left| {x - 2} \right| < \left| {2x - 1} \right| \Rightarrow {x^2} - 4x + 4 \ge 4{x^2} - 4x + 1 \Rightarrow 3{x^2} - 3 \le 0 \Rightarrow \\\\ - 1 \le x \le 1 \Rightarrow {D_g} = \left[ { - 1,1} \right]\end{array}\)
مثال
اگر تابع \(f(x) = \left\{ \begin{array}{l}\sqrt {x + 1} ,x \ge 3\\\\\frac{1}{2}x + a,x < 2\end{array} \right.\) صعودي اكيد باشد، بيشترين مقدار a را به دست آورید.
نمودار تابع به صورت زير است.
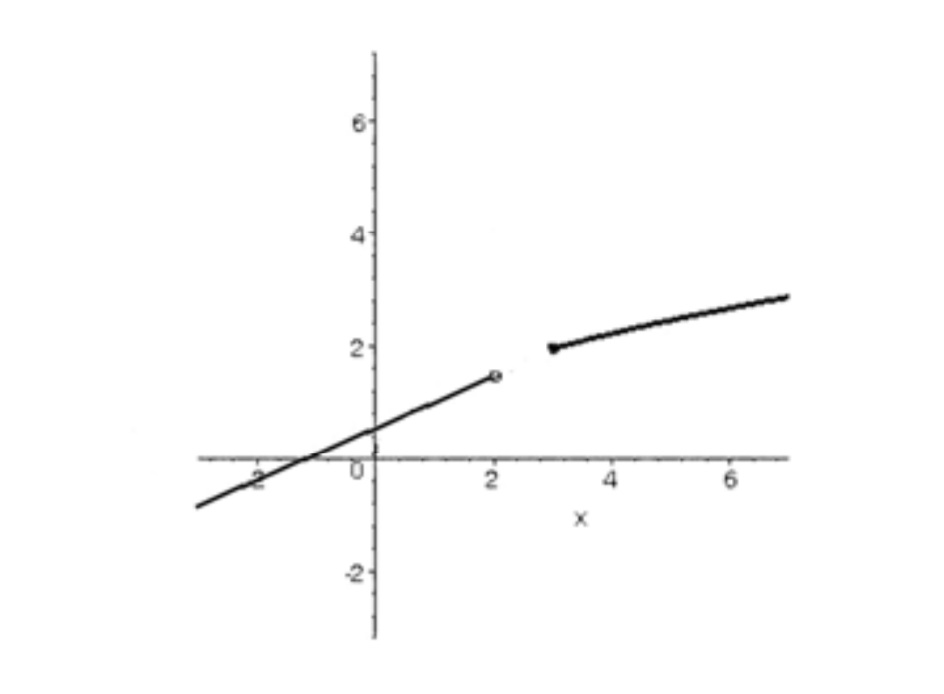
چون تابع f صعودي است پس لازم است \(1 + a \le 2\) يعني \(a \le 1\) بنابراين بيشترين مقدار a ميتواند يك باشد.
توابعي كه يا صعودي باشند يا نزولي، توابع يكنوا ناميده ميشوند.
توابعي كه اكيداً صعودي باشند يا اكيداً نزولي، توابع اكيداً يكنوا ناميده ميشوند.
مثال
تابع \(y = {x^2}\) روی دامنه تعریف خود نه صعودی است نه نزولی پس تابعی غیر یکنوااست.
مثال
اگر تابع f نزولي اكيد و تابع g بر \({R_f}\) نزولی اکید باشدیکنوایی تابعgof رابررسی كنيد.
دو عضو دلخواه \({x_1},{x_2} \in {D_f}\) , را طوري انتخاب ميكنيم كه \({x_1} < {x_2}\) پس داريم:
\({x_1} < {x_2} \Rightarrow f({x_1}) > f({x_2}) \Rightarrow g(f({x_1})) < g(f({x_2}))\)
يعني در واقع داريم
\({x_1} < {x_2} \Rightarrow (gof)({x_1}) < (gof)({x_2})\)
پس تابع gof صعودي اكيد ميباشد، بنابراين يكنواي اكيد ميباشد.
مثال
اگر دو تابع f و g در بازهي I ، صعودي اكيد باشند يكنوايي تابع f+gرا روي I بررسي كنيد.
: \({x_1},{x_2} \in I\)را به طور دلخواه طوري انتخاب ميكنيم كه \({x_1} < {x_2}\) پس داريم:
\(\begin{array}{l}{x_1} < {x_2} \Rightarrow \left( \begin{array}{l}f({x_1}) < f({x_2})\\\\ \Rightarrow g({x_1}) < g({x_2})\end{array} \right. \Rightarrow f({x_1}) < f({x_2}) + g({x_2})\\\\ \Rightarrow (f + g)({x_1}) < (f + g)({x_2})\end{array}\)
تابع f+g صعودي اكيد است . بنابراين تابع f+gيكنواي اكيد ميباشد
مثال
\(y = - {x^3}\) تابع نزولي اكيد است. پس تابع يكنواي اكيد ميباشد.
بعد از فراگيري مبحث مشتق، ميتوانيم در توابع مشتق پذير، يكنوايي را با روش هاي ساده تري بررسي كنیم.
تهیه کننده: حامد دلیجه
تابع يك به يك
فصل 2 : تابع
تابع يك به يك
تابع f يك به يك است، اگر براي هر\({x_1},{x_2} \in {D_f}\) , داشته باشيم:
\(f({x_1}) = f({x_2}) \Rightarrow {x_1} = {x_2}\)
و يا به بيان ديگر
تابع f يك به يك است اگر براي هرداشته باشيم:
\({x_1} \ne {x_2} \Rightarrow f({x_1}) \ne f({x_2})\)
نمودار يك تابع در صورتي نمودار تابع يك به يك است كه هر خط موازي محور x ها حداكثر در يك نقطه آن را قطع كند.
مثال
كدام يك از توابع زير يك به يك هستند.
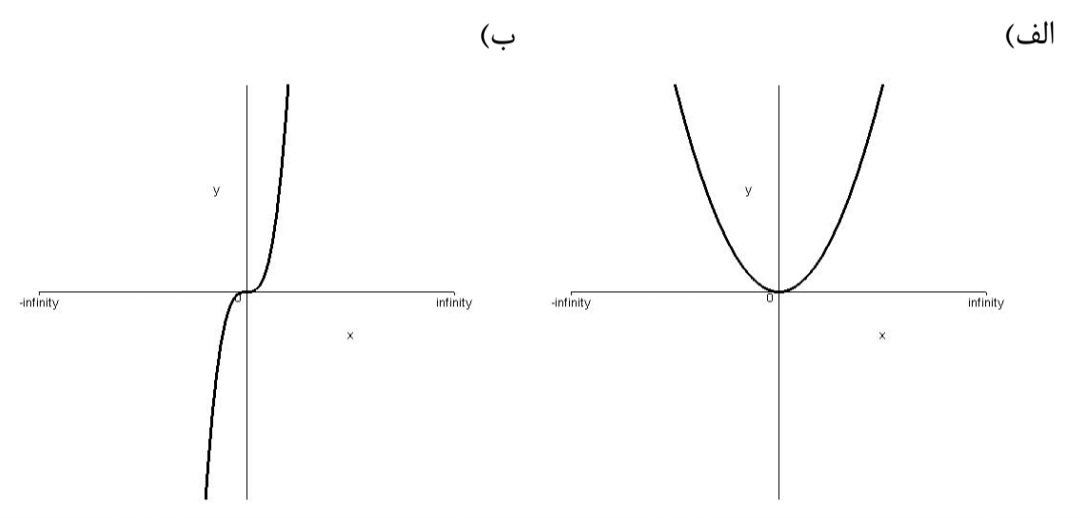
ج)\(f = \left\{ {\left( {1,2} \right)} \right.,\left( {2,3} \right),\left( {4,2} \right)\left. {} \right\}\)
الف) يك به يك نيست زيرا مثلاً خط y=1نمودار را در بيش از يك نقطه قطع ميكند.
ب) هر خط موازي محو x ها رسم كنيم. نمودار را در بيش از يك نقطه قطع نميكند . پس تابع يك به يك است.
ج) يك به يك نيست زيرا \(f(1) = f(4)\) ولي \(1 \ne 4\)
مثال
يك به يك بودن هر يك از توابع زير را بررسي كنيد
الف) \(f(x) = \sqrt {{x^3} + 4} \) ب) \(f(x) = {x^2} + 2x + 3\)
ج) \(f(x) = x + \left| {x - 2} \right|\) د) \(f(x) = \log x\)
ه) \(f(x) = \sin x - \cos x\) و) \(f(x) = \frac{{{3^x}}}{{{3^x} + 1}}\)
الف)
روش اول:
\(\begin{array}{l}f({x_1}) \ne f({x_2}) \Rightarrow \sqrt {x_1^3 + 4} = \sqrt {x_2^3 + 4} \Rightarrow x_1^3 + 4 = x_2^3 + 4 \Rightarrow \\\\x_1^3 = x_2^3 \Rightarrow {x_1} = {x_2}\end{array}\)
بنابراين تابع f يك به يك است.
روش دوم:
\(\begin{array}{l}{x_1} \ne {x_2} \Rightarrow x_1^3 = x_2^3 \Rightarrow x_1^3 + 4 \ne x_2^3 + 4 \Rightarrow \\\\\sqrt {x_1^3 + 4} \ne \sqrt {x_2^3 + 4} \Rightarrow f({x_1}) \ne f({x_2})\end{array}\)
بنابراين تابع f يك به يك است.
ب(
\(\begin{array}{l}f({x_1}) = {x^2} + 2x + 3 = {(x + 1)^2} + 2\\\\f({x_1}) = f({x_2}) \Rightarrow {({x_1} + 1)^2} + 2 = {({x_2} + 1)^2} + 2 = {({x_1} + 1)^2} = {({x_2} + 1)^2}\\\\{x_1} + 1 = \pm x(2 + 1) \Rightarrow \left\{ \begin{array}{l}{x_1} = {x_2}\\\\{x_1} = - {x_2} - 2\end{array} \right.\end{array}\)
پس تابع f يك به يك نيست.
ج)
\(f(0) = f(1) = 2 \Rightarrow 0 \ne 1\)
پس تابع f يك به يك نيست.
د(
\(\begin{array}{l}f({x_1}) = f({x_2}) = \log {x_1} = \log {x_2} \Rightarrow \log {x_1} - \log {x_2} = 0\\\\ \Rightarrow \log \frac{{{x_1}}}{{{x_2}}} = 0 \Rightarrow \frac{{{x_1}}}{{{x_2}}} = 1 \Rightarrow {x_1} = {x_2}\end{array}\)
پس تابع f يك به يك است.
ه(
\(f(0) = f(2\pi ) = - 1 \Rightarrow 0 \ne 2\pi \)
بنابراين تابع f يك به يك نيست.
توجه: توابع متناوب يك به يك نيستند.
و(
\(\begin{array}{l}f({x_1}) = f({x_2}) = \frac{{{3^{{x_1}}}}}{{{3^{{x_1}}} + 1}} = \frac{{{3^{{x_2}}}}}{{{3^{{x_2}}} + 1}} \Rightarrow {3^{{x_1}}} \times {3^{{x_2}}} + {3^{{x_1}}} = {3^{{x_2}}} \times {3^{{x_1}}} + {3^{{x_2}}}\\\\ \Rightarrow {3^{{x_1}}} = {3^{{x_2}}} \Rightarrow {x_1} = {x_2}\end{array}\)
پس تابع f يك به يك است
مثال
ثابت كنيد اگر تابع f يكنواي اكيد باشد آنگاه تابع f يك به يك است.
مثلاً فرض كنيم تابع f صعودي اكيد باشد آنگاه اگر \({x_1} \ne {x_2}\) دو حالت رخ ميدهد: حالت اول : اگر \({x_1} < {x_2}\) باشد، داريم:
\({x_1} > {x_2} \Rightarrow f({x_1}) < f({x_2}) \Rightarrow f({x_1}) \ne f({x_2})\)
لذا f يك به يك است.
حالت دوم اگر \({x_1} > {x_2}\) باشد، داريم:
\({x_1} > {x_2} \Rightarrow f({x_1}) > f({x_2}) \Rightarrow f({x_1}) \ne f({x_2})\)
لذا f يك به يك است.
مثال
اگر توابع f و g يك به يك باشند، يك به يك بودن هر يك از توابع f+g و fog را بررسي كنيد.
تابعf+g همواره نميتواند يك به يك باشد زيرا مثلاً اگر \(f = \left\{ {\left( {0,0} \right)} \right.,(1,1\left. ) \right\}\) و \(g = \left\{ {\left( {0,0} \right)} \right.,(1, - 1\left. ) \right\}\) را در نظر بگيريم، داريم \(f + g = \left\{ {\left( {0,0} \right)} \right.,(1,1\left. ) \right\}\) كه يك به يك نيست.
اما تابع fog يك به يك است زيرا:
\(\begin{array}{l}(fog)({x_1}) = (fog)({x_2}) \Rightarrow f(g({x_1})) = f(g({x_2}))\\\\g({x_1}) = g({x_2})\\\\{x_1} = {x_2}\end{array}\)
مثال
آيا يك تابع ميتواند هم فرد و هم يك به يك باشد.
بلي . مثلاً توابع \(y = {x^3}\) و\(y = x\) است، اما يك به يك نيست.ولی تابع \(y = \sin x\) فرد است امایک به یک نیست
مثال
آيا يك تابع ميتواند هم زوج و هم يك به يك باشد.
فرض كنيم f تابعي زوج و يك به يك باشد . داريم:
F \(x = - x \Rightarrow x = 0\) یک به یک است \(f \Rightarrow f(x) = f( - x)\) تابعی زوج است
پس تنها تابعي كه هم زوج و هم يك به يك است ، تابعی دلخواه با دامنه ي يك عضوي صفر ميباشد. f
يك تابع چند ضابطه اي در صورتي يك به يك است كه هر يك از ها يك به يك بوده و اشتراك برد دوبه دوي ضابطه ها مجموعه تهي باشد.
مثال
يك به يك بودن تابع \(f(x) = \left\{ \begin{array}{l}x + 1,x < 1\\\\2x + 3,x \ge 1\end{array} \right.\) را بررسی کنید.
\({f_1}({x_1}) = {f_1}({x_2}) \Rightarrow {x_1} + 1 \Rightarrow {x_2} + 1 \Rightarrow {x_1} = {x_2}\)
ضابطه اول يك به يك است.
\(\begin{array}{l}{f_2}({x_1}) = {f_2}({x_2}) \Rightarrow 2{x_1} + 3 \Rightarrow 2{x_2} + 3 \Rightarrow 2{x_1} = 2{x_2} \Rightarrow \\\\{x_1} = {x_2}\end{array}\)
ضابطه دوم يك به يك است
\(\left. \begin{array}{l}x < 1 \Rightarrow x + 1 < 2 \Rightarrow R = ( - \infty ,2)\\\\x \ge 1 \Rightarrow 2x \ge 2 \Rightarrow 2x + 3 \ge 5 \Rightarrow {R_2} = (5, + \infty )\end{array} \right\} \Rightarrow {R_1} \cap {R_2} = \emptyset \)
پس اشتراك برد ضابطه ها نيز تهي است . بنابراين f تابعي يك به يك است.
مثال
حدود k را طوري تعيين كنيد تا تابع \(f(x) = \left\{ \begin{array}{l}3x - 2,x > 1\\\\2x + k,x \le 1\end{array} \right.\) يك به يك باشد.
واضح است كه هر يك از ضابطه ها تابعي يك به يك هستند، كافي است اشتراك برد آنها نيز تهي باشد.
\(\left. \begin{array}{l}x > 1 \Rightarrow 3x > 3 \Rightarrow 3x - 2 > 1 \Rightarrow {R_1} = \left( {1, + \infty } \right)\\\\x \le 1 \Rightarrow 2x \le 3 \Rightarrow 2x + k \Rightarrow {R_2} = \left( { - \infty ,2 + k} \right)\end{array} \right\} \Rightarrow 2 + k \le 1 \Rightarrow k \le - 1\)
وارون تابع
اگر وارون \(f = \left\{ {(x,y\left. ) \right|} \right.x \in A,y \in \left. B \right\}\) يك تابع باشد، وارون تابع f به صورت تعريف ميشود. اگر تابع f به صورت \(\left\{ {(y,x\left. ) \right|} \right.(x,y) \in \left. f \right\}\) نمودار نمايش داده شده باشد، براي پيدا كردن وارون آن كافي است قرينه ي نقاط نمودار را نسبت به خط x = y رسم كنيم.
مثال
وارون هر يك از توابع زير را به دست آوريد.
الف) \(f = \left\{ {(1,2),} \right.(3,4),(5,6\left. ) \right\}\) ب) \(f = \left\{ {(1,3),} \right.(2,4),(5,3\left. ) \right\}\)
الف) \(f = \left\{ {(1,2),} \right.(3,4),(5,6\left. ) \right\}\) همانگونه كه مشاهده ميشود وارون تابع f يك تابع را مشخص ميكند.
ب( \(f = \left\{ {(1,3),} \right.(2,4),(5,3\left. ) \right\}\) همانگونه كه مشاهده ميشود وارون تابع g يك تابع نيست
اگر وارون تابع f خود يك تابع باشد، آن را تابع وارون f ميگويند و f را وارونپذير مينامند. بديهي است f وارون پذير است اگر و تنها اگر f يك به يك باشد و وارون f نمايش ميدهيم.
مثال
تابع وارون تابع \(f(x) = 3x + 5\) را در صورت وجود به دست آوريد.
ابتدا يك به يك بودن تابع را بررسي ميكنيم.
\(f({x_1}) = f({x_2}) \Rightarrow 3{x_1} + 1 = 3{x_2} + 5 \Rightarrow 3{x_1} = 3{x_2} \Rightarrow {x_1} = {x_2}\)
تابع f يك به يك است، پس وارون پذير ميباشد . براي به دست آوردن ضابطه ي تابع وارون كافي است y را به جاي قرار دهيم و x را برحسب y به دست آورده، سپس جاي x و y را با هم عوض كنيم.
\(y = 3x + 5 \Rightarrow 3x = y - 5 \Rightarrow x = \frac{{y - 5}}{3} \Rightarrow {f^{ - 1}}(x) = \frac{{x - 5}}{3}\)
مثال
اگر \(f = \left\{ {(1,2),} \right.(3,4\left. ) \right\}\) ، توابع \({f^{ - 1}}\) و \(\frac{1}{f}\) را محاسبه كنيد
f يك به يك است پس \({f^{ - 1}} = \left\{ {(2,1),} \right.(4,3\left. ) \right\}\) و \(\frac{1}{f} = \left\{ {(1,\frac{1}{2}),} \right.(3,\frac{1}{4}\left. ) \right\}\) واضح است كه \({f^{ - 1}}\) و \(\frac{1}{f}\) با هم مساوي نيستند.
مثال
تابع وارون هر يك از توابع وارون پذير زير را به دست آوريد.
الف) \(f(x) = {x^3} + 4\) ب) \(f(x) = {x^2} - 4,x < 0\)
ج) \(f(x) = 2{x^3} + 6{x^2} + 6x\) د) \(f(x) = \log _5^x\)
ه) \(f(x) = \sqrt {2 - 3x} \) و) \(f(x) = x + \frac{1}{x},x \ge 1\)
ز) \(f(x) = \frac{{2x + 1}}{{3x - 2}}\)
با توجه به اينكه روي وارون پذيري توابع داده شده تصريح شده است، بررسي وارون پذيري لازم نيست.
الف(
\(y = {x^3} + 4 \Rightarrow {x^3} = y - 4 \Rightarrow x{ = ^3}\sqrt {y - 4} \Rightarrow {f^{ - 1}}(x){ = ^3}\sqrt {y - 4} \)
ب)
\(\begin{array}{l}y = {x^2} - 4 \Rightarrow {x^2} = y + 4 \Rightarrow x = \pm \sqrt {y + 4} \\\\x = - \sqrt {y + 4} \Rightarrow {f^{ - 1}}(x) = - \sqrt {x + 4} \end{array}\)
ج)
\(y = 2({x^3} + 3{x^2} + 3x) \Rightarrow y = 2({x^3} + 3{x^2} + 3x + 1 - 1)\)
\(\begin{array}{l}y = 2({x^3} + 6{x^2} + 6x) \Rightarrow y = 2({x^3} + 6{x^2} + 6x + 1 - 1) \Rightarrow \\\\y = 2{(x + 1)^3} - 2 \Rightarrow {(x + 1)^3} = \frac{{y + 2}}{2} \Rightarrow x + 1{ = ^3}\sqrt {\frac{{y + 2}}{2} \Rightarrow } \\\\x = - 1{ + ^3}\sqrt {\frac{{y + 2}}{2} \Rightarrow } {f^1}(x){ = ^3}\sqrt {\frac{{x + 2}}{2}} \end{array}\)
د)
\(y = \log _5^x \Rightarrow x = {5^y} \Rightarrow {f^{ - 1}}\left( x \right) = {5^x}\)
ه)
\(\begin{array}{l}fy = \sqrt {2 - 3x} \to {y^2} = 2 - 3x \Rightarrow 2 - 3x - {y^2} \Rightarrow x = \frac{{2 - {y^2}}}{3} \Rightarrow \\\\{f^{ - 1}}(x) = \frac{{2 - {x^2}}}{3}\end{array}\)
و)
\(\begin{array}{l}y = x + \frac{1}{x} \Rightarrow y = \frac{{{x^2} + 1}}{x} \Rightarrow {x^2} - yx + 1 = 0 \Rightarrow \\\\\\x = \frac{{y \pm \sqrt {{y^2} - 4} }}{2}x = \frac{{y + \sqrt {{y^2} - 4} }}{2} \to {f^{ - 1}}(x) = \frac{{x + \sqrt {{x^2} - 4} }}{2}\end{array}\)
ز)
\(\begin{array}{l}f(x) = \frac{{2x + 1}}{{3x - 2}} \Rightarrow 3xy - 2y = 2x + 1 \Rightarrow 3xy - 2x = 2y + 1 \Rightarrow \\\\x(3y - 2) = 2y + 1 \Rightarrow \frac{{2y + 1}}{{3y - 2}} \Rightarrow {f^{ - 1}}(x) = \frac{{2x + 1}}{{3x - 2}}\end{array}\)
اگر دو تابع f و g وارون يكديگر باشند داريم:
\({D_g} = {R_f},{R_g} = {D_f}\)
و برای هر \(x \in {D_f}\) داریم :
\(g(f(x)) = x\)
و برای هر \(x \in {D_g}\) داریم :
\(f(g(x)) = x\)
مثال
نشان دهيد توابع \(f(x) = 2x + 5\) و \(g(x) = \frac{{x\_2}}{2}\) وارون يكديگرند.
\(x \in {D_g}:f(g(x)) = f\left( {\frac{{x - 5}}{2}} \right) = 2 \times \frac{{x - 5}}{2} + 5 = x\) دلخواه
\(x \in {D_F}:g(f(x)) = g\left( {2x + 5} \right) = \frac{{2x + 5 - 5}}{2} = x\) دلخواه
مثال
آيا دو تابع \(f(x) = \frac{{x + 1}}{2}\) و \(g(x) = 2x + 1\) وارون يكديگر هستند؟
روش اول:
\(x \in {D_g}:f(g(x)) = f(2x + 1) = \frac{{2x + 1 + 1}}{2} = x + 1 \ne x\)
بنابراين f و g وارون يكديگر نيستند.
مثال
برد تابع وارون تابع\(f(x) = \frac{x}{{\sqrt {x + 4 - 2} }}\) را به دست آوريد.
\(\begin{array}{l}\left\{ \begin{array}{l}x + 4 \ge 0\\\\\sqrt {x + 4} - 2 \Rightarrow \sqrt {x + 4} \ne 2 \Rightarrow x \ne 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x \ge 4\\\\x \ne 0\end{array} \right.\\\\{D_f} = \left( { - 4,0} \right) \cup (0, + \infty ) = {D_{{f^{ - 1}}}} = \left( { - 4,0} \right) \cup (0, + \infty )\end{array}\)
مثال
\(2 \le x < 4\), ,\(f(x) = \frac{{1 - 3x}}{4}\) داده شده است . دامنه تابع را بدست آورید
ميدانيم \({R_{{f^{ - 1}}}} = {R_f}\) پس كافي است برد تابع f را به دست آوريم.
\(\begin{array}{l}2 \le x < 4 \Rightarrow - 12 < - 3x < - 6 \Rightarrow - 11 \le 1 - 3x < - 5 \Rightarrow \\\\\frac{{ - 11}}{4} < \frac{{1 - 3x}}{4} < - \frac{5}{4} \Rightarrow \frac{{ - 11}}{4} < y < - \frac{5}{4} \Rightarrow {R_f} = (\frac{{ - 11}}{4},\left. { - \frac{{ - 5}}{4}} \right] \Rightarrow \\\\{D_f}^{ - 1} = (\frac{{ - 11}}{4},\left. { - \frac{{ - 5}}{4}} \right]\end{array}\)
براي به دست آوردن تابع وارون يك تابع چند ضابطه اي در صورت وجود وارون هر يك مياز ضابطه ها را به دست آوريم. بديهي است دامنه ،ي هر ضابطه برد ضابطهي نظير در تابع اصلي است.
مثال
تابع وارون تابع وارون پذير \(f(x) = \left\{ \begin{array}{l}x - 2,x < 1\\\\2x + 4,x \ge 1\end{array} \right.\) را بدست آورید .
برای ضابطه اول داریم:
\(x < 1 \Rightarrow x - 2 < - 1 \Rightarrow {R_1} = ( - \infty , - 1)\)
در نتیجه
\(y = x - 2 \Rightarrow x = y + 2 \Rightarrow f_1^{ - 1}(x) = x + 2\)
برای ضابطه دوم داریم
\(x \ge 1 \Rightarrow 2x \ge 2 \Rightarrow 2x + 4 \ge 6 \Rightarrow {R_2} = \left[ {6, + \left. \infty \right\}} \right.\)
در نتیجه
\(y = 2x + 4 \Rightarrow 2x = y - 4 \Rightarrow x = \frac{{y - 4}}{2} \Rightarrow f_2^{ - 1}(x) = \frac{{x - 4}}{2}\)
بنابراين ضابطه ي تابع وارون f به صورت زير خواهد بود.
\(f(x) = \left\{ \begin{array}{l}x + 2,x < - 1\\\\\frac{{x + 4}}{2},x \ge 6\end{array} \right.\)
اگر f تابع صعودي اكيد باشد، محل برخورد f و \({f^{ - 1}}\) در صورت وجود روی خط y=xقرار دارد.
مثال
اگر \(f(x) = {x^3} + x\_8\) فاصله ی نقطه ی fتلاقی و \({f^{ - 1}}\) تا مبدأ مختصات را محاسبه ، كنيد.
\(\begin{array}{l}{x_1} < {x_2} \Rightarrow \left\{ \begin{array}{l}x_1^3 < x_2^3\\\\{x_1} < {x_2}\end{array} \right. \Rightarrow x_3^1 + {x_1} < x_2^3 + {x_2} \Rightarrow x_3^1 + {x_1} - 8 < x_2^3 + {x_2} - 8\\\\ \Rightarrow f({x_1}) < f({x_2})\end{array}\)
در نتيجه تابع f صعودي اكيد است
بنابراين براي محاسبه محل تلاقي f و \({f^{ - 1}}\) كافي است محل تلاقي f و خط x = y را در صورت وجود محاسبه كنيم.
\(\begin{array}{l}\left\{ \begin{array}{l}y = {x^3} + x - 8\\\\y = x\end{array} \right. \Rightarrow {x^3} + x - 8 = x \Rightarrow {x^3} = 8 \Rightarrow x = 2,y = 2\\\\ \Rightarrow d = \sqrt {4 + 4} = 2\sqrt 2 \end{array}\)
مثال
نقاط برخورد تابع \(f(x) = x - \sqrt {x + 1} \) را با وارونش، در صورت وجود پيدا كنيد.
\(\begin{array}{l}{x_1},{x_2} \in \left[ { - 1, + \left. \infty \right)} \right.,{x_1} < {x_2}\\\\{x_1} < {x_2} \Rightarrow \left\{ \begin{array}{l}{x_1} < {x_2}\\\\{x_1} + 1 < {x_2} + 1 \Rightarrow \sqrt {{x_1} + 1} < \sqrt {{x_2} + 1} \end{array} \right.\\\\ \Rightarrow {x_1} + \sqrt {{x_1} + 1} < {x_2} + \sqrt {{x_2} + 1} \Rightarrow f({x_1}) < f({x_2})\end{array}\) دلخواه
تابع f صعودي اكيد است.
براي پيدا كردن نقطه ي برخورد داريم:
\(\left\{ \begin{array}{l}y = x\\\\y = x + \sqrt {x + 1} \end{array} \right. \Rightarrow x = x + \sqrt {x + 1} \Rightarrow \sqrt {x + 1} = 0 \Rightarrow x = - 1,y = - 1\)
تهیه کننده: حامد دلیجه
توابع متناوب
فصل 2 : تابع
توابع متناوب
تابع f را متناوب ناميم هرگاه يك عدد حقيقي مثبت مانند T موجود باشد، كه برای هر \(x \in {D_f}\) داشته باشيم:
\(f(x + T) = f(x),x + T \in {D_f}\)
براي هر
كوچكترين عدد T با خاصيت هاي بالا را دوره تناوب f مينامند.
مثال
با استفاده از رسم نمودار دوره تناوب تابع \(y = \sin x\) را تعيين كنيد.
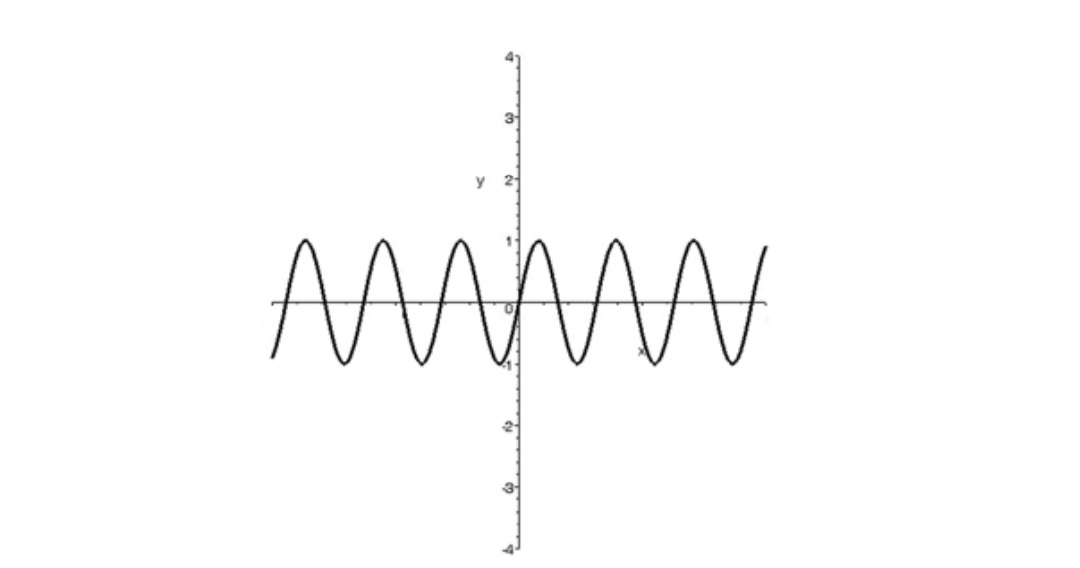
حل: همانگونه كه از نمودار مشاهده ميشود كمترين طولي كه نمودار تابع در آن عيناً تكرار ميشود \(2\pi \) است. پس دوره تناوب تابع \(T = 2\pi \) ميباشد.
مثال
دوره تناوب تابع \(y = 3\sin x - 1\) را تعيين كنيد.
با توجه به اينكه براي رسم نموار تابع \(y = 3\sin x - 1\) ميتوانيم ابتدا نمودار تابع \(y = \sin x\) را رسم و نمودار را با يك انبساط در جهت محور y ها و يك انتقال به راست، نمودار تابع را رسم كنيم در واقع دوره تناوب اين تابع با تابع \(y = \sin x\) يكسان است. اين مطلب در شكل زير به خوبي قابل مشاهده ميباشد.
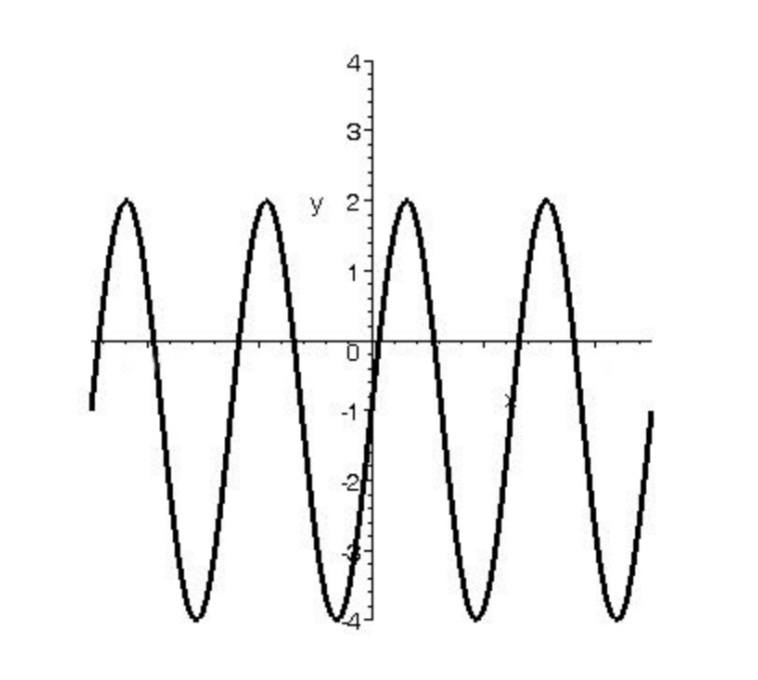
توجه: در حالت كلي اگر f تابعي متناوب با دوره تناوب T باشد توابع \(y = af(x) + b\) نيز متناوب با همان دوره تناوب T خواهند بود. ولي دوره تناوب تابع \(y = f(ax)\) برابر \(\frac{{2\pi }}{{\left| a \right|}}\) است ( . به علت π2 انقباض و انبساط در جهت محور x ها(
مثال
آيا تابع \(y = \sqrt {1 - {x^2}} \) متناوب است؟ چرا؟
خير - زيرا \({D_f} = \left[ { - 1,1} \right]\) و شرط \(x + T \in {D_f}\) نميتواند براي تابع برقرار باشد.
مثال
آيا تابع y=2متناوب است؟ در صورت متناوب بودن دوره تناوب آن را تعيين كنيد.
دامنه تعريف تابع برابر ℜ است. پس T هر عدد حقيقي مثبت كه باشد داريم
\(\left\{ \begin{array}{l}x + T \in {D_f}\\\\f(x + T) = f(x)\end{array} \right.\)
پس تابع متناوب است. اما چون كوچكترين عدد حقيقي مثبت وجود ندارد، پس دوره تناوب ندارد.
براي تعيين دوره تناوب ميتوانيم از دستورهاي زير استفاده كنيم:
\(\begin{array}{l}1)y = {\sin ^{2n - 1}}(ax).y = {\cos ^{2n - 1}}(ax)T = \frac{{2\pi }}{{\left| a \right|}}\\\\2)y = {\sin ^{2n - 1}}(ax).y = {\cos ^{2n - 1}}(ax)T = \frac{{2\pi }}{{\left| a \right|}}\\\\3)y = {\sin ^{2n}}(ax),y = {\cos ^{2n}}(ax),y = {\tan ^n}(ax),y = {\cot ^n}(ax)T = \frac{\pi }{{\left| a \right|}}\\\\y = \left| {\sin (ax)} \right|,y = \left| {\cos (ax)} \right|,y = \left| {A\sin (ax) + B\cos (ax)} \right| \Rightarrow T = \frac{\pi }{{\left| a \right|}}\\\\\end{array}\)
مثال
دوره تناوب توابع زير را تعيين مي کنیم
\(\begin{array}{l}1)y = {\sin ^3}(2x) \Rightarrow T = \frac{{2\pi }}{2} = \pi \\\\2)y = {\sin ^2}(2x) \Rightarrow T = \frac{\pi }{2}\\\\3)y = - 3\sin (2x) \Rightarrow T = \frac{{2\pi }}{2} = \pi \\\\4)y = {\sin ^3}(2x) \Rightarrow T = \frac{{2\pi }}{2} = \pi \\\\5)y = \frac{\pi }{4} - 3\sin (1 - 2x) \Rightarrow T = \frac{{2\pi }}{{\left| { - 2} \right|}} = \pi \\\\6)y = {\tan ^2}(3x) \Rightarrow T = \frac{\pi }{3}\\\\7)y = 4 - 2\cot (\frac{\pi }{4} - 3\pi x) \Rightarrow T = \frac{\pi }{{\left| { - 3\pi } \right|}} = \frac{1}{3}\end{array}\)
مثال
دوره تناوب تابع \({y_1} = \sin (\frac{2}{3}x + \frac{\pi }{6}) - 1\) چند برابر دوره تناوب تابع \({y_2} = {\sin ^2}(\frac{2}{3}x)\) است.
\({T_1} = \frac{{2\pi }}{{\frac{2}{3}}} = 3\pi ,{T_2} = \frac{{2\pi }}{{\frac{2}{3}}} = \frac{{2\pi }}{3} \Rightarrow \frac{{{T_1}}}{T} = \frac{{3\pi }}{{\frac{2}{3}}} = \frac{9}{2}\)
توابع زير متناوب نيستند:
توابع مثلثاتي كه در آن كمان x زير راديكال و يا تواني غير از يك داشته باشد متناوب نيستند.
هر گاه در تابع، كمان با يكي از چهار عمل اصلي با نسبت مثلثاتي قرار گيرد، تابع متناوب نيست.
مثال
توابع زير متناوب نيستند
الف)\(y = \cos \left| x \right|\) ب) \(y = x\cos x\)
ج) \(y = \sqrt x + \tan x\) د) \(y = x - \cos x\)
ه)\(y = \sin \left| x \right|\)
جزء صحيح
براي هر عدد حقيقي x جزء صحيح آن بزرگترين عدد صحيحي است كه از x بيشتر نيست. جزء صحيح x را با نماد \(\left[ x \right]\) يا \(\left\lfloor x \right\rfloor \) نمايش ميدهيم. يعني براي هر عدد حقيقي x يك عدد صحيح p موجود است به طوري که:
\(p \le x < p + 1 \Rightarrow \left[ x \right] = p\)
مثال
الف)\(\left[ x \right] < 2\) ب)\(\left[ x \right] \le 2\)
ج)\(\left[ x \right] < - \frac{1}{2}\) د)\(\left[ x \right] \le - \sqrt 2 \)
ه)\(\left[ {\frac{{3x + 1}}{2} < 4} \right]\) و)\({\left[ x \right]^2} - 3\left[ x \right] + 2 < 0\)
ز)\(\left[ {\log _2^x} \right] < 8\)
\(\left[ x \right] < 2 \Rightarrow \left[ x \right] \le 2 \Rightarrow x < 2\) (الف
\(\left[ x \right] \le 2 \Rightarrow x < 3\) (ب
\(\left[ x \right] < - \frac{1}{2} \Rightarrow \left[ x \right] < - \frac{1}{2} < 0 \Rightarrow x < 0\) (ج
\(\left| x \right| \le - \sqrt 2 \Rightarrow \left| x \right| \le - \sqrt 2 < - 1 \Rightarrow x < - 1\) (د
\(\left[ {\frac{{3x + 1}}{2}} \right] < 4 \Rightarrow \frac{{3x + 1}}{2} < 4 \Rightarrow 3x + 1 < 8 \Rightarrow x < \frac{7}{3}\) (ه
\(\begin{array}{l}{\left[ x \right]^2} - 3\left[ x \right] + 2 < 0{t^2} - 3t + 2 < 0 \Rightarrow 1 < t < 2\\\\ \Rightarrow 1 < \left[ x \right] < 2\end{array}\)
\(\left[ {\log _2^x} \right] < 9 \Rightarrow \log _2^x < 9 \Rightarrow x < {2^9}\) (ز
دستور های زیر برای جز صحیح همواره برقرار است
\(\begin{array}{l}\left[ {x + k} \right]\left[ x \right] \pm k\\\\\left[ x \right] + \left[ { - x} \right] = \left\{ \begin{array}{l}0,x \in z\\\\ - 1,x \notin z\end{array} \right.\\\\0 \le x - \left[ x \right] < 1\\\\x - 1 \le \left[ x \right] \le x\\\\\left[ x \right] + \left[ {x + \frac{1}{n}} \right] + \left[ {x + \frac{n}{2}} \right] + ... + \left[ {x + \frac{{n - 1}}{n}} \right] = \left[ {nx} \right]\\\\x > 0 \Rightarrow \left[ x \right] \ge 0\\\\x < 0 \Rightarrow \left[ x \right] < 0\end{array}\)
مثال
معادله ي \(\left[ x \right] + \left[ {x + 3} \right] - \left[ {x + 2} \right] = 5\) را حل كنيد.
\(\left[ x \right] + \left[ x \right] + 3 - \left[ x \right] - 2 = 5 \Rightarrow \left[ x \right] = 4 \Rightarrow 4 \le x < 5\)
مثال
معادله ی \(4\left[ x \right.\left. {^2} \right] + x = 5\) را حل كنيد.
\(\left\{ \begin{array}{l}\left\{ {4\left[ x \right.\left. {^2} \right]} \right. \in z\\\\\left\{ {4\left[ x \right.\left. {^2} \right]} \right. + x = 5\end{array} \right. \Rightarrow x \in z \Rightarrow {x^2} \in z \Rightarrow 4{x^2} + x - 5 = 0 \Rightarrow \left\{ \begin{array}{l}x = 1\\\\x = - \frac{5}{4}\end{array} \right.\)
مثال
معادله ي \(\left[ x \right] + \left[ { - x} \right] = \frac{1}{{x - \left[ x \right]}}\) را حل كنيد.
ميدانيم
\(\left[ x \right] + \left[ { - x} \right] = \left\{ \begin{array}{l}0,x \in z\\\\ - 1,x \notin z\end{array} \right.\)
باتوجه به اینکه صورت کسر طرف دوم عدد یک یک است پس طرف اول صفر نمی تواند باشد بنابراین \(x \in z\) و برابر 1- است و داریم :
مهادله جواب ندارد \( - 1 = \frac{1}{{x - \left[ x \right]}} \Rightarrow x - \left[ x \right] = - 1 \to 0 < x - \left[ x \right] < 1\)
مثال
دامنه و برد تابع \(y = \frac{1}{{\sqrt {x - \left| x \right|} }}\) را تعيين كنيد
لازم است \(x - \left| x \right| > 0\) باشد،
\(\begin{array}{l}0 \le x - \left| x \right| < 1x - \left| x \right| \ne 0 \Rightarrow x \ne z \Rightarrow {D_f} = R - Z\\\\x \in R - Z \Rightarrow 0 < x - \left| x \right| < 1 \Rightarrow \sqrt {x - \left| x \right| < 1} \Rightarrow \frac{1}{{\sqrt {x - \left| x \right|} }} > 1 \Rightarrow {R_f} = \left( {, + \infty } \right)\end{array}\)
مثال
نمودار تابع \(y = - 2\left| x \right| - 1\) را رسم كنيد.
ميدانيم نمودار تابع \(y = \left| x \right|\) به صورت مقابل است.
پس لازم است ابتدا y هاي نقاط اين نمودار در -2 ضرب شود، سپس تمام نقاط آن يك واحد به سمت پايين انتقال يابد. بنابراين نمودار به صورت زير در مي آيد.
مثال
نمودار تابع \(y = \left| {\sqrt x } \right|\) را در فاصله ي ( 90 ,0 ] رسم كنيد.
داريم
\(\begin{array}{l}0 \le x < 9 \Rightarrow 0 \le \sqrt x < 3 \Rightarrow \left| {\sqrt x } \right| = 0,1,2\\\\\left| {\sqrt x } \right| = 0 \Rightarrow 0 \le \sqrt x < 1 \Rightarrow 0 \le x < 1,y = 0\\\\\left| {\sqrt x } \right| = 1 \Rightarrow 1 \le \sqrt x < 2 \Rightarrow 1 \le \sqrt x < 4,y = 1\\\\\left| {\sqrt x } \right| = 2 \Rightarrow 2 \le \sqrt x < 3 \Rightarrow 4 \le \sqrt x < 9,y = 2\end{array}\)
و نمودار به صورت زير در مي آيد.
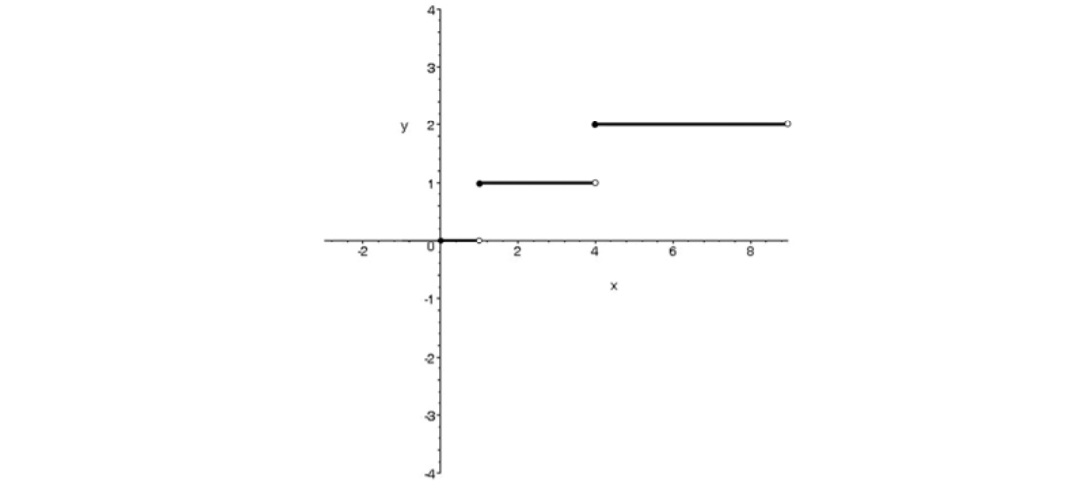
مثال
نمودار تابع \(y = x\left| {\sqrt x } \right| + 2x - 5\) را در فاصله ي ( 40 ,0 ] رسم كنيد.
\(0 \le x < 4 \Rightarrow 0 \le \sqrt x < 2 \Rightarrow \left[ {\sqrt x } \right] = 0,1 \Rightarrow \left\{ \begin{array}{l}\left[ {\sqrt x } \right] = 0 \Rightarrow 0 \le \sqrt x < 1 \Rightarrow \left\{ \begin{array}{l}0 \le x < 1\\\\y = 2x - 5\end{array} \right.\\\\\left[ {\sqrt x } \right] = 1 \Rightarrow 1 \le \sqrt x < 2 \Rightarrow \left\{ \begin{array}{l}1 \le x < 4\\\\y = 3x - 5\end{array} \right.\end{array} \right.\)
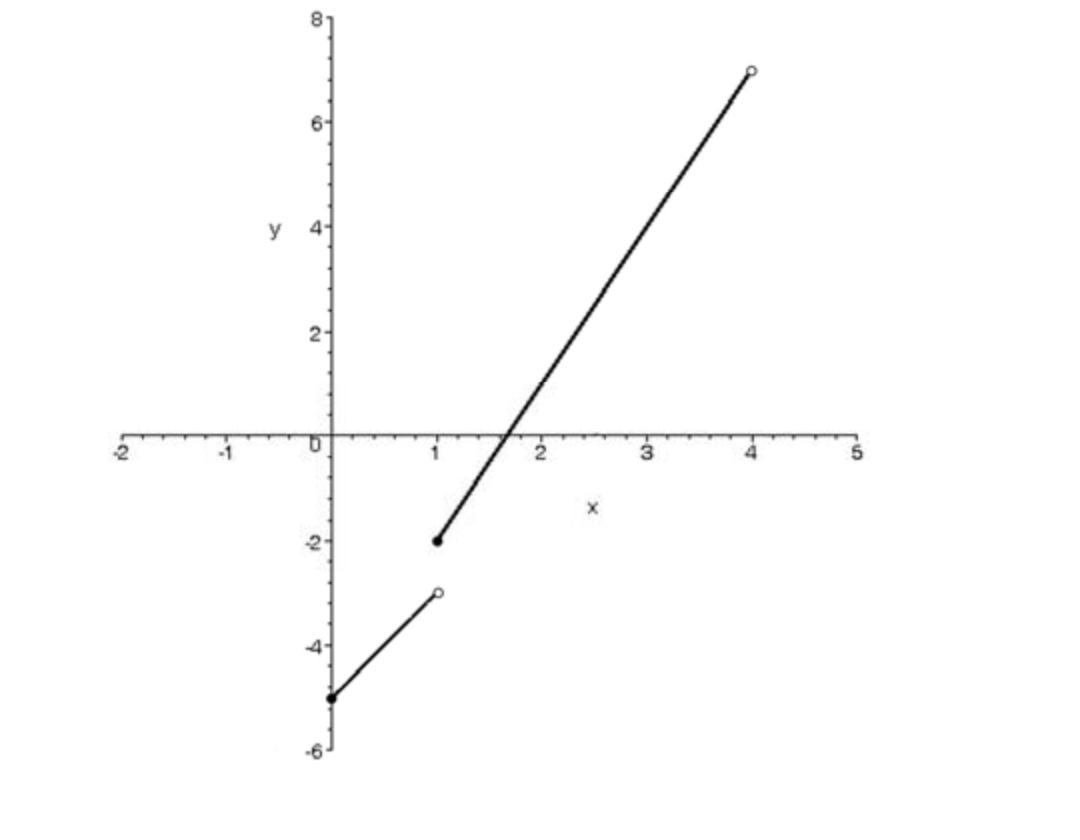
براي رسم نمودار تابع \(f(x) = \left[ {g(x)} \right]\) ميتوانيم ابتدا نمودار تابع \(y = g(x)\) را رسم كنيم. سپس خطوط\(y = k\) , \(k \in z\) را رسم نموده و در انتها هر قسمت از نمودار را كه بين دو خط افقي متوالي قرار گرفت را روي خط پاييني تصوير كنيم. محل تلاقي خطوط افقي با نمودار نقطه اي توپر ميباشد.
مثال
نمودار تابع \(y = \left| {{x^2}} \right|\) رارسم کنید
مثال
نمودار تابع \(y = \left| {\log x} \right|\) رارسم کنید
مثال
نمودار تابع\(y = \left[ {\sin x} \right]\) را در فاصله ی \(\left[ {0,2\pi } \right]\) رسم کنید
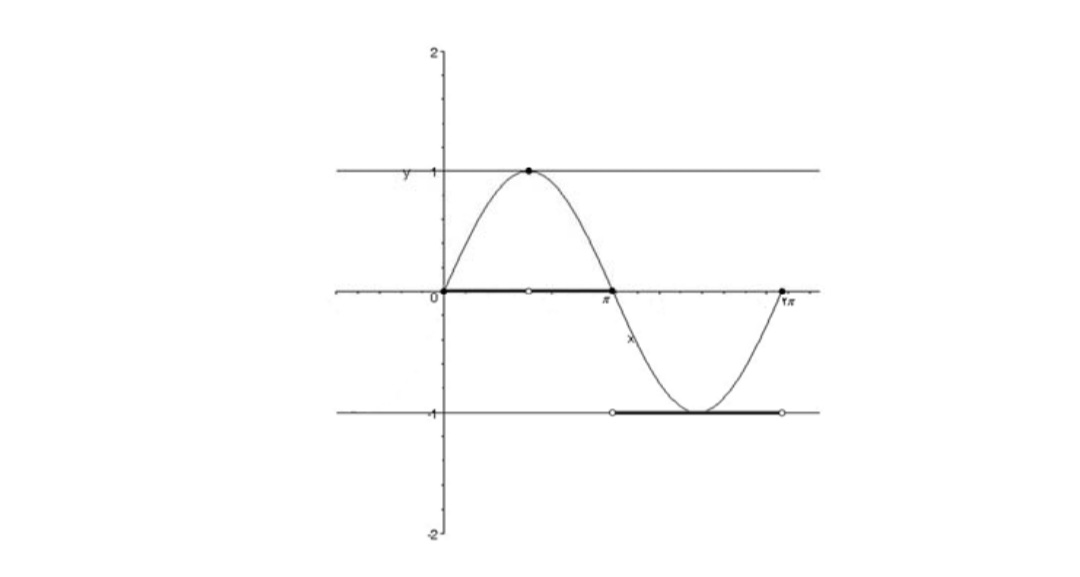
تهیه کننده: حامد دلیجه
- آزمون آنلاین تمامی دروس پایه یازدهم
- گام به گام تمامی دروس پایه یازدهم
- ویدئو های آموزشی تمامی دروس پایه یازدهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه یازدهم
- فلش کارت های آماده دروس پایه یازدهم
- گنجینه ای جامع از انشاء های آماده پایه یازدهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه یازدهم
لُگاریتم
فصل 3 : توابع نمایی و لگاریتمی
لگاریتم
فرض کنید می خواهیم با سه عدد 2، 3، و 8 به همراه یک عمل ریاضی، یک تساوی منطقی بنویسیم. پاسخ شما چیست؟
حدس می زنم شما بنویسید: \({2^3} = 8\)
خُب این پاسخ در سطح بچه های هفتم و هشتم است و من انتظار پاسخ در سطح نُهم و دهُم را دارم!
آفرین درست حدس زدید: \(\sqrt[3]{8} = 2\)
در تساوی \({2^3} = 8\) حاصل عمل، عدد 8 است و در تساوی \(\sqrt[3]{8} = 2\)
حاصل عمل، عدد 2 می باشد. در این درس، عملی را معرفی می کنیم که برای اعداد فوق، حاصل آن عدد 3 باشد.
این عمل لگاریتم نام دارد، به این صورت که می نویسیم: \({\log _2}8 = 3\)
و می خوانیم: «لگارتیم 8 در پایه ی (مبنای) 2 برابر 3 است.
تعریف:
به ازای عداد حقیقی مثبت a و b و با فرض \(b \ne 1\) ، تعریف می کنیم:
\({\log _b}a = x \Leftrightarrow {b^x} = a\)
مثال
تساوی های زیر را به صورت لگاریتمی بنویسید.
\({3^4} = 81\) الف
\({\log _3}81 = 4\)
\(0/{1^3} = 0/001\) ب
\({\log _{0/1}}0/001 = 3\)
\({(\sqrt 2 )^{ - 2}} = \frac{1}{2}\) پ
\({\log _{\sqrt 2 }}\frac{1}{2} = - 2\)
\({5^0} = 1\) ت
\({\log _5}1 = 0\)
مثال
تساوی های لگاریتمی زیر را به صورت نمایی بنویسید.
\({\log _2}32 = 5\) الف
\({2^5} = 32\)
\({\log _2}0/125 = - 3\) ب
\({2^{ - 3}} = 0/125\)
\({\log _5}\sqrt {125} = 1/5\) پ
\({5^{1/5}} = \sqrt {125} \)
\({\log _a}a = 1\) ت
\({a^1} = a\)
اگر \({\log _{50}}A = \frac{1}{2}\) و \({\log _{32}}B = \frac{1}{2}\) باشد، حاصل \(\frac{{A + B}}{{A - B}}\) کدام است؟
- 8
- 4
- 5
- 9
گزینه 4 پاسخ صحیح می باشد:
\(\left. \begin{array}{l}{\log _{50}}A = \frac{1}{2} \Rightarrow A = {50^{\frac{1}{2}}} = \sqrt {50} = 5\sqrt 2 \\\\{\log _{32}}B = \frac{1}{2} \Rightarrow B = {32^{\frac{1}{2}}} = \sqrt {32} = 4\sqrt 2 \end{array} \right\} \Rightarrow \frac{{A + B}}{{A - B}} = \frac{{9\sqrt 2 }}{{\sqrt 2 }} = 9\)
معادله \({\log _3}(x - 1) = 4\) را حل کنید.
\({\log _3}(x - 1) = 4 \Rightarrow {3^4} = x - 1 \Rightarrow x - 1 = 81 \Rightarrow x = 82\)
اگر \({\log _{10}}\left( {98 + {{\log }_5}(x - 1)} \right) = 2\) مقدار \({\log _3}(x + 1)\) کدام است؟
- 3
- 2
- 4
- \(\frac{3}{2}\)
گزینه 1 پاسخ صحیح می باشد:
\( \Rightarrow 98 + {\log _5}(x - 1) = {10^2} = 100 \Rightarrow {\log _5}(x - 1) = 100 - 98 = 2\) فرض
\(\begin{array}{l} \Rightarrow x - 1 = {5^2} \Rightarrow x = 26\\\\ \Rightarrow {\log _3}(x + 1) = {\log _3}27 = 3\end{array}\)
تهیه کننده: استاد ملاسعیدی
دامنه توابع لُگاریتمی
فصل 3 : توابع نمایی و لگاریتمی
دامنه توابع لُگاریتمی
همانطور که در تعریف اشاره شد، \({\log _b}a\) وقتی تعریف شده است که a>0 و b>0 و \(b \ne 1\) باشد.
مثال
دامنه توابع زیر را تعیین کنید.
\(f(x) = lo{g_{(3 - x)}}(x + 2)\) الف
\( \Rightarrow \left\{ \begin{array}{l}x + 2 > 0 \Rightarrow x > - 2\\\\3 - x > 0 \Rightarrow x < 3\\\\3 - x \ne 1 \Rightarrow x \ne 2\end{array} \right.\,\,\,\,\,\,\,\,\mathop \Rightarrow \limits^ \cap \,\,\,\,\,{D_f} = ( - 2\,,\,3) - \{ 2\} \)
\(g(x) = {\log _3}(2 - |x|)\) ب
می دانیم که 0<3 و \(3 \ne 1\) است، لذا کافی است \(2 - |x| > 0\) باشد:
\( \Rightarrow |x|\, < 2 \Rightarrow - 2 < x < 2 \Rightarrow {D_f} = ( - 2\,,\,2)\)
نکات مقدماتی از لگاریتم
1 از تساوی های \({a^0} = 1\) و \({a^1} = a\) می توان نتیجه گرفت:
لگاریتم 1 در هر مبنای تعریف شده ای برابر صفر است؛ یعنی:
\({\log _a}1 = 0\)
و لگاریتم هر عدد در مبنای خودش برابر یک است؛ یعنی:
\({\log _a}a = 1\)
2 قرارداد می شود به جای \({\log _{10}}a\) می نویسیم \(\log \,\,a\)
3 اگر مبنای لگاریتم e (عدد نپر که تقریبا برابر 2/7 است) باشد، آن را با نماد Ln نمایش می دهیم. به عبارت دیگر به جای \({\log _e}a\) می نویسیم \(Ln\,\,a\)
4 اگر ab=1 ، آنگاه \({\log _b}a = - 1\) است؛ زیرا ab=1 نتیجه می دهد \(a = \frac{1}{b}\) یعنی \(a = {b^{ - 1}}\)
مثال
حاصل هر عبارت را بنویسید.
\(\log \,\,100 = \) الف
2
\(Ln\,\,1 = \) ب
0
\(Ln\,\,e = \) پ
1
\(\log \,\,0/1 = \) ت
-1
\({\log _{\cot \theta }}\,\,\tan \theta = \) ث
-1
زیرا \(\tan \theta .\cot \theta = 1\) بوده و طبق نکته 4 جواب برابر 1- است.
\({\log _{(\sqrt 3 + \sqrt 2 )}}\,\,(\sqrt 3 - \sqrt 2 ) = \) ج
-1
زیرا \((\sqrt 3 - \sqrt 2 )(\sqrt 3 + \sqrt 2 ) = 1\) است.
معادلات زیر را حل کنید.
\(\log \,\,(2x - 1) = 2\) الف
\( \Rightarrow 2x - 1 = {10^2} = 100 \Rightarrow 2x = 101 \Rightarrow x = \frac{{101}}{2}\)
\(Ln\,\,(x - 2) = 3\) ب
\( \Rightarrow x - 2 = {e^3} \Rightarrow x = {e^3} + 2\)
\(Ln\,\left( {\,\log \,\,(x + 7)} \right) = 0\) پ
\(\begin{array}{l} \Rightarrow \,\log \,\,(x + 7) = {e^0} = 1\\\\ \Rightarrow x + 7 = {10^1}\\\\ \Rightarrow x = 3\end{array}\)
مثال
نشان دهید توابع زیر وارون پذیرند، سپس تابع وارون آن ها را بنویسید.
\(f(x) = \log \,\,(3x + 1)\) الف
\(\begin{array}{l}f(a) = f(b) \Rightarrow \log \,\,(3a + 1) = \log \,\,(3b + 1) \Rightarrow 3a + 1 = 3b + 1\\\\ \Rightarrow 3a = 3b \Rightarrow a = b\end{array}\)
بنابراین تابع f یک به یک است و در نتیجه وارون پذیر می باشد. وارون تابع f برابر است با:
\(\begin{array}{l}\log \,\,(3x + 1) = y \Rightarrow 3x + 1 = {10^y} \Rightarrow 3x = {10^y} - 1\\\\ \Rightarrow x = \frac{{{{10}^y} - 1}}{3}\,\,\,\,\,\mathop \Rightarrow \limits^{f \to {f^{ - 1}}} \,\,\,\,\,y = \frac{{{{10}^x} - 1}}{3} \Rightarrow {f^{ - 1}}(x) = \frac{{{{10}^x} - 1}}{3}\end{array}\)
\(g\,\,(x) = {e^{2x}} - 5\) ب
\(g(a) = g(b) \Rightarrow {e^{2a}} - 5 = {e^{2b}} - 5 \Rightarrow {e^{2a}} = {e^{2b}} \Rightarrow 2a = 2b \Rightarrow a = b\)
بنابراین تابع g یک به یک است و در نتیجه وارون پذیر می باشد. وارون تابع g برابر است با:
\(\begin{array}{l}{e^{2x}} - 5 = y \Rightarrow {e^{2x}} = y + 5 \Rightarrow 2x = Ln\,\,(y + 5)\\\\ \Rightarrow x = \frac{1}{2}Ln\,\,(y + 5)\,\,\,\,\,\mathop \Rightarrow \limits^{g \to {g^{ - 1}}} \,\,\,\,\,y = \frac{1}{2}Ln\,\,(x + 5)\end{array}\)
حاصل هر یک از عبارات زیر را بنویسید.
\({\log _2}16 = \) الف
4
\({\log _7}49 = \) ب
2
\({\log _5}125 = \) پ
3
\(\log \,\,10 = \) ت
1
\(Ln\,\,{e^2} = \) ث
2
\(Ln\,\,\,\sqrt[3]{e} = \) ج
\(\frac{1}{3}\)
\({\log _{(\sqrt 3 - \sqrt 2 )}}(5 - 2\sqrt 5 ) = \) چ
\({\log _{(\sqrt 3 - \sqrt 2 )}}{(\sqrt 3 - \sqrt 2 )^2} = 2\)
\({\log _{\frac{1}{{\sqrt 2 - 1}}}}(\sqrt 2 + 1) = \) ح
می دانیم که \(\frac{1}{{\sqrt 2 - 1}} = \frac{1}{{\sqrt 2 - 1}} \times \frac{{\sqrt 2 + 1}}{{\sqrt 2 + 1}} = \frac{{\sqrt 2 + 1}}{{2 - 1}} = \sqrt 2 + 1\) ؛ بنابراین:
\({\log _{\frac{1}{{\sqrt 2 - 1}}}}(\sqrt 2 + 1) = {\log _{(\sqrt 2 + 1)}}(\sqrt 2 + 1) = 1\)
با فرض \({\log _2}\,\,({x^2} - x) = 1\) و x<0 ، مقدار \({3^x} + {x^3}\) را محاسبه نمایید.
\(\begin{array}{l}{\log _2}\,\,({x^2} - x) = 1 \Rightarrow \,({x^2} - x) = 2 \Rightarrow {x^2} - x - 2 = 0\\\\ \Rightarrow (x - 2)(x + 1) = 0 \Rightarrow \left\{ \begin{array}{l}x = 2\\\\x = - 1\end{array} \right.\,\,\,\,\,\mathop \Rightarrow \limits^{x < 0} \,\,\,\,\,x = - 1\\\\ \Rightarrow {3^x} + {x^3} = {3^{ - 1}} + {( - 1)^3} = \frac{1}{3} - 1 = - \frac{2}{3}\end{array}\)
حاصل \(A = {\log _4}\,\,\left( {{{\log }_3}\,\,\left( {{{\log }_2}\,\,512} \right)} \right)\) را بیابید.
می دانیم \({2^9} = 512\) است، بنابراین \({\log _2}\,\,512 = 9\) و در نتیجه \(A = {\log _4}\,\,\left( {{{\log }_3}\,\,9} \right)\) است.
از طرفی \({3^2} = 9\) ، پس \({\log _3}\,\,9 = 2\) بوده و داریم \(A = {\log _4}\,\,2\) . حال مقدار A به راحتی بدست می آید:
\(A = {\log _4}\,\,2 = \frac{1}{2}\)
ثابت کنید \({\log _2}\,\,3 + {\log _2}\,\,5 = {\log _2}\,\,15\)
این تساوی به صورت زیر اثبات می شود:
\(\begin{array}{l}\left. \begin{array}{l}{\log _2}\,\,3 = x \Rightarrow {2^x} = 3\\\\{\log _2}\,\,5 = y \Rightarrow {2^y} = 5\end{array} \right\}\,\,\,\mathop \Rightarrow \limits^ \times \,\,\,15 = {2^{x + y}} \Rightarrow x + y = {\log _2}\,\,15\\\\ \Rightarrow {\log _2}\,\,3 + {\log _2}\,\,5 = {\log _2}\,\,15\end{array}\)
تهیه کننده: استاد ملاسعیدی
توابع مثلثاتي
فصل 4 : مثلثات
توابع مثلثاتي
توابع \(y = \sin x\) و\(y = \cos x\) از ساده ترين توابع مثلثاتي هستند كه به ازاي هر مقدار x تعريف شده اند به عبارتي دامنه اين توابع، مجموعه اعداد حقيقي ℜ است و با تغيير x مقاديري كه براي \(\sin x\) و\(\cos x\) به دست مي آيد اعدادي بين 1 و1_ميباشند كه در حقيقت برد اين توابع \(\left[ { - 1,1} \right]\) می شود.
در حالت كلي تر، بيش ترين مقدار توابع \(a = \sin bx + c\) و \(a = \cos bx + c\)، \(\left| a \right|\)و كمترين \( - \left| a \right|\)مقدار و دوره تناوب آنها \(\frac{{2\pi }}{b}\)ميباشند.
همچنين بيش ترين و كمترين \(a = \sin bx + c\)مقدار و\(a = \cos bx + c\) عبارتست از
\(\min = - \left| a \right| + c\) و \(\max = \left| a \right| + c\)
مثال
در تابع \(f(x) = - 2\sin 3x\) مقادير حداقل و حداكثر و T، دوره تناوب تابع را مشخص كرده، نمودار آن را در بازه ي \(\left[ {0,T} \right]\) رسم كنيد.
\(\min f = - \left| 2 \right| = - 2,\max f = \left| { - 2} \right| = 2,T = \frac{{2\pi }}{3}\)
براي رسم، نقاطي كه تابع مقادير حداكثر و حداقل دارد را به دست آورده، همچنين نقاطي كه تابع صفر مي شود را نيز مشخص كنيم . سپس با توجه به نمودار توابع \(y = \sin x\) و \(y = \cos x\)شكل را كامل ميكنيم.
\(\begin{array}{l}2 = - 2\sin 3x \Rightarrow \sin 3x = - 1 \Rightarrow \frac{{3\pi }}{2} \Rightarrow x = \frac{{2\pi }}{3}\\\\ - 2 = - 2\sin 3x \Rightarrow \sin 3x = 1 \Rightarrow \frac{\pi }{2} \Rightarrow x = \frac{\pi }{3}\\\\0 = - 2\sin 3x \Rightarrow \sin 3x = 0 \Rightarrow 3x = 0 \Rightarrow x = 0\left\{ \begin{array}{l}3x = 0 \Rightarrow x = 0\\\\3x = \pi \Rightarrow x = \frac{\pi }{3}\\\\3x = 2\pi \Rightarrow x = \frac{{2\pi }}{3}\end{array} \right.\end{array}\)
نمودار تابع به صورت زير است:
مثال
تابع مثلثاتي مربوط به نمودار رسم شده را بنويسيد (موج كسينوسي)
\(\left. \begin{array}{l}\min y = - 1 = - \left| a \right| + c\\\max y = 3 = \left| a \right| + c\end{array} \right\}c = 1,\left| a \right| = 2\)
باتوجه به شكل \(a = 2\) ميباشد چون موج كسينوسي از بالا شروع شده است. همچنين:
\(t = \pi \Rightarrow \pi = \frac{{2\pi }}{b} \Rightarrow x = 2 \Rightarrow y = 2\cos (2x) + 1\)
مثال
اگر آونگ يك ساعت بزرگ، نوسانات عمودي داشته باشد و ضابطه اين نوسانات \(d(t) = \frac{{\pi t}}{{10}}\) باشد (t بر حسب ثانيه و d برحسب متر)
الف) آونگ از حالت تعادل حداكثر چند متر بالا ميرود.
ب) چه مدت طول ميكشد تا يك نوسان كامل انجام گيرد.
ج) پاندول چند نوسان كامل در مدت 2 دقيقه انجام ميدهد
د ) نمودار تابع را در يك دوره تناوب رسم كنيد.
الف)
در واقع بايد بيشترين مقدار تابع را محاسبه نمود، بنابراين كافيست به جاي \(\cos \frac{{\pi t}}{{10}}\)
ب) در 20 ثانيه يك نوسان كامل انجام ميگيرد \(b = \frac{\pi }{{10}} \Rightarrow t = \frac{{2\pi }}{{\left| b \right|}} = \frac{{2\pi }}{{\frac{\pi }{{10}}}} = 20\)
ج) نوسان كامل ثانيه \(2 \times 60 = 120 \Rightarrow 12 + 2 = 6\)
د)
\(\begin{array}{l}\max d = 8 \Rightarrow 8 = 2\cos \frac{\pi }{{10}}t + 6 \Rightarrow \cos \frac{\pi }{{10}}t = 1 \Rightarrow \frac{\pi }{{10}}t = 0,\frac{\pi }{{10}}t = 2\pi \Rightarrow t = 0,t = 20\\\\\min d = 4 \Rightarrow 4 = 2\cos \frac{\pi }{{10}}t + 6 \Rightarrow \cos \frac{\pi }{{10}}t = - 1 \Rightarrow \frac{\pi }{{10}}t = \pi ,\pi = 20\\\\d = 0 \Rightarrow \cos (\frac{{\pi t}}{{10}}) = 0 \Rightarrow \frac{\pi }{{10}}t = \frac{\pi }{2},\frac{\pi }{{10}}t = \frac{{3\pi }}{2} \Rightarrow t = 5,t = 15\\\\\max d = 8 \Rightarrow 8 = 2\cos \frac{\pi }{{10}}t + 6 \Rightarrow \cos \frac{\pi }{{10}}t = 1 \Rightarrow \frac{\pi }{{10}}t = 0,\frac{\pi }{{10}}t = 2\pi \Rightarrow t = 0,t = 20\\\\\min d = 4 \Rightarrow 4 = 2\cos \frac{\pi }{{10}}t + 6 \Rightarrow \cos \frac{\pi }{{10}}t = - 1 \Rightarrow \frac{\pi }{{10}}t = \pi ,\pi = 20\\\\d = 0 \Rightarrow \cos (\frac{{\pi t}}{{10}}) = 0 \Rightarrow \frac{\pi }{{10}}t = \frac{\pi }{2},\frac{\pi }{{10}}t = \frac{{3\pi }}{2} \Rightarrow t = 5,t = 15\\\\\end{array}\)معادله ي توابع
سينوسي و كسينوسی در حالت كلي به صورت\(y = a\sin \left[ {b(t - c)} \right] + d\) و \(y = a\cos \left[ {b(t - c)} \right] + d\)ميباشد كه مقدار c نمايشگر تعداد واحدي است كه \(y = a\sin (bt)\) و\(y = a\cos (bt)\)در راستاي محور طولها انتقال می یابند . هرگاه \(a > 0\)انتقال به طرف راست محور طول ها و هرگاه\(a < 0\)انتقال در جهت چپ محور طول ها صورت ميگيرد d تعداد واحدي است كه توابع\(y = a\sin \left[ {b(t - c)} \right] + d\) و\(y = a\cos \left[ {b(t - c)} \right] + d\) در راستاي محور عرض ها منتقل ميشود. اگر \(a > 0\)انتقال به طرف بالا و اگر \(b < 0\)انتقال در جهت پايين صورت ميگيرد.
مثال
معادله تابع مربوط به نمودار مثلاتي زير كه در يك دورهي تناوب رسم شده است را بنويسيد ( با شرط\(a > 0\))
\(\begin{array}{l}a = \frac{{4/5 - 1/5}}{2} = 1/5\\\\t = \frac{{5\pi }}{4} - \frac{\pi }{4} = \pi \Rightarrow \frac{{2\pi }}{b} = \pi \Rightarrow b = 2\end{array}\)
همچنين با توجه به شكل، نمودار شبيه نمودار سينوسي است كه از\(\pi = \frac{\pi }{4}\) شروع شده است. يعني موج سينوسي به اندازه \(\frac{\pi }{4}\)به طرف راست منتقل شده است . پس \(c = \frac{\pi }{4}\)و مقدار d نيز برابر است با:
\(d = \frac{{\max y + \min y}}{2} = \frac{{4/5 + 1/5}}{2} = 3\)
در نتيجه معادله ي تابع به صورت زير است:
\(y = 1/5\sin \left[ {2(t - \frac{\pi }{4})} \right] + 3\)
مثال
ارتفاع يك موج سوار نسبت به سطح زمين در حركت بر روي آب از رابطه ی
\(h(t) = 10\sin \left[ {\frac{\pi }{{30}}\left( {t - 15} \right)} \right] + 12\)
بدست می آيد)hبرحسب متر و t برحسب ثانيه)
الف) بيشترين و كمترين ارتفاع موج سوار چقدر است؟
ب) چه مدت طول ميكشد تا موج سوار از نقطه با كمترين ارتفاع به نقطه با بيشترين ارتفاع برسد؟
ج)چه مدت طول ميكشد تا يك حركت نوساني كامل انجام گیرد؟
د ) در طول يك دقيقه در چه زمانهايي ارتفاع موج سوار نسبت به سطح زمين 17 متر خواهد بود؟
الف)
\(\begin{array}{l}\max h = 10 + 12 = 22\\\\\max h = 12 - 10 = 2\end{array}\)
ب)
\(\begin{array}{l}10\sin \left[ {\frac{\pi }{{30}}(t - 15)} \right] + 12 = 22 \Rightarrow \sin \left[ {\frac{\pi }{{30}}(t - 15)} \right] = 1\\\\ \Rightarrow \frac{\pi }{{30}}(t - 15) = \frac{\pi }{2} \Rightarrow t - 15 = 15 \Rightarrow 15 \Rightarrow at = 3\\\\10\sin \left[ {\frac{\pi }{{30}}(t - 15)} \right] + 12 = 2 \Rightarrow \sin \frac{\pi }{{30}}(t - 15) = 1\\\\\frac{\pi }{{30}}(t - 15) = - \frac{\pi }{2} \Rightarrow t - 15 = - 15 \Rightarrow t = 0\end{array}\)
ج)
\(t = \frac{{2\pi }}{b} = \frac{{2\pi }}{{\frac{\pi }{{30}}}} = 60s\)
با استفاده از قسمت ب نيز ميتوان تشخيص داد كه دوره تناوب \(2 \times 30 = 60\) ثانیه می شود
د)
\(h(t) = 17 \Rightarrow \left( {} \right)\sin \left[ {\frac{\pi }{{30}}(t - 15)} \right] = \frac{1}{2} \Rightarrow \frac{\pi }{{30}}(t - 15) = \frac{\pi }{6},\frac{\pi }{{30}}(t - 15) = \frac{{5\pi }}{6} \Rightarrow t = 20,t = 40\)
يكي ديگر از توابع مثلثاتي\(y = \tan x\)است كه از رابطه \(\tan x = \frac{{\sin x}}{{\cos x}}\)به دست مي آيد. بنابراين \(\tan x\)به ازاي x هايي که \(\cos x = 0\)تعريف نمي شود . يعني تانژانت زوايايي كه 2 كمان آن ها بر حسب راديان به صورت \(x = k\pi + \frac{\pi }{2}\)تعريف نمي شوند. بنابراين دامنه تابع تانژانت برابر است با\(R - \left\{ {\left. x \right|} \right.x = k\pi + \left. {\frac{\pi }{2}} \right\},k \in z\)،و با توجه به اینکه \(\tan (x + \pi ) = \tan x\)دوره تناوب تابع تانژانت \(t = \pi \) مي باشد.
يكي ديگر از توابع مثلثاتي \(y = \cot x\) است كه برابر است با \(y = \frac{1}{{\tan x}}\)و چون \(\cot x = \frac{{\cos x}}{{\sin x}}\)بنابراين تابع \(y = \cot x\)به ازاي هر x كه \(\sin x = 0\) تعريف نمي شود. يعني دامنه ي تابع كتانژانت برابر است با \(D = R - \left\{ {\left. x \right|} \right.x = k\left. \pi \right\},k \in z\)
نمودار تابع \(y = \tan x\)در فاصله ي \( - \frac{{3\pi }}{2} < x < \frac{{3\pi }}{2}\)به صورت زير ميباشد :
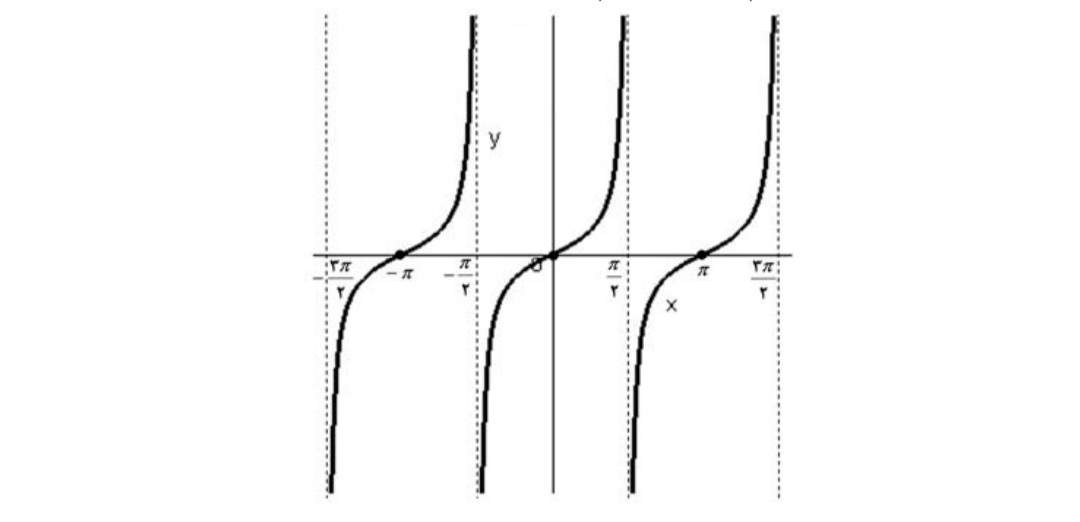
ديده ميشود كه هر شاخه در فاصله هاي به طول π تكرار ميگردد. واضح است كه هر شاخه از منحني صعودي است . اما تابع در دامنه اش نه صعودي و نه نزولي است
همچنين نمودار تابع\(y = \cot x\) در فاصله ي \( - \pi < x < \pi \)به صورت زير ميباشد:
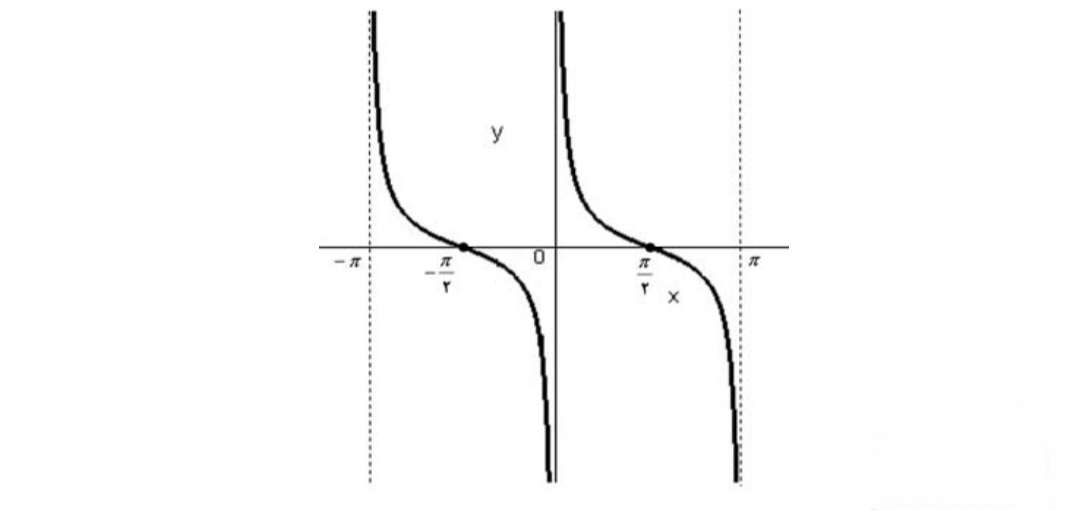
واضح است كه هر شاخه از منحني نزولي است
مثال
اگر \(0 < x < \frac{\pi }{2}\) و آنگاه مقادیر تابع \(y=tanx\) در بازه ی قرار دارند
مثال
اگر \( - \pi < x < \frac{{ - \pi }}{2}\)و \(\tan \alpha = \frac{2}{{m - 1}}\) آنگاه مقادیر تابع در بازه ي (∞ +, 0) قرار ميگيرند
روابط زير بين توابع مثلثاتي برقرار است ( اتحادهاي مثلثاتي)
\(\begin{array}{l}1)\sin 2\alpha = 2\sin \alpha \cos \alpha \\\\2)\cos 2\alpha = {\cos ^2}\alpha - {\sin ^2}\alpha = 1 - 2{\sin ^2}\alpha = 2{\cos ^2}\alpha - 1\\\\3){\sin ^2}\alpha = \frac{{1 - {{\cos }^2}\alpha }}{2}\\\\4){\cos ^2}\alpha = \frac{{1 + {{\cos }^2}\alpha }}{2}\\\\5){\mathop{\rm s}\nolimits} {\tan ^2}\alpha = \frac{{2{{\tan }^2}\alpha }}{2}\\\\6)\sin (\alpha \pm \beta ) = \sin \alpha \cos \beta \pm \cos \alpha \sin \beta \\\\7){\mathop{\rm s}\nolimits} \cos (\alpha \pm \beta ) = {\mathop{\rm s}\nolimits} \cos \alpha \sin \beta \pm \sin \alpha \sin \beta \\\\8)\tan (\alpha \pm \beta ) = \frac{{\tan \alpha \pm \tan \beta }}{{1 \pm \tan \alpha \tan \beta }}\end{array}\)
مثال
درستي اتحادهاي زير را بررسي كنيد.
\(\begin{array}{l}\sin 2x = \frac{{2\tan x}}{{1 + {{\tan }^2}x}}\\\\\cos 2x = \frac{{1 - {{\tan }^2}x}}{{1 + {{\tan }^2}x}}\\\\\frac{{2\sin 2x}}{{2{{\cos }^2}x + 1}} = \frac{{\sin x}}{{2\cos x - 1}} + \frac{{\sin x}}{{2\cos x + 1}}\end{array}\)
\(\begin{array}{l}\frac{{2\tan x}}{{1 + {{\tan }^2}x}} = \frac{{\frac{{2\sin x}}{{\cos x}}}}{{\frac{1}{{{{\cos }^2}x}}}}\\\\\frac{{1 - {{\tan }^2}x}}{{1 + {{\tan }^2}x}} = \frac{{\frac{{1 - {{\sin }^2}x}}{{{{\cos }^2}x}}}}{{\frac{1}{{{{\cos }^2}x}}}} = \frac{{{{\cos }^2}x - {{\sin }^2}x}}{{{{\cos }^2}x}} = {\cos ^2}x - {\sin ^2}x = {\cos ^2}x\\\\\frac{{\sin x}}{{2\cos x - 1}} + \frac{{\sin x}}{{2\cos x + 1}} = \frac{{2\sin x\cos x + 2\sin x\cos x - \sin x}}{{4{{\cos }^2}x - 1}} = \frac{{4\sin x\cos x}}{{4{{\cos }^2} - 1}} = \frac{{2\sin 2x}}{{2(2{{\cos }^2}x - 1) + 1}} = \frac{{2\sin 2x}}{{2\cos 2x + 1}}\\\\\cos 2x = \frac{{1 - {{\tan }^2}x}}{{1 + {{\tan }^2}x}}\\\\\frac{{2\sin 2x}}{{2{{\cos }^2}x + 1}} = \frac{{\sin x}}{{2\cos x - 1}} + \frac{{\sin x}}{{2\cos x + 1}}\end{array}\)
مثال
مقدار نسبت هاي مثلثاتي زاویه ی 75 درجه را بيابيد.
\(\begin{array}{l}\sin 75 = \sin (45 + 30) = \sin 45\cos 30 + \cos 45\sin 30 = \frac{{\sqrt 2 }}{2}(\frac{{\sqrt 3 }}{2} + \frac{1}{2}) = \frac{{\sqrt 6 + \sqrt 2 }}{4}\\\\\sin 75 = \sin (45 + 30) = \cos 45\cos 30 - \sin 45\sin 30 = \frac{{\sqrt 2 }}{2}(\frac{{\sqrt 3 }}{2} - \frac{1}{2}) = \frac{{\sqrt 6 - \sqrt 2 }}{2}\\\\\tan 75 = \sin (45 + 30) = \frac{{\tan 45 + \tan 30}}{{1 - \tan 45\tan 30}} = \frac{{1 + \frac{{\sqrt 3 }}{{\sqrt 3 }}}}{{1 - \frac{{\sqrt 3 }}{{\sqrt 3 }}}} = \frac{{3 + \sqrt 3 }}{{3 - \sqrt 3 }}\\\\\cot 75 = \frac{1}{{\tan 75}} = \frac{{3 - \sqrt 3 }}{{3 + \sqrt 3 }}\end{array}\)
روابط مثلثاتي زير همواره برقرار است:
قوانين ضرب به جمع
\(\begin{array}{l}1)\sin \alpha \cos \beta = \frac{1}{2}\left[ {\sin (\alpha + \beta ) + \sin (\alpha - \beta )} \right]\\\\2)\sin \alpha \cos \beta = \frac{1}{2}\left[ {\cos (\alpha - \beta ) - \cos (\alpha + \beta )} \right]\\\\3)\cos \alpha - \sin \beta = \frac{1}{2}\left[ {\cos (\alpha + \beta ) + \cos (\alpha - \beta )} \right]\end{array}\)
قوانين جمع به ضرب
\(\begin{array}{l}1)\sin \alpha + \cos \beta = 2\left[ {\cos (\frac{{\alpha + \beta }}{2})\cos (\frac{{\alpha - \beta }}{2})} \right]\\\\2)\sin \alpha + \sin \beta = 2\sin (\frac{{\alpha + \beta }}{2})\cos (\frac{{\alpha - \beta }}{2})\\\\3)\cos \alpha - \cos \beta = - 2\sin (\frac{{\alpha + \beta }}{2})\sin (\frac{{\alpha - \beta }}{2})\\\end{array}\)
اثبات روابط فوق به عنوان تمرين واگذار ميگردد.
مثال
\(\begin{array}{l}\sin x + \cos x = \sin x + \sin (\frac{\pi }{2} - x) = \\2\sin \frac{\pi }{4}\cos \frac{{x - \frac{\pi }{2} + x}}{2} = \sqrt 2 \cos (\frac{\pi }{4} - x) = \sqrt 2 \cos (\frac{\pi }{4} + x)\end{array}\)
مثال
\(\begin{array}{l}\sin x - \cos x = \sin x - \sin (\frac{\pi }{2} - x) = \sin x + \sin (x - \frac{\pi }{2})\\\\2\sin \frac{{x + x - \frac{\pi }{2}}}{2}\cos \frac{\pi }{4} = \sqrt 2 \sin (x - \frac{\pi }{4}) = \\\\\sqrt 2 \cos (\frac{{3\pi }}{4} - x)\end{array}\)
مثال
درستي اتحادهاي زير را تحقيق كنيد.
\(\begin{array}{l}\frac{{\sin 7x + \sin x}}{{\cos 7x + \cos x}} = \tan 4x\\\\\cos 5x\cos 2x + \sin 4x\sin 3x - \cos 4x\cos x = \sin 2x\sin 3x\end{array}\)
الف)
\(\begin{array}{l}\frac{{\sin 7x + \sin x}}{{\cos 7x + \cos x}} = \frac{{2\sin (\frac{{7x + x}}{2})\cos (\frac{{7x - x}}{2})}}{{2\cos (\frac{{7x + x}}{2})\cos (\frac{{7x - x}}{2})}} = \frac{{\sin 4x}}{{\cos 4x}} = \tan 4x\\\\\cos 5x\cos 2x + \sin 4x\sin 3x - \cos 4x\cos x = \sin 2x\sin 3x\\\\\\\\\\\cos 5x\cos 2x + \sin 4x\sin 3x - \cos 4x\cos x = \sin 2x\sin 3x\end{array}\)
ب)
\(\begin{array}{l}\cos 5x\cos 2x + \sin 4x\sin 3x - \cos 4x\cos x = \frac{1}{2}\left[ {\cos (5x + 2x) + \cos (5x - 2x)} \right]\\\\ + \frac{1}{2}\left[ {\cos (4x - 3x) + \cos (4x + 3x)} \right]\\ - \frac{1}{2}\left[ {\cos (4x + x) + \cos (4x - x)} \right]\\ = \frac{1}{2}\left[ {\cos 7x + \cos 3x + \cos x - \cos 7x - \cos 5x - \cos 3x} \right]\\\\ = \frac{1}{2}\left[ {\cos x - \cos 5x} \right]\\\\ = \frac{1}{2}( - 2)\sin (\frac{{x + 5x}}{2})\sin (\frac{{x0 - 5x}}{2})\\\\ - \sin 3x\sin ( - 2x)\\\\ = \sin 3x\sin 2x\end{array}\)
حل 4 معادله ي مثلثاتي اصلي به صورت هاي زير است:
\(\begin{array}{l}1)\sin x = \sin \alpha \Rightarrow x = 2k\pi + \alpha ,x = 2k\pi + \pi - \alpha \\\\2)\cos x = \cos \alpha \Rightarrow x = 2k\pi \pm \alpha \\\\3)\tan x = \tan \alpha \Rightarrow k\pi \pm \alpha \\\\4)\cot x = \cot \alpha \Rightarrow k\pi \pm \alpha \end{array}\)
مثال
معادلات مثلثاتي زير را حل كنيد
\(\begin{array}{l}2{\cos ^2}\theta + \cos \theta = 1\\\\1 - 3\cos 2x = 2{\sin ^2}x\\\\4\tan x + cotx = 5\end{array}\)
الف)
\(\begin{array}{l}2{\cos ^2}\theta + \cos \theta = 1 \Rightarrow 2{\cos ^2}\theta + \cos \theta - 1 = 0 \Rightarrow \\\\(2\cos - 1)(\cos \theta + 1) = 0 \Rightarrow \\\\\left\{ \begin{array}{l}2{\cos ^2}\theta - 1 = 0 \Rightarrow \cos \theta = \frac{1}{2} = \cos \frac{\pi }{3} \Rightarrow \theta = 2k\pi \pm \frac{\pi }{3}\\\\(\cos \theta + 1) = 0 \Rightarrow \cos \theta = - 1 = \cos \pi \Rightarrow \theta = 2k\pi + \pi \end{array} \right.\end{array}\)
ب)
 \(\begin{array}{l}1 - 3(1 - 2{\sin ^2}x) = 2{\sin ^2}x \Rightarrow 1 - 3 + 2 = 6{\sin ^2}x = 2{\sin ^2}x \Rightarrow + 4{\sin ^2}x = + 2\\\\ \Rightarrow {\sin ^2}x = \frac{1}{2} \Rightarrow \sin x = \pm \frac{{\sqrt 2 }}{2}\\\\\sin x = \frac{{\sqrt 2 }}{2} \Rightarrow \sin x = \sin \frac{\pi }{4} \Rightarrow x = 2k\pi + \frac{\pi }{4}\\\\\sin x = \frac{{ - \sqrt 2 }}{2} \Rightarrow \sin x = \sin ( - \frac{\pi }{4}) \Rightarrow x = 2k\pi - \frac{\pi }{4},x = 2k\pi + \frac{{5\pi }}{4}\\\end{array}\)
\(\begin{array}{l}1 - 3(1 - 2{\sin ^2}x) = 2{\sin ^2}x \Rightarrow 1 - 3 + 2 = 6{\sin ^2}x = 2{\sin ^2}x \Rightarrow + 4{\sin ^2}x = + 2\\\\ \Rightarrow {\sin ^2}x = \frac{1}{2} \Rightarrow \sin x = \pm \frac{{\sqrt 2 }}{2}\\\\\sin x = \frac{{\sqrt 2 }}{2} \Rightarrow \sin x = \sin \frac{\pi }{4} \Rightarrow x = 2k\pi + \frac{\pi }{4}\\\\\sin x = \frac{{ - \sqrt 2 }}{2} \Rightarrow \sin x = \sin ( - \frac{\pi }{4}) \Rightarrow x = 2k\pi - \frac{\pi }{4},x = 2k\pi + \frac{{5\pi }}{4}\\\end{array}\)
چهار جواب معادله ي مثلثاتي فوق را ميتوان به صورت زير خلاصه كرد:
\(x = k\pi + \frac{\pi }{4},k \in z\)
ج)
\(\begin{array}{l}4\tan x + \cot x = 5 \Rightarrow 4\tan x + \frac{1}{{\tan x}} = 5 \Rightarrow 4{\tan ^2}x + 1 = 5\tan x(x \ne \frac{{k\pi }}{2})\\\\ \Rightarrow 4{\tan ^2}x - 5\tan x + 1 = 0\left\{ \begin{array}{l}\tan x = 1 = \tan \frac{\pi }{4} \Rightarrow x = k\pi + \frac{\pi }{4}\\\\\tan x = \frac{1}{4} = \tan \alpha \Rightarrow x = k\pi + \alpha \end{array} \right.\end{array}\)
چون كوچكترين زاويه اي كه مقدار تانژانت آن برابر با\(\frac{1}{4}\)  است را بدون ماشين حساب نميتوان يافت از 1 زاويه αاستفاده كرديم.
است را بدون ماشين حساب نميتوان يافت از 1 زاويه αاستفاده كرديم.
تهیه کننده: حامد دلیجه
- آزمون آنلاین تمامی دروس پایه یازدهم
- گام به گام تمامی دروس پایه یازدهم
- ویدئو های آموزشی تمامی دروس پایه یازدهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه یازدهم
- فلش کارت های آماده دروس پایه یازدهم
- گنجینه ای جامع از انشاء های آماده پایه یازدهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه یازدهم
حل معادلات مثلثاتي به روش نمودار
فصل 4 : مثلثات
حل معادلات مثلثاتي به روش نمودار
بعضي از معادلات مثلثاتي از طريق جبري قابل حل نيستند و فقط با استفاده از رسم نمودار ميتوان تعداد جوابها را بدست آورد و مقدار آنها را تخمين زد.
مثال
معادله\(\sin x + 2x = 1\) را حل كنيد.
ابتدا معادله را به صورت \(\sin x = - 2x + 1\)مينويسيم . سپس نمودارهاي\(f(x) = \sin x\)و\(g(x) = - 2x + 1\)را رسم ميكنيم طول نقاط تلاقي اين دو نمودار جواب معادله مورد نظر ميباشد.
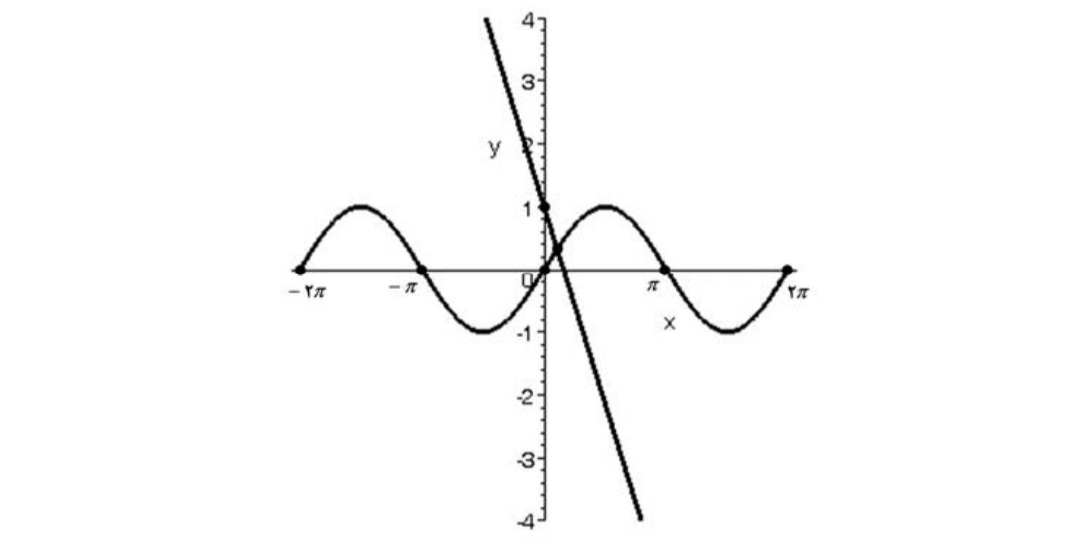
همانطوركه مشاهده ميكنيد معادله يك جواب دارد كه بين صفر و\(\frac{\pi }{2}\) است با روش آزمايش و خطا π ميتوان جواب تقريبي را بدست آورد .
مثلا:
\(\begin{array}{l}x = \frac{\pi }{4} \Rightarrow \left\{ \begin{array}{l}f(\frac{\pi }{4}) = \sin \frac{\pi }{4} = \frac{{\sqrt 2 }}{2} \approx \frac{{1/4}}{2} = 0/7\\\\g(x) = - \frac{\pi }{2} + 1 \approx \frac{{3/14}}{2} + 1 = - 0/75\end{array} \right.\\\\x = \frac{\pi }{6} \Rightarrow \left\{ \begin{array}{l}f(\frac{\pi }{6}) = \sin \frac{\pi }{6} = \frac{1}{2}\\\\g(x) = - \frac{\pi }{3} + 1 \approx - \frac{{3/14}}{2} + 1 = - 0/05\end{array} \right.\\x = 15^\circ = \frac{\pi }{{12}} \Rightarrow \left\{ \begin{array}{l}f(\frac{\pi }{{12}}) = \sin 15^\circ \approx 0/25\\g(x) - \frac{\pi }{6} + 1 \approx \frac{{2/86}}{6} = 0/48\end{array} \right.\end{array}\)
\(\)ً
لذا جواب معادله ي فوق نزديك به \(\frac{\pi }{{12}} \approx 026\) است و با ادامه ي اين روش و با استفاده از ماشين حساب ميتوان تقريب هاي بهتري يافت.
تهیه کننده: حامد دلیجه
وارون معادله مثلثاتی
فصل 4 : مثلثات
وارون توابع مثلثاتي
ميدانيم تابعي وارون پذير است كه يك به يك باشد بنابراين براي بدست آوردن وارون توابع مثلثاتي كه يك به يك نيستند، بايد دامنه ي آنها را تحديد كنيم تا آنها تبديل به يك تابع يك به يك شوند.
تحديد تابع \(y = \sin x\)به بازه ي \(\left[ { - \frac{\pi }{2},\frac{\pi }{2}} \right]\)يك به يك بوده و معكوس پذير است.
\(y = \sin x,x \in \left[ { - \frac{\pi }{2},\frac{\pi }{2}} \right]\)
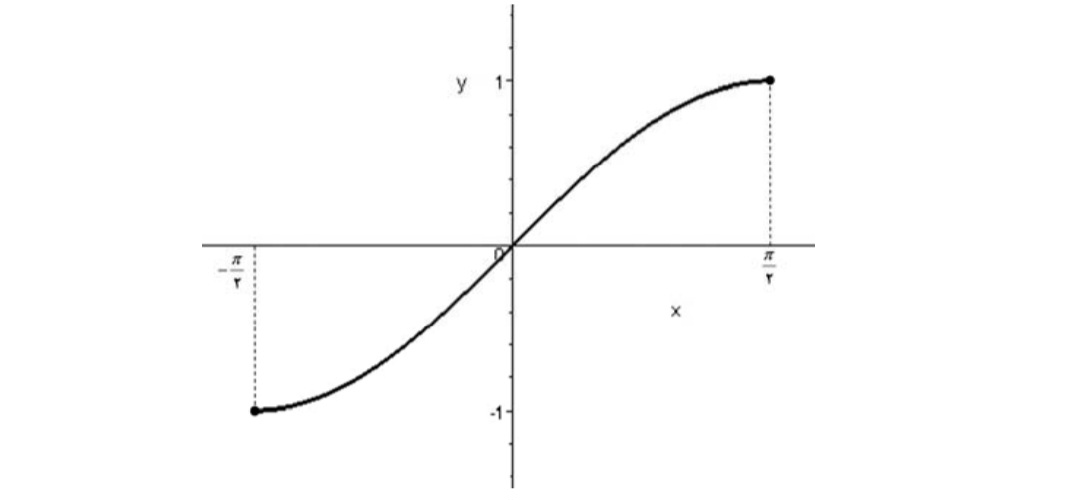
معكوس \(y = \sin x\)را با نمادهاي \(y = \arcsin x\)يا \(y = si{n^{ - 1}}\)
نمایش می دهیم پس:
\(y = si{n^{ - 1}}x:\left[ { - 1,1} \right] \to \left[ { - \frac{\pi }{2},\frac{\pi }{2}} \right]\)
نمودار آن بصورت زیر است:
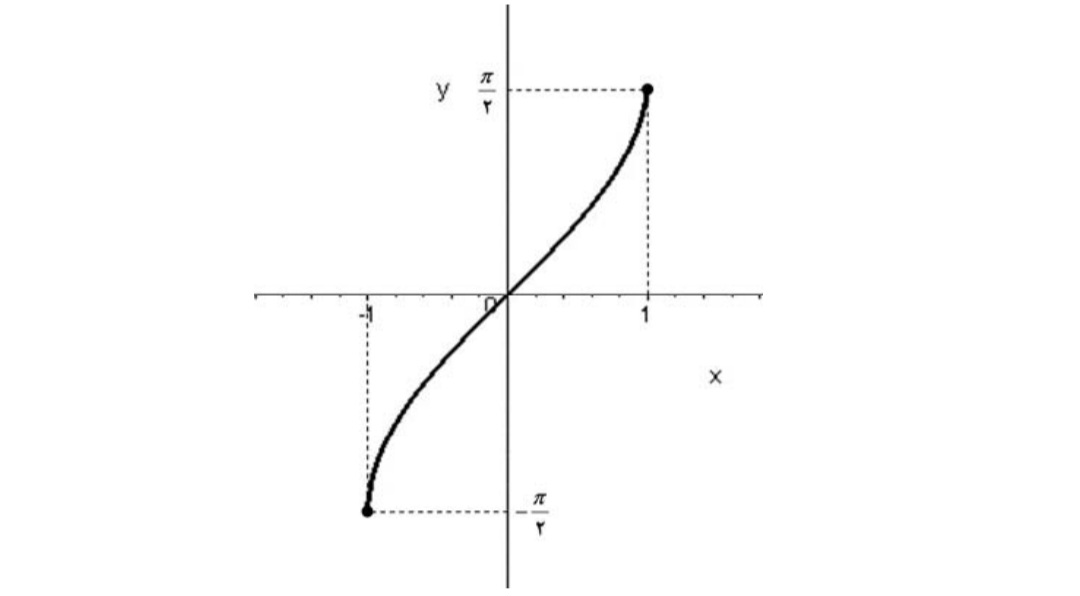
تحدید تابع \(y = \cos x\) به بازه ی \(( {-0,\pi } )\)یک به یک بوده و معکوس پذیر است.
\(y = \cos x,x \in \left[ {0,\pi } \right]\)
\(y = \cos x\)معکوس را با نماد های\(y = ars\cos x\)یا \(y = {\cos ^{ - 1}}x\)نمایش میدهیم پس
\(y = {\cos ^{ - 1}}x:\left[ { - 1,1} \right] \to \left[ {0,\pi } \right]\)
و نمودار آن به صورت زیر است:
تحدید تابع\(y=tanx\) به بازه ی \(( - \frac{\pi }{2},\frac{\pi }{2})\)یک به یک بوده و معکوس پذیر است
\(y = \tan x,x \in ( - \frac{\pi }{2},\frac{\pi }{2})\)
معکوس \(y = \tan x\)را با نماد های \(x = \arctan x\)یا \(y = {\tan ^{ - 1}}\) نمایش می دهیم
\(y = {\tan ^{ - 1}}x:R \to ( - \frac{\pi }{2},\frac{\pi }{2})\)
تابع \(y=cotx\)به بازه ی \((0,\pi )\)يك به يك بوده و معكوس پذير است.
\(y = \cot x,x \in \left( {0,\pi } \right)\)
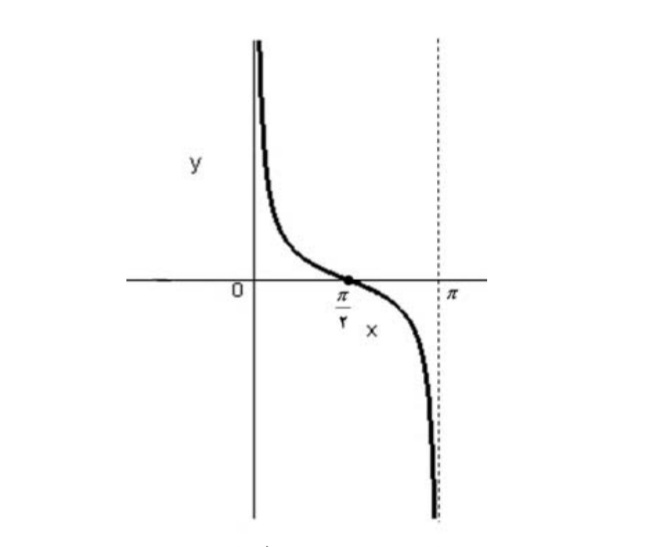
معكوس \(y = \cot x\) را با نمادهاي \(y = arc\cot x\)يا\(y = {\cot ^{ - 1}}x\)
\(y = \cot x\) را با نمادهاي \(y = arc\cot x\)يا\(y = {\cot ^{ - 1}}x\)
نمایش میدهیم پس:
\(y = {\cot ^{ - 1}}x:R \to (0,\pi )\)
و نمودار آن به صورت زير است:
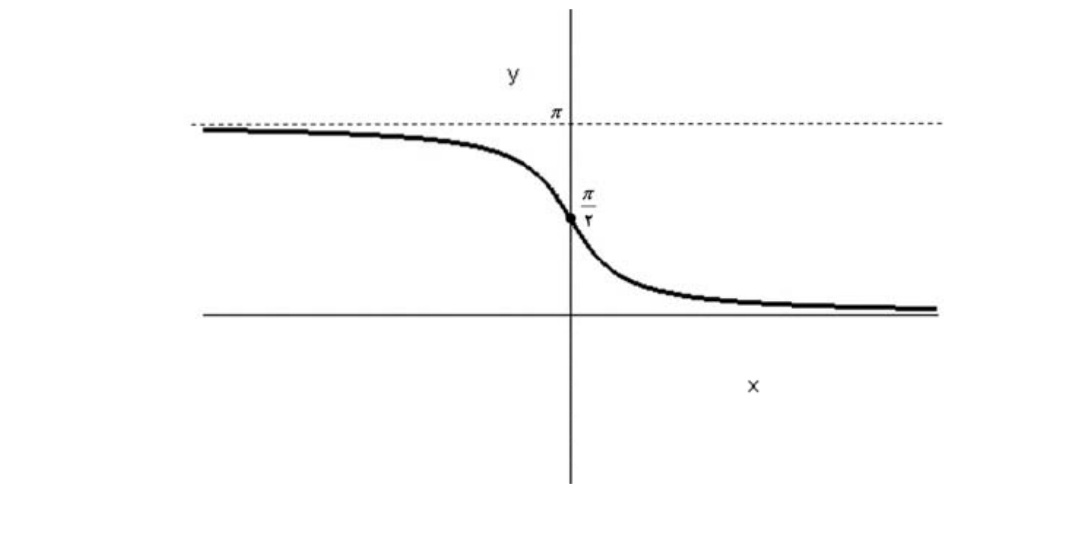
مثال
حاصل عبارتهاي زير را بدست آوريد.
\(\cos \left[ {2{{\sin }^{ - 1}}} \right.( - \frac{{\sqrt 3 }}{2}) + {\cos ^{ - 1}}(\frac{{ - 1}}{2}\left. ) \right]\)(الف
\(\cos \left[ {{{\sin }^{ - 1}}} \right.( - \frac{4}{2}))\)(ب
\({\sin ^{ - 1}}\left( a \right) = b\)یعنی\(\sin b = a\) به این توضیح داریم:
\({\cos ^{ - 1}}(\frac{{\sqrt 2 }}{2}) = \frac{\pi }{4}\) \({\sin ^{ - 1}}\left( 0 \right) = 0\)
\({\cot ^{ - 1}}( - 1) = \frac{{3\pi }}{4}\) \({\tan ^{ - 1}}(1) = \frac{\pi }{4}\)
تهیه کننده: حامد دلیجه
همسايگي يك نقطه
فصل 5 : حد و پیوستگی
همسايگي يك نقطه
اگر a عددي حقيقي و δ يك عدد مثبت باشد، بازه ي\((a - \delta + \delta )\) را يك همسايگي a مينامند a) مركز و δ شعاع همسايگي نام دارند(. اگر a را از اين همسايگي حذف كنيم، آن را يك همسايگي محذوف a مينامند.
مثال
هر يك از بازه هاي\(\left( {1/9,2/1} \right),\left( {0,4} \right),\left( {1,3} \right)\) يك همسايگي 2 هستند.
مثال
هر يك از مجموعه هاي \((0,2) \cup (2,4),(1,3) - \left\{ 2 \right\}\)و\(\left\{ {\left. x \right|} \right.1/9 < x < 2/1,x \ne \left. 2 \right\}\) يك همسايگي محذوف 2 هستند.
مثال
اگر \((3k - 2,k + 4)\)يك همسايگي 3 باشد، a و δ را به دست آوريد؟
عدد 3 نقطه ي وسط بازه است، پس
\(3 = \frac{{(3k - 2) + (k + 4)}}{2} \Rightarrow 4k + 2 = 6 \Rightarrow k = 1\)
بنابراين همسايگي به صورت \((1,5)\)در مي آيد و \(a = \frac{{1 + 5}}{2} = 3\) و\(\delta = 3 - 1 = 2\)
مثال
اگر مجموعه ی \(( - 3,y) \cup (2,{x^2} + 1)\)نمايشگر يك همسايگي محذوف باشد، حاصل \(3{x^2} + y\)را به دست آوريد؟
ابتدا طوري دو بازه را مينويسيم كه اعداد از كوچك به بزرگ مرتب شوند و داريم \(y = 2\) چون همسايگي محذوف 2 است، بايد:
\(2 = \frac{{ - 2 + {x^2} + 1}}{2} \Rightarrow {x^2} - 2 = 4 \Rightarrow x = \pm \sqrt 6 \)
بنابراين داريم:
\(3{x^2} + y = 3( \pm \sqrt 6 ) + 2 = 20\)
مثال
كداميك از مجموعه هاي زير يك همسايگي محذوف a را نمايش ميدهند؟
الف) \(\left\{ {x \in \left. R \right|} \right.0 < \left| {x - a} \right| < \left. \delta \right\}\) ب)\(\left\{ {x \in \left. R \right|} \right.\left| {x - a} \right| < \left. \delta \right\}\)
الف)
\(\begin{array}{l}0 < \left| {x - a} \right| < \delta \Rightarrow \left\{ \begin{array}{l}\left| {x - a} \right| < \delta \\\\\left| {x - a} \right| \ne 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l} - \delta < x - a < a + \delta \\\\x \ne a\end{array} \right.\\\\x \in (a - \delta ,a + \delta ) - \left\{ a \right\}\end{array}\)
بنابراين يك همسايگي محذوف a را نمايش ميدهد.
ب)
\(\left| {x - a} \right| < \delta \Rightarrow - \delta < x - a < \delta \Rightarrow a - \delta < x < a + \delta \)
بنابراین یک همسايگي هست ولی همسایگی محذوف نیست.
همسایگی چپ و راست یک نقطه
اگر a عددي حقيقي و δ يك عدد مثبت باشد، بازه به صورت\((a - \delta ,a)\) را يك همسايگي چپ a و بازه به صورت\((a,a + \delta )\) را يك همسايگي راست a ميناميم.
مثال
هر يك از بازه هاي\(\left( {3,3/1} \right)\) و \(\left( {3,4} \right)\) و\(\left( {3,5} \right)\) يك همسايگي راست 3 و هر يك از بازه هاي \(\left( {2/9,3} \right)\)و \(\left( {2,3} \right)\)و\(\left( { - 1,3} \right)\) يك همسايگي چپ 3 هستند.
مثال
همسايگي \(\left( {2,3} \right) \cup \left( {3,4} \right)\)در واقع از اجتماع يك همسايگي چپ 3 يعني \(\left( {2,3} \right)\) و يك همسايگي راست 3 يعني\(\left( {3,4} \right)\) تشكيل شده است.
اگر I يك همسايگي نقطه ي a باشد، گوييم تابع f در همسايگي I تعريف شده است، . هرگاه\(I \subseteq {D_f}\)
مثال
تابع \(y = \sqrt x \)در كداميك از همسايگي هاي زير تعريف شده است
الف) \(\left( {2,3} \right)\) ب) \(\left( {0,4} \right)\)
ج)\(\left( { - 2,1} \right)\) د) \(\left( { - 1, - 3} \right)\)
می دانیم پس داريم :
الف) \(\left( {2,3} \right) \subseteq {D_f}\)پس تابع در همسايگي \(\left( {2,3} \right)\) تعريف شده است.
ب)\(\left( {0,2} \right) \subseteq {D_f}\) پس تابع در همسايگي \(\left( {0,4} \right)\)تعريف نشده است.
ج)\(\left( { - 2,1} \right) \not\subset {D_f}\) پس تابع در همسايگي \(\left( { - 2,1} \right)\) تعريف نشده است
د) \(\left( { - 1, - 3} \right) \not\subset {D_f}\)پس تابع در همسایگی \(\left( { - 1, - 3} \right)\)تعریف نشده است.
مثال
تابع \(y = \sqrt {x - 1} \)در كداميك از همسايگي هاي عدد يك تعريف شده است.
الف)\(\left( {1,1 + \delta } \right)\) ب)\((1 - \delta ,1 + \delta )\) ج) \((1 - \delta ,1)\)
می دانیم\({D_f} = \left[ {1, + \infty )} \right.\) پس \(\delta \)هر عدد مثبتي كه باشد تابع در همسايگي\((1,1 + \delta )\) تعريف شده است . ولي به ازاي هيچ مقدار مثبتي از δ در همسايگي هاي \((1 - \delta ,1 + \delta )\)و \((1 - \delta ,1)\) تعريف نشده است.
مثال
نمودار تابع f زيربه صورت رسم شده است. با توجه به نمودار مشخص كنيد تابع f در كداميك از همسايگي هاي زير تعريف شده است.
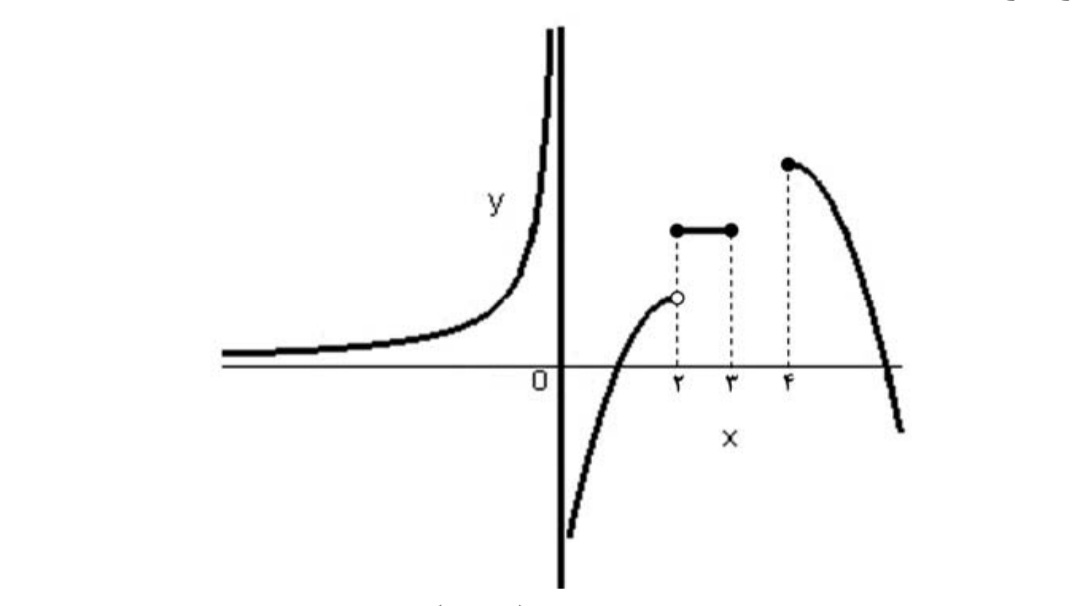
الف) \(\left( { - 3, - 1} \right)\) ب) \(\left( { - 2,2} \right)\)
ج) \(\left( {1,2} \right)\) د) \(\left( {0,3} \right)\)
هـ)\(\left( {0,7} \right)\) و) \(\left( {3,4} \right)\)
ز) \(\left( {2,3} \right)\)
با توجه به شكل داريم:
\({D_f} = \left( { - \infty ,0} \right) \cup \left( {0,3} \right) \cup \left( {4, + \infty } \right)\)
بنابراين تابع در همسايگي هاي\(\left( {0,3} \right),\left( {1,2} \right),\left( { - 3, - 1} \right)\) و \(\left( {2,3} \right)\) تعريف شده ولي در همسايگي هاي \(\left( {0,7} \right),\left( { - 2,2} \right)\)و \(\left( {3,4} \right)\)تعريف نشده است.
وقتي ميگوييم متغير مستقل x به عدد ثابت a نزديك ميشود . يعني هر اندازه كه بخواهيم متغير x به a نزديك ميشود ولي هيچگاه مساوي a نميشود. به بيان ديگر به ازاي هر عدد دلخواه و مثبت مانند ε داريم:
\(0 < \left| {x - a} \right| < \delta \)
مثال
با رسم يك جدول و نوشتن چند مقدار در آن مفهوم نزديك شدن متغير x را به عدد 2 نمايش دهيد.

مثال
با رسم یک جدول و نوشتن چند مقدار در آن مفهوم نزدیک شدن متغیر x رابه عدد ثابت -2نمایش دهید.

برای یک تابع fاگر مقادیر متغیر مستقل x(در دامنه f )به عددی مانند a نزدیک شوند و مشاهده شود که مقادیرf(x) به عددی مانندl نزدیک می شوند.(ممکن است مساوی l هم بشوند) گوییم تابعf در نقطه ی aحد داردو حد آن برابرl است و می نویسیم:
\(\mathop {\lim }\limits_{x \to a} f(x) = l\)
مثال
با رسم يك جدول حاصل حد تابع\(f(x) = 2x + 3\) را در\(x = 5\) محاسبه کنید.

همانگونه که از جدول مشاهده می شود بانزدیک شدن مقادیر متغیر x به عدد 5 مقادیر تابعf به عدد 13 نزدیک می شوند و داریم :
\(\mathop {\lim }\limits_{x \to 5} (2x + 3) = 13\)
توجه:تابع fدر\(x = 5\) تعریف شده است و \(f(5) = 13\)می باشد.
مثال
بارسم یک جدول حاصل حد تابع \(f(x) = \frac{{{x^2} - 4}}{{x - 2}}\)را در x=2محاسبه کنید.

همانگونه که از جدول مشاهده می شود با نزدیک شدن مقادیر متغیر x به عدد 2مقادیر تابع f به عدد 4 نزدیک می شوندو داریم:
\(\mathop {\lim }\limits_{x \to 2} \frac{{{x^2} - 4}}{{x - 2}}\)
توجه:تابعf در x=2 تعریف نشده است ولی حد دارد.
مثال
با رسم یک جدول رفتار تابع\(f(x) = \frac{1}{{x - 1}}\) را وقتی متغیر X به عدد یک نزدیک می شود بررسی کنید.

همانگونه که از جدول مشاهده می شود وقتی متغیر به عدد یک نزدیک می شودمقادیر تابع به هیچ عددی نزدیک نمی شوندو از نظر قدر مطلق مرتبا افزایش می یابند.بنابراین میگوییم تابع fدرx=1 حد ندارد.
توجه:تابع fدرx=1 نه تعریف شده است و نه حد دارد.
شرط لازم برای انکه بتوان درمورد حد تابع F درx=a صحبت کرد ان است که تابع F دست کم در یک همسایگی A تعریف شده باشد
مثال
در کدامیک از توابع زیرمیتوان از حد تابعf در نقطه ی داده شده صحبت کرد.
الف)  \(f(x) = \frac{1}{{\left| x \right|}},x = \frac{1}{2}\) ب) \(f(x) = x - \left| x \right|\)
\(f(x) = \frac{1}{{\left| x \right|}},x = \frac{1}{2}\) ب) \(f(x) = x - \left| x \right|\)
ج)\(f(x) = \left\{ \begin{array}{l}x - 1,x < 1\\\\1 - x,x > 1\end{array} \right.,x = 1\)
الف)
باتوجه به اینکه\({D_f} = ( - \infty ,0) \cup \left[ {1, + \infty )} \right.\) پس تابع f در هیچ همسایگی \(\frac{1}{2}\) تعریف نشده است.یعنی نمیتوان از حدتابع fدر\(x = \frac{1}{2}\) صحبت کرد.
\(\frac{1}{2}\) تعریف نشده است.یعنی نمیتوان از حدتابع fدر\(x = \frac{1}{2}\) صحبت کرد.
ب)
با توجه به اين كه \({D_f} = R\)پس میتوان درمورد حد تابع در x=2صحبت کرد
ج)
با توجه به اين كه \({D_f} = R - \left\{ 1 \right\}\)پس میتوان درمورد حد تابع در x=2 را بررسي کرد

همانگونه كه از جدول مشاهده ميشود داريم:
\(\mathop {\lim }\limits_{x \to 1} f(x) = 0\)
توجه: تابع f در x=1تعريف نشده است ولي حد دارد.
در تابع f اگر متغير x با مقدارهاي بزرگتر از عدد a به a نزديك شود و مقدارهايf(x) به عددي مانند l نزديك شوند، گوييم تابع f در نقطه يا به طول a حد راست دارد و مينويسيم:
\(\mathop {\lim }\limits_{x \to {a^ + }} f(x) = l\)
مثال
بارسم جدول اگر \(f(x) = \frac{{\left| x \right|}}{x}\)حاصل \(\mathop {\lim }\limits_{x \to {0^ + }} f(x)\)را محاسبه كنيد.

بنابراین داریم:
\(\mathop {\lim }\limits_{x \to {0^ + }} \frac{{\left| x \right|}}{x} = 1\)
مثال
اگر \(f(x) = \left\{ \begin{array}{l}3 - x,x < 1\\\\3,x = 1\\\\x + 1,x > 1\end{array} \right.\)مقدار\(\mathop {\lim }\limits_{x \to {1^ + }} f(x) = \) را با استفاده از رسم نمودار محاسبه کنید
نمودار تابع f در فاصله ی \((1, + \infty )\)به صورت زیر است.
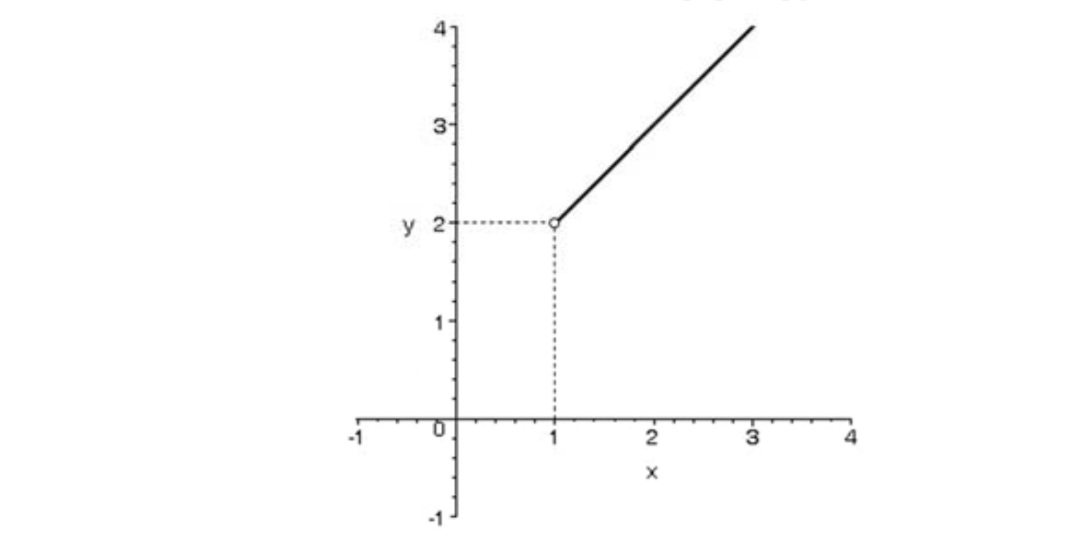
همانگونه كه از نمودار مشاهده مي شود با نزديك شدن مقادير x از طرف راست ( مقادير بزرگتر از يك ) به يك، مقادير f(x)به عدد 2 نزديك ميشوند. بنابراين داريم:
\(\mathop {\lim }\limits_{x \to {1^ + }} f(x) = 2\)
در تابع f اگر متغير x با مقدارهاي کوچک تر از عدد a به a نزديك شود و مقدارهاي f(x)به عددي مانند k نزديك شوند، گوييم تابع f در نقطه يا به طول a حد چپ دارد و مينويسيم:
\(\mathop {\lim }\limits_{x \to {a^ - }} f(x) = k\)
مثال
اگر\(f(x) = \frac{{\left| x \right|}}{x}\) با رسم جدول حاصل \(\mathop {\lim }\limits_{x \to {0^ - }} f(x)\)را محاسبه كنيد.

بنابراين داريم:
\(\mathop {\lim }\limits_{x \to {0^ - }} \frac{{\left| x \right|}}{x} = 1\)
مثال
اگر \(f(x) = \left\{ \begin{array}{l}3 - x,x < 1\\\\3,x = 1\\\\x + 1,x > 1\end{array} \right.\)حاصل\(\mathop {\lim }\limits_{x \to {1^ - }} f(x)\) را با استفاده از رسم نمودار تابع محاسبه كنيد.
نمودار تابع f در فاصله ي \(\left( { - \infty ,1} \right)\)به صورت زير است.

همانگونه كه از نمودار مشاهده مي شود با نزديك شدن مقادير x از طرف چپ ( مقادير كوچكتر از يك) به يك، مقادير f(x)به عدد 2 نزديك ميشوند. بنابراين داريم:
\(\mathop {\lim }\limits_{x \to {1^ - }} f(x) = 2\)
اگر حدهاي چپ و راست تابع در نقطه اي مساوي باشند، تابع در آن نقطه حد دارد و حد آن همان مقدار حد چپ و راست در آن نقطه است.
مثال
ابتدا نمودار هر يك از توابع زير را رسم كنيد و سپس با استفاده از نمودار، حدهاي چپ و راست و حد تابع را در صورت وجود در نقطه ي داده شده محاسبه كنيد
 الف) \(f(x) = \left\{ \begin{array}{l} - x,x < 0\\\\3,x = 0\\\\x + 1,x > 0\end{array} \right.,x = 0\)
الف) \(f(x) = \left\{ \begin{array}{l} - x,x < 0\\\\3,x = 0\\\\x + 1,x > 0\end{array} \right.,x = 0\)
نمودار تابع به صورت زير است.
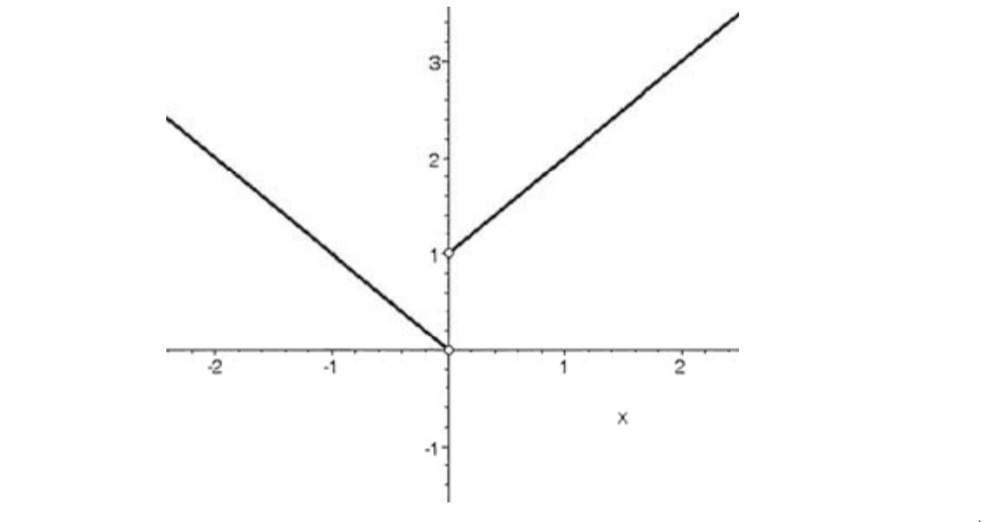
با توجه به نمودار داريم
\(\left\{ \begin{array}{l}\mathop {\lim }\limits_{x \to {0^ - }} f(x) = 0\\\\\mathop {\lim }\limits_{x \to {0^ + }} f(x) = 1\end{array} \right. \Rightarrow \mathop {\lim }\limits_{x \to 0} f(x)\)
وجود ندارد
ب)\(f(x) = \left\{ \begin{array}{l}{x^2} - 2x,x \ne 1\\\\0,x = 1\end{array} \right.,x = 1\)
نمودار تابع به صورت زير است.
با توجه به نمودار داريم:
\(\left\{ \begin{array}{l}\mathop {\lim }\limits_{x \to {1^ - }} f(x) = - 1\\\\\mathop {\lim }\limits_{x \to {1^ + }} f(x) = - 1\end{array} \right. \Rightarrow \mathop {\lim }\limits_{x \to 1} f(x) = - 1\)
ج) \(=f(x) = \left[ x \right],x = 2\)
ج)نمودار تابع به صورت زير است.
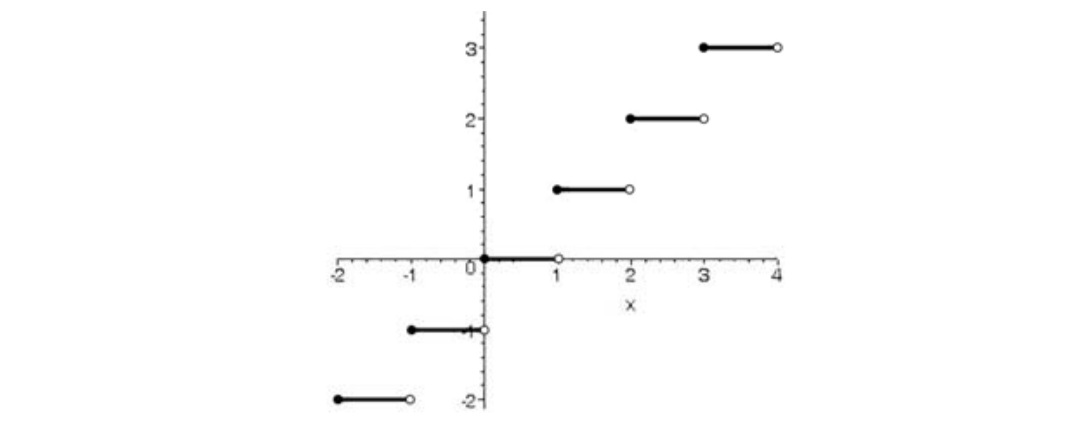
با توجه به نمودار داريم:
\(\left\{ \begin{array}{l}\mathop {\lim }\limits_{x \to {2^ - }} f(x) = 1\\\\\mathop {\lim }\limits_{x \to {2^ + }} f(x) = 2\end{array} \right. \Rightarrow \mathop {\lim }\limits_{x \to 2} f(x) = 1\)
وجود ندارد
مثال
نمودار توابع f ، g و h به صورت زير رسم شده است. با استفاده از نمودار، حد توابع f ، g و h را در نقطه ای به طول x=2 محاسبه كنيد.
الف
با توجه به نمودار تابع در x=2از چپ حد ندارد و از راست نيز حد ندارد. بنابراين تابع در x=2حد ندارد .
ب)تابع g در x=2از چپ حد ندارد ولي \(\mathop {\lim }\limits_{x \to {2^ + }} f(x) = 0\) بنابراين g در x=2حد ندارد.
ج)به دليل عدم تعريف تابع h در يك همسايگي چپ ،2 بحث از وجود حد چپ در اين نقطه معنادار نيست. ازدر واقع منظور حد تابع h در x=2همان حد راست تابع h در x=2است. يعني:
\(\mathop {\lim }\limits_{x \to 2} h(x) = 1\)
مثال
اگر تابع \(f(x) = \left\{ \begin{array}{l}{x^2} + x,x > 2\\\\ax + b,x < 2\end{array} \right.\)در x=2 داراي حد باشد، چه رابطه اي بين a و b برقرار است.
\(\left. \begin{array}{l}\mathop {\lim }\limits_{x \to {2^ + }} f(x) = \mathop {\lim }\limits_{x \to {2^ + }} ({x^2} + x) = 6\\\\\mathop {\lim }\limits_{x \to {2^ - }} f(x) = \mathop {\lim }\limits_{x \to {2^ - }} (ax + b) = 2a + b\end{array} \right\}\)
مثال
نمودار تابع زوج f به صورت زير رسم شده است.
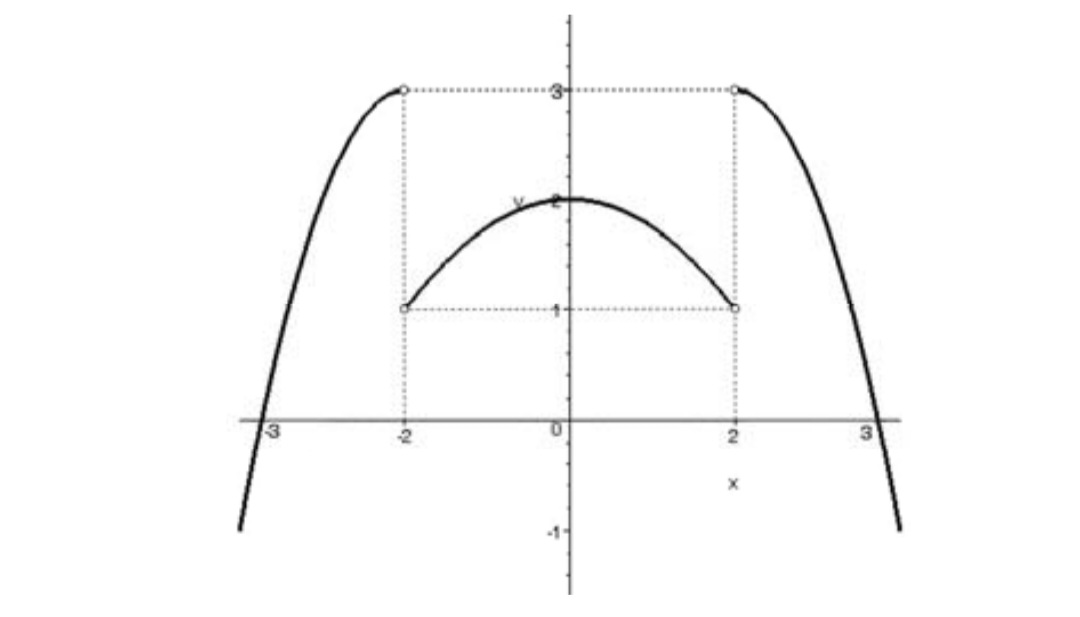
با توجه به نمودار، حدود زير را محاسبه كنيد.
الف) \(\mathop {\lim }\limits_{x \to - {2^ - }} f(x)\)ب) \(\mathop {\lim }\limits_{x \to - 3} f(x)\) ج) \(\mathop {\lim }\limits_{x \to - {2^ + }} f(x)\)
با توجه به اين كه f تابعي زوج است، نمودار آن نسبت به محور y ها متقارن است. بنابراين داريم:
\(\mathop {\lim }\limits_{x \to - {2^ - }} f(x) = \mathop {\lim }\limits_{x \to - {2^ + }} f(x) = 3\)(الف
\(\mathop {\lim }\limits_{x \to - 3} f(x) = \mathop {\lim }\limits_{x \to 3} f(x) = 0\)(ب
\(\mathop {\lim }\limits_{x \to - {2^ + }} f(x) = \mathop {\lim }\limits_{x \to - {2^ - }} f(x) = 1\)(ج
مثال
نمودار تابع زوج f به صورت زير رسم شده است.
با توجه به نمودار، حدود زير را محاسبه كنيد
الف)\(\mathop {\lim }\limits_{x \to - {2^ - }} f(x)\)
ب)\(\mathop {\lim }\limits_{x \to - 3} f(x)\)
ج) \(\mathop {\lim }\limits_{x \to - {2^ + }} f(x)\)
با توجه به اين كه f تابعي زوج است، نمودار آن نسبت به محور y ها متقارن است. بنابراين داريم:
\(\mathop {\lim }\limits_{x \to - {2^ - }} f(x) = \mathop {\lim }\limits_{x \to - {2^ + }} f(x) = 3\)(الف
\(\mathop {\lim }\limits_{x \to - 3} f(x) = \mathop {\lim }\limits_{x \to 3} f(x) = 0\)(ب
\(\mathop {\lim }\limits_{x \to - {2^ + }} f(x) = \mathop {\lim }\limits_{x \to {2^ - }} f(x) = 1\)(ج
تابع ثابت f(x)=cدر همه ی نقاط حد داردو حد آن در همه ی نقاط c است یعنی:
\(\mathop {\lim }\limits_{x \to a} c = c\)
تابع f(x)=x در همه ی نقاط حد داردو حد آن در هر نقطه به طول aبرابرa است یعنی:
\(\mathop {\lim }\limits_{x \to a} x = a\)
اگر\(\mathop {\lim }\limits_{x \to a} f(x) = l\) و\(\mathop {\lim }\limits_{x \to a} g(x) = k\) آنگاه:
\(\begin{array}{l}\mathop {\lim }\limits_{x \to a} (f(x) + g(x)) = \mathop {\lim }\limits_{x \to a} f(x) + \mathop {\lim }\limits_{x \to a} g(x) = l + k\\\\\mathop {\lim }\limits_{x \to a} (f(x) - g(x)) = \mathop {\lim }\limits_{x \to a} f(x) - \mathop {\lim }\limits_{x \to a} g(x) = l - k\\\\\mathop {\lim }\limits_{x \to a} (f(x) \times g(x)) = \mathop {\lim }\limits_{x \to a} f(x) \times \mathop {\lim }\limits_{x \to a} g(x) = l \times k\end{array}\)
اين قضايا را براي تعداد متناهي تابع نيز ميتوان تعميم داد.
اگر p(x) يك تابع چندجمله اي باشد، آنگاه:
\(\mathop {\lim }\limits_{x \to a} p(x) = p(a)\)
مثال
حدود زير را محاسبه كنيد.
الف)\(\mathop {\lim }\limits_{x \to 4} (2x + 3)\) ب)\(\mathop {\lim }\limits_{x \to 1} ({x^2} - 3x + 5)\)
ج)\(\mathop {\lim }\limits_{x \to \sqrt 2 } ({x^3} - 2{x^2} + x)\) د)\(\mathop {\lim }\limits_{x \to 7} \frac{{1 - 5x}}{3}\)
الف)
\(\mathop {\lim }\limits_{x \to 4} (2x + 3) = 1 \times 4 + 3 = 11\)
ب)
\(\mathop {\lim }\limits_{x \to 1} ({x^2} - 3x + 5) = {1^2} - 3(1) + 5 = 3\)
ج)
\(\mathop {\lim }\limits_{x \to \sqrt 2 } ({x^3} - 2{x^2} + x) = {\left( {\sqrt 2 } \right)^3} + 2{\left( {\sqrt 2 } \right)^2} + \sqrt 2 = 3\sqrt 2 + 4\)
د)
\(\mathop {\lim }\limits_{x \to 7} \frac{{1 - 5x}}{3} = \mathop {\lim }\limits_{x \to 7} ( - \frac{5}{3}x + \frac{1}{3}) = - \frac{5}{3}(7) + \frac{1}{3} = - \frac{{34}}{3}\)
اگر a عضوي از دامنه ي تابع باشد، آن گاه:
\(\begin{array}{l}{\mathop {\lim }\limits_{x \to a} ^k}\sqrt x { = ^k}\sqrt a ,\mathop {\lim }\limits_{x \to a} {b^x} = {b^a}\\\\\mathop {\lim }\limits_{x \to a} \sin x = \sin x,\mathop {\lim }\limits_{x \to a} \cos x = \cos a\end{array}\)
مثال
حدود زير را محاسبه كنيد(
الف) \(\mathop {\lim }\limits_{x \to 0} \sqrt x \) ب)\({\mathop {\lim }\limits_{x \to 0} ^3}\sqrt x \)
ج) \(\mathop {\lim }\limits_{x \to 8} (\sqrt x { + ^3}\sqrt x - 2)\) د)\(\mathop {\lim }\limits_{x \to \frac{\pi }{4}} \sin x\)
هـ)\(\mathop {\lim }\limits_{x \to \frac{\pi }{2}} {\sin ^2}x\) و)\(\mathop {\lim }\limits_{x \to \frac{\pi }{4}} (2\sin x - 3\cos x)\)
ز)\(\mathop {\lim }\limits_{x \to - 2} {3^x}\) ح)\(\mathop {\lim }\limits_{x \to 4} {2^x}\)
الف)
\(\mathop {\lim }\limits_{x \to 0} \sqrt x = \sqrt 0 = 0\)
توجه: منظور از\(\mathop {\lim }\limits_{x \to 0} \sqrt x \)درواقع\(\mathop {\lim }\limits_{x \to {0^ + }} \sqrt x \) است . زيرا تابع\(y = \sqrt x \) تنها در همسايگي راست صفر تعريف شده است.
ب(
\({\mathop {\lim }\limits_{x \to 0} ^3}\sqrt x { = ^3}\sqrt 0 = 0\)
ج)
\(\mathop {\lim }\limits_{x \to 8} (\sqrt x { + ^3}\sqrt x - 2) = \mathop {\lim }\limits_{x \to 8} \sqrt {x + } {\mathop {\lim }\limits_{x \to 8} ^3}\sqrt x - \mathop {\lim }\limits_{x \to 8} 2 = \sqrt 8 { + ^3}\sqrt 8 - 2 = 2\sqrt 2 + 2 - 2 = 2\sqrt 2 \)
د)
\(\mathop {\lim }\limits_{x \to \frac{\pi }{4}} \sin x = \sin x\frac{\pi }{4} = \frac{{\sqrt 2 }}{2}\)
هـ)
\(\mathop {\lim }\limits_{x \to \frac{\pi }{2}} {\sin ^2}x = \mathop {\lim }\limits_{x \to \frac{\pi }{2}} (\sin x\sin x) = \mathop {\lim }\limits_{x \to \frac{\pi }{2}} \sin x \times \mathop {\lim }\limits_{x \to \frac{\pi }{2}} \sin x = 1 \times 1 = 1\)
و)
\(\begin{array}{l}\mathop {\lim }\limits_{x \to \frac{\pi }{4}} (2\sin x - 3\cos x) = \mathop {\lim }\limits_{x \to \frac{\pi }{4}} 2\sin x - \mathop {\lim }\limits_{x \to \frac{\pi }{4}} 3\cos x\\\\2\mathop {\lim }\limits_{x \to \frac{\pi }{4}} \sin x - 3\mathop {\lim }\limits_{x \to \frac{\pi }{4}} \cos x\\\\2\sin x\frac{\pi }{4} - 3\cos \frac{\pi }{4}\\\\\sqrt 2 - 3\frac{{\sqrt 2 }}{2} = - \frac{{\sqrt 2 }}{2}\end{array}\)
ز)
\(\mathop {\lim }\limits_{x \to - 2} {3^x} = {3^{ - 2}} = \frac{1}{9}\)
ح)
\(\mathop {\lim }\limits_{x \to 4} {2^x} = {2^4} = 16\)
اگر توابع f و g در a حد داشته باشند و\(\mathop {\lim }\limits_{x \to a} g(x) \ne 0\) آنگاه تابع\(\frac{f}{g}\) نيز در a حد دارد و f داريم:
\(\mathop {\lim }\limits_{x \to a} \frac{{f(x)}}{{g(x)}} = \frac{{\mathop {\lim }\limits_{x \to a} f(x)}}{{\mathop {\lim }\limits_{x \to a} g(x)}}\)
مثال
حدود زير را محاسبه كنيد
الف)\(\mathop {\lim }\limits_{x \to 2} \frac{{{x^2} + 4x + 3}}{{2x - 1}}\) ب)\(\mathop {\lim }\limits_{x \to \frac{\pi }{2}} \frac{{\cos x + \sin x}}{{2\sin x - \cos x}}\)
ج)\(\mathop {\lim }\limits_{x \to 4} \frac{{\sqrt x + 2x}}{{{x^2} - 3}}\) (د \(\mathop {\lim }\limits_{x \to 1} \frac{1}{{x - 1}}\)
ه)\(\mathop {\lim }\limits_{x \to \frac{\pi }{4}} \tan x\)
الف )
\(\mathop {\lim }\limits_{x \to 2} \frac{{{x^2} + 4x + 3}}{{2x - 1}} = \frac{{4 + 8 + 3}}{{4 - 1}} = \frac{{15}}{3} = 5\)
ب)
\(\mathop {\lim }\limits_{x \to \frac{\pi }{2}} \frac{{\cos x + \sin x}}{{2\sin x - \cos x}} = \frac{{0 + 1}}{{2 - 0}} = \frac{1}{2}\)
ج)
\(\mathop {\lim }\limits_{x \to 4} \frac{{\sqrt x + 2x}}{{{x^2} - 3}} = \frac{{2 + 4}}{{16 - 3}} = \frac{6}{{13}}\)
د)
\(\mathop {\lim }\limits_{x \to 1} (x - 1) = 0\)پس وقتي x به 1 نزديك ميشود، قدرمطلق مقادير \(\frac{1}{{x - 1}}\)به طور نامحدود افزايش مييابد و به عدد خاصي نزديك نميشوند. بنابراين \(\mathop {\lim }\limits_{x \to 1} \frac{1}{{x - 1}}\) وجود ندارد.
هـ)
\(\mathop {\lim }\limits_{x \to \frac{\pi }{4}} \tan x = \mathop {\lim }\limits_{x \to \frac{\pi }{4}} \frac{{\sin x}}{{\cos x}} = \frac{{\sin \frac{\pi }{4}}}{{\cos \frac{\pi }{4}}} = 1\)
توجه: اگر داريم \(a \ne kz + \frac{\pi }{2}\)، داريم \(\mathop {\lim }\limits_{x \to a} \tan x = \tan a\)، اگر \(a \ne k\pi \)داریم\(\mathop {\lim }\limits_{x \to a} \cot a = \cot a\) و اگر \(\mathop {\lim }\limits_{x \to a} f\left( x \right) = 0\) و \(\mathop {\lim }\limits_{x \to a} g\left( x \right) = 0\) و اگر در يك همسايگي a ،\(f(x) \ne 0\) و \(g(x) \ne 0\)، در اين صورت گوييم \(\mathop {\lim }\limits_{x \to a} \frac{{f\left( x \right)}}{{g(x)}}\) مبهم است. براي محاسبه ي حد تابع \(\frac{{f\left( x \right)}}{{g(x)}}\) درx=a در صورت وجود، با ساده كردن و حذف عامل هاي مشترك \(\frac{{f\left( x \right)}}{{g(x)}}\)، به كسري تبديل ميشود كه حد آن را به كمك قضايايي كه ذكر آن رفت ميتوان محاسبه نمود.
مثال
الف)\(\mathop {\lim }\limits_{x \to 0} \frac{{{{\cos }^2}x}}{{1 - \sin x}}\) ب)\(\mathop {\lim }\limits_{x \to 0} \frac{{1 - \cos x}}{{{{\sin }^2}x}}\)
ج )\(\mathop {\lim }\limits_{x \to \frac{\pi }{4}} \frac{{1 - \sin 2x}}{{\sin x - \cos x}}\) د)\(\mathop {\lim }\limits_{x \to \frac{\pi }{2}} \frac{{\tan (x - \frac{\pi }{4})}}{{2\sin (\frac{\pi }{4} - x)}}\)
ه)\(\mathop {\lim }\limits_{x \to 0} \frac{{{{\sin }^2}x - {{\sin }^3}x}}{{{{\cos }^2}x - {{\cos }^3}x}}\) و)\(\mathop {\lim }\limits_{x \to \frac{\pi }{4}} \frac{{1 - \tan x}}{{\sin x - \cos x}}\)
ز)\(\mathop {\lim }\limits_{x \to \frac{{2\pi }}{3}} \frac{{\sin x + \sin 2x + \sin 3x}}{{2\cos x + 1}}\)
الف)
\(\mathop {\lim }\limits_{x \to 0} \frac{{{{\cos }^2}x}}{{1 - \sin x}}\mathop {\lim }\limits_{x \to 0} \frac{{1 - {{\sin }^2}x}}{{1 - \sin x}} = \mathop {\lim }\limits_{x \to 0} \frac{{(1 - {{\sin }^2}x)(1 + {{\sin }^2}x)}}{{1 - \sin x}} = \mathop {\lim }\limits_{x \to 0} (1 + \sin x) = 1\)
ب)
\(\mathop {\lim }\limits_{x \to 0} \frac{{1 - \cos x}}{{{{\sin }^2}x}}\mathop {\lim }\limits_{x \to 0} \frac{{1 - \cos x}}{{1 - {{\cos }^2}x}} = \mathop {\lim }\limits_{x \to 0} \frac{{1 - \cos x}}{{(1 - \cos )(1 + \cos )}} = \mathop {\lim }\limits_{x \to 0} \frac{1}{{1 + \cos }} = \frac{1}{2}\)
ج)
\(\begin{array}{l}\mathop {\lim }\limits_{x \to \frac{\pi }{4}} \frac{{1 - \sin 2x}}{{\sin x - \cos x}}\mathop {\lim }\limits_{x \to \frac{\pi }{4}} \frac{{\sin 2x + {{\cos }^2}x - 2\sin x\cos x}}{{\sin x - \cos x}} = \mathop {\lim }\limits_{x \to \frac{\pi }{4}} \frac{{{{(\sin x - \cos x)}^2}}}{{\sin x - \cos x}}\\\\\mathop {\lim }\limits_{x \to \frac{\pi }{4}} (\sin x - \cos x) = \sin \frac{\pi }{4} - \cos \frac{\pi }{4} = 0\end{array}\)
د)
\(\mathop {\lim }\limits_{x \to \frac{\pi }{2}} \frac{{\tan (x - \frac{\pi }{4})}}{{2\sin (\frac{\pi }{4} - x)}}\mathop {\lim }\limits_{x \to \frac{\pi }{2}} \frac{{\frac{{\sin (x - \frac{\pi }{4})}}{{\cos (x - \frac{\pi }{4})}}}}{{ - 2\sin (x - \frac{\pi }{4})}} = \mathop {\lim }\limits_{x \to \frac{\pi }{2}} \frac{1}{{ - 2\sin (x - \frac{\pi }{4})}} = - \frac{1}{2}\)
ه)
\(\begin{array}{l}\mathop {\lim }\limits_{x \to 0} \frac{{{{\sin }^2}x - {{\sin }^3}x}}{{{{\cos }^2}x - {{\cos }^3}x}}\mathop {\lim }\limits_{x \to 0} \frac{{{{\sin }^2}x(1 - \sin x)}}{{{{\cos }^2}x(1 - \cos x)}} = \mathop {\lim }\limits_{x \to 0} \frac{{(1 - {{\cos }^2}x)(1 - \sin x)}}{{{{\cos }^2}x(1 - \cos x)}}\\\\ = \mathop {\lim }\limits_{x \to 0} \frac{{(1 - {{\cos }^2}x)(1 + \cos x)(1 - \sin x)}}{{{{\cos }^2}x}}\\\\ = \mathop {\lim }\limits_{x \to 0} \frac{{(1 + \cos x)(1 - \sin x)}}{{{{\cos }^2}x}} = 2\end{array}\)
و)
\(\begin{array}{l}\mathop {\lim }\limits_{x \to \frac{\pi }{4}} \frac{{1 - \tan x}}{{\sin x - \cos x}}\mathop {\lim }\limits_{x \to \frac{\pi }{4}} \frac{{1 - \frac{{\sin x}}{{\cos x}}}}{{\sin x - \cos x}} = \mathop {\lim }\limits_{x \to \frac{\pi }{4}} \frac{{1 - \frac{{\cos x - \sin x}}{{\cos x}}}}{{\sin x - \cos x}}\\\\\mathop {\lim }\limits_{x \to \frac{\pi }{4}} \frac{{1 - \frac{{(\sin x - \cos x)}}{{\cos x}}}}{{\sin x - \cos x}}\end{array}\)
ز)
\(\begin{array}{l}\mathop {\lim }\limits_{x \to \frac{{2\pi }}{3}} \frac{{\sin x + \sin 2x + \sin 3x}}{{2\cos x + 1}}\mathop {\lim }\limits_{x \to \frac{{2\pi }}{3}} \frac{{(\sin x + \sin 3x) + \sin 2x}}{{2\cos x + 1}}\\\\ = \mathop {\lim }\limits_{x \to \frac{{2\pi }}{3}} \frac{{2\sin x2x\cos x + \sin 2x}}{{2\cos x + 1}}\\\\ = \mathop {\lim }\limits_{x \to \frac{{2\pi }}{3}} \frac{{\sin x(2x\cos x + 1)}}{{2\cos x + 1}}\\\\\mathop {\lim }\limits_{x \to \frac{{2\pi }}{3}} \sin 2x = \sin \frac{{4\pi }}{3} = - \frac{{\sqrt 2 }}{3}\\\end{array}\)
اگر P(x) وQ(x) دو چند جمله اي باشند و در محاسبه ي حد\(\frac{{P(x)}}{{Q(x)}}\) در نقطه اي به طول a به حالت مبهم\(\frac{0}{0}\)  برخورد كنيم، اين به معناي آن است كه \(P(a) = 0\) و\(Q(a) = 0\) يعني صورت 0 و مخرج برx-a بخش پذيرند و ميتوان عامل ( عامل هاي )x-a را در صورت و مخرج ظاهر ساخته، از صورت و مخرج حذف كنيم. سپس حد را در صورت وجود محاسبه كنيم.
برخورد كنيم، اين به معناي آن است كه \(P(a) = 0\) و\(Q(a) = 0\) يعني صورت 0 و مخرج برx-a بخش پذيرند و ميتوان عامل ( عامل هاي )x-a را در صورت و مخرج ظاهر ساخته، از صورت و مخرج حذف كنيم. سپس حد را در صورت وجود محاسبه كنيم.
مثال
حدود زير را محاسبه كنيد؟
الف)\(\mathop {\lim }\limits_{x \to 3} \frac{{{x^2} - 9}}{{{x^3} - 27}}\) ب)\(\mathop {\lim }\limits_{x \to - 2} \frac{{{x^5} + 32}}{{{x^3} + 8}}\)
ج)\(\mathop {\lim }\limits_{x \to 1} \frac{{{x^3}2x - 3}}{{{x^4} - 1}}\)
الف)
\(\mathop {\lim }\limits_{x \to 3} \frac{{{x^2} - 9}}{{{x^3} - 27}}\mathop {\lim }\limits_{x \to 3} \frac{{(x - 3)(x + 3)}}{{(x - 3)({x^2} + 3x + 9)}} = \mathop {\lim }\limits_{x \to 3} \frac{{x + 3}}{{{x^2} + 3x + 9}} = \frac{6}{{27}} = \frac{2}{9}\)
با توجه به اينكه x=3صورت و مخرج را صفر ميكند. صورت و مخرج بر x-3 بخشپذير هستند.
ب)
\(\begin{array}{l}\mathop {\lim }\limits_{x \to - 2} \frac{{{x^5} + 32}}{{{x^3} + 8}}\mathop {\lim }\limits_{x \to - 2} \frac{{{x^5} + {2^5}}}{{{x^3} + {2^3}}}\\\\\mathop {\lim }\limits_{x \to - 2} \frac{{(x + 2)({x^4}\_2{x^3} + 4{x^2} - 8x + 16)}}{{(x + 2)({x^2} - 2x + 4)}}\\\\\mathop {\lim }\limits_{x \to - 2} \frac{{{x^4}\_2{x^3} + 4{x^2} - 8x + 16)}}{{{x^2} - 2x + 4}} = \frac{{80}}{{12}} = \frac{{20}}{3}\end{array}\)
ج)
\(\mathop {\lim }\limits_{x \to 1} \frac{{{x^3}2x - 3}}{{{x^4} - 1}}\mathop {\lim }\limits_{x \to 1} \frac{{(x - 1)({x^2} + x + 3)}}{{(x - 1)(x + 1)({x^2} + 1)}} = \mathop {\lim }\limits_{x \to 1} \frac{{{x^2} + x + 3}}{{(x + 1)({x^2} + 1)}} = \frac{5}{4}\)
مثال
در تساوي زير مقادير a و b را به دست آوريد؟
\(\mathop {\lim }\limits_{x \to 1} \frac{{{x^2} - 6x + 5}}{{{x^2} + ax + b}} = 2\)
عدد يك، صورت را صفر ميكند. با توجه به اينكه جواب حد عدد 2 است. لازم است  x=1ريشه ي چندجمله اي مخرج نيز باشد. يعني \(1 + a + b = 0\)بنابراين صورت و مخرج هر دو عامل x-1دارند. پس داريم:
x=1ريشه ي چندجمله اي مخرج نيز باشد. يعني \(1 + a + b = 0\)بنابراين صورت و مخرج هر دو عامل x-1دارند. پس داريم:
\(\begin{array}{l}\mathop {\lim }\limits_{x \to 1} \frac{{{x^2} - 6x + 5}}{{{x^2} + ax + b}} = \mathop {\lim }\limits_{x \to 1} \frac{{{x^2} - 6x + 5}}{{{x^2} + ax + ( - a - 1)}}\\\\\mathop {\lim }\limits_{x \to 1} \frac{{(x - 1)(x - 5)}}{{(x - 1)(x + a + 1)}}\\\\ = \frac{{ - 4}}{{2 + a}}\\\\ \Rightarrow \frac{{ - 4}}{{2 + a}} = 2 \Rightarrow 4 + 2a = - 4 \Rightarrow a = - 4\\\\1 + a + b = 0b = 3\end{array}\)
مثال
اگر\(\mathop {\lim }\limits_{x \to 2} \frac{{{x^n} - {2^n}}}{{x - 2}} = 80\) ، مقدار n را به دست آوريد؟
\(\begin{array}{l}\mathop {\lim }\limits_{x \to 2} \frac{{{x^n} - {2^n}}}{{x - 2}}\mathop {\lim }\limits_{x \to 2} \frac{{(x - 2)({x^{n - 1}} + 2{x^{n - 2}} + 4{x^{n - 3}} + ... + {2^{n - 1}})}}{{x - 2}}\\\\ = \mathop {\lim }\limits_{x \to 2} ({x^{n - 1}} + 2{x^{n - 2}} + 4{x^{n - 3}} + ... + {2^{n - 1}})\\\\ = {2^{n - 1}} + {2^{n - 1}} + {2^{n - 1}} + ... + {2^{n - 1}}\\\\ = n \times {2^{n - 1}}\\\\ = 80\\\\ \Rightarrow n = 5\end{array}\)
اگر P(x) يا Q(x) عبارت هاي راديكالي باشند، براي محاسبه ي \(\mathop {\lim }\limits_{x \to a} \frac{{P(x)}}{{Q(x)}}\)در حالت مبهم \((\frac{0}{0})\) لازم است با گويا كردن و يا روش هاي ديگر عامل صفر كننده را ظاهر ساخته و پس از 0 حذف آن، حد را در صورت وجود محاسبه ميكنيم.
مثال
حدود زير را محاسبه كنيد؟
الف)\(\mathop {\lim }\limits_{x \to 1} \frac{{\sqrt {x + 3} - 2}}{{x - 1}}\) ب)\(\mathop {\lim }\limits_{x \to 1} \frac{{1 - \sqrt x }}{{{x^2} + x - 2}}\)
ج)\(\mathop {\lim }\limits_{x \to 1} \frac{{\sqrt {x + 2} - \sqrt 3 }}{{\sqrt {x + 3} - 2}}\) د)\(\mathop {\lim }\limits_{x \to 5} \frac{{^3\sqrt {x + 3} - 2}}{{{x^2} - 25}}\)
ه)\(\mathop {\lim }\limits_{x \to 27} \frac{{^3\sqrt {x + 3} }}{{\sqrt {x + 3} - 5}}\) و )\(\mathop {\lim }\limits_{x \to 16} \frac{{^4\sqrt {x - 2} }}{{\sqrt {x - 4} }}\)
الف)
\(\begin{array}{l}\mathop {\lim }\limits_{x \to 1} \frac{{\sqrt {x + 3} - 2}}{{x - 1}}\mathop {\lim }\limits_{x \to 1} \frac{{\sqrt {x + 3} - 2}}{{x - 1}} \times \mathop {\lim }\limits_{x \to 1} \frac{{\sqrt {x + 3} - 2}}{{\sqrt {x + 3} - 2}}\\\\ = \mathop {\lim }\limits_{x \to 1} \frac{{x - 1}}{{\left( {x - 1} \right)\left( {\sqrt {x + 3} + 2} \right)}}\\\\ = \mathop {\lim }\limits_{x \to 1} \frac{1}{{\sqrt {x + 3} + 2}} = \frac{1}{4}\end{array}\)
ب)
\(\begin{array}{l}\mathop {\lim }\limits_{x \to 1} \frac{{1 - \sqrt x }}{{{x^2} + x - 2}}\mathop {\lim }\limits_{x \to 1} \frac{{1 - \sqrt x }}{{{x^2} + x - 2}} \times \mathop {\lim }\limits_{x \to 1} \frac{{1 + \sqrt x }}{{1 + \sqrt x }}\\\\\mathop {\lim }\limits_{x \to 1} \frac{{1 - x}}{{(x - 1)(x + 2)(1 + \sqrt x )}}\\\\\mathop {\lim }\limits_{x \to 1} \frac{{ - 1}}{{(x + 2)(1 + \sqrt x )}} = \frac{{ - 1}}{6}\end{array}\)
ج)
\(\begin{array}{l}\mathop {\lim }\limits_{x \to 1} \frac{{\sqrt {x + 2} - \sqrt 3 }}{{\sqrt {x + 3} - 2}}\mathop {\lim }\limits_{x \to 1} \frac{{\sqrt {x + 2} - \sqrt 3 }}{{\sqrt {x + 3} - 2}} \times \mathop {\lim }\limits_{x \to 1} \frac{{\sqrt {x + 2} + \sqrt 3 }}{{\sqrt {x + 2} + \sqrt 3 }} \times \mathop {\lim }\limits_{x \to 1} \frac{{\sqrt {x + 2} + 2}}{{\sqrt {x + 3} + 2}}\\\\\mathop {\lim }\limits_{x \to 1} \frac{{(x - 1) - (\sqrt {x + 3} - 2)}}{{(x - 1) - (\sqrt {x + 3} - 2)}}\\\\\mathop {\lim }\limits_{x \to 1} \frac{{\sqrt {x + 3} + 2}}{{\sqrt {x + 2} + \sqrt 3 )}} = \frac{4}{{2\sqrt 3 }} = \frac{2}{{\sqrt 3 }}\end{array}\)
د)
\(\begin{array}{l}\mathop {\lim }\limits_{x \to 5} \frac{{^3\sqrt {x + 3} - 2}}{{{x^2} - 25}}\mathop {\lim }\limits_{x \to 5} \frac{{^3\sqrt {x + 3} - 2}}{{{x^2} - 25}} \times \frac{{{(^3}\sqrt {x + 3} ) + {2^3}\sqrt {x + 3} + 4}}{{{(^3}\sqrt {x + 3} ) + {2^3}\sqrt {x + 3} + 4}}\\\mathop {\lim }\limits_{x \to 5} \frac{{x - 5}}{{(x - 5)(x + 5)({{{(^3}\sqrt {x + 3} )}^2} + {2^3}\sqrt x + 4}} = \frac{1}{{10 \times 12}} = \frac{1}{{120}}\end{array}\)
ه)
\(\begin{array}{l}\mathop {\lim }\limits_{x \to 27} \frac{{^3\sqrt {x\_3} }}{{\sqrt {x + 3} - 5}}\mathop {\lim }\limits_{x \to 27} \frac{{^3\sqrt {x - 3} }}{{\sqrt {x + 2} - 5}} \times \frac{{{{{(^3}\sqrt x )}^2} + {3^3}\sqrt x + 9}}{{{(^3}\sqrt x ) + {3^3}\sqrt x + 9}} \times \frac{{\sqrt {x - 2} + 5}}{{\sqrt {x - 2} + 5}}\\\\\mathop {\lim }\limits_{x \to 27} \frac{{(x - 27)(\sqrt {x - 2} + 5)}}{{(x - 27)({(^3}\sqrt {x{)^2}} + {3^3}\sqrt x + 9}} = \frac{{10}}{{27}}\end{array}\)
و)با توجه به اتحاد \({a^4} - {b^4} = (a - b)({a^3} + {a^2}b + a{b^2} + {b^3})\)داریم:
\(\begin{array}{l}\mathop {\lim }\limits_{x \to 16} \frac{{^4\sqrt {x - 2} }}{{\sqrt {x - 4} }}\mathop {\lim }\limits_{x \to 16} \frac{{^4\sqrt {x - 2} }}{{\sqrt {x - 4} }} \times \frac{{{(^4}{{\sqrt {x)} }^3} + 2{(^4}{{\sqrt {x)} }^2} + {4^4}\sqrt {x + 8} }}{{{(^4}{{\sqrt {x)} }^3} + 2{(^4}{{\sqrt {x)} }^2} + {3^3}\sqrt x + 9}} \times \frac{{\sqrt {x + 4} }}{{\sqrt {x + 4} }}\\\\ = \mathop {\lim }\limits_{x \to 16} \frac{{(x - 16)(\sqrt x + 4)}}{{(x - 16)({(^4}{{\sqrt {x)} }^3} + 2{(^4}{{\sqrt {x)} }^{^2}} + {4^4}\sqrt x + 8}} = \frac{8}{{32}} = \frac{1}{4}\end{array}\)
هرگاه x زاويه اي بر حسب راديان باشد. آنگاه داريم:
\(\begin{array}{l}1)\mathop {\lim }\limits_{x \to 0} \frac{{\sin x}}{x} = 1\\\\2)\mathop {\lim }\limits_{x \to 0} \frac{x}{{\sin x}} = 1\end{array}\)
مثال
ثابت كنيد:
\(\mathop {\lim }\limits_{x \to \infty } \frac{{\tan x}}{x} = 1\)
\(\mathop {\lim }\limits_{x \to 0} \frac{{\tan x}}{x} = \mathop {\lim }\limits_{x \to 0} \frac{{\frac{{\sin x}}{{\cos x}}}}{x} = \mathop {\lim }\limits_{x \to 0} \frac{{\sin x}}{x} \times \frac{1}{{\cos x}} = \mathop {\lim }\limits_{x \to 0} \frac{{\sin x}}{x} \times \mathop {\lim }\limits_{x \to 0} \frac{1}{{\cos x}} = 1 \times 1 = 1\)
توجه : به طريق مشابه ميتوان ثابت كرد
\(\mathop {\lim }\limits_{x \to 0} \frac{x}{{\tan x}} = 1\)
مثال
حدود زير را محاسبه كنيد.
الف)\(\mathop {\lim }\limits_{x \to 0} \frac{{\sin 3x}}{x}\) ب)\(\mathop {\lim }\limits_{x \to 0} \frac{{\sin x + \sin 3x}}{{5x}}\)
ج)\(\mathop {\lim }\limits_{x \to 0} \frac{{x\sin 2x}}{{\tan {x^2}}}\) د)\(\mathop {\lim }\limits_{x \to 0} \frac{{1 - \cos 2x}}{{3{x^2}}}\)
ه)\(\mathop {\lim }\limits_{x \to 0} \frac{{1 - \cos 7x}}{{1 - \cos 4x}}\) و) \(\mathop {\lim }\limits_{x \to 0} \frac{{\tan x - \sin x}}{{4{x^3}}}\)
\(\mathop {\lim }\limits_{x \to 0} \frac{{\tan x - \sin x}}{{4{x^3}}}\)
ز)\(\mathop {\lim }\limits_{x \to 0} \frac{{\cos x - \cos 2x}}{{\cos 2x - \cos 3x}}\) ح)\(\mathop {\lim }\limits_{x \to 2} \frac{{\sin (x - 2)}}{{\tan ({x^2} - 3x + 2)}}\)
ط)\(\mathop {\lim }\limits_{x \to \frac{\pi }{2}} \frac{{\cos x}}{{2x - \pi }}\)
الف)
\(\mathop {\lim }\limits_{x \to 0} \frac{{\sin 3x}}{x}\mathop {\lim }\limits_{x \to 0} \frac{{\sin 3x}}{{3x}} \times 3 = 1 \times 3 = 3\)
ب)
\(\mathop {\lim }\limits_{x \to 0} \frac{{\sin x + \sin 3x}}{{5x}}\mathop {\lim }\limits_{x \to 0} \frac{{\frac{{\sin x}}{x} + \frac{{\sin 3x}}{x}}}{{\frac{{5x}}{x}}} = \frac{{1 + 3}}{5} = \frac{4}{5}\)
ج)
\(\mathop {\lim }\limits_{x \to 0} \frac{{x\sin 2x}}{{\tan {x^2}}}\mathop {\lim }\limits_{x \to 0} \frac{{x \times \frac{{\sin 2}}{{2x}} \times 2x}}{{\frac{{\tan {x^2}}}{{{x^2}}} \times {x^2}}} = 2\)
د)
\(\mathop {\lim }\limits_{x \to 0} \frac{{1 - \cos 2x}}{{3{x^2}}}\mathop {\lim }\limits_{x \to 0} \frac{{2{{\sin }^2}x}}{{3{x^2}}} = \mathop {\frac{2}{3}\lim }\limits_{x \to 0} {(\frac{{\sin x}}{x})^2} = \frac{2}{3} \times 1 = \frac{2}{3}\)
ه)
\(\mathop {\lim }\limits_{x \to 0} \frac{{1 - \cos 7x}}{{1 - \cos 4x}}\mathop {\lim }\limits_{x \to 0} \frac{{2{{\sin }^2}(\frac{{7x}}{2})}}{{2{{\sin }^2}x}} = \mathop {\lim }\limits_{x \to 0} \frac{{(\frac{{2{{\sin }^2}\frac{{7x}}{2}}}{{\frac{{7x}}{2}}}) \times {{(\frac{{7x}}{2})}^2}}}{{(\frac{{2{{\sin }^2}x}}{{2x}}) \times {{(2x)}^2}}} = \frac{{1 \times \frac{{49}}{4}}}{{1 \times 4}} = \frac{{49}}{{16}}\)
و)
\(\begin{array}{l}\mathop {\lim }\limits_{x \to 0} \frac{{\tan x - \sin x}}{{4{x^3}}}\mathop {\lim }\limits_{x \to 0} \frac{{\frac{{\sin x}}{{\cos x}} - \sin x}}{{4{x^3}}}\\\\\mathop {\lim }\limits_{x \to 0} \frac{{\sin x - \cos x\sin x}}{{4{x^3}\cos x}}\\\\\mathop {\lim }\limits_{x \to 0} \frac{{\sin x(1 - \cos x)}}{{4{x^3}\cos x}}\\\\\mathop {\lim }\limits_{x \to 0} \frac{{\sin x(2{{\sin }^2}x\frac{x}{2})}}{{4{x^3}\cos x}}\\\\\mathop {\frac{1}{2}\lim }\limits_{x \to 0} \frac{{\frac{{\sin x}}{x} \times x \times {{(\frac{{\sin \frac{x}{2}}}{{\frac{x}{2}}})}^2} \times {{\left( {\frac{x}{2}} \right)}^2}}}{{{x^3}\cos x}} = \frac{1}{2} \times \frac{{1 \times \frac{1}{4}}}{1} = \frac{1}{8}\end{array}\)
ز)
\(\begin{array}{l}\mathop {\lim }\limits_{x \to 0} \frac{{\cos x - \cos 2x}}{{\cos 2x - \cos 3x}}\mathop {\lim }\limits_{x \to 0} \frac{{ - 2\frac{{x - 2x}}{x}\sin \frac{{x + 2x}}{x}}}{{ - 2\frac{{x - 3x}}{2}\sin \frac{{x + 3x}}{2}}}\\\\ = \mathop {\lim }\limits_{x \to 0} \frac{{\sin \frac{x}{2}\sin \frac{{3x}}{2}}}{{\sin \frac{x}{2}\sin \frac{{5x}}{2}}}\\\\ = \mathop {\lim }\limits_{x \to 0} \frac{{\frac{{\sin \frac{{3x}}{2}}}{{\frac{{3x}}{2}}} \times \frac{{3x}}{2}}}{{\frac{{\sin \frac{{5x}}{2}}}{{\frac{{5x}}{2}}} \times \frac{{5x}}{2}}} = \frac{3}{5}\end{array}\)
ح)
\(\mathop {\lim }\limits_{x \to 2} \frac{{\sin (x - 2)}}{{\tan ({x^2} - 3x + 2)}}\mathop {\lim }\limits_{x \to 2} \frac{{\frac{{\sin (x - 2)}}{{(x - 2)}} \times (x - 2)}}{{\frac{{\tan ({x^2} - 3x + 2)}}{{({x^2} - 3x + 2)}} \times (x - 2)(x - 1)}} = 1\)
ط)
\(\mathop {\lim }\limits_{x \to \frac{\pi }{2}} \frac{{\cos x}}{{2x - \pi }}\mathop {\lim }\limits_{x \to \frac{\pi }{2}} \frac{{\sin (\frac{\pi }{2} - x)}}{{ - 2(\frac{\pi }{2} - x)}} = - \frac{1}{2}\sin \mathop {\lim }\limits_{x \to \frac{\pi }{2}} \frac{{\sin (\frac{\pi }{2} - x)}}{{(\frac{\pi }{2} - x)}} = - \frac{1}{2} \times 1 = - \frac{1}{2}\)
براي به دست آوردن \(\mathop {\lim }\limits_{x \to a} \left[ {f(x)} \right]\)ابتدا حاصل\(\mathop {\lim }\limits_{x \to a} f(x)\) را محاسبه ميكنيم، فرض ميكنيم\(\mathop {\lim }\limits_{x \to a} f(x) = l\) اگر عددي غير صحيح باشد آنگاه \(\mathop {\lim }\limits_{x \to a} \left[ {f(x)} \right] = \left[ l \right]\)و اگر عددي صحيح باشد، در صورت لزوم حد چپ و راست تابع را در x=a به دست مي آوريم.
عددي غير صحيح باشد آنگاه \(\mathop {\lim }\limits_{x \to a} \left[ {f(x)} \right] = \left[ l \right]\)و اگر عددي صحيح باشد، در صورت لزوم حد چپ و راست تابع را در x=a به دست مي آوريم.
اگر تابع f ميشامل جزء صحيح باشد ابتدا جزء صحيح را محاسبه كنيم و سپس حاصل حد را در صورت وجود مي یابيم .
مثال
حدود زير را محاسبه كنيد.
الف) \(\mathop {\lim }\limits_{x \to \frac{2}{2}} \left[ x \right]\) ب)\(\mathop {\lim }\limits_{x \to 2} \left[ x \right]\)
ج)\(\mathop {\lim }\limits_{x \to 0} \left[ {{x^2}} \right]\) د)\(\mathop {\lim }\limits_{x \to - 2} \left[ {3x - 1} \right]\)
ه)\(\mathop {\lim }\limits_{x \to \frac{3}{2}} \left[ {\sin x} \right]\) و)\(\mathop {\lim }\limits_{x \to 2} \left[ {\frac{{2x + 4}}{{x + 1}}} \right]\)
ز)\(\mathop {\lim }\limits_{x \to 1} \left[ {\frac{{2x + 4}}{{x + 1}}} \right]\) ح)\(\mathop {\lim }\limits_{x \to \frac{{3\pi }}{4}} \left[ {\sqrt 2 \cos x} \right]\)
ط) \(\mathop {\lim }\limits_{x \to 0} \left[ {\frac{{\sin x}}{x}} \right]\) ی)\(\mathop {\lim }\limits_{x \to 1} \left[ {\frac{{\left[ x \right] + 3 + x}}{{\left[ {x + \frac{1}{2}} \right] + \left[ { - 2x} \right] + 4 - x}}} \right]\)
الف)
\(\mathop {\lim }\limits_{x \to 0} \left[ {\sin x} \right]\)\(\mathop {\lim }\limits_{x \to \frac{3}{2}} x = \frac{3}{2} \Rightarrow \mathop {\lim }\limits_{x \to \frac{3}{2}} \left[ x \right] = \left[ {\frac{3}{2}} \right] = 1\)
ب)
\(\left\{ \begin{array}{l}x \to {2^ - } \Rightarrow 1 < x < 2 \Rightarrow \mathop {\lim }\limits_{x \to {2^ - }} \left[ x \right] = 1\\\\x \to {2^ + } \Rightarrow 2 < x < 3 \Rightarrow \mathop {\lim }\limits_{x \to {2^ + }} \left[ x \right] = 2\end{array} \right.\)
پس تابع \(\left[ x \right]\) در x=2حد ندارد.
ج)
\(x \to 0 \Rightarrow 0 < {x^2} < 1 \Rightarrow \mathop {\lim }\limits_{x \to 0} \left[ {{x^2}} \right] = 0\)
د)
\(\left\{ \begin{array}{l}x \to - {2^ - } \Rightarrow 3x \to - {6^ - } \Rightarrow 3x - 1 \to - {7^ - } \Rightarrow \mathop {\lim }\limits_{x \to - {2^ - }} \left[ {3x - 1} \right] = - 8\\\\x \to - {2^ + } \Rightarrow 3x \to - {6^ + } \Rightarrow 3x - 1 \to - {7^ + } \Rightarrow \mathop {\lim }\limits_{x \to - {2^ + }} \left[ {3x - 1} \right] = - 7\end{array} \right.\)
ه)
\(\left\{ \begin{array}{l}x \to {0^ - } \Rightarrow - 1 < \sin x < 0 \Rightarrow \mathop {\lim }\limits_{x \to {0^ - }} \left[ {\sin x} \right] = - 1\\\\x \to {0^ + } \Rightarrow 0 < \sin x < 1 \Rightarrow \mathop {\lim }\limits_{x \to {0^ + }} \left[ {\sin x} \right] = 0\end{array} \right.\)
پس تابع\(\left[ {\sin x} \right]\) در x=0حد ندارد
و)
\(\mathop {\lim }\limits_{x \to 2} \frac{{2x + 4}}{{x + 1}} = \frac{8}{3} \Rightarrow \mathop {\lim }\limits_{x \to 2} \frac{{2x + 4}}{{x + 1}} = \left[ {\frac{8}{3}} \right] = 2\)
ز)
\(\begin{array}{l}\frac{{2x + 4}}{{x + 1}} = \frac{{2x + 2 + 2}}{{x + 1}} = 2 + \frac{2}{{x + 1}}\\\\\\x > 1 \Rightarrow x + 1 > 2 \Rightarrow 0 < \frac{1}{{x + 1}} < \frac{1}{2} \Rightarrow 0 < \frac{2}{{x + 1}} < 1 \Rightarrow \mathop {\lim }\limits_{x \to {1^ + }} \left[ {\frac{2}{{x + 1}}} \right] = 0\\\\0 < x < 1 \Rightarrow 1 < x + 1 < 2 \Rightarrow \frac{1}{2} < \frac{1}{{x + 1}} < 1 \Rightarrow 1 < \frac{2}{{x + 1}} < 2 \Rightarrow \mathop {\lim }\limits_{x \to {1^ - }} \left[ {\frac{2}{{x + 1}}} \right] = 1\end{array}\)
بنابراین
\(\begin{array}{l}\mathop {\lim }\limits_{x \to {1^ + }} \left[ {\frac{{2x + 4}}{{x + 1}}} \right] = \mathop {\lim }\limits_{x \to {1^ + }} \left[ {2 + \frac{2}{{x + 1}}} \right]\\\\\mathop {\lim (2 + }\limits_{x \to {1^ + }} \left[ {\frac{2}{{x + 1}}} \right])\\\\2 + \mathop {\lim }\limits_{x \to {1^\_}} \left[ {\frac{{2x + 4}}{{x + 1}}} \right] = \mathop {\lim }\limits_{x \to {1^ - }} \left[ {2 + \frac{2}{{x + 1}}} \right])\\\\ = \mathop {\lim }\limits_{x \to {1^ - }} \left[ {\frac{{2x + 4}}{{x + 1}}} \right] = \mathop {\lim }\limits_{x \to {1^ - }} \left[ {2 + \frac{2}{{x + 1}}} \right]\\\\\mathop {\lim }\limits_{x \to {1^ - }} (2 + \left[ {\frac{2}{{x + 1}}} \right])\\\\2 + \mathop {\lim }\limits_{x \to {1^ - }} \left[ {\frac{2}{{x + 1}}} \right] = 3\end{array}\)
لذا تابع \(\left[ {\sqrt 2 \cos x} \right]\)در \(x = \frac{{3\pi }}{4}\)حد ندارد
ح)
\(\left\{ \begin{array}{l}x = \frac{{3{\pi ^ - }}}{4} \Rightarrow - \frac{{\sqrt 2 }}{2} < \cos x < 0 \Rightarrow - 1 < \sqrt 2 \cos x < 0 \Rightarrow \mathop {\lim }\limits_{x \to \frac{{3{\pi ^ - }}}{4}} \left[ {\sqrt 2 \cos x} \right] = - 1\\\\x = \frac{{3{\pi ^ + }}}{4} \Rightarrow - 1 < \cos x < - \frac{{\sqrt 2 }}{2} \Rightarrow - \sqrt 2 < \sqrt 2 \cos x < - 1 \Rightarrow \mathop {\lim }\limits_{x \to \frac{{3{\pi ^ + }}}{4}} \left[ {\sqrt 2 \cos x} \right] = - 2\end{array} \right.\)
لذا تابع \(\left[ {\sqrt 2 \cos x} \right]\)در \(x = \frac{{3\pi }}{4}\)حد ندارد
ط)وقتی\(x > 1\)میدانیم\(\sin x < x\)پس\(0 < \mathop {\lim }\limits_{x \to {0^ + }} \left[ {\frac{{\sin x}}{x}} \right] < 1\)بنابراین \(\mathop {\lim }\limits_{x \to {0^ + }} \left[ {\frac{{\sin x}}{x}} \right] = 0\)همچنین با توجه به زوج بودن تابع \(\frac{{\sin x}}{x}\)داریم \(\mathop {\lim }\limits_{x \to {0^ - }} \left[ {\frac{{\sin x}}{x}} \right] = 0\)و لذا\(\mathop {\lim }\limits_{x \to 0} \left[ {\frac{{\sin x}}{x}} \right] = 0\)
ی)اگر \(x \to {1^ - }\)داریم
\(\left\{ \begin{array}{l}\left[ x \right] = 0\\\\1 < x + \frac{1}{2} < \frac{3}{2} \Rightarrow \left[ {x + \frac{1}{2}} \right] = 1\\\\ - 2 < - 2x < - 1 \Rightarrow \left[ { - 2x} \right] = - 2\end{array} \right.\)
پس حد چپ به صورت زیر محاسبه می شود
\(\begin{array}{l}\mathop {\lim }\limits_{x \to {1^ - }} \frac{{\left[ x \right] + 3 + x}}{{\left[ {x + \frac{1}{2}} \right] + \left[ { - 2x} \right] + 4 - x}} = \mathop {\lim }\limits_{x \to {1^ - }} \frac{{0 + 3 + x}}{{1 - 2 + 4 - x}} = \frac{4}{2} = 2\\\end{array}\)
و اگر\(x \to {1^ + }\) داریم :
\(\left\{ \begin{array}{l}\left[ x \right] = 1\\\\\frac{3}{2} < x + \frac{1}{2} < 2 \Rightarrow \left[ {x + \frac{1}{2}} \right] = 1\\\\ - 3 < - 2x < - 2 \Rightarrow \left[ { - 2x} \right] = - 3\end{array} \right.\)
پس حد راست به صورت زیر محاسبه میشود
 \(\mathop {\lim }\limits_{x \to {1^ + }} \frac{{\left[ x \right] + 3 + x}}{{\left[ {x + \frac{1}{2}} \right] + \left[ { - 2x} \right] + 4 - x}} = \mathop {\lim }\limits_{x \to {1^ + }} \frac{{1 + 3 + x}}{{1 - 3 + 4 - x}} = \frac{5}{1} = 5\)
\(\mathop {\lim }\limits_{x \to {1^ + }} \frac{{\left[ x \right] + 3 + x}}{{\left[ {x + \frac{1}{2}} \right] + \left[ { - 2x} \right] + 4 - x}} = \mathop {\lim }\limits_{x \to {1^ + }} \frac{{1 + 3 + x}}{{1 - 3 + 4 - x}} = \frac{5}{1} = 5\)
لذا تابع در x=1حد ندارد
اگر \(\mathop {\lim }\limits_{x \to a} f(x) = l\)باشد آنگاه
\(\mathop {\lim }\limits_{x \to a} \left| {f(x)} \right| = \left| l \right|\)
اگر تابع f شامل قدرمطلق باشد، براي محاسبه ي \(\mathop {\lim }\limits_{x \to a} f(x)\)در صورت لزوم حدود چپ وراست را محاسبه ميكنيم.
مثال
حدود زير را محاسبه كنيد؟
الف)\(\mathop {\lim }\limits_{x \to 2} \left| {x - 2} \right|\) ب)\(\mathop {\lim }\limits_{x \to 1} \left| {x - 2} \right|\)
ج)\(\mathop {\lim }\limits_{x \to 2} \frac{{\left| {x - 2} \right|}}{{x - 2}}\) د)\(\mathop {\lim }\limits_{x \to 1} \frac{{\left| {x - 2} \right| - 3}}{{\left| {x - 2} \right| + 4}}\)
هـ)\(\mathop {\lim }\limits_{x \to \frac{\pi }{2}} \frac{{\left| {\cos x} \right|}}{{x - \frac{\pi }{2}}}\)
الف)
\(\mathop {\lim }\limits_{x \to 2} \left| {x - 2} \right| = \left| {2 - 2} \right| = 0\)
ب)
\(\mathop {\lim }\limits_{x \to 1} \left| {x - 2} \right| = \left| {1 - 2} \right| = 1\)
ج)
تابع در اینجا حد ندارد \(\mathop {\lim }\limits_{x \to 2} \frac{{\left| {x - 2} \right|}}{{x - 2}}\left\{ \begin{array}{l}\mathop {\lim }\limits_{x \to {2^ - }} \frac{{ - (x - 2)}}{{x - 2}} = - 1\\\\\mathop {\lim }\limits_{x \to {2^ + }} \frac{{ - x - 2}}{{x - 2}} = 1\end{array} \right. \Rightarrow x = 2\)
د)
\(\mathop {\lim }\limits_{x \to 1} \frac{{\left| {x - 2} \right| - 3}}{{\left| {x - 2} \right| + 4}} = \mathop {\lim }\limits_{x \to 1} \frac{{\left| {1 - 2} \right| - 3}}{{\left| {1 - 3} \right| + 4}} = \frac{{ - 3}}{6} = - \frac{1}{2}\)
ه)
تابع در \(x = \frac{\pi }{2}\)حد ندارد\(\mathop {\lim }\limits_{x \to \frac{\pi }{2}} \frac{{\left| {\cos x} \right|}}{{x - \frac{\pi }{2}}}\left\{ \begin{array}{l}\mathop {\lim }\limits_{x \to {{\frac{\pi }{2}}^ - }} \frac{{\cos x}}{{x - \frac{\pi }{2}}} = \mathop {\lim }\limits_{x \to {{\frac{\pi }{2}}^ - }} \frac{{\sin (\frac{\pi }{2} - x)}}{{ - (\frac{\pi }{2} - x)}} = - 1\\\\\mathop {\lim }\limits_{x \to {{\frac{\pi }{2}}^ + }} \frac{{ - \cos x}}{{x - \frac{\pi }{2}}} = \mathop {\lim }\limits_{x \to {{\frac{\pi }{2}}^ + }} \frac{{ - \sin (\frac{\pi }{2} - x)}}{{ - (\frac{\pi }{2} - x)}} = 1\\\end{array} \right.\)
قضيه فشردگي: اگر به ازاي هر x از يك همسايگي a داشته باشيم\(h(x) \le f(x) \le g(x)\) و \(\mathop {\lim }\limits_{x \to a} g(x) = \mathop {\lim }\limits_{x \to a} h(x) = L\)آنگاه.\(\mathop {\lim }\limits_{x \to a} f(x) = L\)
مثال
\(\mathop {\lim }\limits_{x \to 1} \left| {x - 1} \right|\cos \frac{1}{{x - 1}}\)را محاسبه كنيد.
\(\begin{array}{l} - 1 \le \cos \frac{1}{{x - 1}} \le 1 \Rightarrow - \left| {x - 1} \right| \le \left| {x - 1} \right|cos\frac{1}{{x - 1}} \le \left| {x - 1} \right|\\\\\\\mathop {\lim - }\limits_{x \to 1} \left| {x - 1} \right| = \mathop {\lim }\limits_{x \to 1} \left| {x - 1} \right| = 0 \Rightarrow \mathop {\lim }\limits_{x \to 1} \left| {x - 1} \right|\cos \frac{1}{{x - 1}} = 0\end{array}\)
مثال
اگر به ازاي هر \(x \in ( - 1,1)\)، داشته باشيم\(\left| {f(x) - 2} \right| \le {(x - 1)^2}\): حاصل \(\mathop {\lim }\limits_{x \to 1} \frac{1}{{f(x)}}\)را محاسبه كنيد.
\(\begin{array}{l}\left| {f(x) - 2} \right| \le {(x - 1)^2} \Rightarrow - {(x - 1)^2} \le f(x) - 2 \le {(x - 1)^2} \Rightarrow \\\\2 - {(x - 1)^2} \le f(x) \le 2 + {(x - 1)^2}\\\\\mathop {\lim }\limits_{x \to 1} (2 + {(x - 1)^2}) = \mathop {\lim }\limits_{x \to 1} (2 - {(x - 1)^2}) = \mathop {\lim }\limits_{x \to 1} f(x) = 2\mathop {\lim }\limits_{x \to 1} \frac{1}{{f(x)}} = \frac{1}{2}\end{array}\)
تهیه کننده: حامد دلیجه
- آزمون آنلاین تمامی دروس پایه یازدهم
- گام به گام تمامی دروس پایه یازدهم
- ویدئو های آموزشی تمامی دروس پایه یازدهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه یازدهم
- فلش کارت های آماده دروس پایه یازدهم
- گنجینه ای جامع از انشاء های آماده پایه یازدهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه یازدهم
پیوستگی
فصل 5 : حد و پیوستگی
پیوستگی
اگر \(a \in {D_f}\)و\(\mathop {\lim }\limits_{x \to a} f(x) = f(a)\)گوییم تابع در x=aپیوسته است.
مثال
نمودار تابعF به صورت زیر رسم شده است باتوجه به نمودار پیوستگی تابعF را در نقاط مشخص شده بررسی کنید.
الف)X=0 ب)X=1 ج)X=2 د)X=3
الف)
\(\mathop {\lim }\limits_{x \to 0} f(x) = f(0) = 0\)
پس تابع در x=0پیوسته است.
توجه:در اصطلاح باتوجه به این که در واقع \(\mathop {\lim }\limits_{x \to {0^ + }} f(x) = f(0)\)میگویند تابع fدر x=0تنهااز راست پیوسته است.
ب)
\(\mathop {\lim }\limits_{x \to 1} f(x) = f(1) = 1\)
پس تابع fدرx=1 پیوسته است.
ج)
\(f(2) = 2\)ولی \(\mathop {\lim }\limits_{x \to 2} f(x) = \frac{1}{2}\)پس\(\mathop {\lim }\limits_{x \to 2} f(x) \ne f(2)\) بنابراین تابعf درx=2 پیوسته نیست
د)
تابع fدر x=3حدندارد پس دراین نقطه پیوسته نیست.
توجه:در اصطلاح می گویند تابع fدر x=3تنها پیوستگی چپ دارد.
مثال
تابع \(y = \left| x \right|\)در چه نقاطی ناپیوسته است.
نمودارتابع \(y = \left| x \right|\) به صورت زیر می باشد باتوجه به نمودار تابع در zناپیوسته است (البته میتوان ثابت کرد تابع\(y = \left| x \right|\) در \(x \in z\)ناپیوسته ودر \(\)پیوسته است.)
مثال
پیوستگی هریک از توابع زیر رادر نقطه یا نقاط داده شده در صورت بامعنی بودن بررسی کنید.
الف)\(f(x) = \sqrt {x - 1,x = 0} \) ب)\(f(x) = {x^2} - 3x + 5,x = 2\)
ج)\(f(x) = \left\{ \begin{array}{l}{x^2} + 1,x < 1\\\\2.x = 1,x = 1\\\\\frac{{{x^2}1}}{{x - 1}},x > 1\end{array} \right.\) د)\(f(x) = \left\{ \begin{array}{l}{x^2} + 1,x < 1\\\\3,x = 1,x = 1\\\\\frac{{{x^2}1}}{{x - 1}},x > 1\end{array} \right.\)
ه) \(f(x) = \left\{ \begin{array}{l}\frac{{\sin x}}{x},x \ne 0\\\\1,x = 0\end{array} \right.,x = 0\)
و) \(\begin{array}{l}f(x) = \left\{ \begin{array}{l}{x^2} + 2,x < - 1\\\\ - 3x, - 1 < x < 1\\\\x - 4,x > 1\end{array} \right.,x = - 1,x = 1\\\end{array}\)
الف)
میدانیم \({D_f} = \left[ {1, + \infty )} \right.\)و \(0 \notin {D_f}\)بنابراین بحث از پیوستگی این تابع در x=0بی معنا است.
ب)
تابعf در x=2پیوسته است زیرا :\(\mathop {\lim }\limits_{x \to 2} f(x) = f(2) = 3\)
توجه :توابع چند جمله ای در هر نقطه ای ازR پیوسته هستند.
ج)
\(\left. \begin{array}{l}f(1) = 2\\\\f( - 1) = 3\\\\\mathop {\lim }\limits_{x \to {1^ - }} f(x) = \mathop {\lim }\limits_{x \to {1^ - }} f({x^2} + 1) = 2\\\\\mathop {\lim }\limits_{x \to {1^ + }} f(x) = \mathop {\lim }\limits_{x \to {1^ + }} \frac{{{x^2} - 1}}{{x - 1}} = 2\\\end{array} \right\} \Rightarrow \mathop {\lim }\limits_{x \to 2} f(x) = 2\)
تابع f در x=1پيوسته است زيرا\(\mathop {\lim }\limits_{x \to 1} f(x) = f(1)\)
د)
 \(\left. \begin{array}{l}f(1) = 3\\\\\mathop {\lim }\limits_{x \to {1^ - }} f(x) = \mathop {\lim }\limits_{x \to {1^ - }} f({x^2} + 1) = 2\\\\\mathop {\lim }\limits_{x \to {1^ + }} f(x) = \mathop {\lim }\limits_{x \to {1^ + }} \frac{{{x^2} - 1}}{{x - 1}} = \mathop {\lim }\limits_{x \to {1^ + }} \frac{{(x - 1)(x + 1)}}{{x - 1}} = 2\\\end{array} \right\} \Rightarrow \mathop {\lim }\limits_{x \to 1} f(x) = 2\)
\(\left. \begin{array}{l}f(1) = 3\\\\\mathop {\lim }\limits_{x \to {1^ - }} f(x) = \mathop {\lim }\limits_{x \to {1^ - }} f({x^2} + 1) = 2\\\\\mathop {\lim }\limits_{x \to {1^ + }} f(x) = \mathop {\lim }\limits_{x \to {1^ + }} \frac{{{x^2} - 1}}{{x - 1}} = \mathop {\lim }\limits_{x \to {1^ + }} \frac{{(x - 1)(x + 1)}}{{x - 1}} = 2\\\end{array} \right\} \Rightarrow \mathop {\lim }\limits_{x \to 1} f(x) = 2\)
تابع f در پيوسته نيست زيرا\(\mathop {\lim }\limits_{x \to 1} f(x) \ne f(1)\)
ه)
\(\begin{array}{l}f(1) = - 3\\\\\mathop {\lim }\limits_{x \to {1^ + }} f(x) = \mathop {\lim }\limits_{x \to {1^ + }} f( - 3x) = 3\\\\\mathop {\lim }\limits_{x \to - {1^ - }} f(x) = \mathop {\lim }\limits_{x \to - {1^ - }} ({x^2} + 1) = 2\end{array}\)
تابع f درx=0پيوسته است زيرا\(\mathop {\lim }\limits_{x \to 0} f(x) = f(0)\)
و)
\(\begin{array}{l}f( - 1) = 3\\\\\mathop {\lim }\limits_{x \to {1^ + }} f(x) = \mathop {\lim }\limits_{x \to {1^ + }} f( - 3x) = - 3\\\\\mathop {\lim }\limits_{x \to - {1^ - }} f(x) = \mathop {\lim }\limits_{x \to - {1^ - }} f({x^2} + 1) = 2\end{array}\)
تابع f در X=-1حد ندارد. بنابراين تابع f در X=-1 پيوسته نيست، زيرا در اين نقطه حد ندارد ( همانگونه كه بيان شد تابع f در X=-1تنها پيوستگي راست دارد)
\(\left. \begin{array}{l}f(1) = - 3\\\\\mathop {\lim }\limits_{x \to {1^ - }} f(x) = \mathop {\lim }\limits_{x \to {1^ - }} f( - 3x) = - 3\\\\\mathop {\lim }\limits_{x \to {1^ + }} f(x) = \mathop {\lim }\limits_{x \to {1^ + }} f(x - 4) = - 3\end{array} \right\} \Rightarrow \mathop {\lim }\limits_{x \to 1} f(x) = - 3\)
تابع f درx=1پيوسته است زيرا \(\mathop {\lim }\limits_{x \to 1} f(x) = f(1)\)
مثال
مقدار a را طوري بيابيد تا تابع \(f(x) = (x + a)\left[ {2x - 5)} \right.\) در x=2پيوسته باشد.
\(\begin{array}{l}f(2) = \left[ {2 + a)} \right.\left[ {4 - 5) = - a - 2} \right.\\\\\mathop {\lim }\limits_{x \to {2^ - }} (x + a)\left[ {2x - 5)} \right. = \mathop {\lim }\limits_{x \to {2^ - }} (x + a)( - 2) = - 4 - 2a\\\\\mathop {\lim }\limits_{x \to {2^ + }} (x + a)\left[ {2x - \left. 5 \right]} \right. = \mathop {\lim }\limits_{x \to {2^ + }} (x + a)( - 1) = 2 - a\end{array}\)
با توجه به اينكه بايد داشته باشيم \(\mathop {\lim }\limits_{x \to {2^ + }} f(x) = f(2)\)پس لازم است\( - a - 2 = - 4 - 2a\) بنابراينa=-2 ميباشد.
مثال
اگرتابع\(f(x) = \left\{ \begin{array}{l}\frac{{\sin x}}{{\sqrt {1 - \cos 2x} }},x < 0\\\\a,x = 0\\\\\left[ x \right] + b,x > 0\end{array} \right.\) در x=0 پیوسته باشد مقدار aو bرابدست آورید.
 \(\begin{array}{l}\mathop {\lim }\limits_{x \to {0^ - }} f(x) = \mathop {\lim }\limits_{x \to {0^ - }} \frac{{\sin x}}{{\sqrt {1 - \cos 2x} }} = \mathop {\lim }\limits_{x \to {0^ - }} \frac{{\sin x}}{{\sqrt {2{{\sin }^2}x} }} = \mathop {\lim }\limits_{x \to {0^ - }} \frac{{\sin x}}{{\sqrt {2\left| {\sin x} \right|} }} = \mathop {\lim }\limits_{x \to {0^ - }} \frac{{\sin x}}{{ - \sqrt {2\sin x} }} = \\\\\sqrt 2 \frac{{\sin x}}{{ - \sqrt {2\sin x} }} = \frac{{ - \sqrt 2 }}{2}\\\\\mathop {\lim }\limits_{x \to {0^ + }} f(x) = \mathop {\lim }\limits_{x \to {0^ + }} (\left| x \right| + b) = \mathop {\lim }\limits_{x \to {0^ + }} (0 + b) = b\end{array}\)
\(\begin{array}{l}\mathop {\lim }\limits_{x \to {0^ - }} f(x) = \mathop {\lim }\limits_{x \to {0^ - }} \frac{{\sin x}}{{\sqrt {1 - \cos 2x} }} = \mathop {\lim }\limits_{x \to {0^ - }} \frac{{\sin x}}{{\sqrt {2{{\sin }^2}x} }} = \mathop {\lim }\limits_{x \to {0^ - }} \frac{{\sin x}}{{\sqrt {2\left| {\sin x} \right|} }} = \mathop {\lim }\limits_{x \to {0^ - }} \frac{{\sin x}}{{ - \sqrt {2\sin x} }} = \\\\\sqrt 2 \frac{{\sin x}}{{ - \sqrt {2\sin x} }} = \frac{{ - \sqrt 2 }}{2}\\\\\mathop {\lim }\limits_{x \to {0^ + }} f(x) = \mathop {\lim }\limits_{x \to {0^ + }} (\left| x \right| + b) = \mathop {\lim }\limits_{x \to {0^ + }} (0 + b) = b\end{array}\)
براي اينكه تابع f در x=0 پيوسته باشد بايد\(\mathop {\lim }\limits_{x \to 0} f(x) = f(0)\) بنابراین داریم:
\(b = a = - \frac{{\sqrt 2 }}{2}\)
اگر تابعي در تمام نقاط دامنه ي خود پيوسته باشد، آن را تابعي پيوسته مي نامند.
مثال
كدام يك از توابع زير، تابع پيوسته ميباشند.
الف) \(f(x) = \sqrt {2x - {x^2}} \)ب)\(g(x) = \frac{{x + 1}}{{{x^2} - 4}}\)
ج) \(h(x) = \left\{ \begin{array}{l}\frac{{\tan x}}{x},x \ne 0\\\\2,x = 0\end{array} \right.\)
الف(
دامنه ي تابع f ، بازه ي \(\left[ {0,2} \right]\)ميباشد. اگر \(0 < x < 2\) ، آنگاه:
\(\)\(\)
اگر x=0 و \(\mathop {\lim }\limits_{x \to {0^ + }} = f(x) = 0 = f(0)\)واگر x=2، آنگاه. \(\mathop {\lim }\limits_{x \to {2^ - }} = f(x) = 0 = f(2)\) پس تابع f ، تابعي پيوسته ميباشد.
ب)
دلخواه
بنابراين g تابعي پيوسته است.
ج)
\(\begin{array}{l}{D_h} = R\\0 \in {D_h} = \left\{ \begin{array}{l}h(0) = 2\\\\\mathop {\lim h(x) = 1}\limits_{x \to 0} \end{array} \right. \Rightarrow \mathop {\lim h(x) \ne h(0)}\limits_{x \to 0} \end{array}\)
بنابراين h تابعي پيوسته نيست
توابع چندجمله ای \(y = {\tan ^{ - 1}}x,y = {\cos ^{ - 1}}x,y = {\sin ^{ - 1}}x\) و \(y = {\cot ^{ - 1}}x\)روی پیوسته اند
و \(y = {\cot ^{ - 1}}x\)روی پیوسته اند
توابع \(y = {\sin ^{ - 1}}x,y = \cot x,y = \tan x\)و \(y = {\cos ^{ - 1}}x\)در دامنه ی خود که زيرمجموعه اي از ℜ ميباشد تابعي پيوسته هستند.
اگر تابع h از جمع يا تفريق يا ضرب يا تقسيم چند تابع پيوسته تشكيل شده باشد روي دامنه خود تابعي پيوسته است.
اگر f تابعي پيوسته باشد، تابع باشد، تابع \(^n\sqrt f \)روي دامنه ي تعريف خود پيوسته است.
مثال
پيوستگي توابع زير را روي دامنه ي تعريف بررسي كنيد.
الف(\(f(x) = \frac{{{x^2} + 1}}{{{x^2} - 4}}\)
ب)\(g(x) = \sqrt {{x^2} - 4} \)
ج)\(h(x) = \tan x\cot x\)
الف)
صورت و مخرج توابع چند جمله اي هستند و در هر نقطه اي پيوسته، پس تابع f روي \({D_f} = R - \left\{ { - 2} \right\}\)پيوسته است.
ب) تابع \(y = {x^2} - 4\)چند جمله اي است و در هر نقطهاي پيوسته، پس تابع g در دامنه تعريف خود يعني \(\left( { - \infty ,2} \right) \cup \left[ {2, + \infty )} \right.\) تابع پيوسته است.
ج) تابع \(y = \tan x\)روی \(D = \left\{ {\left. x \right|} \right.x \ne k\pi + \left. {\frac{\pi }{2}} \right\}\)و تابع\(y = \cot x\) روی \({D_f} = \left\{ {\left. x \right|} \right.x \ne k\left. \pi \right\}\)پيوسته اند پس تابع h روي\({D_f} = \left\{ {\left. x \right|} \right.x \ne \left. {\frac{{k\pi }}{2}} \right\}\) است پيوسته است.
مثال
فاصله ي پيوستگي تابع\(f(x) = \left\{ \begin{array}{l}\frac{{x + 1}}{{x - 2}},x > 3\\\\\frac{{x + 1}}{{x + 2}},x \le 3\end{array} \right.\) را تعيين كنيد.
میدانیم \({D_f} = R - \left\{ { - 2} \right\}\)و هر يك از رابطه ها روي دامنه ي تعريف خود پيوسته اند. پس كافي است ض ميدانيم \(x = R - \left\{ 2 \right\}\)پيوستگي تابع در x=3را بررسي كنيم .
\(\begin{array}{l}\mathop {\lim }\limits_{x \to {3^ + }} f(x) = \mathop {\lim }\limits_{x \to {3^ + }} \frac{{x + 1}}{{x - 2}} = 4\\\\\mathop {\lim }\limits_{x \to {3^ - }} f(x) = \mathop {\lim }\limits_{x \to {3^ - }} \frac{{x + 1}}{{x + 2}} = \frac{4}{5}\end{array}\)
تابع در x=3پیوسته نیست بنابراین تابع f روي\(\left( { - \infty , - 2} \right) \cup \left( { - 2,3} \right) \cup \left( {3, + \infty } \right)\) پيوسته است.
مثال
حدود k را طوري تعيين كنيد تا تابع\(f(x) = \frac{{{x^2} + x + 7}}{{{x^2} + kx + 1}}\) در ℜ پيوسته باشد
صورت و مخرج توابع چند جمله اي هستند و در هر نقطهاي از ℜ پيوسته ميباشند. پس كافي است دامنه تعریف تابع برابرR باشد.یعنی باید معادله \({x^2} + kx + 1 = 0\)فاقد ريشه باشد بنابراين لازم است:
\(\Delta < 0 \Rightarrow {k^2} - 4 < 0 \Rightarrow \left| k \right| < 2 \Rightarrow - 2 < k < 2\)
اگر ترکیبfog امکان پذیر باشد و\(\mathop {\lim }\limits_{x \to a} g(x) = l\) و تابعی پیوسته در\(\) باشد،انگاه داریم:
\(\mathop {\lim }\limits_{x \to a} f(g(x)) = f\left( {\mathop {\lim g(x)}\limits_{x \to a} } \right)\)
مثال
الف)\(y = \sqrt x \)زیراتابعی پیوسته است\(\mathop {\lim }\limits_{x \to 1} \sqrt {{x^2} + 3} = \sqrt {\mathop {\lim ({x^2} + 3)}\limits_{x \to 1} } = \sqrt 4 = 2\)
ب)زیرا تابع \(y = \left| x \right|\)در  پیوسته نیست \(\mathop {\lim }\limits_{x \to 2} \left| x \right| \ne \left| {\mathop {\lim x}\limits_{x \to 2} } \right|\)
پیوسته نیست \(\mathop {\lim }\limits_{x \to 2} \left| x \right| \ne \left| {\mathop {\lim x}\limits_{x \to 2} } \right|\)
ج)\(\mathop {\lim }\limits_{x \to \frac{1}{2}} \left| {{x^2}} \right| = \left| {\mathop {\lim }\limits_{x \to \frac{1}{2}} {x^2}} \right| = \frac{1}{4} = 0\)
د)زیرا تابع \(y = \left| {\frac{{2x + 1}}{x}} \right|\)در  پیوسته نیست\(\mathop {\lim }\limits_{x \to 1} \left| {\frac{{2x + 1}}{x}} \right| \ne \mathop {\lim }\limits_{x \to 1} \left| {\frac{{2x + 1}}{x}} \right|\)
پیوسته نیست\(\mathop {\lim }\limits_{x \to 1} \left| {\frac{{2x + 1}}{x}} \right| \ne \mathop {\lim }\limits_{x \to 1} \left| {\frac{{2x + 1}}{x}} \right|\)
ه)\(\mathop {\lim }\limits_{x \to 2} \left| {\frac{{2x + 1}}{x}} \right| = \left| {\mathop {\lim \frac{{2x + 1}}{x}}\limits_{x \to 2} } \right| = \frac{5}{2} = 2\)
اگر تابع gدر x=aپیوسته و تابع fدر g(a)پیوسته باشد،تابع fogدر x=aپیوسته است.
مثال
ثابت کنید تابع\(f(x) = {\sin ^3}\sqrt x \) تابعی پیوسته است.
حل روش اول :
تابع y=xتابع چند جمله ای است ودر  دلخواه پیوسته است پس تابع \(g(x){ = ^3}\sqrt x \)در
دلخواه پیوسته است پس تابع \(g(x){ = ^3}\sqrt x \)در پیوسته است و تابع \(h(x) = \sin x\)در هر نقطه ای از جمله
پیوسته است و تابع \(h(x) = \sin x\)در هر نقطه ای از جمله پیوسته است پس تابع
پیوسته است پس تابع
\(f(x) = h(g(x)) = {\sin ^3}\sqrt x \)
در \(\mathop {\lim }\limits_{x \to 1} \sqrt {{x^2} + 3} = \sqrt {\mathop {\lim ({x^2} + 3)}\limits_{x \to 1} } = \sqrt 4 = 2\)پیوسته است.
روش دوم :
بنابراین تابع fروی \({D_f} = R\) تابعی پیوسته است.
تهیه کننده: حامد دلیجه
مشتق
فصل 5 : حد و پیوستگی
مشتق
خط مماس و خط قائم بر منحنی از یک نقطه روی منحنی
با توجه به تغییرهندسی مشتق واضح است که مشتق تابع \( y = f(x)\)در نقطه ی a با شیب خط مماس بر منحنی در این نقطه برابر است.
\(m = {f^`}(a)\)=شیب خط مماس
حال اگر تعریف کنیم که خط قائم خطی است که در نقطه ی aبر خط مماس بر منحنی در این نقطه عمود باشد بدیهی است که اگر شیب خز مماس را عکس و قرینه کنیم شیب خط قائم به دست می اید.
\({m^`} = \frac{{ - 1}}{{{f^`}(a)}}\)شیب خط قائم
بنابراین معادله ی خط مماس و خط قائم بر منحنی در نقطه ی\(M(a,b)\) واقع بر نمودار ان به این شکل خواهند بود.
\(y = m(x - a) + b\)معادله ی خط مماس
\(y = {m^`}(x - a) + b\)معادله ی خط قائم
تهیه کننده: حامد دلیجه
آهنگ تغییرات
فصل 5 : حد و پیوستگی
آهنگ تغییرات
واضح است که کمیت های زیادی وجود دارند که تغییر یکی وابسته به تغییر دیگری است. مانند:
الف:مساحت مربع تابعی از طول ضلع ان است.
ب:مساحت دایره تابعی از شعاع ان است.
ج:محیط دایره تابعی از شعاع مثال ان است.
د:حجم کره تابعی از شعاع ان است.
ه:شتاب حرکت یک متحرک تابعی از سرعت ان است.
حال اگر بین دو کمیت یا دو پدیده که تغییر یکی سبب تغییر در دیگری میشود یکی را به عنوان متغیر(متغیر مستقل یا) و دیگری را به عنوان تابعی از ان متغیر (متغیر وابسته یا )در نظر بگیریم خواهیم داشت:
\(y = f(x)\)
در این صورت تغییرات yنسبت به تغییرات را اهنگ تغییرy نسبت به تغییرx می گوییم.
اهنگ تغییر را میتوان به یکی از دو صورت زیر بررسی کرد.
آهنگ متوسط تغییرات
آهنگ تغییرات متوسط تابعf نسبت به تغییرات xوقتیx از\(x = a\) تا \(x = b\)تغییر کند برابر است با :
\(\frac{{y}}{{x}} = \frac{{f(b) - f(a)}}{{b - a}}\)
تذکر:اگر قرار دهیم \(x = h = b - a\)در این صورت \(b = a + h\)یعنی اگر مقدار کمیتa رابه اندازه یh واحد تغییر دهیم خواهیم داشت:
\(\frac{{y}}{{x}} = \frac{{f(a + h) - f(a)}}{h}\)
آهنگ تغییرات آنی(لحظه ای)
حد آهنگ تغییرات متوسط تابعf نسبت به تغییرات xوقتی تغییرx خیلی ناچیز\((h \to 0)\) باشد را آهنگ لحظه ای رابه اختصار آهنگ تغییر کمیت \(y = f(x)\)به کمیت xدر aمیگویند.
\(\mathop {\lim }\limits_{x \to 0} \frac{{y}}{{x}} = \mathop {\lim }\limits_{h \to 0} \frac{{f(a + b) - f(a)}}{h}\)
تذکر: با توجه به تعریف مشتق تابع در یک نقطه واضح است که
\(\mathop {\lim }\limits_{x \to 0} \frac{{y}}{{x}} = {f^`}(a)\)
مثال
آهنگ تغییرات متوسط حجم مکعبی به ضلع سانتی متر را نسبت به تغییرات وقتی از به تغییر می کند بیابید.
\(\begin{array}{l}v(x) = {x^3}\\\\\frac{{v}}{{x}} = \frac{{v(5) - v(2)}}{{5 - 2}} = \frac{{125 - 8}}{3} = 39\end{array}\)
مثال
اهنگ تغییر مساحت یک دایره را نسبت به تغییرات شعاع آن که \(r = 5\)سانتی متر باشد حساب کنید.
\(\begin{array}{l}s(r) = \pi {r^2} \to {s^`}(r) = 2\pi r\\\\{s^`}(5) = 2\pi r\left( 5 \right) = 10\pi \end{array}\)
مثال
اگر\(f(t) = 30 + 10{t^2}\) نمایش جمعیت یک نوع باکتری باشد (tبر حسب ساعت) آهنگ تغییرات متوسط افزایش جمعیت را در 5ساعت اول پس از زمان\({t_1} = 2\) را حساب کنید.
\(\begin{array}{l}f(t) = 30 + 10{t^2}\\\\f(2) = 30 + 10{(2)^2} = 70\\\\f(7) = 30 + 10{(7)^2} = 520\\\\\frac{{f}}{{x}} = \frac{{f(7) - f(2)}}{{7 - 2}} = \frac{{520 - 70}}{5} = 90\end{array}\)
مثال
طول دو ضلع مثلثی 1و2 و طول ضلع سوم برابر متغیرL است فرض کنید که زاویه ی مقابل به این ضلعa باشد
الف) Lرا برحسب aبنویسید
ب)مشتقL رابر حسب aبه دست اورید.
ج)آهنگ تغییرات L وقتی که \(\alpha = \frac{\pi }{4}\)رابه دست اورید.
\(\begin{array}{l}l = (1) + (2) - 2(1)(2)\cos \alpha \to l(\alpha ) = \sqrt {5 - 4\cos \alpha } \\\\{l^`}(\alpha ) = \frac{{4\cos \alpha }}{{2\sqrt {5 - 4\cos \alpha } }} = \frac{{2\sin \alpha }}{{\sqrt {5 - 4\cos \alpha } }}\\\\{l^`}(\frac{\pi }{4}) = \frac{{2\sin (\frac{\pi }{4})}}{{\sqrt {5 - 4\cos (\frac{\pi }{4})} }} = \frac{{2\sqrt {\frac{2}{2}} }}{{\sqrt {5 - 4(\frac{{\sqrt 2 }}{2})} }} = \frac{{\sqrt 2 }}{{\sqrt {5 - 2\sqrt 2 } }}\end{array}\)
مثال
مساحت هر دایره تابعی از محیط آن است .آهنگ تغییرات مساحت دایره را نسبت به محیط \(5\pi \)ان را برای دایره ای به محیط حساب کنید.
\(\begin{array}{l}s(r) = \pi {r^2}s(p) = \pi {(\frac{p}{{2\pi }})^2} = {\frac{p}{{4\pi }}^2}\\\\s(p) = {\frac{p}{{4\pi }}^2} \to {s^`}(p) = \frac{{2p}}{{4\pi }} = \frac{p}{{2\pi }}\\\\s(5\pi ) = \frac{{5\pi }}{2} = 2/5\end{array}\)
مثال
مخزنی که گنجایش 60لیتر آب را دارد می تواند در مدت200 ثانیه کاملا تخلیه شود لبریز از آب بود. در لحظه ی \(t = 0\)شیر این مخزن باز می شود. اگر حجم اب باقی مانده در مخزن پس ازt ثانیه از رابطه ی\(v = 60{(1 - \frac{t}{{200}})^2}\) به دست آید.
الف) آهنگ تغییرات متوسط تخلیه آب پس از یک دقیقه چقدر است؟
ب) آهنگ تغییرات تخلیه ی آب در\(t = 100\) ثانیه چقدر است ؟
تابع تخلیه آب
\(\begin{array}{l}v(t) = 60 - 60{(1 - \frac{t}{{200}})^2} = 60(1 - (1 - \frac{t}{{100}} + \frac{{{t^2}}}{{4000}}))\\\\ = 60(\frac{t}{{100}} - \frac{{{t^2}}}{{4000}})60 \times \frac{{400t - {t^2}}}{{4000}} = \frac{3}{{2000}}(400t - {t^2})\end{array}\)
الف
\(\begin{array}{l}v(t) = \frac{3}{{2000}}(400t - {t^2})\\\\v(0) = \frac{3}{{2000}}(400(0) - {(0)^2}) = 0\\\\v(60) = \frac{3}{{2000}}(400(60) - {(60)^2}) = 30/6\\\\\frac{{v}}{{t}} = \frac{{v(60) - v(0)}}{{60 - 0}} = \frac{{30/6 - 0}}{{60}} = 0/51\end{array}\)
ب
\(\begin{array}{l}v(t) = \frac{3}{{2000}}(400t - {t^2}) \to v(t) = \frac{3}{{2000}}(400 - 2t) = \frac{3}{{1000}} = (200 - t)\\\\{v^`}(100) = \frac{3}{{1000}}(200 - 100) = \frac{3}{{10}} = 0/3\end{array}\)
نتیجه : می دانیم که نسبت به تغییر مسافت یک متحرک نسبت به زمان را سرعت و همچنین نسبت تغییر سرعت را متحرک نسبت به زمان را شتاب می نامند.بنابراین اگر \(x = f(t)\)معادله ی حرکت یک متحرک باشد .داریم :سرعت اولی و شتاب دومی
مثال
معادله ی حرکت متحرکی به صورت\(x(t) = {t^2} - 5t + 6\) است. مطلوب است
الف)سرعت متوسط متحرک ببین لحظات \({t_1} = 3\)تا \({t_2} = 5\)ثانیه
ب) سرعت لحظه ای متحرک در لحظه ی\({t_0} = 2\)
\(x(t) = {t^2} - t + 6\)
الف
\(\begin{array}{l}x(3) = {(3)^2} - 5(3) + 6 = 9 - 15 + 6 = 0\\\\x(5) = {(5)^2}\_5(5) + 6 = 25 - 25 + 6 = 6\\\\v = \frac{{x}}{{t}} = \frac{{{x_2} - {x_1}}}{{{t_2} - {t_1}}} = \frac{{6 - 0}}{{5 - 3}} = 3\frac{m}{s}\end{array}\)
ب
\({x^`}(t) = 2t - 5 \to {x^`}(2) = 2(2) - 5 = - 1\frac{m}{s}\)
مثال
توپی را در راستای قائم از زمین به بالا پرتاب می کنیم .اگر جهت مثبت به طرف بالا و معادله ی حرکت توپ به صورت \(y(t) = - 5{t^2} + 20t\)باشد (tبرحسب ثانیه و yبر حسب متر)
1: نمودار\(y(t)\)را رسم کنید
2: دامنه ی\(y(t)\) را تعیین کنید
3:سرعت متوسط توپ را از لحظه ی پرتاپ\((t = 0)\) تا پایان ثانیه ی دوم \((t = 2)\)حساب کنید
4: سرعت لحظه ای توپ را در یک ثانیه پس از پرتاپ \((t = 1)\)را حساب کنید
5:سرعت لحظه ای توپ هنگام برخورد با زمین چقدر است ؟
6: در چه زمانی توپ به بالاترین ارتفاع خود می رسد.در این لحظه سرعت توپ چقدر است . معنای آن چیست .
1 معادله ی داده شده یک سهمی و چون در آن \(a = - 5\)پس نمودار سهمی رو به پایین بوده و دارای نقطه یmax است.
2 چون بعد از 4 ثانیه توپ مجددا به زمین بر میگردد .لذا دامنه ی تابع \(D = \left[ {0,4} \right]\)می شود.
3
\(\begin{array}{l}y(t) = - 5{t^2} + 20t\\\\y(0) = - 5{(0)^2} + 20(0) = 0\\\\y(2) = - 5{(2)^2} + 20(2) = - 20 + 4\\\\y(t) = - 5{t^2} + 20t\\\\\frac{{y}}{{t}} = \frac{{y(2) - y(0)}}{{2 - 0}} = \frac{{20 + 0}}{2} = 10\end{array}\)
4
\(\begin{array}{l}y(t) = - 5{t^2} + 20t \to {y^`}(t) = - 10t + 20t\\\\{y^`}(1) = - 10(1) + 20 = 10\frac{m}{s}\end{array}\)
5
\({y^`}(4) = - 10(4) + 20 = - 20\frac{m}{s}\)
6 بالاترین ارتفاع توپ زمانی است که\(t = 2\) باشد.لذا
\({y^`}(2) = - 10(2) + 20 = 0\frac{m}{s}\)
یعنی سرعت لحظه ای توپ در این لحظه برابر صفر است.(ایست لحظه ای )
تهیه کننده: حامد دلیجه
- آزمون آنلاین تمامی دروس پایه یازدهم
- گام به گام تمامی دروس پایه یازدهم
- ویدئو های آموزشی تمامی دروس پایه یازدهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه یازدهم
- فلش کارت های آماده دروس پایه یازدهم
- گنجینه ای جامع از انشاء های آماده پایه یازدهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه یازدهم



1736019749.png)















