درسنامه کامل فیزیک یازدهم ریاضی
تعداد بازدید : 497.8kخلاصه نکات فیزیک یازدهم ریاضی - درسنامه شب امتحان فیزیک یازدهم ریاضی - جزوه شب امتحان فیزیک یازدهم ریاضی نوبت اول
قانون کولن
فصل 1 : الکتریسیتۀ ساکن
قانون کولن
بزرگی نيروی الکتريکی ربايشی يا رانشی بين دو ذره با بارهای \({q_1}\) و \({q_2}\) که در فاصله r از يکديگر قرار دارند، با حاصل ضرب اندازه (بزرگی) بار دو ذره نسبت مستقيم و با مجذور فاصله دو ذره از هم، نسبت وارون دارد.
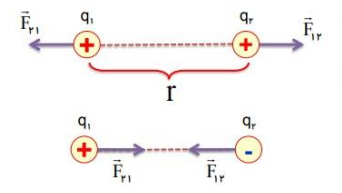
\({F_{12}}\) به معنای نیرویی است که ذره اول به ذره دوم وارد می کند.
\({F_{21}}\) به معنای نیرویی است که ذره دوم به ذره اول وارد می کند.
\(F = K\frac{{\left| {{q_1}} \right| \times \left| {{q_2}} \right|}}{{{r^2}}}\)
در این فرمول
(K) ثابت کولن (\(\frac{{N{m^2}}}{{{C^2}}}\) )
\(\begin{array}{l}K = \frac{1}{{4\pi {\varepsilon _0}}} \approx 9 \times {10^9}\frac{{N{m^2}}}{{{C^2}}}\\{\varepsilon _0} = 8/85 \times {10^{ - 12}}\frac{{{C^2}}}{{N{m^2}}}\end{array}\)
مثال
دو ذره با بارهای الکتریکی \( - 2\mu c\) و \(5\mu c\) در فاصله \(3cm\) از یکدیگر ثابت شده اند، اندازه نیرویی که دو ذره به یکدیگر وارد می کنند و نوع آن را مشخص کنید. (\(K = 9 \times {10^9}\frac{{N{m^2}}}{{{C^2}}}\) )
\(\begin{array}{l}{q_1} = - 2\mu c = 2 \times {10^{ - 6}}C\\{q_2} = 5\mu c = 5 \times {10^{ - 6}}C\\r = 3cm = 3 \times {10^{ - 2}}m\\K = 9 \times {10^9}\frac{{N{m^2}}}{{{C^2}}}\\F = ?\\F = K\frac{{\left| {{q_1}} \right|\left| {{q_2}} \right|}}{{{r^2}}} \to F = 9 \times {10^9}\frac{{\left| {2 \times {{10}^{ - 6}}} \right|\left| {5 \times {{10}^{ - 6}}} \right|}}{{3 \times {{10}^{ - 2}}}} = 100N \to F = 100N\end{array}\)
تکنیک 90
برای سادگی محاسبات می توان قانون کولن را به صورت \(F = 90\frac{{\left| {{q_1}} \right| \times \left| {{q_2}} \right|}}{{{r^2}}}\) نوشت؛ اما توجه کنيد در اين رابطه، اندازه ی بارها بر حسب \(\mu C\) و فاصله بر حسب cm جایگذاری شود.
ترازوی پیچشی
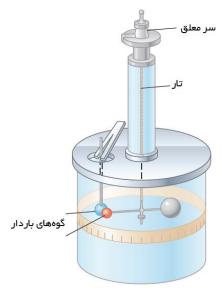
در يک سر ميله نارسانای سبک افقی، يک گوی باردار مثبت کوچک و در سر ديگر آن، يک قرص جهت حفظ تعادل قرار دارد. ميله از وسط توسط يک رشته سيم کشسان و نازک آويخته شده است. يک گوی با بار منفی از حفرهای به داخل استوانه شيشه ای برده می شود. درجه هايی بر سطح استوانه حک شده است که ميزان چرخش ميله را نشان می دهد. نيروی موثر بين اين بارها از اندازه گيری زاويه چرخش تا رسيدن به حالت تعادل بدست می آيد .اين آزمايش اولين بار توسط دانشمندی فرانسوی به نام شارل آگوستين کولُن، جهت محاسبه ی بزرگی نيروی بين دو بار الکتريکی بنا شد و يکای بار الکتريکی به افتخار اين دانشمند فرانسوی، کولن ناميده می شود.
اصل برهم نهی نیرو های الکتریکی
نيروی الکتريکی وارد بر هر ذره، برآيند نيروهايی است که هر يک از ذرات، در غياب ساير ذرات، بر آن ذره وارد می کنند. مثلا فرض کنيد n ذره ی باردار داشته باشيم، که در نزديکی بار نقطه ای \({q_0}\) قرار دارند. آنگاه نيروی خالص وارد بر بار نقطه \({q_0}\) به صورت جمع برداری بدست می آيد:
\({F_{T0}} = {F_{10}} + {F_{20}} + {F_{30}} + .... + {F_{n0}}\)
گام های اساسی حل مسائل بر هم نهی نيروی الکتريکی
- اندازه نيروی الکتريکی ناشی از تک تک بارها را بر بار مورد نظر محاسبه می کنيم.
- جهت نيروی الکتريکی هر بار را بر بارمورد نظر رسم می کنيم.
- اندازه و جهت نيروی برآيند را محاسبه می کنيم.
مثال
دو ذره باردار \({q_1} = + 3\mu c\) و \({q_2} = - 3\mu c\) در فاصله \(6cm\) از یکدیگر واقع شده اند، بار الکتریکی \({q_3} = + 1\mu c\) را در وسط این دو ذره قرار می دهیم. نیروی برآیند وارد بر بار \({q_3}\) را محاسبه کنید. (\(K = 9 \times {10^9}\frac{{N{m^2}}}{{{C^2}}}\) )
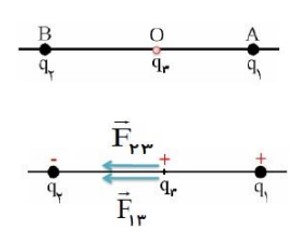
\(\begin{array}{l}{r_{13}} = 3cm = 3 \times {10^{ - 2}}m\\{r_{23}} = 3cm = 3 \times {10^{ - 2}}m\\{F_{13}} = K\frac{{\left| {{q_1}} \right|\left| {{q_3}} \right|}}{{{r_{13}}^2}} \to {F_{13}} = 9 \times {10^9}\frac{{3 \times {{10}^{ - 6}} \times 1 \times {{10}^{ - 6}}}}{{{{\left( {3 \times {{10}^{ - 2}}} \right)}^2}}} \to {F_{13}} = - 30i\\{F_{23}} = K\frac{{\left| {{q_1}} \right|\left| {{q_3}} \right|}}{{{r_{13}}^2}} \to {F_{13}} = 9 \times {10^9}\frac{{\left| { - 3 \times {{10}^{ - 6}}} \right| \times 1 \times {{10}^{ - 6}}}}{{{{\left( {3 \times {{10}^{ - 2}}} \right)}^2}}} \to {F_{23}} = - 30i\\{F_T} = {F_{13}} + {F_{23}}\\{F_T} = - 30i - 30i = - 60i\end{array}\)
- آزمون آنلاین تمامی دروس پایه ریاضی
- گام به گام تمامی دروس پایه ریاضی
- ویدئو های آموزشی تمامی دروس پایه ریاضی
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ریاضی
- فلش کارت های آماده دروس پایه ریاضی
- گنجینه ای جامع از انشاء های آماده پایه ریاضی
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ریاضی
بار الکتریکی
فصل 1 : الکتریسیتۀ ساکن
بار الکتریکی
کوچکترين باری که در طبيعت وجود دارد، بار الکتريکی الکترون و يا پروتون است که آن را با نماد (e) نمايش می دهند و مقدار آن برابر \(1/6 \times {10^{ - 19}}C\) است. مقدار بار الکتريکی جسم از رابطه \(q = \pm ne\) بدست می آيد، (علامت مثبت موقعی که جسم الکترون از دست بدهد، علامت منفی موقعی که جسم الکترون دريافت کند.)
1 از آنجا که تعداد الکترون های جا به جا شده همواره عدد درستی است، بار الکتريکی کميتی ناپيوسته است. يعني بار الکتريکی يک جسم نمي تواند \(1/25e\) و... باشد.
2 (e) را بار پایه (کوانتوم بار) می نامیم.
اصل کوانتيده بودن بار الکتريکی
بار الکتريکی همواره مضرب درستی از بار پايه يعنی الکترون (\( - e\)) و بار پروتون (\( + e\)) که در اتم های ماده وجود دارد، است. يک جسم نمی تواند بار الکتريکی \(5 \times {10^{ - 19}}C\) داشته باشد، ولی می تواند بار الکتريکی \(8 \times {10^{ - 19}}C\) داشته باشد، زیرا:
\(\begin{array}{l}q = 5 \times {10^{ - 19}}C \to n = \frac{q}{e} \to n = \frac{{5 \times {{10}^{ - 19}}}}{{1/6 \times {{10}^{ - 19}}}} = 3/125\\q = 8 \times {10^{ - 19}}C \to n = \frac{q}{e} \to n = \frac{{8 \times {{10}^{ - 19}}}}{{1/6 \times {{10}^{ - 19}}}} = 5\end{array}\)
روش های باردار کردن جسم
روش مالش
در اين روش، در اثر مالش دو ماده، تعدادی الکترون از يکی جدا شده و به ديگری انتقال می يابد. مثلا اگر يک ميله ی پلاستيکی را با پارچه پشمی مالش دهيم، ميله دارای بار منفي و پارچه ی پشمی به همان اندازه دارای بار مثبت می شود و هر گاه يک ميله ی شيشه ای را با پارچه ابريشمی مالش دهيم، ميله دارای بار مثبت و پارچه ی ابريشمی به همان اندازه دارای بار منفی می شود، اين روش معمولا برای باردار کردن اجسام نارسانا بکار می رود. در اين روش؛ دو جسم دارای بار الکتريکی همان اندازه ولی ناهمنام می شوند.
سری تريبو الکتريک (سری الکتريسته ی مالشی)
مثبت يا منفی شدن اجسام در اثر مالش به يکديگر، بر اساس جدول سری تريبو الکتريک مشخص می شود.
باردار کردن با روش تماس
هر گاه يک جسم رسانای باردار را با يک جسم رسانای خنثی تماس دهيم، مقداری بار از جسم باردار به جسم خنثی منتقل شده و بار هر دو همنام شده و يکديگر را می رانند. در اين روش هر دو جسم بايد رسانا باشند.
باردار کردن به روش القاء
در اين روش مطابق شکل، يک جسم باردار را به جسم رسانای بدون باری نزديک می کنند. در اثر القا، جسم دارای بار مثبت و منفی القايی می شود که بنا به قانون پايستگی بار الکتريکی، مقدار بار مثبت و منفی القا شده برابر است. ايجاد بار در رساناها بدون تماس آنها با يکديگر را القای بارالکتريکی گويند و بارهای ايجاد شده را بار القايی گويند.
اصل پايستگی بار الکتريکی (قانون بقای بار)
براثر مالش دو جسم به يکديگر، بار الکتريکی آفريده يا نابود نمی شود، بلکه مقداری بار از يک جسم به جسم ديگر منتقل می شود و دو جسم باردار می شوند ولی بار کل دو جسم ثابت می ماند.
الکتروسکوپ (برق نما)
وسيله ای است متشکل از يک کلاهک فلزی که يک ميله فلزی به آن متصل است و در سر ديگر ميله دو ورقه ی نازک فلزی (يا يک ورقه) قرار دارد. که ميله و ورقه ها در يک ظرف شيشه ای قرار دارند.
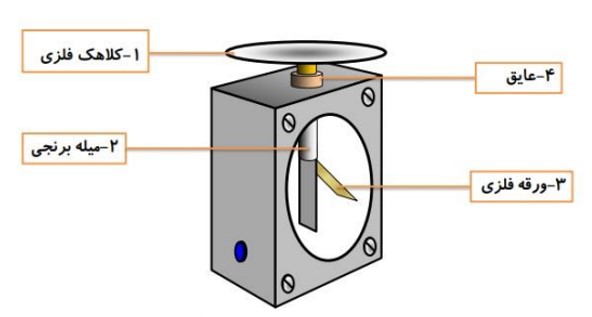
هر گاه به الکتروسکوپ باردار، يک جسم باردار، دارای بار همنام با الکتروسکوپ را به آرامی نزديک کنيم، انحراف ورقه های الکتروسکوپ بيشتر می شود. هر گاه به الکتروسکوپ باردار، جسمی با بار غيرهمنام الکتروسکوپ را به آرامی نزديک کنيم، ورقه های الکتروسکوپ بسته و دوباره باز می شوند. هر گاه جسم خنثی به الکتروسکوپ باردار نزديک کنيم، ورقه ها ابتدا بسته و سپس باز می شوند. هر گاه جسم بدون باری را به کلاهک الکتروسکوپ باردار تماس دهيم، اگر انحراف ورقه ها تغيير محسوسی نکند، جسم نارساناست و اگر انحراف ورقه ها کم شود و يا حتی از بين برود، جسم رساناست.
میدان الکتریکی
فصل 1 : الکتریسیتۀ ساکن
میدان الکتریکی
در فضای اطراف هر جسم باردار خاصيتی بوجود می آيد، که هر گاه جسم باردار ديگری در آن فضا قرار گيرد تحت تاثير قرار می گيرد، به اين خاصيت ميدان الکتريکی می گويند.
تعريف کمی ميدان الکتريکی
نيروی وارد بر يکای بار الکتريکی مثبت را در هر نقطه، ميدان الکتريکی در آن نقطه می ناميم. ميدان الکتريکی بار q در محل بار \({q_0}\) برابر است با: \(E = \frac{F}{{{q_0}}}\)
ميدان الکتريکی کميتی برداری است که آن را با نماد E نشان می دهند و يکای آن در SI، نیوتن بر کولن (\(\frac{N}{C}\) ) است.
مثال
بر بار الکتریکی \(20\mu c\) در یک میدان نقطه از میدان بار q، نیروی \(50 \times {10^{ - 2}}N\) وارد می شود؛ اندازه میدان الکتریکی را در این نقطه محاسبه کنید.
\(\begin{array}{l}{q_0} = 20\mu c = 20 \times {10^{ - 6}}C\\F = 50 \times {10^{ - 2}}N\\E = ?\\E = \frac{F}{{{q_0}}} \to E = \frac{{50 \times {{10}^{ - 2}}}}{{20 \times {{10}^{ - 6}}}} \to E = 2/5 \times {10^4}\frac{N}{C}\end{array}\)
میدان الکتریکی حاصل از ذره باردار
بنا بر قانون کولن نيروی F وارد بر اين بار برابر است با:
\(E = K\frac{{\left| q \right|}}{{{r^2}}}\)
مثال
اندازه و جهت میدان الکتریکی بار ذره \( - 2\mu c\) را در نقطه ای به فاصله \(3cm\) از بار را پیدا کنید.
\(\begin{array}{l}q = - 2\mu c = - 2 \times {10^{ - 6}}C\\r = 3cm = 3 \times {10^{ - 2}}m\\E = ?\\K = 9 \times {10^9}\frac{{N{m^2}}}{{{C^2}}}\\E = K\frac{{\left| q \right|}}{{{r^2}}} \to E = \frac{{9 \times {{10}^9} \times \left| { - 2 \times {{10}^{ - 6}}} \right|}}{{{{\left( {3 \times {{10}^{ - 2}}} \right)}^2}}}\\ \to E = \frac{{18 \times {{10}^{ + 3}}}}{{9 \times {{10}^{ - 4}}}} \to E = 2 \times {10^7}\frac{N}{C}\end{array}\)
1 اگر بار الکتریکی q در یک میدان الکتریکی E قرار گیرد، این میدان بر بار q نیروی \(F = q \times E\) را وارد می کند.
2 جهت نیروی F اگر موافق جهت میدان باشد، مثبت و اگر مخالف جهت میدان باشد، منفی است.
مولد وان دو گراف
دستگاهی است که بار الکتریکی روی کلاهک فلزی آن انباشته می شود. اگر یک جسم رسانا با کلاهک این دستگاه تماس پیدا کند دارای بار الکتریکی می شود.
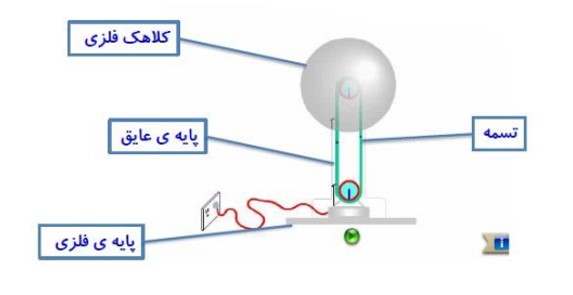
این دستگاه دارای دو غلتک از جنس متفاوت است که توسط تسمه ای به حرکت در می آیند. با حرکت تسمه بار های الکتریکی به کلاهک منتقل می شوند. نوع بار الکتریکی بستگی به جنس غلتک ها دارد.
اصل برهم نهی ميدان های الکتريکی
ميدان الکتريکی ناشی از چند بار الکتريکی در نقطه ای از فضا، برابر مجموع ميدان هايی است که هر بار در نبود ساير بارها در آن نقطه از فضا ايجاد می کند.
\(E = {E_1} + {E_2} + {E_3} + ...\)
گام های اساسی حل مسائل بر هم نهی ميدان الکتريکی
- اندازه ميدان الکتريکي ناشی از تک تک بارها را در نقطه مورد نظر محاسبه می کنيم.
- جهت ميدان الکتريکی هر بار را در نقطه مورد نظر رسم می کنيم.
- اندازه و جهت ميدان برآيند را محاسبه می کنيم.
مثال
شکل زیر، آرایشی از دو بار الکتریکی هم اندازه و غیر همنام (دو قطبی الکتریکی) را نشان می دهد که در آن فاصله دو بار از هم \(6cm\) است. میدان الکتریکی خالص را در نقطه O به دست آورید.
(\(K = 9 \times {10^9}\frac{{N{m^2}}}{{{C^2}}}\) )
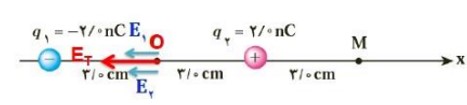
\(\begin{array}{l}{E_1} = \frac{{9 \times {{10}^9} \times \left| { - 2 \times {{10}^{ - 9}}} \right|}}{{{{\left( {3 \times {{10}^{ - 2}}} \right)}^2}}} = \frac{{18}}{{9 \times {{10}^{ - 4}}}} \to {E_1} = 2 \times {10^4}\frac{N}{C}\\{E_2} = \frac{{9 \times {{10}^9} \times 2 \times {{10}^{ - 9}}}}{{{{\left( {3 \times {{10}^{ - 2}}} \right)}^2}}} = \frac{{18}}{{9 \times {{10}^{ - 4}}}} \to {E_2} = 2 \times {10^4}\frac{N}{C}\\{E_T} = {E_1} + {E_2} \to {E_T} = 2 \times {10^4} + 2 \times {10^4} = 4 \times {10^4}\frac{N}{C}\end{array}\)
تجسم ميدان الکتريکی
برای تجسم ميدان الکتريکی در فضای اطراف هر جسم بارداری از خط های ميدان الکتريکی استفاده می شود. ويژگی های اين خطوط عبارتند از:
- خط های ميدان در هر نقطه، هم جهت با نيروی وارد بر بار مثبت (بار آزمون) واقع در آن نقطه است. در نتيجه، جهت اين خط ها از بار مثبت به طرف خارج و به سوی بار منفی
- مماس بر هر خط ميدان در هر نقطه دلخواه، راستای E در آن نقطه را نشان می دهد. سوی خط ها سوی ميدان الکتريکی است.
- خطوط ميدان بايد طوری رسم شوند که تعداد آنها در واحد سطحی عمود بر خط های ميدان با بزرگی E متناسب باشد. به عبارت ديگر هر جا خط های ميدان به هم نزديک تر (متراکم تر) باشند، اندازه E بزرگتر و هر جا که از هم دورتر باشند، اندازه E کوچک تر است.
- خط های ميدان يکديگر را قطع نمی کنند، يعنی از هر نقطه دلخواه در فضای اطراف يک يا چند جسم باردار فقط يک خط ميدان می گذرد که همان ميدان الکتريکی برآيند است.
1 ميدان بر سطح رسانا عمود است.
2 ميدان در داخل رسانا صفر است.
خطوط میدان الکتریکی اطراف بار مثبت
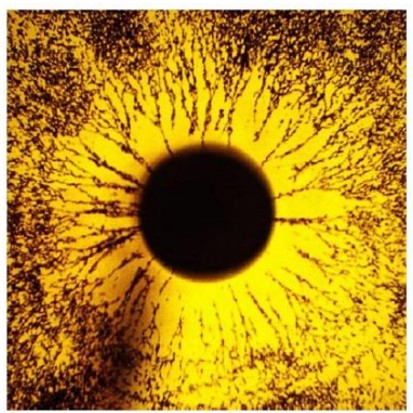
خطوط میدان الکتریکی اطراف بار مثبت و منفی
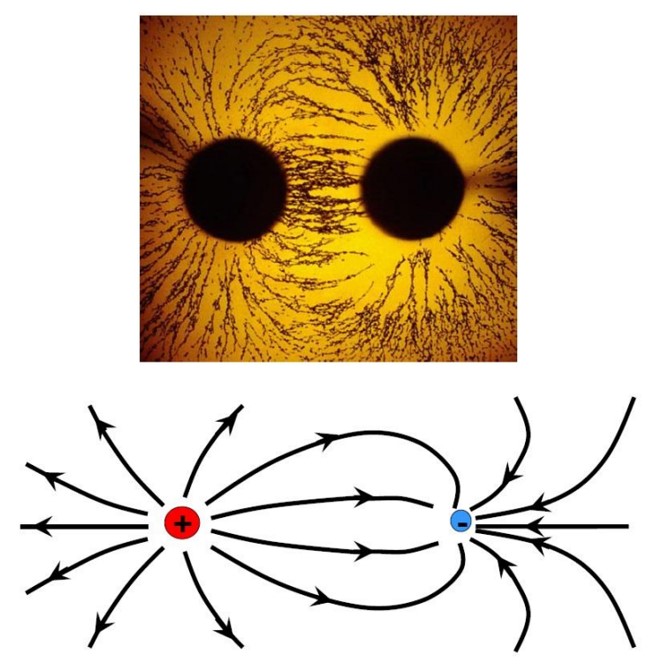
میدان الکتریکی یکنواخت
ميدان الکتريکی را يکنواخت می نامند، که در فضای بين دو صفحه ی رسانا و دور از لبه های صفحات، خطوط ميدان مستقيم، موازی و هم فاصله اند؛ يعنی بردار ميدان در تمام نقاط بين دو صفحه هم اندازه و هم جهت است.

آزمايش قطره روغن ميليکان
اين آزمايش نشان می دهد که بار الکتريکي کميتی کوانتيده است (\(q = \pm ne\) ) .ميليکان بين دو صفحه فلزی موازی و افقی ميدان الکتريکی يکنواخت E را توسط يک منبع ولتاژ قابل تنظيم ايجاد کرد. او در مرکز ورقه ی بالايی چند سوراخ ريز ايجاد کرد که از طريق اين سوراخ ها، قطرات روغن حاصل از يک روغن پاش به ناحيه بين دو ورقه مي پاشيد. بيشتر اين قطره ها در اثر مالش با دهانه خروجی روغن پاش باردار می شدند. ميليکان با تغيير دادن ميدان الکتريکی بين صفحات و با در نظر گرفتن مقاومت هوا، نيروی الکتريکی وارد بر هر قطره را محاسبه کرد و از آنجا بار الکتريکی هر قطره را تعيين کرد.
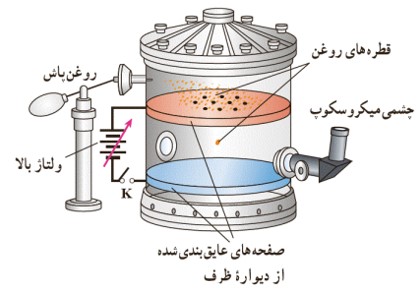
بررسی حرکت بار الکتريکی در ميدان الکتريکی يکنواخت
در يک ميدان الکتريکی يکنواخت قائم، اگر صفحه پايينی منفی باشد بار منفی به حال تعادل درمی آيد و اگر صفحه پايينی مثبت باشد، بار مثبت به حال تعادل درمی آيد و شرط تعادل به صورت زير است.
\({F_E} = W \to Eq = mg\)
شتاب ذره ی باردار، با فرض ناچيز بودن نيروی گرانش از رابطه زير محاسبه می شود.
\(\alpha = \frac{F}{m} = \frac{{Eq}}{m}\)
انرژی پتانسیل الکتریکی
فصل 1 : الکتریسیتۀ ساکن
انرژی پتانسیل الکتریکی
انرژی پتانسيل گرانشی
هميشه ذرهای به جرم m در ميدان گرانشی زمين سقوط می کند، يعنی از پتانسيل گرانشی بيشتر به پتانسيل گرانشی کمتر حرکت می کند.
انرژی پتانسيل الکتريکی
هميشه ذره ای با بار \( + q\) در میدان الکتريکی قائم رو به پايين سقوط می کند، يعنی از پتانسيل الکتريکی بيشتر به پتانسيل الکتريکی کمتر حرکت می کند.
1 رفتار ذره ی باردار، با بار مثبت در ميدان الکتريکی؛ همانند رفتار ذرهای به جرم m در میدان گرانشی زمين است.
2 هر گاه حرکتی، خود به خودی رخ دهد، از پتانسيل (گرانشی – الکتريکی) بيشتر به پتانسيل کمتر مي رود و انرژی پتانسيل (گرانشی – الکتريکی) آن کاهش می يابد.
3 هر گاه در جهت خطوط ميدان (گرانشی – الکتريکی) جابجا شويم، پتانسيل (گرانشی – الکتريکی) مستقل از نوع بار الکتريکی کاهش می يابد.
تغيير انرژی پتانسيل الکتريکی يک ذره ی باردار در ميدان الکتريکي E در يک جابجايی مشخص برابر با منفی کار انجام شده توسط نيروی الکتريکی در همان جابجايی است.
\(\Delta U = - {W_E} = - \left| q \right|Ed.\cos \alpha \)
تغيير انرژی پتانسيل الکتريکی يک ذره ی باردار در ميدان الکتريکی E در يک جابجايی مشخص برابر با مثبت کار انجام شده توسط نيروی عامل خارجی در همان جابجايی است.
\(\Delta U = + W\)
\(\Delta U = + W = - {W_E}\)
هر گاه بار الکتريکی به طرف صفحه همنام حرکت کند، انرژی پتانسيل الکتريکی افزايش می يابد؛ هر گاه به طرف صفحه غير همنام حرکت کند انرژی پتانسيل الکتريکی آن بار کاهش می يابد
اگر کاری که برای جايجايی بار الکتريکی (با سرعت ثابت) انجام می دهيم مثبت باشد (\(W\rangle 0\) ) انرژی پتانسيل الکتريکی بار افزايش می يابد (\(\Delta U\rangle 0\) ) در نتيجه: \({U_2}\rangle {U_1}\)
اگر کاری که برای جايجايی بار الکتريکی (با سرعت ثابت) انجام می دهيم منفی باشد (\(W\langle 0\) ) انرژی پتانسيل الکتريکی بار کاهش می يابد (\(\Delta U\langle 0\) ) در نتيجه: \({U_2}\langle {U_1}\)
تغيير انرژی پتانسيل بار الکتريکی به مسير حرکت بستگی ندارد.
اختلاف پتانسيل الکتريکی
اختلاف پتانسيل الکتريکی دو نقطه، برابر تغيير انرژی پتانسيل الکتريکی يکای بار الکتريکی مثبت است، وقتی يکای بار از نقطه اول تا نقطه دوم جا به جا شود.
بنابراين اگر انرژی پتانسيل الکتريکی بار مثبت q در يک نقطه برابر \({U_1}\) و در نقطه دوم برابر \({U_2}\) باشد، اختلاف پتانسيل الکتريکی بين اين دو نقطه که با نماد \(\Delta V\) نشان داده می شود عبارت است از:
\(\Delta V = \frac{{\Delta U}}{q} \to \Delta V = {V_2} - {V_1} \to \Delta U = {U_2} - {U_1}\)
در این فرمول
(\(\Delta U\) ) بر حسب ژول
(q) بر حسب کولن
(\(\Delta V\) ) بر حسب ولت می باشد.
ولت
يک ولت اختلاف پتانسيل بين دو نقطه از ميدان الکتريکی است که برای جابجا کردن يک کولن بار الکتريکی، يک ژول کار انجام دهيم.
اثبات رابطه \(V = Ed\) در يک ميدان الکتريکی يکنواخت:
اگر فاصله ميان صفحات يک ميدان يکنواخت را با d نشان دهيم و ذره ی باردار در راستای خطوط ميدان الکتريکی حرکت کند، آنگاه داریم:
\(\Delta V = \frac{{\Delta U}}{q} = \frac{{qEd.\cos (0)}}{q} = Ed\)
1 از رابطه \(E = \frac{V}{d}\) می فهميم که واحد ميدان الکتريکی \(\frac{V}{m}\) می باشد. يعنی \(1\frac{V}{m} = 1\frac{N}{C}\)
2 اگر بار الکتريکی مثبت در جهت ميدان الکتريکی حرکت کند، انرژی پتانسيل الکتريکی آن کاهش می يابد. تغيير پتانسيل الکتريکی به تغيير انرژی پتانسيل الکتريکی بستگی دارد.
3 هرگاه بار الکتريکی مثبت در جهت ميدان الکتريکی جا به جا شود، از پتانسيل الکتريکی بيشتر به پتانسيل کمتر رفته است و هرگاه بار الکتريکی مثبت در خلاف جهت ميدان حرکت کند، از پتانسيل الکتريکی کمتر به پتانسيل الکتريکی بيشتر رفته است.
4 هرگاه بار الکتريکی منفی در خلاف جهت ميدان الکتريکی جابجا شود، از پتانسيل الکتريکی کمتر به بيشتر رفته است و هرگاه در جهت ميدان الکتريکی جا به جا شود، از پتانسيل الکتريکی بيشتر به کمتر رفته است.
5 معمولا پتانسيل زمين را صفر در نظر می گيريم و پتانسيل هر جسم را نسبت به آن می سنجيم در اين صورت پتانسيل هر جسم متصل به زمین برابر صفر است.
- آزمون آنلاین تمامی دروس پایه ریاضی
- گام به گام تمامی دروس پایه ریاضی
- ویدئو های آموزشی تمامی دروس پایه ریاضی
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ریاضی
- فلش کارت های آماده دروس پایه ریاضی
- گنجینه ای جامع از انشاء های آماده پایه ریاضی
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ریاضی
توزيع و القای بار در رساناها
فصل 1 : الکتریسیتۀ ساکن
توزيع و القای بار در رساناها
رسانای منزوی
جسم رسانايی که توسط عايقی از محيط اطراف خود جدا شده است را رسانای منزوی می گويند. وقتی به يک جسم رسانای منزوی بار الکتريکی اضافی بدهيم، بار الکتريکی در محل داده شده ساکن نمی ماند و در جسم خارجی رسانا توزيع می شود (آزمايش فارادی.(
اگر يک رسانای خنثی منزوی درون ميدان الکتريکی خارجی قرار گيرد، الکترون های آزاد رسانا طوری روی سطح خارجی آن توزيع می شوند که اثر ميدان خارجی را درون رسانا خنثی کنند و ميدان خالص درون رسانا صفر شود و ميدان روی سطح رسانا همواره عمود است.
چون ميدان درون رسانايی که در حال تعادل الکترو استاتيکی است، برابر صفر است و ميدان روی سطح رسانا عمود بر سطح رساناست، کار نيروی الکتريکی در هر جابجايی بار در داخل و روی سطح رسانا صفر است و در نتيجه همه نقاط داخل و روی سطح رسانا، پتانسيل يکسانی دارند. (سطح هم پتانسيل(
جسم نارسانا
وقتی به يک جسم نا رسانا بار الکتريکی بدهيم، بار در محل داده شده به جسم باقی می ماند و در جسم جا به جا نمی شود.
چگالی سطحی بار \(\sigma \) (سیگما)
بار الکتريکی موجود در واحد سطح خارجی يک جسم رسانا را چگالی سطحی بار الکتريکی می ناميم.
\(\sigma = \frac{q}{A}\)
1 در SI يکای چگالی سطحی بار بر حسب کولن بر متر مربع (\(\frac{c}{{{m^2}}}\) ) بیان می شود.
2 آزمايش نشان می دهد، که شکل يک رسانا در چگونگی توزيع بار الکتريکی روی سطح آن تاثير دارد.
3 اگر سطح خارجی رسانا يکنواخت باشد چگالی سطحی بار در تمام نقاط آن يکسان است.
4 در مکان های نوک تيز و برجسته جسم رسانا چگالی سطحی بار بيشتر از نقاط ديگر جسم است. يعنی فاصله بار های داده شده به جسم در مکان های نوک تيز کمتر از فاصله آنها در مکان های پهن است.
مقايسه چگالی سطحی بار الکتريکی دو جسم رسانا از رابطه زير بدست می آيد.
\(\frac{{{\sigma _1}}}{{{\sigma _2}}} = \frac{{{q_1}}}{{{q_2}}} = \frac{{{A_2}}}{{{A_1}}}\)
خازن
فصل 1 : الکتریسیتۀ ساکن
خازن
دو رسانا با هر شکلی، در مجاورت هم که از هم عايق شده باشند، را خازن می ناميم. خازن وسيله ای الکتريکی است که می تواند بار و انرژی الکتريکی در خود ذخيره کند. خازن ها در مدارهای الکترونيک بسيار کاربرد دارند. از جمله در يک موبايل تا 700 خازن ممکن است بکار گرفته شده باشد.
خازن ها اندازه ها و شکل های مختلف دارند. ساده ترين خازن متشکل از دو صفحه رسانای تخت به مساحت A است که به فاصله (d) که در مقابل ابعاد صفحه ها ناچيز است از هم قرار گرفته اند. برای باردار کردن خازن هر صفحه آن را به يک قطب باتری متصل می کنند. بار از باتری به صفحات خازن جريان پيدا می کند تا بار صفحه متصل به قطب مثبت \( + Q\) و صفحه متصل به قطب منفی \( - Q\) شود. در نتيجه بين صفحات خازن ميدان يکنواختی (که جهت آن از صفحه مثبت به منفی است) ايجاد می شود.
ظرفيت خازن را با رابطه \(C = \frac{Q}{V}\) تعريف می کنند. يکای ظرفيت خازن در SI فاراد (که با F نشان داده می شود) است. يک فاراد ظرفيت خازنی است که اگر اختلاف پتانسيل يک ولت به آن وارد شود يک کولن بار در آن ذخيره گردد. با توجه به بزرگی يک کولن بار، يک فاراد نيز ظرفيت بزرگی براي يک خازن است. بيشتر خازن های بکار رفته در ابزارهايی مانند موبايل ظرفيت هايی در حدود پيکو فاراد يا ميکرو فاراد دارند.
مثال
اگر اختلاف پتانسيل 6 ولت به دو سر يک خازن 20 ميکرو فاراد متصل شود، مقدار بار ذخيره شده در آن چقدر خواهد بود؟
\(\begin{array}{l}V = 6V\\C = 20\mu F = 20 \times {10^{ - 6}}F\\Q = ?\\C = \frac{Q}{V} \to Q = CV \to Q = 20 \times {10^{ - 6}} \times 6 = 120\mu C\end{array}\)
ماده نارسايی که بين دو صفحه خازن قرار می گيرد را دی الکتريک می نامند. ظرفيت يک خازن تخت ساده متشکل از دو صفحه رسانای تخت به مساحت A است که به فاصله d تنها به خصوصيات ساختاری آن وابسته است و برای يک خازن تخت از رابطه زير بدست می آيد:
\(C = {\varepsilon _0}\frac{A}{d}\)
که در آن \({\varepsilon _0}\) ضريب گذردهی خلأ (\({\varepsilon _0} = 8 - 85 \times {10^{ - 12}}\frac{F}{m}\) ) است. اگر بين صفحات خازن ماده دی الکتريک قرار گيرد، ظرفيت خازن بسته به ثابت دی الکتريک آن افزايش يافته، و از رابطه زير بدست می آيد.
\(C = \kappa {C_0}\)
اين رابطه برای خازن تخت به صورت زير است.
\(C = \kappa {\varepsilon _0}\frac{A}{d}\)
هر ماده دی الکتريک تحمل ولتاژ معينی را دارد. اگر اختلاف پتانسيل متصل به دو سر خازن از اين مقدار بالاتر رود، پديده فروريزش الکتريکی رخ می دهد. در اين حالت شدت ميدان الکتريکی به قدری قوی است که باعث کنده شدن الکترون ها و حرکت آن در ماده دی الکتريک می شود و معمولا منجر به سوختن دی الکتريک و خازن می گردد.
يک خازن علاوه بر بار می تواند ابزاری برای ذخيره انرژی در مدارها باشد. انرژی ذخيره شده در خازن از روابط زير) بر حسب بار و اختلاف پتانسيل و ظرفيت خازن) بدست می آيد:
\(U = \frac{1}{2}QV = \frac{1}{2}C{V^2} = \frac{1}{2}\frac{{{Q^2}}}{C}\)
که در آن U انرژی پتانسيل الکتريکی خازن بوده و يکای آن ژول است.
مثال
ظرفيت خازن مسطحی 5 پيکو فاراد و بار الکتريکی ذخيره شده بر صفحات آن \(0/2\) نانو کولن و فاصله بين دو صفحه خازن از هم 1 ميلی متر است. شدت ميدان الکتريکی بين دو صفحه خازن را تعيين کنيد.
\(\begin{array}{l}Q = 0/2nC = 0/2 \times {10^{ - 9}}C\\C = 5PF = 5 \times {10^{ - 12}}F\\V = ?\\d = 1mm = 1 \times {10^{ - 3}}m\\E = ?\\V = \frac{Q}{C} = \frac{{0/2 \times {{10}^{ - 9}}}}{{5 \times {{10}^{ - 12}}}} = 40V \to E = \frac{V}{d} = \frac{{40}}{{1 \times {{10}^{ - 3}}}} = 4 \times {10^4}\frac{N}{C}\end{array}\)
1 در خازنی که به باتری متصل است، همواره اختلاف پتانسيل و سر خازن برابر اختلاف پتانسيلی است که باتر ايجاد می کند.
2 در خازن بارداری که از باتری جدا شده است، آنچه همواره پايدار می ماند بار خازن است.
مدارهای الکتريکی
فصل 2 : جریان الکتریکی و مدارهای جریان مستقیم
مدارهای الکتريکی
جريان الکتريکی
ناشی از شارش بارهای متحرک است به عبارت ديگر، عبور بارهای الکتريکی از يک رسانا را جريان الکتريکی گويند.
جهت جريان الکتريکی
جهت حرکت بارهای مثبت، يعنی در خلاف جهت الکترون ها را جهت جريان الکتريکی گويند. (جريان الکتريکی هم جهت با E است.) بنا به قرارداد جهت جريان از قطب مثبت به طرف قطب منفی است.
عامل برقراری جريان، اختلاف پتانسيلی است که در دو سر رسانا اعمال می شود و وسايل توليد اين اختلاف پتانسيل، پيله ای شيميايی، ژنراتورها و . . . هستند.
سرعت سوق
سرعت متوسط شارش الکترون ها در يک رسانا، با اعمال ميدان الکتريکی را که به کُندی حرکت يک حلزون (يعني کمتر از \(1\frac{{mm}}{s}\) ( در خلاف جهت ميدان می باشد، را سرعت سوق می ناميم. اين سرعت باعث ايجاد جريان الکتريکی در يک رسانا می شود.
جريان الکتريکی متوسط
مقدار باری که در واحد زمان از مقطع مداری می گذرد، جريان الکتريکی ناميده می شود و واحد آن آمپر است.
\(I = \frac{{\Delta q}}{{\Delta t}}\)
اگر در تمام بازه های زمانی جهت جريان با زمان تغيير نکند و مقدار جريان ثابت باشد، جريان را مستقيم می نامند، در اين حالت جريان لحظه ای با جريان متوسط برابر است و داريم:
\(I = \frac{q}{t} \to q = It\)
در دستگاه SI، جریان (]) بر حسب آمپر (A)، بار الکتریکی (q) بر حسب کولن (C) و زمان (t) بر حسب ثانیه (s) می باشد.
اگر (I) بر حسب آمپر (A)، و زمان (t) بر حسب ساعت (h) باشد، بار الکتریکی (q) بر حسب آمپر ساعت (Ah) بيان می شود. هر چه آمپر- ساعت يک باتری بيشتر باشد، حداکثر باری که می تواند از مدار عبور دهد تا به طور ايمن تخيله شود، بيشتر است.
\(1Ah = 3600As = 3600C\)
مدار الکتريکی
برای آنکه جريانی برقرار شود، بار الکتريکی به يک مسير بسته نياز دارد تا در آن شارش کند. مسير بسته ای که بارهای الکتريکی در آن حرکت می کنند، مدار الکتريکی ناميده می شود. مدار الکتريکی شامل رساناهای فلزی (سيم يا لامپ)، منبع تامين انرژی الکتريکی (باتری- پيل يا منبع تغذيه) کليد قطع و وصل، وسيله های اندازه گيری اختلاف پتانسيل، شدت جريان و مقاومت الکتريکی (ولت سنج، آمپر سنج و اهم متر يا آوومتر) است. شکل ساده ی مدار الکتريکی در زير رسم شده است.
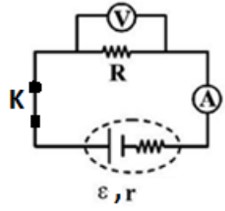
طريقه قرار گرفتن ولت سنج و آمپرسنج در مدار الکتريکی
ولت سنج، وسيله اندازه گيری اختلاف پتاسيل الکتريکی است که به طور موازی در مدار قرار می گيرد و مقاومت آن بسيار زياد می باشد، چون از ولت سنج بايد جريان کمی بگذرد تا ولت سنج اختلاف پتانسيل وسيله مورد نظر را اندازه بگيرد. اگر ولت سنج به صورت متوالی در مدار قرار گيرد، به علت مقاومت زيادی که دارد؛ مانع عبور جريان می شود و جريان شاخه ای از مدار که ولت سنج در آن قرار گرفته است، صفر می شود.
آمپرسنج وسيله اندازه گيری جريان است که بطور سری (متوالی) در مدار قرار می گيرد و مقاومت آن بسيار ناچيز است. زيرا درحد امکان بايد تمام جريان از آمپرسنج بگذرد، تا آمپرسنج جريان آن مصرف کننده را اندازه گيری کند. اگر آمپرسنج به صورت موازی در مدار قرارگيرد، در مدار اتصال کوتاه می شود و آمپرسنج نيز آسيب می بيند.
مقاومت الکتريکی (R)
هنگامی که اختلاف پتانسيلی در دو سر سيم ايجاد شود و باعث حرکت الکترون های آزاد در سيم مدار شود، اين الکترون ها با اتم های رسانا که در حال نوسان اند؛ برخورد می کنند و اين موضوع باعث گرم شدن رسانا می شود. در واقع هر رسانايی در برابر عبور الکترون های آزاد (جريان الکتريکی) از خود مقاومتی نشان می دهد که معمولا به صورت گرما در اجزای مدار الکتريکی ظاهر می شود و اصطلاحاً می گوييم، رسانا دارای مقاومت الکتريکی است
- آزمون آنلاین تمامی دروس پایه ریاضی
- گام به گام تمامی دروس پایه ریاضی
- ویدئو های آموزشی تمامی دروس پایه ریاضی
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ریاضی
- فلش کارت های آماده دروس پایه ریاضی
- گنجینه ای جامع از انشاء های آماده پایه ریاضی
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ریاضی
قانون اهم
فصل 2 : جریان الکتریکی و مدارهای جریان مستقیم
قانون اهم
در دمای ثابت، نسبت اختلاف پتانسيل دو سر رسانا به جريانی که از آن می گذرد، مقدار ثابتی است که برابر مقاومت الکتريکی مدار (R) است.
\(R = \frac{V}{I}\)
1 در رابطه قانون اهم، مقاومت الکتريکي مدار (R) بر حسب اهم (\(\Omega \)) ، اختلاف پتانسيل الکتريکی (V) بر حسب ولت (v) و جريان الکتريکی (I) بر حسب آمپر (A) می باشد.
2 وسايل زيادی وجود دارند که از قانون اهم پيروی نمی کنند، يکی از آنها ديود نور گسيل (LED) است.
تعريف اهم
يک اهم، مقاومت سيمی است که اگر اختلاف پتانسيل يک ولت در دو سر آن برقرار شود، جريان \(1A\) از سيم عبور کند.
\(1\Omega = \frac{{1v}}{{1A}}\)
نمودار قانون اهم
نمودار قانون اهم، خط راستی است که از مبدأ مختصات می گذرد.
اگر محور عمودی را (V) بناميم و محور افقی را (I) بناميم، شيب اين خط برابر مقاومت الکتريکی رسانا است.
اگر محور عمودی را (I) بناميم و محور افقی را (V) بناميم، شيب اين خط برابر عکس مقاومت الکتريکی رسانا است.
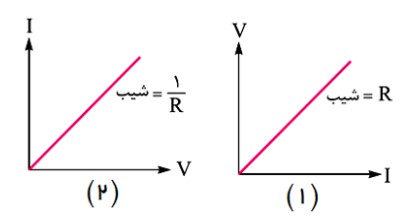
\(\begin{array}{l}1)\tan \alpha = \frac{V}{I} = R\\2)\tan \alpha = \frac{I}{V} = \frac{1}{R}\end{array}\)
با افزايش ولتاژ، در يک دمای ثابت جريان الکتريکی به همان نسبت زياد می شود، اما مقاومت سيم عوض نمی شود.
مثال
بار الکتریکی \(60C\) در مدت زمان \(30s\) از مقطع مداری با اختلاف پتانسیل \(100V\) می گذرد، مقاومت الکتریکی آن را بدست آورید.
\(\begin{array}{l}q = 60C\\t = 30s\\V = 100v\\I = ?\\R = ?\\I = \frac{q}{t} \to I = \frac{{60}}{{30}} = 2\\R = \frac{V}{I} = \frac{{100}}{2} = 50\Omega \end{array}\)
عوامل موثر بر مقاومت الکتریکی
فصل 2 : جریان الکتریکی و مدارهای جریان مستقیم
عوامل موثر بر مقاومت الکتریکی
مقاومت يک سيم در دمای ثابت، به عوامل ساختمانی اش از جمله طول، مساحت مقطع و جنس آن بستگی دارد. اگر سطح مقطع سيم در تمام طول آن ثابت باشد، مقاومت آن از رابطه ی \(R = \rho \frac{L}{A}\) بدست می آید.
در این رابطه \(\rho \)، مقاومت ويژه رساناست و به جنس سيم بستگی دارد، واحد آن (\(\Omega m\) ) است؛ L طول سیم بر حسب متر، A سطح مقاومت سیم بر حسب متر مربع است.
ديد ديگر درباره عوامل موثر بر مقاومت الکتريکی
هر چه طول رسانا بيشتر باشد، الکترون ها هنگام عبور از آن برخوردهای بيشتری با اتم ها دارند، بنابراين مقاومت الکتريکی جسم بيشتر می شود. کوچکتر شدن سطح مقطع جسم باعث کاهش عبور جريان از سيم می شود و اين به معنای افزايش مقاومت در برابر عبور جريان است.
1 مقاومت ويژه يک ماده به ساختار اتمی و دمای آن بستگی دارد، رساناهای الکتريکی خوب مقاومت ويژه بسيار کم و عايق های خوب مقاومت ويژه بسيار زيادی دارند. ژرمانيم و سيليسيم که مقاومت ويژه آن ها بين مقاومت ويژه رساناها و نارسانا است را نيمه رسانا می ناميم مقاومت ويژه نيمه رساناها با افزايش دما کاهش می يابد.
2 نسبت مقاومت دو ميله رسانا از رابطه زير بدست می آيد.
\(\frac{{{R_1}}}{{{R_2}}} = \frac{{{\rho _1}}}{{{\rho _2}}} \times \frac{{{L_1}}}{{{L_2}}} \times \frac{{{A_2}}}{{{A_1}}}\)
اثر دما بر مقاومت ويژه رساناهای فلزی و نيم رساناها
در اثر افزايش دمای يک رسانای فلزی، تعداد حامل های بار (الکترون های آزاد) تقريباً ثابت می ماند، ولی ارتعاشات کاتوره ای اتم ها و يون های آن افزايش می يابد. اين عامل موجب افزايش برخورد حامل های بار با شبکه اتمی رسانای فلزی می شود. و به اين ترتيب مقاومت رسانا در برابر عبور جريان زياد می شود. مثلا مقاومت لامپ معمولی روشن با رشته تنگستن از لامپ خاموش مشابه آن بيشتر می باشد؛ آزمايش نشان می دهد مقاومت ويژه فلزات در يک گستره دمايی نسبتاً بزرگ با دما تقريباً به طور خطی تغيير می کند. بر اثر تغيير دما به اندازه ی \(\Delta T\) مقاومت سيم \({R_1}\) برابر \({R_2}\) می شود.
تغیرات مقاومت به صورت \(\Delta R = {R_1}\alpha \Delta T\) نوشته می شود؛ (\(\alpha \)، ضریب دمایی مقاومت است، برای فلزات \(\alpha \rangle 0\) و برای نیم رسانا ها \(\alpha \langle 0\) می باشد.)
1 درصد تغيير مقاومت برای يک سيم به صورت \(\frac{{\Delta R}}{{{R_1}}} \times 100 = \alpha \Delta T \times 100\) نوشته می شود.
2 تغييرات مقاومت ويژه توسط رابطه روبرو بيان می شود. \(\Delta \rho = {\rho _0}\alpha (T - {T_0}) = {\rho _0}\alpha \Delta T\) و یا \(\rho = {\rho _0}\left[ {1 + \alpha (T - {T_0})} \right]\)
اثر دما بر مقاومت ويژه نيم رساناها
در دماهای پايين تعداد حامل های بار نيم رساناها ناچيز است، و نيم رسانا مانند نارسانا رفتار می کند. با افزايش دما بر تعداد اين حامل های بار افزوده می شود؛ گرچه با افزايش دما بر تعداد حامل های بار افزوده می شود و تعداد برخوردهای کاتوره ای نيز افزايش می يابد، اما تأثير افزايش تعداد حامل های بار بيشتر از افزايش اين برخوردهای کاتوره ای است. بنابراين با افزايش دما مقاومت ويژه نيم رسانا کاهش می يابد.
ضريب دمايی مقاومت ويژه برای رساناها مثبت و برای نيم رساناها منفی است، بنابراين مقاومت رساناها با افزايش دما، افزايش می يابد و مقاومت نيم رساناها با افزايش دما، کاهش می يابد.
مثال
ضريب دمايي مس در دماي \(20{}^0C\) برابر با \(0/007{}^0{C^{ - 1}}\) است. اگر مقاومت سیمی مس در دمای \(20{}^0C\) برابر \(5\Omega \) باشد، مقاومت این سیم در دمای \(100{}^0C\) چقدر است؟
\(\begin{array}{l}\Delta R = {R_1}\alpha \Delta T \to \Delta R = 5 \times 7 \times {10^{ - 3}} \times 80 \to \Delta R = 2/8\Omega \\\Delta R = {R_2} - {R_1} \to 2/8 = {R_2} - 5 \to {R_2} = 7/8\Omega \end{array}\)
انواع مقاومت ها
فصل 2 : جریان الکتریکی و مدارهای جریان مستقیم
انواع مقاومت ها
مقاومت ها برای کنترل جريان ولتاژ در وسايل الکترونيکی بکار می روند. اندازه ی مقاومت ها می تواند کمتر از \(1\Omega \) تا مگا اهم باشد. انواع اصلی مقاومت ها بر دو نوع است؛ مقاومت های پیچه ای و مقاومت های ترکیبی
مقاومت های پیچه ای
شامل پيچه ای از يک سيم نازک هستند که معمولا جنس آنها از آلياژهايی مانند نيکروم (نيکل- کروم) يا منگانين (مس-نيکل- منگنز) است. اين پيچه ها به دور هسته ای از جنس سراميک، پلاستيک يا شيشه پيچيده شده اند و در غلافی از سراميک قرار گرفته اند.
مقاومت های پيچه ای، قديمی ترين نوع مقاومت هاست که امروزه همچنان توليد می شوند، زيرا می توانند برای حصول مقاومت های پايين بسيار دقيق و همچنين توان های بالا ساخته شوند.
یکی از معروفترين مقاومت های پيچه ای، رئوستا نام دارد که در مدارهای الکتريکی پتانسيومتر ناميده می شود.
رئوستا يا مقاومت تغيير
در آزمايشگاه برای تنظيم و کنترل جريان از يک مقاومت متغير استفاده می شود که رئوستا نام دارد. اين وسيله از يک سيم دراز با مقاومت ويژه نسبتاً زياد (تنگستن) تشکيل شده است. اين سيم روی استوانه ای پيچيده شده است. با استفاده از يک دکمه لغزنده که روي ريلی بالای استوانه قرار دارد و انتهای آن با سيم در تماس است می توان قسمت های دلخواه سيم را در مسير جريان قرار داده و مقاومت را به طور دلخواه تغيير داد.
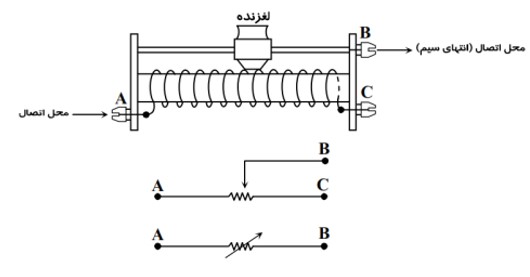
در هنگام استفاده از رئوستا ابتدا آن را با بيشترين مقاومت درمدار قرار می دهيم سپس با دکمه لغزنده، مقاومت مناسب را برای جريان مورد نظر تنظيم می کنيم.
مقاومت های ترکيبی (رنگی)
اين گونه مقاومت ها معمولا از کربن، برخی نيم رساناها، و يا فيلم های نازک فلزی ساخته شده اند که در داخل پوشش پلاستيکی قرار گرفته اند. کارخانه های سازنده اين گونه مقاومت ها، آنها را در اندازه های خاص توليد می کنند. اندازه ی آنها يا بر روی آنها نوشته شده و يا بوسيله ی کدی رنگی نشان داده شده است. مشخصه ی اصلی اين مقاومت ها بيشينه ی توان الکتريکی است که مقاومت ها می تواند بدون آن که بسوزد، تحمل کند.
کد گذاری مقاومت های ترکيبی (مقاومت های کربنی)
در استانداردهای مهندسی، سيم ها را بر حسب قطر و مساحت سطح مقطع آنها نمره بندی می کنند و اندازه ی مقاومت های الکتريکی را با حلقه های رنگی کدگذاری می نمايند. روی مقاومت ها چهار خط رنگی وجود دارد. اگر مقاومت را طوری نگه داريم که در سمت راست، رنگ نقره ای يا طلايی که مشخص کننده ضريب خطا است قرار گيرد، از سمت چپ به ترتيب اولين رنگ، دهگان (a)، دومين رنگ يکان (b) و سومين رنگ، توان 10 (n) می باشند.
\(R = ab \times {10^n}\)
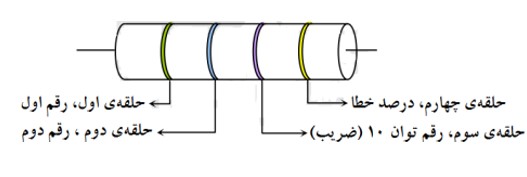
1 دقت کنید اعداد a و b را در هم ضرب نکنید.
2 مقدار خطای حلقه ی چهارم، تلرانس ناميده می شود و ميزان انحراف از مقدار دقيق را بر حسب درصد مشخص می کند.
3 درصد خطای طلایی 5%، درصد خطای نقره ای 10% و درصد خطای بی رنگ 20% است.
- آزمون آنلاین تمامی دروس پایه ریاضی
- گام به گام تمامی دروس پایه ریاضی
- ویدئو های آموزشی تمامی دروس پایه ریاضی
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ریاضی
- فلش کارت های آماده دروس پایه ریاضی
- گنجینه ای جامع از انشاء های آماده پایه ریاضی
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ریاضی
مقاومت های خاص
فصل 2 : جریان الکتریکی و مدارهای جریان مستقیم
مقاومت های خاص
ترميستور
ترميستور نوعی مقاومت الکتريکی است که وابستگی مقاومت الکتريکی آن به دما، با مقاومت های معمولی متفاوت است. از ترميستور به عنوان حسگر دما در مدارهای حساس به دما مانند زنگ خطر آتش، دماپا و دماسنج استفاده می شود. رايج ترين ترميستورها ديسکی، مهره ای و ميله ای است.
به مقاومت های حساس به دما که از مواد نيمه هادی ساخته می شود، ترميستور می گويند.
در ترميستور مقاومت الکتريکی با دما به طور غير خطی تغيير می کند. رنج دمای آن \( - 70\) تا 150 و نهايتا 316 درجه سانتيگراد می باشد. در اکثر کاربردها مقاومت آن در دمای 25 درجه سانتيگراد بين 100 تا 100 کيلو اهم می باشد.
1 اندازه کوچک، پاسخ سريع, حساسيت بسيار بالا از مزایای ترمیستور ها است.
2 غير خطی، محدوده دمايی کم، شکننده، مقاومت بالا و مشکلات نويز، ناپايداری و کاليبره نبودن از معایب ترمیستور ها است.
مقاومت های نوری (LDR)
نوعی مقاومت است که مقاومت الکتريکی آن به نور تابيده شده به آن بستگی دارد. به طوری که با افزايش شدت نور، از مقاومت آن کاسته می شود. اندازه ی مقاومت های نوری از چند مگا اهم در تاريکی تا چند صد اهم در روشنايی قابل تغيير است.
نوعی از اين مقاومت ها از جنس نيم رسانای خالص، مانند سيليسيم هستند که با افزايش شدت نور تابيده شده، بر تعداد حامل های بار الکتريکي آنها افزوده شده و در نتيجه از مقاومت آنها کاسته می شود. مقاومت الکتريکی چنین LDR هایی را بر حسب روشنایی (LUX) سنجیده می شوند. از (LDR) در چشم های الکترونیکی، دزدگيرها، کنترل کننده های خودکار و چراغ روشنايی خيابان ها استفاده می شود.
ديودها (يکسوکننده جريان)
ديود قطعه ای است که هر گاه در مداری قرار گيرد، حريان را تنها از يک سو عبور می دهد و مقاومت آن در برابر عبور جريان در اين سو ناچيز است. معروف ترين ديودها، ديودهای نوری يا (LED) هستند. از LED در چراغ خودررو، روشنايی منازل، تابلوهای تبليغاتی، نمايشگرهای LED و ... استفاده می شود. LED ها در مقايسه با لامپ رشته ای عمر طولانی تری دارند و به دليل نداشتن رشته سيم در آنها به هنگام توليد نور، گرمای زيادی توليد نمی کنند.
محاسبه انرژی الکتريکی مصرف شده در يک مقاومت
هنگامی که بار مثبت q در جهت ميدان الکتريکی يکنواخت حرکت کند، انرژی پتانسيل الکتريکی آن به اندازه \(q.\Delta V\) کاهش می يابد.
\(\Delta U = q \times \Delta V\)
اين کاهش انرژی پتانسيل به صورت انرژی جنبشی در می آيد. در اثر برخورد اين بارها با اتم ها اين انرژی به اتم های رسانا منتقل می شود و انرژی درونی رسانا را افزايش می دهد، در نتيجه در اثرعبور جريان الکتريکی رسانا گرم می شود.
اگر جريان ثابت I در مدت t ثانيه در سيمی به مقاومت R برقرار شود، داريم:
\(1)U = (It).(RI) = R{I^2}t\)
U: انرژی که بار هنگام عبور از سيم از دست می دهد و به انرژی درونی سيم تبديل می شود.
با توجه به رابطه (1) و رابطه قانون اهم (\(V = RI\) ) روابط ديگری برای انرژی بدست می آوريم:
\(2)U = VIt\)
\(3)U = \frac{{{V^2}}}{R}t\)
توان الکتريکی مصرفی در يک مقاومت (P)
مقدارانرژی مصرف شده در واحد زمان را توان الکتريکی می نامند و با نماد P نشان می دهند.
\(P = \frac{U}{t}\)
1 يکای توان الکتريکی در SI، ژول بر ثانيه است که آنرا وات (W) می نامیم.
2 با توجه به رابطه ی \(U = R{I^2}t = VIt = \frac{{{V^2}}}{R}t\) و رابطه \(P = \frac{U}{t}\) ، رابطه های زير برای توان الکتريکی مصرف شده در مقاومت به دست می آيد.
\(P = R{I^2} = VI = \frac{{{V^2}}}{R}\)
توان و انرژی الکتريکی مصرفی يا (گرما) در مقاومت
برای محاسبه انرژی الکتريکی مصرفی يا گرمای توليد شده توسط يک مقاومت کافيست که توان آن مقاومت را در زمان ضرب کنيد، \(U = P \times t\) . دقت کنيد؛ توان، انرژی الکتريکی مصرفی کل مدار را می توان به دو شکل حساب کرد.
راه اول: برای هر مقاومت حساب کرد و بدون توجه به جايگاهشان همگی را با هم جبری جمع کرد.
راه دوم: اگر ولتاژ کل يا جريان کل را داشتيم با محاسبه ی مقاومت معادل، از \(P = R{I^2}\) یا \(P = \frac{{{V^2}}}{R}\) استفاده کنيم.
نيروی محرکه الکتريکی و مولدها
فصل 2 : جریان الکتریکی و مدارهای جریان مستقیم
نيروی محرکه الکتريکی و مولدها
بارهای الکتريکی ضمن شارش در مدار الکتريکی انرژی جنبشی از دست می دهند،کار مولد اين است که اين انرژی را دوباره تامين کند. همانطور که می دانيم بارهای الکتريکی از پتانسيل پايين تر شارش می کند و وارد مولد می شوند؛ مولد با صرف انرژی بارهای الکتريکی را از پتانسيل پايين تر به پتانسيل بالاتر می برد و سبب شارش آنها در مدار می شود. بارهای الکتريکی هنگام شارش انرژی خود را از دست می دهند برای اينکه شارش بار در مدار تداوم يابد اين انرژی بايد بوسيله مولد تامين شود.
وسيله ای که با انجام کار روی بار الکتريکی اختلاف پتانسيل را ثابت نگه می دارد، منبع نيروی محرکه الکتريکی ناميده می شود.
منبع نيروهای الکتريکی بارهای الکتريکی مثبت را در خلاف جهت ميدان الکتريکی از پتانسيل پايين تر به پتانسيل بالاتر می برند و با افزايش انرژی پتانسيل آنها، جريان ثابتی در مدار برقرار می کنند.
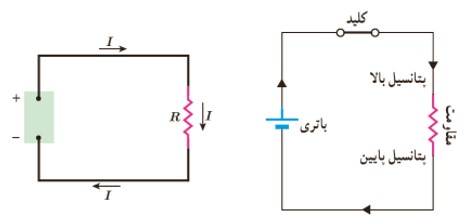
باتری، پيل سوختی، سلول خورشيدی و مولدهايی الکتريکی نمونه هايی از منبع نيروی محرکه الکتريکی اند.
کاری که منبع نيروی محرکه روی واحد بار الکتريکی مثبت انجام می دهد تا آن را از پايانه با پتانسيل کمتر به پايانه با پتانسيل بيشتر ببرد، نيروی محرکه الکتريکی (emf) می نامند.
\(\varepsilon = \frac{{\Delta W}}{{\Delta q}}\)
يکای نيروی محرکه مولد، ژول برکولن (\(\frac{J}{C}\) ) یا ولت (V) است.
منبع نيروهای محرکه الکتريکی يا آرمانی (\(r = 0\) ) و یا واقعی (\(r \ne 0\) ) هستند، در حالت آرمانی اختلاف پتانسيل الکتريکی ميان اين دو پايانه با نيروی محرکه الکتريکی برابر است.
\({V_b} - {V_a} = \varepsilon \)
در حالت واقعی هنگامی جريان از مولد می گذرد، اختلاف پتانسيل بين پايانه های آنها بر خلاف منابع آرمانی، متفاوت از نيروی محرکه الکتريکی خواهد شد، يعنی اختلاف پتانسيل در مقايسه با نيروی محرکه مولد بيشتر و يا کمتر خواهد شد.
هر مولد دارای مقاومت درونی است که آن را با r نمايش می دهند و علامت آن در مدارهای الکتريکی به صورت شکل روبرو است.
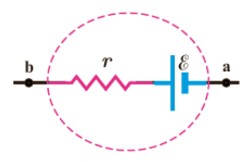
قواعد حل مدارهای تک حلقه ای
در هر دور زدن کامل حلقه ای از مدار، جمع جبری اختلاف پتانسيل های اجزای مدار صفر است.
برای حل مدارهای تک حلقه ای بايد يک جهت دلخواه برای جريان الکتريکی و يک جهت دلخواه برای گردش حلقه در نظر بگيريم. اگر در سوالی جهت جريان و گردش حلقه مشخص باشد، بايد از همان جهت های مشخص پيروی کنيم اين جهت ها ساعتگرد و يا پاد ساعتگردند.
الف) هرگاه روی مداری در جهت جريان از مقاومت R و یا r بگذريم، پتانسيل به اندازه IR یا Ir کاهش می يابد و اگر درخلاف جهت جريان از مقاومت ها بگذريم، پتانسيل به اندازه IR یا Ir افزایش می یابد.
ب) هرگاه برای گذر از مولد (بدون توجه به جهت جريان) از پايانه منفی به پايانه مثبت برويم، پتانسيل به اندازه نيروی محرکه مولد افزايش می يابد و اگر از پايانه مثبت به منفی (بدون توجه به جهت جريان) بگذريم، پتانسيل به اندازه نيروی محرکه مولد کاهش می يابد.
1 برای محاسبه جريان يک حلقه حتماً بايد حلقه را يک دورکامل بگرديم. يعنی بايد از يک نقطه فرضی شروع کنيم و در جهت دلخواه گردش کنيم و هنگام گذر از هر جزء را اضافه کنيم. (اگر اين تغييرات افزايش يابند، با علامت مثبت و اگر کاهش يابند، با علامت منفی جايگذاری می کنيم.(
2 برای محاسبه اختلاف پتانسيل بين دو نقطه از مدار، ابتدا پتانسيل نقطه اول را می نويسيم آنگاه از اين نقطه روی مدار در جهت دلخواه به طرف نقطه دوم می رويم و ضمن گذر از هر جزء تغييرات پتانسيل هر جزء را اضافه می کنيم تا به نقطه دوم برسيم، حاصل برابر پتانسيل نقطه دوم است.
3 اگر درحل مداری جريان بدست آمده مثبت باشد، معلوم می شود که جهت انتخاب شده درست است و اگر جريان بدست آمده منفی باشد، معلوم می شود که جهت جريان در مدار، خلاف جهتی است که انتخاب شده است.
مدار تک حلقه با چند مولد
مولدها وسايلی هستند که انرژی لازم را جهت حرکت الکترون در مدار تامين می کنند. مولدها تمايل دارند جريان را از پايانه مثبت خود خارج کنند، البته در شرايطی که تحت تأثير مولدی قرار بگيرند که از خودشان قوی تر باشد، جريان را از پايانه منفی خود خارج می کنند که در اين صورت به آنها مولدهای مصرف کننده (ضد مولد) نيز می گوييم، توان اين مولدها را توان ورودی ميناميم.
در مدارهای تک حلقه ای که چند مولد در يک شاخه حضور دارد، گام صفر اين است که بر اساس زور سنج ها (\(\varepsilon \)) نيرو محرکه ها جهت جريان را مشخص کنيم، سپس اندازه ی آن را تعيين کنيم.
اندازه ی جريان را در اين گونه حلقه ها، از رابطه ی \(I = \frac{{\sum \varepsilon - \sum {\varepsilon '} }}{{\sum {(R + r)} }}\) بدست می آيد که \(\sum \varepsilon \) مجموع تمام نيروی های محرکه مولد (مولد توليد کننده) و \(\sum {\varepsilon '} \) مجموع تمام نيرومحرکه های ضد مولد (مولد مصرف کننده( هستند.
در مدار روبرو، فرض کنيد ؛ \(({\varepsilon _1} + {\varepsilon _3})\rangle {\varepsilon _2}\)
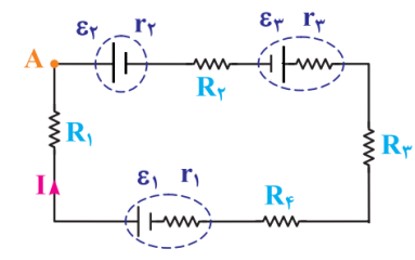
زور نيرو محرکه ی مولدهای ساعتگرد (مولد اول و سوم) از نيرو محرکه های مولدهای پاد ساعتگرد (مولد دوم) بيشتر است.
مولد اول: جريان از سر مثبت خارج شده – پس توليد کننده است.
مولد دوم: جريان به سر مثبتش وارد شده – پس مصرف کننده است.
مولد سوم: جريان از سر مثبت خارج شده – پس توليد کننده است.
\(I = \frac{{({\varepsilon _1} + {\varepsilon _3}) - {\varepsilon _2}}}{{{R_1} + {R_2} + {R_3} + {R_4} + {r_1} + {r_2} + {r_3}}}\)
باتری که جريان از سر مثبتش خارج شود را مولد (يا مولد توليد کننده يا مولد برنده) و باطری که، جريان از سر منفی اش خارج شود؛ را ضد مولد (يا مولد مصرف کننده يا مولد بازنده) می ناميم. اگر در مداری فقط يک باتری داشته باشيم، قطعاً مولد (مولد توليد کننده) است و جريان از سر مثبتش خارج می شود.
مثال
در مدار شکل زیر
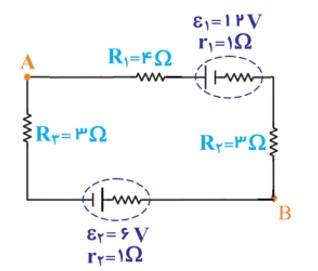
الف شدت جریان چند آمپر است؟
\(\begin{array}{l}{V_A} - i{R_1} - i{r_1} - {\varepsilon _1} - i{R_2} - i{r_2} - {\varepsilon _2} - i{R_3} = {V_A}\\ \to i = \frac{{{\varepsilon _1} + {\varepsilon _2}}}{{{R_1} + {R_2} + {R_3} + {r_1} + {r_2}}} = \frac{{12 + 6}}{{4 + 3 + 3 + 1 + 1}} = \frac{{18}}{{12}} = 1/5V\end{array}\)
ب اختلاف پانسیل دو نقطه ی A و B، (\({V_B} - {V_A}\) ) چند ولت است؟
\({V_B} - {\varepsilon _2} - i{r_2} - i{R_3} = {V_A} \to {V_B} - {V_A} = {\varepsilon _2} + i{r_2} + i{R_3} = 6 + 1/5 \times 1 + 1/5 \times 3 = 12V\)
ج اختلاف پتانسیل باتری (1) را بدست آورید؟
\({V_c} + {\varepsilon _1} - i{r_1} = {V_d} \to {V_d}\rangle {V_c} \to {V_d} - {V_c} = {\varepsilon _1} - i{r_1} = 12 - 1/5 \times 1 = 10/5V\)
اگر نقطه ای از مدار به زمين متصل باشد، پتانسيل آن نقطه برابر صفر در نظر گرفته می شود.
افت پتانسيل در مولد
فصل 2 : جریان الکتریکی و مدارهای جریان مستقیم
افت پتانسيل در مولد
مولدهای ايده آل دارای مقاومت درونی نيستند، ولی مولدهای معمولی دارای مقاومت کمی هستند به همين علت مقداری از انرژی داده شده توسط مولد در خود مولد به صورت گرما تلف می شود.
مقدار انرژی مصرف شده توسط واحد بار در داخل مولد را افت پتانسيل مولد می ناميم.
با توجه به مدار مقابل می توان افت پتانسيل در يک مولد را حساب کرد.
در حالتی که جريان از مولد نگذرد (\(Ir = 0\) ) يعني مدار باز باشد، اختلاف پتانسيل دوسر مولد با نيروی محرکه مولد برابر است. بنابراين نيروی محرکه مولد برابر اختلاف پتانسيل دو سر مولد است وقتی که جريانی از مولد نگذرد، پس :
\(1){V_A} - {V_B} = IR = V\)
اگر دو سر مولد را به ولت سنجی متصل کنيم، عملا جريانی از ولت سنج نمی گذرد. عددی که ولت سنج نشان می دهد برابر نيروی محرکه مولد است، از طرفی مطابق شکل بالا و حل مدارهای تک حلقه ای داريم:
\(\begin{array}{l}2){V_A} - \varepsilon + Ir = {V_B} \to {V_A} - {V_B} = \varepsilon - Ir\\3)V = {V_A} - {V_B} = \varepsilon - Ir\end{array}\)
از رابطه (1) و (2) نتيجه می گيريم:
يعنی اختلاف پتانسيل دو سر مولد به اندازه Ir از نيروی محرکه مولد کمتر است.
از رابطه (3) و رابطه (1) می توان شدت جريانی را که از يک مولد می گذرد، حساب کرد. پس:
\(I = \frac{\varepsilon }{{R + r}}\)
- آزمون آنلاین تمامی دروس پایه ریاضی
- گام به گام تمامی دروس پایه ریاضی
- ویدئو های آموزشی تمامی دروس پایه ریاضی
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ریاضی
- فلش کارت های آماده دروس پایه ریاضی
- گنجینه ای جامع از انشاء های آماده پایه ریاضی
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ریاضی
توان در مدارهای الکتريکی
فصل 2 : جریان الکتریکی و مدارهای جریان مستقیم
توان در مدارهای الکتريکی
به طور کلی اگر يک عنصر مداری (مقاومت و يا مولد) داری اختلاف پتانسيل \(\Delta V\) باشد، بار \(\Delta q\) در مدت زمان \(\Delta t\) از اين عنصر می گذرد. کار خارجی برای انتقال چنين باری برابر است با:
\(W = \Delta q.\Delta V\)
از طرفی توان الکتريکی برابر است با:
\(P = \frac{{\Delta W}}{{\Delta t}} = \frac{{\Delta q \times \Delta V}}{{\Delta t}} = \left( {\frac{{\Delta q}}{{\Delta t}}} \right) \times \Delta V = I \times \Delta V = I \times \left( {{V_b} - {V_a}} \right)\)
اگر \(P\rangle 0\) باشد، اين عنصر به مدار انرژی می دهد و اگر \(P\langle 0\) باشد، اين عنصر از مدار انرژی می گيرد.
توان مولد
فصل 2 : جریان الکتریکی و مدارهای جریان مستقیم
توان مولد
مقدار انرژی مصرف شده در واحد زمان در هر مصرف کننده الکتريکی را توان مصرفی آن می ناميم. اگر جريان I از مولد بگذرد انرژی مصرفی آن عبارت است از:
\(U = \varepsilon It\)
توان توليدی مولد از رابطه \(P = \frac{U}{t} = \varepsilon \times I\) بدست می آید.
بخشی از اين توان توليدی، توسط خود مولد به دليل مقاومت درونی مولد (r) در درون مصرف می شود که بنا به آنچه در مورد يک مقاومت ديديم اين مقدار برابر است با:
\(P' = {I^2}r\)
بنابرين داريم:
توان مفید یا خروجی مولد = توان مصرف شده در مولد – توان تولیدی مولد
يعني توان مفيد مولد (توان خروجی) از رابطه \(P'' = \varepsilon I - {I^2}r\) بدست می آید.
مثال
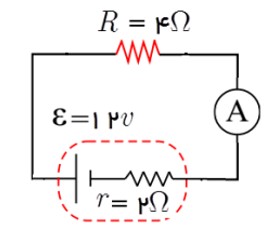
در شکل بالا
الف) توان ذخیره شده در مولد
ب) توان مصرفی مقاومت درونی مولد
ج) توان مصرفی در مقاومت R
الف)
\(I = \frac{\varepsilon }{{R + r}} = \frac{{12}}{{4 + 2}} = 2A,P = \varepsilon I = 12 \times 2 = 24W\)
ب) توان مصرفی درون مولد توسط مقاومت درونی مصرف می شود.
\(P = {I^2}R = {2^2} \times 2 = 8W\)
ج) توان مصرفی مقاومت با توان خروجی مولد برابر است.
\(\begin{array}{l}P = R{I^2} = 4 \times {2^2} = 16W\\P = \varepsilon I - {I^2}r = 12 \times 2 - {2_2} \times 2 = 24 - 8 = 16W\\P'' = P - P' = 24 - 8 = 16W\end{array}\)
معادل گیری مقاومت ها
فصل 2 : جریان الکتریکی و مدارهای جریان مستقیم
معادل گیری مقاومت ها
الف) اتصال متوالی مقاومت ها:
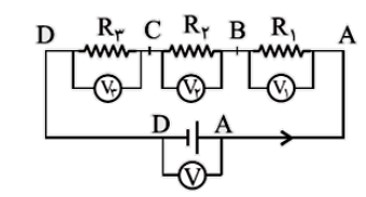
در اين مقاومت ها شدت جريان دو سر هر مقاومت، با شدت جريان کل مدار برابر است. يعنی:
\({I_T} = {I_1} = {I_2} = {I_3} = ...\)
در مقاومت های متوالی اختلاف پتانسيل کل مقاومت ها، برابر مجموع اختلاف پتانسيل تک تک مقاومت هاست. يعنی:
\({V_T} = {V_1} + {V_2} + {V_3} + ...\)
مقاومت معادل، در مقاومت های متوالی برابر مجموع تک تک مقاومت های مدار است.
\({R_T} = {R_1} + {R_2} + {R_3} + ...\)
در اين حالت مقاومت معادل از بزرگترين مقاومت موجود در مجموعه بزرگتر است.
با حذف يک مقاومت که به صورت متوالی در مدار قرار گرفته است، مقاومت مدار کاهش می يابد. در نتيجه بنا به رابطه \(I = \frac{V}{R}\) ، شدت جريان شاخه ای از مدار که آن مقاومت در آن قرار گرفته است افزايش می يابد و بالعکس.
اختلاف پتانسيل کل در مقاومت های سری، به نسبت مقاومت ها توزيع می شود. يعنی هر مقاومتی که بزرگ تر است سهم بيشتری از اختلاف پتانسيل کل را می گيرد.
\({I_1} = {I_2} \to \frac{{{V_1}}}{{{R_1}}} = \frac{{{V_2}}}{{{R_2}}} \to \frac{{{V_1}}}{{{V_2}}} = \frac{{{R_1}}}{{{R_2}}}\)
در حالت متوالی، توان مصرفی با مقاومت الکتريکی رابطه ی مستقيم دارد.
\(\begin{array}{l}{I_1} = {I_2}\\P = R{I^2}\\ \to \frac{{{P_2}}}{{{P_1}}} = \frac{{{R_1}}}{{{R_2}}}\end{array}\)
اگر n مقاومت مشابه با مقاومت \({R_1}\) داشته باشيم،که به طور متوالی بسته شده اند، مقاومت معادل برابر است با:
\({R_T} = n{R_1}\)
در اتصال سری، نبايد از سر مشترک انشعابی خارج گردد؛ شاخه ای که در آن ولت سنج ايده آل، کليد باز، خازن باردار يا مقاومت بی نهايت باشد انشعاب به حساب نمی آيد؛ زيرا مقاومت آنها بی نهايت است و الکترون وارد شاخه ی آنها نمی شود پس جريان در آنها صفر است، بنابراين: سه مقاومت زير سری هستند.
ب) اتصال موازی مقاومت ها
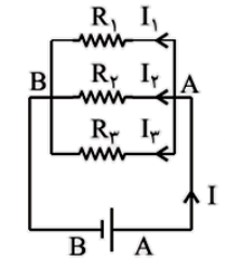
مقاومت هايی را موازی گويند، که دو سر هر يک از آنها به يک نقطه مشترک متصل باشند. در اين اتصال، يک سر همه ی مقاومت ها به يک نقطه و سر ديگر همه ی آنها نيز به يک نقطه ی ديگر متصل است، به همين خاطر اختلاف پتانسيل دو سر همه ی مقاومت ها يکسان است و داريم:
در اين مقاومت ها اختلاف پتانسيل هر مقاومت با اختلاف پتانسيل کل مدار برابر است. یعنی:
\({V_T} = {V_1} = {V_2} = {V_3} = ...\)
شدت جريان کل مدار، با مجموع شدت جريان های عبوری تک تک مقاومت ها برابر است. يعنی:
\({I_T} = {I_1} + {I_2} + {I_3} + ...\)
مقاومت معادل، مقاومت های موازی از رابطه ی زير بدست می آيد.
\(\frac{1}{{{R_T}}} = \frac{1}{{{R_1}}} + \frac{1}{{{R_2}}} + \frac{1}{{{R_3}}} + ...\)
يعنی، وارون مقاومت معادل مقاومت های موازی، برابر مجموع وارون تک تک مقاومت هاست. پس مقاومت معادل از کوچکترين مقاومت موجود در مجموعه کوچکتر است.
اگر يک مقاومت به صورت موازی به مدار اضافه شود، مقاومت مدار کوچک تر می شود و بالعکس، با حذف يک مقاومت موازی، مقاومت معادل بزرگتر می شود.
برای دو مقاومت موازی می توان مقاومت معادل را از رابطه روبرو بدست آورد.
\({R_T} = \frac{{{R_1} \times {R_2}}}{{{R_1} + {R_2}}}\)
اگر n مقاومت مشابه \({R_1}\) به صورت موازی به هم بسته شوند، مقاومت معادل آنها برابر است با:
\({R_T} = \frac{{{R_1}}}{n}\)
اگر دو مقاومت با هم موازی باشند، شدت جريان به نسبت عکس مقاومت ها توزيع می شود. يعنی مقاومتی که بزرگتر است جريان کمتری را از خود عبور می دهد.
\({V_1} = {V_2} \to {R_1}{I_1} = {R_2}{I_2} \to \frac{{{R_1}}}{{{R_2}}} = \frac{{{I_1}}}{{{I_2}}}\)
در حالت موازی شاخه ای که مقاومت کمتری دارد، گرمای بيشتری توليد می کند.
\(\begin{array}{l}{V_1} = {V_2}\\P = \frac{{{V^2}}}{R}\\ \to \frac{{{P_2}}}{{{P_1}}} = \frac{{{R_1}}}{{{R_2}}}\end{array}\)
- آزمون آنلاین تمامی دروس پایه ریاضی
- گام به گام تمامی دروس پایه ریاضی
- ویدئو های آموزشی تمامی دروس پایه ریاضی
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ریاضی
- فلش کارت های آماده دروس پایه ریاضی
- گنجینه ای جامع از انشاء های آماده پایه ریاضی
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ریاضی
میدان مغناطیسی
فصل 3 : مغناطیس
میدان مغناطیسی
آهن ربا
به موادی که براده های آهن را جذب می کند، آهن ربا می گویند. آهن، کبالت، نیکل و آلیاژ های آنها جذب آهن ربا می شوند از موادی که جذب آهن ربا می شوند می توان آهن ربا ساخت.
هر آهن ربایی دو قطب دارد.
ربایش در دو ناحیه از آهن ربا بیشتر از جاهای دیگر است، به این دو قطب می گویند.
1 قطبی را که تقریبا به سوی نیم کره شمالی زمین می ایستد، قطب شمال می نامند.
2 قطبی را که تقریبا به سوی نیم کره جنوبی زمین می ایستد، قطب جنوبی می نامند.
روش های آهن ربا کردن
1) بوسیله جریان الکتریسیته
یک تیغه فولادی را درون یک سیم پیچ قرار می دهیم و به جریان مستقیم وصل می کنیم، در مدت کوتاهی تیغه فولادی آهن ربا می شود.
2) مالش
یک قطب آهن ربا را در یک جهت معین از ابتدا تا انتهای میله ی مغناطیسی، می کشیم؛ به طور منظم این عمل را تکرار می کنیم. در این روش، انتهای میله که مالش به آن ختم می شود، همواره مخالف قطبی است که روی میله کشیده می شود.
3) بوسیله القا
یک آهن ربا را در نظر گرفته و در راستای آن یک تیغه فولادی قرار می دهیم، تیغه فولادی تحت اثر آهن ربایی که در بالای آن قرار دارد آهن ربا می شود. می گوییم در تیغه فولادی خاصیت مغناطیسی القا شده است.
قطب های القای مغناطیسی همواره به گونه ای خواهد بود که قطعه های آهنی جذب آهن ربای اصلی می شوند.
مجزا کردن قطب های مغناطیسی غیر ممکن است، چون هر قطعه جدا شده از آهن ربا، خود یک دو قطبی مجزا می شود.
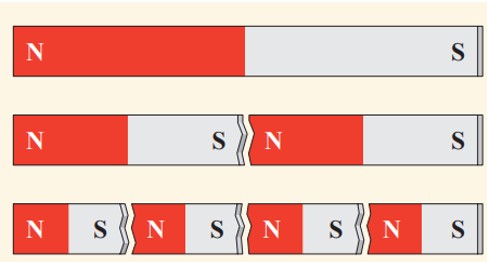
میدان مغناطیسی
خاصیتی در اطراف هر آهن ربا که بر اجسام مغناطیسی موجود در این فضا، نیروی مغناطیسی وارد کند.
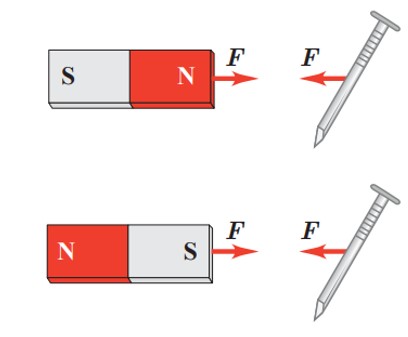
میدان مغناطیسی را با B نمایش می دهند که یک کمیت برداری است و به همین علت هم جهت و هم بزرگی دارد.
جهت میدان مغناطیسی B در هر نقطه از فضای پیرامون یک آهن ربا در جهتی است که وقتی عقربه مغناطیسی در آن نقطه قرار می گیرد، قطب N عقربه، جهت B ر معلوم می کند.
ویژگی های خط های میدان مغناطیسی
- بردار میدان مغناطیسی در هر نقطه، مماس و هم جهت با خط میدانی است که از آن نقطه می گذرد.
- خط های میدان یکدیگر را قطع نمی کنند.
- تراکم خط های میدان در هر ناحیه نشان دهنده بزرگی میدان مغناطیسی در آن ناحیه است.
- خط های میدان مغناطیسی، همواره منحنی های بسته ای هستند و به بیان دیگر تک قطبی وجود ندارد.
میدان مغناطیسی زمین
زمین یک آهن ربای بزرگ است که قطب S آن تقریبا در جهت شمال جغرافیایی زمین و قطب N آن در جنوب قرار دارد. قطب های مغناطیسی زمین دقیقا در محل قطب های جغرافیایی آن قرار ندارند.
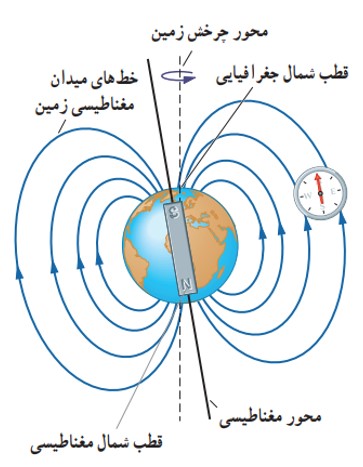
شیب مغناطیسی
در بیشتر نقاط زمین عقربه مغناطیسی، به طور افقی قرار نمی گیرد و امتداد آن با سطح افقی زمین زاویه می سازد. به این زاویه، شیب مغناطیسی گفته می شود.
یا زاویه بی میدان مغناطیسی و راستای افقی را، شیب مغناطیسی می نامند.
میدان مغناطیسی یکنواخت
هر گاه در ناحیه ای از فضا جهت و اندازه میدان مغناطیسی یکسان باشد، به این میدان، میدان مغناطیسی یکنواخت می گویند.
بار متحرک در میدان مغناطیسی
فصل 3 : مغناطیس
بار متحرک در میدان مغناطیسی
نیروی وارد بر ذره باردار متحرک در میدان مغناطیسی
هرگاه ذره بارداری در یک میدان مغناطیسی حرکت کند بر ذره باردار نیرو وارد می شود، بار الکتریکی از مسیر خود منحرف می شود به طوری که راستای نیرو بر راستای میدان و راستای حرکت عمود است.
جهت نیروی وارد بر بار متحرک
چهار انگشت باز شده دست راست را در جهت سرعت (V) ذره باردار مثبت طوری قرار می دهیم که، هنگامی که خم می شود، در جهت میدان مغناطیسی قرار گیرد، انگشت شست، سوی نیروی وارد بر ذره ی باردار مثبت را نشان می دهد.
جهت نیروی وارد بر ذره مثبت را با دست راست و نیروی وارد بر ذره منفی را با دست چپ نشان می دهیم.
تعریف کمی میدان مغناطیسی
بزرگی نیرویی که بر \(1c\) بار الکتریکی که با سرعت \(1\frac{m}{s}\) در راستای عمود بر خط های میدان قرار گرفته باشد، وارد می شود.
یکای میدان مغناطیسی تسلا نام دارد.
\(\begin{array}{l}B = \frac{F}{{qV\sin \alpha }}\\F = qVB\sin \alpha \end{array}\)
یکای کوچکتر میدان مغناطیسی گاوس نام دارد و با نماد G نمایش داده می شود.
\(\begin{array}{l}1T = {10^4}G\\1G = {10^{ - 4}}T\end{array}\)
اندازه میدان مغناطیسی زمین در نزدیکی سطح زمین در قطب ها بیشترین (\(0/65G\) ) و در استوا کمترین (\(0/25G\) ) است.
نمایش بردار عمود بر صفحه کاغذ
هر بار داخل صفحه کاغذ را به صورت شکل روبرو نمایش می دهند:
اگر برداری عمود بر صفحه کاغذ و به سمت داخل باشد به صورت \( \otimes \) نمایش می دهند.
اگر برداری عمود بر صفحه کاغذ و به سمت خارج باشد به صورت \( \odot \) نمایش می دهند.
مثال
بر پروتونی که با زاویه \(\theta = {30^0}\) نسبت به میدان مغناطیسی یکنواختی به اندازه \(B = 320G\) در حرکت است، نیرویی به اندازه \(F = 5/12 \times {10^{ - 14}}N\) وارد می شود. تندی پروتون چند کیلومتر بر ثانیه است؟
\(\begin{array}{l}q = 1/6 \times {10^{ - 19}}c\\\theta = {30^0}\\B = 320 \times {10^{ - 4}}T\\F = 5/12 \times {10^{ - 14}}N\\V = ?\\F = qVB\sin \theta \to V = \frac{F}{{qC\sin \theta }}\\V = \frac{{5/12 \times {{10}^{ - 14}}}}{{1/6 \times {{10}^{ - 19}} \times 320 \times {{10}^{ - 4}} \times 0/5}}\\V = 2 \times {10^7}\frac{m}{s} = 2 \times {10^4}\frac{{Km}}{s}\end{array}\)
سیم حامل جریان در میدان مغناطیسی
فصل 3 : مغناطیس
سیم حامل جریان در میدان مغناطیسی
نیروی مغناطیسی وارد بر سیم حامل جریان به عوامل زیر بستگی دارد:
- با جریانی که از سیم می گذرد رابطه مستقیم دارد.
- با طول قسمتی از سیم که در میدان مغناطیسی قرار می گیرد رابطه مستقیم دارد.
- با بزرگی میدان مغناطیسی، رابطه مستقیم دارد.
- با سینوس زاویه ای که جریان با میدان مغناطیسی می سازد، رابطه مستقیم دارد.
فرمول نیروی مغناطیسی وارد بر سیم حامل جریان در میدان مغناطیسی
\(F = BIL\sin \alpha \)
در این فرمول
F نیروی مغناطیسی
B میدان مغناطیسی
I جریان الکتریکی
L طول سیم
\(\sin \alpha \) زاویه بین جریان با میدان
برای حفظ بهتر این فرمول می توان از اختصار بیل سینا استفاده کرد.
جهت نیروی مغناطیسی
نیروی مغناطیسی وارد بر سیم حامل جریان الکتریکی، بر راستای جریان و نیز بر میدان مغناطیسی عمود است.
جهت نیروی مغناطیسی را از قاعده دست راست بدست می آوریم.
قاعده دست راست
اگر چهار انگشت دست راست خود را در جهت جریان بگیرید به طوری که اگر انگشتان خود را خم کنید. در جهت میدان مغناطیسی قرار گیرد، در این صورت انگشت شست شما جهت نیروی وارد بر سیم حامل جریان را نشان خواهد داد.
بردار میدان همواره از کف دست خارج می شود.
مثال
یک سیم حامل جریان در میدان مغناطیسی به بزرگی \(0/04mT\) در راستایی که با جهت میدان زاویه 30 درجه می سازد، قرار دارد. اگر شدت جریانی که از سیم می گذرد \(5A\) باشد، نیروی مغناطیسی وارد بر یک متر از این سیم را محاسبه کنید.
\(\begin{array}{l}B = 0/04mT = 4 \times {10^{ - 5}}T\\\alpha = {30^0}\\I = 5A\\L = 1m\\F = ?\\\sin {30^0} = 0/5\\F = BIL\sin \alpha \\ \to F = 4 \times {10^{ - 5}} \times 5 \times 1 \times 0/5 \to F = 10 \times {10^{ - 5}} = {10^{ - 4}}N\end{array}\)
- آزمون آنلاین تمامی دروس پایه ریاضی
- گام به گام تمامی دروس پایه ریاضی
- ویدئو های آموزشی تمامی دروس پایه ریاضی
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ریاضی
- فلش کارت های آماده دروس پایه ریاضی
- گنجینه ای جامع از انشاء های آماده پایه ریاضی
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ریاضی
میدان مغناطیسی اطراف سیم دراز مستقیم
فصل 3 : مغناطیس
میدان مغناطیسی اطراف سیم دراز مستقیم
آثار مغناطیسی ناشی از جریان الکتریکی (آزمایش اورستد)
هرگاه یک عقربه مغناطیسی در اطراف سیمی که به باتری و کلید وصل شده است قرار گیرد، در لحظه وصل کلید، ملاحظه می شود که عقربه مغناطیسی منحرف می شود، بنابراین در اطراف سیم حامل جریان میدان مغناطیسی ایجاد می کند.
خطوط میدان مغناطیسی در اطراف یک سیم راست حامل جریان الکتریکی

روی صفحه مقوایی که در وسط آن سیم راست حامل جریان قرار دارد؛ براده های آهن بپاشیم، این براده ها به صورت دایره هایی هم مرکز در خواهند آمد.
خطوط میدان مغناطیسی حاصل از یک سیم راست حامل جریان به صورت دایره های هم مرکزی در اطراف سیم راست هستند.
جهت میدان مغناطیسی در اطراف یک سیم راست حامل جریان الکتریکی
به این ترتیب است که اگر انگشت شست دست راست را در جهت جریان بگیریم، بسته شدن چهار انگشت، جهت میدان مغناطیسی را به ما می دهد.
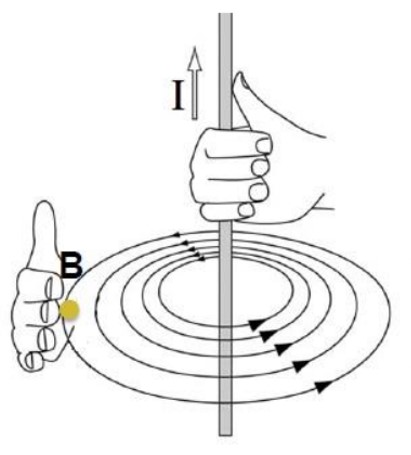
نیروی بین سیم های موازی حامل جریان
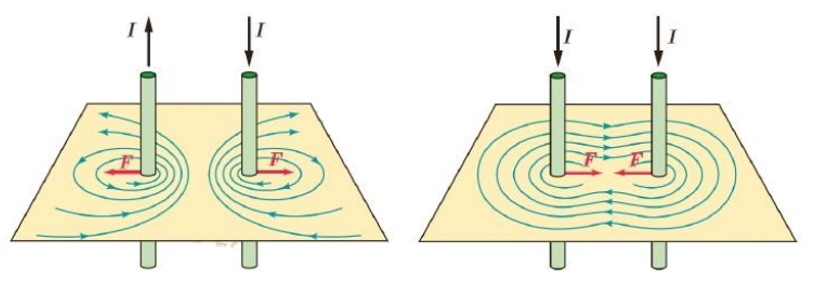
آزمایش نشان می دهد اگر از دو سیم راست و موازی جریان های الکتریکی عبور کند این دو سیم همدیگر را جذب یا دفع می کنند.
یعنی
اگر جریان ها هم جهت باشند همدیگر را جذب و اگر مخالف باشند همدیگر را دفع می کنند و علت آن ایجاد میدان یک سیم در محل سیم دیگر است.
میدان مغناطیسی ناشی از یک حلقه دایره ای سیملوله حامل جریان
پیچه مسطح، از چند دور سیم ناز به شکل حلقه به هم فشرده شده تشکیل شده است.

خطوط میدان مغناطیسی حاصل از یک پیچه ی مسطح:
یک مقوا را از وسط پیچه مسطح می گذرانیم و از آن جریان عبور می دهیم سپس روی مقوا براده می ریزیم شکل میدان در مقطع سیم ها به شکل دایره و در وسط حلقه به صورت یک خط راست خواهد بود.
خط های میدان مغناطیسی در ناحیه داخل پیچه به یکدیگر نزدیکترند. یعنی میدان در این ناحیه قوی تر است.
جهت میدان مغناطیسی دریچه
روش اول
اگر نوک انگشت شست دست راست را در جهت جریان قرار دهیم، بسته شدن انگشت دست راست، جهت میدان مغناطیسی را نشان می دهد.
روش دوم
اگر چهار انگشت دست راست را به صورت خمیده در جهت جریان در سیم پیچ قرار دهیم، آنگاه نوک انگشت شست، قطب N که همان جهت B هست.
سیملوله
اگر جریان الکتریکی از سیملوله عبور کند در فضای اطراف سیملوله خاصیت مغناطیسی ایجاد می شود.
اگر شعاع سیملوله نسبت به طولش کوچک باشد و حلقه های آن خیلی بهم نزدیک باشند. به این سیم لوله سیم لوله آرمانی گفته می شود.
میدان مغناطیسی داخل یک سیملوله آرمانی در نقطه های دور از لبه ها یکنواخت است.
بزرگی میدان مغناطیسی در محور سیملوله به عوامل زیر بستگی دارد:
- با شدت جریانی که از سیملوله می گذرد، نسبت مستقیم دارد.
- با تعداد حلقه های سیملوله نسبت مستقیم دارد.
- با طول سیملوله نسبت عکس دارد.
ضریب تناسب در SI برابر \({\mu _0}\) تراوایی مغناطیسی خلا است.
\(B = {\mu _0}\frac{N}{L}I\)
در این فرمول:
B بزرگی میدان
L طول سیملوله
N تعداد دور
I جریان الکتریکی
تعیین نوع قطب های سیملوله
روش اول
اگر نوک انگشت دست راست را در جهت جریان قرار دهیم، بسته شدن چهار انگشت دست راست، جهت میدان مغناطیسی را نشان می دهد.
روش دوم
اگر چهار انگشت دست راست خود را به صورت خمیده در جهت جریان در سیملوله قرار دهیم آنگاه انگشت شست قطب N که همان جهت B هست.
جهت میدان مغناطیسی در خارج از سیملوله از N به S و در داخل آن از S به N می باشد.
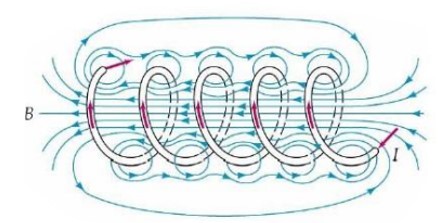
ویژگی های میدان مغناطیسی سیملوله
- خط های میدان داخل سیملوله، بسیار متراکم نر از خط های میدان در خارج آن است.
- میدان در داخل سیملوله دور از لبه ها یکنواخت است.
- جهت میدان در داخل و خارج سیملوله، خلاف هم هستند.
- شکل میدان سیملوله مانند میدان یک آهنربای میله ای است. که خطوط میدان منحنی های بسته ای را تشکیل می دهند.
مثال
جهت میدان مغناطیسی در سیملوله ی زیر را مشخص کنید.

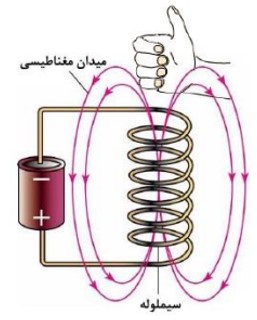
مثال
روی محور یک سیملوله ی حامل جریان به طول \(62/8cm\) ، میدان مغناطیسی به بزرگی \(0/02T\) ایجاد شده است. اگر تعداد حلقه های آن 2000 باشد، جریان گذرنده از آن چند آمپر است؟
\(\begin{array}{l}L = 62/8cm\\B = 0/02T\\N = 2000\\I = ?\\B = {\mu _0}\frac{N}{L}I \to I = \frac{{BL}}{{{\mu _0}N}}\\ \to I = \frac{{0/02 \times 62/8 \times {{10}^{ - 2}}}}{{4 \times 3/14 \times {{10}^{ - 7}} \times 2000}} \to I = 5A\end{array}\)
سیملوله با هسته آهنی – آهنربای الکتریکی
اگر داخل یک سیم لوله متصل به جریان یک هسته آهنی قرار دهیم، مجموعه را آهنربای الکتریکی می نامند.
توانایی آهنربای الکتریکی در ربایش قطعات آهنی به عوامل زیر بستگی دارد:
- جریانی که از سیملوله می گذرد.
- تعداد دور های واحد طول سیملوله
- جنس هسته آهنی سیملوله
قدرت آهنربای الکتریکی با افزایش شدت جریا و افزایش شمار دور های سیم لوله افزایش می یابد.
کاربرد های آهربای الکتریکی
هرگاه هسته ی درونی سیم پیچ از آهن خالص باشد، با برقراری جریا، هسته آهن ربا می شود و با قطع جریان، خاصیت خود را از دست می دهد. از این آهنربا ها در زنگ اخبار و جرثقیل های مغناطیسی و ... استفاده می شود.
خاصیت مغناطیسی مواد
فصل 3 : مغناطیس
خاصیت مغناطیسی مواد
منشاء اصلی مغناطیسی
خاصیت مغناطیسی ناشی از حرکت الکترون به دور خودش است.
مواد دیامغناطیس:
اتم های این مواد به طور ذاتی فاقد خاصیت مغناطیسی اند. اتم های این مواد در حضور میدان مغناطیسی خارجی، می تواند سبب القای دو قطبی های مغناطیسی در خلاف سوی میدان خارجی، در مواد دیا مغناطیسی شود.
وقتی که در یک میدان مغناطیسی بسیار قوی قرار بگیرند میدان در داخل آنها اندکی ضعیف می شوند و از قطب های آهن ربا رانده می شونئ.
مانند: نقره، طلا، مس، نمک ها، ترکیب های آلی و تمام غیر فلز ها بجز اکسیژن
مواد مغناطیسی
موادی را که اتم های آن ها به طور ذاتی دارای دو قطبی مغناطیسی هستند.
نحوه سمت گیری دو قطبی های مغناطیسی کوچک در مواد مختلف، متفاوت است به همین دلیل مواد از لحاظ ویژگی های مغناطیسی نیز باهم تفاوت دارند.
مواد مغناطیسی
مواد پارا مغناطیس
مواد فرو مغناطیس
مواد فرو مغناطیس نرم
مواد فرو مغناطیس سخت
مواد پارا مغناطیس
دو قطبی های مغناطیسی این مواد، به طور کاتوره ای سمت گیری کرده اند و میدان مغناطیسی خالصی ایجاد نمی کنند. با قرار دادن مواد پارا مغناطیسی درون میدان مغناطیسی خارجی قوی دو قطبی های مغناطیسی آنها، در راستای خط های میدان مغناطیسی منظم می شوند. با دور کردن آهنربا از این مواد، دو قطبی های مغناطیسی آنها، دوباره به طور کاتوره ای سمت گیری می کنند.
مانند: اورانیم، پلاتین، آلومینیم، سدیم، اکسیژن، اکسید نیتروژن، فلز های قلیایی و قلیایی خاکی از جمله مواد پارامغناطیسی اند.
مواد پارا مغناطیس در حضور میدان های مغناطیسی قوی، خاصیت مغناطیسی ضعیف و موقت پیدا می کنند.
مواد فرومغناطیس
در برخی از مواد مغناطیسی، دو قطبی های مغناطیسی کوچک به طور خود به خود با دو قطبی های مجاور خود هم خط می شوند. این گونه مواد را فرو مغناطیس می نامند.
حوزه مغناطیسی
به ابعاد خیلی کوچکتر از میلی متر که تقریبا \({10^{19}}\) اتم وجود دارد و دو قطبی های مغناطیسی وابسته به آنها هم جهت اند. حوزه مغناطیسی می گویند.
مواد فرو مغناطیس در ابتدا آهنربا نمی شوند زیرا؛ سمت گیری و اندازه حوزه های مغناطیسی در ماده فرومغناطیس به گونه ای است که در کل اثر یکدیگر را خنثی می کنند لذا در مجموع آهنربا نیستند.
فرومغناطیس نرم
در برخی از مواد فرومغناطیس حجم حوزه ها در حضور میدان مغناطیسی به سهولت تغییر می کند و در نبود میدان مغناطیسی خاصیت آهنربایی خود را به آسانی از دست می دهند.
مانند: آهن، نیکل و کبالت در صورتی که خالص باشند.
کاربرد: ساخت آهنربای الکتریکی
شار مغناطیسی
فصل 4 : القای الکترومغناطیسی و جریان متناوب
شار مغناطیسی
پدیده القای الکترو مغناطیسی
هرگاه جریان الکتریکی در یک رسانا القا گردد، به این پدیده (القای الکترو مغناطیسی) می گویند.
جریان القایی
حرکت آهنربا به سمت پیچه (دور و نزدیک شدن آهنربا از پیچه) باعث القای جریانی در پیچه می گردد، که به آن جریان القایی می گویند.
عوامل موثر در ایجاد جریان القایی
- با دور و نزدیک کردن آهنربا به پیچه، میدان در محل پیچه تغییر کرده و جریان القایی در مدار ایجاد می گردد. (تغییر در اندازه میدان مغناطیسی، در محل پیچه مدار بسته)
- اگر پیچه (انعطاف پذیر) در یک میدان مغناطیسی قرار دهید و از دو نقطه گرفته و بکشید، بطوری که شکل آن عوض شود، در اثر تغییر شکل، مساحت پیچه تغییر کرده و جریان در مدار به وجود می آید. (تغییر مساحت مدار بسته در میدان مغناطیسی)
- تغییر زاویه ین حلقه و راستای میدان مغناطیسی نیز می تواند عامل برقراری جریان الکتریکی القایی شود. (تغییر زاویه بین حلقه و راستای میدان مغناطیسی)
علت ایجاد جریان القایی در مدار
در اثر تغییر میدان مغناطیسی، یک میدان الکتریکی القایی در فضا ایجاد می شود و از آنجایی که مدار در این میدان الکتریکی قرار دارد بر الکترون های آزاد داخل آن نیرو وارد می شود و حرکت الکترون ها باعث ایجاد نیروی محرکه و جریان القایی، می شود.
تعریف شار مغناطیسی \(\Phi \)
معرف تعداد خطوط مغناطیسی که به طور عمود از یک سطح بسته می گذرند، شار مغناطیسی می گویند.
شار کمیتی نرده ای است.
بردار سطح
برای نمایش یک سطح، نیم خطی بر سطح پیچه عمود می کنیم. جهت این نیم خط همان جهت برداری سطح خواهد بود.
اگر یک سطح بچرخد، نیم خط عمود بر سطح N نیز با همان اندازه می چرخد.
فرمول شار مغناطیسی
\(\Phi = B \times A \times \cos \theta \)
در این فرمول
\(\Phi \) شار مغناطیسی و بر حسب وبر (wb)
B میدان مغناطیسی
A مساحت پیچه
\(\theta \) زاویه بین نیم خط عمود بر سطح پیچه و راستای میدان
1 بردار N را بر هر طرف سطح حلقه عمود کنیم، اهمیت ندارد. البته با تعویض جهت N، علامت \(\Phi \) تغییر خواهد کرد، ولی اندازه آن تغییر نمی کند.
2 در مسائل شار، اگر زاویه بین سطح قاب با سوی مثبت میدان مغناطیسی (\(\alpha \)) را داده باشند آنگاه:
3 زاویه بین نیم خط عمود بر سطح و سوی مثبت میدان مغناطیسی یعنی \(\alpha \) از رابطه ی زیر پیدا می شود.
\(\theta = \left| {90 - \alpha } \right|\)
تغییر شار مغناطیسی عبوری از یک حلقه
همواره دو جهت برای رسم نیم خط عمود بر یک سطح معین وجود دارد. علامت شار مغناطیسی عبوری از این سطح نیز به انتخاب این جهت بستگی دارد. در حل یک مسئله، همواره باید یک جهت را انتخاب کنیم و تا پایان آن را تغییر ندهیم، بنابراین ممکن است شار مثبت، منفی یا صفر شود.
\(\Delta \Phi = {\Phi _2} - {\Phi _1} \to \Delta \Phi = AB(\cos {\theta _2} - \cos {\theta _1})\)
یکای شار مغناطیسی
اگر قابی به مساحت \(1m{}^2\) عمود بر میدان مغناطیسی یکنواختی به بزرگی \(1T\) قرار گیرد، شار مغناطیسی گذرنده از آن برابر یک وبر (\(1wb\)) خواهد شد.
\(\Phi = BA\cos \theta \to 1wb = 1T \times 1{m^2} \times \cos 0\)
1 هرگاه سطح قاب عمود بر میدان مغناطیسی باشد، آنگاه \(\alpha = {90^0}\) بوده یعنی؛ شار عبوری از قاب ماکزیمم می شود.
\(\begin{array}{l}\theta = \left| {90 - \alpha } \right|\\\theta = \left| {90 - 90} \right| = {0^0} \to {\Phi _{\max }} = BA\\\cos {0^0} = 1\end{array}\)
2 هرگاه سطح قاب موازی میدان مغناطیسی باشد، آنگاه \(\alpha = 0\) بوده یعنی؛ شار عبوری از قاب صفر می شود.
\(\begin{array}{l}\theta = \left| {90 - \alpha } \right|\\\theta = \left| {90 - 0} \right| = {90^0} \to {\Phi _{\min }} = 0\\\cos {90^0} = 0\end{array}\)
تغییر شار مغناطیسی
هنگامی رخ می دهد که میدان مغناطیسی یا مساحت سطح و یا زاویه نیم خط عمود بر سطح رسانا با میدان، تغییر کند.
مثال
صفحه ای مربع شکل به ضلع \(20cm\) در یک میدان مغناطیسی یکنواخت به بزرگی \(3\mu T\) قرار دارد؛ به طوری که خط های میدان با سطح صفحه زاویه \({37^0}\) می سازند. شار مغناطیسی گذرنده از صفحه چند وبر است؟ (\(\cos 53 = 0/6\))
\(\begin{array}{l}a = 20cm = 0/2m \to A = {a^2} \to A = 4 \times {10^{ - 2}}{m^2}\\\alpha = {37^0} \to \theta = \left| {90 - \alpha } \right| \to \theta = \left| {90 - 37} \right| = {53^0}\\B = 3\mu T = 3 \times {10^{ - 6}}T\\\Phi = ?\\\Phi = BA\cos \theta \to \Phi = 3 \times {10^{ - 6}} \times 4 \times {10^{ - 2}} \times 0/6\\\Phi = 7/2 \times {10^{ - 8}}Wb\end{array}\)
- آزمون آنلاین تمامی دروس پایه ریاضی
- گام به گام تمامی دروس پایه ریاضی
- ویدئو های آموزشی تمامی دروس پایه ریاضی
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ریاضی
- فلش کارت های آماده دروس پایه ریاضی
- گنجینه ای جامع از انشاء های آماده پایه ریاضی
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ریاضی
قانون فارادی
فصل 4 : القای الکترومغناطیسی و جریان متناوب
قانون فارادی
هرگاه شار مغناطیسی ای که بسته ای می گذرد تغییر کند، نیروی محرکه ای در آن القا می شود که بزرگی نیروی محرکه القایی با آهنگ تغییر شار مغناطیسی متناسب است.
\(\varepsilon = - N\frac{{\Delta \Phi }}{{\Delta t}}\)
1 علامت منفی در رابطه به خاطر رعایت قانون لنز می باشد.
2 هنگامی که آهنگ تغییر شار مغناطیسی ثابت بماند، نیروی محرکه القایی متوسط \(\varepsilon \) برابر نیروی محرکه ای لحظه ای بوده و با نماد \(\varepsilon \) نمایش می دهیم.
مقدار شدت جریان القا شده از رابطه زیر بدست می آید:
\(I = \frac{\varepsilon }{R} \to I = - \frac{N}{R}\frac{{\Delta \Phi }}{{\Delta t}}\)
هر چه آهنگ تغییر شار مغناطیسی بیشتر باشد، نیروی محرکه القایی و در نتیجه جریان القایی تولید شده در مدار بیشتر خواهد بود.
هرگاه حلقه ای به هر وضعیتی که در یک میدان مغناطیسی قرار داشته باشد و شار عبوری از آن \(\Phi \) باشد، اگر حلقه حول خطی که در سطح حلقه است \({180^0}\) دوران نماید، شار عبوری از آن \( - \Phi \) می شود.
مثال
سیملوله ای با 500 دور در یک میدان مغناطیسی متغیر با زمان قرار گرفته است. مساحت مقطع سیملوله \(25c{m^2}\) و آهنگ تغییر میدان \(8 \times {10^{ - 3}}\frac{T}{s}\) است. بیشینه نیروی محرکه القایی متوسط در سیملوله را محاسبه کنید.
\(\begin{array}{l}N = 500\\A = 25 \times {10^{ - 4}}{m^2}\\\frac{{\Delta B}}{{\Delta t}} = 8 \times {10^{ - 3}}{m^2}\\\theta = 0\\\varepsilon = ?\\\varepsilon = - NA\frac{{\Delta B}}{{\Delta t}}\cos \theta \to \varepsilon = - 500 \times 25 \times {10^{ - 4}} \times 8 \times {10^{ - 3}} \times \cos 0 \to \varepsilon = - 0/01v = - {10^{ - 2}}v\end{array}\)
قانون لنز
فصل 4 : القای الکترومغناطیسی و جریان متناوب
قانون لنز
جریان حاصل از نیروی محرکه القایی در یک مدار در جهتی است که آثار مغناطیسی ناشی از آن، با عامل به وجود آورنده جریان القایی، یعنی تغییر شار مغناطیسی، مخالفت می کند.
علامت منفی در رابطه فارادی نشان دهنده همین مخالفت است.
به قوانین فارادی و لنز، قانون های القای الکترومغناطیسی می گویند.
1 جهت جریان القایی ایجاد شده در حلقه هم با افزایش شار و هم با کاهش شار عبوری از حلقه، مخالفت می کند.
2 هنگامی که شار گذرنده از حلقه در حال افزایش می باشد، میدان مغناطیسی القایی در خلاف جهت میدان اصلی به وجود می آید تا اثر تضعیف کننده آن با افزایش شار مخالفت کند.
3 هنگامی که شار گذرنده از حلقه در حال کم شدن باشد، میدان مغناطیسی القایی در جهت میدان مغناطیسی اصلی به وجود می آید تا اثر تقویت کننده آن با کاهش شار مخالف کند.
مثال
در شکل رو به رو با توجه به جهت جریان القایی در حلقه توضیح دهید، جریان در سیم راست در حال افزایش است یا کاهش؟
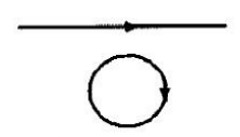
در حال کاهش، چون میدان مغناطیسی سیم راست هم جهت با میدان مغناطیسی حلقه است، طبق قانون لنز باید شار مغناطیسی در حال کاهش باشد یعنی جریان در حال کاهش است.
خود-القاوری
فصل 4 : القای الکترومغناطیسی و جریان متناوب
خود-القاوری
القاگر وسیله ای الکتریکی شبیه سیم پیچ با دو سر اتصال است که برای تولید میدان مغناطیسی و ذخیره انرژی مغناطیسی استفاده می شود.
القاگر می توانند میدان های مغناطیسی را در حجم های کوچک نگه دارند؛ همچنین می توان از آنه برای ذخیره کردن انرژی استفاده کرد.
خود-القاوری
در مدار شامل القاگری (پیچه یا سیملوله) باتری و رئوستا، آمپرسنج و القاگری است که به طور متوالی به یکدیگر بسته شده اند.
با تغییر مقاومت رئوستا، جریان در مدار تغییر می کند. تغییر جریان در مدار، سبب تغییر میدان مغناطیسی القاگر شده و در نتیجه شار مغناطیسی عبوری از آن نیز تغییر می کند. این فرایند سبب القای نیروی محرکه ای در القاگر می شود که بنابر قانون لنز با تغییر جریان عبوری از آن مخالفت می کند. این پدیده را اثر خود-القاوری نامیده می شود.
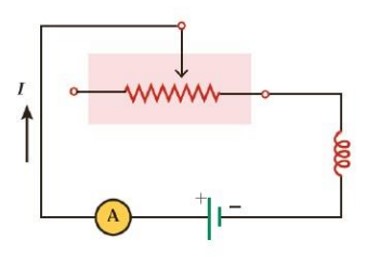
تغییر جریان در یک مدار باعث ایجاد نیروی محرکه ای القایی در همان مدار می شود، این پدیده را خود-القاوری می نامند.
نیروی محرکه ی خود القاوری \({\varepsilon _L}\)
اگر جریان گذرنده از سیملوله تغییر کند، به علت تغییر شار مغناطیسی گذرنده از آن، نیروی محرکه ای در خود مدار القا می شود که با عامل تغییر شار مغناطیسی که در اینجا تغییر جریان است مخالفت کند.
1 هرگاه جریان در مدار اصلی رو به افزایش باشد، جهت جریان خود- القاوری خلاف جهت جریان در مدار اصلی است.
2 هرگاه جریان در مدار اصلی رو به کاهش باشد، جهت جریان خود-القاوری هم جهت با جهت جریان در مدار اصلی است.
3 به هر قسمتی از یک مدار که خاصیت خود القاوری داشته باشد، القاگر می گویند.
4 پیچه و سیملوله در مداری با جریان متغیر القاگرند.
5 اثر خود-القاوری مخصوص جریان های متغیر است و در مدار های جریان پیوسته تنها به هنگام قطع و وصل کلید در مدار ایجاد می گردد.
ضریب القاوری (با نماد l نمایش می دهند.)
این پارامتر، ویژگی های فیزیکی القاگر را نشان می دهد و به عواملی همچون تعداد دور، طول و سطح مقطع القاگر و جنس هسته ای که داخل آن قرار می گیرد بستگی دارد.
یکای ضریب القاوری در SI، اهم در ثانیه (\(\Omega \times S\)) است که هانری نامیده و با H نشان داده می شود.
ضریب القاوری فقط به مشخصات ساختمانی سیم لوله بستگی دارد.
فرمول ضریب القاوری سیملوله
\(L = \frac{{AK{\mu _0}{N_2}}}{I}\)
در این فرمول
L ضریب القاوری
A مساحت هر حلقه ی سیملوله
K ضریب تراوایی نسبی هسته
\({\mu _0}\) ضریب تراوایی مغناطیسی خلاء
N تعداد دور های سیملوله
مثال
تعداد حلقه های سیملوله ای بدون هسته، به طول \(2/8cm\) و سطح \(10c{m^2}\) چه تعداد باشد تا ضریب القاوری آن \(1H\) شود؟
\(\begin{array}{l}K = 1\\I = 2/8 \times {10^{ - 2}}m\\A = 10 \times {10^{ - 4}}{m^2}\\N = ?\\L = 1H\\{\mu _0} = 4\pi \times {10^{ - 7}}\frac{{Tm}}{A}\\L = \frac{{AK{\mu _0}{N^2}}}{I} \to {N^2} = \frac{{IL}}{{AK{\mu _0}}}\\{N^2} = \frac{{2/8 \times 10 - 2 \times 1}}{{{{10}^{ - 3}} \times 1 \times 4 \times 3/14 \times {{10}^{ - 7}}}} \to {N^2} = 22 \times {10^6} \to N = 4/7 \times {10^3}\end{array}\)
القای متقابل
تغییر جریان در یک مدار باعث تغییر شار مغناطیسی در مدار دیگر و ایجاد نیروی محرکه القایی می شود.
با تغییر مقاومت رئوستا و تغییر جریان عبوری از پیچه 1 شار عبوری از پیچه 2 نیز تغییر می کند. این تغییر شار، سبب ایجاد نیروی محرکه القایی در پیچه 2 می شود. هم زمان تغییر جریان در پیچه 2، سبب ایجاد نیروی محرکه القایی در پیچه 1 می گردد.
انرژی ذخیره شده در القاگر
هنگامی که به دو سر القاگری اختلاف پتانسیل وصل کنیم، از طرف مولد به القاگر انرژی داده می شود. بخشی از این انرژی در مقاومت R تلف شده و بقیه آن در میدان مغناطیسی سیملوله ذخیره می شود. این انرژی از رابطه زیر بدست می آید:
\({U_L} = \frac{1}{2}L{I^2}\)
در این فرمول
\({U_L}\) انرژی ذخیره شده در القاگر
L ضریب القاوری
I شدت جریان در القاگر
- آزمون آنلاین تمامی دروس پایه ریاضی
- گام به گام تمامی دروس پایه ریاضی
- ویدئو های آموزشی تمامی دروس پایه ریاضی
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ریاضی
- فلش کارت های آماده دروس پایه ریاضی
- گنجینه ای جامع از انشاء های آماده پایه ریاضی
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ریاضی
جریان متناوب
فصل 4 : القای الکترومغناطیسی و جریان متناوب
جریان متناوب
تولید جریان متناوب
ساده ترین راه برای تغییر شار مغناطیسی و ایجاد جریان، تغییر زاویه است.
بنابراین معادله شار به صورت زیر می باشد:
\(\Phi = BA\cos \theta \)
که در آن \(\theta \) در حال تغییر است.
اجزای یک مولد (ژنراتور) جریان متناوب
حرکت یک میله گردان، باعث چرخش پیچه در فضای میدان مغناطیسی ناشی از یک آن ربا می شود. با گردش پیچه، زاویه آن با خطوط میدان و در نتیجه شار گذرنده از پیچه تغییر و نیروی محرکه و جریان الکتریکی در آن القا می شود.
دوره یا زمان تناوب T
زمانی که طول می کشد تا پیچه یک دور کامل بچرخد را دوره می نامند. یکای آن در SI ثانیه است.
\(T = \frac{t}{N}\)
بسامد یا فرکانس f
تعداد چرخش های کامل در مدت یک ثانیه را بسامد می نامند.
یکای بسامد (\({S^{ - 1}}\)) است که معادل هرتز HZ است.
\(f = \frac{1}{T}\)
مثال
قابی در دقیقه، 300 بار دور خود می چرخد. زمان تناوب و بسامد قاب را به دست آورید؟
\(\begin{array}{l}t = 1\min = 60s\\N = 300\\T = ?\\f = ?\\T = \frac{t}{N} \to T = \frac{{60}}{{300}} = 0/2s\\f = \frac{1}{T} \to f = \frac{1}{{0/2}} = 5HZ\end{array}\)
معادله نیروی محرکه متناوب
اگر هر دور کامل برابر \(2\pi \) و زمان یک دور چرخش کامل پیچه T باشد، \(\theta \) زاویه پیچه در مدت زمان t ثانیه چرخیدن از رابطه ی زیر پیدا می شود.
\(\varepsilon = {\varepsilon _m}\sin \frac{{2\pi }}{T}t\)
جریان متناوب
اگر جریان الکتریکی تولید شده در مدار، به طور سینوسی تغییر کند به چنین جریانی جریان متناوب می گویند.
\(I = {{\mathop{\rm I}\nolimits} _M}\sin \frac{{2\pi }}{T}t\)
انواع جریان
جریان مستقیم D.C
اگر مقدار و جهت شدت جریان متوسط در تمام بازه های زمانی ثابت بماند.
جریان متناوب A.C
اگر جهت جریان در زمان های مساوی به طور متناوب عوض می شود.
مبدل ها
فصل 4 : القای الکترومغناطیسی و جریان متناوب
مبدل ها
مزایای مولد های AC نسبت به DC
1) در انتقال توان در فاصله های دور، از ولتاژ هرچه بالاتر و جریان هر چه متری استفاده کنیم، باعث کاهش اتلاف \(R{I^2}\) در خط های انتقال می شود.
2) در افزایش انرژی الکتریکی از نیروگاه به محل مصرف کننده توسط یک مبدل ولتاژ را افزایش و جریان را کاهش می دهند (طبق رابطه \(P = VI\) اگر توان تولیدی را ثابت فرض کنیم افزایش ولتاژ توسط یک مبدل با کاهش جریان همراه است) تا توان تلف شده در سیم ها انتقال (\(R{I^2}\)) به کمترین مقدار برسد.
نحوه کارکرد مبدل
مبدل شامل دو پیچه با روکش عایق که روی یک هسته آهنی پیچیده شده اند. اگر پیچه اولیه را به یک مولد جریان متناوب وصل کنیم، شار عبوری از آن نیز تغییر می کند، این شار متغییر از راه هسته از پیچه ثانویه عبور می کند و در اثر پدیده القای متقابل باعث القای نیروی محرکه الکتریکی در پیچه ثانویه می شود.
رابطه تعداد دور ها با ولتاژ در مبدل ها
میدان و شار مغناطیسی در داخل هسته آهنی بسیار بیشتر از خارج هسته است و می توان فرض کرد تمام شار تولید شده در پیچه اولیه از پیچه ثانویه عبور می کند.
\(\frac{{\Delta {\Phi _1}}}{{\Delta t}} = \frac{{\Delta {\Phi _2}}}{{\Delta t}} \to \frac{{{\varepsilon _2}}}{{{\varepsilon _1}}} = \frac{{ - {N_2}\frac{{\Delta {\Phi _2}}}{{\Delta t}}}}{{ - {N_1}\frac{{\Delta {\Phi _1}}}{{\Delta t}}}} \to \varepsilon = V \to \frac{{{V_2}}}{{{V_1}}} = \frac{{{N_2}}}{{{N_1}}}\)
رابطه تعداد دور ها با شدت جریان در مبدل های ایده آل (آرمانی)
مبدلی را ایده آل گویند که هیچگونه اتلاف انرژی در آن وجود نداشته باشد. در نتیجه توان ورودی به مبدل آرمانی برابر توان خروجی از آن است.
\(P{}_{_1} = {P_2} \to {V_1}{I_1} = {V_2}I{}_2 \to \frac{{{I_2}}}{{{I_1}}} = \frac{{{V_1}}}{{{V_2}}} \to \frac{{{I_2}}}{{{I_1}}} = \frac{{{N_1}}}{{{N_2}}}\)
فرمول مبدل ها (ترانسفورماتور ها)
\(\frac{{{V_2}}}{{{V_1}}} = \frac{{{N_2}}}{{{N_1}}} = \frac{{{I_1}}}{{{I_2}}}\)
استفاده از مبدل برای کاهش اتلاف انرژی الکتریکی
در انتقال انرژی الکتریکی از نیروگاه به محل مصرف کنندخ توسط یک مبدل، ولتاژ را تا حد امکان افزایش و جریان را تا حد امکان کاهش می دهند تا توان تلف شده در سیم های انتقال برق (\(R{I^2}\)) به حداقل برسد.
توان تلف شده در خط انتقال
اگر توان تولیدی نیروگاه P ولتاژ بین خط های انتقال V باشد، شدت جریان در خط های فشار قوی \(I = \frac{P}{V}\) می شود. فرض می کنیم که مقاومت خط های انتقال برابر R باشد. در این صورت توان تلف شده \(P'\) در خط انتقال برابر می شود با:
\(P' = R\frac{{{P^2}}}{{{V^2}}}\)
رابطه ی مقایسه ای توان تلف شده در دو خط انتقال
خط انتقال توان، توان الکتریکی ثابت P را تحویل می گیرد. اگر انشعابی در مسیر نیروگاه تا مقصد وجود نداشته باشد، نسبت توان تلف شده در دو خط انتقال به صورت رابطه زیر است.
\(P' = R{I^2} \to P' = R\frac{{{P^2}}}{{{V^2}}} \to \frac{{{{P'}_1}}}{{{{P'}_2}}} = (\frac{{{R_1}}}{{{R_2}}}){(\frac{{{V_2}}}{{{V_1}}})^2}\)
مثال
توان تولیدی نیروگاهی \(2MW\) است. می خواهیم این انرژی را با کابل های مسی به طول \(20Km\) و سطح مقطع \(2c{m^2}\) انتقال دهیم. اگر ولتاژ خط های انتقال \(400kv\) باشد، توان تلف شده در خط های انتقال، چند ولت می شود؟
\(\begin{array}{l}P = 2 \times {10^6}W\\L = 20 \times {10^3}m\\A = 2 \times {10^{ - 4}}{m^2}\\V = 400 \times {10^3}kv\\P' = ?\\\rho = 1/8 \times {10^{ - 8}}\Omega m\\R = \rho \frac{L}{A} \to R = 1/8 \times {10^{ - 8}} \times \frac{{2 \times {{10}^4}}}{{2 \times {{10}^{ - 4}}}} \to R = 1/8\Omega \\P' = R\frac{{{P^2}}}{{{V^2}}} \to P' = 1/8 \times \frac{{{{(2 \times {{10}^6})}^2}}}{{{{(400 \times {{10}^3})}^2}}} \to P' = 45W\end{array}\)



1736019749.png)