درسنامه کامل ریاضیات گسسته فصل 2 گراف و مدل سازی
تعداد بازدید : 7.27Mخلاصه نکات ریاضیات گسسته فصل 2 گراف و مدل سازی - درسنامه شب امتحان ریاضیات گسسته فصل 2 گراف و مدل سازی - جزوه شب امتحان ریاضیات گسسته نوبت اول فصل 2 گراف و مدل سازی
معرفی گراف
معرفی گراف
گراف از مجموعه ای از نقاط (که به هر کدام راس می گوییم) و مجموعه ای از خطوط (که به هرکدام یال می گوییم) تشکیل شده است. هر یال بین دو راس قرار دارد. در گراف G مجموعه ی راس ها را با (Vertex) V (G) و مجموعه یال ها را با (Edge) E (G) نشان می دهیم.
گراف یک روش مدل سازی برای نشان دادن رابطه بین اعضای یک مجموعه است.
مثال
1 برای گراف زیر یک مجموعه ی احاطه گر بنویسید.
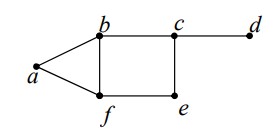
\(\{ a,b,e,d\} \)
2 یک گراف 5 راسی با عدد احاطه گری 2 رسم کنید.
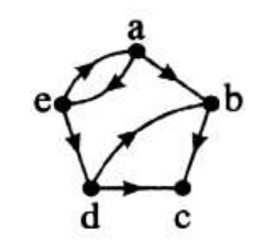
به گرافی که یال های آن جهت داشته باشند، گراف جهت دار می گوییم. در نمایش گراف جهت دار با استفاده از نماد های ریاضی، یال هارا با زوج مرتب نشان می دهیم.
مثال
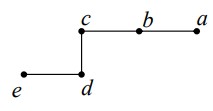
مجموعه ی راس ها و یال های گراف زیر را بنویسید.
\(\begin{array}{l}V = \{ a,b,c,d,e\} \\E = \{ (a,b),(b,c),(d,c),(d,b),(e,d),(e,a),(a,e)\} \end{array}\)
برای رسم نمودار یک گراف روش یکتایی وجود ندارد و شکل گراف صرفا باید مشخص کند که کدام راس ها به هم متصل اند.
مثلا دو نمودار زیر هر دو یک گراف را نمایش می دهند.
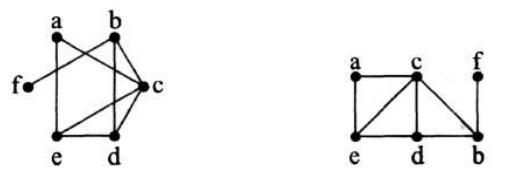
بین هر دو راس گراف ممکن است بیش از یک یال موجود باشد و همچنین یک یال ممکن است یک راس را به خود آن راس وصل کند که در این صورت به آن یال طوقه می گویند.
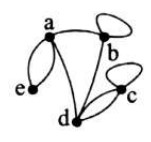
به گرافی که طوقه نداشته باشد و بین هر دو راس آن حداکثر یک یال وجود داشته باشد، گراف ساده می گوییم. در این فصل با گراف های ساده سر و کار خواهیم داشت و هر کجا از گراف نام ببریم، منظور گراف ساده است.
مرتبه و اندازه گراف
به تعداد راس های گراف G، مرتبه ی گراف گفته و آن را با P نشان می دهیم. به تعداد یال های گراف G، اندازه ی گراف گفته و آن را با q نشان می دهیم.
تعریف درجه راس گراف
به تعداد یال های متصل به گراف G که به راس V متصل اند، درجه ی آن راس گفته و آن را با \({\deg _G}(v)\) یا \(\deg (v)\) نشان می دهیم. اگر درجه یک راس عددی فرد باشد، به آن راس فرد و اگر درجه زوج باشد، به آن راس زوج می گوییم. در صورتی که \(\deg (v) = 0\) باشد (یعنی راس مورد نظر به راس دیگر متصل نباشد) به v راس تنها یا ایزوله می گوییم.
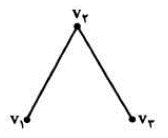
دو راس مجاور
دو راس که توسط یالی به هم متصل شده باشند را مجاور (یا همسایه) می نامیم. مثلا در گراف زیر راس های مجاور و غیر مجاور عبارت اند از:
مجموعه های همسایه های یک راس
فرض کنیم \(v \in V(G)\)، به مجموعه راس هایی از گراف g که به راس v متصل هستند، همسایگی باز راس v می گوییم و با \({N_G}(v)\) نمایش می دهیم. اضافه کردن خود راس v به \({N_G}(v)\) همسایگی بسته ی راس v را به دست می دهد که آن را با \({N_G}[v]\) نمایش می دهیم. می توان این دو مجموعه را به صورت زیر نشان داد:
\(\begin{array}{l}{N_G}(v) = \{ u \in V(G):uv \in E(G)\} \\{N_G}[v] = {N_G}(v) \cup \{ v\} \end{array}\)
مثال
مجموعه های همسایه های یک راس گراف زیر را بنویسید.
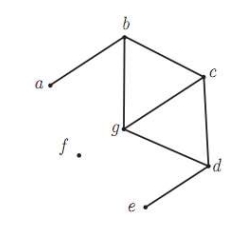
\(\begin{array}{l}{N_G}(a) = \{ b\} \\{N_G}(c) = \{ b,d,g\} \\{N_G}(f) = \emptyset \\{N_G}[a] = \{ a,b\} \\{N_G}[c] = \{ b,c,d,g\} \\{N_G}[f] = \{ f\} \end{array}\)
در صورتی که \({N_G}[v] = \emptyset \) باشد، راس v ایزوله است.
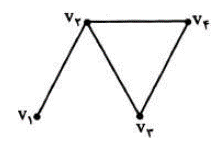
دو یال مجاور
دو یال را مجاور می نامیم هر گاه راسی وجود داشته باسد که هر دو یال به آن وصل باشند. مثلا در گراف زیر یال های \({v_1}{v_2}\) و \({v_2}{v_3}\) مجاورند. ولی یال های \({v_1}{v_2}\) و \({v_3}{v_4}\) مجاور نیستند.
بزرگ ترین و کوچک ترین درجه گراف
بزرگ ترین درجه در بین راس های یک گراف را ماکزیمم درجه نامیده و آن را با نماد \(\Delta (G)\) نمایش می دهیم. به صورت مشابه، کوچک ترین درجه را مینیمم درجه نامیده و با نماد \(\delta (G)\) نمایش می دهیم.
برای مثال در گراف زیر \(\Delta = 3\) و \(\delta = 1\)
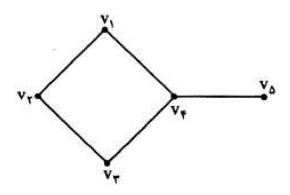
حواستان باشد ممکن است چند راس از درجه ماکسیمم یا مینیمم وجود داشته باشد.
همواره داریم \(\Delta \le p - 1\)
در گراف از مرتبه p، راسی که با همه رئوس دیگر مجاور باشد، را راس فول (پر) می نامیم. در واقع راس فول دارای درجه \(p - 1\) است.
اگر گرافی از مرتبه p، دارای k راس فول باشد آنگاه \(\delta \ge K\)
ارتباط درجه راس ها با تعداد یال ها
فرض کنید گراف G از مرتبه ی p و اندازه ی q باشد، در این صورت:
\(\sum\limits_{i - 1}^p {\deg ({v_i}) = } \deg ({v_1}) + \deg ({v_2}) + ... + \deg ({v_p}) = 2q\)
در نتیجه تعداد راس های فرد هرگراف عددی زوج است.
تمرین
1 در گراف شکل زیر
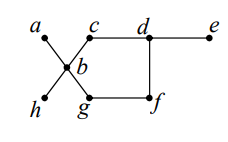
الف) مجموعه احاطه گری بنویسید که مینیمال باشد ولی مینیمم نباشد.
\(\{ a,h,c,e,f\} \)
ب) عدد احاطه گری این گراف را تعیین کنید.
\(\left[ {\frac{8}{{4 + 1}}} \right] = 2 \le \gamma (G)\) و چون \(\{ b,d\} \) یک مجموعه ی احاطه گر پس \(\gamma (G) = 2\)
2 شهری دارای 11 میدان است و هر میدان شهر از طریق خیابان ها حداکثر به 4 میدان دیگر متصل است. می خواهیم در بعضی از میدان ها نمازخانه بسازیم به طوری که هر شخصی در هر یک از میدان های شهر که باشد، یا در همانی میدانی که ایستاده به نمازخانه دسترسی داشته باشد یا در میدان مجاور آن. آیا با ساخت 2 نمازخانه می توانیم به این هدف برسیم؟ چرا؟
چون کران پایین عدد احاطه گری 3 است. پس با تعداد کمتر از 3 نمازخانه به هدف نمی رسیم و حداقل به 3 نماز خانه لازم است.
\(\gamma (G) = \left[ {\frac{{11}}{{4 + 1}}} \right] = 3\)
تهیه کننده: جابر عامری و الماسی کیا
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه گسسته- آزمون آنلاین تمامی دروس پایه گسسته
- گام به گام تمامی دروس پایه گسسته
- ویدئو های آموزشی تمامی دروس پایه گسسته
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه گسسته
- فلش کارت های آماده دروس پایه گسسته
- گنجینه ای جامع از انشاء های آماده پایه گسسته
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه گسسته
انواع گراف
انواع گراف
گراف های منتظم
گرافی که درجه ی همه راس های آن r باشد، گراف r-منظم (از مرتبه p) نامیده می شود. برای نمونه گراف های زیر 2-منتظم و 3-منتظم هستند:
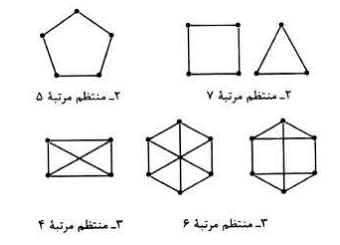
گفتیم هر گراف، مجموع درجه ها برابر  می شود. حال در گراف r-منتظم p راسی داریم:
می شود. حال در گراف r-منتظم p راسی داریم:
مجموع درجه ها = \(r + r + ... + r = 2q \Rightarrow pr = 2q\)
یعنی در گراف های منتظم ضرب مرتبه در درجه راس ها، دو برابر تعداد یال ها می شود.
یعنی pr همواره عددی زوج است؛ پس p و r نمی توانند هر دو فرد باشد (یعنی گراف فرد-منتظم از مرتبه فرد نداریم).
مثال
1 یک گراف 2-منتظم 5 راسی رسم کنید که دارای بیش از یک مجموعه ی احاطه گر مینیمم با اندازه 2 باشد. حداقل دو تا از مجموعه های احاطه گر مینیمم آن را بنویسید.
مجموعه های احاطه گر مینیمم، مجموعه های زیر می باشند.
\(\{ a,c\} ,\{ a,d\} \)
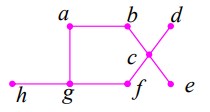
2 یک گراف 8 راسی با عدد احاطه گری 2 رسم کنید که دارای فقط یک مجموعه ی احاطه گر باشد.
در گراف زیر تنها مجموعه ی \(\{ c,g\} \) احاطه گر مینیمم می باشد.
گراف های کامل
گرافی از مرتبه ی p که هر دو راس آن مجاور باشند را گراف کامل نامیده و با \({K_p}\) نشان می دهیم.
در واقع گراف های کامل حداکثر تعداد یال ها را در مرتبه ی خود دارند و دیگر نمی توانیم به آن ها یال اضافه کنیم.
در جدول زیر گراف های کامل تا مرتبه 5 را مشاهده کنید:
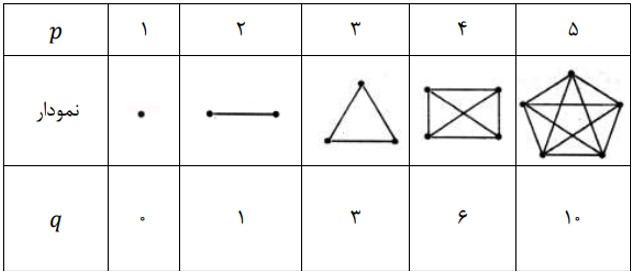
1 درجه ی هر راس در گراف کامل p راسی \(p - 1\) است. یعنی گراف کامل \({K_p}\)، یک گراف \(p - 1\) منتظم است.
2 تعداد یال ها در گراف کامل p راسی برابر است با:
مجموع درجه ها = \((p - 1) + (p - 1) + ... + (p - 1) = 2q \Rightarrow q = \frac{{p(p - 1)}}{2}\)
مکمل گراف
مکمل گراف G که آن را با \({G^c}\) یا \(\bar G\) نشان می دهیم، گرافی است که مجموعه راس های آن همان مجموعه ی راس ها است و دو راس در \(\bar G\) مجاورند اگر در G مجاور نباشند. برای مثال در شکل زیر یک گراف کامل و مکمل آن را می بینید:
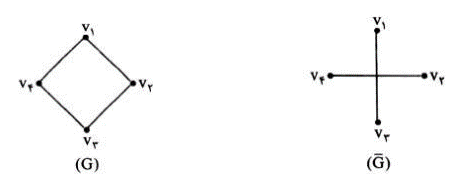
اگر تعداد یال های G و \(\bar G\) را با هم جمع کنیم، برابر تعداد یال های گراف کامل می شود؛ یعنی:
\(q(G) + q(\bar G) = \frac{{p(p - 1)}}{2}\)
مکمل گرافی r-منتظم گرافی \(\bar r\)-منتظم بوده و \(r + \bar r = p - 1\)
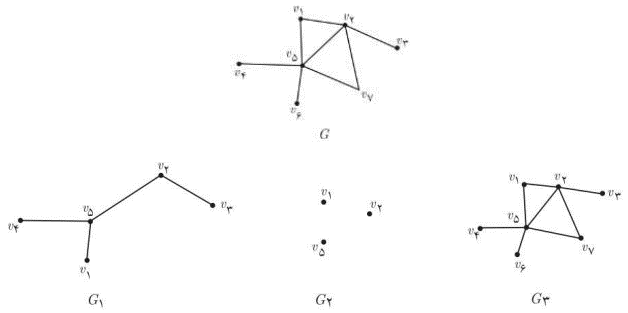
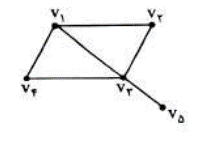
زیر گراف
گراف H را یک زیر گراف از G می گوییم هر گاه \(E(H) \subseteq E(G),V(H) \subseteq V(G)\)
برای مثال گراف G و سه زیر گراف آن را در زیر مشاهده می کنید:
تهیه کننده: جابر عامری و الماسی کیا
جزوات جامع پایه گسسته
جزوه جامع ریاضیات گسسته فصل 1 آشنایی با نظریۀ اعداد
جزوه جامع ریاضیات گسسته فصل 2 گراف و مدل سازی
جزوه جامع ریاضیات گسسته فصل 3 ترکیبیّات (شمارش)
مسیر در گراف
مسیر در گراف
فرض کنیم u و v دو راس از گراف G باشند. یک مسیر از u به v در G دنباله ای متشکل از راس های دو به دو متمایز است که از u شروع و به v ختم می شود به طوری که هر دو راس متوالی در این مسیر، مجاور هستند. طول مسیر همان تعداد یال های طی شده است که یکی کمتر از تعداد راس ها است.
قرارداد
هر راس به تنهایی، یک مسیر به طول صفر از خودش به خودش است.
گرافی که تنها از یک مسیر n راسی تشکیل شده باشد با \({P_n}\) نمایش می دهیم.
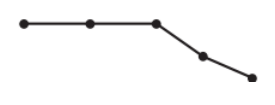
گراف های همبند
گراف G را همبند گوییم، هر گاه بین هر دو راس آن حداقل یک مسیر وجود داشته باشد، مانند گراف زیر:
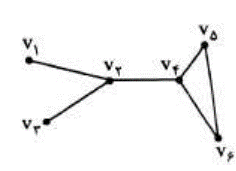
گرافی که همبند نباشد را ناهمبند می نامیم. مانند گراف های زیر:
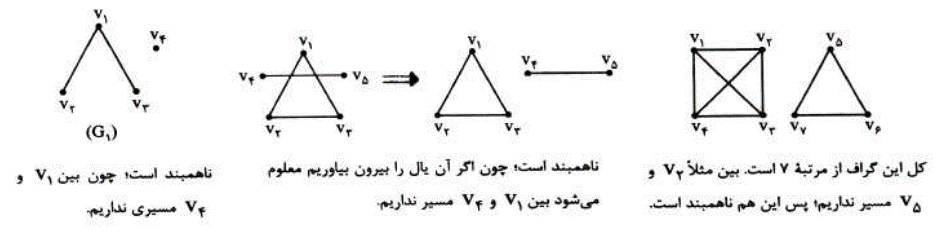
1 اگر \(q\langle p - 1\) باشد، گراف قطعا نا همبند است.
2 اگر \(q\rangle (\frac{{p - 1}}{2})\) باشد، گراف قطعا همبند است. همچنین اگر در گرافی \(\Delta = p - 1\) باشد (یعنی یک راس به همه وصل باشد) گراف قطعا همبند است.
دور در گراف
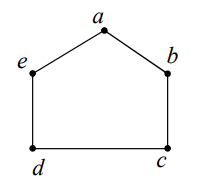
یک دور به طول m در گراف G دنباله ای از \(m + 1\) راس، که راس های متوالی مجاور بوده و m راس اول آن دو به دو متمایز بوده و راس آخر همان راس اول باشد. در شکل زیر دور \({v_1}{v_2}{v_3}{v_4}{v_1}\) را ببینید. این دور به طول 4 است.
1 حداقل طول دور می تواند 3 باشد.
2 طول دور همان تعداد یال های طی شده است.
گرافی را که تنها از یک دور n راسی تشکیل شده باشد با \({C_n}\) نمایش می دهیم.
برای مثال \({C_5}\) را در شکل زیر می بینید:
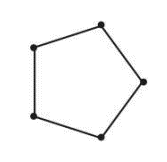
تمرین
1 با توجه به گراف زیر یک مجموعه ی احاطه گر مینیمال بنویسید که مینیمم نباشد.
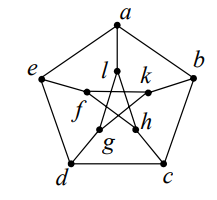
مجموعه ی \(\{ a,b,c,d,e\} \) احاطه گر مینیمال است ولی مینیمم نیست، مجموعه ی احاطه گر مینیمم این گراف \(\{ c,l,f\} \) می باشد.
2 درستی یا نادرستی گزاره های زیر را برسی کنید.
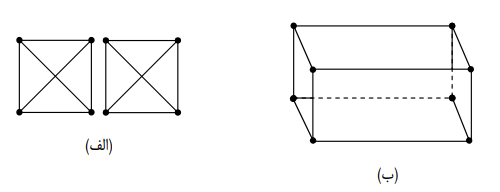
الف) مجموعه ی احاطه گر هر گراف، مساوی مجموعه ی احاطه گر مینیمم آن است.
نادرست
ب) مجموعه احاطه گر مینیمم هر دو گراف زیر یک مجموعه ی دو عضوی است.
درست
تهیه کننده: جابر عامری و الماسی کیا



1736019749.png)















