درسنامه کامل ریاضیات گسسته فصل 3 ترکیبیّات (شمارش)
تعداد بازدید : 7.27Mخلاصه نکات ریاضیات گسسته فصل 3 ترکیبیّات (شمارش) - درسنامه شب امتحان ریاضیات گسسته فصل 3 ترکیبیّات (شمارش) - جزوه شب امتحان ریاضیات گسسته نوبت اول فصل 3 ترکیبیّات (شمارش)
مباحثی در ترکیبیات
مباحثی در ترکیبیات
اصل ضرب
اگر کاری در مرحله اول به m روش و در مرحله دوم به n روش و در مرحله سوم به P روش و ... انجام شود کل کار به \(m \times n \times P \times ...\) روش انجام می شود.
مثال
1 با حروف کلمه Stop چند کلمه چهار حرفی با تکرار حروف می توان نوشت در صورتی که:
الف) با حرف T شروع شود؟
\(1 \times 4 \times 4 \times 4 = 64\)
ب) با حرف P شروع شده و به حرف O ختم شود؟
\(1 \times 4 \times 4 \times 1 = 16\)
2 می خواهیم 5 توپ با شماره های \(1,2,3,4,5\) را در 3 جعبه به رنگ های آبی، زرد و قرمز توزیع کنیم. این کار به چند طریق امکان پذیر است؟
برای هر توپ 3 انتخاب وجود دارد؛ بنابراین طبق اصل ضرب \(3 \times 3 \times 3 \times 3 \times 3 = {3^5}\) است.
جایگشت
تعداد حالت های کنار هم قرار گرفتن n شی متمایز را جایگشت آن n شی متمایز نامیده و برابر است با: \(n!\)
مثال
5 دانش آموز به چند طریق می توانند در یک صف بایستند؟
\(5! = 5 \times 4 \times 3 \times 2 \times 1 = 120\)
N نفر به چند طریق می توانند در یک صف بایستند به طوری که:
الف) k نفر مشخص همواره کنار هم باشند.
\((n - k + 1)! \times k!\)
ب) k نفر مشخص همواره کنار هم نباشند.
\(n! - (n - k + 1)! \times k!\)
مثال
به چند طریق می توان 7 دانش آموز را در یک صف قرار داد به طوری که:
الف) دو نفر از آنها که برادرند کنار هم باشند؟
\(\begin{array}{l}(n - k + 1)! \times k!\\(7 - 2 + 1)! \times 2! = 6! \times 2! = 720 \times 2 = 1440\end{array}\)
ب) دو نفر از آنها که برادرند کنار هم نباشند؟
\(\begin{array}{l}n! - (n - k + 1)! \times k!\\7! - (7 - 2 + 1)! \times 2! \to 7! - 6! \times 2! = 5040 - 1440 = 3600\end{array}\)
\(\begin{array}{l}0! = 1\\1! = 1\end{array}\)
جایگشت k شی از n شی متمایز
تعداد حالت های کنار هم قرار گرفتن k شی از n شی متمایز را با علامت \(P(n,k)\) نشان داده و از فرمول زیر حساب می کنیم:
\(P(n,k) = \frac{{n!}}{{(n - k)!}}\)
مثال
1 با حروف کلمه FAMILY و بدون تکرار حروف چند کلمه 4 حرفی شامل حرف M می توان ساخت؟
قرار دادن حرف M در یکی از چهار مکان به 4 طریق ممکن است و پر کردن سه مکان باقی مانده توسط 5 حرف باقی مانده به صورت زیر ممکن است:
\(P(5,3) = \frac{{5!}}{{(5 - 3)!}} = 60\)
طبق اصل ضرب = \(4 \times 60 = 240\)
2 شرکتی در نظر برای هر یک از شغل های نگهبانی، دفترداری، روابط عمومی و مسئول رایانه، یک نفر را استخدام کند، 10 نفر برای استخدام در این شغل ها داوطلب شده اند. شرکت به چند روش می تواند افراد را برای این مشاغل استخدام کند؟
برای نگهبانی هر کدام از 10 نفر را می توان انتخاب کرد پس 10 روش، برای دفترداری نیز 9 روش و برای روابط عمومی 8 روش و برای مسئول رایانه نیز 7 روش وجود دارد. در نتیجه \(10 \times 9 \times 8 \times 7\) طریق وجود دارد. (یا می توان ابتدا 4 نفر از 10 نفر را انتخاب کرده و سپس آن چهار نفر را برای شغل ها انتخاب نمود)
\(\left( {\begin{array}{*{20}{c}}{10}\\4\end{array}} \right) \times 4! = \frac{{10!}}{{6!}}\)
ترکیب k شی از n شی متمایز
اگر از بین n شی متمایز بخواهیم k شی (\(k \le n\)) را انتخاب کنیم و حالت های کنار هم قرار گرفتن آنها اهمیتی نداشته باشد آن را یک ترکیب k شی از n شی می گوییم و با علامت \(C(n,k)\) یا \(\left( {\begin{array}{*{20}{c}}n\\k\end{array}} \right)\) نشان داده و از فرمول زیر محاسبه می کنیم:
\(C(n,k) = \frac{{n!}}{{k! \times (n - k)!}}\)
مثال
1 به چند طریق می توان از بین 8 نفر، یک تیم 3 نفری انتخاب کرد؟
\(C(8,3) = \frac{{8!}}{{3! \times 5!}} = 56\)
2 شرکتی در نظر برای هر یک از شغل های نگهبانی، دفترداری، روابط عمومی و مسئول رایانه، به ترتیب \(3,2,2,1\) را استخدام کند، 10 نفر برای استخدام در این شغل ها داوطلب شده اند. شرکت به چند روش می تواند افراد را برای این مشاغل استخدام کند؟
\(\left( {\begin{array}{*{20}{c}}{10}\\3\end{array}} \right) \times \left( {\begin{array}{*{20}{c}}7\\2\end{array}} \right) \times \left( {\begin{array}{*{20}{c}}5\\2\end{array}} \right) \times \left( {\begin{array}{*{20}{c}}3\\1\end{array}} \right)\)
جایگشت های با تکرار
اگر n شی متمایز داشته باشیم به طوری که P تای آنها از نوع اول، q تای آنها از نوع دوم و r تای آنها از نوع سوم و ... باشد تعداد کل جایگشت های اشیا برابر است با:
\(\frac{{n!}}{{p! \times q! \times r! \times ...}}\)
مثال
1 9 نفر به چند طریق می توانند در سه اتاق 2 نفره، 3 نفره و 4 نفره در یک هتل اسکان یابند؟
\(\begin{array}{l}\frac{{n!}}{{p! \times q! \times r! \times ...}}\\\frac{{9!}}{{2! \times 3! \times 4!}} = \frac{{362880}}{{288}} = 1260\end{array}\)
2 با حروف کلمات (انتخابات) چند کلمه 8 حرفی بدون توجه به مفهوم آن می توان ساخت؟
با توجه به اینکه 3 حرف (الف) و 2 حرف (ت) وجود دارد، در نتیجه \(\frac{{8!}}{{3! \times 2!}}\) است.
اگر یک شبکه \(n \times m\) مطابق شکل زیر داشته باشیم و فقط به راست یا بالا حرکت کنیم تعداد مسیر ها از A به B برابر است با:
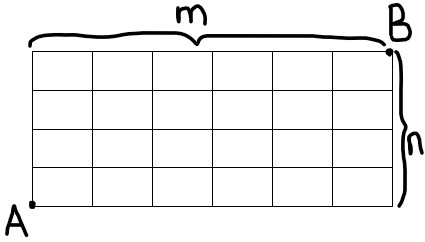
تعداد مسیر ها = \(\frac{{(n + m)!}}{{n! \times m!}}\)
مثال
چند مسیر از A به B وجود دارد به طوری که فقط مجاز باشیم به راست یا بالا جرکت کنیم؟

\(\begin{array}{l}\frac{{(n + m)!}}{{n! \times m!}}\\\frac{{(4 + 5)!}}{{4! \times 5!}} = \frac{{362880}}{{2880}} = 126\end{array}\)
حل معادله سیاله خطی با ضرایب واحد:
تعداد جواب های صحیح و نا منفی معادله \({x_1} + {x_2} + ... + {x_k} = n\) برابر است با:
\(\left( {\begin{array}{*{20}{c}}{n + k - 1}\\{k - 1}\end{array}} \right)\)
که همان تعداد انتخاب های دلخواه n شاخه گل از بین k نوع گل است.
مثال
1 معادله \({x_1} + {x_2} + {x_3} = 7\) چند جواب صحیح و نا منفی دارد؟
n = 7
k = 3
\(\left( {\begin{array}{*{20}{c}}{n + k - 1}\\{k - 1}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}{7 + 3 - 1}\\{3 - 1}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}9\\2\end{array}} \right) = \frac{{9!}}{{2! \times 7!}} = 36\)
2 به چند طریق می توان از بین 4 نوع گل، دسته گلی شامل 8 شاخه گل را به دلخواه انتخاب کرد؟
تعداد گل های نوع اول را \({x_1}\) و نوع دوم را \({x_2}\) و .... آنگاه در نظر می گیریم:
\(\begin{array}{l}{x_1} + {x_2} + {x_3} + {x_4} = 8\\n = 8,k = 4\\\left( {\begin{array}{*{20}{c}}{n + k - 1}\\{k - 1}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}{8 + 4 - 1}\\{4 - 1}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}{11}\\3\end{array}} \right) = \frac{{11!}}{{3! \times 8!}} = 165\end{array}\)
تعداد جواب های طبیعی معادله \({x_1} + {x_2} + ... + {x_k} = n\) برابر است با:
\(\left( {\begin{array}{*{20}{c}}{n - 1}\\{k - 1}\end{array}} \right)\)
مثال
1 معادله \({x_1} + {x_2} + {x_3} = 5\) چند جواب صحیح و مثبت (طبیعی) دارد؟
n = 5
k = 3
\(\left( {\begin{array}{*{20}{c}}{n - 1}\\{k - 1}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}{5 - 1}\\{3 - 1}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}4\\2\end{array}} \right) = \frac{{4!}}{{2! \times 2!}} = 6\)
2 به چند طریق می توان دسته گلی شامل 9 شاخه گل را از بین 4 نوع گل انتخاب کرد به شرط آن که از هر نوع گل حداقل 1 شاخه انتخاب شود؟
چون از هر نوع گل حداقل 1 شاخه باید انتخاب شود و جواب های معادله عدد طبیعی هستند، آنگاه:
\(\begin{array}{l}{x_1} + {x_2} + {x_3} + {x_4} = 9\\n = 9,k = 4\\\left( {\begin{array}{*{20}{c}}{n - 1}\\{k - 1}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}{9 - 1}\\{4 - 1}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}8\\3\end{array}} \right) = 56\end{array}\)
حل معادله \({x_1} + {x_2} + ... + {x_k} = n\) به روش تغییر متغیر
اگر در مساله سیاله شرط هایی به صورت \({x_1} \ge a\) و \({x_2} \ge b\) و ... داشته باشیم در این صورت متغیر را تغییر داده و معادله را طبق شرایط زیر حل می کنیم:
\(\begin{array}{l}{x_1} \ge a \to {x_1} - a \ge 0 \to {x_1} - a = {y_1} \to {x_1} = {y_1} + a,{y_1} \ge 0\\{x_2} \ge b \to {x_2} - b \ge 0 \to {x_2} - b = {y_2} \to {x_2} = {y_2} + b,{y_2} \ge 0\end{array}\)
مثال
1 معادله \({x_1} + {x_2} + {x_3} = 7\) چند جواب طبیعی دارد؟
\(\begin{array}{l}{x_1} \ge {x_1} = {y_1} + 1\\{x_2} \ge {x_2} = {y_2} + 1\\{x_3} \ge {x_3} = {y_3} + 1\\{y_1} + 1 + {y_2} + 1 + {y_3} + 1 = 7 \to {y_1} + {y_2} + {y_3} = 4\\n = 4,k = 3\\\left( {\begin{array}{*{20}{c}}{n + k - 1}\\{k - 1}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}{4 + 3 - 1}\\{3 - 1}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}6\\2\end{array}} \right) = 15\end{array}\)
2 به چند طریق می توان 8 توپ یکسان را بین 4 نفر توزیع کرد، هرگاه بخواهیم هر نفر حداقل یک توپ داشته باشد؟
\(\begin{array}{l}{x_1} + {x_2} + {x_3} + {x_4} = 8,{x_i} \ge 1,i = 1,2,3,4\\n = 8,k = 4\\\left( {\begin{array}{*{20}{c}}{n - 1}\\{k - 1}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}{8 - 1}\\{4 - 1}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}7\\3\end{array}} \right) = 35\end{array}\)
تمرین
1 با حروف کلمه (می سی سی پی) چند جایگشت 8 حرفی با معنا یا بی معنا می توان نوشت؟
تعداد (ی) = 4
تعداد (س) = 2
\(\frac{{8!}}{{4! \times 2!}} = 840\)
2 اگر داشته باشیم \(A = \{ 1,2,3,4\} \) و \(B = \{ 5,6,7,8,9\} \) در این صورت چند کد یا رمز 5 رقمی می توان نوشت که هر یک شامل دو رقم متمایز از A و سه رقم متمایز از B باشد؟
\(\left( {\begin{array}{*{20}{c}}4\\2\end{array}} \right) \times \left( {\begin{array}{*{20}{c}}5\\3\end{array}} \right) \times 5! = 7200\)
3 6 کتاب ریاضی مختلف و 5 کتاب فیزیک متمایز را به چند طریق می توان کنار هم در یک ردیف قرار داد به طوری که:
الف) کتاب ها یکی در میان قرار گیرند؟
\(6! \times 5!\)
ب) کتاب های ریاضی کنار هم و کتاب های فیزیک نیز کنار هم باشند؟
\(6! \times 5! \times 2!\)
4 به چند طریق می توان 4 خودکار متفاوت را بین 8 نفر توزیع کرد به شرطی که هیچکس بیشتر از یک خودکار نداشته باشد؟ (به هر نفر حداکثر یک خودکار داده باشیم)
\(P(8,4) = \frac{{8!}}{{(8 - 4)!}} = \frac{{8!}}{{4!}} = 1680\)
5 7 نفر به چند طریق می توانند در دو اتاق دو نفره و یک اتاق سه نفره قرار بگیرند؟
\(\frac{{7!}}{{2! \times 2! \times 3!}} = 210\)
6 به چند طریق می توان 5 توپ یکسان را بین 3 نفر و به دلخواه توزیع کرد؟
\(\begin{array}{l}\left( {\begin{array}{*{20}{c}}{n + k - 1}\\{k - 1}\end{array}} \right)\\{x_1} + {x_2} + {x_3} = 5 \to \left( {\begin{array}{*{20}{c}}{5 + 3 - 1}\\{3 - 1}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}7\\3\end{array}} \right) = 21\end{array}\)
7 به چند طریق می توان 8 توپ یکسان را بین 4 نفر توزیع کرد هر گاه بخواهیم هر نفر حداقل یک توپ داشته باشد؟
\(\left( {\begin{array}{*{20}{c}}{n - 1}\\{k - 1}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}{8 - 1}\\{4 - 1}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}7\\3\end{array}} \right) = 35\)
تهیه کننده: عادل نقدی
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه گسسته- آزمون آنلاین تمامی دروس پایه گسسته
- گام به گام تمامی دروس پایه گسسته
- ویدئو های آموزشی تمامی دروس پایه گسسته
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه گسسته
- فلش کارت های آماده دروس پایه گسسته
- گنجینه ای جامع از انشاء های آماده پایه گسسته
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه گسسته
مربع های لاتین
مربع های لاتین
یک جدول مربعی از اعداد \(1,2,3,...,n\) به شکل یک مربع \(n \times n\) را که سطر ها و ستون های آن با اعداد \(1,2,3,...,n\) پر شده باشد و در هیچ سطر آن و نیز در هیچ ستون آن عدد تکراری وجود نداشته باشد، مربع لاتین می نامیم و به هر یک از اعداد درون مربع لاتین یک درایه می گوییم.
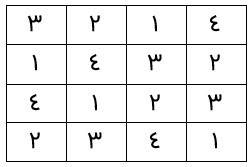
در حالت کلی شکل زیر یک مربع لاتین \(n \times n\) است که به آن مربع لایتن چرخشی می گوییم.

مربع لاتین از هر مرتبه ای وجود دارد.
یک مربع لاتین \(1 \times 1\) داریم:

ساخت مربع لاتین
روش چرخشی
در سطر اول اعداد \(1,2,3,...,n\) را می گذاریم، آخرین عدد سطر اول را که n است در ابتدای سطر دوم نوشته و بقیه عدد ها را در سطر دوم یکی یکی به راست می بریم و این کار را تکرار می کنیم.

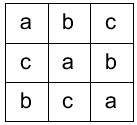
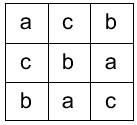
کل مربع های لاتین مرتبه دو نوع هستند.
روی قطر اعداد تکراری
روی قطر اعداد غیر تکراری
روش جا به جایی سطر و ستون
با تعویض جای هر دو سطر یا هر دو ستون یک مربع لاتین می توان مربع لاتین جدیدی ساخت.
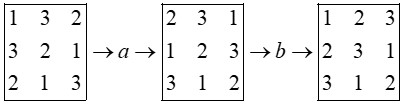
در a ستون 1 با ستون 3 تعویض شد و در b سطر 1 با سطر 2 تعویض شد.
روش جایگشت
می توانیم بدون تغییر جای سطر ها و ستون ها، جای خود عدد ها را با هم عوض کنیم، مثلا به جای تمام 3 ها 2 بنویسیم و برعکس یا همه 1 ها را 2 و همه 2 ها را به 3 و همه 3 ها را به 1 تبدیل کنیم و ... . در این صورت می گوییم جایگشت روی 1 عدد اعمال کرده ایم، با این روش مربع لاتین جدیدی ساخته می شود.
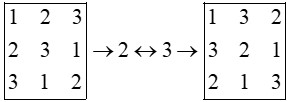
دو مربع لاتین متعامد
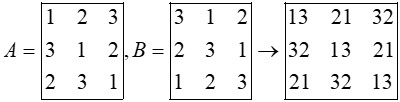
فرض کنیم A و B دو مربع لاتین هم مرتبه باشند به طوری که از کنار هم قرار دادن درایه های نظیر به نظیر این دو مربع، مربع جدیدی از همان مرتبه حاصل شود که هر خانه آن حاوی یک عدد دو رقمی است که تمام رقم های سمت چپ مربوط به مربع a و تمام رقم های سمت راست مربوط به مربع B (و یا برعکس) است، اگر هیچ یک از اعداد دو رقمی موجود در خانه های مربع جدید تکرار نشده باشند می گوییم دو مربع لاتین A و B متعامدند.
متعامد (عدد تکراری ندارد)
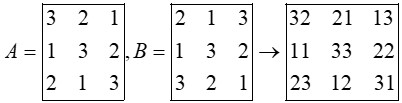
نا متعامد (عدد تکراری دارد)
مثال
دو مربع لاتین متعامد از مرتبه 3 بنویسید و متعامد بودن آنها را نشان دهید.
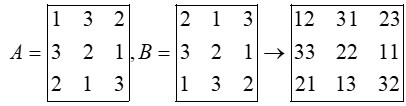
یک روش برای ساختن دو مربع لاتین متعامد از مرتبه یک عدد فرد:
به عنوان مثال نحوه ایجاد دو مربع لاتین متعامد \(3 \times 3\) (مرتبه فرد است) را توضیح می دهیم:
دو شکل مانند زیر ایجاد می کنیم:
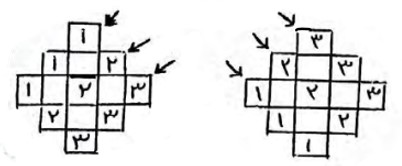
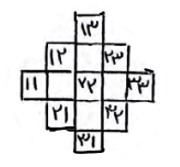
حال دو شکل را با هم ترکیب می کنیم:
تهیه کننده: عادل نقدی
جزوات جامع پایه گسسته
جزوه جامع ریاضیات گسسته فصل 1 آشنایی با نظریۀ اعداد
جزوه جامع ریاضیات گسسته فصل 2 گراف و مدل سازی
جزوه جامع ریاضیات گسسته فصل 3 ترکیبیّات (شمارش)
اصل شمول و عدم شمول
اصل شمول و عدم شمول
اصل شمول و عدم شمول برای دو مجموعه
تعداد عضو هایی که به مجموعه A یا به مجموعه B تعلق دارند برابر است با:
\(\left| {A \cup B} \right| = \left| A \right| + \left| B \right| - \left| {A \cap B} \right|\)
واضح است که تعداد عضو هایی که به هیچ یک از مجموعه های A و B تعلق ندارند برابر است با:
\(\left| {\bar A\bar \cup \bar B} \right| = \left| {\bar A \cap \bar B} \right| = \left| {(A \cup B)'} \right| = \left| S \right| - \left| {A \cup B} \right|\)
تعداد اعداد طبیعی کوچکتر یا مساوی n که بر k بخش پذیرند برابر است با:
خارج قسمت تقسیم = \(\left[ {\frac{n}{k}} \right]\)
مثال
چند عضو از مجموعه \(S = \{ n \in \mathbb{N}|n \le 400\} \) نه بر 2 و نه بر 3 بخش پذیرند؟
\(\begin{array}{l}S = \{ 1,2,3,...,400\} \to \left| S \right| = 400\\ \div 2 = A \to \left| A \right| = \left[ {\frac{{400}}{2}} \right] = 200\\ \div 3 = B \to \left| B \right| = \left[ {\frac{{400}}{3}} \right] = 133\\ \div 3,2 = A \cap B \to \left| {A \cap B} \right| = \left[ {\frac{{400}}{{2 \times 3}}} \right] = \left[ {\frac{{400}}{6}} \right] = 66\\\left| {A \cup B} \right| = \left| A \right| + \left| B \right| - \left| {A \cap B} \right| = 200 + 133 - 66 = 267\\\left| {(A \cup B)'} \right| = \left| S \right| - \left| {A \cup B} \right| = 400 - 267 = 133\end{array}\)
اصل شمول و عدم شمول برای سه مجموعه
تعداد عضو هایی که حداقل به یکی از سه مجموعه A یا B یا C تعلق دارد برابر است با:
\(\begin{array}{l}\left| {A \cup B \cup C} \right| = \left| A \right| + \left| B \right| + \left| C \right| - \left| {A \cap B} \right| - \left| {A \cap C} \right| - \left| {B \cap C} \right| + \left| {A \cap B \cap C} \right|\\\left| {{{\left( {A \cap B \cap C} \right)}^\prime }} \right| = \left| {A' \cap B' \cap C'} \right| = \left| S \right| - \left| {A \cup B \cup C} \right|\end{array}\)
مثال
چند عدد طبیعی مانند n به طوری که \(1 \le n \le 350\) وجود دارد که بر هیچ یک از اعداد 4 و 5 و 6 بخش پذیر نباشد؟
\(\begin{array}{l}\left| S \right| = 350,\left[ {4,5} \right] = 20,\left[ {4,6} \right] = 12,\left[ {5,6} \right] = 30,\left[ {4,5,6} \right] = 60\\\left| A \right| = \left[ {\frac{{350}}{4}} \right] = 87,\left| B \right| = \left[ {\frac{{350}}{5}} \right] = 70,\left| C \right| = \left[ {\frac{{350}}{6}} \right] = 58\\\left| {A \cap B} \right| = \left[ {\frac{{350}}{{20}}} \right] = 17,\left| {A \cap C} \right| = \left[ {\frac{{350}}{{12}}} \right] = 29,\left| {B \cap C} \right| = \left[ {\frac{{350}}{{30}}} \right] = 11\\\left| {A \cap B \cap C} \right| = \left[ {\frac{{350}}{{60}}} \right] = 5 \to \left| {A \cup B \cup C} \right| = 163 \to \left| {A' \cup B' \cup C'} \right| = 350 - 163 = 187\end{array}\)
تابع شماری
اگر A و B دو مجموعه باشند، تعداد توابع از A به B برابر است با:
\({\left| B \right|^{\left| A \right|}}\)
مثال
چند تابع از مجموعه \(A = \{ {a_1},{a_2},{a_3}\} \) به مجموعه \(B = \{ {b_1},{b_2}\} \) می توان نوشت؟
\(\left| A \right| = 3,\left| B \right| = 2 \to {\left| B \right|^{\left| A \right|}} = {2^3} = 8\)
اگر \(\left| A \right| = m\) و \(\left| B \right| = k\) با شرط \(m \le k\) تعداد توابع یک به یک از مجموعه A به مجموعه B برابر است با:
\({(k)_m} = \frac{{k!}}{{(k - m)!}}\)
مثال
به چند طریق می توان 4 خودکار متفاوت را بین 8 نفر توزیع کرد به شرط آن که هیچکس بیشتر از یک خودکار نداشته باشد؟ (به هر نفر حداکثر یک خودکار برسد)
تعداد حالت های ممکن \({\left( 8 \right)_4} = \frac{{8!}}{{4!}} = 1680\) که معادل است با پیدا کردن تعداد تابع های یک به یک از مجموعه ای 4 عضوی به مجموعه ای 8 عضوی
تابع f از مجموعه A به مجموعه B را پوشا می نامند هر گاه برد تابع f، شامل کل اعضای B باشد، به عبارت دیگر به هر عضو B یک پیکان رسم شود و آن را به صورت زیر نشان می دهند.
\(\begin{array}{l}A = \{ {a_1},{a_2},...,{a_n}\} ,B = \{ {b_1},{b_2},...,{b_n}\} \\f:A \to B\\{R_f} = B\end{array}\)
برای پیدا کردن تعداد تابع های پوشا از مجموعه n عضوی A به مجموعه m عضوی B از فرمول های زیر استفاده می کنیم که همان اصل شمول و عدم شمول است:
\(\begin{array}{l}{A_j} = \{ f:A \to B|f({a_i}) \ne {b_j},1 \le i \le n,1 \le j \le m\} \\\left| S \right| = {\left| B \right|^{\left| A \right|}} = {m^n},\left| {{A_1}} \right| = \left| {{A_2}} \right| = ... = \left| {{A_m}} \right| = {2^m}\\\left| {{A_1} \cap {A_2}} \right| = \left| {{A_1} \cap {A_3}} \right| = ... = \left| {{A_2} \cap {A_3}} \right| = ... = 1,\left| {{A_1} \cap {A_2} \cap {A_3} \cap ... \cap {A_m}} \right| = 0\\\left| {{{\bar A}_1} \cap {{\bar A}_2} \cap ... \cap {{\bar A}_m}} \right| = \left| {{{\bar A}_1}\bar \cup {{\bar A}_2}\bar \cup ...\bar \cup {{\bar A}_m}} \right| = \left| S \right| - \left| {{A_1} \cup {A_2} \cup ... \cup {A_m}} \right|\end{array}\)
مثال
با استفاده از اصل شمول و عدم شمول، تعداد توابع پوشا از یک مجموعه 4 عضوی به یک مجموعه 3 عضوی را بدست آورید.
\(\begin{array}{l}{A_j} = \{ f:A \to B|f({a_i}) \ne {b_j},1 \le i \le 4,1 \le j \le 3\} \\A = \{ {a_1},{a_2},{a_3},{a_4}\} ,B = \{ {b_1},{b_2},{b_3}\} \to \left| A \right| = 4,\left| B \right| = 3\\\left| S \right| = {3^4} = 81,\left| {{A_i}} \right| = {2^4} = 16 \to \left| {{A_i} \cap {A_j}} \right| = 1,\left| {{A_1} \cap {A_2} \cap {A_3}} \right| = 0\\\left| {{{\bar A}_1} \cup {{\bar A}_2} \cup {{\bar A}_3}} \right| = \left| S \right| - \left| {{A_1} \cup {A_2} \cup {A_3}} \right| = 81 - \left( {16 + 16 + 16 - 3 + 0} \right) = 36\end{array}\)
تعداد تابع های پوشا از مجموعه m عضوی A به مجموعه 3 عضوی B از فرمول زیر بدست می آید:
\(\begin{array}{l}\left| A \right| = m,\left| B \right| = 3\\f:A \to B,{R_f} = B\\{3^m} - (3 \times {2^m} - 3)\end{array}\)
مثال
تعداد تابع های پوشا از مجموعه 4 عضوی A به مجموعه 3 عضوی B چند تا است؟
\(\begin{array}{l}m = 4\\{3^4} - (3 \times {2^4} - 3) = 36\end{array}\)
تهیه کننده: عادل نقدی
اصل لانه کبوتری
اصل لانه کبوتری
اگر m کبوتر و n لانه داشته باشیم و \(m\rangle n\) و همه کبوتر ها درون لانه ها قرار بگیرند در این صورت لانه ای وجود دارد که حداقل دو کبوتر در آن قرار گرفته است.
مثال
در کلاس 40 نفره، حداقل چند نفر ماه تولدشان یکسان است؟
40 نفر را کبوتر و 12 ماه سال را لانه در نظر می گیریم \(40 \div 12 = 3 \to 3 \times 12 = 36 \to 40 - 36 = 4\) باقی مانده صفر نشد پس حداقل \(3 + 1\) یعنی 4 نفر می توان یافت.
اگر باقی مانده صفر نشود یک واحد به خارج قسمت اضافه می کنیم.
تعمیم اصل لانه کبوتری
هر گاه (\(kn + 1\)) کبوتر یا بیشتر در n لانه قرار بگیرند در این صورت لانه ای وجود دارد که حداقل (\(k + 1\)) کبوتر در آن قرار گرفته است.
مثال
1 در یک اردوی دانش آموزی حداقل چند دانش آموز وجود داشته باشند تا اطمینان داشته باشیم که حداقل 7 نفر از آنها ماه تولد یکسانی دارند؟
\(\begin{array}{l}k + 1 = 7 \to k = 6\\kn + 1 = \left( {6 \times 12} \right) + 1 = 73\end{array}\)
2 در یک دبیرستان حداقل چند دانش آموز وجود داشته باشد تا مطمئن باشیم حداقل 10 نفر از آنها ماه و روز هفته تولدشان یکی است؟
\(\begin{array}{l}year = 12month\\week = 7day\\ \to n = 12 \times 7 = 84\\k + 1 = 10 \to k = 9 \to kn + 1 = 9 \times 84 + 1 = 757\end{array}\)
تمرین
1 54 شاخه گل را حداکثر در چند گلدان قرار دهیم تا اطمینان داشته باشیم گلدانی هست که در آن حداقل 5 شاخه گل قرار گرفته است؟
\(\begin{array}{l}k + 1 = 5 \to k = 4\\kn + 1 = 54 \to 4n + 1 = 54 \to n = \left[ {\frac{{53}}{4}} \right] = 13\end{array}\)
پس n باید حداکثر 13 باشد.
2 در بین اعداد 1 تا 90 چند عدد وجود دارد که بر 2 یا 3 بخش پذیر باشند؟
\(\begin{array}{l}\left| A \right| = \left[ {\frac{{90}}{2}} \right] = 45\\\left| B \right| = \left[ {\frac{{90}}{3}} \right] = 30\\\left| {A \cap B} \right| = \left[ {\frac{{90}}{6}} \right] = 15\\\left| {A \cup B} \right| = \left| A \right| + \left| B \right| - \left| {A \cap B} \right| = 45 + 30 - 15 = 60\end{array}\)
3 در یک اردوی دانش آموزی حداقل چند دانش آموز حضور داشته باشند تا اطمینان داشته باشیم که لااقل 7 نفر از آنها ماه تولد یکسانی دارند؟
\(\begin{array}{l}k + 1 = 7 \to k = 6\\n = 12\\kn + 1 = \left( {6 \times 12} \right) + 1 = 73\end{array}\)
4 چند عدد طبیعی مانند n به طوریکه \(1 \le n \le 350\) وجود دارد که بر هیچ یک از اعداد 4 و 6 بخش پذیر نباشد؟
\(\begin{array}{l}\left| {\bar A \cap \bar B} \right| = \left| {\bar A \cap \bar B} \right| = \left| S \right| - \left( {\left| A \right| + \left| B \right| - \left| {A \cap B} \right|} \right) = 350\\350 - \left( {\left[ {\frac{{350}}{4}} \right] + \left[ {\frac{{350}}{6}} \right] - \left[ {\frac{{350}}{{12}}} \right]} \right) = 234\end{array}\)
تهیه کننده: عادل نقدی
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه گسسته- آزمون آنلاین تمامی دروس پایه گسسته
- گام به گام تمامی دروس پایه گسسته
- ویدئو های آموزشی تمامی دروس پایه گسسته
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه گسسته
- فلش کارت های آماده دروس پایه گسسته
- گنجینه ای جامع از انشاء های آماده پایه گسسته
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه گسسته



1736019749.png)















