درسنامه کامل ریاضی هشتم فصل 1 عددهای صحیح و گویا
تعداد بازدید : 7.27Mخلاصه نکات ریاضی هشتم فصل 1 عددهای صحیح و گویا - درسنامه شب امتحان ریاضی هشتم فصل 1 عددهای صحیح و گویا - جزوه شب امتحان ریاضی هشتم نوبت اول فصل 1 عددهای صحیح و گویا
اعداد صحیح
اعداد صحیح
اعداد صحیح از سه دسته تشکیل شده اند:
اعداد مثبت، صفر واعداد منفی
اعداد صحیح را با حرف انگلیسی \(\mathbb{Z}\) نشان می دهند:
\(\mathbb{Z} = \left\{ { \cdots \,,\, - 2\,,\, - 1\,,\, \circ \,,\,1\,,\,2\,,\, \cdots } \right\}\)
حرکت روی محور اعداد صحیح
جا به جایی از یک نقطه به نقطه ی دیگر را «حرکت» می گویند؛ اگر این حرکت در جهت مثبت (سمت راست) باشد، با علامت مثبت (+) و اگر در جهت منفی (سمت چپ) باشد، علامت منفی (-) خواهد داشت؛ به عنوان مثال:
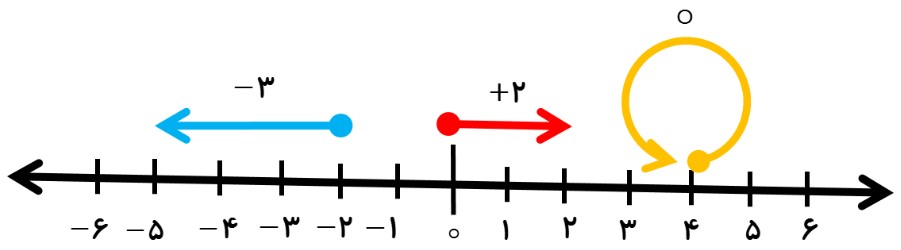
قرینه
به اعدادی که فاصله آن ها تا «صفر» با هم برابر باشد، دو عدد قرینه می گویند؛ مانند 3+ و 3- ، 2+ و 2-.
10- = قرینه 10
5+ = قرینه 5-
1 قرینه را با علامت (−) نمایش می دهند. قرینه ی هر عدد صحیح را می توان با تغییر علامت آن بدست آورد.
8- = قرینه 8
3+ = قرینه 3-
2 قرینه ی عدد صفر برابر صفر می باشد.
-0=0
3 قرینه قرینه عر عدد خود عدد می باشد.
\(\begin{array}{l} - \left[ { - \,( - \,3)} \right] = - \,3\\\\ - \left[ { + \,( - \,6)} \right] = + \,6\end{array}\)
مثال
قرینه قرینه قرینه عدد 10 کدام است؟
هر کلمه قرینه را با نماد – نشان می دهیم:
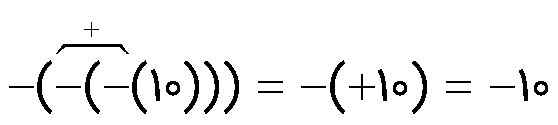
مثال
اگر عدد 25- را 1023 بار قرینه کنیم، نتیجه حاصل چه عددی می شود؟
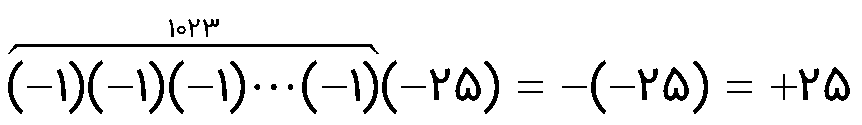
تهیه کنندگان: فاطمه بنده زاده - سارا جاویدپور
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه هشتم- آزمون آنلاین تمامی دروس پایه هشتم
- گام به گام تمامی دروس پایه هشتم
- ویدئو های آموزشی تمامی دروس پایه هشتم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه هشتم
- فلش کارت های آماده دروس پایه هشتم
- گنجینه ای جامع از انشاء های آماده پایه هشتم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه هشتم
جمع و تفریق اعداد صحیح
جمع و تفریق اعداد صحیح
برای محاسبه ی حاصل جمع و یا تفریق عددهای صحیح ابتدا مختصر نویسی (ساده نویسی) می کنیم، به این صورت که پرانتزها رو حذف کرده، سپس اگر عددی بیشتر از یک علامت داشته باشد، علامت های آن ها را در هم ضرب می کنیم تا به یک علامت تبدیل شود. آنگاه با یکی از دو حالت زیر مواجه می شویم:
1- حالت اول:
عددها هم علامت باشند؛ در این حالت یکی از علامت ها را نوشته، سپس عددها را با هم جمع می کنیم؛ مانند:
10- = (7–) + (3–)
14+ = 6 + 8+ = (6–) – (8+)
2- حالت دوم:
عددها هم علامت نباشند؛ در این حالت علامت عددی که بزرگتر است (بدون در نظر گرفتن علامت( را نوشته سپس عددها را از هم کم می کنیم؛ مانند:
2+ = 8 + 6- = (8+) + (6-)
5- = 30 - 25 = (30+) - 25
اگر تعداد عددها بیشتر از دو تا بود، می توان عددهای مثبت را با هم و عددهای منفی را با هم جمع کرد، سپس حاصل نهایی را بدست آورد.
مثال
حاصل عبارت زیر را بدست آورید.
= 7 + (3+) - (6+) + 4-
6+ = 13 + 7- = 7 + 3 - 6 + 4- = 7 + (3+) - (6+) + 4-
تهیه کنندگان: فاطمه بنده زاده - سارا جاویدپور
جزوات جامع پایه هشتم
جزوه جامع ریاضی هشتم فصل 1 عددهای صحیح و گویا
جزوه جامع ریاضی هشتم فصل 2 عددهای اول
جزوه جامع ریاضی هشتم فصل 3 چندضلعی ها
جزوه جامع ریاضی هشتم فصل 4 جبر و معادله
جزوه جامع ریاضی هشتم فصل 5 بردار و مختصات
جزوه جامع ریاضی هشتم فصل 6 مثلث
جزوه جامع ریاضی هشتم فصل 7 توان و جذر
جزوه جامع ریاضی هشتم فصل 8 آمار و احتمال
جزوه جامع ریاضی هشتم فصل 9 دایره
ضرب و تقسیم اعداد صحیح
ضرب و تقسیم اعداد صحیح
ابتدا علامت ها را در هم ضرب کرده، سپس اعداد را با توجه به علامت بین آن ها ضرب یا تقسیم می کنیم.
جدول ضرب علامت ها
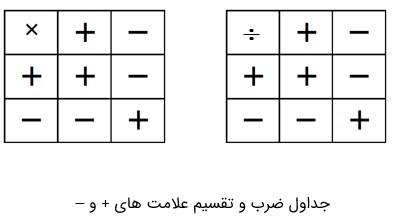
مثال
حاصل ضرب و تقسیم های زیر را بیابید.
= (3-) ÷ [(4+) × (6-)] (1
= [(4+) ÷ 12] × 8- (2
8+ = (3-) ÷ (24-)= (3-) ÷ [(4+) × (6-)] (1
24- = (2+) × (8-) = [(4+) ÷ 12] × 8- (2
تهیه کنندگان: فاطمه بنده زاده - سارا جاویدپور
اولویت های انجام عملیات در ریاضی
اولویت های انجام عملیات در ریاضی
برای محاسبه ی عبارت ترکیبی جمع، تفریق، ضرب، تقسیم باید بر اساس ترتیب اولویت ها شروع به پاسخ دادن کرد:
1( مجموعه یا کروشه یا پرانتز
2( توان و جذر
3( ضرب و تقسیم (از سمت چپ)
4) جمع و تفریق
مثال
حاصل عبارت مقابل را به دست آورید.
\(4 - 4 \times {3^2} \div 6 - (9 - {2^3}) = \)
ابتدا حاصل داخل پرانتز را محاسبه می کنیم:
\(9 - {2^3} = 9 - 8 = 1\)
حال داریم:
\(4 - 4 \times {3^2} \div 6 - 1 = \)
سپس از سمت چپ مطابق ترکیب عملیات پیش می رویم (توان و جذر):
\(4 - 4 \times 9 \div 6 - 1 = \)
مجدد از سمت چپ طبق ترتیب عملیات پیش می رویم:
\(4 - 36 \div 6 - 1 = 4 - 6 - 1 = - 3\)
تهیه کنندگان: فاطمه بنده زاده - سارا جاویدپور
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه هشتم- آزمون آنلاین تمامی دروس پایه هشتم
- گام به گام تمامی دروس پایه هشتم
- ویدئو های آموزشی تمامی دروس پایه هشتم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه هشتم
- فلش کارت های آماده دروس پایه هشتم
- گنجینه ای جامع از انشاء های آماده پایه هشتم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه هشتم
جمع اعداد یک مجموعه منظم
جمع اعداد یک سری (مجموعه) منظم
برای جمع اعداد یک سری منظم، از رابطه های زیر استفاده می کنیم:

مثال
حاصل عبارت های زیر را به دست آورید.
\(3 + 6 + 9 + \cdots + 204 = \)
\( = \,\,\frac{{204 - 3}}{3} + 1 = 67 + 1 = 68\) تعداد اعداد
\( = \,\,\frac{{204 + 3}}{2} \times 68 = 207 \times 34 = 7038\) مجموع اعداد
برای جمع اعداد یک سری منظم که یک در میان مثبت و منفی باشند ابتدا دو به دو اعداد را جواب می دهیم؛ مانند:
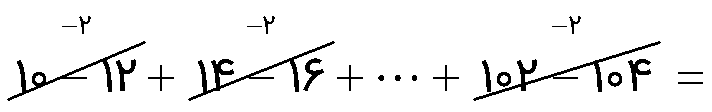
\( = \,\,\frac{{104 - 10}}{2} + 1 = 47 + 1 = 48\) تعداد اعداد
\(\begin{array}{l}48 \div 2 = 24\\\\10 - 12 + 14 - 16 + \cdots + 102 - 104 = 24 \times ( - 2) = - 48\end{array}\)
تهیه کنندگان: فاطمه بنده زاده - سارا جاویدپور
جزوات جامع پایه هشتم
جزوه جامع ریاضی هشتم فصل 1 عددهای صحیح و گویا
جزوه جامع ریاضی هشتم فصل 2 عددهای اول
جزوه جامع ریاضی هشتم فصل 3 چندضلعی ها
جزوه جامع ریاضی هشتم فصل 4 جبر و معادله
جزوه جامع ریاضی هشتم فصل 5 بردار و مختصات
جزوه جامع ریاضی هشتم فصل 6 مثلث
جزوه جامع ریاضی هشتم فصل 7 توان و جذر
جزوه جامع ریاضی هشتم فصل 8 آمار و احتمال
جزوه جامع ریاضی هشتم فصل 9 دایره
اعداد گویا
اعداد گویا
هر عدد را که بتوان به صورت یک کسر نوشت، به طوری که صورت و مخرج آن عدد صحیح بوده و مخرج آن صفر نباشد را عدد گویا می نامند.
اعداد گویا را با حرف انگلیسی \(\mathbb{Q}\) نمایش می دهند:
\(\mathbb{Q} = \left\{ {\left. {\frac{a}{b}} \right|a\,,\,b\, \in \mathbb{Z}\,,\,b \ne \circ } \right\}\)
عددهای طبیعی، حسابی، صحیح، کسری، اعشاری، مخلوط و رادیکال هایی که عدد زیر رادیکال آن مجذور کامل باشد یک عدد گویا می باشند؛ مانند:
\(\begin{array}{l} - \frac{5}{6}\,\,\,\,\,\,\,\,\,13 = \frac{{13}}{1}\,\,\,\,\,\,\,\,\,\frac{8}{{ - 3}}\,\,\,\,\,\,\,\,\,0/7 = \frac{7}{{10}}\,\,\,\,\,\,\,\,\, - 2\frac{3}{4}\\\\\sqrt {25} = 5 = \frac{5}{1}\,\,\,\,\,\,\,\,\, \circ = \frac{ \circ }{1}\end{array}\)
اگر مخرج کسری صفر باشد، کسر را «تعریف نشده» می نامند.
نمایش اعداد گویا روی محور
برای نمایش هر عدد گویا روی محور طبق مراحل زیر عمل می کنیم:
1) واحدهای محور را به تعداد عدد مخرج کسر تقسیم می کنیم.
2) با توجه به علامت عدد، جهت حرکت را مشخص می کنیم، علامت + حرکت به سمت راست و علامت − حرکت به سمت چپ است.
3) به تعداد عدد صورت کسر از صفر ، واحدهای تقسیم شده را شمارش می کنیم.
مثال
عددهای مقابل را مانند نمونه روی محور نمایش دهید.
\( - \frac{3}{4}\,\,\,\,\,,\,\,\,\,\,\frac{1}{4}\,\,\,\,\,,\,\,\,\,\, - 2\frac{1}{4}\)
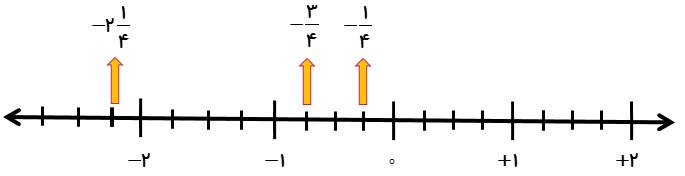
1 قرینه ی اعداد گویا همانند قرینه عددهای صحیح می باشد؛ مانند:
\( - ( - \frac{7}{5}) = + \frac{7}{5}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - ( + \frac{2}{3}) = - \frac{2}{3}\)
2 برای نوشتن معکوس اعداد گویا ، جای صورت و مخرج آن را عوض می کنیم:
\( - \frac{{11}}{6}\,\, \to \,\, - \frac{6}{{11}}\,\,\,\,\,\,\,,\,\,\,\,\,\, - 4\frac{2}{3} = - \frac{{14}}{3}\,\, \to \,\, - \frac{3}{{14}}\)
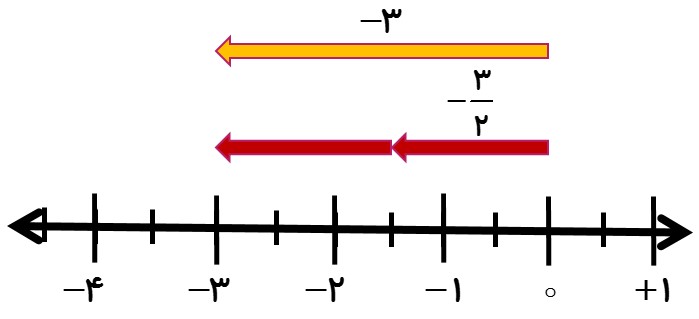
3 علامت کسر را می توان در کنار خود کسر، کنار صورت و یا کنار مخرج کسر نوشت. به محور زیر دقت کنید. می دانیم \(\frac{{ - 3}}{2}\) یعنی 2 ÷ 3- . برای نمایش این عدد برداری به طول 3- رسم می کنیم و آن را به دو قسمت مساوی تقسیم می کنیم. هر تکه برداری در جهت منفی محور اعداد و به طول \(\frac{3}{2}\) واحد است. پس عدد متناطر با هر قسمت کوچک \(\frac{{ - 3}}{2}\) است. بنابراین داریم:
\(\frac{{ - 3}}{2} = - 3 \div 2 = - \frac{3}{2}\)
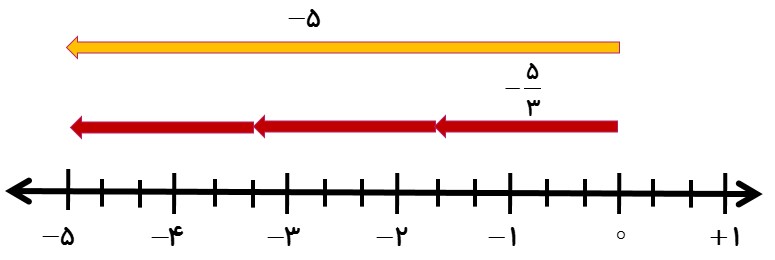
مثال
تساوی \(\frac{{ - 5}}{3} = - \frac{5}{3}\) را به کمک محور کامل کنید.
تهیه کنندگان: فاطمه بنده زاده - سارا جاویدپور
محدوده ی اعداد
محدوده ی اعداد
اعداد بزرگتر از 2 را به صورت \(x > 2\) نمایش می دهیم و شامل تمامی اعدادی است که از 2 بزرگترند.
اعداد بزرگتر یا مساوی با 2 را به صورت \(x \ge 2\) نمایش می دهیم و شامل عدد 2 و همه ی اعداد بزرگتر از 2 است.
اعداد بین 1 و 2 را به صورت \(1 < x < 2\) نمایش می دهیم.
اعداد کوچکتر یا مساوی با 2 و بزرگتر از 1 را با \(1 < x \le 2\) نمایش می دهند و شامل عدد 2 و تمام اعداد بین 1 و 2 است.
مثال
برای هر کدام از محدوده های زیر دو عدد مثال بزنید.


تهیه کنندگان: فاطمه بنده زاده - سارا جاویدپور
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه هشتم- آزمون آنلاین تمامی دروس پایه هشتم
- گام به گام تمامی دروس پایه هشتم
- ویدئو های آموزشی تمامی دروس پایه هشتم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه هشتم
- فلش کارت های آماده دروس پایه هشتم
- گنجینه ای جامع از انشاء های آماده پایه هشتم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه هشتم
تساوی کسرها
تساوی کسرها
اگر صورت و مخرج کسر را در عددی غیر از صفر ضرب کنیم، یا بر عددی غیر از صفر تقسیم کنیم، کسر حاصل با کسر اول مساوی می باشد؛ مانند:
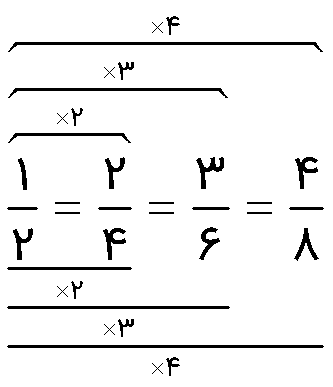
مثال
برای کسر زیر 2 کسر مساوی بنویسید.
\(\frac{3}{5} = \)
\(\frac{3}{5} = \frac{6}{{10}} = \frac{9}{{15}}\)
در تساوی دو کسر اگر یکی از عددها مجهول باشد، به کمک تساوی کسرها می توان مقدار مجهول را به دست آورد.
مانند نمونه مقدار مجهول را به دست آورید.
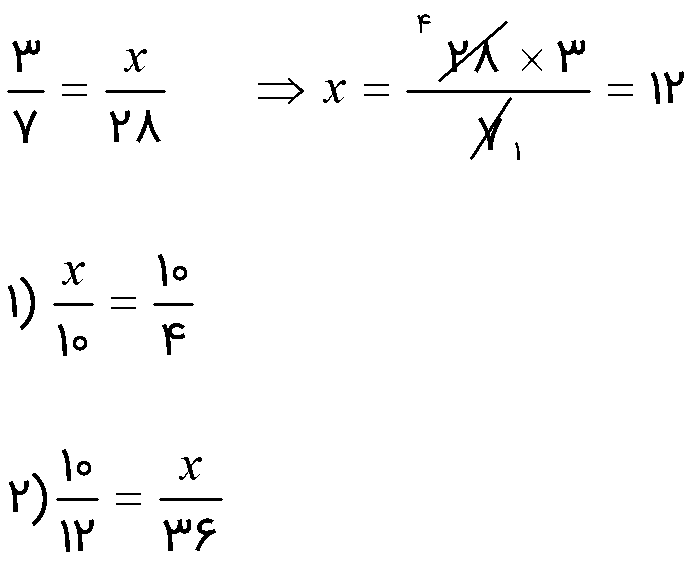
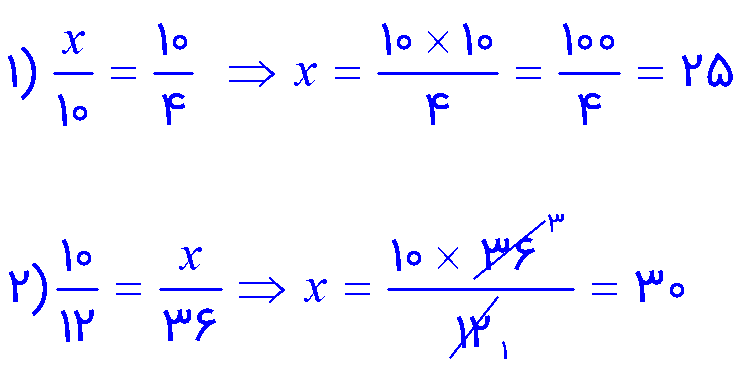
1 برای اینکه یک کسر را تا حد ممکن ساده کنیم باید صورت و مخرج آن را بر «ب.م.م» صورت و مخرج تقسیم کنیم.
2 برای به دست آوردن ب.م.م، ابتدا دو عدد را به عامل های اول تجزیه می کنیم، سپس حاصل ضرب عامل های مشترک دو عدد با توان کمتر را حساب می کنیم.
مثال
کسر زیر را مانند نمونه تا حد امکان ساده کنید.
\(\begin{array}{l}\frac{{ - 56}}{{210}} = \\\\\frac{{48}}{{100}} = \end{array}\)
\(\begin{array}{l}56 = {2^3} \times 7\\\\210 = 2 \times 3 \times 5 \times 7\\\\\left( {56\,,\,210} \right) = 2 \times 7 = 14\\\\\frac{{ - 56}}{{210}} = \frac{{ - 56 \div 14}}{{210 \div 14}} = \frac{{ - 4}}{{15}}\\\\ - - - - - - - - - - - - - - - - - \\48 = {2^4} \times 3\\\\100 = {2^2} \times {5^2}\\\\\left( {48\,,\,100} \right) = {2^2} = 4\\\\\frac{{48}}{{100}} = \frac{{48 \div 4}}{{100 \div 4}} = \frac{{12}}{{25}}\end{array}\)
1 از تساوی کسرها می توان نتیجه گرفت که هر کسر گویا بی شمار نمایش مختلف دارد.
2 نوشتن عددی گویا بین دو عدد به چند روش است که یک روش کاربردی آن در زیر آورده شده ابتدا مخرج مشترک گرفته سپس صورت و مخرج را در یک واحد بیشتر از تعداد کسرهای خواسته شده ضرب می کنیم.
3 با توجه به تقسیم شدن فاصله ی بین دو عدد، کسرهای مختلفی بین هر دو عدد صحیح می توان نوشت.
4 بین هر دو عدد کسری نیز می توان کسرهای بی شماری پیدا کرد.
مثال
ما بین دو عدد گویای زیر دو عدد گویا (دو کسر) پیدا کنید.
\(\frac{3}{4}\,\,,\,\,\frac{5}{7}\)
\(\begin{array}{l}\left. \begin{array}{l}\frac{3}{4} = \frac{{21}}{{28}} = \frac{{21 \times 3}}{{28 \times 3}} = \frac{{63}}{{84}}\\\\\frac{5}{7} = \frac{{20}}{{28}} = \frac{{20 \times 3}}{{28 \times 3}} = \frac{{60}}{{84}}\,\end{array} \right\}\\\\ \Rightarrow \frac{5}{7} = \frac{{60}}{{84}} < \frac{{61}}{{84}} < \frac{{62}}{{84}} < \frac{{63}}{{84}} = \frac{3}{4}\\\\ \Rightarrow \frac{5}{7} < \frac{{61}}{{84}} < \frac{{62}}{{84}} < \frac{3}{4}\end{array}\)
تهیه کنندگان: فاطمه بنده زاده - سارا جاویدپور
جزوات جامع پایه هشتم
جزوه جامع ریاضی هشتم فصل 1 عددهای صحیح و گویا
جزوه جامع ریاضی هشتم فصل 2 عددهای اول
جزوه جامع ریاضی هشتم فصل 3 چندضلعی ها
جزوه جامع ریاضی هشتم فصل 4 جبر و معادله
جزوه جامع ریاضی هشتم فصل 5 بردار و مختصات
جزوه جامع ریاضی هشتم فصل 6 مثلث
جزوه جامع ریاضی هشتم فصل 7 توان و جذر
جزوه جامع ریاضی هشتم فصل 8 آمار و احتمال
جزوه جامع ریاضی هشتم فصل 9 دایره
جمع و تفریق اعداد گویا
جمع و تفریق اعداد گویا
1- روش اول با استفاده از محور:
از حرکت های علامت دار روی محور استفاده می کنیم:
\(( + \frac{5}{3}) + ( - \frac{8}{3}) = - \frac{3}{3} = - 1\)
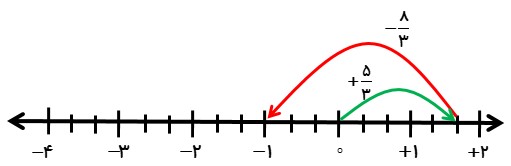
2- روش دوم:
الف) هنگامی که دو عدد گویا دارای مخرج های برابر باشند، جمع و تفریق آن ها به سادگی و مانند عددهای صحیح صورت می گیرد:
\(\begin{array}{l}\frac{3}{4} + \frac{5}{4} = \frac{{3 + 5}}{4} = \frac{8}{4} = 2\\\\\frac{7}{3} - \frac{5}{3} = \frac{{7 - 5}}{3} = \frac{2}{3}\end{array}\)
ب) در صورتی که مخرج ها یکسان نباشند، ابتدا مخرج ها را با استفاده از مخرج کسر دیگر یکسان می کنیم (ک.م.م(، سپس مانند قبل محاسبات جمع و یا تفریق را انجام می دهیم.
\(\frac{2}{3} + \frac{3}{4} = \frac{{2 \times 4}}{{3 \times 4}} + \frac{{3 \times 3}}{{4 \times 3}} = \frac{8}{{12}} + \frac{9}{{12}} = \frac{{17}}{{12}}\)
روش بدست آوردن ک.م.م
ابتدا هر عدد را به عامل های اول تجزیه می کنیم سپس عامل های مشترک هر دو عدد را در عامل های غیر مشترک ضرب می کنیم.
\(\begin{array}{l}\left[ {8\,,\,12} \right] = ?\\\\\left. \begin{array}{l}8 = {2^3}\\12 = {2^2} \times 3\end{array} \right\} \Rightarrow \left[ {8\,,\,12} \right] = 24\end{array}\)
مثال
حاصل عبارت مقابل را بدست آورید.
\( - \frac{2}{3} - (\frac{4}{{15}}) = \)
\(\begin{array}{l}\left[ {10\,,\,15} \right] = 30\\\\ \Rightarrow - \frac{2}{3} - (\frac{4}{{15}}) = \frac{{ - 9 + 8}}{{30}} = - \frac{1}{{30}}\end{array}\)
بهترین مخرج مشترک دو کسر ، همان ک.م.م عددهای مخرج هاست .
مثال
حاصل عبارت های زیر را به دست آورید.
\(\begin{array}{l}1)\,\,\frac{8}{{12}} - \frac{{12}}{{16}} = \\\\2)\, - \frac{7}{4} - ( - \frac{{13}}{4}) = \end{array}\)
\(\begin{array}{l}1)\,\,\left[ {12\,,\,16} \right] = 48\\\\ \Rightarrow \frac{8}{{12}} - \frac{{12}}{{16}} = \frac{{32 - 36}}{{48}} = - \frac{4}{{48}} = - \frac{1}{{12}}\\\\2)\, - \frac{7}{4} - ( - \frac{{13}}{4}) = \frac{{ - 7 + 13}}{4} = \frac{6}{4} = \frac{3}{2}\end{array}\)
تهیه کنندگان: فاطمه بنده زاده - سارا جاویدپور
ضرب اعداد گویا
ضرب اعداد گویا
هنگام ضرب دو عدد گویا مراحل زیر انجام می شود:
1) ابتدا صورت را با مخرج یا بالعکس ساده کنید. (در صورت امکان)
2) علامت های دو عدد را طبق قانون ضرب علامت ها در هم ضرب کنید.
3) سپس صورت های دو کسر را در هم و مخرج ها نیز در هم ضرب کنید.
4) در ضرب اعداد گویا، اگر عددی مخلوط بود، ابتدا عدد مخلوط را به کسر تبدیل کنید.
مثال
حاصل عبارات زیر را بدست آورید.
\(\begin{array}{l}1)\,\,( - \frac{3}{5}) \times ( + \frac{7}{9}) = \\\\2)\,( - \frac{{20}}{{21}}) \times ( + \frac{{28}}{{80}}) = \end{array}\)
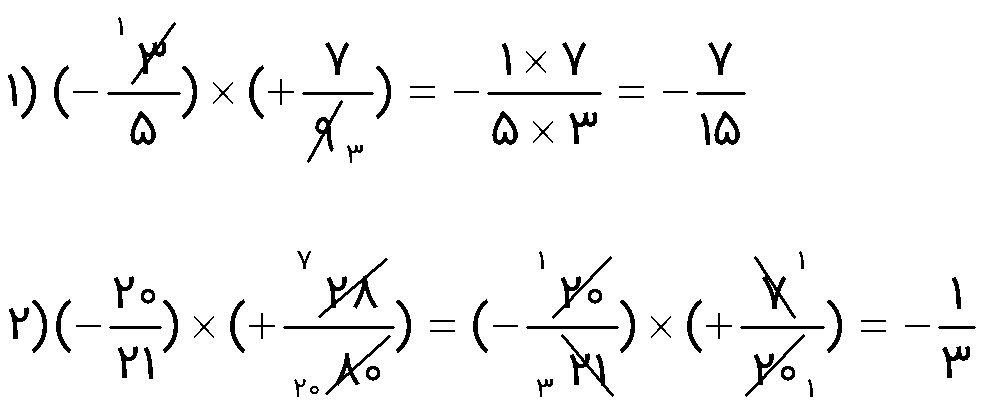
اگر در ضرب اعداد گویا عددی، عدد مخلوط بود ابتدا عدد مخلوط را به کسر تبدیل کنید؛ به عنوان مثال:
\(2\frac{3}{5} = \frac{{2 \times 5 + 3}}{5} = \frac{{13}}{5}\)
تهیه کنندگان: فاطمه بنده زاده - سارا جاویدپور
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه هشتم- آزمون آنلاین تمامی دروس پایه هشتم
- گام به گام تمامی دروس پایه هشتم
- ویدئو های آموزشی تمامی دروس پایه هشتم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه هشتم
- فلش کارت های آماده دروس پایه هشتم
- گنجینه ای جامع از انشاء های آماده پایه هشتم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه هشتم
تقسیم اعداد گویا
تقسیم اعداد گویا
هنگام تقسیم دو عدد گویا مراحل زیر را انجام دهید.
1) کسر اول را بدون تغییر بنویسید.
2) علامت تقسیم را به ضرب تبدیل کرده و کسر دوم را به صورت معکوس بنویسید.
3) ضرب به دست آمده را انجام دهید.
به عنوان مثال:
\(( - \frac{3}{5}) \div \left( { + \frac{7}{4}} \right) = ( - \frac{3}{5}) \times \left( { + \frac{4}{7}} \right) = - \frac{{3 \times 4}}{{5 \times 7}} = - \frac{{12}}{{35}}\)
1 اگر جای صورت و مخرج یک کسر را تغییر دهیم معکوس آن کسر به دست می آید.
2 ساده کردن کسر ها در تقسیم بعد از اینکه به ضرب تبدیل شد الزامی است.
3 در صورت وجود عدد مخلوط ایتدا به کسر تبدیل کنید.
حل کنید.
\(( - \frac{3}{5}) \div \left( {\frac{2}{{15}}} \right) = \)
\(( - \frac{3}{5}) \div \left( {\frac{2}{{15}}} \right) = ( - \frac{3}{5}) \times \left( {\frac{{15}}{2}} \right) = - \frac{{3 \times 15}}{{10}} = - \frac{{3 \times 5}}{2} = - \frac{{15}}{2}\)
تقسیم \(\frac{2}{5} \div \frac{3}{8}\) را در نظر بگیرید. این تقسیم را می توان به صورت \(\frac{{\,\,\frac{2}{5}\,\,}}{{\frac{3}{8}}}\) نیز نوشت. محاسبه این کسر با ضرب عدد های مشخص شده انجام می شود؛ یعنی ضرب عدد های دور را در صورت و ضرب عدد های نزدیک را در مخرج می نویسیم. به این عمل «دور در دور _ نزدیک در نزدیک» گفته می شود:
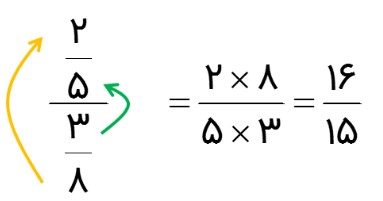
حل کنید.
\(\frac{{\frac{9}{5}}}{{ - \frac{{12}}{{15}}\,\,}} = \)
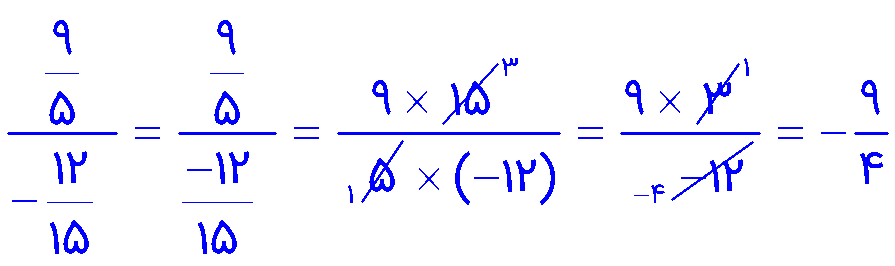
1 تنها عددی که معکوس ندارد عدد صفر است.
2 حاصل ضرب هر عدد در معکوس خودش برابر 1 می شود.
3 معکوس عدد 1 خود عدد یک می شود.
تهیه کنندگان: فاطمه بنده زاده - سارا جاویدپور



1736019749.png)















