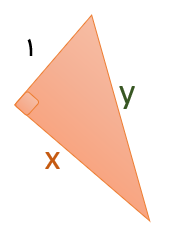درسنامه کامل ریاضی هشتم فصل 6 مثلث
تعداد بازدید : 7.26Mخلاصه نکات ریاضی هشتم فصل 6 مثلث - درسنامه شب امتحان ریاضی هشتم فصل 6 مثلث - جزوه شب امتحان ریاضی هشتم نوبت اول فصل 6 مثلث
مثلث و اجزاء آن
انواع مثلث ها
۱) مثلث مختلف الاضلاع
۲) مثلث متساوی الساقين
۳) مثلث متساوی الاضلاع
۴) مثلث قائم الزاويه
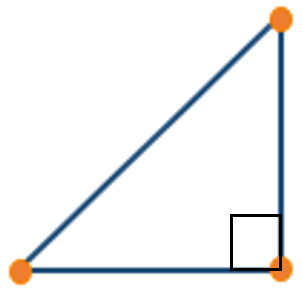
۵) مثلث قائم الزاویه ی متساوی الساقین
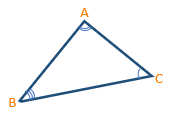
می دانید که هر مثلث دارای اجزایی است. به سه زاویه و سه ضلع مثلث اجزای اصلی آن می گویند. به طور مثال A,B,Cراس های مثلث، AC AB و BC نام اضلاع و\(\hat a,\hat b,\hat c\) نام زوایای مثلث هستند.
اجزاء فرعی مثلث
به نیمساز ارتفاع عمود منصف و .... اجزای فرعی مثلث می گویند .
نیمساز :
نیم خطی است که از راس شروع شده و زاویه را به دو قسمت مساوی تقسیم می کند.
ارتفاع:
پاره خطی است که از راس مثلث به ضلع مقابل متصل شده و بر آن عمود باشد .
عمود منصف :
خطی است که از وسط ضلع بر آن عمود شده باشد.
میانه:
پاره خطی که از یک راس مثلث به وسط ضلع مقابلش وصل شده باشد.
تهیه کنندگان: شهریار ارم و ندا بهرامی نیا
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه هشتم- آزمون آنلاین تمامی دروس پایه هشتم
- گام به گام تمامی دروس پایه هشتم
- ویدئو های آموزشی تمامی دروس پایه هشتم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه هشتم
- فلش کارت های آماده دروس پایه هشتم
- گنجینه ای جامع از انشاء های آماده پایه هشتم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه هشتم
رابطه ی فیثاغورس
رابطه ی فیثاغورس
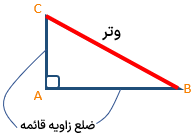
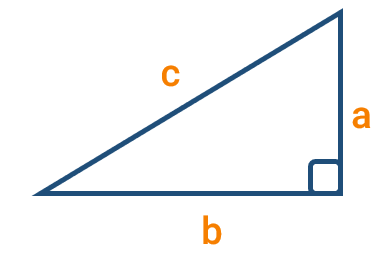
همانطور که می دانید یکی از انواع مثلث ها مثلث قائم الزاویه است در مثلث قائم الزاویه ضلع مقابل به زاویه ی قائمه که بزرگترین ضلع مثلث است را وتر می نامیم در شکل زیر مثلث ABC قائم الزاویه و \(\hat A = 90^\circ \) این مثلث دو ضلع AB و AC اضلاع زاویه ی قائمه و ضلع BC وتر مثلث است.
فيثاغورس ( فیلسوف و ریاضیدان یونانی ) با تحقیق بر روی مثلث قائم الزاویه به این نتیجه رسید:
(مساحت مربعی که با وتر مثلث قائم الزاویه ساخته میشود برابر است با مجموع مساحت دو مربعی که با اضلاع زاویه ی قائمه ساخته می شود.)
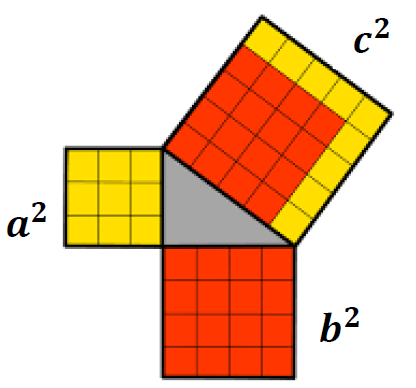
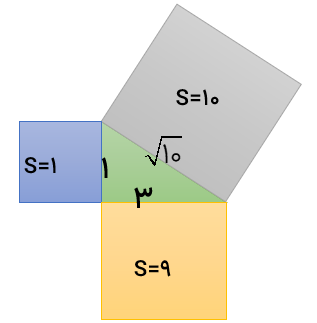
این رابطه بعدها رابطه ی فیثاغورس نامیده شد. طبق شکل زیر مساحت هر شکل کنار آن نوشته شده است . بنابراین :
\(c = 5 \Rightarrow \) مساحت مربع روی وتر:\({c^2} = 25\)
\(\left. \begin{array}{l}a = 3 \Rightarrow {a^2} = 9\\\\b = 4 \Rightarrow {b^2} = 16\end{array} \right\} \Rightarrow \) مجموع مساحت ها :9+16=25
با مقایسه ی دو عبارت داریم:
\({c^2} = {a^2} + {b^2}\)
در هر مثلث قائم الزاويه مجذور وتر برابر است با مجموع مجذور دو ضلع زاویه ی قائمه.
(توضیح: به توان دوم یک عدد مربع یا مجذور آن عدد می گویند به طور مثال مربع یا مجذور ۷ برابر است با \({7^2}\) یا 49)
برعکس این رابطه نیز برقرار است یعنی اگر در مثلثی رابطه ی فیثاغورس برقرار باشد ( مجذور وتر با مجموع مجذور دو ضلع زاویه ی قائمه برابر باشد) آن مثلث حتما قائم الزاویه است.
از این ویژگی برای تعیین اندازه ی اضلاع مثلث قائم الزاویه یا تشخیص نوع مثلث استفاده می کنیم.
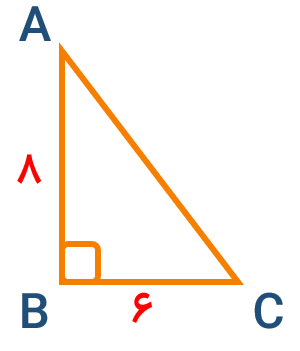
برای مثلث ABC را در نظر بگیرید.
۶۴=۸×۸ : مساحت مربعی به ضلع AB
۳۶=۶×۶ : مساحت مربعی به ضلع BC
بنابراین طبق رابطه ی فیثاغورس داریم64+36=100 : مساحت مربعی به ضلع AC پس \(AC = \sqrt {100} = 10\)
مثال
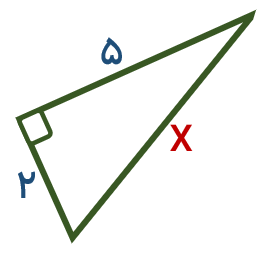
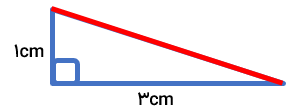
با توجه به اندازه های داده شده در شکل مقابل مقدار x را به دست آورید.
طبق رابطه فیثاغورس داریم :
\(\begin{array}{l}{x^2} = {2^2} + {5^2} = 4 + 25 = 29\\ \Rightarrow \sqrt {29} \end{array}\)
با توجه به این مثال که \({(\sqrt 3 )^2} = \sqrt 3 \times \sqrt 3 = \sqrt 9 = 3\) ؛ اگر a عددی مثبت باشد همواره رابطه ی\({(\sqrt a )^2} = a\) برقرار است.
آیا مثلثی با اضلاع \(\sqrt {11} ,6,5\) قائم الزاویه است؟
\(\left. \begin{array}{l}{6^2} = 36\\\\{5^2} + {(\sqrt {11} )^2} = 11 + 25 = 36\end{array} \right\} \Rightarrow {6^2} = {5^2} + {(\sqrt {11} )^2}\)
بنابراین مثلث مورد نظر قائم الزاویه است.
دقت کنیم در شکل هایی که مجهول ، ضلع زاویه ی قائمه است از معادل های دیگر رابطه ی فیثاغورس
استفاده کنیم.
\({c^2} = {a^2} + {b^2} \Rightarrow \left\{ \begin{array}{l}{a^2} = {c^2} - {b^2}\\{b^2} = {c^2} - {a^2}\end{array} \right.\)
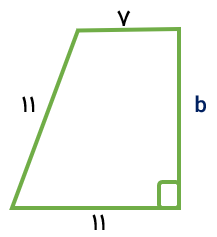
در شکل مقابل مقدار b را به دست آورید.
با توجه به شکل زیر مثلث قائم الزاویه ای به وتر ۱۱ و ضلع قائمه ی ۲ واحد به وجود می آید و بنا به رابطه ی فیثاغورس داریم:
\(\begin{array}{l}{b^2} = {11^2} - {2^2} = 121 - 4 = 117\\ \Rightarrow b = \sqrt {117} \end{array}\)
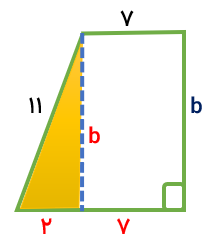
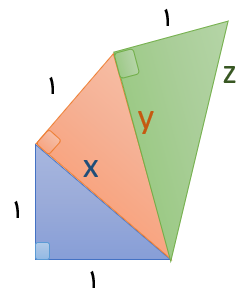
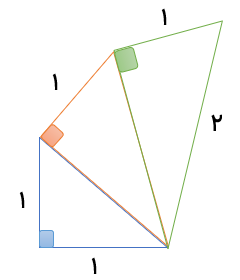
به کمک رابطه ی فیثاغورس محیط شکل زیر را به دست آورید.
برای محاسبه ی محیط باید مقدار z را به دست آورد بنابراین باید به ترتیب مقادیر x و y و z را محاسبه کنیم.
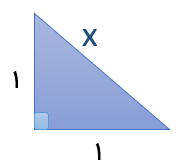
طبق شکل شماره ۱, X وتر مثلث قائم الزاویه ی متساوی الساقین است.بنابراین داریم:
\({x^2} = {1^2} + {1^2} = 1 + 1 = 2 \Rightarrow x = \sqrt 2 \)
با جایگذاری مقدار x در شکل شماره ۲ داریم:
\({y^2} = {1^2} + {(\sqrt 2 )^2} = 1 + 2 = 3 \Rightarrow y + \sqrt 3 \)
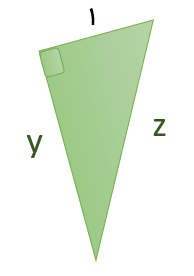
و با جایگذاری مقدار ۷ در شکل شماره ۳ داریم:
\({z^2} = {1^2} + {(\sqrt 3 )^2} = 1 + 3 = 4 \Rightarrow z = \sqrt 4 = 2\)
بنابراین مقدار محیط شکل عبارت است از:
\(p = 1 + 1 + 1 + 1 + 2 = 6\)
با استفاده از رابطه ی فیثاغورس پاره خطی به طول \(\sqrt {10} \) رسم کنید.
به کمک رابطه ی فیثاغورس به دو مربع نیاز داریم که مجموع مساحت آنها ۱۰ باشد. به طور مثال با انتخاب مربع هایی به مساحت های ۱ و ۹ (به ضلع ۱ و ۳ سانتیمتر) برای اضلاع مثلث قائم الزاويه طبق رابطه ی فیثاغورس مساحت مربعی که روی وتر ساخته می شود ۱۰ سانتیمتر مربع است پس ضلع این مربع \(\sqrt {10} \) خواهد بود.
\({x^2} = {1^2} + {3^2} = 1 + 9 = 10 \Rightarrow x = \sqrt {10} \)
بنابراین کافی است به کمک خط کش و گونیا مثلثی قائم الزاویه که اضلاع زاویه ی قائمه ی آن ۱ و ۳ سانتی متر هستند، ترسیم کنیم. وتر مثلث ترسیم شده همان پاره خط موردنظر به اندازه ی \(\sqrt {10} \) خواهد بود.
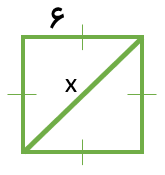
در شکل مقدار xرا به کمک رابطه فیثاغورس به دست اورید.
\(\begin{array}{l}{x^2} = {6^2} + {6^2} = 36 + 36 = 72\\ \Rightarrow x = \sqrt {72} \end{array}\)
تهیه کنندگان: شهریار ارم و ندا بهرامی نیا
جزوات جامع پایه هشتم
جزوه جامع ریاضی هشتم فصل 1 عددهای صحیح و گویا
جزوه جامع ریاضی هشتم فصل 2 عددهای اول
جزوه جامع ریاضی هشتم فصل 3 چندضلعی ها
جزوه جامع ریاضی هشتم فصل 4 جبر و معادله
جزوه جامع ریاضی هشتم فصل 5 بردار و مختصات
جزوه جامع ریاضی هشتم فصل 6 مثلث
جزوه جامع ریاضی هشتم فصل 7 توان و جذر
جزوه جامع ریاضی هشتم فصل 8 آمار و احتمال
جزوه جامع ریاضی هشتم فصل 9 دایره
شکل های هم نهشت
شکل های هم نهشت
اگر بتوانیم شکلی را با یک یا چند تبدیل (انتقال تقارن و دوران) بر شکل دیگری منطبق کنیم طوری که کاملا یکدیگر را بپوشانند میگوییم آن دو شکل هم نهشتند در واقع دو شکل هم نهشت با هم قابل انطباق اند.
مثال 1 دو شکل A و B با انتقال بر هم منطبق می شوند.
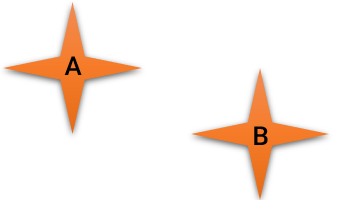
مثال ۲ دو شکل E و F با تقارن محوری نسبت به خط d بر هم منطبق می شوند .
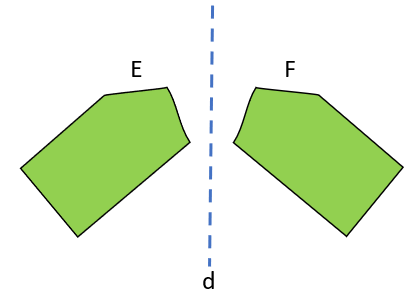
برای نشان دادن هم نهشتی بین دو شکل از علامت\( \cong \) استفاده می کنیم به طور مثال در بالا داریم:
\(E \cong F{\rm{ }},{\rm{ }}A \cong B\)
اجزاء متناظر
اضلاع و زاویه هایی هستند که در هر دو شکل هم نهشت با هم برابرند.
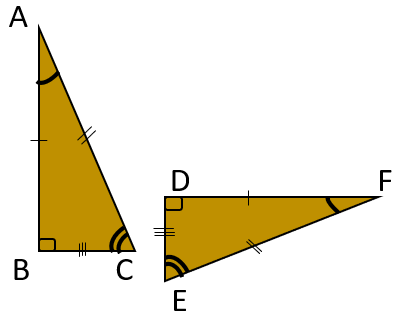
مثال دو مثلث ABC و DEF با دوران بر هم منطبق می شوند. اجزاء متناظر در این دو شکل عبارتند از :
\(A\mathop B\limits^\Delta C \cong D\mathop E\limits^\Delta F \Rightarrow \left\{ \begin{array}{l}\overline {AB} = \overline {DF} ,\hat A = \hat F\\\overline {AC} = \overline {EF} ,\hat B = \hat D\\\overline {BC} = \overline {DE} ,\widehat C = \hat E\end{array} \right.\)
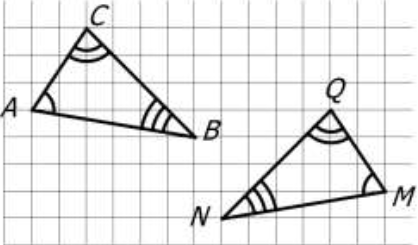
در شکل داده شده دو مثلث هم نهشتند تساوی اجزای متناظر را بنویسید.
\(A\mathop B\limits^\Delta C \cong M\mathop N\limits^\Delta Q \Rightarrow \left\{ \begin{array}{l}\overline {AB} = \overline {MN} ,\widehat A = \hat M\\\overline {AC} = \overline {QM} ,\widehat B = \widehat N\\\overline {BC} = \overline {QN} ,\widehat C = \widehat Q\end{array} \right.\)
دقت کنیم محیط یا مساحت دو شکل هم نهشت با هم برابرند ولی برعکس این جمله صحیح نیست.
یعنی اگر محیط یا مساحت دو شکل برابر باشد ممکن است آن دو شکل هم نهشت نباشند.
به این دو مثال دقت کنید.
مثال (الف) مساحت مربعی به ضلع ۴ و مستطیلی به ابعاد ۲ و ۸ با هم برابر است.ولی این دو شکل هم نهشت نیستند.
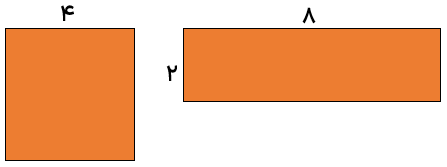
مثال (ب) محیط این لوزی و مربع هر دو برابر است ولی هم نهشت نیستند.
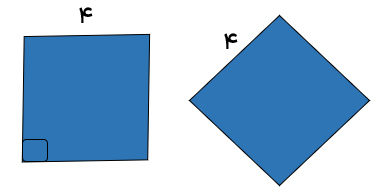
به کمک هم نهشتی دو مثلث و تساوی اجزاء آنها میتوان مقادیر مجهول را محاسبه نمود.
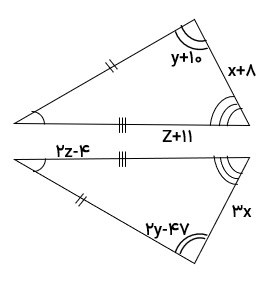
دو مثلث داده شده با تقارن محوری بر هم منطبق میشوند با توجه به اندازه های داده شده مقادیر مجهول را بیابید.
با توجه به تناظر بین اضلاع و زاویه ها داریم:
\(\begin{array}{l}3x = x + 8 \Rightarrow 2x = 8 \Rightarrow x = 4\\2y - 47 = y + 10 \Rightarrow y = 10 + 47 \Rightarrow y = 57\\2z - 4 = z + 11 \Rightarrow 2z - {\rm{z = 11 + 4}} \Rightarrow z = 15\end{array}\)
دو مثلث مقابل هم نهشتند محیط هر کدام چقدر است؟
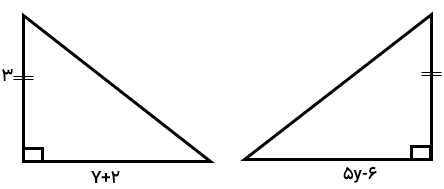
با توجه به تناظر اضلاع دو مثلث داریم
\(5y - 6 = y + 2 \Rightarrow 4y = 2 + 6 = 8 \Rightarrow y = \frac{8}{4} = 2\)
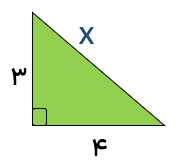
با جایگزین کردن مقدار ۲ = y در هر کدام از روابط بالا اندازه ی ضلع دوم مثلث را محاسبه می کنیم\(5 \times 2 - 6 = 10 - 6 = 4\) پس دو ضلع زاویه ی قائمه در این مثلث ۳ و ۴ هستند. به کمک رابطه ی فیثاغورس داریم:
\({x^2} = {4^2} + {3^2} = 16 + 9 = 25 \Rightarrow x = \sqrt {25} = 5\)
بنابراین محیط این دو مثلث برابر است با ۱۲ = ۳ + ۴ + ۵ = p
تهیه کنندگان:شهریار ارم و ندا بهرامی نیا
هم نهشتی مثلث ها
هم نهشتی مثلث ها
برای اینکه نشان دهیم دو مثلث هم نهشت هستند می توانیم از یکی از حالت های زیر استفاده کنیم و لازم نیست برابری تمامی اضلاع و زاویه ها بررسی گردد.
1- برابری سه ضلع ( ض ض ض )
2- برابری دو ضلع و زاویه ی بین آن ها ( ض ز ض )
3- برابری دو زاویه و ضلع بین آن ها ( ز ض ز )
4- برابری وتر و یک ضلع زاویه ی قائمه در مثلث قائم الزاويه ( و ض )
5- برابری وتر و یک زاویه ی تند از مثلث قائم الزاویه ( و ز )
تهیه کنندگان: شهریار ارم و ندا بهرامی
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه هشتم- آزمون آنلاین تمامی دروس پایه هشتم
- گام به گام تمامی دروس پایه هشتم
- ویدئو های آموزشی تمامی دروس پایه هشتم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه هشتم
- فلش کارت های آماده دروس پایه هشتم
- گنجینه ای جامع از انشاء های آماده پایه هشتم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه هشتم
برابری سه ضلع ( ض ض ض )
برابری سه ضلع ( ض ض ض )
اگر سه ضلع از مثلث اول با اضلاع مثلث دوم دو به دو با هم برابر باشند آن دو مثلث حتما هم نهشت هستند.
مثال
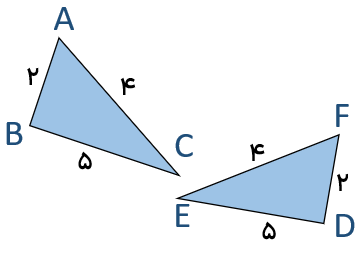
آیا دو مثلث ABC و DEF هم نهشتند؟
\(\left. \begin{array}{l}\overline {AB} = \overline {FD} = 2\\\overline {AC} = \overline {EF} = 4\\\overline {BC} = \overline {ED} = 5\end{array} \right\} \Rightarrow A\mathop B\limits^\Delta C \cong F\mathop D\limits^\Delta E\) بنا به حالت (ض ض ض)
مثال
مثلث ABC متساوی الساقین و AM میانه ی وارد بر قاعده BC است . چرا دو مثلث ABM و ACMهم نهشتند؟
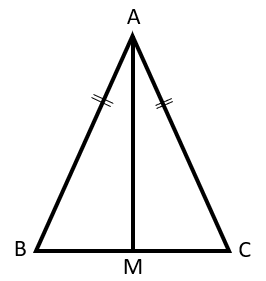
ابتدا توجه کنیم که میانه قاعده را به دو قسمت مساوی تقسیم می کند بنابراین داریم
\(\overline {AB} = \overline {AC} \) :زیرا مثلث متساوی الساقین است
\(\overline {BM} = \overline {CM} \) :زیرا AM میانه است
\(\overline {AM} = \overline {AM} \) :زیرا ضلع مشترک دو مثلث است
بنا به حالت (ض ض ض)\(\left. \begin{array}{l}\overline {AB} = \overline {AC} \\\overline {BM} = \overline {CM} \\\overline {AM} = \overline {AM} \end{array} \right\} \Rightarrow A\mathop B\limits^\Delta M \cong A\mathop C\limits^\Delta M\)
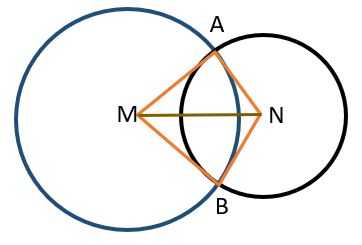
نقاط M و N مرکز دو دایره هستند چرا دو مثلث AMN و BMN هم نهشتند؟
دقت کنیم در یک دایره شعاع ها با هم برابرند.
بنابراین :
چون شعاع دایره بزرگ هستند : AM = BM
\( \Rightarrow {\rm A}\mathop {\rm M}\limits^\Delta {\rm N} \cong {\rm B}\mathop {\rm M}\limits^\Delta {\rm N}\) چون شعاع دایره کوچک هستند : AN = BN
چون ضلع مشترک دو مثلث است : MN = M
تهیه کنندگان: شهرام ارم و ندا بهرامی
جزوات جامع پایه هشتم
جزوه جامع ریاضی هشتم فصل 1 عددهای صحیح و گویا
جزوه جامع ریاضی هشتم فصل 2 عددهای اول
جزوه جامع ریاضی هشتم فصل 3 چندضلعی ها
جزوه جامع ریاضی هشتم فصل 4 جبر و معادله
جزوه جامع ریاضی هشتم فصل 5 بردار و مختصات
جزوه جامع ریاضی هشتم فصل 6 مثلث
جزوه جامع ریاضی هشتم فصل 7 توان و جذر
جزوه جامع ریاضی هشتم فصل 8 آمار و احتمال
جزوه جامع ریاضی هشتم فصل 9 دایره
برابری دو ضلع و زاویه ی بین آن ها ( ض ز ض )
برابری دو ضلع و زاویه ی بین آن ها ( ض ز ض )
اگر دو ضلع از مثلث اول با دو ضلع از مثلث دوم برابر و زاویه ی بین آن دو ضلع در هر دو مثلث برابر باشد، آن دو مثلث حتما هم نهشت هستند.
مثال
آیا دو مثلث زیر هم نهشتند؟
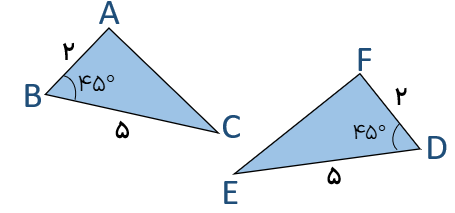
بله، بنا به حالت ( ض ز ض)
\(\left. \begin{array}{l}\overline {AB} {\rm{ }} = {\rm{ }}F\overline D = 2\\\overline B {\rm{ }} = {\rm{ }}\bar D = 45^\circ \\\overline {BC} {\rm{ }} = {\rm{ }}\overline {ED} {\rm{ }} = 5\end{array} \right\} \Rightarrow A\mathop B\limits^\Delta C \cong F\mathop D\limits^\Delta E\) بنا به حالت (ض ز ض)
مثال
مثلث ABC متساوی الساقین و AM نیمساز زاویه ی A است چرا دو مثلث ABM وACMهم نهشتند؟
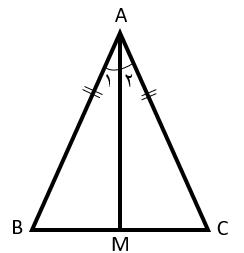
ابتدا توجه کنیم که نیم ساز زاویه ی A را به دو قسمت مساوی تقسیم می کند بنابراین داریم:
زیرا مثلث متساوی الساقین است\(\overline {AB} = \overline {AC} \)
زیرا AM نیمساز \(\widehat A\) است \({\widehat A_1} = {\widehat A_2}\)
زیرا ضلع مشترک دو مثلث است\(\overline {AM} = \overline {AM} \)
\(\left. \begin{array}{l}\overline {AB} = \overline {AC} \\{\widehat A_1} = {\widehat A_2}\\\overline {AM} = \overline {AM} \end{array} \right\} \Rightarrow A\mathop B\limits^\Delta M \cong A\mathop C\limits^\Delta M\) بنا به حالت (ض ز ض)
نقطه ی O مرکز دایره و AC و BD قطر های دایره هستند. چرا دو مثلث OAB و OCD هم نهشتند؟
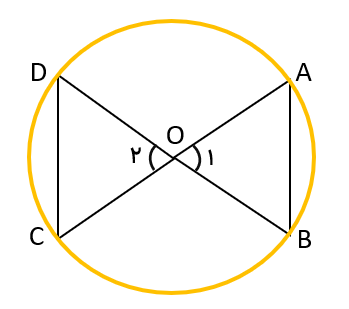
دقت کنیم به زوایایی مانند دو زاویه ی ۱ و ۲ متقابل به راس می گویند و دو زاویه ی متقابل به راس همیشه با هم برابرند. بنابراین داریم:
\(\left. \begin{array}{l}\overline {OB} = \overline {OC} \\{\widehat O_1} = {\widehat O_2}\\\overline {OA} = \overline {OD} \end{array} \right\} \Rightarrow O\mathop A\limits^\Delta B \cong O\mathop D\limits^\Delta C\) بنا به حالت (ض ز ض)
دقت کنیم در این حالت (ض ز ض) زاویه ی مساوی باید حتما بین دو ضلع متناظر قرار داشته باشد.
تهیه کنندگان:شهریار ارم و ندا بهرامی نیا
برابری دو زاویه و ضلع بین آن ها ( ز ض ز )
برابری دو زاویه و ضلع بین آن ها ( ز ض ز )
اگر دو زاویه از مثلث اول با دو زاویه از مثلث دوم برابر و ضلع بین آن دو زاویه در هر دو مثلث برابر باشد، آن دو مثلث حتما هم نهشت هستند.
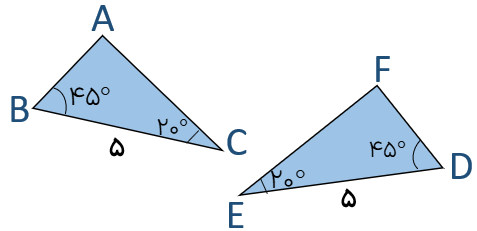
مثال : دو مثلث زیر هم نهشتند زیرا :
\(\left. \begin{array}{l}\widehat B = \widehat D = 45^\circ \\\overline {BC} = \overline {ED} = 5\\\widehat C = \widehat E = 20^\circ \end{array} \right\} \Rightarrow A\mathop B\limits^\Delta C \cong F\mathop D\limits^\Delta E\) بنا به حالت (ز ض ز)
مثال
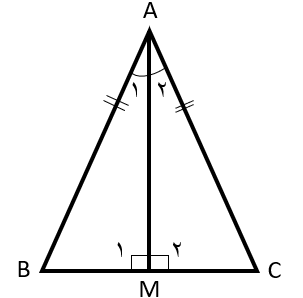
در مثلث ABC پاره خط AM نیمساز زاویه ی A و بر BC عمود است چرا دو مثلث ABM و ACMهم نهشتند؟
ابتدا توجه کنیم که نیم ساز AM زاویه A را به دو قسمت مساوی تقسیم می کند.و چون بر قاعده یBCعمود است زوایای M و M قائمه هستند.بنابراین داریم:
زیرا AM برBC عمود است \({\widehat M_1} = \widehat {{M_2}}\)
زیرا AMنیمساز A است. \(\widehat {{A_1}} = \widehat {{A_2}}\)
زیرا ضلع مشترک دو مثلث است.\(\overline {AM} = \overline {AM} \)
\(\left. \begin{array}{l}{\widehat M_1} = \widehat {{M_2}} = 90^\circ \\\widehat {{A_1}} = \widehat {{A_2}}\\\overline {AM} = \overline {AM} \end{array} \right\} \Rightarrow A\mathop B\limits^\Delta M \cong A\mathop C\limits^\Delta M\)
مثال
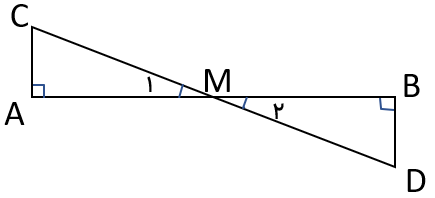
نقطه ی M وسط پاره خط AB است چرا دو مثلث ACM و BDM هم نهشتند؟
\({\widehat M_1} = \widehat {{M_2}}\) : زیرا متقابل به راس هستند
\(\overline {AM} = \overline {MB} \) :زیرا M وسط پاره خط ABاست.
\(\left. \begin{array}{l}{\widehat M_1} = \widehat {{M_2}}\\\widehat A = \widehat B = 90^\circ \\\overline {AM} = \overline {MB} \end{array} \right\} \Rightarrow A\mathop C\limits^\Delta M \cong B\mathop D\limits^\Delta M\)
دقت کنیم اگر ضلع بین دو زاویهی مساوی نباشد دو مثلث هم نهشتند زیرا در صورت تساوی دو زاویه در دو مثلث ، زوایای سوم نیز با هم برابرند و به حالت سوم دو مثلث هم نهشت خواهند بود. برای درک بیشتر به مثال زیر دقت کنید.
در این دو مثلث دو زاویه مساوی وجود دارد بنابر این زاویه ی سوم در هر دو مثلث برابر است با:
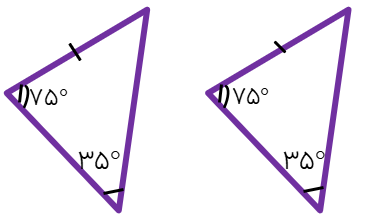
پس زاویه سوم در هر دو مثلث ۷۰ درجه است و ضلع متناظر بین دو زاویه ی مساوی در دو مثلث دو زاویه ی ۷۰ و ۷۵ درجه قرار میگیرد و بنا به حالت سوم دو مثلث هم نهشتند.
تهیه کنندگان:شهریار ارم و ندا بهرامی نیا
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه هشتم- آزمون آنلاین تمامی دروس پایه هشتم
- گام به گام تمامی دروس پایه هشتم
- ویدئو های آموزشی تمامی دروس پایه هشتم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه هشتم
- فلش کارت های آماده دروس پایه هشتم
- گنجینه ای جامع از انشاء های آماده پایه هشتم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه هشتم
هم نهشتی مثلث های قائم الزاویه
هم نهشتی مثلث های قائم الزاویه
مثال
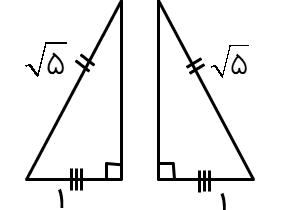
در شکل زیر وتر و یک ضلع از هر دو مثلث با هم برابرند با توجه به شکل های داده شده اندازه ی ضلع سوم در هر مثلث را محاسبه کنید و اندازه ی ضلع سوم را با هم مقایسه کنید.
اگر ضلع سوم را a در نظر بگیریم بنا به رابطه ی فیثاغورس در هر دو مثلث داریم:
\({a^2} = {(\sqrt 5 )^2} - {1^2} = 5 - 1 = 4 \to a = \sqrt 4 = 2\)
با مقایسه متوجه میشویم که اندازه ی ضلع سوم در هر دو مثلث ۲ واحد است. دقت کنیم که دو مثلث هم نهشتند.(به دلیل داشتن سه ضلع مساوی)
طبق مثال بالا برای مثلث های قائم الزاویه علاوه بر سه حالت قبل میتوان حالت هم نهشتی زیر را در نظر گرفت.
تهیه کنندگان:شهریار ارم و ندا بهرامی نیا
جزوات جامع پایه هشتم
جزوه جامع ریاضی هشتم فصل 1 عددهای صحیح و گویا
جزوه جامع ریاضی هشتم فصل 2 عددهای اول
جزوه جامع ریاضی هشتم فصل 3 چندضلعی ها
جزوه جامع ریاضی هشتم فصل 4 جبر و معادله
جزوه جامع ریاضی هشتم فصل 5 بردار و مختصات
جزوه جامع ریاضی هشتم فصل 6 مثلث
جزوه جامع ریاضی هشتم فصل 7 توان و جذر
جزوه جامع ریاضی هشتم فصل 8 آمار و احتمال
جزوه جامع ریاضی هشتم فصل 9 دایره
برابری وتر و یک ضلع زاویه ی قائمه ( و ض )
برابری وتر و یک ضلع زاویه ی قائمه در مثلث قائم الزاويه ( و ض )
دقت کنیم این حالت فقط مخصوص مثلث های قائم الزاویه است.
مثال
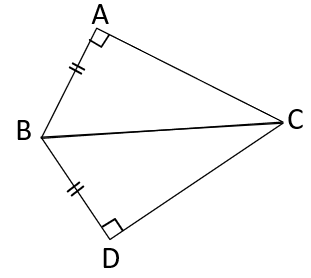
با توجه به شکل داده شده چرا دو مثلث ABC و DBC هم نهشتند؟ ( طبق شکل\(\overline {AB} = \overline {DB} \) )
با توجه به این که دو مثلث قائم الزاویه هستند و وتر هر دوی آن ها BC است داریم:
\(\left. \begin{array}{l}\widehat A = \widehat D = 90^\circ \\\overline {BC} = \overline {BC} \\\overline {AB} = \overline {DB} \end{array} \right\} \Rightarrow A\mathop B\limits^\Delta C \cong D\mathop B\limits^\Delta C\) بنا به حالت (وتر و یک ضلع)
مثال
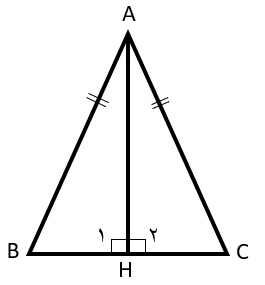
مثلث ABC متساوی الساقین و AH ارتفاع آن است. چرا دو مثلث ABH وACH هم نهشتند؟
ابتدا توجه کنیم چون AH ارتفاع است پس دو مثلث ABH و ACH قائم الزاویه هستند و AB و AC در دو مثلث وتر هستند.
\(\overline {AH} \) :ضلع مشترک دو مثلث است
\(\left. \begin{array}{l}\widehat {{H_1}} = {\widehat H_2} = 90^\circ \\\overline {AB} = \overline {AC} \\\overline {AH} \end{array} \right\} \Rightarrow A\mathop B\limits^\Delta C \cong D\mathop B\limits^\Delta C\) بنا به حالت (وتر و یک ضلع)
مثال
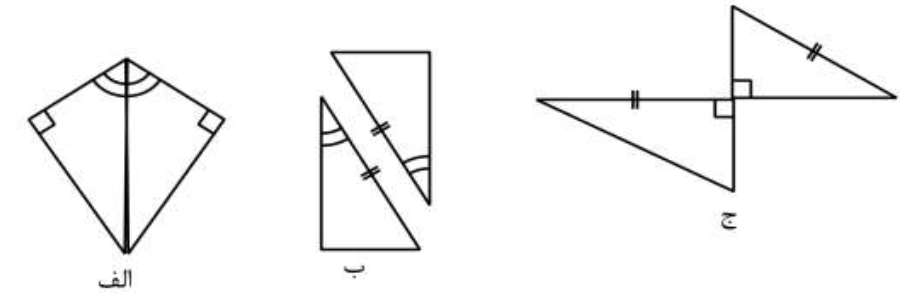
با توجه به اطلاعات داده شده برای هم نهشتی کدام مثلث ها دلایل کافی داریم؟
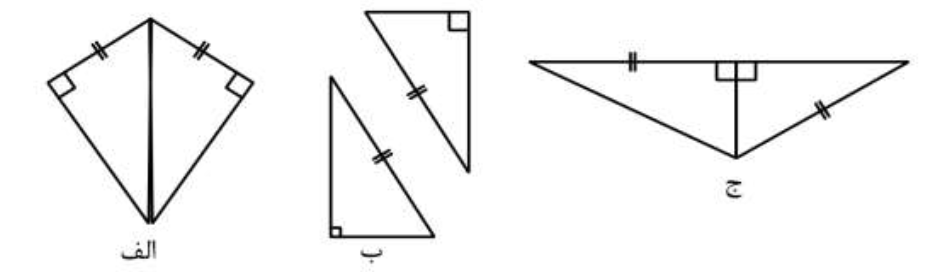
الف) دو مثلث وتر مشترک دارند و یک ضلع زاویه ی قائمه در هر دو مثلث با هم برابرند.
بنابراین به حالت وتر و یک ضلع که برای خلاصه تر شدن به صورت )و ض) نوشته می شود،هم نهشتند.
ب) وتر دو مثلث قائم الزاویه در هر دو برابر است ولی در مورد تساوی اضلاع دیگر اطلاعات مساله کافی نیست.
پس در این حالت دو مثلث هم نهشت نیستند.
ج) دو مثلث قائم الزاویه هستند و یک ضلع زاویهی قائمه در هر دو مشترک است ولی اضلاعی که با هم مساوی هستند و تساوی آنها با علامت مشخص شده در یکی از مثلثها وتر و در دیگری ضلع زاویه ی قائمه است. پس دو مثلث هم نهشت نیستند.
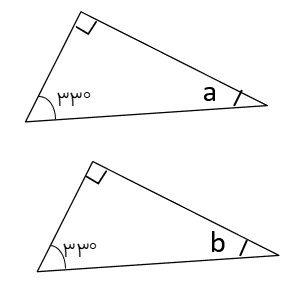
در شکل زیر وتر و یک زاویه ی تند از دو مثلث با هم برابرند با توجه به اندازه های داده شده اندازه ی a و b را در هر مثلث محاسبه کنید. پاسخ در مثلث قائم الزاویه دو زاویه تند متمم یکدیگرند( یعنی مجموع دو زاویه ی تند ۹۰ درجه است.) بنابراین برای محاسبه ی a یا b کافی است اندازه ی زاویه ی تند دیگر را از ۹۰ درجه کم کنیم. پس:
\(a = b = 90^\circ - 32^\circ = 58^\circ \)
دقت کنیم که دو مثلث هم نهشتند(به دلیل داشتن دو زاویه و ضلع بین آن ها)
تهیه کنندگان:شهریار ارم و ندا بهرامی نیا
برابری وتر و یک زاویه ی تند ( و ز )
برابری وتر و یک زاویه ی تند از مثلث قائم الزاویه ( و ز )
دقت کنیم این حالت هم مانند حالت قبل فقط مخصوص مثلث های قائم الزاویه است.
مثال
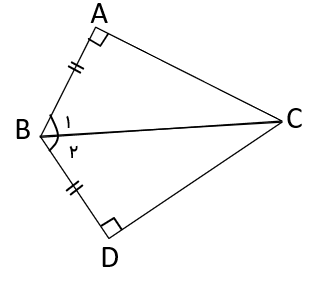
در شکل داده شده BC نیمساز زاویه ی B است چرا دو مثلث ABC و DBC هم نهشتند؟
با توجه به این که دو مثلث قائم الزاویه هستند و وتر هر دوی آن ها BC است داریم
\(\left. \begin{array}{l}\widehat A = \widehat D = 90^\circ \\\overline {BC} = \overline {BC} \\\widehat {{B_1}} = \widehat {{B_2}}\end{array} \right\} \Rightarrow A\mathop B\limits^\Delta C \cong D\mathop B\limits^\Delta C\) بنا به حالت (وتر و یک زاویه تند)
مثال
با توجه به اطلاعات داده شده برای هم نهشتی کدام مثلث ها دلایل کافی داریم؟
الف دو مثلث وتر مشترک دارند و یک زاویه ی تند در هر دو مثلث با هم برابرند. بنا بر این به حالت وتر و یک زاویه ی تند دو مثلث هم نهشتند.
ب یک ضلع و یک زاویه در هر دو مثلث برابرند ولی در مورد تساوی اجزای دیگر اطلاعات مساله کافی نیست، پس در این حالت دو مثلث هم نهشت نیستند.
ج دو مثلث قائم الزاویه هستند و و ترهای دو مثلث برابرند ولی اطلاعات سوال در مورد تساوی دیگر اجزاء کافی نیست.پس دو مثلث هم نهشت نیستند.
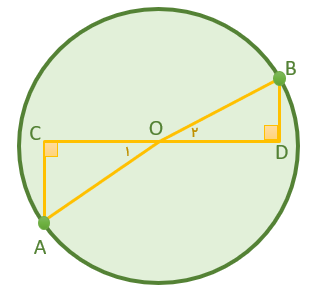
در شکل مقابل AB قطر دایره است چرا دو مثلث OAC و OBD هم نهشتند؟
دقت کنیم A و OB شعاع دایره و و ترهای این دو مثلث قائم الزاویه هستند پس برای نشان دادن هم نهشتی دو مثلث از حالتهای مخصوص مثلث قائم الزاویه با داشتن وتر مساوی استفاده میکنیم داریم:
\(\left. \begin{array}{l}\widehat C = \widehat D = 90^\circ \\\widehat {{O_1}} = \widehat {{O_2}}\\\overline {OA} = \overline {OB} \end{array} \right\} \Rightarrow O\mathop A\limits^\Delta C \cong O\mathop B\limits^\Delta D\) بنا به حالت (وتر و یک زاویه ی تند)
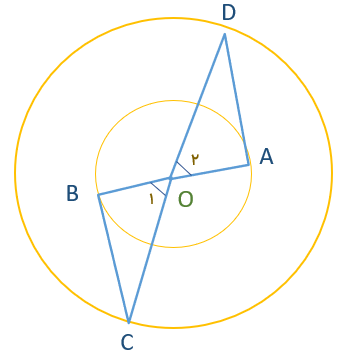
دو دایره ی داده شده هم مرکز هستند و چرا دو مثلث OAD و OBC هم نهشتند؟
دقت کنیم OA و OB شعاعهای دایره ی کوچک و OC و OD شعاع های دایره ی بزرگ هستند و دو زاویه ی o متقابل به راس هستند. بنابراین داریم:
\(\left. \begin{array}{l}\overline {OA} = \overline {OD} \\\widehat {{O_1}} = \widehat {{O_2}}\\\overline {OB} = \overline {OA} \end{array} \right\} \Rightarrow O\mathop B\limits^\Delta C \cong O\mathop A\limits^\Delta D\) بنا به حالت (ض ز ض)
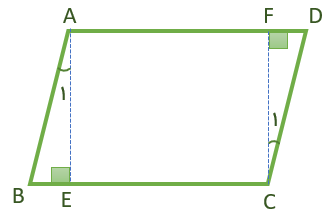
چهار ضلعی ABCD متوازی الاضلاع و AE و CF بر قاعده های آن عمودند.
الف) چرا دو مثلث ABE و CDF هم نهشتند؟
می دانیم در هر متوازی الاضلاع اضلاع و زاویه های رو به رو دو به دو با هم برابرند، از طرفی دو مثلث قائم الزاویه و AB و CD و ترهای آن هستند. پس داریم:
\(\overline {AB} = \overline {CD} \) : وتر
\(\widehat B = \widehat D\) :دو زاویه تند
\(\left. \begin{array}{l}\widehat E = \widehat F = 90^\circ \\\overline {AB} = \overline {CD} \\\widehat B = \widehat D\end{array} \right\} \Rightarrow A\mathop B\limits^\Delta E \cong C\mathop D\limits^\Delta F\) بنا به حالت (وتر و یک زاویه تند)
ب( با توجه به قسمت الف و هم نهشتی دو مثلث تساوی های زیر را کامل کنید.
\(\begin{array}{l}\overline {AE} = ...{\rm{ }}\\\\\overline {FD} = ...{\rm{ }}\\\\{\widehat A_1} = ...\end{array}\)
\(\begin{array}{l}\overline {AE} = \overline {FC} \\\\\overline {FD} = \overline {BE} {\rm{ }}\\\\{\widehat A_1} = {\widehat C_1}\end{array}\)
تهیه کنندگان:شهریار ارم و ندا بهرامی نیا
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه هشتم- آزمون آنلاین تمامی دروس پایه هشتم
- گام به گام تمامی دروس پایه هشتم
- ویدئو های آموزشی تمامی دروس پایه هشتم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه هشتم
- فلش کارت های آماده دروس پایه هشتم
- گنجینه ای جامع از انشاء های آماده پایه هشتم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه هشتم



1736019749.png)