درسنامه کامل فیزیک دهم ریاضی فصل 2 ویژگی های فیزیکی مواد
تعداد بازدید : 7.27Mخلاصه نکات فیزیک دهم ریاضی فصل 2 ویژگی های فیزیکی مواد - درسنامه شب امتحان فیزیک دهم ریاضی فصل 2 ویژگی های فیزیکی مواد - جزوه شب امتحان فیزیک دهم ریاضی نوبت اول فصل 2 ویژگی های فیزیکی مواد
حالات ماده
حالات ماده
ساختار ماده
ابعاد
- اتم (\({10^{ - 10}}m\)) است.
- مولکول (\({10^{ - 9}}m\)) است.
- هسته اتم در حدود (\({10^{ - 15}}m\)) است.
حالت ماده به چگونگی حرکت ذره های سازنده مواد و اندازه نیروی بین آنها بستگی دارد.
حالت های ماده
جامد ها
مایع ها
گاز ها
پلاسما
جامد
نیروی بین مولکولی در جامد ها، مانند فنر عمل می کند. این نیرو نمی گذارد تا مولکول ها از یک فاصله ی معین نسبت به هم دورتر یا نزدیک تر شوند.
وقتی جامد مانند یک تکه آهن، گرما می گیرد محدوده و دامنه این نوسان ها بیشتر می شود و جسم جامد منبسط می شود.
جامد ها در دو نوع تقسیم بندی می شوند:
الف) جامد بلورین
ب) جامد بی شکل (آمورف)
الف) جامد بلورین:
اتم های برخی از جامد ها در طرح های منظمی کنار هم قرار می گیرند. جامد هایی را که در یک الگوی سه بعدی تکرار شونده از این واحد های منظم ساخته می شود.
نحوه تشکیل جامدات بلورین:
وقتی مایع به آرامی سرد شود، مولکول های مایع فرصت پیدا می کنند که به شکل منظم و ثابتی به خود بگیرند.
مانند: فلزات، نمک ها، الماس، یخ و بیشتر مواد معدنی
ب) جامد بی شکل (آمورف)
مولکول های این جامد در طرح های منظمی قرار نمی گیرند و اصطلاحا به صورت درهم و بی شکل هستند.
نحوه تشکیل جامدات بی شکل:
وقتی مایعی به سرعت سرد شود مولکول های مایع دیگر فرصت ندارند که شکل منظم و ثابتی به خود بگیرند.
مانند: شیشه، چوب، پنبه، عاج
ویژگی مایع ها
1) فاصله مولکول ها در حالت مایع نسبت به حالت جامد آن بیشتر است.
2) مولکول های مایع آزادانه با اطراف حرکت می کنند. همچنین بر روی هم می لغزند.
3) مایع ها تقریبا تراکم ناپذیرند و در نتیجه حجم آنها ثابت است.
اگر فاصله مولکول ها از حدی کمتر شوند نیروی بین مولکولی، دافعه و اگر از حدی بیشتر باشد جاذبه می شوند.
ویژگی گازها
- فاصله مولکول ها حدود چند ده برابر (A35) فاصله مولکول ها در مایع و جامد است. و مولکول ها آزادانه به اطراف حرکت می کنند.
- تراکم پذیرند.
- انرژی جنبشی مولکول های گاز بسیار زیاد است.
علت پخش محلول (نمک و جوهر)
به دلیل حرکت های نامنظم و کاتوره ای (تصادفی) مولکول های آب و برخورد آنها با ذرات سازنده نمک و جوهر، این گونه مواد در آب پخش می شوند.
حرکت بروانی:
حرکت ذره های دود به طور نامنظم و درهم و برهم (کاتوره ای) و در یک مسیر زیگزاگی را حرکت براونی می نامند.
نیروی بین مولکولی در جامدات بیشتر از مایعات و نیروی بین مولکولی در مایعات بیشتر از گاز ها است.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه ریاضی- آزمون آنلاین تمامی دروس پایه ریاضی
- گام به گام تمامی دروس پایه ریاضی
- ویدئو های آموزشی تمامی دروس پایه ریاضی
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ریاضی
- فلش کارت های آماده دروس پایه ریاضی
- گنجینه ای جامع از انشاء های آماده پایه ریاضی
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ریاضی
نیروی بین مولکولی
نیروی بین مولکولی
انواع نیروی بین مولکولی:
- نیروی هم چسبی
- نیروی دگر چسبی
1) نیروی هم چسبی
نیروی جاذبه بین مولکول های همسان است.
مانند نیروی بین مولکول های یک قطره آب یا جیوه
2) نیروی دگر چسبی
نیروی جاذبه بین مولکول های ناهمسان است.
مانند نیروی بین مولکولی بین سطح شیشه و آبی که روی آن ریخته شده است.
نیروی کشش سطحی
به علت هم چسبی مولکول های سطح مایع، سطح یک ماده مانند یک پوسته تحت کشسان عمل می کند، این رفتار سطح را کشش سطحی می گویند.
1 در سطح مایع به دلیل تغییر از وضعیت مایع به بخار فاصله بین مولکول ها افزایش و نیرو های بین مولکولی به صورت جاذبه (سطح مایع تحت کشش) ظاهر می شود.
2 افزایش دما موجب کاهش نیروی هم چسبی و دگر چسبی می شود.
لوله های مویین:
لوله هایی معمولا از جنس شیشه با قطر های مختلف بسیار نازک که هر دو سر آنها باز می باشد. (قطر داخلی آنها حدود یک میلی متر است.)
مویینگی:
به بالا رفتن وپایین آمدن مایع ها از لوله های بسیار باریک را مویینگی می گوییم.
1 چون جهت نیرویی که سطح لوله مویین به آب وارد می کند به سمت بالا است. در نتیجه آب درون لوله بالا می رود و سطح آب درون لوله به صورت فرورفتگی است.
2 ارتفاع مایع درون لوله با شعاع لوله و چگالی مایع نسبت وارون دارد.
3 چون جهت نیرویی که سطح لوله مویین به جیوه وارد می کند به سمت پایین است. در نتیجه جیوه درون لوله پایین می رود و سطح آب درون لوله به صورت برآمدگی است.
جزوات جامع پایه ریاضی
جزوه جامع فیزیک دهم ریاضی فصل 1 فیزیک و اندازه گیری
جزوه جامع فیزیک دهم ریاضی فصل 2 ویژگی های فیزیکی مواد
جزوه جامع فیزیک دهم ریاضی فصل 3 کار، انرژی و توان
جزوه جامع فیزیک دهم ریاضی فصل 4 دما و گرما
جزوه جامع فیزیک دهم ریاضی فصل 5 ترمودینامیک
فشار در شاره های ساکن
فشار در شاره های ساکن
فشار متوسط:
بزرگی نیروی عمودی که بر واحد سطح جسم وارد می شود.
فرمول فشار (P)
\(P = \frac{{{F_ \bot }}}{A}\)
که در فرمول (P) به معنای فشار
(\({F_ \bot }\)) به معنای نیروی عمودی
و (A) به معنای مساحت سطح است.
1 یکای فشار در SI به صورت نیوتن بر متر مربع (\(\frac{N}{{{m^2}}}\)) است که به آن در اصطلاح پاسکال، (Pa) گفته می شود.
2 فشار کمیتی نرده ای می باشد و فاقد جهت و راستا است.
مثال
اگر انگشتتان را روی سطح میز طوری قرار دهیم که سطح تماس حدود\(1c{m^2}\) باشد، چه نیروی باید وارد کنیم تا فشار در محل انگشتتان تقریبا \(1 \times {10^5}Pa\) باشد؟
\(\begin{array}{l}A = 1c{m^2} = 1 \times {10^{ - 4}}{m^2}\\F = ?\\P = {10^5}Pa\\ \to P = \frac{F}{A} \to F = PA \to F = {10^5} \times {10^{ - 4}} = 10N\end{array}\)
اختلاف فشار ستون شاره در دو سطح شاره های یکسان:
نیروی وارد بر سطح 2 برابر با حاصل جمع وزن مایع بین دو سطح و نیروی وارد از ظرف سطح 1 می باشد.
\({P_2} = {P_1} + \rho gh\)
فشار در مایع ها به شکل ظرف بستگی ندارد.
قانون هم فشاری:
فشار نقاط هم تراز درون یک مایع یکسان است.
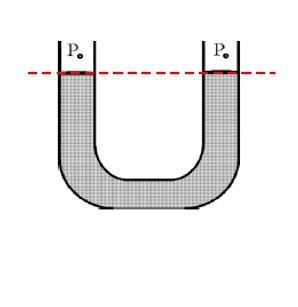
اختلاف فشار مایع در دو سطح به عوامل زیر بستگی دارد:
- با عمق مایع (ارتفاع از سطح آب) نسبت مستقیم دارد.
- با چگالی مایع نسبت مستقیم دارد.
- با شتاب گرانش (زمین، ماه) رابطه ی مستقیم دارد.
فشار مایع ها به چه عواملی بستگی ندارد:
- با وزن مایع
- به اندازه ی مساحت قاعده ظرف
- به شکل ظرف
مثال
جسمی مکعبی به طول ضلع \(20cm\) درون شاره ای غوطه ور و در حال تعادل است. فشار در بالا و زیر جسم برابر 105 و \(106/8\) کیلو پاسکال است. چگالی شاره چند کیلوگرم بر متر مکعب است؟
\(\begin{array}{l}h = 20cm = 0/2m\\{P_1} = 105KPa = 105000Pa\\{P_2} = 106/8KPa = 106000Pa\\g = 10\frac{N}{{Kg}}\\\rho = ?\\{P_2} = {P_1} + \rho gh \to 106000 = 105000 + \rho \times 10 \times 0/2\\ \to 1800 = 2\rho \to \rho = 900\frac{{Kg}}{{{m^3}}}\end{array}\)
عامل وجود فشار هوا
1) بر جسم های روی زمین:
نیروی وزن هوای اطراف زمین است.
2) در ظرف بسته:
عامل فشار، جنبش مولکولی گاز است.
فشار کل در عمق h درون یک شاره، از جمع فشار هوا با فشار ارتفاع ستون مایع، فشار کل درون ظرف، بدست می آید.
\(P = \rho gh + {P_0}\)
در این فرمول:
(P) فشار کل در مایع،
(\(\rho \)) چگالی مایع،
(g) شتاب گرانش،
(h) ارتفاع ستون مایع
و (\({P_0}\)) فشار هوا است.
مثال
فشار آب در عمق 3 متری از سطح آزاد آن، چند پاسکال است؟
\(\begin{array}{l}P = ?\\\rho = 1000\frac{{Kg}}{{{m^3}}}\\g = 10\frac{N}{{Kg}}\\h = 3m\\{P_0} = {10^5}Pa\\ \to P = \rho gh + {P_0} \to P = 1000 \times 10 \times 3 + {10^5}\\ \to P = 130000Pa\end{array}\)
1 هرچه از سطح زمین بالاتر برویم، به علت رقیق شدن هوا و کاهش تعداد ذره ها، فشار هوا کاهش می یابد و هرچه به سطح دریا نزدیک تر می شویم، فشار هوا افزایش می یابد.
2 تا ارتفاع 2000 متری از سطح زمین: به ازای هر 10m که از سطح زمین بالا می رویم فشار هوا تقریبا یک میلی متر جیوه کاهش می یابد.
3 چگالی آب بسیار کمتر از چگالی جیوه است.
فشار سنج توریچلی
فشار سنج توریچلی
چگونه با استفاده از جو سنج جیوه ای (بارو متر) می توان فشار هوای محیط را اندازه گرفت؟(آزمایش توریچلی)
- ابتدا یک لوله شیشه ای به طول حدود 80cm را که یک سر آن بسته است، از جیوه پر می کنیم.
- سپس دهانه لوله را محکم با انگشت گرفته و آن را درون یک ظرف محتوی جیوه واژگون می کنیم.
- با برداشتن انگشت، جیوه درون لوله کمی پایین می آید و در ارتفاعی (که متناسب با فشار هوا در محل آزمایش است) ثابت می ماند، ارتفاع ستون جیوه ی درون لوله، نشان دهنده ی فشار هوای محیط است.
فرمول برای پیدا کردن فشار هوا:
\({P_0} = \rho g{h_0}\)
با اندازه گیری ارتفاع ستون جیوه در آزمایش توریچلی \({h_0}\)، می توان فشار هوا را در محل آزمایش از رابطه ی زیر به دست می آورد.
مثال
آزمایش توریچلی را در محلی که در کنار سطح دریای آزاد است، انجام داده ایم. ارتفاع ستون جیوه 76 سانتی متر شده است. فشار هوا چند پاسکال است؟ (\(g = 9/8\frac{N}{{Kg}}\) و چگالی جیوه \(\rho = 13600\frac{{Kg}}{{{m^3}}}\))
\(\begin{array}{l}{h_0} = 76cm = 0/76m\\{\rho _{Hg}} = 13600\frac{{Kg}}{{{m^3}}}\\g = 9/8\frac{N}{{Kg}}\\{P_0} = ?\\{P_0} = {\rho _{Hg}}g{h_0} \to {P_0} = 13600 \times 9/8 \times 0/76 \to {P_0} = 101292Pa\end{array}\)
فشار هوای درون لوله به ارتفاع عمودی مایع درون لوله بستگی دارد.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه ریاضی- آزمون آنلاین تمامی دروس پایه ریاضی
- گام به گام تمامی دروس پایه ریاضی
- ویدئو های آموزشی تمامی دروس پایه ریاضی
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ریاضی
- فلش کارت های آماده دروس پایه ریاضی
- گنجینه ای جامع از انشاء های آماده پایه ریاضی
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ریاضی
فشار گازهای مخزن
فشار گازهای مخزن
علت فشار گاز ها:
به علت برخورد مداوم مولکول های گاز به جداره ظرف، فشار ایجاد می شود و هر چقدر دمای گاز بیشتر باشد، انرژی جنبشی مولکول های گاز نیز بیشتر شده و فشار آن افزایش پیدا می کند.
فشار پیمانه ای (سنجه ای) \({P_g}\)
به اختلاف فشار گاز درون مخزن و فشار هوا، فشار پیمانه ای می گویند.
فشار سنج، فشارپیمانه ای را اندازه می گیرد.
\({P_g} = P - {P_0}\)
فشار گاز ها را با فشار سنج U شل اندازه گیری می کنند.
اندازه گیری فشار گاز درون مخزن (مانومتر):
فشار سنج: لوله U شکل محتوی یک مایع است که یک سر لوله U شکل را به مخزن متصل نموده و سر دیگر آن در تماس با هوای آزاد قرار می دهند.
پس از باز کردن شیر مخزن، گاز به مایع درون لوله فشار آورده و آن را پایین می راند، در نتیجه سطح مایع در دو شاخه لوله به اندازه ارتفاع h بالا می رود. از روی همین اختلاف ارتفاع، می توان فشار گاز را حساب کرد.
فشار گاز
چون در سطح های هم تراز فشار یکسان است، خواهیم داشت:
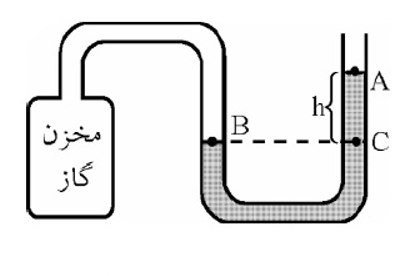
فشار نقطه B = فشار نقطه C
فشار در نقطه C = فشار ستون مایع + فشار هوا
\(\begin{array}{l}{P_B} = {P_C}\\{P_C} = \rho gh + {P_0}\\{P_B} = P\\P = \rho gh + {P_0}\\{P_g} = \rho gh\end{array}\)
در این فرمول
(P) فشار گاز
(\(\rho \)) چگالی مایع (جیوه)
(g) شتاب گرانش
(h) ارتفاع ستون مایع
(\({P_g}\)) فشار پیمانه ای
(\({P_0}\)) فشار هوا
اگر فشار مخزن کمتر از فشار هوا باشد، مایع درون لوله سمت چپ به سمت بالا می رود. در نتیجه سطح مایع در دو شاخه لوله به اندازه ارتفاع h بالا می رود، از روی همین اختلاف ارتفاع، می توان فشار گاز را حساب کرد.
\(\begin{array}{l}{P_C} = {P_B}\\{P_0} = \rho gh + P\\P = {P_0} - \rho gh\end{array}\)
جزوات جامع پایه ریاضی
جزوه جامع فیزیک دهم ریاضی فصل 1 فیزیک و اندازه گیری
جزوه جامع فیزیک دهم ریاضی فصل 2 ویژگی های فیزیکی مواد
جزوه جامع فیزیک دهم ریاضی فصل 3 کار، انرژی و توان
جزوه جامع فیزیک دهم ریاضی فصل 4 دما و گرما
جزوه جامع فیزیک دهم ریاضی فصل 5 ترمودینامیک
اصل ارشمیدس
اصل ارشمیدس
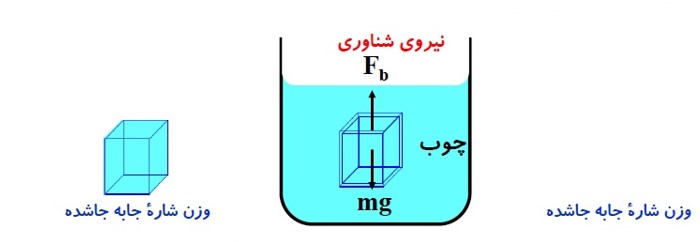
وقتی تمام یا قسمتی از یک جسم در شاره ای فرو رود، شاره نیرویی بالاسو بر آن وارد می کند که با وزن شاره جا به جا شده توسط جسم برابر است.
به جسم های درون یک شاره یا غوطه ور در آن، همواره نیروی بالاسوی خالصی به نام نیروی شناوری از طرف شاره وارد می شود.
عامل نیروی شناوری چیست؟
چون فشار شاره در قسمت های عمیق تر بیشتر است؛ نیرویی که از طرف شاره به بخش های عمیق تر وارد می شود نیز بیش تر است در نتیجه نیروی خالصی که به جسم وارد می شود به سمت بالا خواهد بود.
نیروی شناوری \({F_b}\)
به نیروی بالا سوی خالصی که به جسم درون شاره وارد شده و با وزن شاره جا به جا شده برابر است؛ نیروی شناوری می گویند.
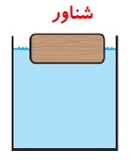
حالت های ممکن برای جسم قرار گرفته در شاره:
1) شناوری: حجم جسم بیشتر از حجم شاره جا به جا شده برابر است.
2) غوطه ور: حجم جسم و حجم شاره جا به جا شده برابر است.
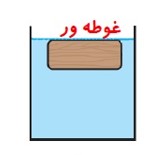
3) فرورفته: حجم جسم با حجم شاره جا به جا شده برابر است.
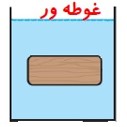
1 شرط غوطه وری و فرو رفتن این است که چگالی جسم بزرگتر یا برابر چگالی شاره باشد.
2 شناور ماندن روی آب ربطی به وزن اجسام ندارد و فقط به چگالی آنها بستگی دارد.
نیروی شناوری
جسمی مکعبی شکل به ضلع L را در نظر بگیرید که درون شاره ساکنی با چگالی \(\rho \) غوطه ور است. شکل زیر نیروهایی را نشان می دهد که شاره به سطح این جسم وارد می کند.
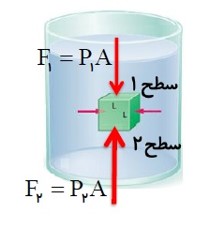
نیروی های افقی وارد به جسم یکدیگر را خنثی می کنند.
\({F_b} = \rho vg\)
در این فرمول
(\(\rho \)) چگالی شاره
(v) حجم شاره جا به جا شده است.
نیروی شناوری به عوامل زیر بستگی دارد:
- چگالی شاره
- حجم شاره جا به جا شده
- شتاب گرانش در آن محل
- جرم شاره جا به جا شده
نیروی شناوری به عوامل زیر بستگی ندارد:
- وزن جسم
- چگالی جسم
- عمق شاره
اصل برنولی
اصل برنولی
اصل برنولی، برای شاره ای که به طور لایه ای و در امتداد افق حرکت می کند:
در مسیر حرکت شاره، با افزایش تندی شاره، فشار داخل شاره کاهش می یابد.
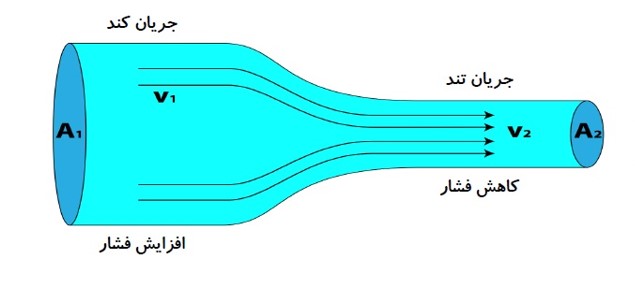
جریان پایا:
به جریانی که در آن تندی همه ذراتی که از یک نقطه می گذرند، ثابت باشد.
1 اصل برنولی بر طبق این فرضیات است:
2 شاره تراکم ناپذیر است.
3 هنگام حرکت شاره اصطکاک داخلی وجود ندارد.
4 حرکت شاره پایا است (متلاطم نیست).
آهنگ جریان شاره:
نسبت حجم شاره جا به جا شده به زمان سپری شده
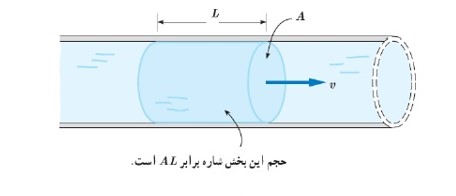

\(\frac{{AL}}{t} = Av\)
در این فرمول
(A) سطح مقطه لوله
(v) تندی شاره است.
معادله پیوستگی
در یک شاره تراکم ناپذیر، مقدار شاره ای که در زمان t از سطح مقطع \({A_1}\) می گذرد. درست برابر مقدار شاره ای است که در همین زمان از سطح مقطع \({A_2}\) می گذرد.
\({A_1}{v_1} = {A_2}v{}_2\)
در معادله پیوستگی باید یکاهای A و v در دو طرف معادله یکسان باشد.
مثال
سطح مقطع یک سرنگ پر از آب \(0/4c{m^2}\) و سطح مقطع دهانه خروجی آن \(0/4m{m^2}\) است. اگر سرنگ با تندی \(1/5\frac{{cm}}{s}\) فشرده شود، تندی خروجی آب از دهانه آن چقدر است؟
\(\begin{array}{l}{A_1} = 0/4c{m^2}\\{A_2} = 0/4m{m^2} = 0/4 \times {10^{ - 2}}c{m^2}\\{v_1} = 1/5\frac{{cm}}{s}\\{v_2} = ?\\1mm = 0/1cm\\{A_1}{v_1} = {A_2}{v_2}\\0/4 \times 1/5 = 0/4 \times {10^{ - 2}} \times {v_2} \to {v_2} = \frac{{1/5}}{{{{10}^{ - 2}}}} = 150\frac{{cm}}{s}\end{array}\)
کاربرد های اصل برنولی:
- باریک شدن ستون آب وقتی شیر آّ را کمی باز می کنیم.
- حرکت ورق کاغذ وقتی در دهان خود بر سطح بالایی کاغذ به سرعت بدمیم.
- پف کردن پوشش برزنتی روی اتاقک عقب کامیون هنگام حرکت
- طراحی بال هواپیما
- دستگاه سمپاش
رابطه مقایسه ای اصل برنولی:
\(\begin{array}{l}{A_1}{v_1} = {A_2}{v_2} \to \frac{{{v_2}}}{{{v_1}}} = \frac{{{A_1}}}{{{A_2}}}\\A = \pi {r^2}\\r = \frac{D}{2} \to A = \pi \frac{{{D^2}}}{4}\\ \to \frac{{{v_2}}}{{{v_1}}} = {(\frac{{{D_1}}}{{{D_2}}})^2}\end{array}\)
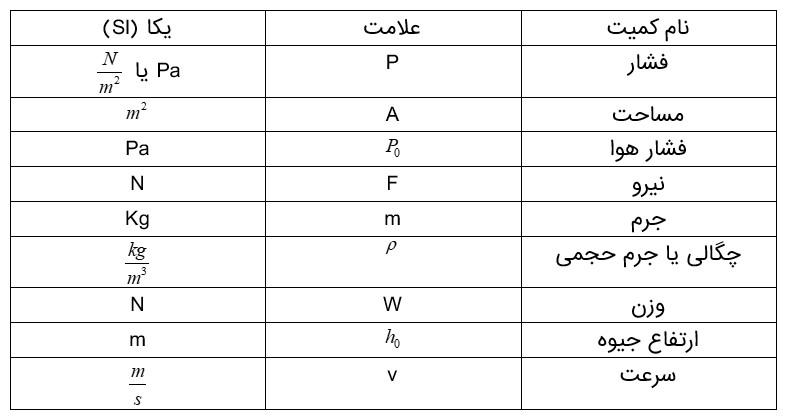
شناسنامه ویژگی های فیزیکی مواد
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه ریاضی- آزمون آنلاین تمامی دروس پایه ریاضی
- گام به گام تمامی دروس پایه ریاضی
- ویدئو های آموزشی تمامی دروس پایه ریاضی
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ریاضی
- فلش کارت های آماده دروس پایه ریاضی
- گنجینه ای جامع از انشاء های آماده پایه ریاضی
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ریاضی



1736019749.png)















