درسنامه کامل فیزیک دهم ریاضی فصل 5 ترمودینامیک
تعداد بازدید : 7.27Mخلاصه نکات فیزیک دهم ریاضی فصل 5 ترمودینامیک - درسنامه شب امتحان فیزیک دهم ریاضی فصل 5 ترمودینامیک - جزوه شب امتحان فیزیک دهم ریاضی نوبت اول فصل 5 ترمودینامیک
معادله حالت، فرآیند های ترمودینامیک
معادله حالت، فرآیند های ترمودینامیک
ترمودینامیک
شاخه ای از علم فیزیک که رابطه بین گرما و کار تبدیل گرما به کار مکانیکی را مورد مطالعه قرار می دهد، ترمودینامیک نام دارد.
دستگاه:
ماده خاصی که معمولا به شکل گاز یا مایع است و با محیط پیرامون خود مبادله گرما و کار می کند و در فرآیند های ترمودینامیکی شرکت می کند، دستگاه می گوییم.
محیط:
اجسام پیرامون دستگاه را که می توانند با آن تبادل انرژی داشته باشند، محیط می نامیم.
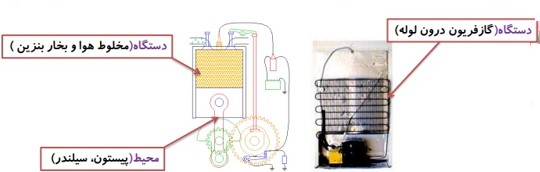
مثال
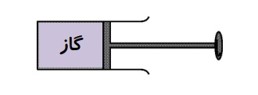
در این مثال گاز درون سیلندر، دستگاه نامیده می شود. پیستون، سیلندر و مکانی که سیلندر در آن واقع است، محیط نامیده می شوند.
انواع کمیت های ترمودینامیکی
کمیت های ماکروسپیک (مشاهده پذیر):
کمیت هایی که وضعیت ماده را در مقیاس بزرگ توصیف می کنند بدون آنکه درگیر جزئیات رفتار تک تک مولکول های گاز شود.
مانند فشار، حجم، دما، گرما، گرمای ویژه و ... .
کمیت های میکروسکوپیک:
کمیت هایی که به جزئیات رفتار تک تک مولکول ها مربوط می شوند.
مانند: سرعت، مکان، انرژی جنبشی، شتاب نیروی بین ذرات و ....
متغیر های ترمودینامیکی:
کمیت های ماکروسکوپی مانند فشار، دمای مطلق و حجم که حالت تعادل با آن ها توصیف می شوند، متغیر های ترمودینامیکی نامیده می شوند.
1 دستگاه موقعی در حالت تعادل ترمودینامیکی است که متغیر های ترمودینامیکی آن به طور خود به خودی تغییر نکند.
2 متغیر های ترمودینامیکی از یکدیگر مستقل نیستند.
حالات دستگاه
1) حالت تعادل:
متغیر های ترمودینامیکی گاز (دما، فشار و حجم) مقدار های ثابت و مشخصی دارند و به طور خود به خود تغییر نمی کنند.
2) حالت ناپایدار:
در تمام متغیر های ترمودینامیکی (دما، فشار و حجم) یکسان نباشد و حالت گاز ثابت و پایدار نباشد.
معادله حالت
رابطه ی بین متغیر های ترمودینامیکی، معادله ی حالت دستگاه نامیده می شود.
(رابطه بین سه کمیت P، V و T)
اگر گاز آرمانی (کامل) باشد، معادله حالت آن ساده و مستقل از نوع گاز است و با قانون گاز کامل معادله \(PV = nRT\) داده می شود.
1 برای نمایش حالت گاز باید از سه محور عمود بر هم P، V و T استفاده کرد، ولی حل مسئله ها با نمایش حالت در صفحه مختصات ساده تر می شود.
2 هنگامی که دو کمیت از معادله حالت معلوم باشد، می گوییم ه حالت دستگاه مشخص است.
3 از رابطه قانون گاز های کامل می توان کمیت سوم را که مجهول است را پیدا کرد.
فرآیند های ترمودینامیکی
به تحول هایی که در آنها دستگاه از یک حالت تعادل (\({T_1},{V_1},{P_1}\) ) به حالت تعادل دیگر (\({T_2},{V_2},{P_2}\) ) می رود.
برای مثال وقتی هوای درون سرنگی را متراکم کنیم، می گوییم گاز یک فرآیند ترمودینامیکی را پیموده است.
فرآیند ایستاوار:
هرگاه در طول فرآیند، دستگاه همواره بسیار نزدیک به حالت تعادل بوده (و گرمای داده شده به دستگاه در هر مرحله بسیار کوچک باشد) و سریع به تعادل برسد. چنین فرآیندی را فرایند ایستاوار می نامند.
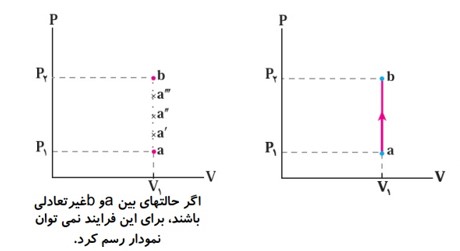
نمودار های مختلف فرآیند آرمانی:
در فرآیند های ترمودینامیکی یک دستگاه از یک حالت ابتدایی (i) به یک حالت نهایی (f) می رود می توان همه مراحل فرآیند را در نمودار های (P-V) یا (P-T) یا (V-T) نمایش داد.
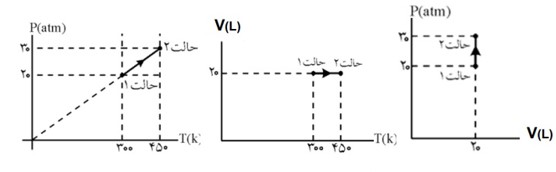
از رابطه زیر می توان یکی از کمیت های مجهول در نقاط (i) یا (f) را پیدا کرد.
\(\frac{{{P_1}{V_1}}}{{{T_1}}} = \frac{{{P_2}{V_2}}}{{{T_2}}}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه ریاضی- آزمون آنلاین تمامی دروس پایه ریاضی
- گام به گام تمامی دروس پایه ریاضی
- ویدئو های آموزشی تمامی دروس پایه ریاضی
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ریاضی
- فلش کارت های آماده دروس پایه ریاضی
- گنجینه ای جامع از انشاء های آماده پایه ریاضی
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ریاضی
تبادل انرژی، قانون اول ترمودینامیک
تبادل انرژی، قانون اول ترمودینامیک
انواع تبادل انرژی بین محیط و دستگاه:
گرما: نوعی انرژی است که به علت اختلاف دما بین دستگاه و محیط مبادله می شود.
بنا به قرارداد:
گرمایی که دستگاه می گیرد را با علامت مثبت نشان می دهیم. \(Q = mc\Delta \theta \)
گرمایی که دستگاه از دست می دهد با علامت منفی نشان می دهیم.
کار: عبارت است از حاصل ضرب نیرو در جا به جایی پیستون در کسینوس زاویه بین نیرو و جا به جایی \(W = F \times d \times \cos \theta \)
1 در شکل زیر، نیرویی را که پیستون به گاز وارد می کند با F و نیرویی را که گاز به پیستون اثر می دهد با \(F'\) نشان داده ایم.
چه پیستون ثابت بماند و چه نماند، جهت این نیرو ها تغییر نمی کند.
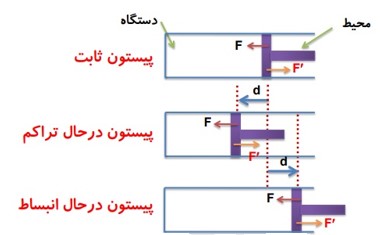
2 کاری را که محیط روی دستگاه انجام می دهد با W نشان می دهیم، در واقع کاری است که نیروی F روی گاز انجام می دهد.
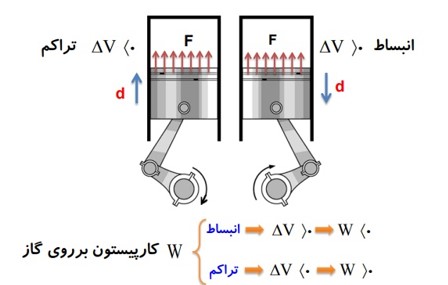
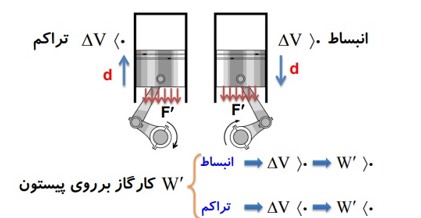
3) همزمان با کاری را که محیط روی دستگاه انجام می دهد W، دستگاه هم روی محیط کار انجام می دهد که آن را با نماد \(W'\) نشان می دهیم.
با توجه به عمل و عکس العمل بودن نیرو هایی که محیط و دستگاه به هم وارد می کنند میفهمیم که همیشه \(W = - W'\) است.
کار پیستون روی گاز = منفی کار گاز روی پیستون
منبع گرمایی:
جسمی است که جرم آن در مقابل جرم دستگاهی که با آن تبادل گرما دارد، چنان بزرگ است که می تواند مقدار گرمای زیادی بگیرد، یا از دست بدهد، بی آنکه تغییر دمای محسوسی بکند.
مثلا سوزن را حرارت دهیم و داخل یک استخر بزرگ حاوی آب بیاندازیم، آب استخر منبع گرمایی برای سوزن محسوب می شود.
انرژی درونی:
به مجموع انرژی های جنبشی و پتانسیل مولکول های یک دستگاه انرژی درونی آن نامیده می شود.
1 تغییر انرژی درونی گاز کامل فقط تابع دمای مطلق گاز است.
2 طبق معادله حالت چون T دمای مطلق یک گاز متناسب با PV (حاصل ضرب فشار گاز در حجم گاز) است.
اصل پایستگی انرژی برای هر دستگاه:
گرمای افزوده شده به دستگاه = کار انجام شده توسط دستگاه + افزایش انرژی درونی دستگاه
\(Q = \Delta U + W'\)
قانون اول ترمودینامیک
تغییر انرژی درونی دستگاه برابر است با مجموع گرمایی که دستگاه دریافت می کند و کاری که بر روی آن انجام می شود.
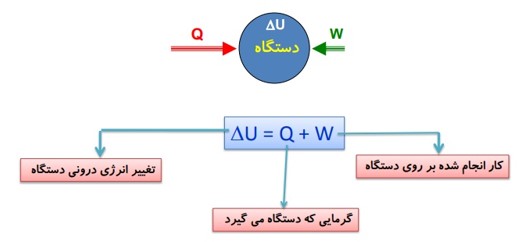
کار انجام شده و گرمای مبادله شده در فرآیند های ترمودینامیکی یک دستگاه، به نوع فرآیند ها در مسیر بستگی دارد.
\(\Delta U = Q + W\)
سوخت ساز بدن و قانون اول ترمودینامیک:
انرژی درونی بدن ما از انرژی شیمیایی ذخیره شده در مواد غذایی تامین می شود. با انجام فعالیت های مختلف، انرژی درونی بدن طبق قانون اول ترمودینامیک به کار و گرما تبدیل می شود.
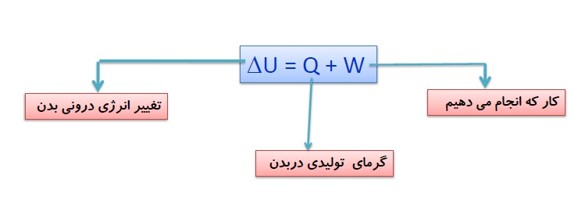
آهنگ سوخت و ساز بدن
آهنگ تبدیل انرژی شیمیایی مواد غذایی به انرژی درونی بدن را آهنگ سوخت و ساز بدن می نامند.
این آهنگ برحسب کیلو کالری بر ساعت یا بر حسب وات بیان می شود.
جزوات جامع پایه ریاضی
جزوه جامع فیزیک دهم ریاضی فصل 1 فیزیک و اندازه گیری
جزوه جامع فیزیک دهم ریاضی فصل 2 ویژگی های فیزیکی مواد
جزوه جامع فیزیک دهم ریاضی فصل 3 کار، انرژی و توان
جزوه جامع فیزیک دهم ریاضی فصل 4 دما و گرما
جزوه جامع فیزیک دهم ریاضی فصل 5 ترمودینامیک
فرآیند هم حجم
فرآیند هم حجم
انواع فرآیند های ترمودینامیکی:
- فرایند هم حجم \({V_1} = {V_2}\)
- فرایند هم فشار \({P_1} = {P_2}\)
- فرایند هم دما \({T_1} = {T_2}\)
- فرایند بی در رو \(Q = 0\)
1) فرایند هم حجم
تحولی از یک گاز که در طول آن، حجم گاز ثابت است را فرآیند هم حجم می نامند.
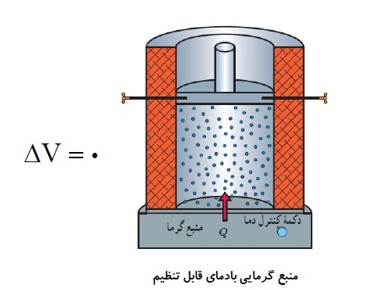
نمونه ای از یک فرایند هم حجم:
اتومبیل هنگام طی یک مسیر، حجم لاستیک اش تغییر نمی کند.
در یک فرایند هم حجم، گاز در حین گرفتن گرمای \({Q_V}\) از چشمه، دما و فشارش افزایش می یابد.
کار انجام شده در فرایند هم حجم
در این فرایند کار انجام شده صفر، فقط بین دستگاه و محیط گرما مبادله می شود.
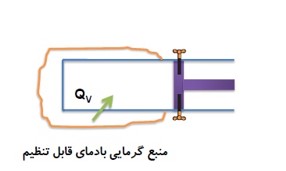
\(W = 0J\)
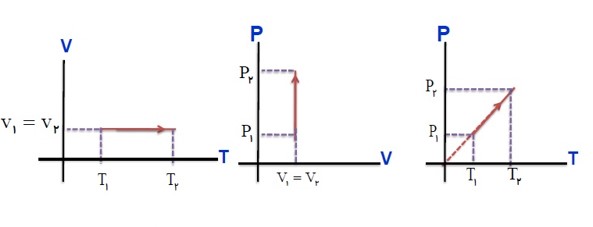
نمودار های مختلف فرایند هم حجم موقعی که دستگاه گرما می گیرد.
\(PV = nRT \to P = \left( {\frac{{nR}}{V}} \right)T \to P \propto T\)
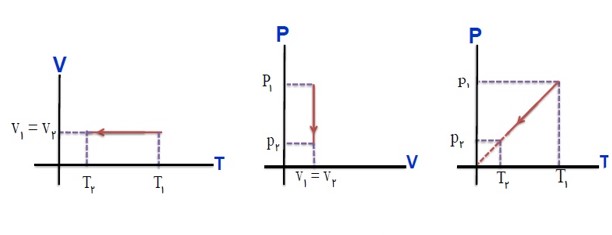
نمودار های مختلف فرایند هم حجم موقعی که دستگاه گرما از دست می دهد.
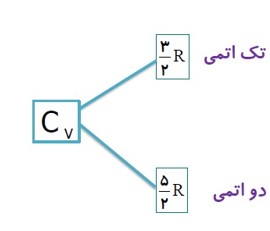
گرمایی ویژه مولی یک گاز در حجم ثابت: \({C_V}\)
مقدار گرمایی است که در حجم ثابت به یک مول گاز داده می شود تا دمای آن یک کلوین بالا رود.
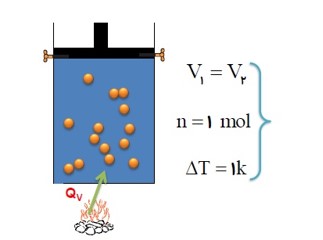
با تقریب خوبی می توان نشان داد که گرمای ویژه مولی در حجم ثابت به جنس گاز بستگی ندارد، برای گاز های کامل:
فرآیند هم فشار
فرآیند هم فشار
تحولی را که در طی آن فشار گاز ثابت بماند، فرآیند هم فشار می نامند.
در این فرآیند دستگاه با دریافت گرما از چشمه گرم منبسط می شود و با از دست دادن گرما متراکم می گردد. (با فرض این که اصطکاک بین پیستون و استوانه ناچیز باشد.)
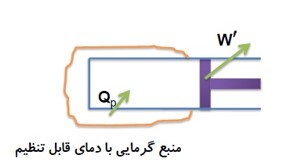
شرایط ایجاد فرایند هم فشار
- باید اصطکاک بین پیستون و استوانه ناچیز باشد.
- مبادله گرما بین منبع گرم و دستگاه خیلی آهسته صورت گیرد تا هم دستگاه در هر لحظه نزدیک به وضعیت تعادل باشد و هم پیستون خیلی آرام حرکت کند.
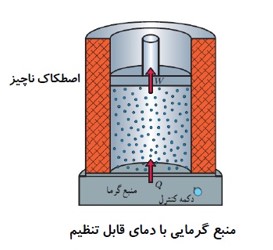
رسم نمودار های فرایند هم فشار: (انبساط)
در فرایند انبساط هم فشار، اگر دستگاه گرمای \({Q_P}\) را بگیرد. کار \(W'\) را انجام می دهد.
\(PV = nRT \to V = \left( {\frac{{nR}}{P}} \right)T \to V \propto T\)
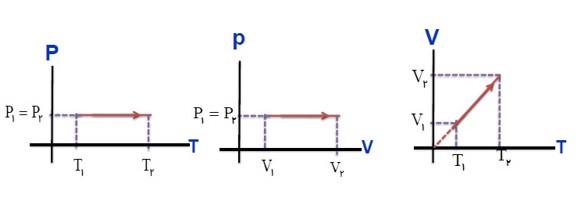
رسم نمودار های فرایند هم فشار: (تراکم)
در تراکم هم فشار، محیط کار W انجام داده و دستگاه گرمای \({Q_P}\) را از دست می دهد.
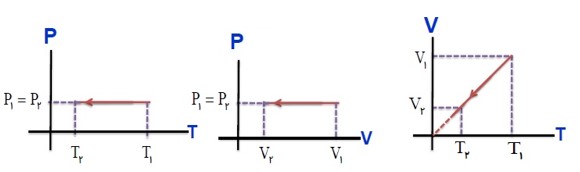
محاسبه کار در یک تحول انبساطی (هم فشار):
کاری که دستگاه (گاز) بر روی محیط (پیستون) انجام می دهد. (انبساط گاز) \(W'\)
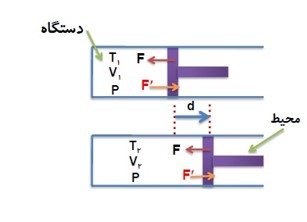
\(\begin{array}{l}1)W' = P.Ad\\Ad = \Delta V\\ \to W' = P.\Delta V\\2)W = - P.Ad\\Ad = \Delta V\\ \to W = - P.\Delta V\end{array}\)
کار انجام شده در فرایند هم فشار
کار انجام شده بر روی دستگاه \(W = - P.\Delta V\)
کار انجام شده بر روی محیط \(W' = P.\Delta V\)
طبق معادله حالت می توان کار را از رابطه ی زیر نیز بدست آورد.
\(W = - nR\Delta T\)
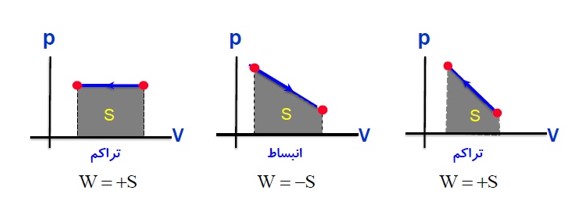
محاسبه ی کار به کمک نمودار:
سطح زیر نمودار (P-V) برابر قدر مطلق کار مبادله شده بین دستگاه و محیط است.
کار انجام شده بر روی گاز در تراکم (\(W\rangle 0\) ) و در انبساط (\(W\langle 0\) )
\(\left| W \right| = S = \left| { - P.\Delta V} \right|\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه ریاضی- آزمون آنلاین تمامی دروس پایه ریاضی
- گام به گام تمامی دروس پایه ریاضی
- ویدئو های آموزشی تمامی دروس پایه ریاضی
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ریاضی
- فلش کارت های آماده دروس پایه ریاضی
- گنجینه ای جامع از انشاء های آماده پایه ریاضی
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ریاضی
فرایند هم دما و بی در رو
فرایند هم دما و بی در رو
فرآیند هم دما
دمای دستگاه در حین این فرایند ثابت می ماند.
در فرایند هم دما با وجود ثابت ماندن دما، بین محیط و دستگاه گرما مبادله می شود.
برای گاز آرمانی که انرژی درونی آن فقط تابعی از دماست، تغییر انرژی درونی صفر است.
\(\Delta U = Q + W \to \Delta U = 0 \to Q = - W \to Q\langle 0\)
رسم نمودار های فرایند هم دما: (تراکم)
در یک فرایند هم دما، با انجام کار W، دستگاه گرمای Q را از دست می دهد.
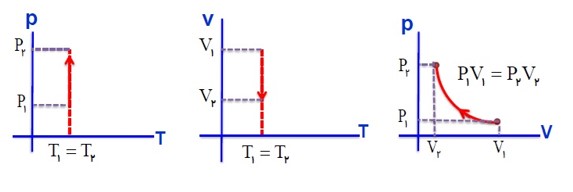
\(PV = nRT \to P = \frac{{nRT}}{V} \to P \propto \frac{1}{V}\)
رسم نمودار های فرایند هم دما: (انبساط)
در یک فرایند هم دما، اگر گاز گرمای Q را بگیرد کار \(W'\) را روی محیط انجام می دهد.
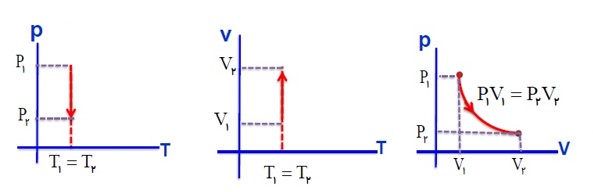
به طور کلی نمودار های فرآیند هم دما به صورت زیر است.
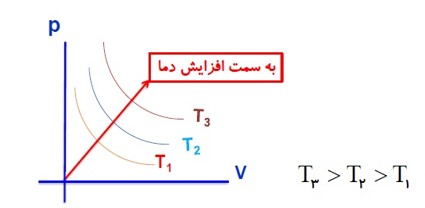
فرآیند بی در رو
در این فرایند بین دستگاه و محیط گرما مبادله نمی شود.
برای انجام فرایند بی در رو
- باید دستگاه را عایق بندی کنیم و عمل تراکم یا انبساط را به آهستگی انجام دهیم.
- گاز چنان با سرعت کم متراکم یا منبسط شود که فرصت مبادله گرما با محیط را پیدا نکند. بنابراین در فرایند بی در رو Q=0 است.
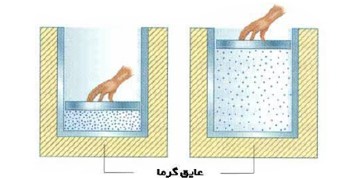
از فرایند بی در رو می توان به دهانه ی تلمبه ی دوچرخه اشاره کرد که دهانه دوچرخه مسدود شده است و پیستون با سرعت به پایین رانده می شود.
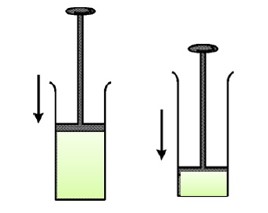
در فرایند تراکم بی در رو که با انجام کار W بر روی گاز، حجم V آن کاهش پیدا کرده فشار و دما افزایش می یابند.
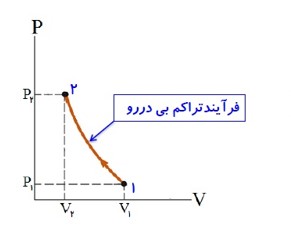
\(\Delta U = Q + W \to Q = 0 \to W\rangle 0 \to \Delta U\rangle 0 \to \Delta T\rangle 0\)
در فرایند انبساط بی در رو که با انجام کار W بر روی گاز، حجم آن افزایش پیدا کرده، فشار و دما کاهش می یابند.
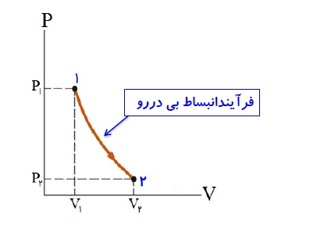
\(\Delta U = Q + W \to Q = 0 \to W\langle 0 \to \Delta U\langle 0 \to \Delta T\langle 0\)
نمودار فرایند بی در رو
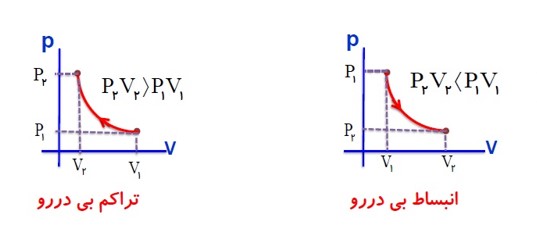
مقایسه تراکم بی در رو و هم دما
در تراکم گاز، فشار و دمای گاز افزایش می یابد. در فرایند هم دما، برای ثابت نگه داشتن دمای گاز باید از آن گرما گرفت ولی در فرایند بی در رو، از گاز گرما گرفته نمی شود و از این رو در انتهای مسیر، فشار و دمای گاز در فرایند بی در رو بیش از فرایند هم دما است.
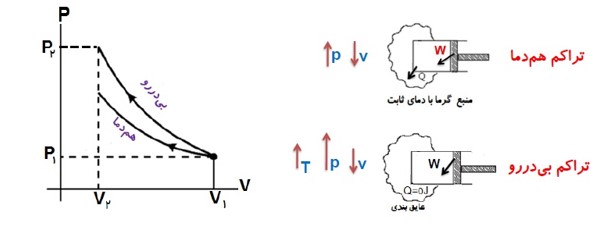
شیب نمودار در فرایندی در رو بیشتر از شیب نموار هم دما است.
مقایسه انبساط بی در رو و هم دما
در انبساط گاز، فشار و دمای گاز کاهش می یابد. در فرایند هم دما، برای ثابت نگه داشتن دمای گاز باید به گاز، گرما دهیم؛ ولی چون در انبساط بی در رو، گاز هیچ گونه گرمایی دریافت نمی کند، در انتهای مسیر، فشار و دمای گاز در فرایند بی در رو پایین تر از فشار و دمای گاز فرایند هم دما خواهد بود.
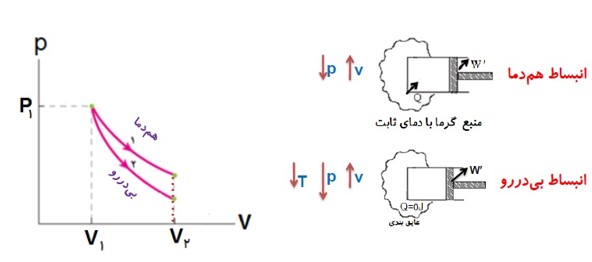
مقایسه کار انجام شده روی دستگاه در سه فرایند هم فشار، هم دما و بی در رو
در انبساط یکسان قدر مطلق کار انجام شده روی دستگاه در فرایند هم فشار از بقیه فرایند ها بیشتر و قدر مطلق تغییرات فشار و دما در فرایند بی در رو از بقیه بیشتر است.
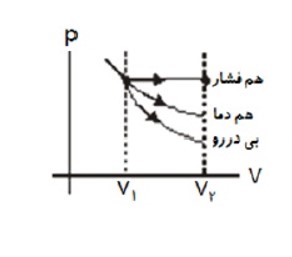
در تراکم یکسان، مقدار کار انجام شده روی دستگاه، در فرایند بی در رو از بقیه فرایند ها بیشتر و دما ی نهایی گاز نیز در فرایند بی در رو از بقیه فرایند ها بیشتر است.
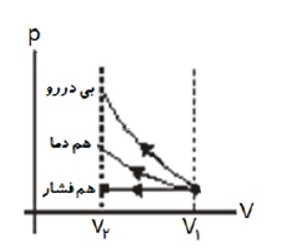
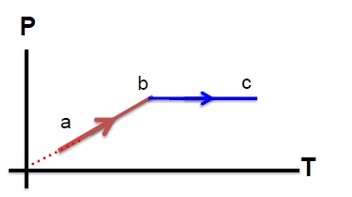
نمودار P-T:
در فرایند ab، V ثابت است و داریم:
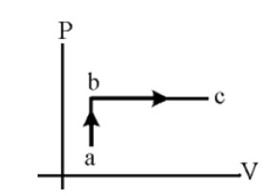
\(PV = nRT \to P = \left( {\frac{{nR}}{V}} \right)T \to P \propto T\)
چون فشار افزایش یافته بنابراین دما نیز افزایش یافته است. در فرایند bc فشار ثابت مانده است و حجم افزایش یافته است، بنابراین دمای گاز نیز افزایش یافته است.
1 تغییر انرژی درونی دستگاه به نوع فرآیند ها بستگی ندارد.
2 تغییر انرژی درونی دستگاه (\(\Delta U\) ) با جرم ثابت فقط بستگی به تغییر دمای مطلق (\(\Delta T\)) دستگاه دارد.
مثال
مقدار معینی از یک گاز کامل در یک فرایند بی در رو 100 ژول کار انجام می دهد، تغییر انرژی درونی گاز چند ژول است؟
\(\begin{array}{l}Q = 0J\\W' = 100J \to W = - 100J\\\Delta U = ?\\\Delta U = Q + W \to \Delta U = 0 - 100 = - 100J\end{array}\)
جزوات جامع پایه ریاضی
جزوه جامع فیزیک دهم ریاضی فصل 1 فیزیک و اندازه گیری
جزوه جامع فیزیک دهم ریاضی فصل 2 ویژگی های فیزیکی مواد
جزوه جامع فیزیک دهم ریاضی فصل 3 کار، انرژی و توان
جزوه جامع فیزیک دهم ریاضی فصل 4 دما و گرما
جزوه جامع فیزیک دهم ریاضی فصل 5 ترمودینامیک
چرخه ترمودینامیکی
چرخه ترمودینامیکی
مجموعه چند فرایند مختلف که دستگاه پس از طی کردن فرایند ها به حالت اولیه خود باز می گردد.
مشخصه اصلی یک چرخه:
بی تغییر ماندن انرژی درونی کل در آن است. (\(\Delta T = 0\) )
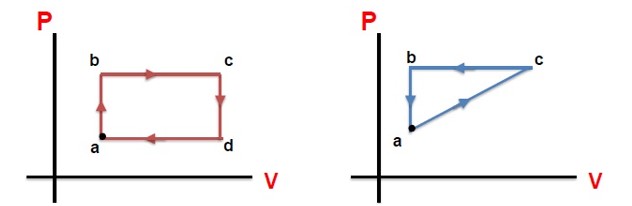
قدر مطلق کار انجام شده در چرخه:
برابر سطح محصور بین فرآیند ها است. \(W = S\)
گرمای مبادله شده در چرخه:
\(\Delta U = 0 \to Q + W = 0 \to Q = - W\)
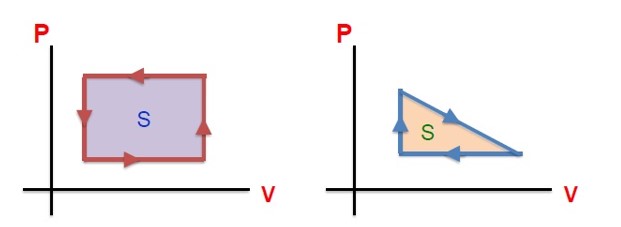
1 اگر جهت چرخه ساعتگرد باشد، کل کار انجام شده روی دستگاه در چرخه منفی و در کل چرخه، گاز گرما دریافت می کند، یعنی:
\(W\langle 0 \to Q = - W \to Q\rangle 0\)
2 اگر جهت چرخه پادساعتگرد باشد، کل کار انجام شده روی دستگاه در چرخه مثبت و در کل چرخه، گاز گرما از دست می دهد، یعنی:
\(W\rangle 0 \to Q = - W \to Q\langle 0\)
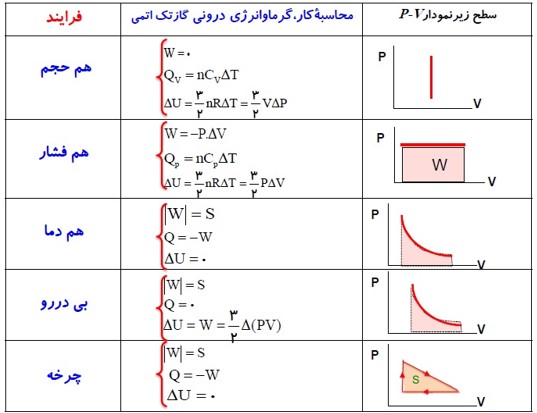
خلاصه ای از قانون اول ترمودینامیک برای چهار حالت زیر:

ماشین گرمایی
ماشین گرمایی
وسیله ای است که با استفاده از فرایند های ترمودینامیکی گرمای حاصل از سوخت را به کار تبدیل می کند.
هر ماشین گرمایی یک چرخه ی معین را تکرار می کنند.
انواع ماشین گرمایی
ماشین گرایی برون سوز:
دستگاه با دو منبع با دمای بالا و دمای پایین در تماس است و گرما از منبع گرم تر در بیرون دستگاه به آن داده شود و کار خالصی توسط دستگاه در طی چرخه انجام می شود.
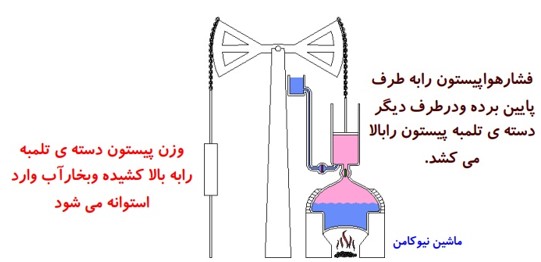
مانند ماشین نیوکامن، ماشین استرلینگ و ماشین بخار وات
ماشین گرمایی درون سوز:
گرما در اثر آتش گرفتن ماده سوختی (دستگاه) که در داخل سیلندر قرار دارد تامین می شود.
مانند موتور های بنزینی و دیزلی
تحلیل دقیق چرخه ی یک ماشین بخار دشوار است. اما با برخی ساده سازی ها می توان به نحلیل این ماشین ها پرداخت و به چرخه ی آرمانی موسوم به چرخه رانکین رسید.
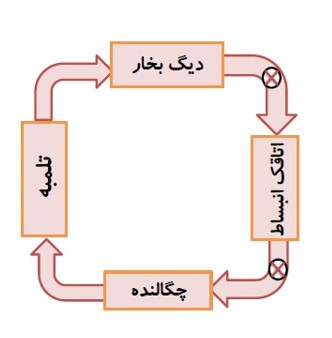
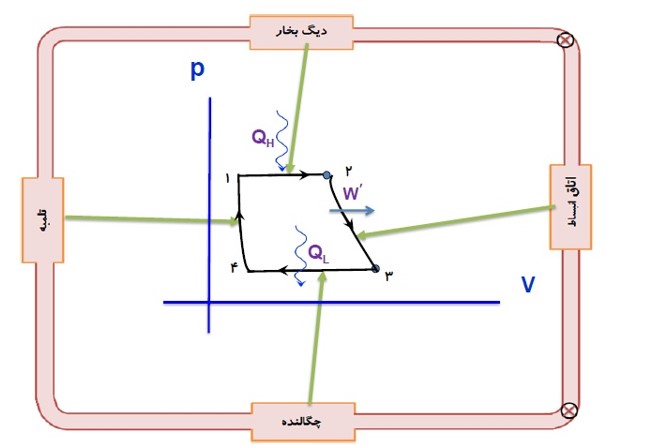
در چرخه ماشین بخار:
- دستگاهی که چرخه را می پیماید، آب است.
- کوره، منبع دمای بالا و گرمای \({Q_H}\) را به دستگاه (آب) می دهد.
- دستگاه روی محیط ار انجام می دهد و باعث انبساط دستگاه می شود.
- منبع دمای پایین چگالنده و لوله های آب سرد است و گرمای \({Q_L}\) را از دستگاه می گیرد.
فرایند هایی که آب در ماشین بخار وات طی می کند، به چهار مرحله اصلی تقسیم می کنیم:
الف) مرحله اول:
در این مرحله آب درون دیگ بخار در فشار ثابت از کوره گرما می گیرد و به بخار تبدیل می شود.
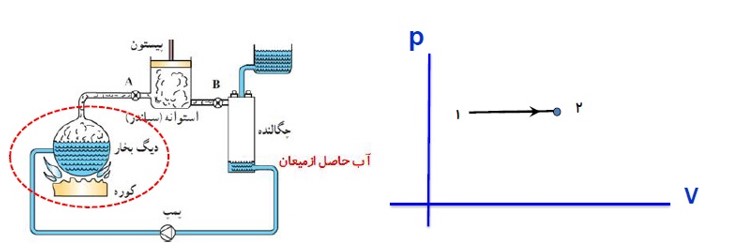
ب) مرحله دوم:
شیر ورودی باز می شود. بخار آب که دما و فشار آن بسیار زیاد است وارد اتاقک انبساط می شود و دما و فشار آن کاهش می یابد در این مرحله بخار آب بر روی محیط کار انجام می دهد.
(چون این انبساط بسیار سریع است این فرایند را بی در رو می توان در نظر گرفت.)
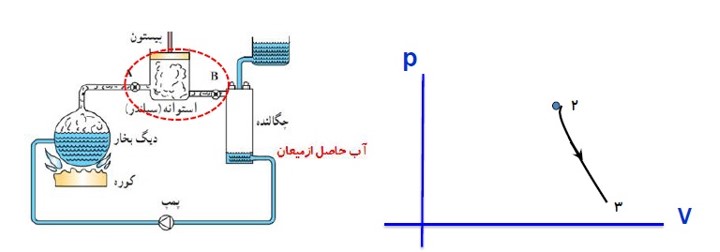
ج) مرحله سوم:
در چگالنده بخار آب در فشار ثابت گرما از دست می دهد و به مایع تبدیل می شود. در این فرایند دما و حجم بخار آب کاهش می یابد.
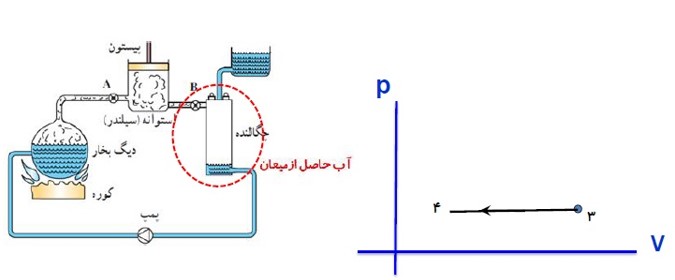
د) مرحله چهارم:
تلمبه (پمپ)، آب حال از میعان را به دیگ بخار بر میگرداند و فشار آن را به طور بی در رو به فشار اولیه می رساند (فقط تغییرات کوچکی در دما و حجم مایع رخ می دهد)
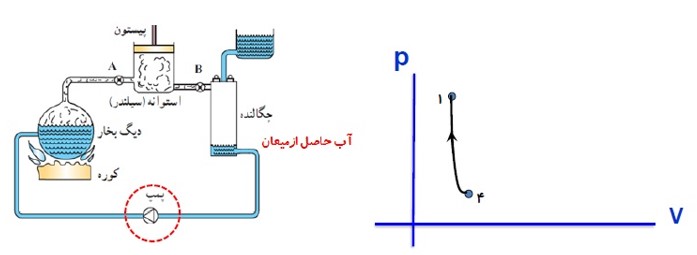
چرخه رانکین
1 در حین کار با ماشین بخار این چرخه دائما تکرار می شود.
2 دستگاه در این چرخه به طور عمده با دو منبع گرما (کوره و چگالنده) تبادل گرما می کند.
3 کوره را که در دمای بالاتری قرار دارد منبع گرم و چگالنده را منبع سرد می نامیم.
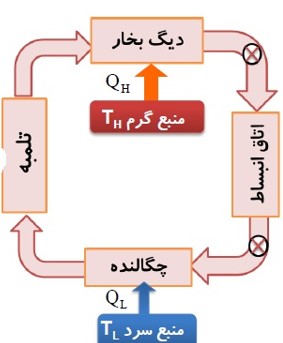
مرحله های کار ماشین گرمایی درون سوز
1) ضربه ی مکش
2) ضربه ی تراکم
3) آتش گرفتن
4) ضربه ی قدرت
5) تخلیه
6) ضربه ی خروج گاز
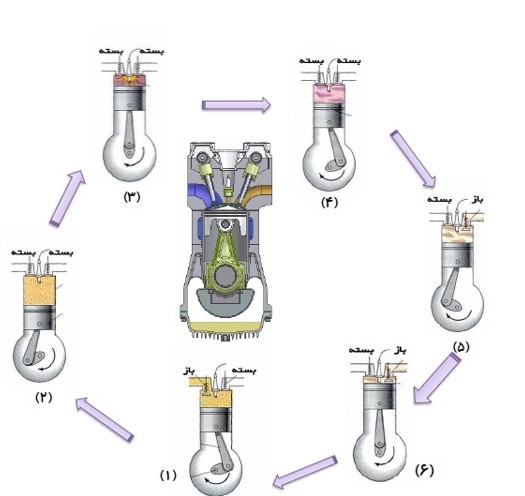
1) ضربه ی مکش
با پایین آمدن پیستون مخلوط بنزین و هوا از طریق دریچه ورودی وارد استوانه می شوند.
وقتی پیستون به پایین ترین وضعیت خود رسید، این دریچه بسته می شود.

2) ضربه ی تراکم
پیستون بالا می آید و مخلوط را متراکم می کند و به حجم اولیه می رساند در این وضعیت دمای مخلوط بسیار بالا می رود.
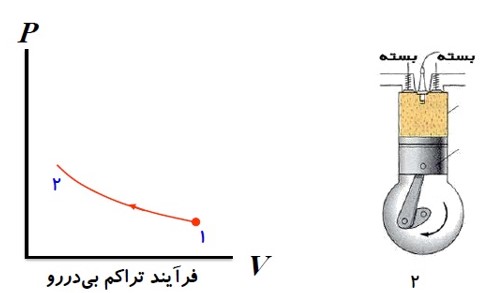
3) آتش گرفتن
هنگامی که پیستون به بالا ترین وضعیت خود رسید، شمع جرقه می زند، مخلوط آتش می گیرد و دما و فشار آن تا مقدار زیادی بالا می رود.
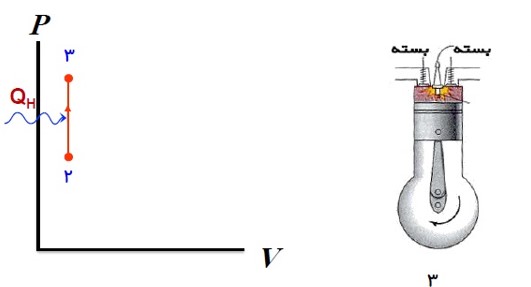
4) ضربه ی قدرت
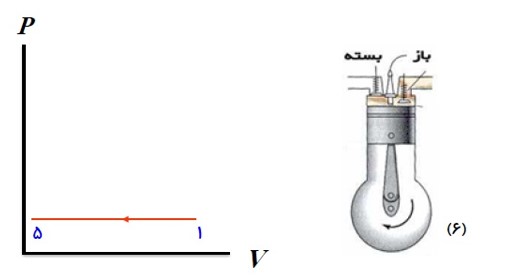
در این مرحله در اثر فشار زیاد دستگاه منبسط می شود و پیستون را به طرف پایین می راند. کاری که دستگاه بر روی محیط انجام می دهد در این مرحله حاصل می شود.
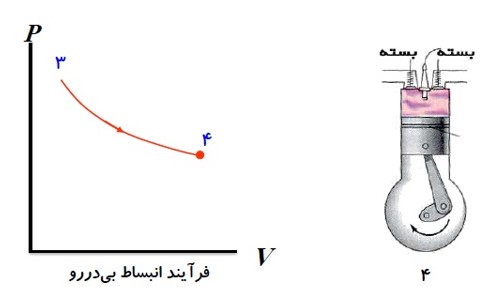
5) تخلیه
در حالی که پیستون در پایین ترین وضعیت حجمی قرار دارد، سوپاپ درچه خروجی باز می شود و قسمتی از محصولات احتراق به صورت دود از دریچه خروجی خارج می شود. به این ترتیب مقدار زیادی گرما به بیرون رانده می شود.
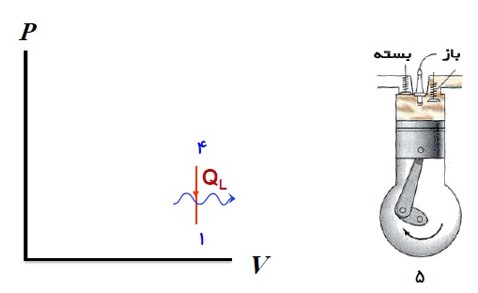
6) ضربه ی خروج گاز
پیستون بالا می آید و بقیه محصولات احتراق را بیرون می راند و حجم فضای بالای پیستون از بیشترین به مقدار اولیه می رسد
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه ریاضی- آزمون آنلاین تمامی دروس پایه ریاضی
- گام به گام تمامی دروس پایه ریاضی
- ویدئو های آموزشی تمامی دروس پایه ریاضی
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ریاضی
- فلش کارت های آماده دروس پایه ریاضی
- گنجینه ای جامع از انشاء های آماده پایه ریاضی
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ریاضی
بازده، قانون دوم ترمودینامیک
بازده، قانون دوم ترمودینامیک
بازده ماشین گرمایی: \(\eta \) (اتا)
نسبت کار بدست آمده \(\left| W \right|\) به مقدار گرمای گرفته شده \({Q_H}\) از چشمه ی گرمایی را بازده ماشین گرمایی می گویند.
\(\eta = \frac{{\left| W \right|}}{{{Q_H}}}\)
مفهوم بازده ماشین گرمایی:
نشان می دهد که چه کسری از گرمای حاصل از سوخت به انرژی مفید خروجی تبدیل می شود.
علامت کار و گرمای مبادله شده در ماشین گرمایی
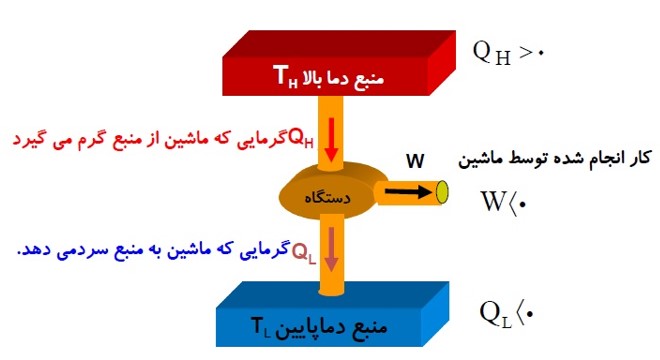
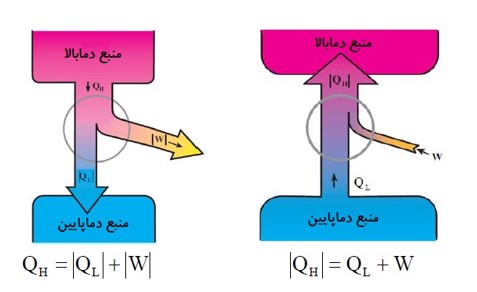
قانون اول ترمودینامیک برای ماشین گرمایی
چون ماشین یک چرخه را طی می کند، \(\Delta U = 0\) است.
\(\begin{array}{l}\Delta U = Q + W\\ \to \Delta U = 0,Q = {Q_H} - \left| {{Q_L}} \right|,W = - \left| W \right|\\ \to 0 = {Q_H} - \left| {{Q_L}} \right| - \left| W \right| \to {Q_H} = \left| W \right| + \left| {{Q_L}} \right|\end{array}\)
رابطه ی بازده ماشین گرمایی با قانون اول ترمودینامیک:
بازدهی ماین گرمایی همواره کوچک تر از یک است زیرا \(\left| W \right|\langle {Q_H}\)
\(\begin{array}{l}\left| W \right| = {Q_H} - \left| {{Q_L}} \right|\\\eta = \frac{{\left| W \right|}}{{{Q_H}}}\\ \to \eta = \frac{{{Q_H} - \left| {{Q_L}} \right|}}{{{Q_H}}} \to \eta = 1 - \frac{{\left| {{Q_L}} \right|}}{{{Q_H}}}\end{array}\)
1 بازده ماشین گرمایی واقعی از بازده ماشین های آرمانی کمتر است.
2 بازده تقریبی ماشین های گرمایی به صورت زیر است:
- بازده ماشین های درون سوز بنزینی: در حدود 20 تا 30 درصد
- بازده ماشین های درون سوز دیزلی: در حدود 30 تا 35 درصد
- بازده ماشین های برون سوز بخار: در حدود 30 تا 40 درصد
روش های افزایش بازده ماشین گرمایی:
- کاهش اصطکاک میان پیستون و سیلندر
- با عایق بندی مناسب، می توانیم تا حدی از اتلاف گرمای کوره جلوگیری کنیم.
- دمای منبع گرم را افزایش و دمای منبع سرد را کاهش دهیم.
هر ماشین گرمایی بخشی از انرژی گرمایی دریافتی از منبع گرم را تبدیل به کار می کند و بقیه را به منبع سرد می سپارد.
ماشین گرمایی نمی تواند تمام گرما را تبدیل به کار کند.
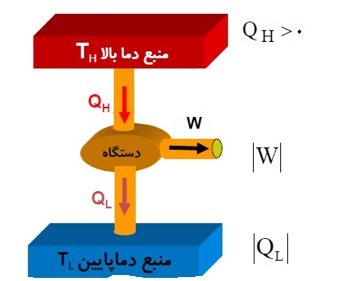
قانون دوم ترمودینامیک (به بیان ماشین گرمایی)
ممکن نیست دستگاه چرخه ای را بپیماید که در طی آن مقداری گرما را از منبع دما بالا جذب و تمام آن را به کار تبدیل کند.
یعنی ممکن نیست بازده یک ماشین گرمایی برابر 100 درصد باشد.
جزوات جامع پایه ریاضی
جزوه جامع فیزیک دهم ریاضی فصل 1 فیزیک و اندازه گیری
جزوه جامع فیزیک دهم ریاضی فصل 2 ویژگی های فیزیکی مواد
جزوه جامع فیزیک دهم ریاضی فصل 3 کار، انرژی و توان
جزوه جامع فیزیک دهم ریاضی فصل 4 دما و گرما
جزوه جامع فیزیک دهم ریاضی فصل 5 ترمودینامیک
یخچال
یخچال
بیان قانون دوم ترمودینامیک (به بیان یخچالی)
ممکن نیست گرما به طور خود به خود از جسم با دمای پایین تر به جسم با دمای بالاتر منتقل شود.

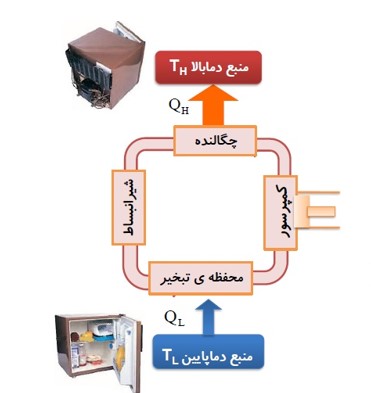
ساختمان یخچال
سرد سازی به وسیله دستگاه (گاز فریون)
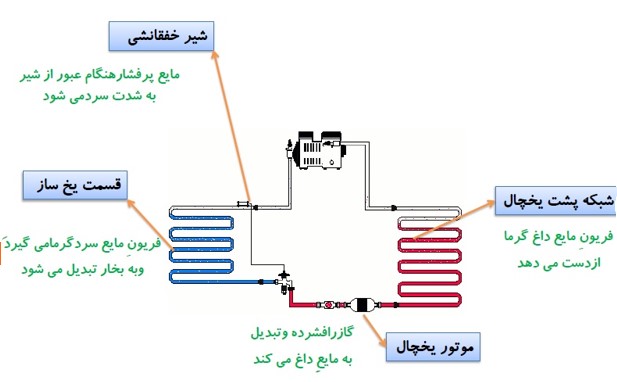
ساز و کار یخچال
اصول کار یخچال
این است که باید از جسمی که درون آن گذاشته ایم مقداری گرما بگیرد (\({Q_L}\) ) و سپس با انجام مقداری کار W (که همان موتور یخچال است) مقداری گرمای گرفته شده را به منبع با دمای بالا بدهد (\({Q_H}\) ).
طرز کار کولر گازی
مانند یخچال است. در کولر گازی منبع دما پایین هوای اتاق و منبع دمای بالا هوای بیرون است. کولر با انجام این کار، گرما را از داخل اتاق می گیرد و به هوای بیرون می دهد.
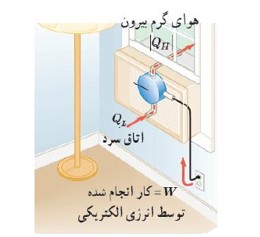
از نظر اقتصادی بهترین یخچال، یخچالی است که با انجام کار کمتر گرمای بیشتری را از درون یخچال به بیرون یخچال منتقل کند.
علامت کار و گرمای مبادله شده در یخچال
یخچال: نوعی ماشین گرمای است که در جهت وارون کار می کند.
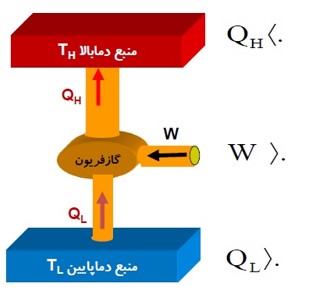
قانون اول ترمودینامیک برای یخچال
چون یخچال یک چرخه را تکرار می کند، در هر چرخه \(\Delta U = 0\) است، داریم:
\(\begin{array}{l}\Delta U = Q + W\\\Delta U = 0\\Q = {Q_L} - \left| {{Q_H}} \right|\\ \to 0 = {Q_L} - \left| {{Q_H}} \right| + W \to \left| {{Q_H}} \right| = {Q_L} + W\end{array}\)
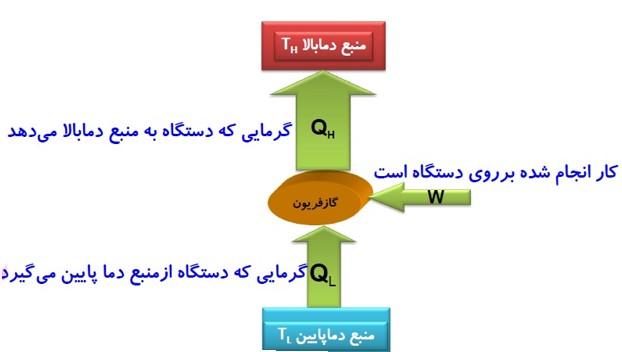
فرق ماشین گرمایی با یخچال
قانون های ترمودینامیک
به بیان ماشین گرمایی
قانون اول ترمودیناک: \({Q_H} = \left| {{Q_L}} \right| + \left| W \right|\)
قانون دوم ترمودینامیک: \({Q_L} \ne 0,\eta \ne 1\)
ممکن نیست دستگاه چرخه ای را بپیماید که در طی آن مقداری گرما را از منبع با دمای بالا جذب و تمام آن را به کار تبدیل کند.
به بیان یخچال
قانون اول ترمودینامیک: \({Q_H} = {Q_L} + W\)
قانون دوم ترمودینامیک: \(W \ne 0\)
ممکن نیست گرما به طور خود به خود از جسم با دمای پایین تر به جسم با دمای بالا تر منتقل شود.



1736019749.png)