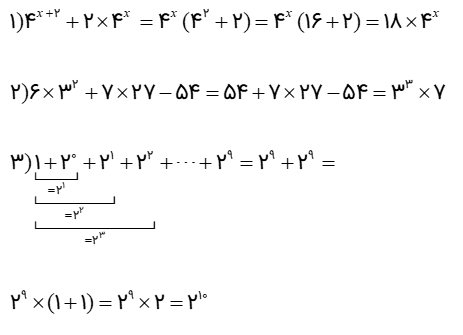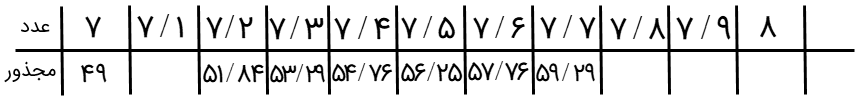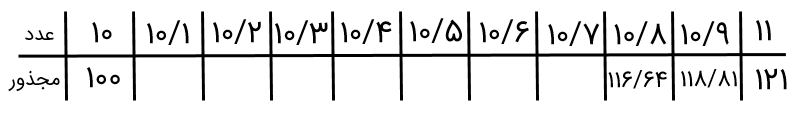حاصل عبارات زیر را به دست آورید.
\(\begin{array}{l}1)\frac{{{{( - 11)}^0} - {{( - 3)}^3} - {{( - 2)}^5}}}{{{{( - 1)}^7} - {{( - 1)}^{11}} - {{(1)}^0}}}\\\\2)3 \times {2^3} - 2 \times {( - 3)^2}\\\\3){(x)^2} - ( - {x^2})\end{array}\)
با استفاده از فاکتور گیری و ویژگی های توان، عبارات زیر را ساده کنید.
\(\begin{array}{l}1)6 \times {3^2} + 3 \times {3^2}\\\\2){6^5} + {6^5} + {6^5} + {6^5} + {6^5} + {6^5}\\\\3)9 \times {4^3} + 5 \times {4^3} - 2 \times {4^3} - 5 \times {4^3}\end{array}\)
حاصل عبارات زیر را به صورت توان دار بنویسید.
\(\begin{array}{l}1){3^5} \times {3^6} \times {2^7} \times {2^4}\\\\2)4 \times {9^2} - {9^2}\\\\3){x^5} \times {x^4} \div {( - {x^3})^2}\\\\4){( - {x^2})^3} \times {( - x)^5} \div {x^4}\end{array}\)
حاصل عبارت های زیر را به صورت یک عدد توان دار به دست آورید.
\(\begin{array}{l}1)\frac{{{{( - a)}^3} \times {{( - {a^3})}^2}}}{{{{({a^5})}^2} \times {{( - {a^2})}^3}}}\\\\2)\frac{{0/12 \times {{10}^3} + 0/24 \times {{10}^6}}}{{0/06 \times {{10}^5}}}\end{array}\)
حاصل هر یک از عبارات زیر را به صورت عددی توان دار بنویسید.
\(\begin{array}{l}1){6^{12}} \div {({6^3})^2}\\\\2)4 \times {2^2} \times \frac{1}{{16}}\\\\3)\frac{{3 \times {2^8} + 5 \times {2^8}}}{{3 \times {4^2} + 16}}\end{array}\)
عبارت های جبری زیر را ساده کنید و به یک ضرب تبدیل کنید.
\(\begin{array}{l}1){4^{x + 2}} + 2 \times {4^x}\\\\2)6 \times {3^2} + 7 \times 27 - 54\\\\3)1 + {2^0} + {2^1} + {2^2} + \cdots + {2^9}\end{array}\)
کسر های زیر را ساده کنید.
\(\begin{array}{l}1)\frac{{125 + 125 + 125 + 125 + 125}}{{8 + 8}}\\\\2)\frac{{{9^x} + {9^x} + {9^x}}}{{{3^{x - 2}}{x^2} + {3^{x - 2}}}}\\\\3)\frac{{{3^6} + {3^7} + {3^8}}}{{9 + 3 + 1}}\end{array}\)
مقدار خواسته شده را بیابید.
\(\begin{array}{l}1){2^x} = 5 \Rightarrow {8^x} = ?\\\\2){6^x} = 7 \Rightarrow {216^x} + {6^{x + 2}} = ?\end{array}\)
سه عدد داده شده در هر قسمت را از کوچک به بزرگ مرتب کنید.
\(\begin{array}{l}1){3^9},{9^2},{81^2}\\\\2){128^{200}},{64^{234}},{512^{150}}\end{array}\)
اگر \(A = {2^4}\) و \(B = {3^4}\) باشد، حاصل عبارت زیر را به دست آورید.
\(\frac{{16A \times 81B}}{{8A \times 27B}}\)
حاصل عبارت های رادیکالی زیر را به دست آورید.
\(\begin{array}{l}1)\sqrt {196} - \sqrt {225} + \sqrt 9 \\\\2)\sqrt {\sqrt {100} + \sqrt {49} - } \sqrt {64} \end{array}\)
حاصل عبارات رادیکالی زیر را با استفاده از ویژگی های جذر به دست آورید و به ساده ترین صورت ممکن بنویسید.
\(\begin{array}{l}1)\sqrt {1/21} - \sqrt {0/81} \\\\2)\sqrt {1 - \frac{8}{9}} + \sqrt {1 + \frac{{44}}{{81}}} \end{array}\)
عبارات رادیکالی زیر را ساده کنید.
\(\begin{array}{l}1)\sqrt 2 + \sqrt 8 + \sqrt {50} \\\\2)\sqrt {20} - \sqrt 5 + \sqrt {605} \end{array}\)
با استفاده از ویژگی های جذر، حاصل هر عبارت را به ساده ترین صورت بنویسید.
\(\begin{array}{l}1)\sqrt {2\sqrt {14} \times 7\sqrt {14} } \\\\2)(\sqrt {27} + \sqrt {12} )\sqrt 3 \\\\3)\sqrt {{3^5}} + \sqrt {27} \\\\4)\sqrt {108} - \sqrt {75} + \sqrt 3 \end{array}\)
حاصل عبارت های رادیکالی زیر را بدست آورید.
\(\begin{array}{l}1)\frac{{4\sqrt {10} }}{{\sqrt {20} \times \sqrt 8 }}\\\\2)\frac{{\sqrt {3000} }}{{\sqrt {270} }}\end{array}\)
مقدار مجهول را بدست آورید.
\(\begin{array}{l}1)2\sqrt x - 5 = 3\\\\2)\sqrt {{x^3}} = 2\sqrt 2 \end{array}\)
مشخص کنید هر عدد زیر بین کدام دو عدد صحیح متوالی قرار می گیرد.
\(\begin{array}{l}1)\sqrt {27} \\\\2)\sqrt {179} \\\\3)\sqrt {288} \end{array}\)
جذر تقریبی اعداد زیر را تا یک رقم اعشار بدست آورید.
\(\begin{array}{l}1)\sqrt {54} \\\\2)\sqrt {120} \end{array}\)
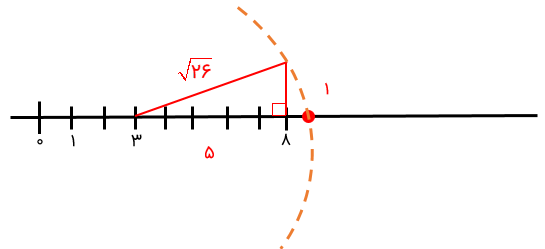
هر یک از اعداد زیر را روی محور اعداد نمایش دهید.
\(\begin{array}{l}1)3 + \sqrt {26} \\\\2)2 - \sqrt {18} \end{array}\)
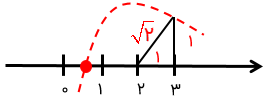
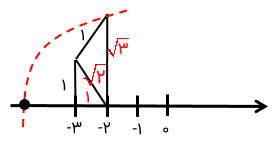
اعداد رادیکالی را از روی نمودار بدست آورید.
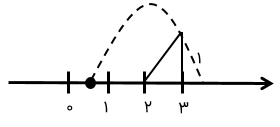

توان یک روش خلاصه سازی ..... است.
هر عدد به توان ..... ، مساوی عدد یک می شود.
عدد ..... به هر توانی برسد، حاصل باز هم یک خواهد شد.
اگر عدد بین صفر و یک باشد، هر چه به توان ..... برسد، کوچکتر می شود.
اگر عددی بزرگتر از یک باشد، هرچه به توان ..... بزرگ تری برسد، ..... می شود.
در محاسبه عبارات توان دار با پایه منفی، اگر منفی داخل پرانتز باشد، ..... نیز به توان می رسد.
در محاسبه عبارات توان دار با پایه منفی، اگر توان زوج باشد، حاصل ..... می شود.
اگر پایه عدد توان دار، عددی منفی باشد و توان فرد باشد، حاصل ..... می شود.
اگر پایه عدد توان دار، عددی منفی باشد و توان فرد باشد، حاصل ..... می شود.
برای محاسبه عبارات توان دار با پایه منفی، اگر علامت منفی، داخل پرانتز نباشد، به ..... نمی رسد.
در محاسبات اعداد توان دار در کنار بقیه عملگر ها مانند جمع و تفریق و ضرب و تقسیم، همواره اولویت با ..... و عبارت توان دار است.
در ضرب دو عبارت توان دار با پایه های مساوی، یک پایه را نوشته و توان ها را با هم ..... می کنیم.
در ..... دو عبارت توان دار اگر توان ها مساوی باشند، پایه ها را در هم ضرب می کنیم و یکی از توان ها را می نویسیم.
اگر یک عدد توان دار به توان برسد، توان ها در هم ..... می شوند.
در تقسیم دو عدد توان دار با پایه های مساوی، یکی از ..... ها را می نویسیم و توان ها را از هم کم می کنیم.
در تقسیم دو عدد توان دار با ..... پایه ها را برهم تقسیم می کنیم و یکی از توان ها را می نویسیم.
..... به نوعی عکس عمل توان رسانی است.
جذر هر عدد مثبت که به توان دو برسد، نتیجه ..... خواهد بود.
جذر اعداد .....، در ناحیه اعداد حقیقی جواب ندارد.
حاصل عبارت \({(\sqrt 3 + \sqrt {12} )^2}\) برابر ..... می باشد.



1736019749.png)