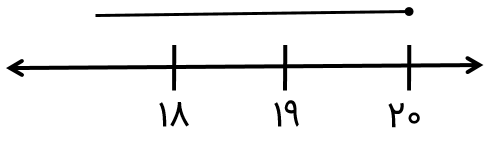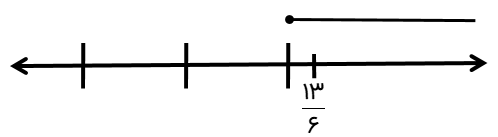تک جمله ای های جبری را مشخص کنید.
\( - 5{x^3},\sqrt {13} , - 3\sqrt x ,3{x^{\frac{5}{3}}},6x{y^3},\frac{2}{{4{x^2}}},3| - x - 1|,x + 1\)
حاصل هر تک جمله ای جبری را به ازای مقادیر داده شده به دست آورید.
\(\begin{array}{l}1) - 4\sqrt 2 {a^3}{b^2} \Rightarrow a = \sqrt 2 ,b = \sqrt 3 \\\\2)\frac{1}{{\sqrt 5 }}(a{b^6}) \Rightarrow a = \sqrt {50} ,b = - 1\end{array}\)
عبارات چند جمله ای زیر را به ساده ترین صورت بنویسید.
\(\begin{array}{l}1)4{y^2} - 5{x^3} - 3{y^2} + 4{x^3} = \\\\2)3x{y^2} - x + 4\sqrt 2 x{y^2} + 5x - y = \end{array}\)
هر عبارات را ابتدا ساده کنید و سپس بر حسب متغیر خواسته شده مرتب کنید.
\(\begin{array}{l}1)5{x^2}y - 10x + 4y - 10x{y^2} + 4{x^2}y - 3 \Rightarrow y\\\\2)({x^5} + 2)(1 - x) + 2({x^6} + 2)(x - 1) \Rightarrow x\end{array}\)
عبارت زیر را کاملا ساده کنید؛ سپس قسمت های خواسته شده را تکمیل نمایید.
\((x + y)({x^2} + {y^2} - 2xy) - (x + y)(x - y)\)
تعداد جملات:
درجه نسبت به x:
درجه نسبت به y:
درجه نسبت به همه متغیر ها:
در هر قسمت، مساحت شکل خواسته شده را به دست آورید.
الف) مساحت مستطیلی به طول x+y و عرض x-y
ب) مساحت مثلث متساوی الاضلاعی به ضلع \(a + \sqrt a \)
هر کسر را به کمک تجزیه ساده کنید.
\(\begin{array}{l}1)\frac{{{x^2} - {y^2}}}{{{x^2} + 2xy + {y^2}}}\\\\2)\frac{{{x^3} + {y^3}}}{{x + y}}\\\\3)\frac{{{{(x + y)}^2} + (x + y)(x - y)}}{x}\end{array}\)
طرف دوم هر تساوی را بنویسید.
\(\begin{array}{l}1){(2a + b - 2c)^2}\\\\2){(a - b - c)^2}\end{array}\)
با کمک اتحاد مزدوج، طرف دوم تساوی های زیر را به دست آورید.
\(\begin{array}{l}1)(\sqrt 3 + \sqrt 5 )(\sqrt 3 - \sqrt 5 )(5 + 3)\\\\2)(x - y)(x + y)({x^2} + {y^2})\end{array}\)
مساحت ذوزنقه ای با ارتفاع \(5x + 4y\) و دو ضلع \(x - 2y\) و \(4x + 3y\) را به دست آورید.
هر عبارت را به کمک اتحاد جمله مشترک تجزیه کنید.
\(\begin{array}{l}1)2{x^2} + 14x + 20\\\\2){x^2} - 11x + 28\\\\3){x^3} + 5x{}^2 + 6x\end{array}\)
طرف دوم تساوی را بنویسید.
\(\begin{array}{l}1){2^{10}} - {2^9} + {2^6}\\\\2){3^8} - 2 \times {6^4} + {2^8}\end{array}\)
حاصل هر عبارت را به کمک اتحاد های به دست آورید.
\(\begin{array}{l}1)104 \times 96\\\\2){5^2} - 5 \times {2^3} + {2^4}\end{array}\)
هر عبارت را تجزیه کنید.
\(\begin{array}{l}1)9{x^2} - 36{y^2}\\\\2){(x - \frac{1}{x})^2} - {(x + \frac{1}{x})^2}\\\\3){x^3} + 27\\\\4)8 - 216{y^3}\end{array}\)
متناظر با محور های زیر، یک نابرابری بنویسید.
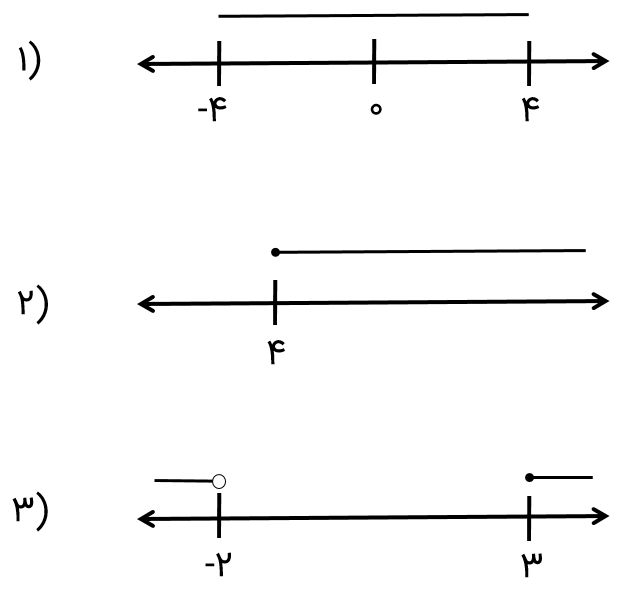
در جای خالی، علامت های \( < \,, = \,, > \) بگذارید تا خواسته مسئله مشخص گردد.
الف) \(1 < b < a\) ، آن گاه \({a^2} \cdots {b^2}\)
ب) \(|a| > |b|,ab > 0\) ، آن گاه \(\frac{{{a^2}}}{{{b^2}}} \cdots 1\)
پ) اگر \(|a| < b\) ، آن گاه \( - a \cdots - b\)
با توجه به اطلاعات داده شده، در هر بخش علامت عبارت را تعیین کنید.
\(\begin{array}{l}1)a < b < c < 0 \to \frac{{a{b^2}}}{{{c^3}}}\\\\2)c < 0 < b < a \to \frac{{ac}}{{ - \sqrt {{b^2}{c^2}} }}\end{array}\)
عبارت های کلامی زیر را به صورت نماد های ریاضی بنویسید.
الف) 2 برابر عددی به علاوه 5 از 4- کوچک تر است.
ب) قدر مطلق هر عدد حقیقی، بزرگ تر یا مساوی خود عدد است.
مجموعه جواب های هر نامعادله را به دست آورید و آن را روی محور نمایش دهید.
\(\begin{array}{l}1)\frac{{x + 4}}{3} - \frac{{x - 2}}{6} \le 5\\\\2)4x + 2(x - 5) > 3\end{array}\)
اگر 4 برابر سن شخصی را با سن دو سال پیش او جمع کنیم، حاصل 4 برابر سن دو سال بعد او است. سن 5 سال آینده این شخص چقدر می باشد؟
هر یک از حروفی که برای نشان دادت رابطه های علمی استفاده می کنیم، ........... می گوییم.
هر یک جمله ای جبری، از دو قسمت ........... و ........... ساخته شده است.
در چند جمله ای های جبری، به قسمت عددی، ........... هم می گوییم.
هر گاه در دو جمله جبری، قسمت حرفی (هم متغیر ها و هم توان های آن ها) کاملا یکسان باشد، به آن ها ........... می گوییم.
از جمع یا تفریق دو یا چند جمله جبری غیر متشابه، عبارتی ایجاد می شود که به آن ........... می گوییم.
هر گاه حاصل دو عبارت جبری به ازای مقادیر مختلفی که برای متغیر ها قرار می دهیم، برابر شود، اصطلاحا می گوییم این دو عبارت متحد هستند یا تشکیل ........... داده اند.
حاصل عبارت برابر با ........... است.
در تجزیه عبارت \({a^8} - {b^8}\) از اتحاد ........... باید استفاده کرد.
حاصل عبارت \(95 \times 105\) را می توان با استفاده از اتحاد ........... به دست آورد.
در اتحاد جمله مشترک \((x + a)(x + b)\) اگر a و b ........... باشند، اتحاد مزدوج ساخته می شود.
حاصل تجزیه عبارت \({x^2} - 10x + 25\) به کمک اتحاد ........... برابر با ........... می شود.
در تجزیه \({x^8} - {y^8}\) می توان ........... مرتبه، عبارت را با اتحاد مزدوج تجزیه نمود.
اگر a و b هم علامت باشند و a<b، همواره رابطه \({a^2} < ab\) برقرار ........... .
اگر \({x^2} < {y^2}\) ........... نتیجه گرفت که x>y.
چنانچه برای \(n \in W\) داشته باشیم \({a^{2n + 1}} < 0\) ، در این صورت علامت a ........... است.
صورت جبری ( توان دوم عددی به علاوۀ 6، حداقل برابر 3 است) را با ........... نمایش می دهیم.
اگر x و y دو عدد حقیقی باشند و \({x^2}y \le 0\) ، آن گاه قطعا y ........... نمی باشد.
مجموعه جواب نامعادله \(2x - 5 \le 3x - 4\) برابر با ........... است.
نامعادله \(6y + 5 < - 6\) را ........... می نامیم.
عبارت \(\sqrt 3 - \sqrt 7 \) را باید در ........... ضرب کنیم تا جواب (4-) شود.



1736019749.png)