جواب تمرین صفحه 109 درس 4 حسابان یازدهم (مثلثات)
تعداد بازدید : 80.84Mپاسخ تمرین صفحه 109 حسابان یازدهم
-گام به گام تمرین صفحه 109 درس مثلثات
-تمرین صفحه 109 درس 4
-شما در حال مشاهده جواب تمرین صفحه 109 حسابان یازدهم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
توابع مثلثاتی زیر را با نمودارهای داده شده نظیر کنید.
الف \(y = - \left| {\sin x} \right|\)
ب \(y = \cos (x + \frac{\pi }{6})\)
پ \(y = \sin (x - \frac{\pi }{3})\)

الف
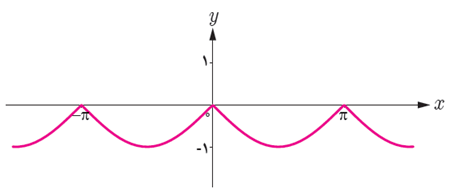
ب

پ

2 در هر یک از نمودارهای زیر بخشی از یک تابع مثلثاتی رسم شده است. با توجه به بخش رسم شده، توابع مثلثاتی داده شده در زیر را به نمودارها نظیر کنید و سپس نمودار را کامل سازید.
الف \(y = - \sin (x + \frac{\pi }{6})\)
ب \(y = \cos (x - \frac{\pi }{3}) - 1\)
پ \(y = 1 + \left| {\cos \,x} \right|\)

الف
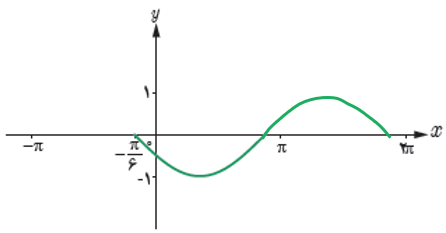
ب

پ
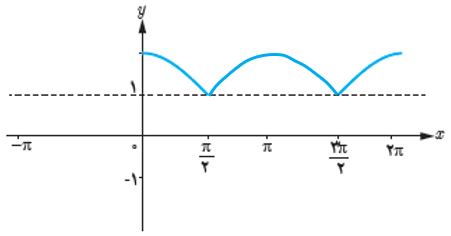
3 با توجه به نمودارهای بالا در سؤال 2، بیشترین و کمترین مقدار توابع مثلثاتی داده شده در آن سؤال در چه نقاطی رخ می دهد؟
الف
\(\left\{ \begin{array}{l}{y_{Max}} = 1 \Rightarrow \left( {\frac{{4\pi }}{3}\;,\;1} \right)\\{y_{Min}} = - 1 \Rightarrow \left( {\frac{\pi }{3}\;,\; - 1} \right)\end{array} \right.\)
ب
\(\left\{ \begin{array}{l}{y_{Max}} = 0 \Rightarrow \left\{ {\left( {\frac{\pi }{3}\;,\;0} \right)\;,\;\left( {\frac{{7\pi }}{3}\;,\;0} \right)} \right\}\\{y_{Min}} = - 2 \Rightarrow \left( {\frac{{4\pi }}{3}\;,\; - 2} \right)\end{array} \right.\)
پ
\(\left\{ \begin{array}{l}{y_{Max}} = 2 \Rightarrow \left\{ {\left( {0\;,\;2} \right)\;,\;\left( {\pi \;,\;2} \right)\;,\;\left( {2\pi \;,\;2} \right)} \right\}\\{y_{Min}} = 0 \Rightarrow \left\{ {\left( {\frac{\pi }{2}\;,\;1} \right)\;,\;\left( {\frac{{3\pi }}{2}\;,\;1} \right)\;} \right\}\end{array} \right.\)
4 با توجه به نمودارهای سؤال 2، کدام یک از توابع مثلثاتی داده شده در آن سؤال در بازهٔ \([0,π]\) یک به یک است؟
اگر بازه بین \(\left[ {0\;,\;\pi } \right]\) که هیچ کدام از نمودارها؛ ولی اگر بازه مورد نظر سوال \(\left[ {\frac{\pi }{3}\;,\;\pi } \right]\) بوده باشد، نمودار (ب).
5 در طراحی روبات های صنعتی برای انعطاف بیشتر در حرکت روبات ها، معمولاً دو مفصل مکانیکی برای بازوی آن به صورت روبه رو در نظر می گیرند.
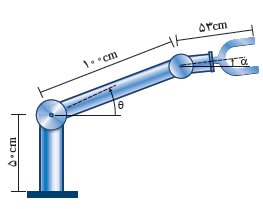 پ
پ
الف ارتفاع نوک گیره این روبات را، از سطح زمین، بر اساس توابعی از \(\theta \) و α مدل سازی کنید. \(\left( { - \frac{\pi }{2} \le \alpha \le \frac{\pi }{2}\;\;,\;\,0 \le \theta \le \frac{\pi }{2}} \right)\)
ب فرض کنید این روبات برای گرفتن یک شیء در ارتفاع \(23/5 cm\) مفصل دوم خود را در حالت \(a = - 30^\circ \) قرار داده است. تعیین کنید زاویه \(\theta \) در این وضعیت چند درجه است؟
الف
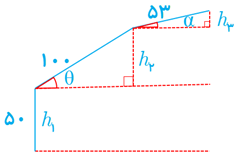
\(\begin{array}{l}{h_1} = 50\\{h_2} = 100\sin \theta \\{h_3} = 53\sin \alpha \\H = {h_1} + {h_2} + {h_3} = 50 + 100\sin \theta + 53\sin \alpha \end{array}\)
ب
\(\begin{array}{l}H = 50 + 100\sin \theta + 53\sin \alpha \\23/5 = 50 + 100\sin \theta + 53\sin \left( { - {{30}^ \circ }} \right)\\ \Rightarrow 23/5 = 50 + 100\sin \theta - 26/5\\ \Rightarrow 100\sin \theta = 0\mathop \Rightarrow \limits^{0 \le \theta \le \frac{\pi }{2}} \theta = {0^ \circ }\end{array}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















