گام به گام فعالیت صفحه 10 درس مجموعه، الگو و دنباله ریاضی (1)
تعداد بازدید : 46.92Mپاسخ فعالیت صفحه 10 ریاضی (1)
-گام به گام فعالیت صفحه 10 درس مجموعه، الگو و دنباله
-فعالیت صفحه 10 درس 1
-1- یک تیم کوه نوردی متشکل از 4 دانش آموز و 3 دانشجوی عضو یک مؤسسهٔ طرفدار محیط زیست است. اعضای این تیم به طور داوطلبانه در روزهای جمعهٔ هر هفته کوه های اطراف شهر خود را از وجود زباله پاک سازی می کنند.
اعضای دانش آموز این تیم مجموعه {آنیتا، زهرا، الناز، الهام} \(A = \) و اعضای دانشجوی آن مجموعه {فاطمه، معصومه، فرزانه} \(B = \) همان گونه که دیده می شود، این دو مجموعه هیچ عضو مشترکی ندارند؛ به عبارت دیگر \(A \cap B = \emptyset \).
الف) اعضای \(A \cup B\) را که بیانگر اعضای تیم کوه نوردی می باشد، بنویسید و جدول زیر را تکمیل کنید.
\(A \cup B = \)
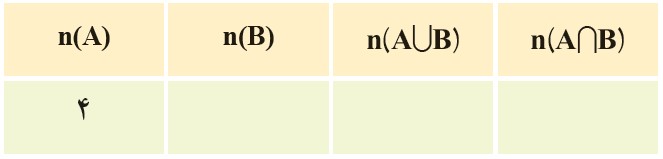
{آنیتا ، زهرا ، الناز ، الهام ، فاطمه ، معصومه ، فرزانه}\(A \cup B = \)
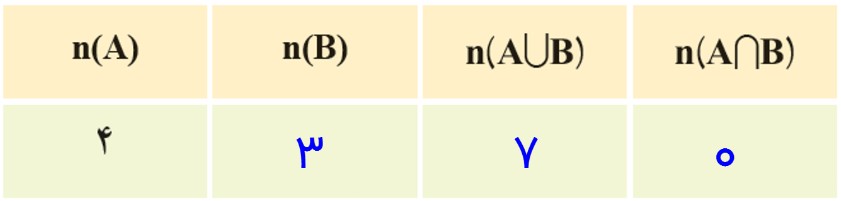
ب) تعداد عضوهای \(A \cup B\) چه رابطه ای با \(n(A)\) و \(n(B)\) دارد؟ این رابطه را به صورت یک فرمول بنویسید.
تعداد عضوهای مجموعه \(A \cup B\) برابر مجموع \(n(A)\) و \(n(B)\) است؛ یعنی:
\(n(A \cup B) = n(A) + n(B)\)
پ) تحت چه شرایطی این فرمول برای دو مجموعه دلخواه A و B برقرار است؟
با این شرط که اشتراک دو مجموعه A و B برابر تهی باشد؛ به عبارت دیگر:
\(A \cap B = \emptyset \)
2- الف) مجموعهٔ شمارنده های طبیعی دو عدد 28 و 30 را به ترتیب A و B می نامیم. موارد خواسته شده را بنویسید.
\(A = \{ \cdots \,,\, \cdots \,,\, \cdots \,,\, \cdots \,,\, \cdots \,,\, \cdots \} \Rightarrow n(A) = 6\) : مجموعه شمارنده های عدد 28
\(A = \{ 1\,,\,2\,,\,4\,,\,7\,,\,14\,,\,28\} \Rightarrow n(A) = 6\)
\(B = \{ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\} \Rightarrow n(B) = \): مجموعه شمارنده های عدد 30
\(B = \{ 1\,,\,2\,,\,3\,,\,5\,,\,6\,,\,10\,,\,15\,,\,30\} \Rightarrow n(B) = 8\)
\(A \cap B = \{ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\} \Rightarrow n(A \cap B) = \) : شمارنده های مشترک 28 و 30
\(A \cap B = \{ 1\,,\,2\} \Rightarrow n(A \cap B) = 2\)
\(A \cup B = \{ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\} \Rightarrow n(A \cup B) = \)
\(A \cup B = \{ 1\,,\,2\,,\,3\,,\,4\,,\,5\,,\,6\,,\,7\,,\,10\,,\,14\,,\,15\,,\,28\,,\,30\} \Rightarrow n(A \cup B) = 12\)
ب) جدول زیر را کامل کنید.
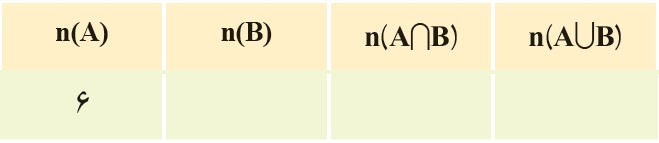
پ) چرا رابطه ای را که در فعالیت (1) به دست آوردید؛ یعنی \(n(A \cup B) = n(A) + n(B)\) در این مثال برقرار نیست؟
زیرا \(n(A \cup B) = 12\) و \(n(A) + n(B) = 14\) است و همچنین مجموعه های A و B با هم اشتراک دارند.
ت) با تکمیل نمودار مقابل، سعی کنید رابطهٔ درست برای \(n(A \cup B)\) را حدس بزنید.
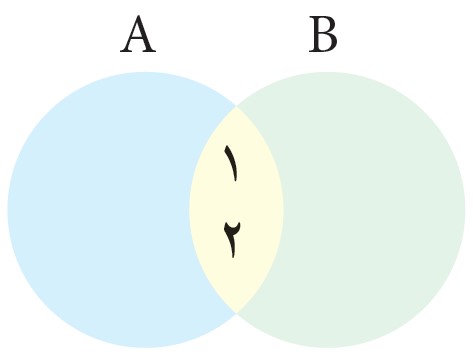
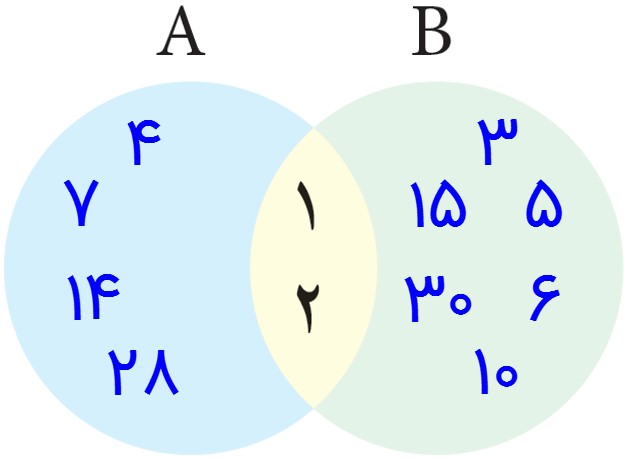
\(n(A \cup B) = n(A) + n(B) - n(A \cap B)\)
همان طور که دیدیم، اگر A و B دو مجموعه متناهی دلخواه باشند، داریم:
\(n(A \cup B) = n(A) + n(B) - n(A \cap B)\)
با توجه به نمودار فوق، در مورد علت درستی این رابطه با دوستان خود بحث کنید.
هنگامی که دو مجموعه ای که با هم اعضایی را اشتراک دارند، با هم اجتماع می گیریم، آن تعداد اعضای مشترک دوبار در جمع ظاهر می شوند و برای اینکه بخواهیم یک بار در جمع شرکت کنند، از مجموع تعداد اعضای دو مجموعه، همان تعداد مشترک را کم می کنیم.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
