جواب فعّالیت صفحه 36 درس 2 هندسه یازدهم (تبدیل های هندسی و کاربردها)
تعداد بازدید : 80.84Mپاسخ فعّالیت صفحه 36 هندسه یازدهم
-گام به گام فعّالیت صفحه 36 درس تبدیل های هندسی و کاربردها
-فعّالیت صفحه 36 درس 2
-شما در حال مشاهده جواب فعّالیت صفحه 36 هندسه یازدهم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
می خواهیم با استدلال دقیق تری نشان دهیم بازتاب، تبدیلی طولپا است. حالت های مختلف یک پاره خط را نسبت به خط بازتاب d در نظر می گیریم و در هر حالت نشان می دهیم که اندازه پاره خط با اندازه تصویر آن برابر است.
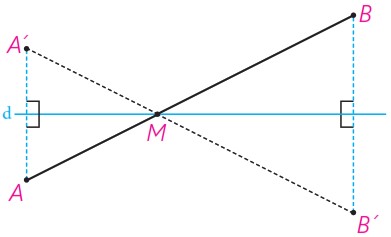
الف ابتدا مسئله را برای حالتی در نظر می گیریم که AB با خط d موازی است.
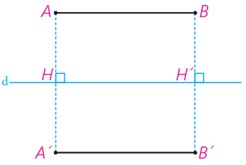
بازتاب A و B را نسبت به خط d پیدا می کنیم و آن را ′A و ′B می نامیم.
چهارضلعی ′ABA′B چه چهارضلعی است؟ چرا؟
طول پاره خط های AB و ′A′B نسبت به هم چگونه اند؟
ب حال فرض می کنیم که فقط یکی از نقاط انتهایی پاره خط داده شده روی خط بازتاب باشد.
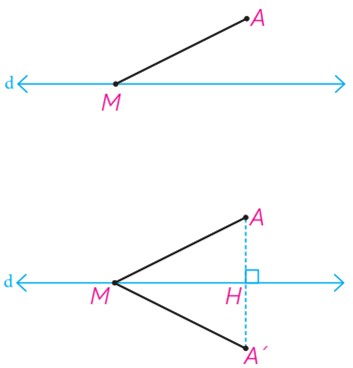
(اگر هر دو نقطه ابتدا و انتهای پاره خط داده شده روی خط بازتاب باشد، اثبات بدیهی است؛ چرا؟)
بازتاب A نسبت به خط d، نقطه ′A و بازتاب M، خود M است.
به عبارتی: ′S(A) = A و S(M) = M
آیا می توانید به کمک هم نهشتی مثلث ها، دلیلی برای تساوی ′MA=MA ارائه کنید؟
آیا می توانید این تساوی را به روش دیگری نشان دهید؟ (از خاصیت عمود منصف یک پاره خط کمک بگیرید).
پ در حالتی که پاره خط AB با خط بازتاب، d نه موازی و نه متقاطع باشد، پاره خط AB را امتداد می دهیم تا خط بازتاب را در نقطه M قطع کند.
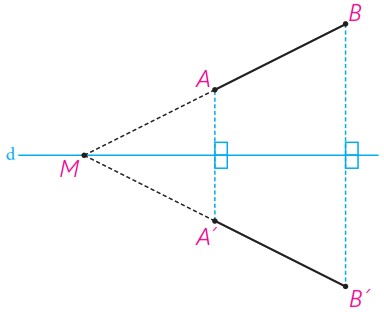
نقطه ′B بازتاب نقطه B را نسبت به خط بازتاب پیدا، و پاره خط ′MB را رسم می کنیم.
ادعا می کنیم که تصویر نقطه A نیز روی خط ′MB واقع می شود؛ چرا؟
حال داریم:
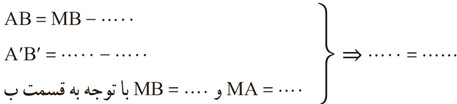
ت در حالتی که پاره خط AB خط بازتاب را در نقطه ای مثل M قطع کند، بازتاب نقطه A را نسبت به خط d پیدا می کنیم و آن را نقطه ′A می نامیم.
پاره خط ′MA را رسم می کنیم و امتداد می دهیم و ادعا می کنیم که بازتاب نقطه B یعنی نقطه ′B هم بر امتداد ′MA واقع است؛ چرا؟
حال داریم:
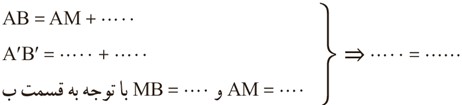
الف
\(\left. \begin{array}{l}AB\parallel d\;,\;AH\begin{array}{*{20}{c}}{}&{}\end{array}\widehat A = \widehat H = {90^ \circ }\\AB\parallel d\;,\;BH'\begin{array}{*{20}{c}}{}&{}\end{array}\widehat B = \widehat {H'} = {90^ \circ }\end{array} \right\} \Rightarrow \)
بنابراین چهارضلعی AHH’A’ یک مستطیل است.
\(\left. \begin{array}{l} \Rightarrow AH = BH' \Rightarrow 2AH = 2BH'\,\,\,\,\,\mathop \Rightarrow \limits_{BH' = B'H'}^{AH = A'H} \,\,\,\,\,AA' = BB'\\\begin{array}{*{20}{c}}{}&{}&{}&{}\end{array}\begin{array}{*{20}{c}}{}&{}&{}&{}\end{array}\begin{array}{*{20}{c}}{}&{}\end{array}\;\;\left. \begin{array}{l}AA' \bot d\\BB' \bot d\end{array} \right\} \Rightarrow AA'\parallel BB'\end{array} \right\} \Rightarrow \)
بنابراین چهارضلعی ABB’A’ یک متوازی الاضلاع است.
\( \Rightarrow \left. \begin{array}{l}AB\parallel A'B'\\AB \bot d\end{array} \right\}A'B' \bot d \Rightarrow \)
بنابراین چهارضلعی ABB’A’ یک مستطیل است.
ب
\(\left. \begin{array}{l}S\left( A \right) = A\\S\left( M \right) = M\end{array} \right\} \Rightarrow MA = MA\)
در این حالت بازتاب پاره خط MA بر روی خط و بر روی خودش منطبق است.
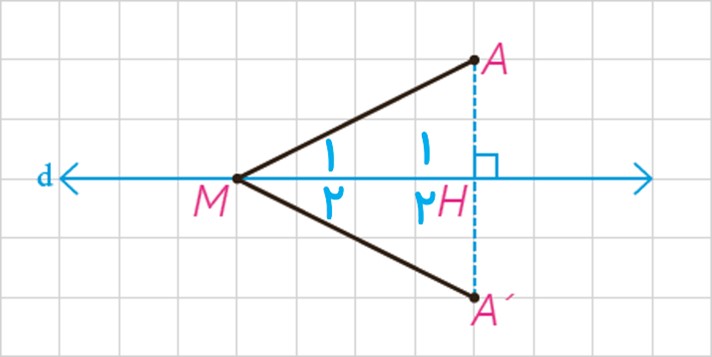
\(:\,\,\,\,\,\left\{ \begin{array}{l}MA = MA'\\\widehat {{M_1}} = \widehat {{M_2}}\end{array} \right.\) بنا به حالت (ض ز ض) \(\left. \begin{array}{l}AH = A'H\\\widehat {{H_1}} = \widehat {{H_2}}\\MH = \begin{array}{*{20}{c}}{}&{}&{}\end{array}\end{array} \right\} \Rightarrow \)
اجزای متناظر \(M\mathop A\limits^\Delta H \cong M\mathop {A'}\limits^\Delta H \Rightarrow \)
خط d عمودمنصف پاره خط AA’ است؛ بنابراین هر نقطه مانند M روی خط d از دو سر پاره خط AA’ به یک فاصله است؛ یعنی: MA=MA’
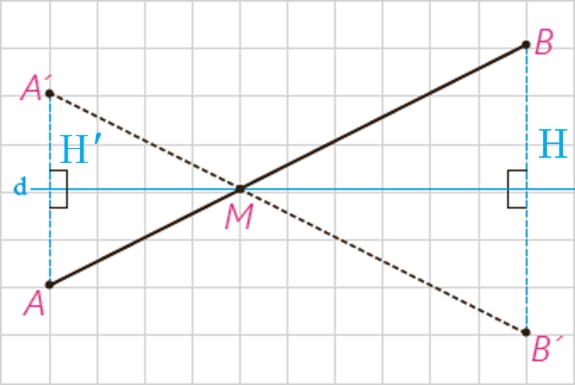
پ
H وسط BB’ و H’ وسط AA’ است. بنا بر تعریف بازتاب، نقاط H و H’ روی خط d یعنی خط بازتاب قرار دارند. با توجه به بند (ب) خط d نیمساز زاویه های AMA’ و BMB’ است:
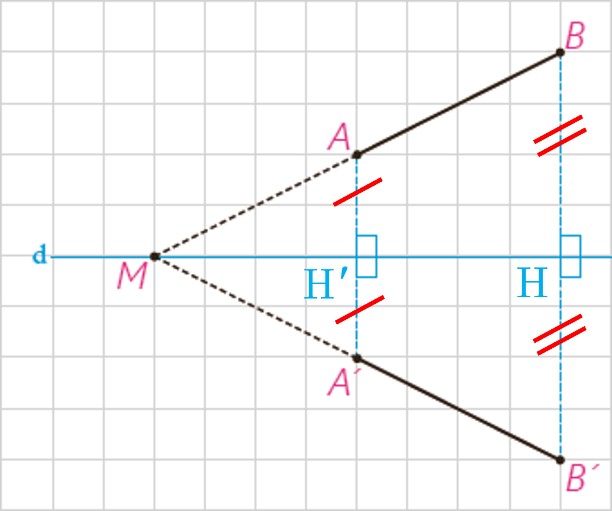
\(\left. \begin{array}{l}\left. \begin{array}{l}\widehat {AMH'} = \widehat {BMH}\\\widehat {A'MH'} = \widehat {AMH'}\end{array} \right\} \Rightarrow \widehat {A'MH'} = \widehat {BMH}\\\begin{array}{*{20}{c}}{}&{}&{}&{}\end{array}\begin{array}{*{20}{c}}{}&{}&{}\end{array}\;\;\;\widehat {B'MH} = \widehat {BMH}\end{array} \right\} \Rightarrow \widehat {A'MH'} = \widehat {B'MH}\)
یک ضلع (MH و MH’) و رأس این دو زاویه بر هم منطبق است، پس اضلاع دیگر هم یعنی MA’ و MB’ بر هم منطبق هستند.
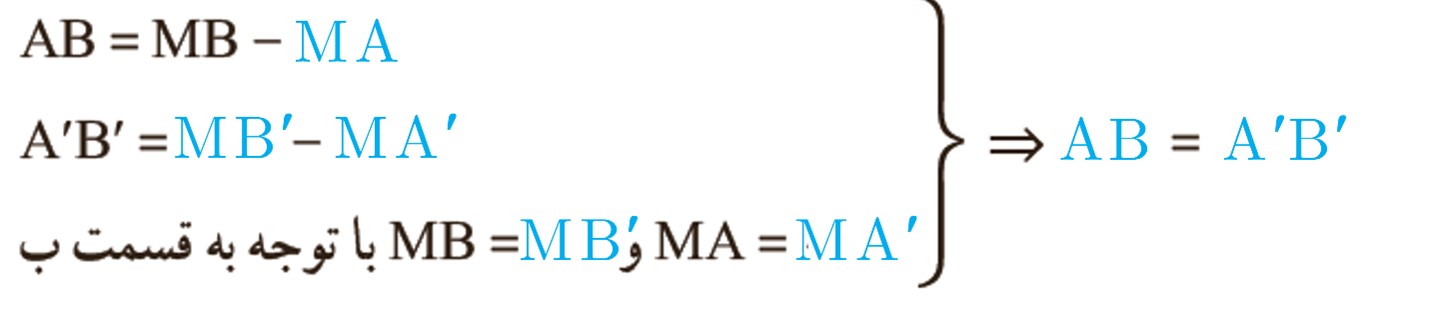
ت
H وسط BB’ و H’ وسط AA’ است. بنا بر تعریف بازتاب، نقاط H و H’ روی خط d یعنی خط بازتاب قرار دارند. با توجه به بند (ب) خط d نیمساز زاویه های AMA’ و BMB’ است:
\(\left. \begin{array}{l}\left. \begin{array}{l}\widehat {AMH'} = \widehat {BMH}\\\widehat {A'MH'} = \widehat {AMH'}\end{array} \right\} \Rightarrow \widehat {A'MH'} = \widehat {BMH}\\\begin{array}{*{20}{c}}{}&{}&{}&{}\end{array}\begin{array}{*{20}{c}}{}&{}&{}\end{array}\;\;\;\widehat {B'MH} = \widehat {BMH}\end{array} \right\} \Rightarrow \widehat {A'MH'} = \widehat {B'MH}\)
یک ضلع (MH و MH’) و رأس این دو زاویه بر هم منطبق است، پس اضلاع دیگر هم یعنی MA’ و MB’ بر هم منطبق هستند.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















