جواب فعّالیت صفحه 40 درس 2 هندسه یازدهم (تبدیل های هندسی و کاربردها)
تعداد بازدید : 80.84Mپاسخ فعّالیت صفحه 40 هندسه یازدهم
-گام به گام فعّالیت صفحه 40 درس تبدیل های هندسی و کاربردها
-فعّالیت صفحه 40 درس 2
-شما در حال مشاهده جواب فعّالیت صفحه 40 هندسه یازدهم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
می خواهیم نشان دهیم دوران، تبدیلی طولپاست.
برای دوران دادن هر پاره خط نظیر AB کافی است نقاط A و B را دوران دهیم تا نقاط ′A و ′B حاصل شود و پاره خط ′A′B را رسم کنیم.
مسئله را برای حالت های مختلف در نظر می گیریم:
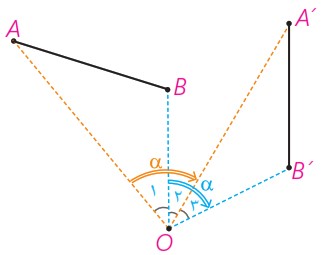
الف مرکز دوران O بر پاره خط AB و امتداد آن واقع نباشد و زاویه دوران از زاویه AOB بیشتر باشد.
با توجه به شکل \(O1 + … = O2 + … = α\)
پس می توان مدعی شد که .......... = ...........
به کمک همنهشتی دو مثلث OAB و ′OA′B نشان دهید AB و ′A′B هم اندازه اند.
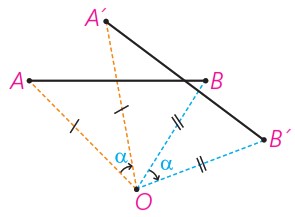
ب به طور مشابه نشان دهید که اگر O بر پاره خط AB واقع نباشد ولی زاویه دوران از زاویه AOB کمتر باشد، باز هم تساوی ′AB =A′B برقرار است.
تذکر: در حالتی که AOB با زاویه دوران α برابر است با هریک از روش های فوق می توان درستی رابطه را نمایش داد.
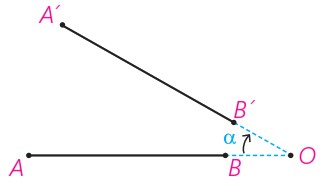
پ اگر نقطه O روی پاره خط AB باشد:

ت به طریق مشابه نشان دهید اگر نقطه O روی امتداد پارخط AB باشد، حکم برقرار است.پ
الف
مرکز دوران O بر پاره خط AB و امتداد آن واقع نباشد و زاویه دوران از زاویه AOB بیشتر باشد.
با توجه به شکل \(O1 + O2 = O2 + O2 = α\)
پس می توان مدعی شد که \(\widehat {AOB} = \widehat {A'OB'}\)
با توجه به تعریف دوران داریم:
\(\,\,\,\,\, \Rightarrow \,\,\,\,\,A\mathop O\limits^\Delta B = A'\mathop O\limits^\Delta B'\) بنا به حالت (ض ز ض)\(\left. \begin{array}{l}\left\{ \begin{array}{l}OA = OA'\\\\OB = OB'\end{array} \right.\\\\\widehat {AOB} = \widehat {A'OB'}\end{array} \right\}\,\,\,\,\, \Rightarrow \,\,\,\,\,\)
\(\,\,\,\,\, \Rightarrow AB = A'B'\) اجزای متناظر
ب
با توجه به شکل:
\(\left. \begin{array}{l}\widehat {AOB} = \alpha + \widehat {A'OB}\\\widehat {A'OB'} = \alpha + \widehat {A'OB}\end{array} \right\} \Rightarrow \widehat {AOB} = \widehat {A'OB'}\)
در نتیجه:
با توجه به تعریف دوران داریم:
\(\,\,\,\,\, \Rightarrow \,\,\,\,\,A\mathop O\limits^\Delta B = A'\mathop O\limits^\Delta B'\) بنا به حالت (ض ز ض) \(\left. \begin{array}{l}\left\{ \begin{array}{l}OA = OA'\\\\OB = OB'\end{array} \right.\\\\\widehat {AOB} = \widehat {A'OB'}\end{array} \right\}\,\,\,\,\, \Rightarrow \,\,\,\,\,\)
\(\,\,\,\,\, \Rightarrow AB = A'B'\) اجزای متناظر
پ
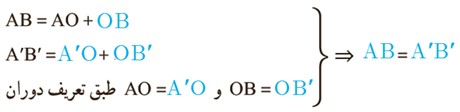
ت
طبق تعریف دوران: \(AO = A'O\quad ,\quad OB = OB'\)
\(\left. \begin{array}{l}AB = AO - OB\\A'B' = A'O - OB'\\AO = A'O\quad ,\quad OB = OB'\end{array} \right\} \Rightarrow AB = A'B'\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















