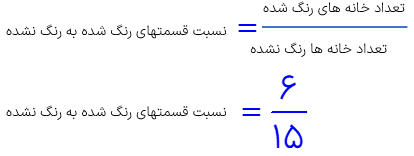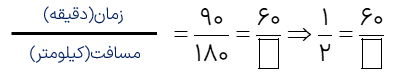درسنامه کامل ریاضی پنجم فصل 3 نسبت، تناسب و درصد
تعداد بازدید : 7.26Mخلاصه نکات ریاضی پنجم فصل 3 نسبت، تناسب و درصد - درسنامه شب امتحان ریاضی پنجم فصل 3 نسبت، تناسب و درصد - جزوه شب امتحان ریاضی پنجم نوبت اول فصل 3 نسبت، تناسب و درصد
نسبت
نسبت
برای مقایسه دو مقدار از مفهوم نسبت استفاده می کنیم. برای مثال در یک کتابخانه 20 عدد كتاب داريم،که 6 تا از آنها کتاب داستان است ؛ نسبت کتاب های داستان به کل کتاب ها 6 به 20 می باشد.
همچنین می توانیم این نسبت را به صورت کسری زیر نمایش دهیم:
\(\frac{6}{{20}}\)
نسبت جزء به کل
در این خصوص تعداد کل را در مخرج نوشته و تعدادی که مربوط به یک مورد خاصی است را در صورت کسر می نویسیم.
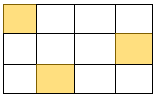
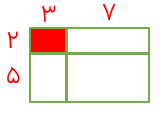
مثال
در شکل زیر نسبت قسمت های رنگ شده به کل قسمت ها را بنویسید.
نسبت جزء به جزء
در این حالت نسبت دو ویژگی خاص را با نوشتن آنها به ترتیب در صورت و مخرج کسر مشخص میکنیم.
مثال
در شکل زیر تعداد خانه های رنگ شده به رنگ نشده را بنویسید.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه پنجم- آزمون آنلاین تمامی دروس پایه پنجم
- گام به گام تمامی دروس پایه پنجم
- ویدئو های آموزشی تمامی دروس پایه پنجم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه پنجم
- فلش کارت های آماده دروس پایه پنجم
- گنجینه ای جامع از انشاء های آماده پایه پنجم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه پنجم
نسبت در مساحت
نسبت در مساحت
نسبت مساحت ها را میتوان به 2 صورت زیر تعیین کرد:
الف) میتوان با تقسیم بندی شکل به واحدهای مساوی این نسبت ها را تعیین کرد.
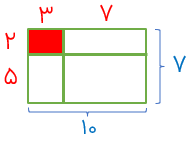
مثال
مساحت قسمت رنگی به مساحت کل شکل چه قدر است؟
\(\frac{{12}}{{24}}\)
ب) در شکل هایی که محاسبه مساحت طبق رابطه های مربوطه به راحتی امکان پذیر است با داشتن اندازه های لازم و بدون تقسیم بندی شکل میتوان نسبت مساحتها را محاسبه کرد و بعد نسبت ها را نوشت.
مثال
در شکل زیر مساحت قسمت رنگی به مساحت کل را بنویسید.
برای مساحت مستطیل بزرگ ، باید طول عرض مستطیل بزرگ را در نظر داشته باشیم.
۶ = ۳×۲ = مساحت قسمت رنگی
۷۰ = ۱۰×۷ = مساحت کل
مساحت قسمت رنگی به مساحت کل \( = \frac{6}{{70}}\)
جزوات جامع پایه پنجم
جزوه جامع ریاضی پنجم فصل 1 عددنویسی و الگوها
جزوه جامع ریاضی پنجم فصل 2 کسر
جزوه جامع ریاضی پنجم فصل 3 نسبت، تناسب و درصد
جزوه جامع ریاضی پنجم فصل 4 تقارن و چندضلعی ها
جزوه جامع ریاضی پنجم فصل 5 عددهای اعشاری
جزوه جامع ریاضی پنجم فصل 6 اندازه گیری
جزوه جامع ریاضی پنجم فصل 7 آمار و احتمال
مقایسه نسبت ها
مقایسه نسبت ها
برای مقایسه عملکرد دو نفر یا دو چیز از نسبت ها استفاده می کنیم.
مثال
مقایسه سرعت دو خودرو در اصل مقایسه نسبت میزان حرکت در واحد زمان آن دو خودرو می باشد.
مقایسه پیشرفت کار دو نقاش مقایسه نسبت میزان رنگ کاری در مدت زمان معین آنها می باشد.
نسبت را با خط کسری نشان می دهیم پس تمام خواص یک کسر را دارا بوده و میتوان مانند کسرها آن را ساده کرد پس در مقایسه نسبت،ها جهت سهولت در کار می توانیم ابتدا آنها را ساده کنیم و بعد ساده شده با هم مقایسه کنیم
مثال
على 540 متر مربع زمین را در 6 روز چمن کاری می کند و رضا 400 متر مربع زمین را در در 5 روز چمن کاری می کند نسبت زمین چمن کاری شده به روز را برای هر دو نفر حساب کنید و عملکرد آنها را با هم مقایسه کنید.

\(\frac{{540}}{6}\left\lfloor > \right\rfloor \frac{{400}}{5}\)
نسبت های مساوی
نسبت های مساوی
همان طور که پیش از این گفته شد، نسبت ها تمامی خواص کسرها را دارند.
مثلا میتوانی هر دو جز نسبت را بر عددی یکسان ضرب یا تقسیم کنیم . در این صورت نسبت جدیدی که با این ضرب یا تقسیم به دست می آید با نسبت اولیه برابر است.
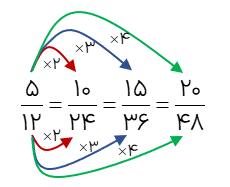
مثال
برای نسبت زیر 3 نسبت دیگر بنویسید.
\(\frac{5}{{12}}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه پنجم- آزمون آنلاین تمامی دروس پایه پنجم
- گام به گام تمامی دروس پایه پنجم
- ویدئو های آموزشی تمامی دروس پایه پنجم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه پنجم
- فلش کارت های آماده دروس پایه پنجم
- گنجینه ای جامع از انشاء های آماده پایه پنجم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه پنجم
تناسب
تناسب
دو نسبت ،مساوی با یکدیگر تناسب تشکیل می دهند. مانند:
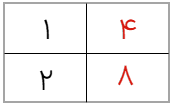
\(\frac{1}{2} = \frac{4}{8}\)
معمولا تناسب را با جدول نشان می دهیم برای مثال تناسب بالا را در جدول به صورت زیر میتوان نشان داد:
در حل مسائل مربوط به نسبت ها می توانیم هم از روش تساوی کسرها و هم از جدول تناسب استفاده کنیم.
مثال
نقاشی در دو ساعت 7 متر مربع را نقاشی می و در چهار روز 16 متر مربع را نقاشی می نسبت تعداد روز به میزان نقاشی شده را در هر دو حالت به دست آورید و بررسی کنید آیا این نسبتها با هم متناسب هستند؟
بعد از ساده کردن، نسبتها با هم برابر نمیشوند لذا تشکیل تناسب نمی دهند و با هم متناسب نیستند.
\(\frac{4}{{16}} = \frac{2}{8},\,\frac{2}{7}\)
جزوات جامع پایه پنجم
جزوه جامع ریاضی پنجم فصل 1 عددنویسی و الگوها
جزوه جامع ریاضی پنجم فصل 2 کسر
جزوه جامع ریاضی پنجم فصل 3 نسبت، تناسب و درصد
جزوه جامع ریاضی پنجم فصل 4 تقارن و چندضلعی ها
جزوه جامع ریاضی پنجم فصل 5 عددهای اعشاری
جزوه جامع ریاضی پنجم فصل 6 اندازه گیری
جزوه جامع ریاضی پنجم فصل 7 آمار و احتمال
حل مسئله به کمک تناسب
حل مسئله به کمک تناسب
منظور از حل تناسب اینست که مقدار خواسته شده را در دو نسبت مساوی به دست بیاوریم.
باید توجه کرد هر کدام از اجزای تناسب اول در چه عدد ضرب یا بر چه عددی تقسیم شده است تا جزء مقابل آنها در تناسب دوم به دست آمده است. البته باید دقت کنیم واحدها در دو تناسب یکسان باشد.
مثال
اتومبیلی 180 کیلومتر را در 1 ساعت و نیم کند این اتومبیل در هر ساعت چند طی می کیلومتر طی می کند؟
۹۰ دقیقه = ۱ ساعت و نیم
۶۰ دقیقه = ۱ ساعت
\(\ 2 \times 60 = 120\)
جدول تناسب
برای حل مسائلی که در آن دو مقدار داده شده باشد از جدول تناسب استفاده میکنیم حالا اگر غیر از خود ،نسبت ها مجموع یا تفاضل نسبت ها هم داده شده باشد میتوانیم یک ردیف به جدول تناسب اضافه کرده و جدول سه طبقه تشکیل دهیم و باز با همان روش تناسب مقادیر خواسته شده را به دست آوریم.
به بیان دیگر در حل مسائل نسبت می توانیم هر ترکیبی از نسبتهای داده شده را به عنوان ردیفی در جدول تناسب اضافه کنیم.
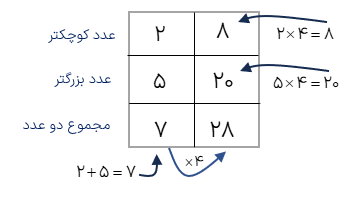
مثال
مجموع دو عدد که نسبت آنها 2 به 5 است برابر 28 میباشد این دو عدد را بیابید.
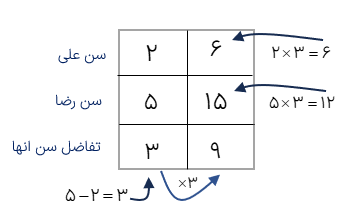
مثال
نسبت سن على به رضا مثل 2 به 5 است. اگر اختلاف سن آنها 9 سال باشد سن هر کدام چقدر است؟
در مسائلی که اختلاف یا مجموع دو مقدار داده شده است ولی در نهایت فقط یکی از مقدارها خواسته می،شود نیازی نیست جدول 3 طبقه درست کنیم و با دست کردن یک جدول 2 طبقه تنها مقادير مجموع یا تفاضل و مقدار خواسته شده را در جدول قرار میدهیم
در برخی موارد نسبت دو مقدار داده میشود و مقدار مجموع یا تفاضل آنها خواسته می شود. در این موارد نیز باید از جدول دو طبقه استفاده کنیم و یک طبقه را به مجموع یا تفاضل نسبت ها اختصاص دهیم.
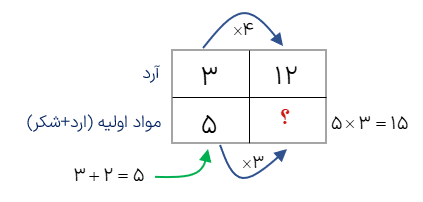
مثال
برای تهیه مواد اولیه ،شیرینی به ازای هر 3 پیمانه آرد 2 پیمانه شکر نیاز داریم با 12 پیمانه آرد در کل چند پیمانه مواد اولیه شیرینی تشکیل می شود؟
درصد
مفهوم درصد
از نظر معنا و مفهوم درصد به معنای کسری از عدد 100 می.باشد یعنی کسری که مخرج آن صد می باشد.
وقتی میخواهیم کسری را که مخرج آن 100 نیست به صورت کسری از صد نشان دهیم می بایست کسر مساوی با آن را طوری بنویسیم مخرج 100 داشته باشد.
مثال
وقتی میگوییم 2 درصد جمعیت یک شهر دانش آموز کلاس پنجم ،هستند یعنی از هر 100 نفر که در این شهر زندگی میکنند 2 نفر در کلاس پنجم درس می خوانند.
میزان 25 درصد تخفیف یعنی از هر 100 تومان 25 تومان گرفته نمی شود و فقط 75 تومان گرفته میشود.
هر نسبتی که مخرج آن 100 باشد را میتوان به صورت درصد بیان کرد، نماد درصد به صورت % می باشد.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه پنجم- آزمون آنلاین تمامی دروس پایه پنجم
- گام به گام تمامی دروس پایه پنجم
- ویدئو های آموزشی تمامی دروس پایه پنجم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه پنجم
- فلش کارت های آماده دروس پایه پنجم
- گنجینه ای جامع از انشاء های آماده پایه پنجم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه پنجم
محاسبه ی درصد
محاسبه ی درصد
می توانیم برخی از نسبت ها را میتوان به صورت درصد بنویسیم.روش کار به این صورت است که کسری با مخرج 100 را مساوی نسبت مورد نظر قرار داده و بعد صورت آن را با روش حل تناسب به دست می آوریم به این ترتیب کسری داریم که از نظر مقدار با نسبت ما مساوی است و مخرج آن صد می باشد.
به طورکلی برای این که یک نسبت را به صورت درصد بنویسیم باید در صورت و مخرج آن نسبت عدد را ضرب کنیم که مخرجش 100 شود.
مثال
در یک مدرسه تعداد دانش آموزان کلاس پنجم به کل دانش آموزان 2 به 5 است. اگر این مدرسه 100 نفر دانش آموز داشته باشد تعداد دانش آموزان کلاس پنجم چند نفر است؟ آن را به صورت درصد بیان کنید.
از هر ۱۰۰ نفر ۴۰ نفر کلاس پنجم هستند ، یعنی ۴۰ دانش آموزان کلاس پنجم هستند.
گاهی اوقات برای اینکه بتوانیم کسر مساوی با مخرج صد را برای کسر موجود بنویسیم، می بایست ابتدا کسر موجود را ساده کنیم و بعد صورت و مخرج آن را در عددی ضرب کنیم که مخرجش 100 شود.
مثال
یک راننده اتوبوس 6 ساعت از شبانه روز را رانندگی میکند او چند درصد از شبانه روز را مشغول رانندگی است؟
هر شبانه روز ۲۴ ساعت می باشد.
\(\left\lfloor {} \right\rfloor = 1 \times 25 = 25\)
برای محاسبه میزان درصد قسمت رنگ شده شکل داده شده می بایست ابتدا نسبت مساحت قسمت رنگی به کل شکل را بنویسیم و بعد با مساوی قرار دادن آن با کسری که مخرج صد دارد به صورت درصد تبدیل کنیم.
مثال
چند درصد شکل زیر رنگ شده است؟
\(\frac{3}{4} = \frac{{\left\lceil {} \right\rceil }}{{100}} \Rightarrow \left\lfloor {\,\,\,} \right\rfloor = 3 \times 25 = 75\)
گاهی درصدی از چیزی داده میشود و بعد مقدار را میخواهند در این صورت باید ابتدا درصد داده شده را به صورت کسری که دارای مخرج 100 میباشد بنویسیم و بعد مقدار را به دست آوریم.
على 3000 تومان پول دارد او 20% از پولش را به برادرش می.دهد حالا او چند تومان پول دارد؟
\(\% 12\) یعنی\(\frac{{12}}{{100}}\)
\(\frac{{12}}{{100}} = \frac{{\left\lceil {} \right\rceil }}{{3000}} \Rightarrow \left\lfloor {\,\,} \right\rfloor = 12 \times 30 = 360\)
۳۶۰ تومان از کل پول (۳۰۰۰ تومان) داده شده است\(3000 - 360 = 2640\)
۲۶۴۰ تومان از پول باقی مانده است.
در مسائل مربوط به "تخفيف" مثل بقيه سوالات ، میتوان با نوشتن نسبتهای متناسب مقادیر مورد نظر را به دست آورد. نکته مهم این که مقدار ،تخفیف، مبلغی است که پرداخت نمی شود.
قیمت یک کتاب 2500 تومان میباشد آن را با %20 تخفیف خریده ایم بدون اینکه مبلغ تخفیف را حساب کنید حساب کنید چقدر باید بپردازیم؟
وقتی %20 تخفیف گرفته ایم یعنی ۸۰%باید پرداخت شود
\(\frac{{80}}{{100}} = \frac{{\left\lceil {} \right\rceil }}{{3000}} \Rightarrow \left\lfloor {} \right\rfloor = 80 \times 30 = 24000\)
۲۴۰۰۰ تومان باید پرداخت شود



1736019749.png)