درسنامه کامل ریاضی پنجم فصل 4 تقارن و چندضلعی ها
تعداد بازدید : 7.27Mخلاصه نکات ریاضی پنجم فصل 4 تقارن و چندضلعی ها - درسنامه شب امتحان ریاضی پنجم فصل 4 تقارن و چندضلعی ها - جزوه شب امتحان ریاضی پنجم نوبت اول فصل 4 تقارن و چندضلعی ها
تعريف خط تقارن
تعريف خط تقارن
خط تقارن خطی است که شکل را به دو قسمت مساوی تقسیم می کند. به طوری که اگر شکل را از روی آن خط تا کنیم آن دو قسمت کاملا بر هم منطبق میشوند. مانند شکل زیر:
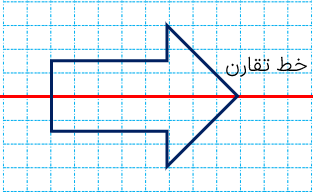
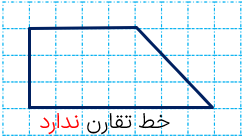
1 بعضی از شکل ها خط تقارن ندارند.
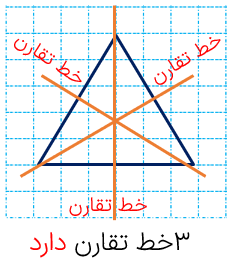
2 برخی شكل ها بیشتر از یک خط تقارن دارند.
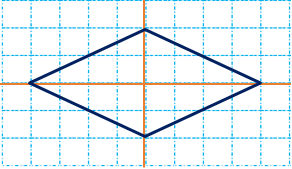
3 در برخی شکل ها قطرها خط تقارن نیز .هستند. مانند: مربع لوزی و دایره.
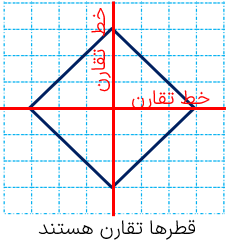
4 با رسم خط های تقارن یک شکل، می توان آن رسم را به چند قسمت مساوی با مساحت های برابر تقسیم کرد. به عنوان نمونه با رسم خط های تقارن لوزی زیر به 4 مثلث مساوی کوچک تقسیم میشود که مساحت همه ی آنها با هم برابر است و مجموع مساحتهای آنها مساحت کل شکل را تشکیل میدهد.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه پنجم- آزمون آنلاین تمامی دروس پایه پنجم
- گام به گام تمامی دروس پایه پنجم
- ویدئو های آموزشی تمامی دروس پایه پنجم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه پنجم
- فلش کارت های آماده دروس پایه پنجم
- گنجینه ای جامع از انشاء های آماده پایه پنجم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه پنجم
قرینه یک نقطه نسبت به خط
قرینه یک نقطه نسبت به خط
برای یافتن قرینه یک نقطه نسبت به یک خط ابتدا به وسیله گونیا از آن نقطه خط عمودی بر خط داده شده رسم کرده و بعد به اندازه خودش ادامه می دهیم و در انتهای خط نقطه مذکور را می گذاریم.
مثال
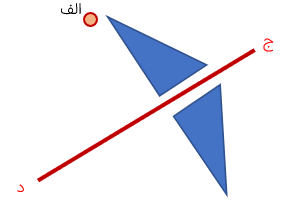
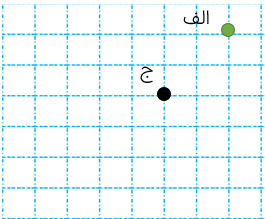
قرینه نقطه ی "الف" را نسبت به خط (ج د) رسم کنید.
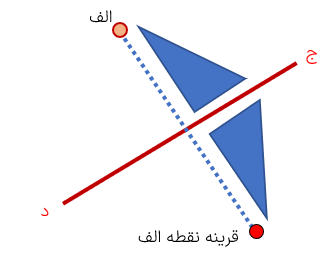
1 قرینه هر نقطه روی خط تقارن، همان نقطه باشد زیرا فاصله آن از خط تقارن صفر میباشد و قابل ادامه دادن نیست تا از خط تقارن خارج شود.
2 در شکل زیر، قرینه ی نقطه ی "الف" که روی روی خط ج د قرار دارد همان نقطه ی "الف" می باشد.
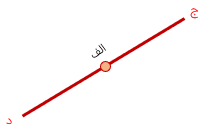
3 برای پیداکردن قرینه ی یک پاره خط نسبت به یک خط ،کافیست قرینه نقاط ابتدا و انتهای پاره خط مذکور را، نسبت به خط تقارن پیدا کنیم و بعد آن دو نقطه را به همدیگر وصل کنیم.پاره خط به دست آمده ی جدید ،قرینه پاره خط اولیه است.
مثال
تقاورن شکل زیر را رسم کنید.
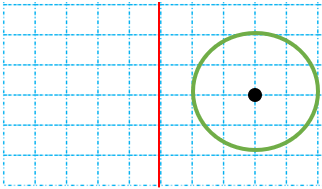
برای رسم قرینه ی یک نقطه نسبت به یک خط باید ابتدا قرینه مرکز دایره را نسبت به خط قرینه داده شده رسم .کنیم بعد به اندازه شعاع دایره اولیه از نقطه قرینه ای که پیدا کرده ایم دایره ای رسم کنیم.
مثال
قرینه دایره زیر را نسبت به خط تقارن رسم کنید.
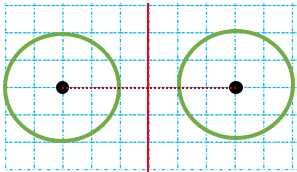
اگر نیمی از یک شکل را در یک طرف خط تقارن داشته باشیم با رسم قرینه شکل نسبت به خط تقارن شکل تکمیل میشود.
جزوات جامع پایه پنجم
جزوه جامع ریاضی پنجم فصل 1 عددنویسی و الگوها
جزوه جامع ریاضی پنجم فصل 2 کسر
جزوه جامع ریاضی پنجم فصل 3 نسبت، تناسب و درصد
جزوه جامع ریاضی پنجم فصل 4 تقارن و چندضلعی ها
جزوه جامع ریاضی پنجم فصل 5 عددهای اعشاری
جزوه جامع ریاضی پنجم فصل 6 اندازه گیری
جزوه جامع ریاضی پنجم فصل 7 آمار و احتمال
مرکز تقارن
مرکز تقارن
مرکز شکل نقطه ای است که اگر هر نقطه از محیط شکل را به آن وصل کنیم و به اندازه خودش ادامه دهیم،دوباره به نقطه ای روی محیط شکل برسیم.
مثال
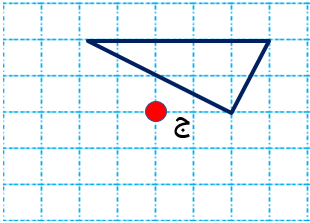
مرکز تقارن شکل زیر را پیدا کنید.
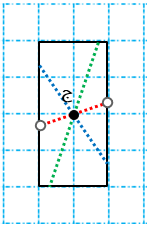
برای پیدا کردن قرینه هرنقطه نسبت به نقطه دیگر، نقطه اول را به نقطه دوم وصل می کنیم و پاره خطی تشکیل می شود که آن را به اندازه خودش در طرف دیگر نقطه دوم ادامه می دهیم.
مثال
قرینه نقطه الف نسبت به نقطه ج را رسم کنید.
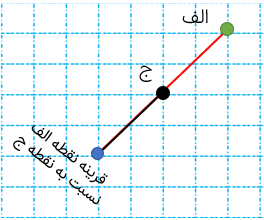
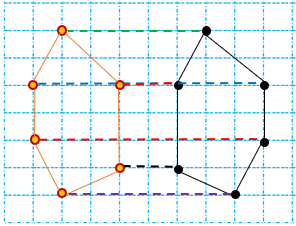
برای رسم قرینه یک شکل نسبت به یک نقطه ابتدا قرینه راس های آن را نسبت به نقطه داده شده به دست می آوریم و سپس آن ها را به هم وصل میکنیم تا قرینه شکل نسبت به نقطه به دست آید.
مثال
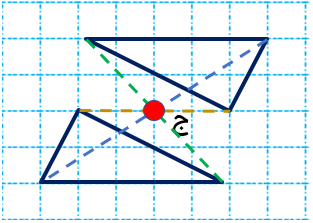
در مثال زیر قرینه شکل ،را نسبت به نقطه "ج" رسم کنید.
همه شکل ها دارای مرکز تقارن نیستند. مانند: انواع مثلث و ذوزنقه.
چند ضلعی ها
چند ضلعی ها
در سال ،گذشته با چند ضلعی ها آشنا شدیم. اکنون به آشنایی بیشتر و ارائه نکاتی می پردازیم.
مجموع زاویه های داخلی هر مثلث 180 درجه می باشد. در این خصوص نوع مثلث مهم نیست.
مثال
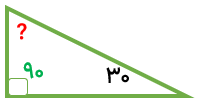
اندازه زاویه خواسته شده را پیدا کنید.
مثلث قائم الزاویه است. پس زاویه دیگر 90 درجه است.
در هر مثلث متساوى الساقين اندازه دو ضلع با هم برابر است و همچنین اندازه دو زاویه کنار قاعده با هم برابر است.
مثال
اندازه زاویه خواسته شده را حساب کنید.
چون مثلث متساوی الساقین است دو زاویه کنار قاعده با هم برابرند جمع دو زاویه با هم ۸۰ میباشد
۱۸۰-۱۰۰ = ۸۰
پس اندازه هر زاویه ۴۰ میشود:
۲÷80=۴۰
1 در هر مثلث متساوی الاضلاع، اندازه همه اضلاع برابر است و همچنین اندازه همه زاویه ها . با هم برابر است و هر کدام 60 درجه می باشد.
2 در هر مثلث قائم الزاویه اندازه یک ،زاویه همواره 90 دذرجه است بنابراین مجموع دو زاویه دیگر ، برابر با 90 درجه می باشد.
مثال
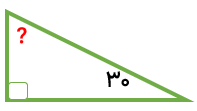
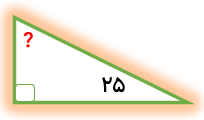
مثلث زیر قائم الزاویه است. اندازه زاویه خواسته شده را به دست آورید.
در مثلث قائم الزاویه، مجموع دو زاویه دیگر غیر از زاویه قائمه ۹۰ درجه است.
90=25=؟
65=25-90=؟
1 دو زاویه که مجموع آنها با هم 90 درجه باشد را متمم .گویند برای مثال دو زاویه زیر متمم هستند.
2 اگر دو زاویه با همدیگر تشکیل زاویه نیم صفحه دهند (یعنی مکمل یکدیگر باشند) در این صورت برای به دست آوردن زاویه نامشخص باید اندازه زاویه دیگر که) مشخص شده است را از 180 درجه کم کنیم.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه پنجم- آزمون آنلاین تمامی دروس پایه پنجم
- گام به گام تمامی دروس پایه پنجم
- ویدئو های آموزشی تمامی دروس پایه پنجم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه پنجم
- فلش کارت های آماده دروس پایه پنجم
- گنجینه ای جامع از انشاء های آماده پایه پنجم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه پنجم
نیمساز
نیمساز
نیمساز زاویه نیم خطی است که زاویه را به دو قسمت مساوی تقسیم می کند.جهت رسم نیمساز ابتدا به کمک نقاله زاویه را اندازه میگیریم و نصف اندازه آن را مشخص کرده و علامت می.گذاریم اگر از نقطه علامت گذاری شده به راس ،زاویه یک خط راست رسم کنیم نیمساز زاویه رسم می شود.
مثال
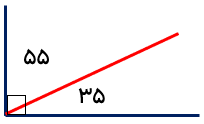
در شکل زیر ابتدا زوايه (ب ج س) را اندازه می گیریم که 80 درجه میباشد. نصف آن می شود 40 درجه حالا زاویه 40 درجه را علامت زده و از راس ،زاویه به آن خطی وصل میکنیم. این خط نیمساز زاویه است.
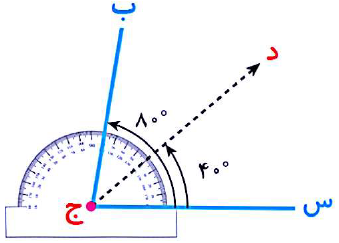
برای محاسبه اندازه دو زاویه ای که از نیمساز به دست می آیند کافیست اندازه زاویه را بر 2 تقسیم کنیم
جزوات جامع پایه پنجم
جزوه جامع ریاضی پنجم فصل 1 عددنویسی و الگوها
جزوه جامع ریاضی پنجم فصل 2 کسر
جزوه جامع ریاضی پنجم فصل 3 نسبت، تناسب و درصد
جزوه جامع ریاضی پنجم فصل 4 تقارن و چندضلعی ها
جزوه جامع ریاضی پنجم فصل 5 عددهای اعشاری
جزوه جامع ریاضی پنجم فصل 6 اندازه گیری
جزوه جامع ریاضی پنجم فصل 7 آمار و احتمال
مجموع زاویه های چند ضلعی ها
مجموع زاویه های چند ضلعی ها
می دانیم مجموع زاویه های داخلی هر مثلث از هر نوعی که باشند برابر با 180 درجه می باشد. حالا با استفاده از ،این می توانیم زاویه های داخلی چند ضلعی ها را حساب کنیم فقط کافیست چند ضلعی ها را به چند مثلث تبدیل کنیم.
مثال
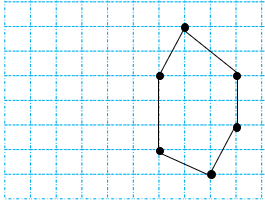
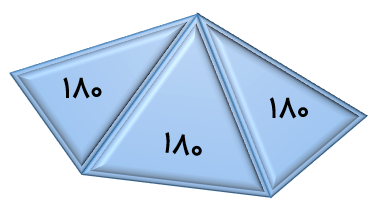
جمع زاویه های داخلی شکل زیر را حساب کنید.
با توجه به اینکه شکل 5 ضلعی می باشد و می توان 3 مثلث در آن درست ،کرد جواب به صورت زیر حساب میشود.
۵۴۰ = ۱۸۰× ۳ = مجموع زاویه های پنج ضلعی
مجموع زاویه های هر چهار ضلعی برابر با 360 درجه است.
مثال
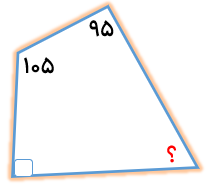
مقدار زاویه خواسته شده را حساب کنید.
شکل داده شده چهار ضلعی می باشد. لذا مجموع زاویه های داخلی 360 درجه می باشد. چون میتواند شامل دو تا مثلث شود زاوییه های داخلی هر مثلث هم 180 در جه است).
360=؟+95+105+90=مجموع زاویه های چهار ضلعی
1 در مربع مستطیل متوازی الاضلاع و لوزی مجموع دو زاویه کنار هم همواره 180 درجه است.
2 در لوزی و ،مربع قطرها نیمساز و بر هم عمود هستند.
3 در مربع و لوزی چهارضلع با هم برابرند ولی در متوازی الاضلاع و مستطیل فقط ضلع های روبرو برابرند.
4 در مربع لوزی متوازی الاضلاع و مستطیل قطرها همدیگر را نصف می کنند.
5 برای رسم انواع متوازی الاضلاع، با توجه به ویژگی آنها با داشتن اندازه قطرها، تنها کافیست به این نکته توجه کنیم که قطرها طوری رسم شوند که یکدیگر را نصف کنند.



1736019749.png)