درسنامه کامل ریاضی پنجم فصل 6 اندازه گیری
تعداد بازدید : 7.26Mخلاصه نکات ریاضی پنجم فصل 6 اندازه گیری - درسنامه شب امتحان ریاضی پنجم فصل 6 اندازه گیری - جزوه شب امتحان ریاضی پنجم نوبت اول فصل 6 اندازه گیری
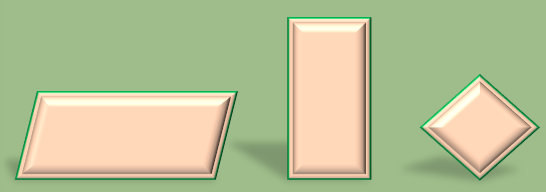
چهار ضلعی ها
چهار ضلعی ها
هر چهار ضلعی از برخورد چهار پاره خط تشکیل می شود.
متوازی الاضلاع
هر چهار ضلعی که در آن ضلع های رو به رو با هم موازی ،باشند متوازی الاضلاع نام دارد. مانند شکل های زیر:
خواص متوازی الاضلاع
ضلع های رو به رو با هم برابرند.
ضلعهای رو به رو با هم موازی اند.
زاویه های رو به رو با هم برابرند
قطرها همیشه یک دیگر را نصف می کنند
هر قطر، شکل را به دو مثلث مساوی تقسیم می کند.
مجموع زاویه های کنار هم 180 درجه است.
مساحت متوازی الاضلاع
با داشتن اندازه قاعده و ارتفاع نظیر آن با استفاده از فرمول ،زیر میتوانیم مساحت متوازی الاضلاع را به دست آوریم
ارتفاع × قاعده = مساحت متوازی الاضلاع
ارتفاع در متوازی الاضلاع میتواند در داخل یا خارج از شکل باشد
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه پنجم- آزمون آنلاین تمامی دروس پایه پنجم
- گام به گام تمامی دروس پایه پنجم
- ویدئو های آموزشی تمامی دروس پایه پنجم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه پنجم
- فلش کارت های آماده دروس پایه پنجم
- گنجینه ای جامع از انشاء های آماده پایه پنجم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه پنجم
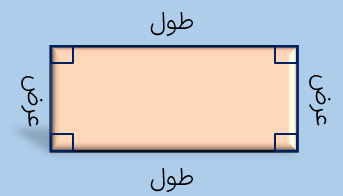
مستطيل و مربع
مستطيل و مربع
مستطیل چهار ضلعی ای است که دارای چهار زاویه ی 90 درجه باشد همچنین میتوان گفت مستطيل نوعى متوازی الاضلاع می باشد.
خواص مستطيل
ضلع های رو به رو با هم برابرند.
ضلع های رو به رو با هم موازی اند.
همه زاویه ها با هم برابرند.
قطرها با هم برابرند
قطرها یک دیگر را نصف می کنند.
قطرها شکل را به دو مثلث مساوی تقسیم می کنند.
محیط و مساحت مستطیل
با داشتن طول و عرض یک مستطیل می توان محیط و مساحت آن را مطابق فرمول زیر حساب کرد.
عرض × طول = مساحت مستطیل
۲ ×(عرض + طول) = محیط مستطیل
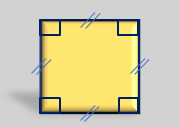
مربع
مربع چهار ضلعی ای است که دارای چهار ضلع برابر و چهار زاویه 90 درجه است همچنین میتوان گفت ؛ مربع نوعی مستطیل میباشد که دارای اضلاع برابر می باشد.
خواص مربع
ضلع های رو به رو موازی اند.
قطرها با هم برابرند
قطرها همدیگر را نصف می کنند
قطرها بر هم عمود هستند.
محیط و مساحت مربع
با داشتن اندازه ضلع ،مربع میتوان از طریق فرمول زیر محیط و مساحت آن را حساب کرد.
خودش× یک ضلع = مساحت مربع
۴ × یک ضلع = محیط مربع
جزوات جامع پایه پنجم
جزوه جامع ریاضی پنجم فصل 1 عددنویسی و الگوها
جزوه جامع ریاضی پنجم فصل 2 کسر
جزوه جامع ریاضی پنجم فصل 3 نسبت، تناسب و درصد
جزوه جامع ریاضی پنجم فصل 4 تقارن و چندضلعی ها
جزوه جامع ریاضی پنجم فصل 5 عددهای اعشاری
جزوه جامع ریاضی پنجم فصل 6 اندازه گیری
جزوه جامع ریاضی پنجم فصل 7 آمار و احتمال
لوزی
لوزی
چهار ضلعی ای که دارای چهار ضلع مساوی است را لوزی می نامیم. همچنین میتوان گفت لوزی، نوعی متوازی الاضلاع است که ضلع های آن با هم برابر است.
خواص لوزی
اضلاع رو به رو با هم موازی اند.
زاویه های رو به رو با هم برابرند.
قطرها همدیگر را نصف می کنند.
قطرها بر هم عمودند.
مجموع زوایای کنار هم 180 درجه است.
مساحت لوزی
با داشتن اندازه دو قطر لوزی مساحت آن را طبق فرمول زیر محاسبه میکنیم:
۲ ×حاصل ضرب دو قطر = مساحت لوزی
مثال
قطر بزرگ یک لوزی 6 و قطر کوچک آن 4 می باشد. مساحت لوزی را حساب کنید.
۲ ÷حاصل ضرب دو قطر = مساحت لوزی
\((6 \times 4) \div 2 = 24 \div 2 = 12\) = مساحت لوزی
مربع، نوعی لوزی است که زاویه ها یا قطرهای آن با هم برابرند لذا مساحت مربع را میتوان از رابطه ی گفته شده برای مساحت لوزی به صورت فرمول زیر نیز محاسبه کرد.
۲ ÷خودش × قطر = مساحت مربع
مثال
در شکل زیر قطر مربع را داریم. حالا مساحت مربع زیر را به دست می آوریم.
۲ ÷خودش × قطر = مساحت مربع
\(\left( {6 \times 6} \right) \div 2 = 36 \div 2 = 18\)
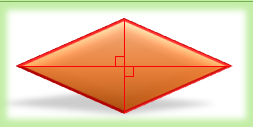
اگر قطرهای یک لوزی را رسم کنیم به 4 مثلث قائم الزاویه با مساحت های برابر تقسیم میشود.
محیط لوزی
با داشتن اندازه یک ضلع لوزی میتوان فرمول را به صورت زیر به دست آورد:
۴ × یک ضلع = محیط لوزی
رسم لوزی
برای رسم ،لوزی کافیست اندازه دو قطر را داشته باشیم این دو قطر را طوری رسم می که دو قطر همدیگر را قطع کرده بر هم عمود باشند و همدیگر را نصف کرده باشند.
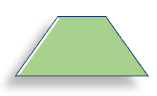
ذوزنقه
ذوزنقه
هر چهار ضلعی ای که فقط دارای دو ضلع موازی باشد ذوزنقه نام دارد.
انواع ذوزنقه
ذوزنقه متساوى الساقين: ذوزنقه ای است که در آن دو ضلع غیر موازی با هم برابر هستند.
ذوزنقه قائم الزاويه: ذوزنقه ای است که دارای دو زاویه ی قائمه می باشد.
فقط در یک ذوزنقه ی متساوی الساقین است که قطرها با هم برابرند.
مساحت ذوزنقه
مساحت ذوزنقه از طریق فرمول زیر به دست می آید:
۲ ÷(ارتفاع ×مجموع دو قاعده)= مساحت ذوزنقه
مثال
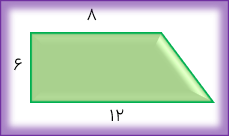
مساحت ذوزنقه زیر را حساب کنید.
۲ ÷(ارتفاع ×مجموع دو قاعده)= مساحت ذوزنقه
.\((8 + 12 \times 6) \div 2 = 120 \div 2 = 60\) =مساحت ذوزنقه
مساحت شکل های ترکیبی
گاهی اوقات با تقسیم بندی های مناسب می توانیم شکلها را به چند شکل شناخته شده که برای محاسبه مساحت آنها فرمول ارائه شده است تبدیل کنیم و مساحت آنها را یک به یک محاسبه کرده و در نهایت با هم جمع میکنیم تا مساحت کل شکل به دست آید.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه پنجم- آزمون آنلاین تمامی دروس پایه پنجم
- گام به گام تمامی دروس پایه پنجم
- ویدئو های آموزشی تمامی دروس پایه پنجم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه پنجم
- فلش کارت های آماده دروس پایه پنجم
- گنجینه ای جامع از انشاء های آماده پایه پنجم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه پنجم
دایره
دایره
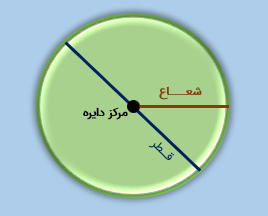
هر دایره شامل اجزای زیر می باشد:
مرکز : نقطه ای در وسط دایره که از تمام قسمت های آن به یک فاصله است.
شعاع: پاره خطی که مرکز را به محیط دایره وصل می کند.( شعاع نصف قطر است).
قطر: پاره خطی که دو نقطه از محیط دایره را به هم وصل میکند و از مرکز هم عبور می کند.(قطر دو برابر شعاع است).
هر دایره بی نهایت شعاع و قطر دارد.
محیط دایره
جهت محاسبه محیط دایره از فرمول زیر استفاده می کنیم:
۳/۱۴ × قطر = محیط دایره
به عدد3/14 که نسبت محیط دایره به قطر آن می باشد عدد پی نیز گفته می شود.
مثال
محیط دایره ای با شعاع 3 سانتی متر را حساب کنید.
۶ = ۲×۳ = ۲× شعاع = قطر
3/14 × قطر = محیط دایره
18/84=محیط دایره
1 هرگاه شعاع یا قطر یک دایره در عددی ضرب شود، محیط آن نیز در همان عدد ضرب می شود. به عنوان مثال اگر قطر یک دایره دو برابر شود محید آن نیز دو برابر میشود و یا اگر قطر یک دایره نصف شود محیط آن نیز نصف می شود.
2 برای تبدیل دقیقه به ساعت باید نسبت زیر را تشکیل دهیم.
مثال
یک ربع چه کسری از ساعت است؟
\(\frac{{{{15}_{ \div 3}}}}{{{{60}_{ \div 3}}}} = \frac{{{5_{ \div 5}}}}{{{{20}_{ \div 5}}}} = \frac{1}{4}\)
مقدار حرکت نوک عقربه دقیقه شمار در ساعت
اگر شعاع یا قطر صفحه ی ساعتی را داشته باشیم از رابطهی رو به رو میتوانیم میزان جا به جایی نوک عقربه ی دقیقه شمار را به دست آوریم.
مثال
اگر شعاع یک ساعت 10 سانتی متر باشد میزان جابجایی نوک عقربه ی دقیقه شمار از ساعت 2:45 به ساعت 3:00 چند سانتی متر است؟
میزان جابجایی 7/15 سانتی متر می باشد.
۲۰ = ۲×۱۰ = ۲ × شعاع = قطر
8/62=14/3×۲۰=14/3× قطر = محیط دایره
میزان جابجایی \(\frac{{15}}{{60}} \times 62/8 = \frac{1}{4} \times \frac{{628}}{{10}} = \frac{{157}}{{10}} = 15/7\)
اگر یک استوانه داشته باشیم، طول خط یا برچسب دور آن برابر با محیط دایره ی سقف یا کف آن می باشد.
محیط نیم دایره
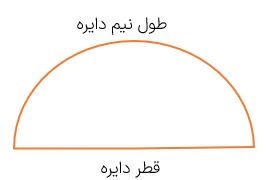
محیط یک نیم دایره از دو بخش تشکیل شده است:
الف) طول نیم دایره (نصف محیط دایره)
ب) قطر دایره
قطر دایره + طول نیم دایره = محیط شکل
جزوات جامع پایه پنجم
جزوه جامع ریاضی پنجم فصل 1 عددنویسی و الگوها
جزوه جامع ریاضی پنجم فصل 2 کسر
جزوه جامع ریاضی پنجم فصل 3 نسبت، تناسب و درصد
جزوه جامع ریاضی پنجم فصل 4 تقارن و چندضلعی ها
جزوه جامع ریاضی پنجم فصل 5 عددهای اعشاری
جزوه جامع ریاضی پنجم فصل 6 اندازه گیری
جزوه جامع ریاضی پنجم فصل 7 آمار و احتمال
حجم
حجم
مقدار فضایی که یک جسم اشغال میکند را حجم آن جسم می گویند.
مكعب
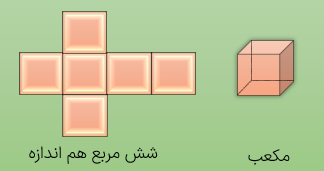
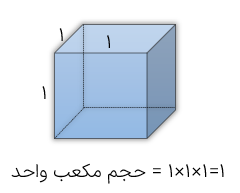
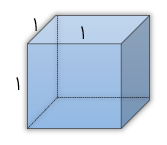
به جسم حاصل از تا کردن و به هم چسباندن شش مربع هم اندازهی مانند شکل زیر مکعب می گوییم.
مكعب واحد
مكعب واحد مکعبی است که از شش مربع با اندازه 1 واحد درست شده باشد. اگر واحد اندازه گیری سانتی متر باشد حجم مكعب واحد که از شش مربع با اندازه هر ضلع 1 سانتی متر درست شده برابر با یک سانتی متر “مکعب" است.
واحد اندازه گیری حجم
برای اندازه گیری حجم یک جسم از مکعب واحد استفاده میکنیم
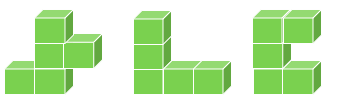
حجم یک جسم با تغییر شکل ظاهری آن تغییر نمی کند.
هر سه تا شکل از ۷ مکعب درست شده اند پس حجم همه ی آنها با هم برابر است
مكعب مستطيل
مكعب مستطيل
دو نوع مكعب مستطیل داریم:
نوع اول: مستطیلی که از تا کردن و چسباندن 6 مستطیل که دو به دو با هم برابر هستند درست می شود.
نوع دوم: از تا کردن و جسباندن 2 مربع و 4 مستطیل هم اندازه درست میشود.
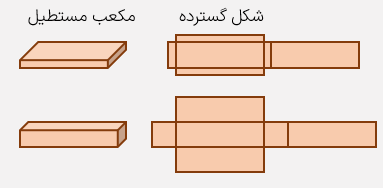
هر مکعب مستطیل دارای "طول" ، "عرض" و عدد"ارتفاع" است.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه پنجم- آزمون آنلاین تمامی دروس پایه پنجم
- گام به گام تمامی دروس پایه پنجم
- ویدئو های آموزشی تمامی دروس پایه پنجم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه پنجم
- فلش کارت های آماده دروس پایه پنجم
- گنجینه ای جامع از انشاء های آماده پایه پنجم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه پنجم
حجم مكعب مستطيل
حجم مكعب مستطيل
برای محاسبه حجم مكعب مستطیل از فرمول زیر استفاده می کنیم:
ارتفاع ×عرض×طول = حجم مکعب مستطیل
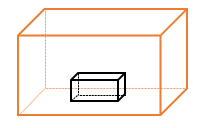
اگر مکعبی داخل مکعب دیگر باشد برای محاسبهی فضای بین آن دو مکعب باید ابتدا حجم مكعب بیرونی را حساب کنیم در مرحله دوم حجم مکعب داخلی را حساب میکنیم در نهایت حجم مکعب داخلی را از حجم مكعب بیرونی کم میکنیم:
حجم مکعب داخلی - حجم مکعب بیرونی = حجم فضای بین دو مکعب
مثال
در یک جعبه به شکل مکعب و با ابعاد 20 سانتی متر جعبه کوچکتری با ابعاد ،5، 20 و 30 سانتی متر قرار داده ایم فضای خالی بین جعبه و کارتن چند یانتی متر مکعب است؟
۸۰۰۰ = ۲۰×۲۰×۲۰ = حجم مکعب بزرگتر
۳۰۰۰ ۳۰×۲۰×۵ = حجم مکعب مستطیل کوچک
۵۰۰۰ = ۸۰۰۰-۳۰۰۰ = حجم فضای بین مکعب و مکعب مستطیل
اگر بخواهیم مکعب مستطیل بزرگی را با تعدادی مكعب مستطیل کوچک تر پر کنیم برای اینکه بدانیم چند تا مکعب مستطیل کوچک برای این کار نیاز داریم باید حم مكعب مستطیل بزرگتر را به حجم مکعب مستطیل کوچکتر تقسیم کنیم تا مشخص شود چند برابر آن است.
مثال
در یک کارخانه کبریت سازی هر 12 تا کبریت با ابعاد 1، 4 و 5 سانتی متر در یک جعبه قرار می گیرد. حجم جعبه چند سانتی متر مکعب است؟
سانتی متر مکعب ۲۰ = ۵×۴×۱ = حجم هر کبریت
سانتی متر مکعب ۲۴۰ = ۲۰×۱۲= حجم جعبه
برخی اجسام شکل مشخصی ندارند و به دست آوردن حجم آنها به سادگی امکان پذیر نیست. برای این کار ابتدا حجم مشخصی از آب را درون یک ظرف درجه بندی شده میریزیم و بعد جسم مورد نظر را داخل ظرف آب قرار میدهیم. تا آب روی جسم را بگیرد. حالا بررسی میکنیم سطح آب چقدر بالاتر ر آمده است.
مثال
ظرف به شکل مكعب مستطيل داریم که طول و عرض آن به ترتیب 2 و 10 می باشد ابتدا ارتفاع آب 5 بوده است وقتی سنگی را داخل آن می اندازیم، ارتفاع آب به 7 می رسد. حجم سنگ را حساب کنید.
سانتی متر ۲ = 7-5= تغییر ارتفاع آب
سانتی متر مکعب ۴۰=۲×۱۰×۲ = حجم
جزوات جامع پایه پنجم
جزوه جامع ریاضی پنجم فصل 1 عددنویسی و الگوها
جزوه جامع ریاضی پنجم فصل 2 کسر
جزوه جامع ریاضی پنجم فصل 3 نسبت، تناسب و درصد
جزوه جامع ریاضی پنجم فصل 4 تقارن و چندضلعی ها
جزوه جامع ریاضی پنجم فصل 5 عددهای اعشاری
جزوه جامع ریاضی پنجم فصل 6 اندازه گیری
جزوه جامع ریاضی پنجم فصل 7 آمار و احتمال
گنجایش
گنجایش
مقدار مایعی که درون یک ظرف قرار میگیرد را گنجایش آن ظرف می نامند. برای مثال اگر یک ظرف برای پر شدن از آب برای مثال اگر یک ظرف برای پر شدن از آب نیاز به 5 لیتر آب داشته باشد، می گوییم گنجایش این ظرف 5 لیتر میباشد.
شباهت و تفاوت حجم و گنجایش
شباهت: روش محاسبه حجم و گنجایش از نظر فرمول یکسان میباشد
تفاوت: حجم جسم مقدار فضایی است که جسم اشغال کرده است ولی گنجایش یک جسم مقدار فضای خالی درون یک جسم است.
مثال
فرض کنیم یک ظرف تواند حداكثر 5 لیتر آب را در خود جای دهد و اکنون 3 لیتر آب در آن باشد یعنی هنوز امکان اضافه کردن 2 لیتر دیگر آب جهت پر شدن داشته باشد. در این صورت میگوییم حجم ظرف 5 لیتر است و گجایش آن 2 لیتر می باشد.
واحدهای اندازه گیری مایعات
جهت اندازه گیری مایعات از واحدهای زیر استفاده می شود.
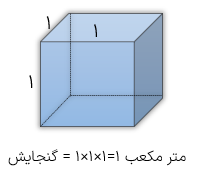
الف) متر مكعب
اگر ظرفی به شکل مکعب که هر ضلع آن 1 متر باشد را در نظر بگیریم گنجایش آن یک متر مکعب خواهد بود.
ب) ليتر
اگر ظرفی به شکل مکعب که هر ضلع آن 10 سانتی متر باشد را در نظر بگیریم، گنجایش آن یک لیتر خواهد بود.
اگر ظرفی به شکل مکعب که هر ضلع آن 10 سانتی متر باشد را در نظر بگیریم، گنجایش آن یک لیتر خواهد بود.
سانتی متر مکعب ۱۰۰۰=۱۰×۱۰×۱۰ = گنجایش
سانتی متر مکعب ۱۰۰۰=۱ لیتر
ج) سی سی (میلی لیتر)
اگر ظرفی به شکل مکعب که هر ضلع آن 1 سانتی متر باشد را در نظر بگیریم، گنجایش آن یک سی خواهد بود.
سانتی متر مکعب ۱ = 1×1×1= گنجایش
سانتی متر مکعب ۱ = ۱ سی سی (میلی لیتر)
مثال
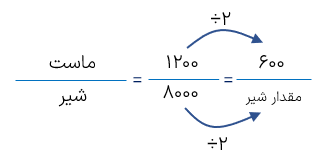
اگر از هر 8 لیتر شیر بتوانیم 1/2 لیتر ماست تهیه کنیم برای تهیه 600 سی سی ماست لیتر شیر نیاز داریم؟
۸۰۰۰ سیسی = ۸ لیتر
۱۲۰۰ سی سی =1/2 لیتر
مقدار شیر \( = 8000 \div 2 = 4000\,cc\,\, = 4L\)



1736019749.png)