گام به گام تمرین صفحه 12 درس 1 ریاضی (1) (مجموعه، الگو و دنباله)
تعداد بازدید : 51.15Mپاسخ تمرین صفحه 12 ریاضی (1)
-گام به گام تمرین صفحه 12 درس مجموعه، الگو و دنباله
-تمرین صفحه 12 درس 1
-1- \(\mathbb{R}\) را به عنوان مجموعهٔ مرجع درنظر بگیرید و سپس متمم هر یک از مجموعه های زیر را روی محور نشان دهید.
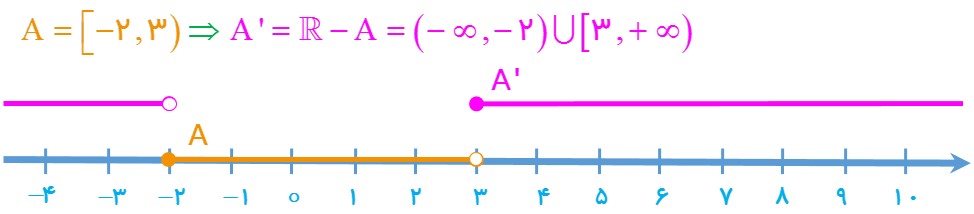
الف) \(A = [ - 2\,,\,3)\)
ب) \(B = \{ 0\,,\,1\,,\,2\,,\,3\,,\,4\,,\, \cdots \} \)
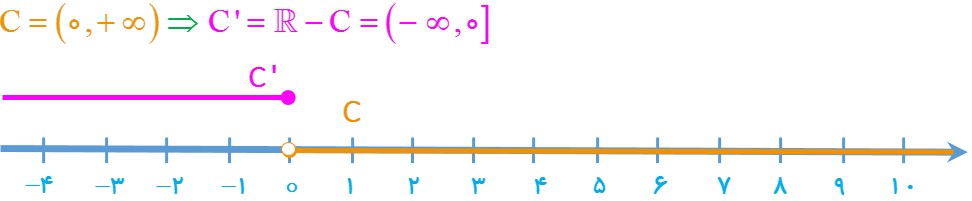
پ) \(C = (0\,,\, + \infty )\)
ت) \(D = ( - \infty \,,\,1]\)
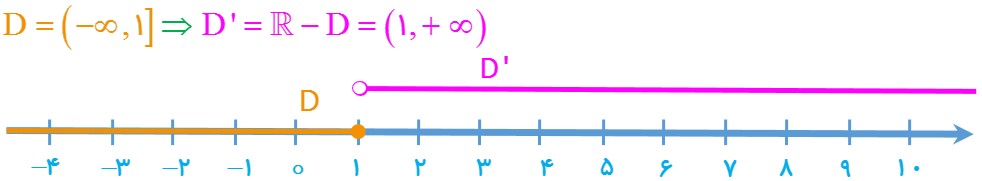
2- \(\mathbb{N}\) را به عنوان مجموعه مرجع درنظر بگیرید.
الف) مجموعه ای نامتناهی مثل A مثال بزنید که A’ هم نامتناهی باشد.
مجموعه اعداد فرد که متمم آن مجموعه اعداد زوج است:
A={1 , 3 , 5 , 7 , …}
B={2 , 4 , 6 , 8 , …}
ب) مجموعه ای نامتناهی مثل B مثال بزنید که B’ متناهی باشد.
مجموعه اعداد غیر یک رقمی که متمم آن مجموعه اعداد یک رقمی است :
B={10 , 11 , 12 , 13 , …}
B’={1 , 2 , 3 , … , 9}
پ) مجموعه ای متناهی مثل C مثال بزنید و C’ . را به دست آورید. C’ متناهی است یا نامتناهی؟
مجموعه اعداد یک رقمی:
C={1 , 2 , 3 , … , 9}
C’={10 , 11 , 12 , 13 , …}
C’ نامتناهی است.
3- اگر \(n(A) = 15\)، \(n(A \cap B) = 5\) و \(n(A \cup B) = 30\) آنگاه \(n(B)\) را محاسبه کنید.
\(\begin{array}{l}n(A \cup B) = n(A) + n(B) - n(A \cap B)\\\\ \Rightarrow 30 = 15 + n(B) - 5 \Rightarrow n(B) = 20\end{array}\)
4- فرض کنیم A و B زیر مجموعه هایی از مجموعهٔ مرجع U باشند، به طوری که \(n(U) = 100\)، \(n(A) = 60\) ، \(n(B) = 40\) و \(n(A \cap B) = 20\) مطلوب است:
الف) \(n(A \cup B)\)
\(\begin{array}{l}n(A \cup B) = n(A) + n(B) - n(A \cap B)\\\\ \Rightarrow n(A \cup B) = 60 + 40 - 20 = 80\end{array}\)
ب) \(n(A \cap B')\)
\(\begin{array}{l}n(A \cap B') = n(A) - n(A \cap B)\\\\ \Rightarrow n(A \cap B') = 60 - 20 = 40\end{array}\)
پ) \(n(A' \cap B)\)
\(\begin{array}{l}n(A' \cap B) = n(B \cap A') = n(B) - n(A \cap B)\\\\ \Rightarrow n(A' \cap B) = 40 - 20 = 20\end{array}\)
ت) \(n(A' \cap B')\)
\(\begin{array}{l}n(A' \cap B') = n((A \cup B)') = n(U) - n(A \cup B)\\\\ \Rightarrow n(A' \cap B') = 100 - 80 = 20\end{array}\)
5- در یک کلاس 31 نفری، تعداد 14 نفر از دانش آموزان عضو گروه سرود و 19 نفر آنها عضو گروه تئاترند. اگر 5 نفر از دانش آموزان این کلاس عضو هر دو گروه باشند، مطلوب است:
الف) تعداد دانش آموزانی که فقط عضو گروه سرودند.
\(\left. \begin{array}{l}n(U) = 31\\\\n(S) = 14\\\\n(T) = 19\\\\n(S \cap T) = 5\end{array} \right\} \Rightarrow n(S - T) = n(S) - n(S \cap T) = 14 - 5 = 9\)
ب) تعداد دانش آموزانی که عضو هیچ یک از این دو گروه نیستند.
\(\begin{array}{l}n(S \cup T) = n(S) + n(T) - n(S \cap T) = 14 + 19 - 5 = 28\\\\n(S' \cap T') = n((S \cup T)') = n(U) - n(S \cup T) = 31 - 28 = 3\end{array}\)
6- در یک نظرسنجی از 110 مشتری یک فروشگاه زنجیره ای، مشخص شد که 70 نفر آنها در یک ماه گذشته از محصولات شرکت A و 57 نفرشان از محصولات شرکت B خرید کرده اند. همچنین 32 نفر از آنان نیز اعلام کردند که در این مدت از هر دو شرکت خرید کرده اند. چه تعداد از این 110 نفر در یک ماه گذشته:
الف) دست کم از یکی از این دو شرکت خرید کرده اند.
\(\begin{array}{l}\left. \begin{array}{l}n(U) = 110\\\\n(A) = 70\\\\n(B) = 57\\\\n(A \cap B) = 32\end{array} \right\}\\\\ \Rightarrow n(A \cup B) = n(A) + n(B) - n(A \cap B) = 70 + 57 - 32 = 95\end{array}\)
ب) فقط از شرکت A خرید کرده اند.
\(n(A - B) = n(A) - n(A \cap B) = 70 - 32 = 38\)
پ) دقیقاً از یکی از این دو شرکت خرید کرده اند.
\(\begin{array}{l}n(A - B) + n(B - A) = \\\\(n(A) - n(A \cap B)) + (n(B) - n(A \cap B)) = \\\\(70 - 32) + (57 - 32) = 38 + 25 = 63\end{array}\)
ت) از هیچ یک از این دو شرکت خرید نکرده اند.
\(\begin{array}{l}n(A' \cap B') = n((A \cup B)') = n(U) - n(A \cup B)\\\\ = 110 - 95 = 15\end{array}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
