جواب تمرین صفحه 24 درس 1 ریاضی دهم (مجموعه، الگو و دنباله)
تعداد بازدید : 81.09Mپاسخ تمرین صفحه 24 ریاضی دهم
-گام به گام تمرین صفحه 24 درس مجموعه، الگو و دنباله
-تمرین صفحه 24 درس 1
-شما در حال مشاهده جواب تمرین صفحه 24 ریاضی دهم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
1- از بین دنباله های زیر، دنباله های حسابی را مشخص کنید و در هر یک از آنها با تعیین قدرنسبت، جملهٔ بیست و یکم را بیابید.
(الف \(3\,,\,10\,,\,17\,,\,24\,,\, \ldots \)
\(\left\{ \begin{array}{l}d = 7\\\\{t_{21}} = 143\end{array} \right.\)
(ب \(1\,,\,2\,,\,4\,,\,8\,,\, \ldots \)
دنباله حسابی نمی باشد.
\(\sqrt 3 \,,\,2\sqrt 3 \,,\,3\sqrt 3 \,,\,4\sqrt 3 \,,\, \ldots \) (پ
\(\left\{ \begin{array}{l}d = \sqrt 3 \\\\{t_{21}} = 21\sqrt 3 \end{array} \right.\)
(ت \(10\,,7\,,\,4\,,\,1\,,\, \ldots \)
\(\left\{ \begin{array}{l}d = - 3\\\\{t_{21}} = - 50\end{array} \right.\)
(ث \(\frac{2}{5}\,,\,\frac{3}{5}\,,\,\frac{4}{5}\,,\,1\,,\, \ldots \)
\(\left\{ \begin{array}{l}d = \frac{1}{5}\\\\{t_{21}} = \frac{{22}}{5}\end{array} \right.\)
(ج \(2\,,\,2\,,\,2\,,\,2\,,\, \ldots \)
\(\left\{ \begin{array}{l}d = 0\\\\{t_{21}} = 2\end{array} \right.\)
2- در یک دنبالهٔ حسابی، جملات سوم و هفتم به ترتیب 20 و 56 است. دنباله را مشخص کنید؛ یعنی با به دست آوردن جملهٔ اول و قدرنسبت، جملات دنباله را بنویسید.
\(\begin{array}{l}{t_n} = {t_1} + d(n - 1)\\\\\left\{ \begin{array}{l}{t_3} = {t_1} + 2d = 20\\\\{t_7} = {t_1} + 6d = 56\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{t_1} = 2\\\\d = 9\end{array} \right. \Rightarrow {t_n} = 2 + 9(n - 1)\\\\ \Rightarrow {t_n} = 9n - 7\end{array}\)
3- در یک دنبالهٔ حسابی، مجموع سه جملهٔ اول 3 و مجموع سه جملهٔ بعدی آن 39 است. دنباله را مشخص کنید.
\(\begin{array}{l}{t_n} = {t_1} + d(n - 1)\\\\\left\{ \begin{array}{l}{t_1} + {t_2} + {t_3} = 3{t_1} + 3d = 3\\\\{t_4} + {t_5} + {t_6} = 3{t_1} + 12d = 39\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{t_1} = - 3\\\\d = 4\end{array} \right.\\\\ \Rightarrow {t_n} = - 3 + 4(n - 1) \Rightarrow {t_n} = 4n - 7\end{array}\)
4- الف) دو جملهٔ بعدی الگوی مقابل را با رسم شکل بیابید و نوع دنباله را مشخص کنید.
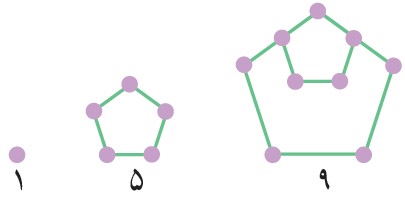
نوع دنباله، دنباله حسابی است، زیرا اختلاف هر دو جمله متوالی یک مقدار ثابت است.
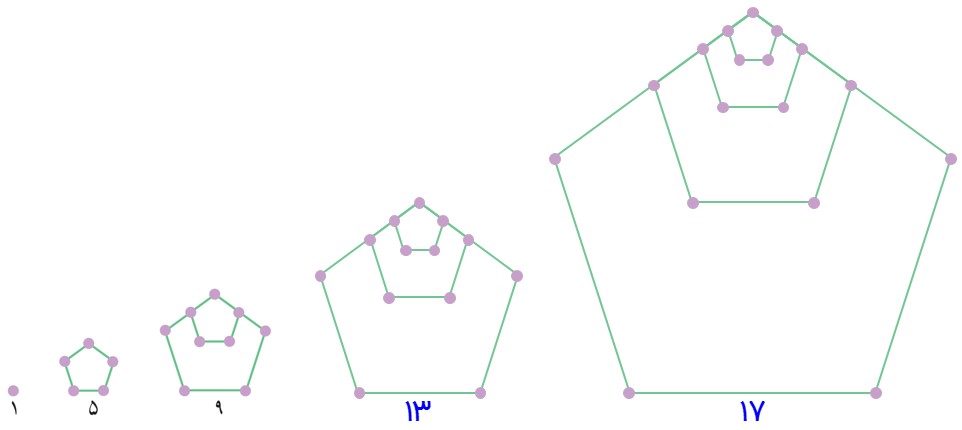
ب) جملهٔ عمومی آن را مشخص کنید.
\(\left\{ \begin{array}{l}{t_1} = 1\\\\d = 4\end{array} \right. \Rightarrow {t_n} = 1 + 4(n - 1) \Rightarrow {t_n} = 4n - 3\)
پ) جملهٔ چندم این دنباله 397 است؟
\({t_{}} = 397 \Rightarrow 4m - 3 = 397 \Rightarrow m = 100\)
5- الف) واسطهٔ حسابی بین 5 و 11 چه عددی است؟
\(\left. \begin{array}{l}\left\{ \begin{array}{l}{t_1} = 5\\\\{t_3} = 11\end{array} \right. \Rightarrow d = \frac{{{t_3} - {t_1}}}{{3 - 1}} = \frac{{11 - 5}}{2} = 3\\\\ \Rightarrow {t_2} = {t_1} + d = 8\end{array} \right\} \Rightarrow 5\,,\,8\,,\,11\)
ب) واسطهٔ حسابی بین 20 و 30 چه عددی است؟
\(\left. \begin{array}{l}\left\{ \begin{array}{l}{t_1} = 20\\\\{t_3} = 30\end{array} \right. \Rightarrow d = \frac{{{t_3} - {t_1}}}{{3 - 1}} = \frac{{30 - 20}}{2} = 5\\\\ \Rightarrow {t_2} = {t_1} + d = 25\end{array} \right\} \Rightarrow 20\,,\,25\,,\,30\)
پ) از دو قسمت قبل چه نتیجه ای می گیرید؟
واسطه حسابی بین دو عدد، میانگین آن دو عدد است. به عبارتی دیگر اگر c ، b ، a دنباله حسابی باشند، داریم:
\(b = \frac{{a + c}}{2}\)
6- مسئلهٔ زیر در پاپیروس رایند آمده است. آن را حل کنید.
«100 قرص نان را بین 5 مرد چنان تقسیم کنید که سهم های دریافت شده، دنبالهٔ حسابی تشکیل دهند و یک سومِ مجموع سه سهم بزرگ تر، مساوی مجموع دو سهم کوچک تر باشد».
\(\begin{array}{l}{t_n} = {t_1} + d(n - 1)\\\\{t_1}\,,\,{t_2}\,,\,{t_3}\,,\,{t_4}\,,\,{t_5}\\\\\left\{ \begin{array}{l}{t_1} + {t_2} + {t_3} + {t_4} + {t_5} = 100 \Rightarrow 5{t_1} + 5d = 100\\\\{t_1} + {t_2} = \frac{{{t_3} + {t_4} + {t_5}}}{3} \Rightarrow {t_1} - 2d = 0\end{array} \right.\\\\ \Rightarrow \left\{ \begin{array}{l}{t_1} = 10\\\\d = 5\end{array} \right. \Rightarrow {t_n} = 10 + 5(n - 1) \Rightarrow {t_n} = 5n + 5\\\\ \Rightarrow \,10\,,\,15\,,\,20\,,\,25\,,\,30\end{array}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















