جواب مثال صفحه 33 درس 2 ریاضی دهم (مثلثات)
تعداد بازدید : 80.71Mپاسخ مثال صفحه 33 ریاضی دهم
-گام به گام مثال صفحه 33 درس مثلثات
-مثال صفحه 33 درس 2
-شما در حال مشاهده جواب مثال صفحه 33 ریاضی دهم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
یک موشک در ارتفاع 15 متری از سطح زمین و با زاویهٔ °30 پرتاب می شود. می خواهیم بدانیم پس از طی 2000 متر با همین زاویه، موشک به چه ارتفاعی از سطح زمین می رسد؟
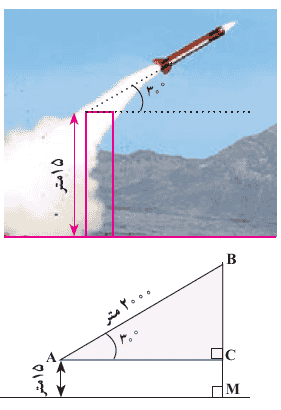
حل: ابتدا یک مدل ریاضی برای حل این مسئله می سازیم. با توجه به شکل زیر، به سادگی می توان دید، ارتفاع موشک از سطح زمین برابر است با :
BC + MC = BC + ………
بنابراین کافی است طول BC را پیدا کنیم. می دانیم \(\sin 30^\circ = \frac{1}{2}\). پس در مثلث قائم الزاویه ABC داریم:
\(\sin 30^\circ = \frac{1}{2} = \frac{{BC}}{{}}\;\; \Rightarrow \;\;BC = \)
و از این رو
ارتفاع موشک = ……….. + ……….. = ……….
حل: ابتدا یک مدل ریاضی برای حل این مسئله می سازیم. با توجه به شکل زیر، به سادگی می توان دید، ارتفاع موشک از سطح زمین برابر است با :
BC + MC = BC + 15
بنابراین کافی است طول BC را پیدا کنیم. می دانیم \(\sin 30^\circ = \frac{1}{2}\). پس در مثلث قائم الزاویه ABC داریم:
\(\sin 30^\circ = \frac{1}{2} = \frac{{BC}}{{AB}}\)
\( \Rightarrow \;BC = \frac{1}{2}AB = \frac{1}{2} \times 2000 = 1000\) متر
و از این رو
ارتفاع موشک = 15 + 1000 = 1015 متر
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















