درسنامه کامل حسابان یازدهم فصل 2 تابع
تعداد بازدید : 7.27Mخلاصه نکات حسابان یازدهم فصل 2 تابع - درسنامه شب امتحان حسابان یازدهم فصل 2 تابع - جزوه شب امتحان حسابان یازدهم نوبت اول فصل 2 تابع
تابع
تابع
يك تابع از مجموعه A به مجموعه B رابطهاي بين دو مجموعه است كه به هر عضو A دقيقاً يك عضو از B را نسبت ميدهد. اعضاي A و B هر شيء ميتوانند باشند اما اگر \(A \subseteq R\) و\(B \subseteq R\) تابع f را تابع حقيقي ميناميم
A را دامنه تابع ، B را هم دامنه آن و مجموعه\(\left\{ {f\left. {\left( x \right)} \right|} \right.x \in \left. A \right\}\) را برد تابع f گوييم.
مثال
تابع حقيقي\(A \to B\) :را كه در آن \(A = \left\{ {1,2,3,4,\left. 5 \right\}} \right.\)و هر عضواز f به صورت \((t,2t)\) ميباشد را در نظر بگيريد
الف) مجموعه B را توصيف كنيد.
ب) تابع f را با اعضايش مشخص كنيد.
ج) ضابطه تابع f را مشخص كنيد؟
د) اگر N) \(B = N\) مجموعه اعداد طبيعي است)، معرفي كاملي از تابع f را بنويسيد.
الف) مجموعه B هر زير مجموعه اي از اعداد حقيقي شامل مجموعه \(\left\{ {2,4,6,8,\left. {10} \right\}} \right.\) ميتواند باشد
ب) اعضاي تابع f به صورت\(f = \left\{ {\left( {1,2} \right)} \right.,\left( {2,4} \right),\left( {3,6} \right),\left( {4,8} \right),\left. {\left( {5,10} \right)} \right\}\) ميباشد.
ج) ضابطه تابع f را ميتوان به صورت \(f(x) = 2x\) نوشت.
د) تابعfراميتوان به صورتهاي\(\left\{ \begin{array}{l}f:A \to N\\f(x) = 2x\end{array} \right.\) يا\(\left\{ \begin{array}{l}\left\{ {f:\left\{ {1,2,3,4,\left. 5 \right\}} \right.} \right. \to \left\{ {1,2,3,4,5,\left. {...} \right\}} \right.\\f(x) = 2x\end{array} \right.\) نوشت كه به طوركامل تابع فوق را معرفي ميكنند توجه كنيد كه مجموعه A دامنه تابع f و مجموعه N ، هم دامنه تابع و همچنين برد تابع مجموعه \(\left\{ {2,4,6,8\left. {,10} \right\}} \right.\) ميباشد.
مثال
مجموعه A داراي m عضو و مجموعه B داراي n عضو ميباشد و تابع g از A به B تعريف شده است.
الف) در نمودار ون مربوط به تابع g چند پيكان بايد وجود داشته باشد.
ب) نمودار ون تابع g را طوري رسم كنيد كه.\(m < n\)
ج) نمودار ون تابع g را طوري رسم كنيد كه \(m = n\)
د) نمودار ون تابع g را طوري رسم كنيد كه \(m > n\)
الف) با توجه به اينكه از هر عضو A دقيقاً يك پيكان بايد خارج شده باشد بنابراين دقيقاً بايد m پيكان از A به B كشيده شود.
ب) بيشمار تابع براي g ميتوان در نظر گرفت.به عنوان مثال ميتوان g را چنين در نظر گرفت:
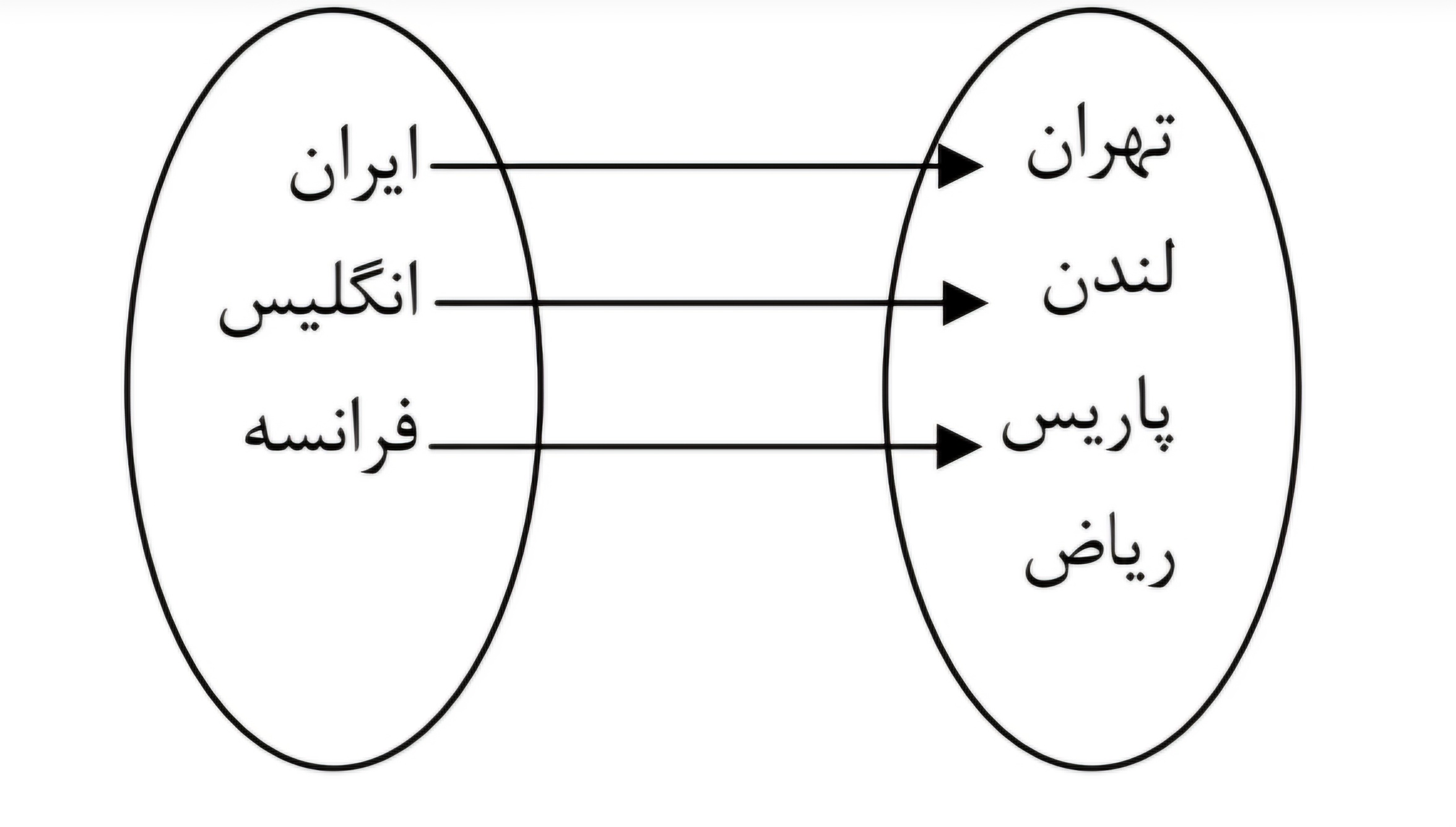
مجموعه {فرانسه، انگليس، ايران} دامنه تابع و مجموعه { رياض، پاريس، لندن، تهران} هم دامنه تابع و مجموعه {پاريس، لندن، تهران} باشندبرد تابع مي باشند.
ج) ميتوان g را چنين در نظر گرفت.
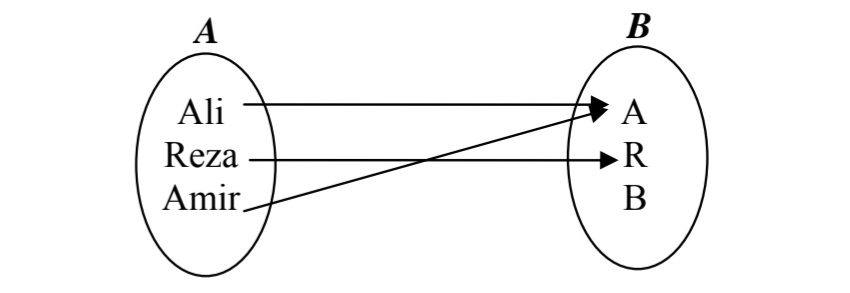
مجموعه \(\left\{ {ali,reza,ami} \right.\left. r \right\}\) دامنه تابع و\(\left\{ {A,R,\left. B \right\}} \right.\) هم دامنه تابع و مجموعه \(\left\{ {A,\left. R \right\}} \right.\) برد تابع ميباشند.
د) تابع g را ميتوان چنين در نظر گرفت
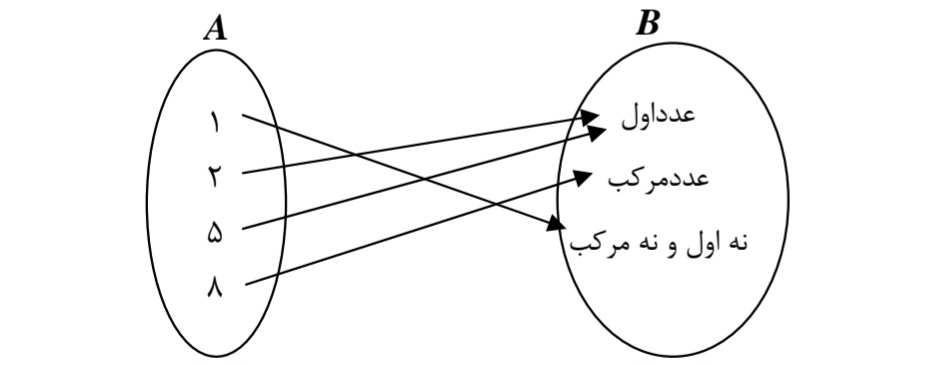
مجموعه \(\left\{ {1,2,5,\left. 8 \right\}} \right.\) دامنه تابع و مجموعه {نه اول و نه مركب، عدد مركب، عدد اول} هم دامنه و برد تابع هستند.
مثال
تابع:\(A \to B\) را طوري مشخص كنيد كه:
الفA (متناهي و B نامتناهي باشد.
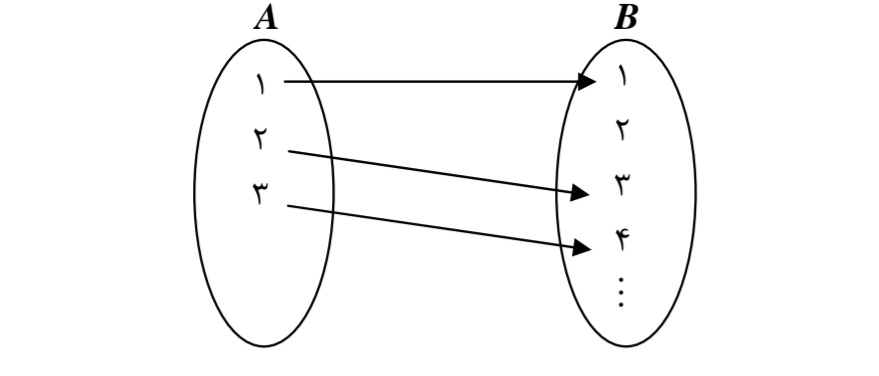
ب A (نامتناهي و B متناهي باشد.
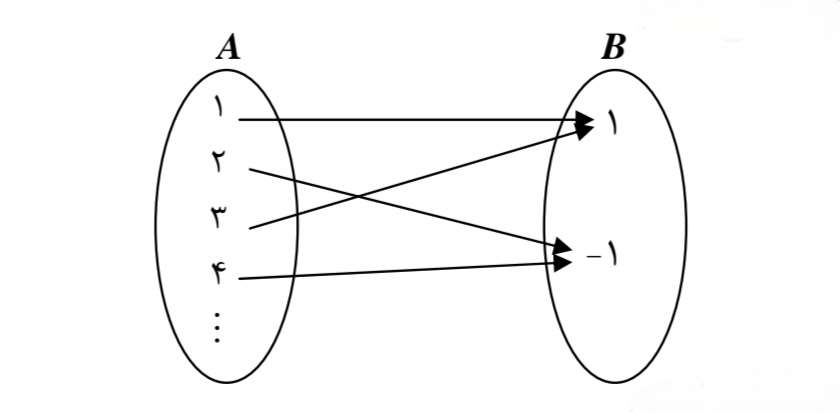
جA ( و B هر دو نامتناهي باشند.
مثال
الف) تابع f با ضابطه \(y = \frac{9}{5}x + 32\) را رسم كنيد.
ب) تابع \(g:\left[ { - 20,20} \right] \to R\) با ضابطه \(g(x) = \frac{9}{5}x + 32\) را رسم كنيد.
ج) آيا تابع h را ميتوان به قسمي در نظر گرفت كه دامنه و ضابطه آن با تابع g يكي باشد اما هم دامنه آن مجموعه Z باشد.
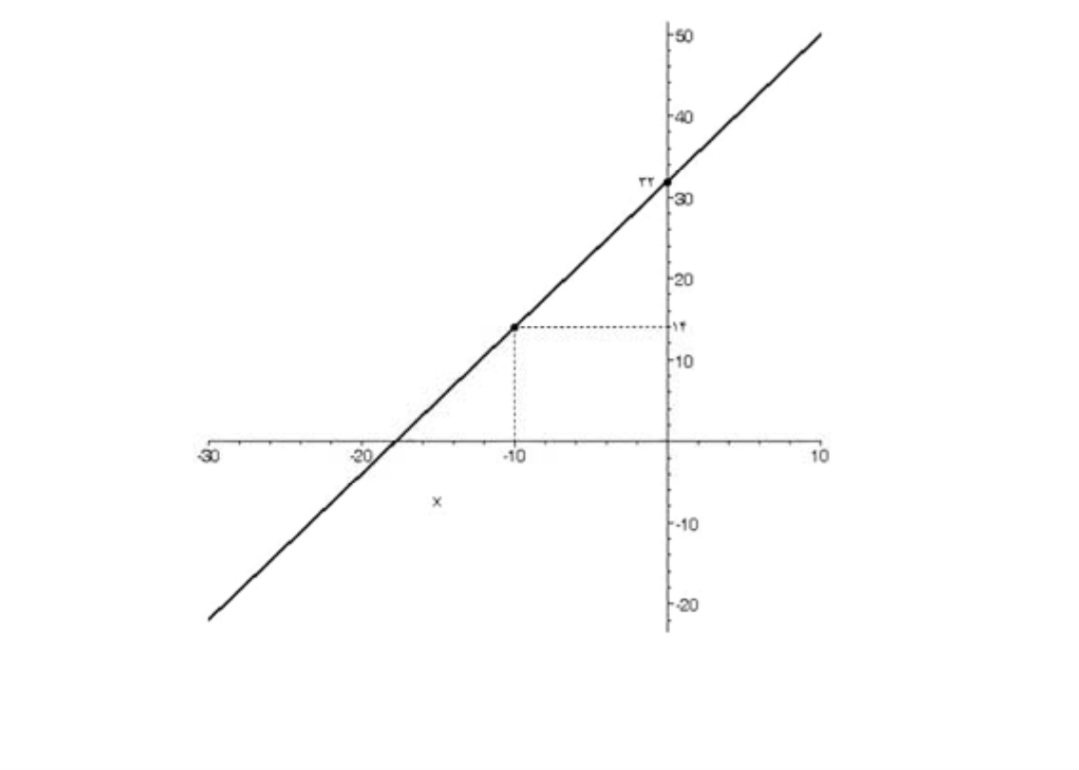
الف) با توجه به اينكه نمودار ضابطه داده شده يك خط است و هر خط با 2 نقطه مشخص ميشود كافي است 2 نقطه از اين خط را يافته و خط را رسم كرد.
به عنوان مثال:
\(x = 0 \Rightarrow y = 32 \Rightarrow (0,32) \in f,x = - 10 \Rightarrow y = 14 \Rightarrow ( - 10,14) \in f\)
لذا شكل آن به صورت زير خواهد بود.
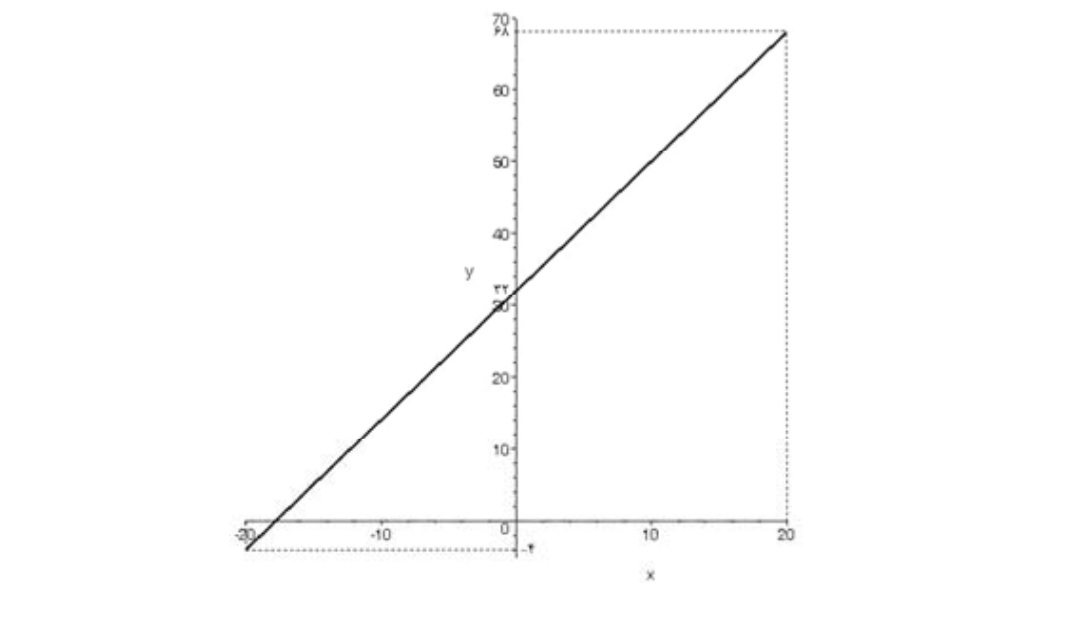
ب) نموار اين تابع قسمتي از تابع f است كه در آن \( - 20 \le x \le 20\) در واقع تابع g را تحديد تابع f ميناميم و نمودار آن چنين است:
ج) با توجه به اينكه\(g\left( 1 \right) = \frac{9}{5} + 32 = \frac{{169}}{5}\) لذا چنين تابعي نميتوان يافت.
مثال
از بين مستطيل هاي قابل محاط شدن در مثلث متساوي الاضلاع به ضلع 1 كدام مستطيل بيشترين مساحت را دارد؟
طبق شكل اگر DC را برابر x بگيريم، داريم\(DFC = 30\) (چرا) و از آنجا\(F{C^2} = 2x\) با توجه به رابطه ي فيثاغورس داريم:
\(F{C^2} = D{C^2} + F{D^2} \Rightarrow {(2x)^2} = {x^2} + F{D^2} = FD = \sqrt 3 x\)
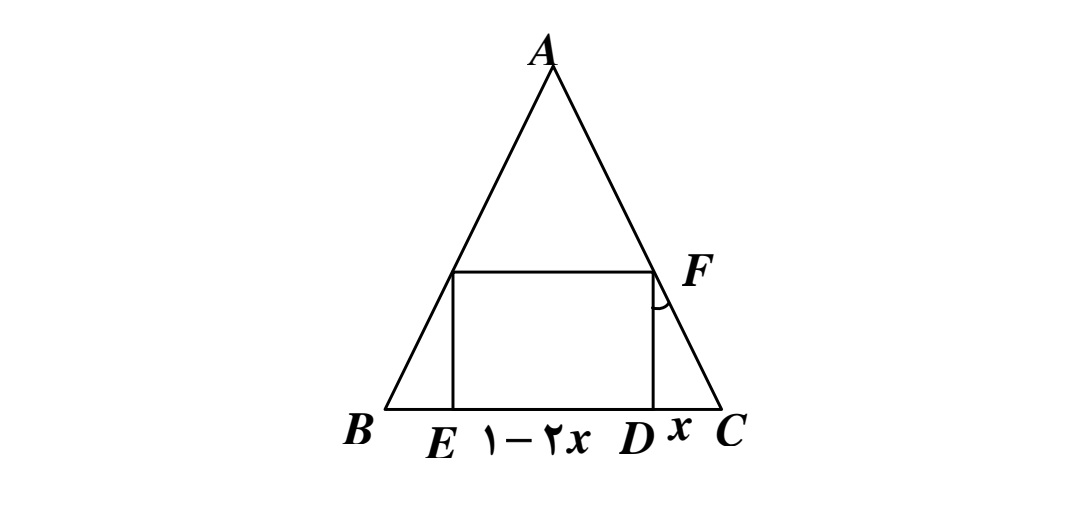
لذا مساحت مستطيل فوق از رابطه\(S = (1 - 2x)x\sqrt 3 \) دست مي آيد و داريم:
\(s = - 2\sqrt 3 ({x^2} - \frac{1}{2}x) = - 2\sqrt 3 \left[ {{{(x - \frac{1}{4})}^2} - \frac{1}{{16}}} \right] = - 2\sqrt 3 {(x - \frac{1}{4})^2} + \frac{{\sqrt 3 }}{8}\)
اما بيشترين مقدار عبارت \( - 2\sqrt 3 {(x - \frac{1}{4})^2}\) صفر است كه به ازاي\(x = \frac{1}{4}\) به دست مي آيد و لذا ماكزيمم S برابر \(\frac{{\sqrt 3 }}{8}\) است و طول و عرض اين مستطيل برابر است با\(x\sqrt 3 = \frac{1}{4}\sqrt 3 \) و
\(1 - 2x = 1 - 2(\frac{1}{4}) = \frac{1}{2}\)
دوتابع f و g در صورتي مساويند كه هردو شرط زير برقرار باشد:
الف) دامنه دو تابع با هم برابر باشند.
ب) به ازاي هر عضو از دامنه آنها داشته باشيم\(f(x) = g(x)\).
مثال
توابع \(g = \left\{ {\left( {3,4} \right)} \right.,(7,5),(9, - 1\left. ) \right\}\) و \(f = \left\{ {(3,4)(7, - 1),(9,5\left. ) \right\}} \right.\) را در نظر بگيريد. آيا اين دو تابع با هم مساويند.
دامنه اين دو تابع مجموعه \(\left\{ {3,7,\left. 9 \right\}} \right.\) است كه با هم مساوي است . \(f(7) = - 1\) ولي \(g(7) = 5\) پس دو تابع با هم مساوي نيستند .
مثال
توابع \(\left\{ \begin{array}{l}f:A \to R\\f(x) = 3{x^3} + 1\end{array} \right.\) و \(\left\{ \begin{array}{l}g:A \to R\\g = \left\{ {(1,a),(b,2),(a,c\left. ) \right\}} \right.\end{array} \right.\) را در نظر بگيريد a ، b وc را طوري بيابيد كه دو تابع با هم مساوي باشند.
چون\(1 \in {D_g}\) لذا بايد \(1 \in {D_f}\) و \(f(1) = 4\) پس بايد \(g(1) = 4\) يعني \(a = 4\) همچنين \(g(b) = 2\) و از حل معادله\(f(x) = 2\) نتيجه ميشود كه \(x = \frac{1}{{^3\sqrt 3 }}\)لذا \(b = \frac{1}{{^3\sqrt 3 }}\) با استدلال هاي مشابه \(4 \in {D_g}\)و در نتیجه باید\(4 \in {D_f}\) و چون \(f(4) = 193\) لذا \(g(4) = 193\) يعني \(c = 193\)
پس تابع gبه صورت \(g(x) = \left\{ {(1,4),(\frac{1}{{^3\sqrt 3 }}} \right.),(4,193\left. ) \right\}\) بوده و A نيز چنين است \(A = \left\{ {(1,4),(\frac{1}{{^3\sqrt 3 }}} \right.),\left. 4 \right\}\)
توابع \(f(x) = {\sin ^2}x + {\cos ^2}x\) و\(g(x) = 1\) با هم برابرند دقت كنيد كه دامنه هر دو تابع مجموعه R است.
مثال
آیا توابع \(f(x) = \sqrt {{x^2}} \) و\(g(x) = x\) با هم مساويند؟
دامنه هر دو تابع مجموعه اعداد حقیقی است اما به ازای هر \(x < 1\) مقادیر هر دو تابع برابر نیست مثلا\(f( - 5) = \sqrt {(5} {)^2} = 25 = 5\) ولی \(g( - 5) = - 5\)
مثال
آيا توابع \(f(x) = \tan x\) و \(g(x) = \frac{1}{{\cot x}}\) باهم برابرند؟
ميدانيد كه \(\tan x\) به ازاي هر\(x = k\pi + \frac{\pi }{2}\) , \(K \in Z\) تعريف نشده است يعني اين نقاط در دامنه تابع f قرار ندارند.
اما \(\cot x\) به ازاي هر \(x = k\pi \) ,\(K \in Z\) تعريف نشده و به ازاي هر\(x = k\pi + \frac{\pi }{2}\) , \(K \in Z\) صفر 2 ميشود لذا مجموعه اين نقاط يعني نقاط به طول\(x = k\frac{\pi }{2}\) \(K \in Z\) , عضو دامنه تابع g نميباشد.
بنابراين دامنه اين دو تابع برابر نيست . به عنوان مثال \(f(0)\) تعريف شده و برابر صفر است اما تابع g به ازاي \(x = 0\) تعريف نشده است
مثال
به طور مشابه با مثال قبل توابع\(f(x) = \log {x^2}\) و \(g(x) = 2\log x\) باهم برابر نیستند زیرا دامنه تابع f مجموعه \(R - \left\{ {\left. 0 \right\}} \right.\) است ولي دامنه تابع g مجموعه \(\left\{ {\left. x \right|} \right.x > \left. 0 \right\}\) مي باشد كه برابر نيستند.
مثال
M و L را طوري بيابيد كه توابع f و g باهم برابر باشند.
\(f(x) = \left\{ {\begin{array}{*{20}{l}}{\frac{{x + 2}}{{{x^2} - 4}},x \ne - 2,2}\\{L,x = - 2}\\{5,x = 2}\end{array}} \right.\,\,\,,\,\,\,g(x) = \left\{ {\begin{array}{*{20}{l}}{\frac{1}{{x - 2}},x \ne 2}\\{}\\{M,x = 2}\end{array}} \right.\)
اولاً دامنه هر دو تابع مجموعه اعداد حقيقي است و \(g(2) = M\) و \(M = 5\) بنابراين 5 همچنين \(f( - 2) = L\) و \(g( - 2) = \frac{1}{{ - 4}}\) لذا.\(L = - \frac{1}{4}\) توجه كنيد كه اگر \(x \ne 2\), \(x \ne - 2\) آنگاه:
\(f(x) = \frac{{x + 2}}{{x - 2}} = \frac{{x + 2}}{{(x - 2)(x + 2)}} = \frac{1}{{x - 2}}\)
تهیه کننده: حامد دلیجه
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه یازدهم- آزمون آنلاین تمامی دروس پایه یازدهم
- گام به گام تمامی دروس پایه یازدهم
- ویدئو های آموزشی تمامی دروس پایه یازدهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه یازدهم
- فلش کارت های آماده دروس پایه یازدهم
- گنجینه ای جامع از انشاء های آماده پایه یازدهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه یازدهم
توابع چند ضابطه اي
توابع چند ضابطه اي
توابعي كه در بخش هاي مختلف دامنه آن با ضابطه هاي مختلف تعريف مي شوند توابع چند ضابطه اي مينامند.
امروزه توابعي كه در سازمانها جهت محاسبه ي هزينه ي آب، برق، گاز، تلفن و ... مشتركين مورد محاسبه قرار مي گيرد به صورت توابع چند ضابطه اي ميباشد.
مثال
يك مغازه زنجيرهاي جهت جذب مشتري اعلام كرده است كه به مشترياني كه مبلغ خريدشان حداقل 20000 تومان باشد %5 و مشترياني كه مبلغ خريدشان حداقل 100000 تومان باشد %10 تخفيف ميدهد تابع فوق را مشخص كنيد.
x را مبلغ خريد مشتري و \(y = f\left( x \right)\) را مبلغي كه مشتري بايد بپردازد در نظر بگيريد خواهيم داشت.
\(f\left( x \right) = \left\{ \begin{array}{l}x,0 < x < 20000\\\\0/95,200000 \le x < 100000\\\\0/9,x \ge 100000\end{array} \right.\)
مثال
مدرسي تصميم ميگيرد جهت ارفاق به دانشجويان خود، نمره دانشجوياني كه كمتر از 8 است را از فرمول \(6 + \frac{x}{2}\) ودانشجوياني كه نمره 8 تا 20 گرفته اند را از فرمول\(\frac{5}{6}x + \frac{{10}}{3}\) محاسبه كند.
الف) تابع را مشخص كنيد و دامنه و برد آن را بيابيد .
ب)اگر دانشجويي در امتحان نمره 11 گرفته باشد نمره نهايي او چقدر است؟
x را نمره برگه دانشجو و \(y = f(x)\) را نمره نهايي او در نظر بگيريد خواهيم داشت:
\(f(x) = \left\{ \begin{array}{l}6 + \frac{x}{2},0 \le x < 8\\\\\frac{5}{6}x + \frac{{10}}{3},8 \le x \le 20\end{array} \right.\)
بدیهی است دامنه تابع یعن نمراتی که دانشجو گرفته از صفر تا 20 یعنی \(\left[ {0,20} \right]\) می باشد
اما برد آن یعنی نمراتی که مدرس ثبت خواهد کرد چنین به دست می آید:
\(\begin{array}{l}0 \le x \le 8 \Rightarrow 0 \le \frac{x}{2} < 4 \to 6 \le 6 + \frac{x}{2} < 10\\\\8 \le x \le 20 \Rightarrow \frac{{40}}{6} \le \frac{5}{6}x \le \frac{{100}}{6} \to 10 \le \frac{5}{6}x + \frac{{10}}{3} \le 20\end{array}\)
يعني برد تابع يا نمرات نهايي مجموعه [20 , 6] ميباشد.
ب) براي محاسبه نمره نهايي دانشجويي كه نمره 11 گرفته است بايد از ضابطه دوم استفاده كرد، يعني:
\( = \frac{5}{6} \times 11 + \frac{{10}}{3} = \frac{{95}}{6} = 12/5\)
مثال
تابع چند ضابطه اي زير را در نظر بگيريد
\(g(x) = \left\{ \begin{array}{l}{x^2},x < - 2\\\\5, - 2 \le x \le 2\\\\4 - 2x,x > 2\end{array} \right.\)
الف) دامنه و برد تابع را مشخص كنيد.
ب) مقدار \(g(g( - 3))\) را بيابيد..
الف)دامنه به وضوح مجموعه اعداد حقيقي است.
براي محاسبه برد آن ملاحظه ميكنيم كه
\(\left. \begin{array}{l}x < - 2 \Rightarrow {x^2} > 4 \Rightarrow g(x0 > 4\\\\ - 2 \le x \le 2 \Rightarrow g(x) = 5\\\\x > 2 \Rightarrow - 2x < - 4 \Rightarrow 4 - 2x < 0 \Rightarrow g(x) < 0\end{array} \right\} \Rightarrow {R_g} = ( - \infty ,0) \cup (4, + \infty )\)
ب(
\(g( - 3) = {( - 3)^2} = 9 \Rightarrow g(g( - 3)) = g(9) = 4 - 2 \times 9 = - 14\)
مثال
نمودار تابع f به شكل زير است ضابطه آن را مشخص كنيد.
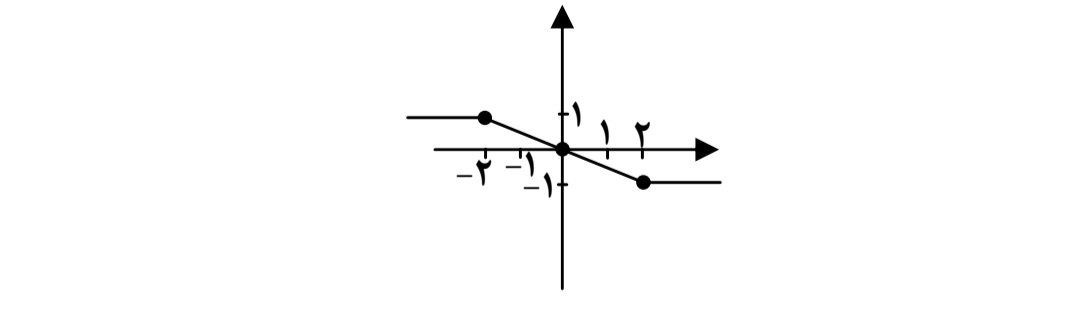
واضح است كه اگر \(x \le - 2\) آن گاه \(f(x) = - 1\) و اگر \(x \ge 2\) آن گاه \(f(x) = - 1\) اما به ازاي \( - 1 \le x \le 1\) نمودار تابع خطي است لذا با داشتن دو نقطه از آن مثلاً نقاط \(( - 2,1)\) و \((0,0)\) ميتوان معادله آن را به دست آورد. شيب خط برابر است با \(\frac{{1 - 0}}{{ - 2 - 0}} = - \frac{1}{2}\) و معادله آن به صورت \(y - 0 = - \frac{1}{2}(x - 1)\) يا \(y - 0 = - \frac{1}{2}x\) است لذا ضابطه تابع f به صورت
\(f(x) = \left\{ \begin{array}{l}1,x < - 2\\\\ - \frac{1}{2}x, - 2 \le x \le 2\\\\ - 1,x > 2\end{array} \right.\)
ميباشد توجه كنيد كه اين تابع را توان به صورت \(f(x) = \frac{1}{4}(\left| {x - 2} \right| - \left| {x + 2} \right|)\) نيز نوشت .
تهیه کننده: حامد دلیجه
جزوات جامع پایه یازدهم
جزوه جامع حسابان یازدهم فصل 1 جبر و معادله
جزوه جامع حسابان یازدهم فصل 2 تابع
جزوه جامع حسابان یازدهم فصل 3 توابع نمایی و لگاریتمی
جزوه جامع حسابان یازدهم فصل 4 مثلثات
جزوه جامع حسابان یازدهم فصل 5 حد و پیوستگی
معادلات و توابع
معادلات و توابع
در رابطه هايي كه شامل x و y هستند اگر به ازاي هر x تنها يك y داشته باشيم اين رابطه نسبت به متغير مستقل x تابعي را مشخص ميكند بهويژه اگر بتوان y را بر حسب x محاسبه كرد اگر به رابطه اي به فرم \(y = \pm f(x)\) كه y همواره صفر نباشد، برسيم؛ رابطه فوق تابعي را مشخص نميكند به عبارت ديگر f تابع است اگر و تنها اگر بتوان نشان داد:
\(f({x_1}) = f({x_2}) \Rightarrow {x_1} = {x_2}\)
يا به طور معادل
\(f({x_1}) \ne f({x_2}) \Rightarrow {x_1} \ne {x_2}\)
مثال
بررسي كنيد روابط زير تابعاند يا خير؟
الف)\({y^2} - {x^2} = 1\) ب)\({y^2} - {x^2}2y = - 1\)
ج)\({y^3} - {x^2} = 2\) د)\(x + \left| y \right| = 0\)
الف) داريم:
يعني به ازاي هر \(x > - 1\) بيش از يك y داريم . مثلاً اگر \(x = 0\) داريم \(y = \pm 1\) .
لذا اين رابطه مشخص كننده ي يك تابع نيست . البته تنها ذكر اين مطلب كه هر دو نقطه \((0,1)\) و \((0, - 1)\) روي نمودار اين رابطه قرار دارد نشان دهنده ي اين است كه رابطه ي فوق تابع نميباشد.
ب) داريم:
\(\begin{array}{l}{x^2} - {y^2} - 2y = - 1 \Rightarrow {x^2} + {(y - 1)^2} = 0 \Rightarrow {(y - 1)^2} = - {x^2}\\\\ \Rightarrow y - 1 = \pm \sqrt { - {x^2}} \Rightarrow y = 1 \pm \sqrt { - {x^2}} \end{array}\)
ما x تنها مقدار صفر را ميتواند اختيار كند كه خروجي آن تنها يك ميباشد يعني در اين رابطه تنها زوج مرتب ( 10 , 0) صدق ميكند لذا y تابعي از x است.
ج) داريم:
\({y^3} + {x^2} = 2 \Rightarrow {y^3} = 2 - {x^2}{ \Rightarrow ^3}\sqrt {2 - {x^2}} \)
يعني به ازاي هر x ، y منحصر به فردي وجود دارد يعني y تابعي از x است براي اثبات اين مطلب ميتوان نوشت:
\({x_1} = {x_2} \Rightarrow x_1^2 = x_2^2 \Rightarrow 2 - x_1^2 = 2 - x_2^2{ \Rightarrow ^3}\sqrt {2 - x_1^2} { = ^3}\sqrt {2 - x_2^2} \Rightarrow {y_1} = {y_2}\)
د) داريم:
\(x + \left| y \right| = 0 \Rightarrow \left| y \right| = - x \Rightarrow y = 9 \pm ( - x),x \le 0\)
يعني اگر\(x > 0\) هيچ نقطه اي در رابطه صدق نميكند . اگر \(x = 0\) ، تنها نقطه ي\((0,0)\) را مشخص ميكند اما اگر \(x < 0\) ، به ازاي هر x ، دو y نظير ميشود؛ لذا y تابعي از x نيست . مثلاً اگر −\(x = - 1\) داريم \(y = \pm 1\) يعني دو نقطه \(( - 1,1)\) و \(( - 1, - 1)\) را مشخص ميكند لذا اين رابطه تابعي را نسبت به x مشخص نميكند . اما اين رابطه يك تابع x بر حسب y را مشخص مي كند .
تهیه کننده: حامد دلیجه
رسم نمودار توابع وابسته به f با استفاده از نمودار تابع f
رسم نمودار توابع وابسته به f با استفاده از نمودار تابع f
(1)نمودار تابع \(g(x) = f(x) + a\) همان نمودار تابع \(f(x)\) است كه a واحد در امتداد محور y ها منتقل شده است ( اگر \(a > 0\) انتقال در جهت مثبت محور y و اگر \(a < 0\) انتقال در جهت منفي ميباشد (
توجه كنيد اگر,\(({x_0},{y_0}) \in f\) يعني \({y_0} = f({x_0})\) آن گاه \(g({x_0}) + a = {y_0} + a\) یا \(({x_0},{y_0} + a) \in g\) یعنی نقطه به اندازه a واحد به موازات محور y ها منتقل شده است.
(2) نمودار تابع \(h(x) = f(x + a)\) همان نمودار تابع f است كه a واحد در امتداد محور x ها منتقل شده است (اگر \(a > 0\) انتقال در جهت منفي محور و اگر \(a > 0\) انتقال در جهت مثبت ميباشد (
توجه كنيد كه اگر \(({x_0},{y_0}) \in f\) يعني \({y_0} = f({x_0})\) انگاه:
\(h({x_0} - 0) = f({x_0} - a + a) = f({x_0}) = {y_0}\)
یا \(({x_0} - a,{y_0})\) یعنی نقطه به اندازه a واحد به موازات محور x ها منتقل شده است
(3 )نمودار تابع \(k(x) = a = af(x)\) با كشيدن نمودار تابع \(y = f(x)\) در امتداد محور y ها به دست ميآيد (اگر \(a > 1\) ، انبساط در امتداد محور y ها و با ضريب a رخ ميدهد و اگر 10, \(0 < a < 1\) ، انقباض و در امتداد محور y ها و با ضريب a رخ ميدهد و اگر براي بدست آوردن نمودار تابع \(y = k(x)\) ابتدا قرينه نمودار f نسبت به محور x ها يعني نموار تابع
\(y = - f(x)\) را رسم ميكنيم سپس نمودار جديد را با ضريب -aمنبسط يا منقبض (بسته به اينكه \( - a > 1\) یا \(0 < - a < 1\) ميكنيم.
.
توجه كنيد اگر \(({x_0},{y_0}) \in f\) یعنی \(({x_0} = f({x_0})\) ان گاه \(k({x_0}) = a,f({x_0}) = a{y_0}\) یعنی \(({x_0},a{y_0}) \in k\) كه مويد نكته گفته شده است
(4 ) نمودار تابع \(t(x) = f(ax)\) \(a > 0\)با كشيدن نمودار تابع \(y = f(x)\) در امتداد محور x ها به دست ميآيد. (اگر \(a > 1\) نمودار f با ضريب \(\frac{1}{a}\) ، منقبض شده و اگر \(0 < a < 1\) نمودار f با ضريب منبسط خواهد شد )
توجه كنيد كه اگر \(({x_0},{y_0}) \in f\) يعني \({y_0} = f({x_0})\) ان گاه \(t(\frac{{{x_0}}}{a}) = f(a \times \frac{{{x_0}}}{a}) = f\left( {{x_0}} \right) = y\) یعنی \((\frac{{{x_0}}}{a},{y_0})\) كه نكات گفته شده را تاييد ميكند
( 5 ) براي رسم نمودار تابع \(M(x) = f(ax)\) كه در آن \(a < 0\) با توجه به آنكه نمودار تابع \(l(x) = f( - x)\) قرينه نمودار تابع \(y = f(x)\) نسبت به محور y ها است براي رسم تابع \(a < 0\) \(M(x) = f(ax)\) , ابتدا ميتوان نمودار تابع \(N(x) = f( - ax)\) را مانند آنچه در ((4 بيان شد، رسم نمود سپس نمودار تابع M كه \(M(x) = N( - x)\) ميباشد را با رسم قرينه نمودار تابع N نسبت به محور y ها رسم كرد.
توجه كنيد كه اگر \(\left( {{x_0},{y_0}} \right) \in f\) یعنی \({y_0} = f\left( {{x_0}} \right)\) ان گاه
\(l( - {x_0}) = f( - ( - {x_0})) = f({x_0}) = {y_0}\)
يعني \(( - {x_0},{y_0}) \in l\) که قرینه نقطه \(({x_0},{y_0})\) نسبت به محورy ها است
(6)براي رسم نمودار تابع \(p(x) = af(bx + c) + d\) مراحل زير را انجام ميدهيم:
الف) اگر \(b > 0\) مطابق مرحله )4(نمودار f را با ضريب \(\frac{1}{b}\)در امتداد محور ط انقباض 1 يا انبساط ميدهيم و اگر \(b < 0\)
مطابق مرحله) 5) عمل ميكنيم)در اين حالت نمودار \(f(x)\) حاصل ميشود (
ب) با توجه به مرحله 2 نموار بدست آمده در مرحله قبل را به اندازه \(\frac{c}{b}\)در راستاي محور x ها و در جهت مخالف علامت \(\frac{c}{b}\)انتقال دارد (در اين حالت نمودار تابع \(y = f(bx + c)\) حاصل ميشود.
ج) با توجه به مرحل 3 نمودار به دست آمده در مرحله قبل را انبساط يا انقباض داد . (با ضريب \(\left| a \right|\) در اين مرحله نمودار تابع\(y = af(bx + c)\) بدست می آيد ).
د) با توجه به مرحله 1 نمودار به دست آمده در مرحله قبل را به اندازه d واحد در جهت محور y ها انتقال ميدهيم (در اين مرحله نموار تابع \(y = (bx + c) + d\) كه همان \(y = p(x)\) است به دست مي آيد(
قابل ذكر است كه در اين مرحله اگر \(a = 1\) يا \(b = 1\) يا \(c = 0\) يا \(d = 0\) مرحله نظير داده شده قابل حذف است.
توجه كنيد كه اگر \(( - {x_0},{y_0}) \in f\) یعنی \(y = f\left( {{x_0}} \right)\) آنگاه:
\((\frac{{ - {x_0} - c}}{b}) = af(b(\frac{{ - {x_0} - c}}{b}) + c) + d = af({x_0}) + d = a{y_0} + d\)
لذا
\(yy = f(2x)\)
كه مويد مطالب فوق است.
مثال
فرض كنيد نمودار تابع \(y = f(x)\) زيربه صورت باشد . مطلوب است رسم نمودار توابع g ،h ، k ، t ، l و p كه در مثال قبل معرفي شدند.
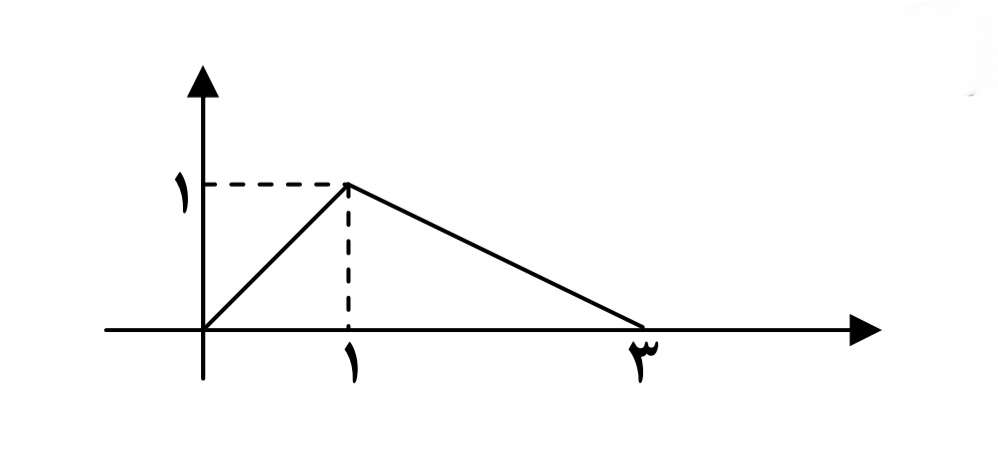
داريم:
الف)
ب)
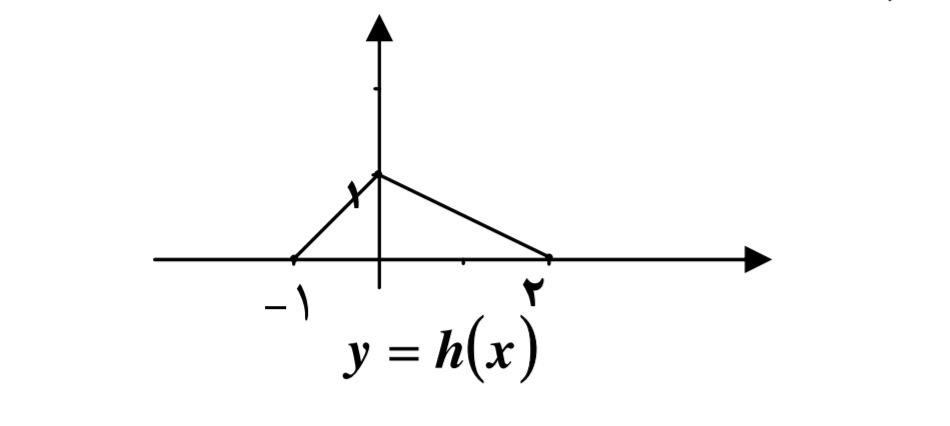
ج)
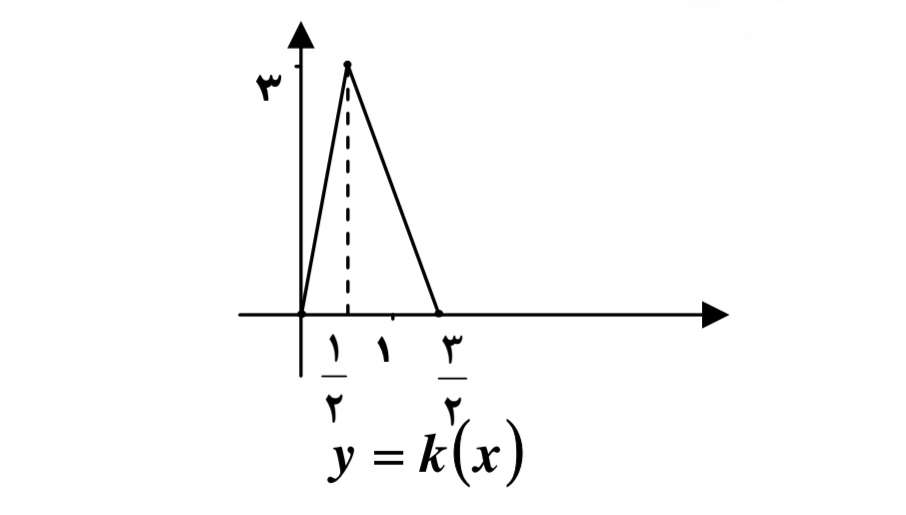
د)
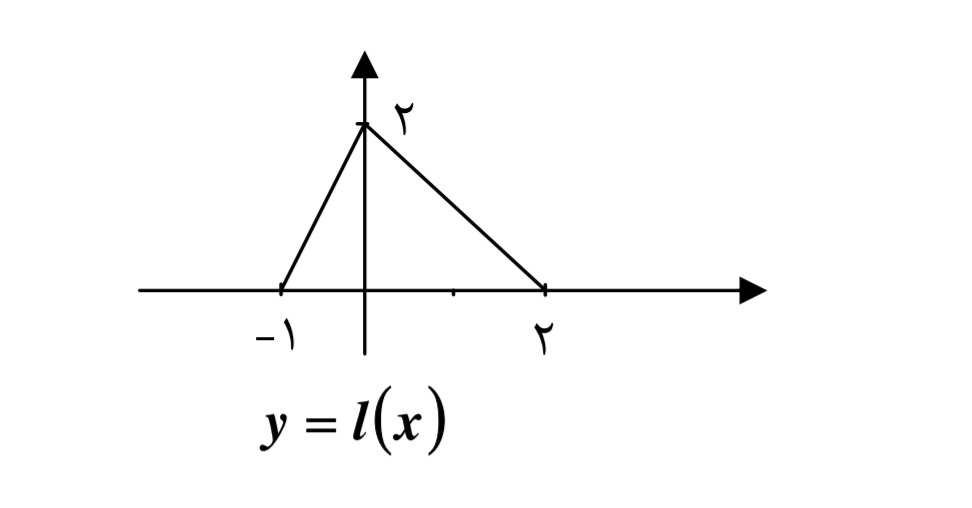
هـ ) توجه كنيد كه نمودار تابع \(y = f( - x)\) به صورت زير است:
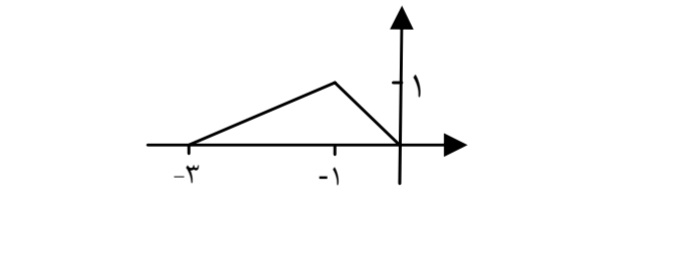
و با توجه به آن نمودار \(y = t(x)\) به صورت زير است:
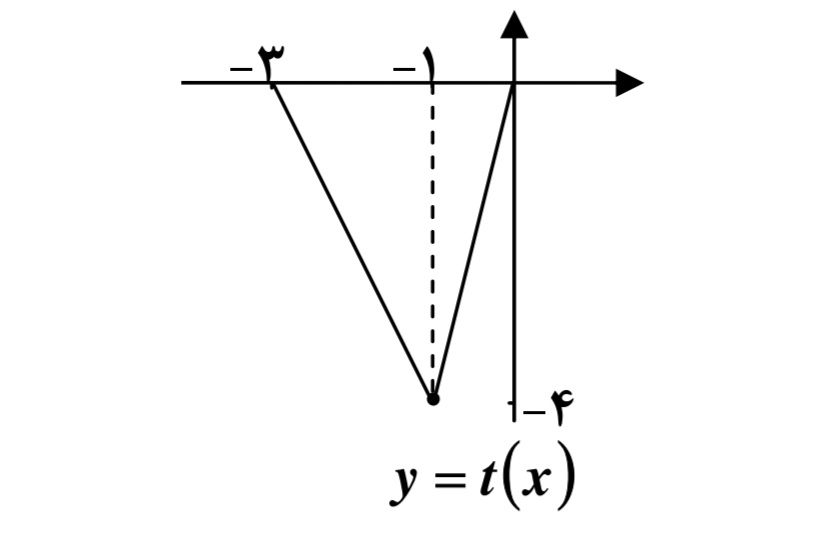
و) براي رسم نمودار تابع p مطابق دستورالعمل 6 به صورت زير عمل ميكنيم: مرحله ي الف) نمودار \(y = f(2x)\)
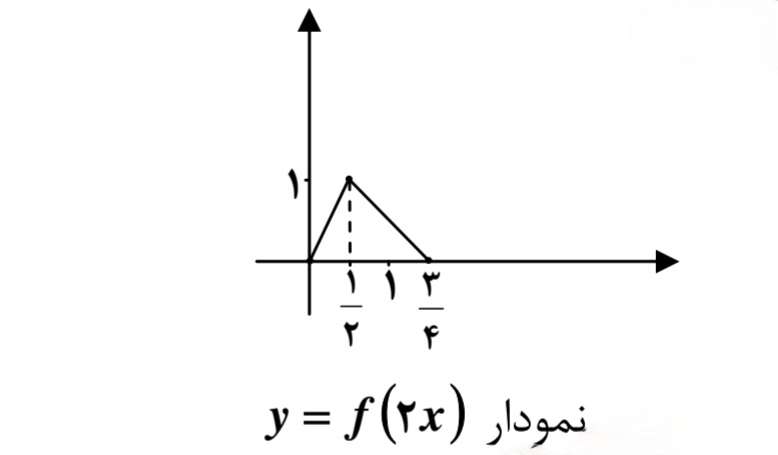
مرحله ي ب) انتقال \(y = f(2x)\) به اندازه\(\frac{1}{2}\) + در جهت محور x ها.
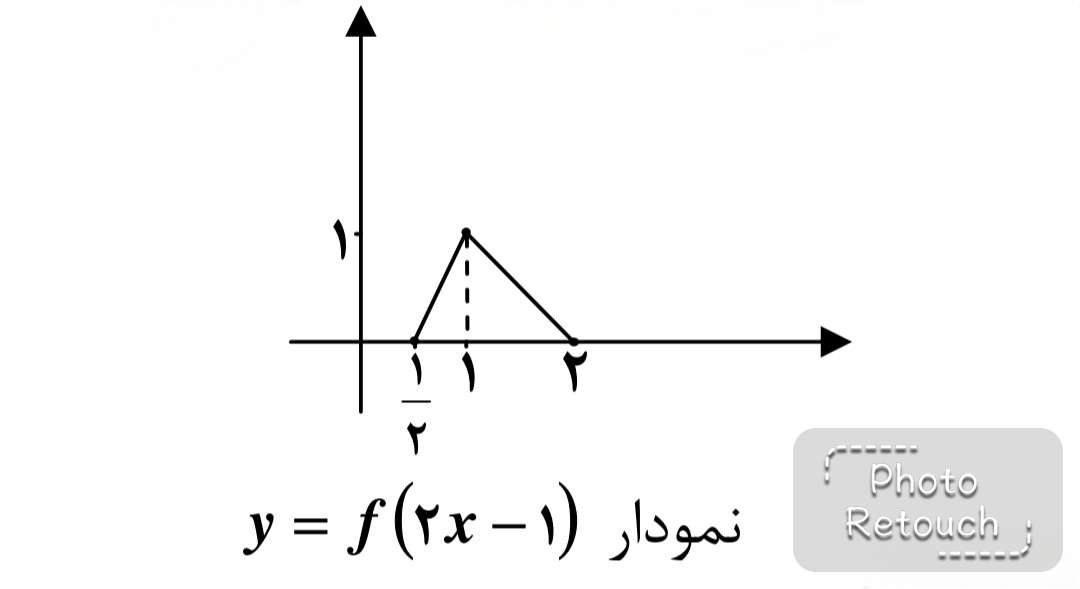
مرحله ي ج) انبساط نمودار \(y = f(2x)\) با ضريب 3 در امتداد محور y ها.
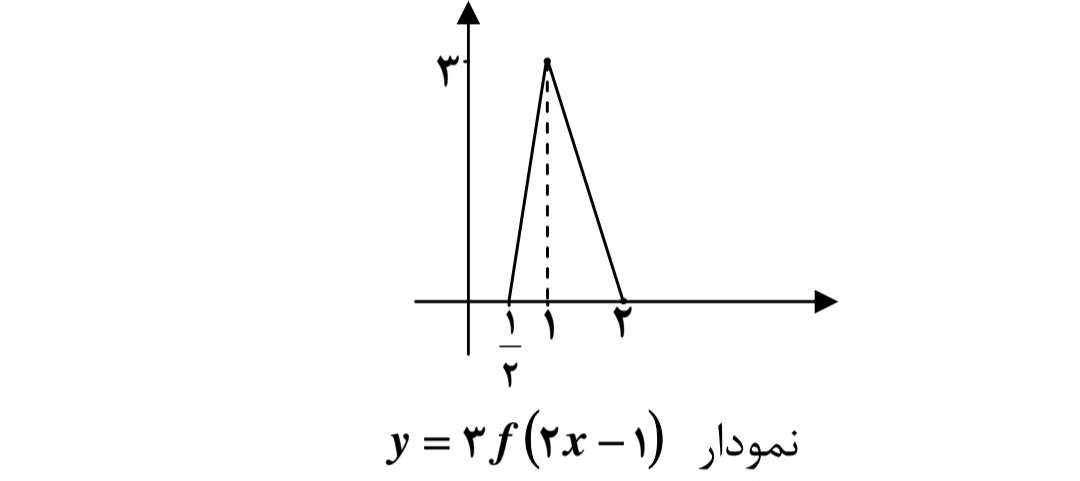
مرحله ی(د) انتقال \(y = 3f(2x - 1)\) به اندازه يك واحد در جهت محور y ها.
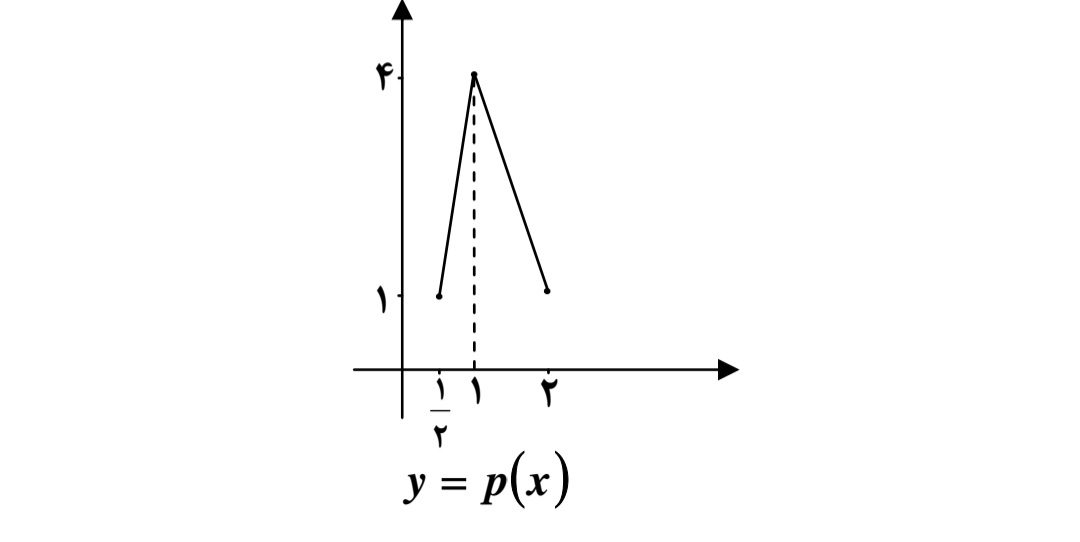
مثال
اگر نمودار تابع \(y = f(x)\) به شكل زير باشد.
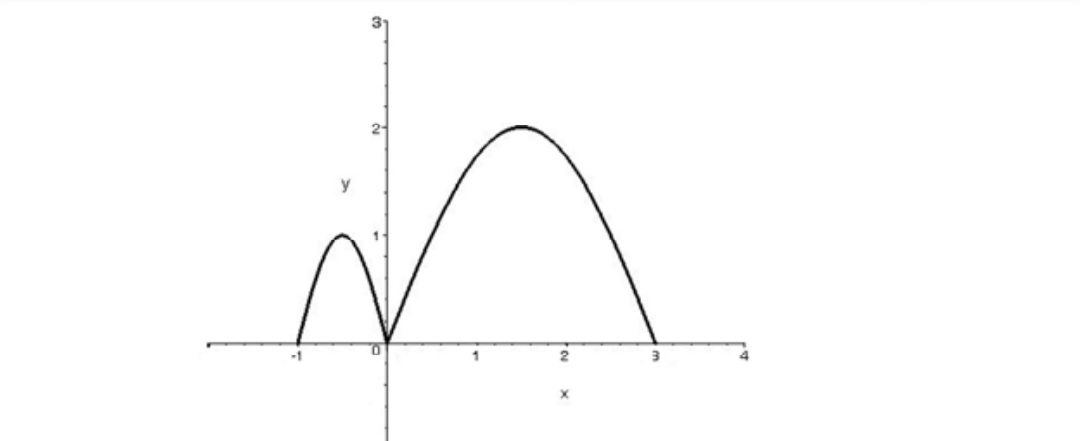
نمودار تابع \(y = f( - 2x)\) را رسم کنید مطابق دستورالعمل 5 و سپس 4 ابتدا نمودار تابع \(y = f(2x)\) را رسم می کنیم .
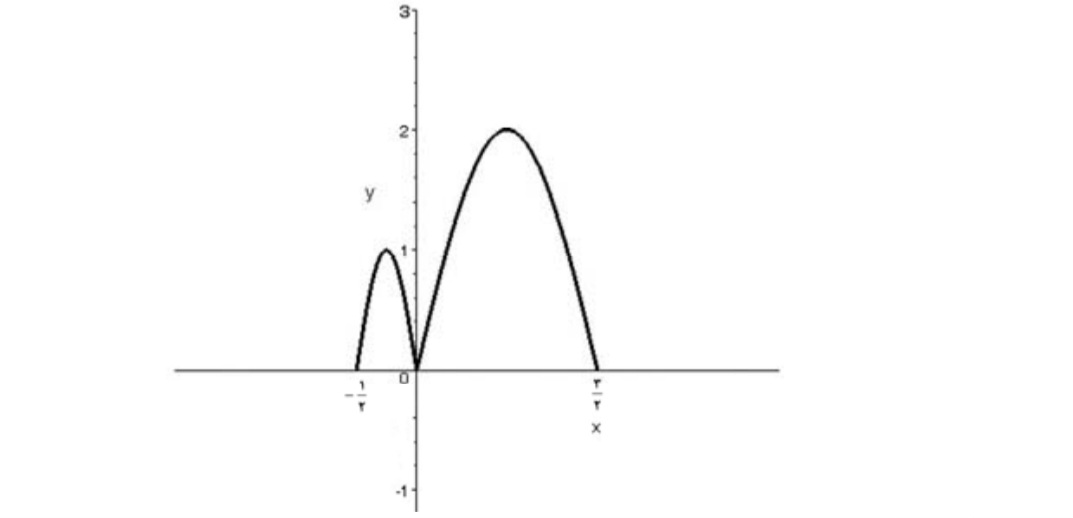
بنابراين نمودار \(y = f( - 2x)\) به صورت ميباشد:
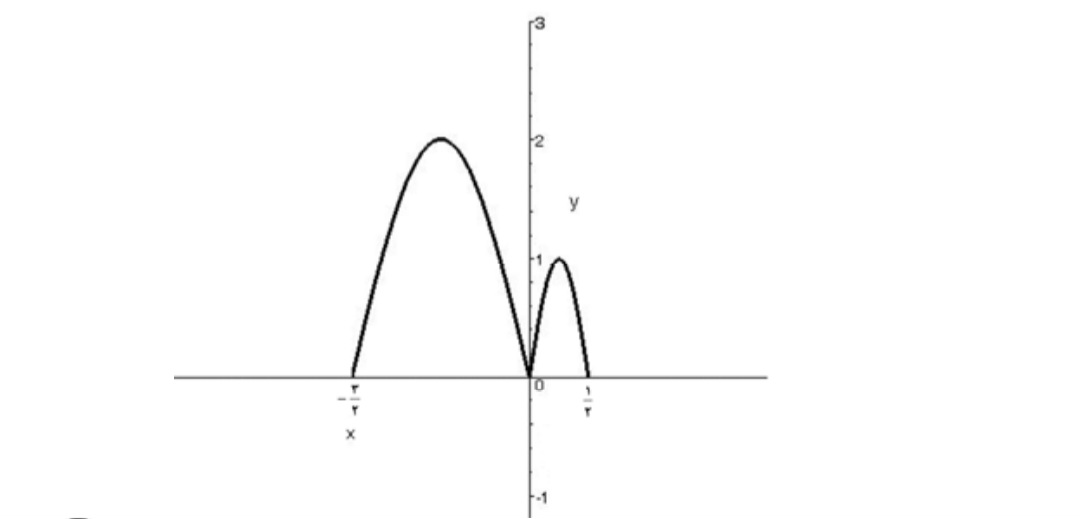
مثال
اگر نمودار تابع \(y = f(x)\) به صورت زير باشد نمودار توابع زير را رسم كنيد و دامنه ي آنها را مشخص كنيد.
الف) \(y = f(3x)\) ب) \(y = f( - 3x)\)
ج) \(y = f( - 3x + 1)\)
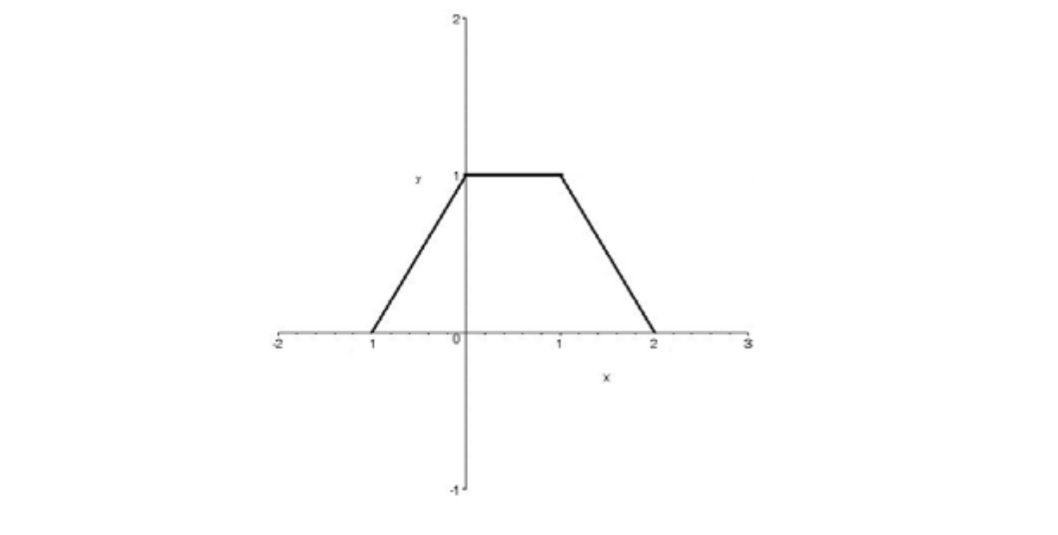
با توجه به دستورالعمل هاي گفته شده مراحل زير را خواهيم داشت.
الف)نمودار \(y = f(3x)\)
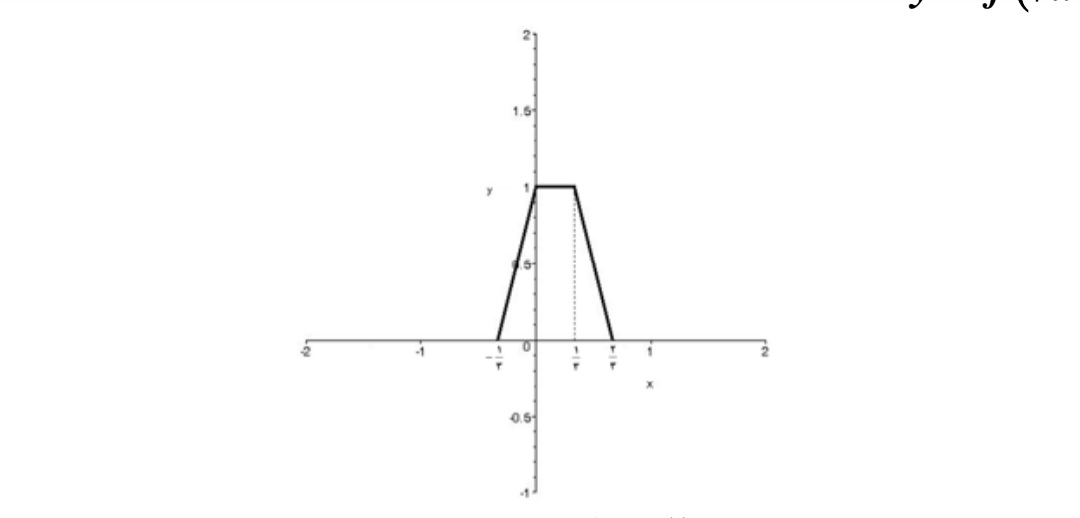
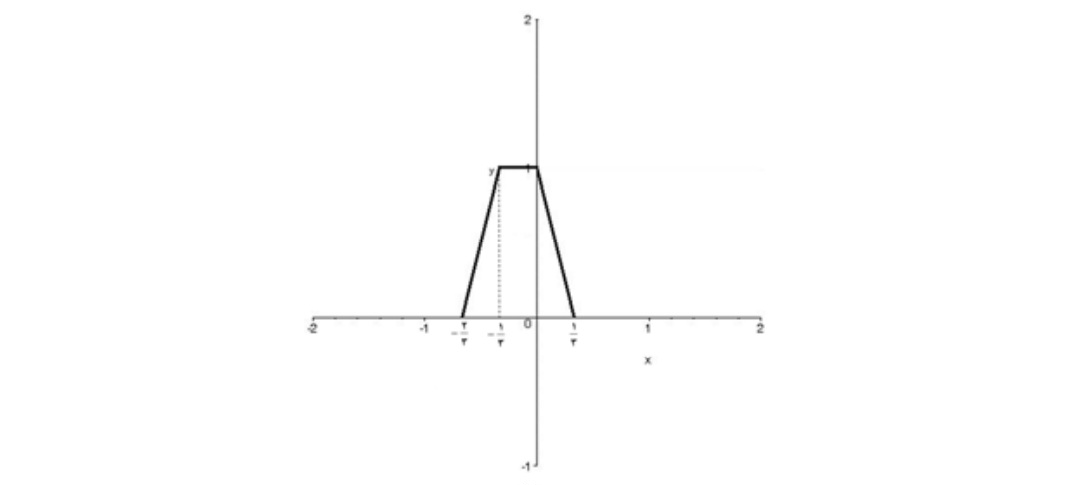
ب)نمودار \(y = f( - 3x)\)
ج)نمودار \(y = f( - 3x + 1)\)
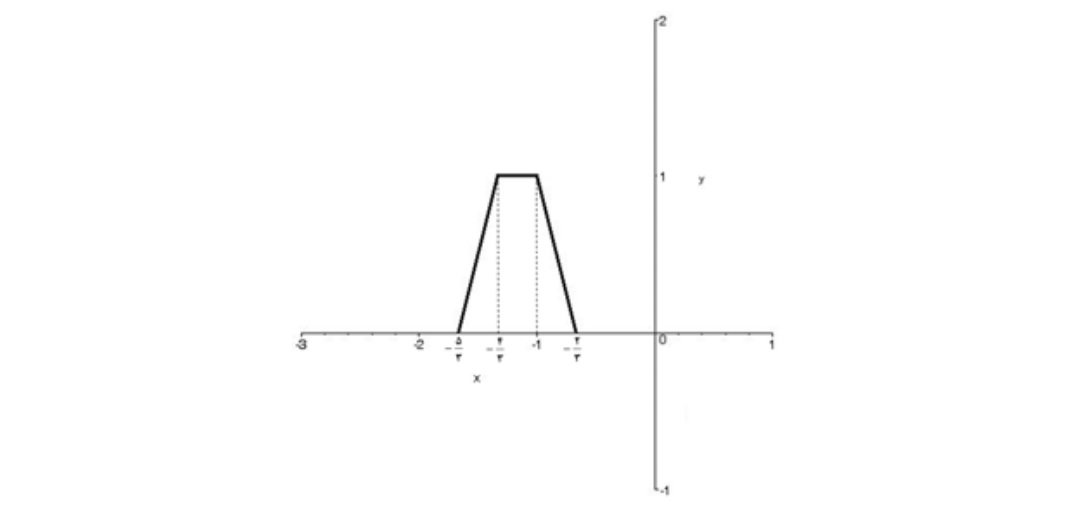
دامنه ي اين تابع با توجه به شكل بازه \(\left[ { - \frac{5}{3}, - \frac{2}{3}} \right]\) است.
تهیه کننده: حامد دلیجه
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه یازدهم- آزمون آنلاین تمامی دروس پایه یازدهم
- گام به گام تمامی دروس پایه یازدهم
- ویدئو های آموزشی تمامی دروس پایه یازدهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه یازدهم
- فلش کارت های آماده دروس پایه یازدهم
- گنجینه ای جامع از انشاء های آماده پایه یازدهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه یازدهم
اعمال جبري روي توابع
اعمال جبري روي توابع
برای دو تابع \(g,f\) تابع روی \(f + g\) تعریف میشود و براي هر مقدار x در \({D_f} \cap {D_g}\) داریم \((f + g)(x) = f(x) + g(x)\) به طور مشابه توابع \(f - g\) و \(f.g\) نيز روي داريم :\({D_f} \cap {D_g}\) داريم تعريف ميشود و به ازای هر \(x \in {D_f} \cap {D_g}\) داریم :
\(\begin{array}{l}(f - g)(x) = f(x) - g(x)\\\\(f.g)(x) = f(x).g(x)\end{array}\)
و تابع \(\frac{f}{g}\) نیز به ازاي \(x \in {D_f} \cap {D_g} - \left\{ {\left. x \right|} \right.g(x) = \left. 0 \right\}\) تعريف مي شود و به ازاي هرعددx در این مجموعه داريم:
\((\frac{f}{g})(x) = \frac{{f(x)}}{{g(x)}}\)
مثال
مدرسه علي تاكنون از دانش آموزان 2 مرحله آزمون گرفته است . در مرحله اول دروس مورد آزمون عبارتند از : حسابان، هندسه، فيزيك، شيمي، ادبيات و دروس آزمون مرحله دوم عبارتند از: حسابان، جبر و احتمال، فيزيك، ادبيات و زبان انگليسي . نمرات علي بر حسب درصد چنين است:
,85 )ادبيات) ,(79 ,شيمي) ,(68 , فيزيك) ,(56 , هندسه) ,(70 , حسابان )f= مرحله اول
,85)زبان انگليسي ) ,(79 ,ادبيات ) ,(68 ,فيزيك) ,(56 ,جبرواحتمال ) ,(74 ,حسابان)g =مرحله دوم
اگر تابع مربوط به اختلاف نمرات مرحله دوم از مرحله اول را بنويسيم اين تابع تنها براي دروسي با معني است كه در هر دو آزمون مورد سنجش واقع شده اند، يعني
(6-,ادبيات ) (0 , فيزيك ) ,( 4 , حسابان)=G-f
و با مشاهده اين تابع مشخص است كه وي در درس حسابان پيشرفت، در فيزيك بدون تغيير و در ادبيات دچار افت شده است.
مثال
فرض كنيد \(f(x) = 2x + 5\) و \(g = ( - 1,3),(0, - 5),(4,0),( - 2/5),(3,2)\) توابع \(\frac{g}{f},\frac{f}{g},f.g,g - f,f - g,f + g\) را مشخص كنيد. G
دامنه تابع f ، مجموعه ℜ و دامنه تابع g مجموعه \(\left\{ { - 1,0,4, - 2/5} \right.,\left. 3 \right\}\) است . لذا دامنه توابع \(f.g,g - f,f - g,f + g\) مجموعه حاصل از اشتراك اين دو مجموعه يعني مجموعه \(\left\{ { - 1,0,4, - 2/5} \right.,\left. 3 \right\}\) است همچنین \(f(0) = 5,f(4) = 13,f( - 2/5) = 0,f(3) = 11\) و بنابراين:
\(\begin{array}{l}f + g = ( - 1,6)\left( {0,0} \right)\left( {4,13} \right)\left( { - 2/5,1} \right)\left( {3,13} \right)\\\\f + g = ( - 1,0)\left( {0,10} \right)\left( {4,13} \right)\left( { - 2/5, - 1} \right)\left( {3,9} \right)\\\\f + g = ( - 1,0)\left( {0, - 10} \right)\left( {4, - 13} \right)\left( { - 2/5, - 1} \right)\left( {3, - 9} \right)\\\\f.g = ( - 1,0)\left( {0, - 25} \right)\left( {4,0} \right)\left( { - 2/5,0} \right)\left( {3,22} \right)\end{array}\)
همچنين دامنه تابع \(\frac{f}{g}\) مجموعه \(\left\{ { - 1,0,4, - 2/5,\left. 3 \right\}} \right.\) به جز اعضايي كه خروجي g به ازاي آنها صفر است؛ يعني عضو ،4 چون \(g(4) = 0\) لذا دامنه آن، مجموعه \(\left\{ { - 1,0, - 2/5,\left. 3 \right\}} \right.\)ميباشد. بنابراين:
\(\frac{f}{g} = \left\{ {( - 1,1)(0, - 1),( - 2/5,\left. {0)(3,\frac{{11}}{2})} \right\}} \right.\)
دامنه تابع \(\frac{g}{f}\) مجموعه \(\left\{ { - 1,0, - 2/5,\left. 3 \right\}} \right.\) به جز اعضايي كه خروجي f به ازاي آنها صفر است؛ يعني عضو \( - \frac{5}{2}\) ، چون \(f( - \frac{5}{2}) = 0\) لذا دامنه آن مجموعه \(\left\{ { - 1,0,4,\left. 3 \right\}} \right.\) بنابراين:
\(\frac{g}{f} = \left\{ ( \right. - 1,1)(0, - 1),( - 2/5,\left. {0)(3,\frac{{11}}{2})} \right\}\)
مثال
فرض كنيد \(f(x) = \sqrt {{x^2} - 4} \) و \(g(x) = \sqrt {\frac{{{x^2} + 2x}}{{2 - x}}} \) ضابطه و دامنه توابع \(\frac{g}{f},\frac{f}{g},f.g,g - f,f - g,f + g\) و را مشخص كنيد.
دامنه تابع f مجموعه \({d_f} = ( - \infty , - \left. 2 \right] \cup \left[ {2, + \infty )} \right.\) است و دامنه تابع g مجموعه \(dg = ( - \infty , - \left. 2 \right] \cup \left[ {0,2)} \right.\) است . بنابراين:
\(\begin{array}{l}(f + g)(x) = f(x) + g(x) = \sqrt {{x^2} - 4} + \sqrt {\frac{{{x^2} + 2x}}{{2 - x}},} {D_{f + g}} = ( - \infty ,2)\\\\(f - g)(x) = f(x) - g(x) = \sqrt {{x^2} - 4} + \sqrt {\frac{{{x^2} + 2x}}{{2 - x}},} {D_{f - g}} = ( - \infty ,2)\\\\(f.g)(x) = f(x).g(x) = \sqrt {{x^2} - 4} .\sqrt {\frac{{{x^2} + 2x}}{{2 - x}},} {D_{f.g}} = ( - \infty ,2)\end{array}\)
اين تابع با تابع \(h(x) = \left| {x + 2} \right|\sqrt { - x} \) كه به دامنه [2 − , ∞ −) تحديد (محدود) شده باشد برابر است ( . واضح است بدون تحديد دو تابع برابر نيستند ).
تابع g به ازاي \(x = 0\) و \(x = - 2\) صفر خواهد شد لذا تابع \(\frac{f}{g}\) عبارتست از :
\(\left( {\frac{f}{g}} \right)(x) = \frac{{f(x)}}{{g(x)}} = \frac{{\sqrt {{x^2} - 4} }}{{\frac{{\sqrt {{x^2} + 2x} }}{{2 - x}}}},{D_{\frac{f}{g}}} = ( - \infty , - 2)\)
اين تابع با تابع \(h(x) = \frac{{\left| {x - 2} \right|}}{{\sqrt { - x} }}\) وقتي كه دامنه آن به مجموعه \(( - \infty , - 2)\) تحديد شده باشد برابر است.
همچنين تابع g به ازاي \(x = 2\) و \(x = - 2\) صفر خواهد شد لذا
\(\left( {\frac{g}{f}} \right)(x) = \frac{{g(x)}}{{f(x)}} = \frac{{\frac{{\sqrt {{x^2} + 2x} }}{{2 - x}}}}{{\sqrt {x - 4} }},{D_{\frac{g}{f}}} = ( - \infty , - 2)\)
و اين تابع با تابع \(m(x) = \frac{{\sqrt { - x} }}{{\left| {x - 2} \right|}}\) ، وقتي دامنه آن به مجموعه \(( - \infty , - 2)\) تحديد شده باشد برابر x است.
مثال
اگر نمودار توابع f و g به صورت زير باشد، نمودار توابع \(f + g\) و \(f - g\) و \(f.g\) را رسم كنيد.
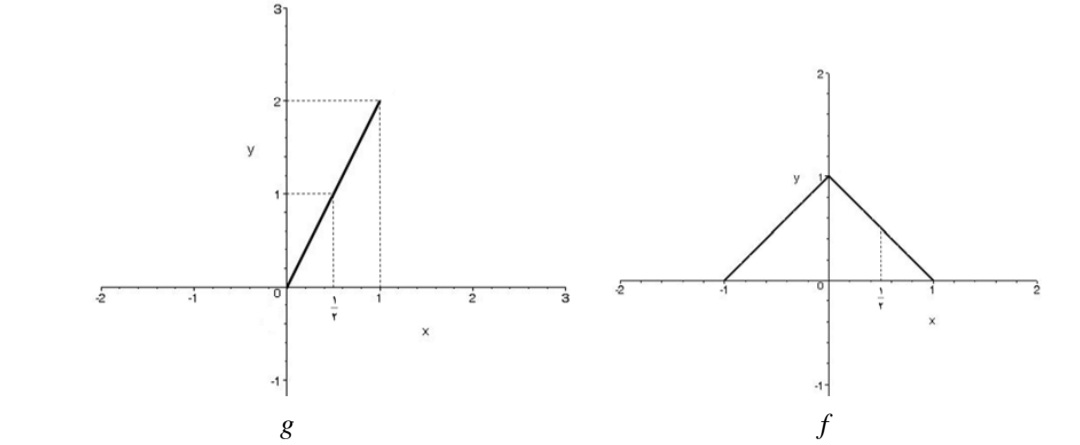
با توجه به شكل تابع f در فاصله [ 11 , 1−] تعريف شده است و تابع g در \(\left[ {0,\infty } \right]\) . لذا توابع \(f + g\) و \(f - g\) و \(f.g\) در فاصله [ 10 ,0 ] تعريف شده اند.
براي رسم \(f + g\) كافي است \((f + g)(x)\) را به ازاي هر مقدار \(0 \le x \le 1\) را محاسبه كنيم يعني مقادير f و g را در هر يك محاسبه نمود و با هم جمع كرد . مثلا:
\(\begin{array}{l}(f + g)(0) = f(0) + g(0) = 1 + 0 = 1\\\\(f + g)(1) = f(1) + g(1) = 0 + 2 = 2\\\\(f + g)(\frac{1}{2}) = f(\frac{1}{2}) + g(\frac{1}{2}) = \frac{1}{2} + 1 = \frac{3}{2}\end{array}\)
لذا شكل \(g + f\) به طور تقريبي چنين خواهد بود.
به طور مشابه مقادير \(f - g\) را به ازاي هر \(0 \le x \le 1\) از تفاضل مقدار تابع g از f وf.g را به ازاي هر \(0 \le x \le 1\) از ضرب مقادير توابع f و g به دست ميآوريم . نمودارهاي تقريبي به صورت زير است:
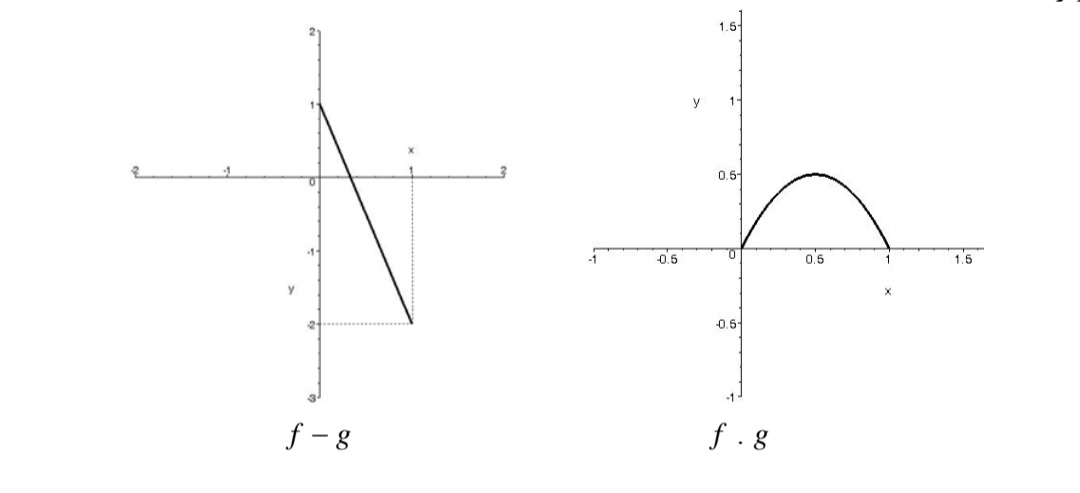
تهیه کننده: حامد دلیجه
جزوات جامع پایه یازدهم
جزوه جامع حسابان یازدهم فصل 1 جبر و معادله
جزوه جامع حسابان یازدهم فصل 2 تابع
جزوه جامع حسابان یازدهم فصل 3 توابع نمایی و لگاریتمی
جزوه جامع حسابان یازدهم فصل 4 مثلثات
جزوه جامع حسابان یازدهم فصل 5 حد و پیوستگی
ترکیب توابع
تركيب توابع
اگر f و g دو تابع باشند، تابع fog تابعي است كه از تركيب دو تابع بوجود ميآيد كه اعضاي آن زوج مرتب هايي از \((x,y)\) هستند كه x در دامنه g قرار دارد و \(g(x)\) هم در دامنه f ميباشد و y مقدار تابع f به ازاي \(g(x)\) ميباشد . يعني:

به عبارت ديگر
مثال
توابع f و g به صورت :\(\begin{array}{l}g = \left\{ {(1,3),(3,5),(5,7),(7,1\left. ) \right\}} \right.\\\\f = \left\{ {(1,2)(2,3)(3,4)(4,5)(6,7\left. ) \right\}} \right.\end{array}\)تعريف شده اند. مطلوب است تعيين توابع fog و gof
براي تعيين تابع fog دقت ميكنيم كه اعضاي دامنه تابع fog اعضايي از دامنه تابع g ميباشد كه در دامنه f قرار داشته باشد . داريم:
\(\left. \begin{array}{l}1 \in {D_f},f(1) = 2,2 \notin {D_g} \to 1 \notin {D_{fog}}\\\\2 \in {D_f},f(2) = 3,3 \notin {D_g} \to 2 \notin {D_{fog}}\\\\3 \in {D_f},f(3) = 4,4 \notin {D_g} \to 3 \notin {D_{fog}}\\\\4 \in {D_f},f(4) = 5,5 \notin {D_g} \to 4 \notin {D_{fog}}\\\\6 \in {D_f},f(6) = 7,7 \notin {D_g} \to 6 \notin {D_{fog}}\end{array} \right\} \Rightarrow {D_{fog}} = \left\{ {2,4,\left. 6 \right\}} \right.\)
و لذا
\(\left. \begin{array}{l}gof(2) = g(f(2)) = g(3) = 5\\\\gof(4) = g(f(4)) = g(5) = 7\\\\gof(6) = g(f(6)) = g(7) = 1\end{array} \right\} \Rightarrow gof = \left\{ {\left( {2,5} \right)} \right.,(4,7),(6,1\left. ) \right\}\)
مثال
فرض كنيد \(g(x) = \sqrt x + 1\) و \(f = \left\{ {\left( { - 2,0} \right)} \right.,(0,1),(1,4\left. {),\left( {2. - 5} \right)} \right\}\)مطلوب است توابع fogو gof
تعيين تابع :fog
دامنه آن اعضايي از دامنه \(\left\{ {\left. x \right|} \right.x \ge \left. 0 \right\}\),g ميباشد كه:
\(\begin{array}{l}g(x) \in {D_f} = \left\{ { - 2} \right.,0,1,\left. 2 \right\}\\\\g(x) = - 2 = \sqrt x + 1 \Rightarrow \sqrt x = - 3\\\\g(x) = 0 \Rightarrow \sqrt x + 1 = 0 \Rightarrow \sqrt x = - 1\\\\g(x) = 1 \Rightarrow \sqrt x + 1 = 1 \Rightarrow \sqrt x = 0 \Rightarrow x = 0\\\\g(x) = 2 \Rightarrow \sqrt x + 1 = 2 \Rightarrow \sqrt x = 1 \Rightarrow x = 1\end{array}\)
دومی غیر ممکن
سومی ممکن
پس از اعضاي دامنه تابع g تنها دو عضو 0 و 1 در دامنه تابع fog وجود دارند و داريم.
\(\begin{array}{l}fog(0) = (f(0)) = f(1) = 4\\\\fog(1) = (f(1)) = f(2) = - 5\end{array}\)
يعني:
\(fog(1) = \left\{ {(0,4),(1, - \left. {5)} \right\}} \right.\)
تعيين تابع: gof
دامنه آن اعضايي از دامنه تابع f ، \(\left\{ { - 2,0,1,\left. 2 \right\}} \right.\) هستند كه \(f(x) \in {D_g} = \left\{ {\left. x \right|} \right.x \ge \left. 0 \right\}\) اما:
\(\begin{array}{l}gof( - 2) = 0,0 \in {D_g} \Rightarrow - 2 \in {D_{fog}}\\\\gof(0) = 1,1 \in {D_g} \Rightarrow 0 \in {D_{fog}}\\\\gof(1) = 4,4 \in {D_g} \Rightarrow 1 \in {D_{fog}}\\\\gof( - 5) = 0, - 5 \in {D_g} \Rightarrow 2 \notin {D_{fog}}\end{array}\)
پس از اعضاي دامنه تابع f تنها سه عضو 2- ، 0 و 1 در دامنه تابع gof حضور دارند و داريم.
\(\begin{array}{l}g( - 2) = 0,0 \in {D_g} \Rightarrow - 2 \in {D_{fog}}\\\\g(0) = g(f(0)) = g(1) = 2\\\\g( - 5) = g(f(1)) = g(1) = 3\end{array}\)
يعني
\(gof = \left\{ {\left( { - 2,1} \right)} \right.,(0,2),(1,3\left. ) \right\}\)
مثال
فرض كنيد \(f(x) = \frac{1}{x}\) و \(g(x) = \sqrt {1 - {x^2}} \) مطلوب است تعيين دامنه و برد توابع fog و . gof
تعيين تابع :fog
دامنه تابع g مجموعه \({D_g} = \left\{ {\left. x \right|} \right. - 1 \le x \le \left. 1 \right\}\) است اماg(x) باید در دامنه تابعf باشدو \({D_f} = \left\{ {\left. x \right|} \right.x \ne \left. 0 \right\}\) پسg(x) نبايد صفر شود. اما g(x)در 1- و 1 صفر ميشود . پس \({D_{fog}} = \left\{ {\left. x \right|} \right. - 1 < x < \left. 1 \right\}\) و به ازای این xها داريم \(fog(x) = f(g(x)) = f(\sqrt {1 - {x^2}} ) = \frac{1}{{\sqrt {1 - {x^2}} }}\) تعيين تابع
دامنه تابع gof عضوهايي از مجموعه \(\left\{ {\left. x \right|} \right.x \ne \left. 1 \right\}\) ميباشد كه \(f(x) \in {D_g}\) باشد يعني \( - 1 \le f(x) \le 1\) یا \( - 1 \le \frac{1}{x} \le 1\) یعنی .\({D_{fog}} = ( - \infty , - \left. 1 \right] \cup \left[ {1, + \infty )} \right.\) پس با در نظر گرفتن هر دو شرط، دامنه gof مجموعه \({D_{fog}} = ( - \infty , - \left. 1 \right] \cup \left[ {1, + \infty )} \right.\) ميباشد و به ازاي اين x ها داريم:
\({D_{fog}} = g(f(x)) = g(\frac{1}{x}) = \sqrt {1 - {{(\frac{1}{x})}^2}} \)
مثال
فرض كنيد \(f(x) = \frac{x}{{2 - x}}\) مطلوب است تعيين دامنه و برد تابع fof
دامنه تابع f مجموعه \(R - \left\{ 2 \right\}\) است . بنابراين
\({D_{fof}} = \left\{ {\left. {x \in {D_f}} \right|} \right.f(x) \in \left. {{D_f}} \right\} = \left\{ {\left. {x \ne 2} \right|} \right.\frac{x}{{2 - x}} \ne \left. 2 \right\}\)
اما
\(\frac{x}{{2 - x}} = 2 \Rightarrow x = 4 - 2x \Rightarrow x = \frac{4}{3}\)
لذا
\({D_{fof}} = \left\{ {x \ne 2,x \ne \left. {\frac{4}{3}} \right\} = ( - \infty ,\frac{4}{3}) \cup } \right.(\frac{4}{3},2) \cup (2, + \infty )\)
همچنين
\(fof(x) = f(f(x)) = f\left( {\frac{x}{{2 - x}}} \right) = \frac{{\frac{x}{{2 - x}}}}{{2 - \frac{x}{{2 - x}}}}\)
توجه كنيد كه اگر اين ضابطه را ساده كنيم حتماً بايد شرط دامنه را قيد كنيم در غير اين صورت تابع حاصل با تابع fof برابر نخواهد بود.
\(fof(x) = \frac{x}{{4 - 3x}},x \ne \frac{4}{3},2\)
البته شرط \(x \ne \frac{4}{3}\) از ضابطه واضح است اما شرط \(x \ne 2\) حتماً بايد قيد شود.
مثال
در پرتاب جسم با سرعت اوليه \({v_0}\) در راستای قائم جسم بر حسب زمان از رابطه ی \(h(t) = \frac{1}{2}g{t^2} + {v_0}t\)\(\) به دست ميآيد كه در آن g ثابت و شتاب ثقل ميباشد . همچنين سرعت جسم بر حسب t از رابطه \(v(t) = {v_0} + gt\) به دست ميآيد. تابع ارتفاع جسم را برحسب متغير v (سرعت جسم) بيابيد.
داريم
\(v = {v_0} + gt \Rightarrow t = \frac{{v - {v_0}}}{g} = t(v) = \frac{{v - {v_0}}}{g}\)
حال از تركيب توابع \(h(t)\) و \(t(v)\) به تابع \(h(t(v))\) ميرسيم . بنابراين:
\(h(t(v)) = \frac{1}{2}g{(\frac{{v - {v_0}}}{g})^2} + {v_0}(\frac{{v - {v_0}}}{g}) \Rightarrow h(t(v)) = \frac{{{v^2} - {v_0}^2}}{{2g}}\)
\(\)
مثال
دامنه تابع \(h(x) = \sqrt {\sqrt {3x - 4} - 6x + 8} \) را بيابيد.
اگر قرار دهيم \(g(x) = 3x - 4\) و \(f(x) = \sqrt {\sqrt x - 2x} \) آنگاه \(h = fog\) و داريم \({D_f} = \left[ {0,\frac{1}{4}} \right]\)
پس
\(\begin{array}{l}{D_h} = {D_{fog}}\left\{ {x\left. { \in {D_g}} \right\}f(x) \in D\left. {_f} \right\}} \right. = \left\{ {x\left. { \in R} \right\}0 \le x \le \left. {\frac{1}{4}} \right\} = \left[ {0,\frac{1}{4}} \right]} \right.\\\end{array}\)
مثال
اگر\(f(x) = \left\{ \begin{array}{l}{x^2},x < 1\\x + 1,x \ge 1\end{array} \right.\) و \(g(x) = \left\{ \begin{array}{l} - 5x,x \le 0\\1,x > 0\end{array} \right.\) ضابطه تابع fog را بيابيد.
توجه كنيد كه x ابتدا به تابع g رفته و خروجي آن وارد تابع f ميشود . حال اگر \(x > 0\) را بعنوان ورودي تابع g در نظر بگيريم خروجي آن عدد 1 ميباشد حال 1 ورودي f را تشكيل ميدهد كه خروجي f به ازاي \(x = 1\) برابر \(1 + 1 = 2\)ميباشد . اين مطلب را چنين نمايش ميدهيم:
\(x > 0 \to 11 + 1 = 2\)
حال اگر \(x \le 0\) ورودي تابع g باشد خروجي آن-5x است . اگر \( - 5x < 1\) باشد، خروجي تابع f ، \(( - 5{x^2}) = 25{x^2}\) است و اگر \( - 5x \ge 1\) باشد خروجي تابع f ، \( - 5x + 1\) است يعني
\(\begin{array}{l}x \le 0 \to - \frac{1}{5} < x \le 0 - 5x{( - 5x)^2} = 25{x^2}\\\\x \le 0 \to x \le - \frac{1}{5} - 5x - 5x + 1\\\\ \Rightarrow fog(x) = \left\{ \begin{array}{l} - 5x + 1,x \le - \frac{1}{5}\\\\25{x^2}, - \frac{1}{5} < x \le 0\\\\2,x > 0\end{array} \right.\\\end{array}\)
مثال
اگر ، تابع \(f(x) = \sqrt x + 1\) و \(fog(x) = \sqrt {{x^2} - 1} + 1\) تابع \(g(x)\) را بيابيد.
داريم
\(\begin{array}{l}f(x) = \sqrt x + 1 \Rightarrow f(g(x)) = \sqrt {g\left( x \right)} + 1\\\\fog(x) = f(g(x)) = \sqrt {{x^2} - 1} + 1\end{array}\)
لذا
\(\sqrt {g\left( x \right)} + 1 = \sqrt {{x^2} - 1} + 1\)
و در نتيجه
\(\sqrt {g\left( x \right)} = \sqrt {{x^2} - 1} \)
يا
\(g(x) = {x^2} - 1\)
اگر
\(\begin{array}{l}fog(x) = f(g(x)) = \sqrt {{{\sin }^4}x + 2{{\sin }^2}x + 2} = \\\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\sqrt {\left( {{{\sin }^2}x + 1} \right)} = \sqrt {{g^2}(x) + 1} \end{array}\)
حالا با قرار دادن x به جاي g(x)در تساوي ها داريم
\(f(x) = \sqrt {{x^2} + 1} \)
تهیه کننده: حامد دلیجه
مجموعه های متقارن
مجموعه هاي متقارن
مجموعه ي \(A \subseteq R\) را متقارن گوييم هر گاه به ازاي هر \(x \in A\) داشته باشيم \( - x \in A\)
مثال
مجموعه ي \(A = \left\{ { - 3, - 2, - 1,0,1,\left. 2 \right\}} \right.\) متقارن نيست، زيرا \( - 3 \in A\) ولي \(3 \notin A\)
مثال
مجموعه ي \(A = \left\{ { - 1,\left. 2 \right\}} \right.\) متقارن نيست، زيرا\(2 \in A\) ولي \( - 2 \notin A\)
مثال
مجموعه ي مثال:مجموعه ی \(A = \left\{ { - 2,\left. 2 \right\}} \right.\) متقارن است زيرا هر عضوي از A انتخاب كنيم قرينه ي آن عضو نيز در A وجود دارد.
مثال
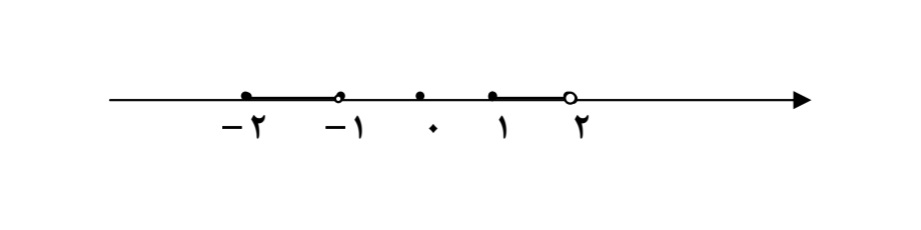
مجموعه ي A كه به صورت زير، روي محور نمايش داده شده، متقارن نيست، زيرا\( - 2 \in A\) و \(2 \notin A\)
توابع زوج و فرد
تابع f با دامنه يي متقارن را زوج گو يم، هر گاه به ازاي هر \(x \in {D_f}\) ، تساوي \(f( - x) = - f(x)\) برقرار باشد.
تابع f با دامنه يي متقارن را فرد گو يم، هر گاه به ازاي هر
\(x \in {D_f}\) تساوي \(f( - x) = - f(x)\) برقرار باشد.
مثال
زوج يا فرد بودن تابع \(f = \left\{ {\left( { - 3, - 1} \right)} \right.,(2,3),( - 2,3\left. {),\left( {3,1} \right)} \right\}\) را بررسي كنيد.
چون \({D_f} = \left\{ { - 3, - 3,2,\left. 3 \right\}} \right.\) ، لذا دامنه f متقارن است \(f( - 3) = - f(3)\) ولي \(f( - 2) = f(2)\) بنابراين تابع f نه زوج است و نه فرد.
مثال
زوج يا فرد بودن تابع \(f(x) = \frac{{x + 1}}{{x - 3}}\) را بررسي كنيد.
داريم \({D_f} = R - 3\) و \( - 3 \in {D_f}\) ولي \(3 \notin {D_f}\) ، پس دامنه تابع f متقارن نيست. بنابراين تابع f نه زوج است نه فرد.
مثال
زوج يا فرد بودن تابع \(f(x) = \frac{{{x^2} - \left| x \right|}}{{{x^2} + 1}}\) را بررسي كنيد.
داريم \({D_f} = R\) و لذا دامنه f متقارن است و
\(f( - x) = \frac{{( - {x^2}) - \left| x \right|}}{{({x^2}) + 1}} = \frac{{{x^2} - \left| x \right|}}{{{x^2} + 1}} = f(x)\)
بنابراين f تابعي زوج است.
مثال
زوج يا فرد بودن تابع \(f(x) = \log (x + \sqrt {{x^2} + 1} )\) رابررسی کنید
باتوجه به \({x^2} + 1 \ge 1\) و اين كه \(x + \sqrt {{x^2} + 1} > 0 \Rightarrow \sqrt {{x^2} + 1} \ge - x\) همواره برقرار است
11 دامنه ي f برابر ℜ است و لذا متقارن است و
\(\begin{array}{l}f( - x) = \log ( - x + \sqrt {({x^2}) + 1} = \log (\frac{{(\sqrt {{x^2} + 1} - x)(\sqrt {{x^2} + 1} + x)}}{{\sqrt {{x^2} + 1} + x}}\\\\ = \log \frac{1}{{\sqrt {{x^2} + 1} - x}} = \log 1 - \log (\sqrt {{x^2} + 1} + x) = - f(x)\end{array}\)
بنابراين f تابعي فرد است.
مثال
زوج يا فرد بودن تابع \(f(x) = \left\{ \begin{array}{l}{x^4} - 2x,x \ge 0\\\\{x^4} + 2x,x < 0\end{array} \right.\) را بررسي كنيد.
\({D_f} = R\) و لذا دامنه f متقارن است.
حالت اول: \(x = 0 \to f(0) = 0\)
حالت دوم: اگر x<0آنگاه –x>0 و داريم:
\(f( - x) = \left( { - {x^4}} \right) + 2\left( { - x} \right) = {x^4} - 2x = f(x)\)
بنابراين f تابعي زوج است.
مثال
زوج يا فرد بودن تابع \(f(x) = \sin x + \cos x\) را بررسي كنيد.
:\({D_f} = R\) و لذا دامنه f متقارن است و
\(f( - x) = \sin ( - x) + \cos ( - x) = - \sin x + \cos x\)
واضح است که \(f( - x) \ne f(x)\) و \(f( - x) \ne - f(x)\) پس تابع نه زوج است نه فرد.
مثال
قسمتي از نمودار تابع f با دامنه ي \(\left[ { - 4,4} \right]\) به صورت
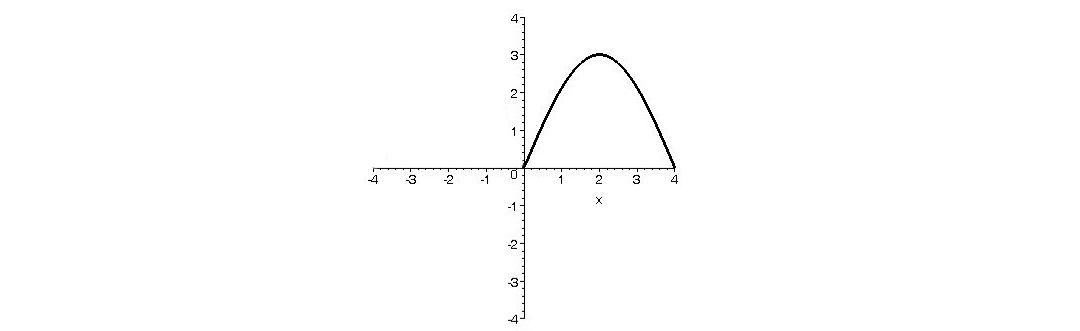
رسم شده است، نمودار تابع را طوري كامل كنيد تا:
الف) f تابعي زوج را نمايش دهد.
ب) f تابعي فرد را نمايش دهد.
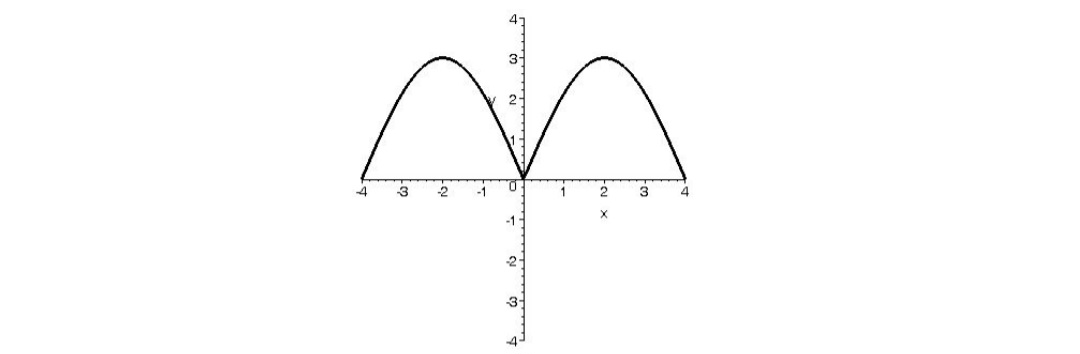
الف) ميدانيم نمودار تابع زوج نسبت به محور y ها متقارن است. پس لازم است نمودار f به صورت مقابل باشد.
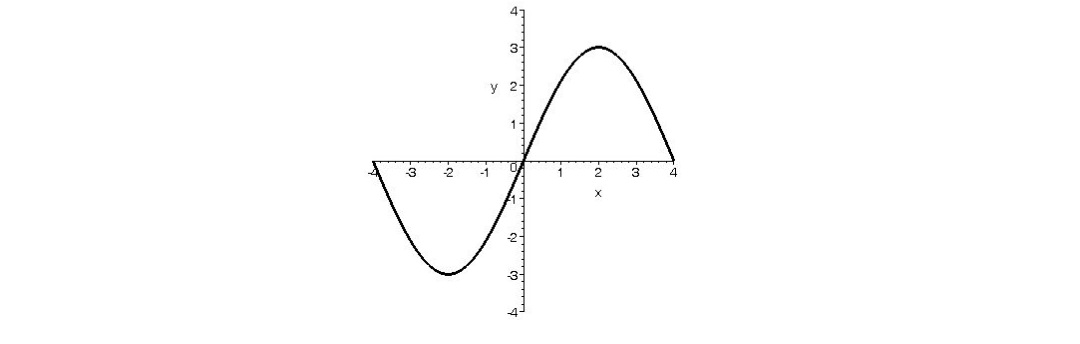
ب) ميدانيم نمودار تابع فرد نسبت به مبدأ مختصات متقارن است. پس لازم است نمودار f به صورت مقابل باشد.
مثال
ثابت كنيد تنها تابعي كه هم زوج است و هم فرد، تابع ثابت صفر با دامنه ي متقارن است.
فرض كنيم f تابعي با دامنهي متقارن باشد، آنگاه به ازاي هر \(x \in {D_f}\) داريم:
تابعی زوج است
\(\left. \begin{array}{l}f \Rightarrow f( - x) = f(x)\\f \Rightarrow f( - x) = - f(x)\end{array} \right\} \Rightarrow f(x) = - f(x) \Rightarrow f(x) = 0\)
تابعی فرد است
مثال
تابع f با ضابطه ي \(f(x) = c{x^3} + {(a - 3)^2} - 2bx + b + 4\) داده شده است.
الف) به ازاي چه مقاديري از a و b تابع f زوج است.
ب) به ازاي چه مقاديري از a و b تابع f فرد است.
واضح است كه \({D_f} = R\)
الف)
\(\begin{array}{l}f( - x) = f(x) \Rightarrow - c{x^3} + (a\_3){x^2} + bx + b + 4 = cx + (a\_3) - 2bx + b + 4\\\\ \Rightarrow \left\{ \begin{array}{l}c = - c\\\\2b = - 2b\\\\a - 3 = a - 3\end{array} \right. \Rightarrow \left\{ \begin{array}{l}c = 0\\\\b = 0\\\\a \in R\end{array} \right.\end{array}\)
براي زوج بودن تابع چند جملهاي f لازم است تنها جملات با درجه ي زوج وجود داشته باشند.
ب(
\(\begin{array}{l}f( - x) = - f(x) \Rightarrow - c{x^3} + (a\_3){x^2} + 2bx + b + 4 = cx - (a\_3){x^2} + 2bx - b - 4\\\\ \Rightarrow \left\{ \begin{array}{l}a - 3 = - (a - 3)\\\\b + 4 = - b + 4\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a = 3\\\\b = - 4\end{array} \right.\end{array}\)
براي فرد بودن تابع چند جمله ای f ، لازم است در ضابطه ی آن تنها جملات با درجه ی فرد وجود داشته باشند.
مثال
اگر f و g هر دو فرد باشند، زوج يا فرد بودن تابع \(\frac{f}{g}\) را بررسي كنيد.
\(\begin{array}{l}x \in {D_{\frac{f}{g}}} \Rightarrow x \in {D_f} \cap {D_g}:g(x) \in {D_{\frac{f}{g}}}\\\left. \begin{array}{l}x \in {D_f} \Rightarrow - x \in {D_f}\\\\x \in {D_g} \Rightarrow - x \in {D_g}\end{array} \right\} \Rightarrow - x \in {D_f} \cap {D_g},g( - x) = - g(x) \ne 0 \Rightarrow - x \in {D_{\frac{f}{g}}}\\\end{array}\)
بنابراين دامنه تابع \(\frac{f}{g}\) متقارن است و داريم:
\(\frac{f}{g}( - x) = \frac{{f( - x)}}{{g( - x)}} = \frac{{ - f( - x)}}{{ - g( - x)}} = \frac{f}{g}(x)\)
پس تابع \(\frac{f}{g}\) تابع زوج است.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه یازدهم- آزمون آنلاین تمامی دروس پایه یازدهم
- گام به گام تمامی دروس پایه یازدهم
- ویدئو های آموزشی تمامی دروس پایه یازدهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه یازدهم
- فلش کارت های آماده دروس پایه یازدهم
- گنجینه ای جامع از انشاء های آماده پایه یازدهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه یازدهم
توابع صعودی و نزولی
توابع صعودي و توابع نزولي
اگر براي هر \({x_2} \in {D_f}\) , كه \({x_1} < {x_2}\) بتوان نتيجه گرفت \(f({x_1}) \le f({x_2})\) ، آنگاه تابع f را صعودي گوييم
اگر براي هر \({x_2} \in {D_f}\) , كه \({x_1} < {x_2}\) بتوان نتيجه گرفت
\(f({x_1}) < f({x_2})\)
و بالعكس، آنگاه تابع f را صعودي اكيد گوييم.
اگر براي هر \({x_2} \in {D_f}\) , كه \({x_1} < {x_2}\) بتوان نتيجه گرفت \(f({x_1}) \ge f({x_2})\) ، آنگاه تابع f را نزولي گوييم
اگر براي هر \({x_2} \in {D_f}\) , كه \({x_1} < {x_2}\) بتوان نتيجه گرفت \(f({x_1}) > f({x_2})\) ، آنگاه تابع f را نزولي اكيد گوييم.
مثال
صعودي يا نزولي بودن هر يك از توابع زير را روي دامنه تعريفشان بررسي كنيد.
الف)
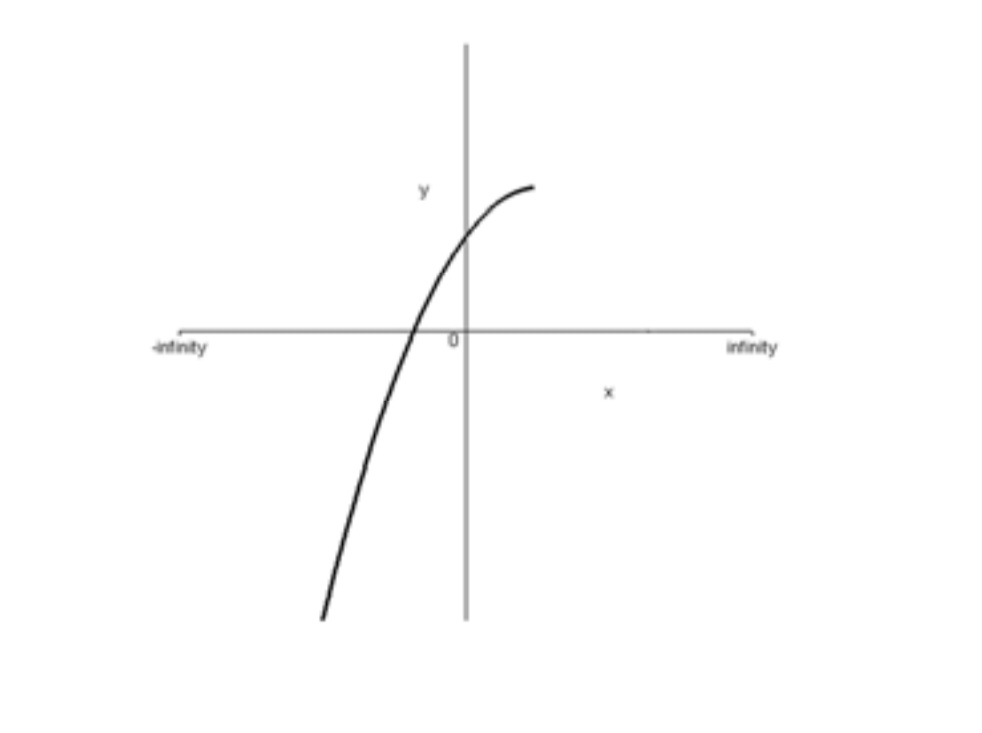
الف) به ازاي هر \({x_2}\) و\({x_1}\) که \({x_1} < {x_2}\) داریم \(f({x_1}) < f({x_2})\) یعنی در واقع با زیاد شدن مقادير x ، مقادير y نيز زياد ميشود. پس تابع صعودي اكيد است.
ب)
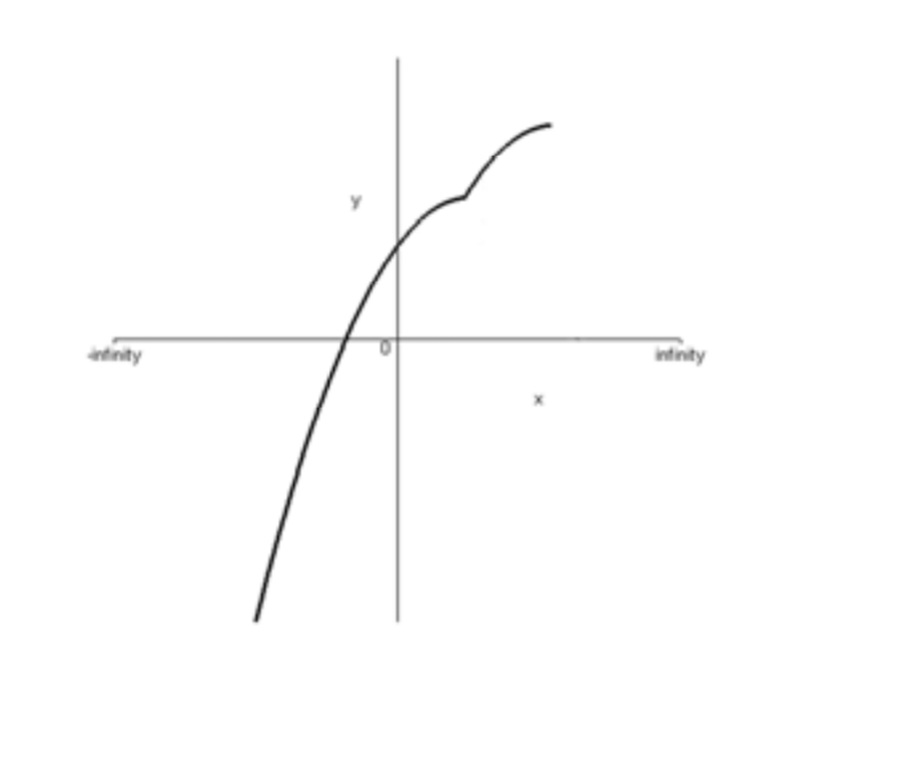
ب) به ازاي هر\({x_2}\) و \({x_1}\) كه \({x_1} < {x_2}\) داريم.\(f({x_1}) \le f({x_2})\) يعني در واقع با زياد شدن مقادير x ، مقادير y زياد ميشود يا ثابت ميماند. پس تابع صعودي است.
ج)
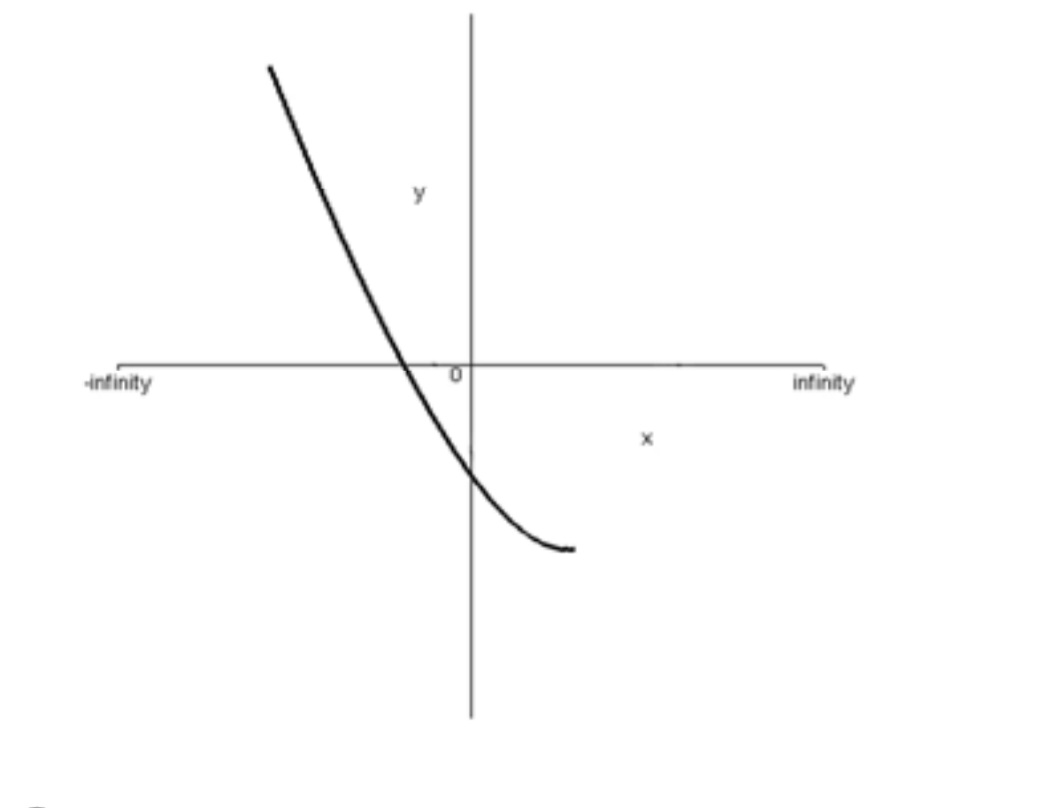
ج) به ازاي هر \({x_2}\) و \({x_1}\) كه \({x_1} < {x_2}\) داريم \(f({x_1}) > f({x_2})\) يعني در واقع با زياد شدن مقادير x ، مقادير y كم ميشود. پس تابع نزولي اكيد است.
د)
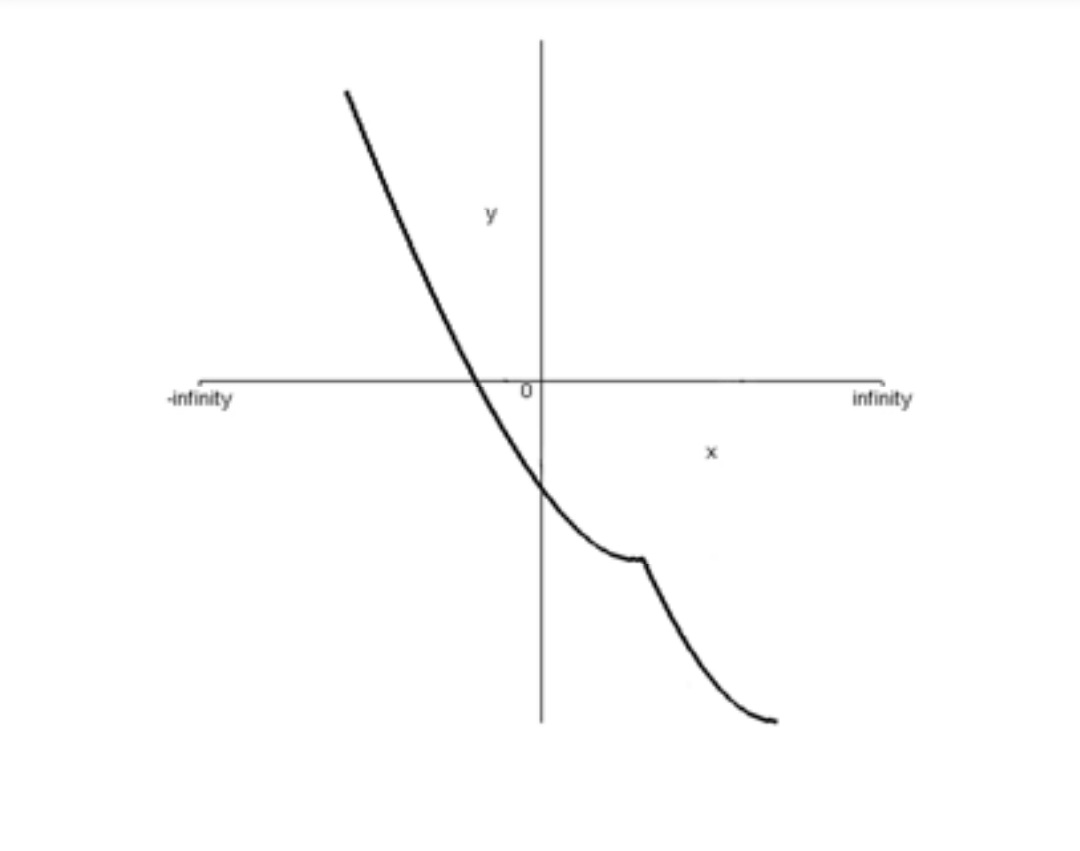
د)به ازای هر \({x_2}\) و\({x_1}\) که داریم \(f({x_1}) \ge f({x_2})\) يعني در واقع با زياد شدن مقاديرداريم كهx و مقادير y كم ميشود يا ثابت ميماند. پس تابع نزولي است.
ه)
ه) اگر \({x_2} \le 0\) و \({x_1}\) و\({x_1} < {x_2}\) آنگاه \(f({x_1}) > f({x_2})\) اين نشان ميدهد تابع f صعودي نيست واز طرف دیگر اگر \({x_2} \ge 0\) و \({x_2} < {x_1}\) آنگاه \(f({x_1}) < f({x_2})\) اين نشان ميدهد تابع f از طرف ديگر، اگر 0 نزولي نيست، بنابراين تابع f نه صعودي است و نه نزولي
و)
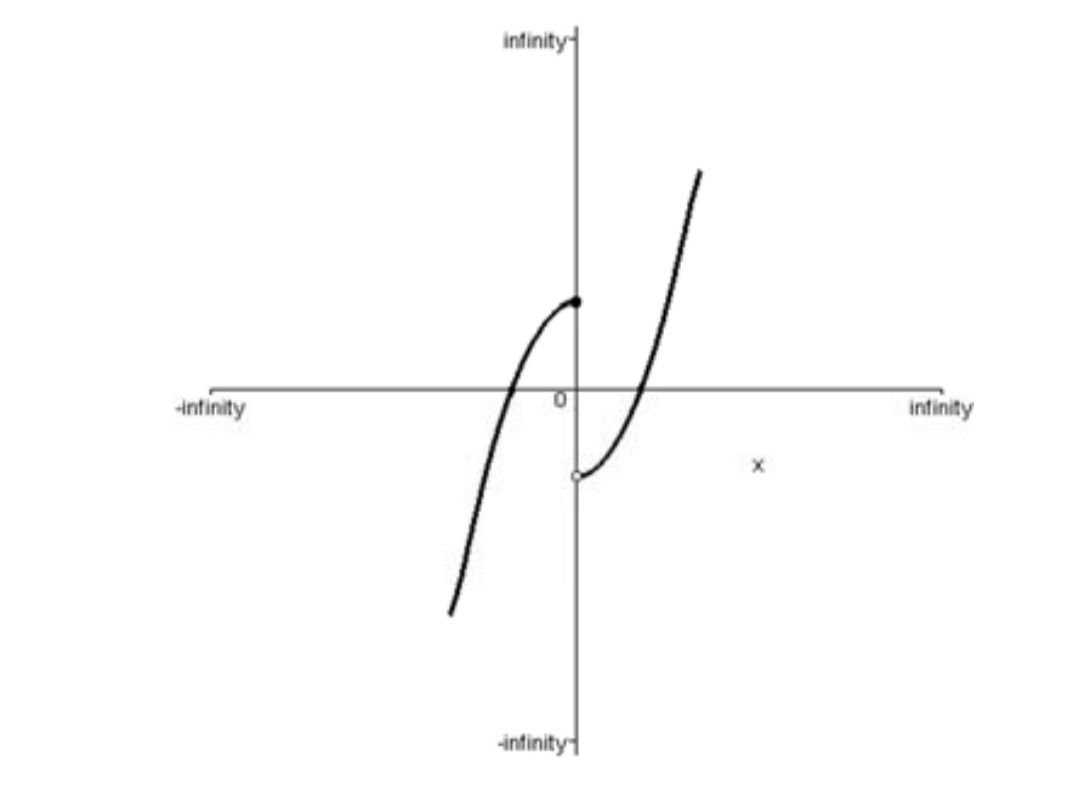
و) تابع در هر يك از بازه هاي [0 , ∞ −) و [∞ + , 0) صعودي اكيد است، ولي مقادير تابع در مجاورت چپ صفر از مقادير تابع در مجاورت راست صفر بيشتر است. بنابراين تابع روي دامنهي تعريف خود يعني بازهي (∞ + , ∞ −) نه صعودي است و نه نزولي.
ز)
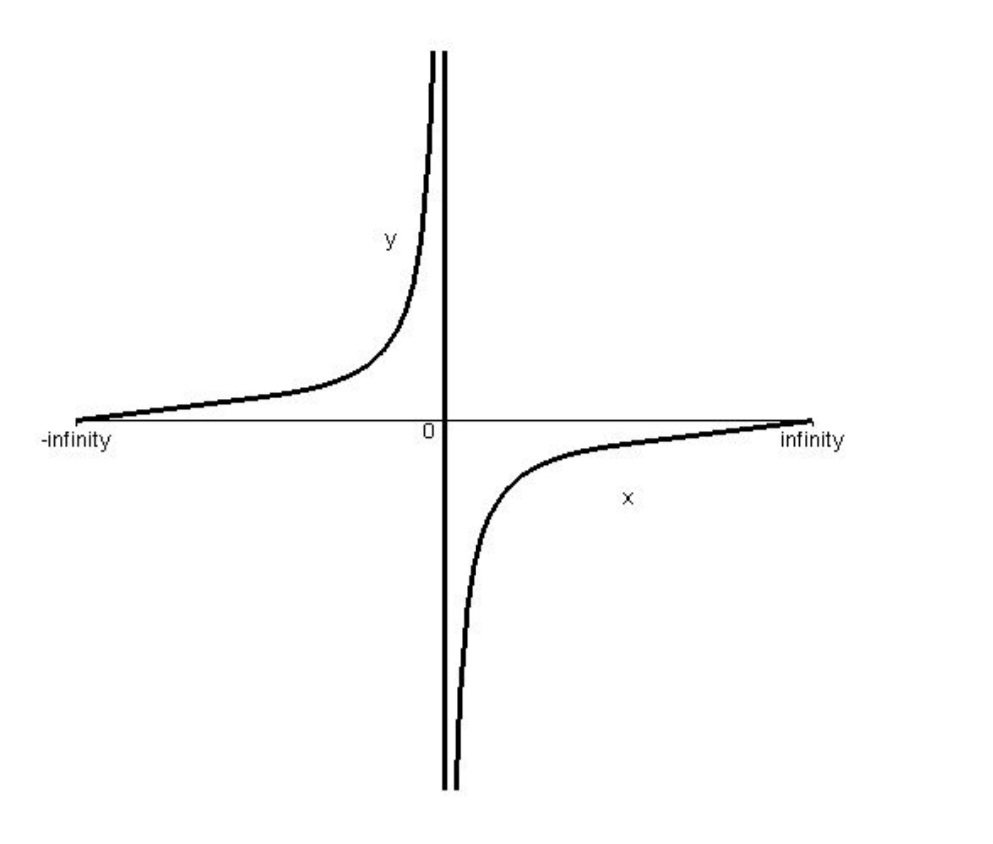
ز) تابع در بازه ي (0 , ∞ −) و (∞ ,+ 0) صعودي اكيد است ولي مقادير تابع در مجاورت چپ صفر از مقادير تابع در مجاورت راست صفر بيشتر است. پس تابع در دامنه ي تعريف خوديعني بازه ي \(( - \infty ,0) \cup (0, + \infty )\) نه صعودي است و نه نزولي.
ح)
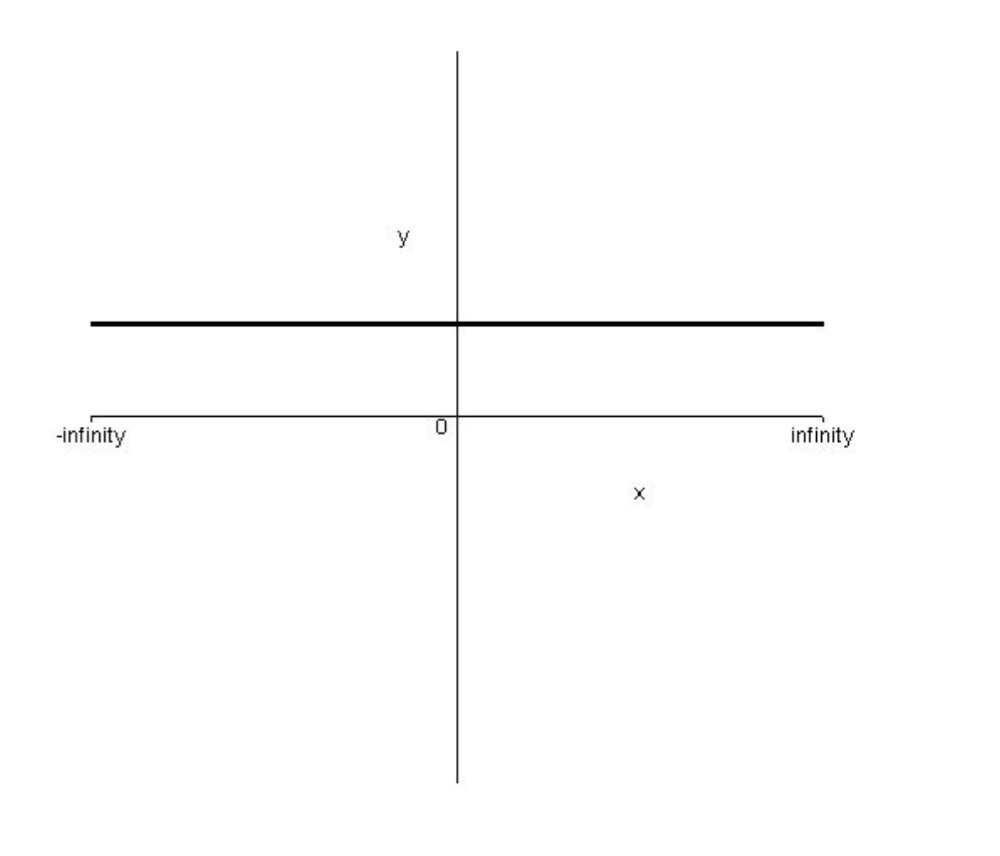
ح) با زياد شدن مقادير x ، مقادير y كم نميشود. پس تابع صعودي است و همچنين با زياد شدن مقادير x ، مقادير y زياد نميشود. پس تابع نزولي است ولي صعودي اكيد يا نزولي اكيد نيست.
مثال
حدود k را طوري به دست آوريد تا تابع \(f = \left\{ {(2,7),( - 1,2),(0,k),( - 2,1\left. ) \right\}} \right.\) صعودي اكيد شود.
چون تابع صعودي اكيد است بايد با زياد شدن مؤلفه هاي اول، مؤلفه هاي دوم نيز زياد شوند. بنابر اين لازم است \(k \in (2,7)\) باشد.
مثال
در تابع f كه نمودار آن به صورت زير رسم شده، مقادير \(f(0)\) در چه بازهاي ميتواند تغيير كند تا تابع f نزولي اكيد باشد.
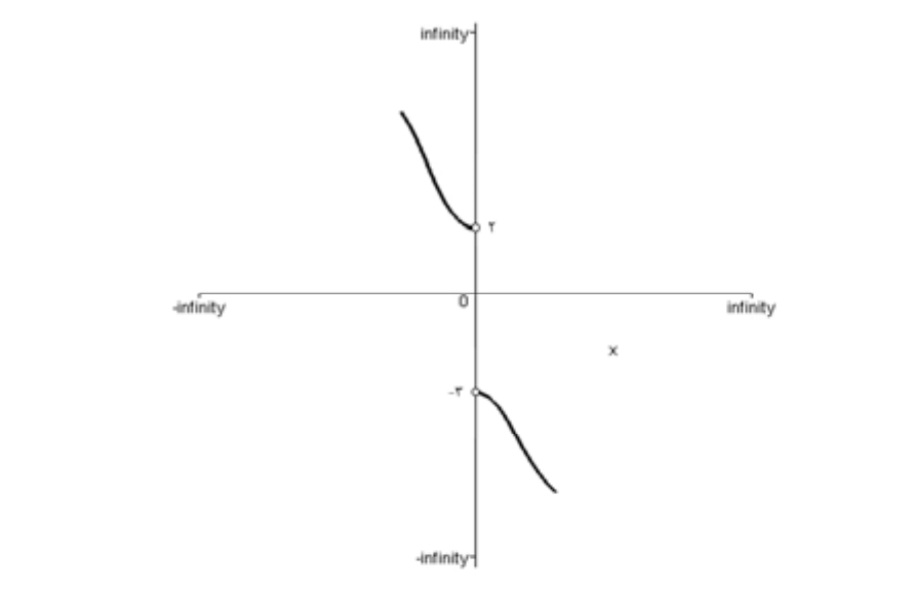
با توجه به اينكه با زياد شدن مقادير x ، مقادير y بايد كم شود. لذا لازم است \(f(0)\) عددي در فاصله ي \(\left[ { - 2,3} \right]\) باشد.
مثال
صعودي يا نزولي بودن هر يك از توابع زير را روي دامنه ي تعريفشان بررسي كنيد.
الف ) \(f(x) = - {x^3}\) ب) \(f(x) = 2{x^3} + 4x - 1\)
ج)\(f(x) = \log _a^x\) د )\(f(x) = \sqrt {3 - 2x} \)
ه) \(f(x) = \left\{ \begin{array}{l}x + 1,x < 0\\\\2 - x,x \ge 0\end{array} \right.\) و) \(f(x) = \left| {x - 1} \right| + 3\)
الف) روش اول نمودار تابع f به صورت زیر است.
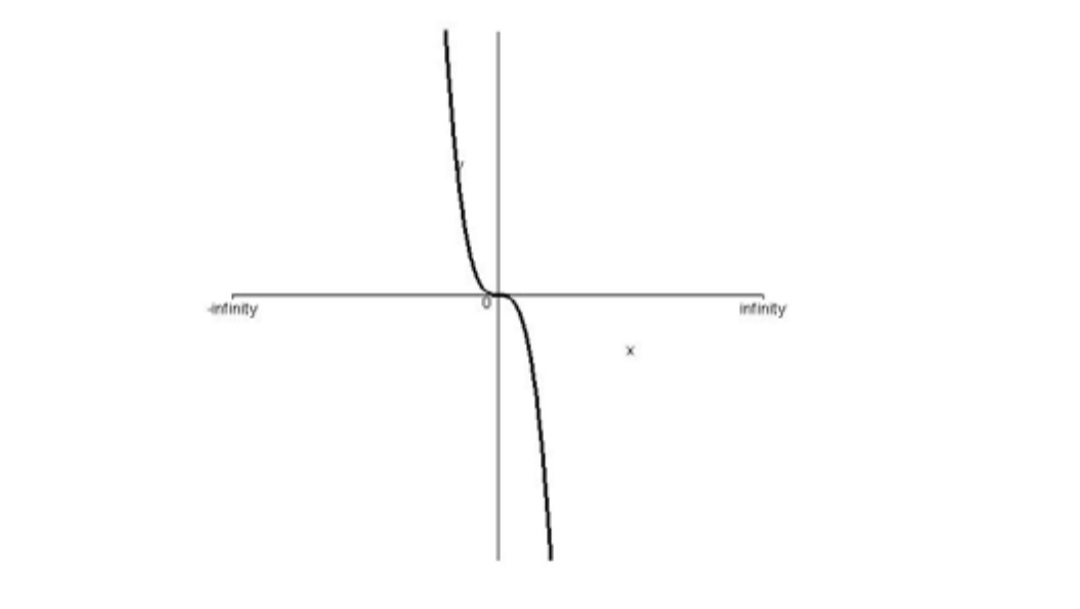
باتوجه به نمودار واضح است كه تابع نزولي اكيد ميباشد. :
ب ) روش اول: نمودار تابع به صورت زير است
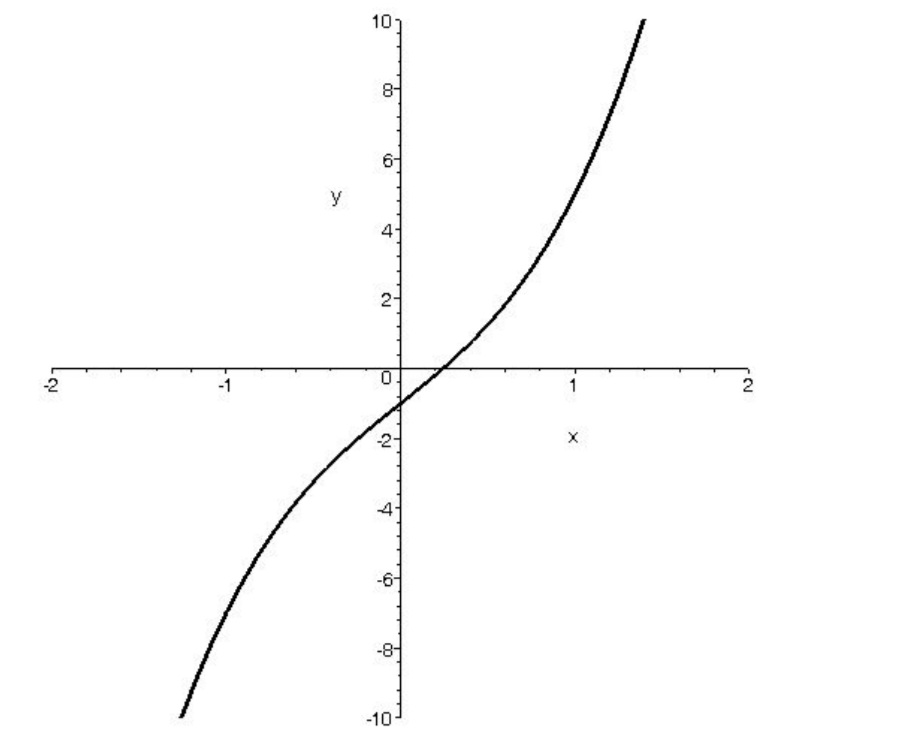
همانگونه که از روی نمودار مشخص است تابع صعودی اکید است.
ج) روش اول: نمودار تابع شبيه يكي از دو نمودار زير است.
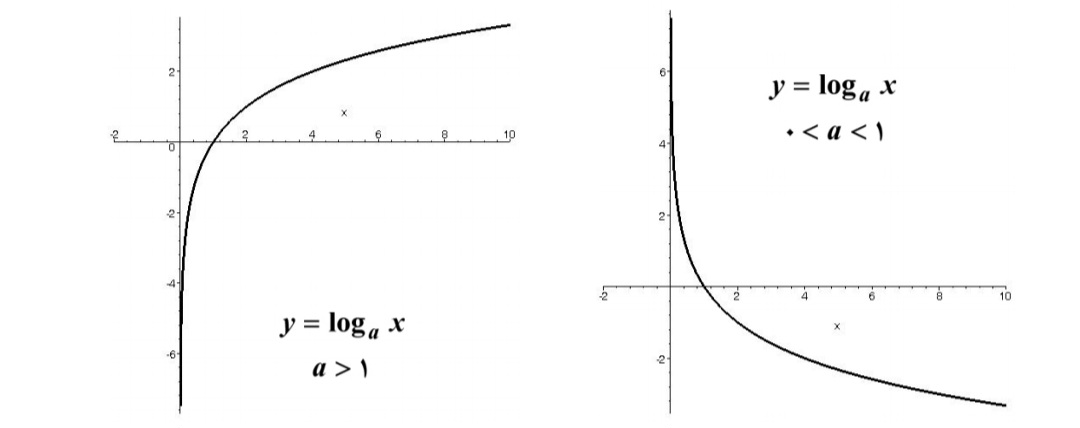
بنابراين اگر a>1باشد تابع صعودي اكيد است و اگر0، تابع نزولي اكيد ميباشد
روش دوم :رابطه های
\({x_1} < {x_2} \Rightarrow \log {x_1} < \log {x_2},\log _a^x = \frac{{\log x}}{{\log a}}\)
را در نظر گرفته دو عضو \({x_1},{x_2} \in {D_f} = \left( {0, + \infty } \right)\) را به دلخواه طوری انتخاب می کنیم که \({x_1} < {x_2}\) سپس دو حالت زیر را در نظر می گیریم
حالت اول :\(\left( {a > 1} \right)\)
\(\begin{array}{l}{x_1} < {x_2} \Rightarrow \log {x_1} < \log {x_2}\frac{{\log {x_1}}}{a} > \frac{{\log {x_2}}}{a} \Rightarrow \log x_a^{{x_1}} > \log x_a^{{x_2}}\\\\ \Rightarrow f({x_1}) > f({x_2})\end{array}\)
در نتيجه fصعودی اكيد است.
حالت دوم: \(\left( {0 < a < 1} \right)\)
در نتيجه f نزولي اكيد است.
د ) روش اول: نمودار تابع به صورت زير است.
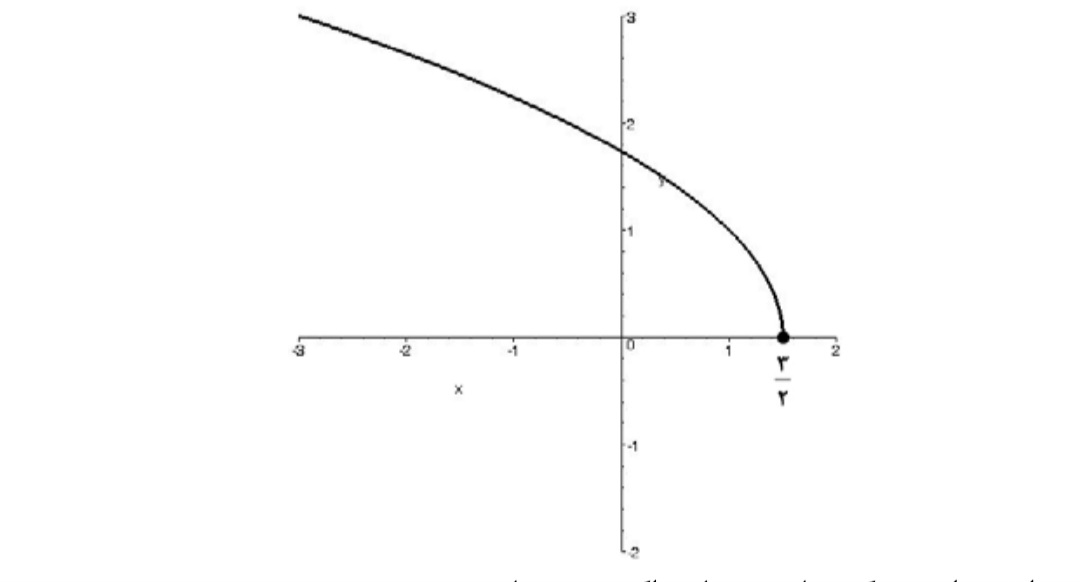
با توجه به نمودار واضح است كه تابع نزولي اكيد ميباشد
روش دوم \({x_1},{x_2} \in {D_f} = ( - \infty ,\left. {\frac{2}{3}} \right]\) را به دلخواه طوري انتخاب ميكنيم كه \({x_1} < {x_2}\) لذا داريم:
\(\begin{array}{l}{x_1} < {x_2} \Rightarrow 3 - 2{x_1} \Rightarrow \sqrt {3 - 2{x_1}} > \sqrt {3 - 2{x_2}} \Rightarrow \\\\f({x_1}) > f({x_2})\end{array}\)
در نتيجه f نزولي اكيد است.
هـ) روش اول: نمودار تابع به صورت زير است.
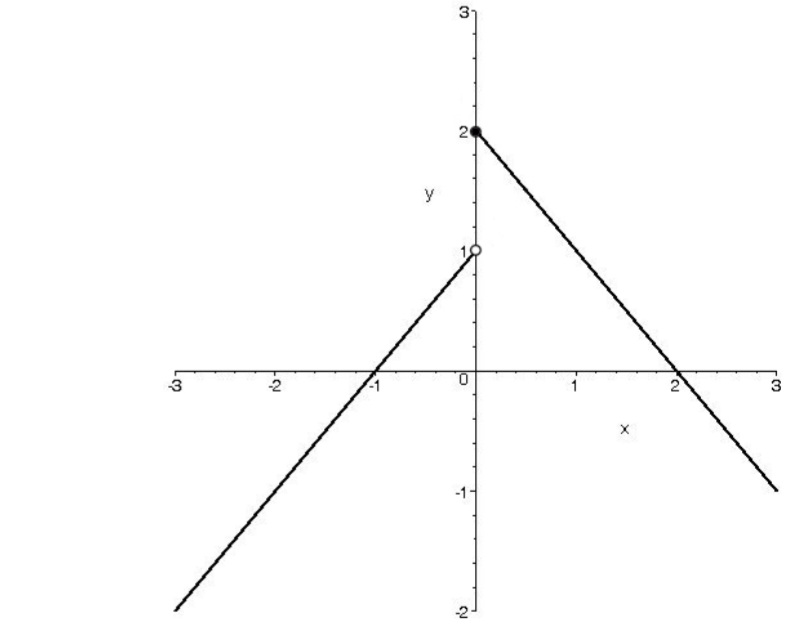
همانگونه كه از نمودار مشخص است تابع f در دامنه ي تعريف خود نه صعودي است نه نزولي .
توجه : تابع روي (0 , ∞ −) صعودي اكيد و روي (∞ + , 0] نزولي اكيد است.
روش دوم: \({x_1}\) و \({x_2}\) را به دلخواه به صورت هاي زير انتخاب ميكنيم . ضابطه قسمت اول تابع صعودي اكيد است.
\(\begin{array}{l}\left\{ \begin{array}{l}{x_1},{x_2} < 0\\\\{x_1} < {x_2}\end{array} \right. \Rightarrow {x_1} + 1 < {x_2} + 1 \Rightarrow f({x_1}) < f({x_2})\\\\\left\{ \begin{array}{l}{x_1},{x_2} > 0\\\\{x_1} < {x_2}\end{array} \right. \Rightarrow - {x_1} < - {x_2} \Rightarrow 2 - {x_1} > 2{x_2} \Rightarrow f({x_1}) > f({x_2})\end{array}\)
ضابطه قسمت دوم، تابع نزولي اكيد است . بنابراين تابع روي دامنهي تعريف خود نه صعودي است و نه نزولي.
و ) روش اول: نمودار تابع به صورت زير است و با توجه به نمودار واضح است كه تابع f روي دامنه ي تعريف خود نه صعودي است نه نزولي
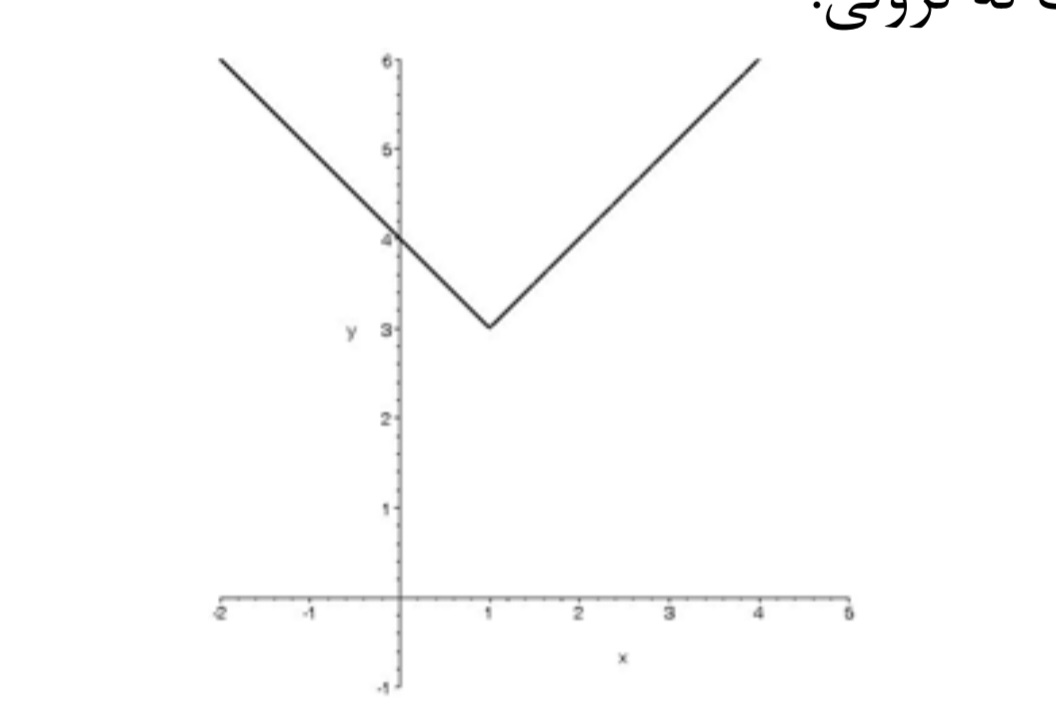
روش دوم : دو عضو دلخواه از \({D_f} = R\) را به هاي زير انتخاب ميكنيم.
\(\begin{array}{l}\\\left\{ \begin{array}{l}{x_1},{x_2} \le 1\\\\{x_1} < x2\end{array} \right. \Rightarrow {x_1} - 1 < {x_2} - 1 \Rightarrow \left| {{x_1} - 1} \right| > \left| {{x_2} - 1} \right| \Rightarrow \left| {{x_1} - 1} \right| + 3 > \left| {{x_2} - 1} \right| + 3 \Rightarrow \\\\f({x_1}) > f({x_2})\end{array}\)
پس تابع f در فاصله ي [,1 ∞ −) نزولي اكيد است.
\(\begin{array}{l}\\\left\{ \begin{array}{l}{x_1},{x_2} \ge 1\\\\{x_1} < {x_2}\end{array} \right. \Rightarrow {x_1} - 1 < {x_2} - 1 \Rightarrow \left| {{x_1} - 1} \right| < \left| {{x_2} - 1} \right| \Rightarrow \left| {{x_1} - 1} \right| + 3 < \left| {{x_2} - 1} \right| + 3 \Rightarrow \\\\f({x_1}) < f({x_2})\end{array}\)
پس تابع f در فاصلهي (∞ + , 1] صعودي اكيد است . اما تابع روي دامنه ي تعريف خود نه صعودي است و نه نزولي.
مثال
اگر f تابعي صعودي با دامنه ي ℜ باشد، دامنه ي تعريف تابع \(g(x) = \sqrt {f\left( {\left| {x - 2} \right|} \right)f\left( {\left| {2x - 1} \right|} \right)} \)را به دست آوريد.
داريم
\(f\left( {\left| {x - 2} \right|} \right) - f\left( {\left| {2x - 1} \right|} \right) \ge 0 \Rightarrow f\left( {\left| {x - 2} \right|} \right) \ge f\left( {\left| {fx - 1} \right|} \right)\)
چون f تابعي صعودي است داريم:
\(\begin{array}{l}\left| {x - 2} \right| < \left| {2x - 1} \right| \Rightarrow {x^2} - 4x + 4 \ge 4{x^2} - 4x + 1 \Rightarrow 3{x^2} - 3 \le 0 \Rightarrow \\\\ - 1 \le x \le 1 \Rightarrow {D_g} = \left[ { - 1,1} \right]\end{array}\)
مثال
اگر تابع \(f(x) = \left\{ \begin{array}{l}\sqrt {x + 1} ,x \ge 3\\\\\frac{1}{2}x + a,x < 2\end{array} \right.\) صعودي اكيد باشد، بيشترين مقدار a را به دست آورید.
نمودار تابع به صورت زير است.
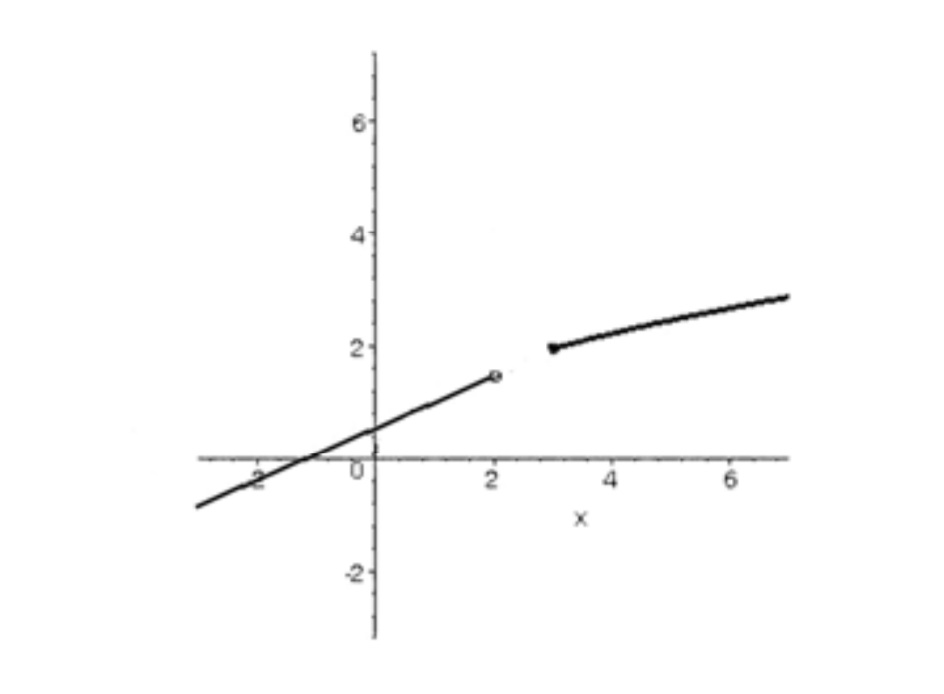
چون تابع f صعودي است پس لازم است \(1 + a \le 2\) يعني \(a \le 1\) بنابراين بيشترين مقدار a ميتواند يك باشد.
توابعي كه يا صعودي باشند يا نزولي، توابع يكنوا ناميده ميشوند.
توابعي كه اكيداً صعودي باشند يا اكيداً نزولي، توابع اكيداً يكنوا ناميده ميشوند.
مثال
تابع \(y = {x^2}\) روی دامنه تعریف خود نه صعودی است نه نزولی پس تابعی غیر یکنوااست.
مثال
اگر تابع f نزولي اكيد و تابع g بر \({R_f}\) نزولی اکید باشدیکنوایی تابعgof رابررسی كنيد.
دو عضو دلخواه \({x_1},{x_2} \in {D_f}\) , را طوري انتخاب ميكنيم كه \({x_1} < {x_2}\) پس داريم:
\({x_1} < {x_2} \Rightarrow f({x_1}) > f({x_2}) \Rightarrow g(f({x_1})) < g(f({x_2}))\)
يعني در واقع داريم
\({x_1} < {x_2} \Rightarrow (gof)({x_1}) < (gof)({x_2})\)
پس تابع gof صعودي اكيد ميباشد، بنابراين يكنواي اكيد ميباشد.
مثال
اگر دو تابع f و g در بازهي I ، صعودي اكيد باشند يكنوايي تابع f+gرا روي I بررسي كنيد.
: \({x_1},{x_2} \in I\)را به طور دلخواه طوري انتخاب ميكنيم كه \({x_1} < {x_2}\) پس داريم:
\(\begin{array}{l}{x_1} < {x_2} \Rightarrow \left( \begin{array}{l}f({x_1}) < f({x_2})\\\\ \Rightarrow g({x_1}) < g({x_2})\end{array} \right. \Rightarrow f({x_1}) < f({x_2}) + g({x_2})\\\\ \Rightarrow (f + g)({x_1}) < (f + g)({x_2})\end{array}\)
تابع f+g صعودي اكيد است . بنابراين تابع f+gيكنواي اكيد ميباشد
مثال
\(y = - {x^3}\) تابع نزولي اكيد است. پس تابع يكنواي اكيد ميباشد.
بعد از فراگيري مبحث مشتق، ميتوانيم در توابع مشتق پذير، يكنوايي را با روش هاي ساده تري بررسي كنیم.
تهیه کننده: حامد دلیجه
جزوات جامع پایه یازدهم
جزوه جامع حسابان یازدهم فصل 1 جبر و معادله
جزوه جامع حسابان یازدهم فصل 2 تابع
جزوه جامع حسابان یازدهم فصل 3 توابع نمایی و لگاریتمی
جزوه جامع حسابان یازدهم فصل 4 مثلثات
جزوه جامع حسابان یازدهم فصل 5 حد و پیوستگی
تابع يك به يك
تابع يك به يك
تابع f يك به يك است، اگر براي هر\({x_1},{x_2} \in {D_f}\) , داشته باشيم:
\(f({x_1}) = f({x_2}) \Rightarrow {x_1} = {x_2}\)
و يا به بيان ديگر
تابع f يك به يك است اگر براي هرداشته باشيم:
\({x_1} \ne {x_2} \Rightarrow f({x_1}) \ne f({x_2})\)
نمودار يك تابع در صورتي نمودار تابع يك به يك است كه هر خط موازي محور x ها حداكثر در يك نقطه آن را قطع كند.
مثال
كدام يك از توابع زير يك به يك هستند.
ج)\(f = \left\{ {\left( {1,2} \right)} \right.,\left( {2,3} \right),\left( {4,2} \right)\left. {} \right\}\)
الف) يك به يك نيست زيرا مثلاً خط y=1نمودار را در بيش از يك نقطه قطع ميكند.
ب) هر خط موازي محو x ها رسم كنيم. نمودار را در بيش از يك نقطه قطع نميكند . پس تابع يك به يك است.
ج) يك به يك نيست زيرا \(f(1) = f(4)\) ولي \(1 \ne 4\)
مثال
يك به يك بودن هر يك از توابع زير را بررسي كنيد
الف) \(f(x) = \sqrt {{x^3} + 4} \) ب) \(f(x) = {x^2} + 2x + 3\)
ج) \(f(x) = x + \left| {x - 2} \right|\) د) \(f(x) = \log x\)
ه) \(f(x) = \sin x - \cos x\) و) \(f(x) = \frac{{{3^x}}}{{{3^x} + 1}}\)
الف)
روش اول:
\(\begin{array}{l}f({x_1}) \ne f({x_2}) \Rightarrow \sqrt {x_1^3 + 4} = \sqrt {x_2^3 + 4} \Rightarrow x_1^3 + 4 = x_2^3 + 4 \Rightarrow \\\\x_1^3 = x_2^3 \Rightarrow {x_1} = {x_2}\end{array}\)
بنابراين تابع f يك به يك است.
روش دوم:
\(\begin{array}{l}{x_1} \ne {x_2} \Rightarrow x_1^3 = x_2^3 \Rightarrow x_1^3 + 4 \ne x_2^3 + 4 \Rightarrow \\\\\sqrt {x_1^3 + 4} \ne \sqrt {x_2^3 + 4} \Rightarrow f({x_1}) \ne f({x_2})\end{array}\)
بنابراين تابع f يك به يك است.
ب(
\(\begin{array}{l}f({x_1}) = {x^2} + 2x + 3 = {(x + 1)^2} + 2\\\\f({x_1}) = f({x_2}) \Rightarrow {({x_1} + 1)^2} + 2 = {({x_2} + 1)^2} + 2 = {({x_1} + 1)^2} = {({x_2} + 1)^2}\\\\{x_1} + 1 = \pm x(2 + 1) \Rightarrow \left\{ \begin{array}{l}{x_1} = {x_2}\\\\{x_1} = - {x_2} - 2\end{array} \right.\end{array}\)
پس تابع f يك به يك نيست.
ج)
\(f(0) = f(1) = 2 \Rightarrow 0 \ne 1\)
پس تابع f يك به يك نيست.
د(
\(\begin{array}{l}f({x_1}) = f({x_2}) = \log {x_1} = \log {x_2} \Rightarrow \log {x_1} - \log {x_2} = 0\\\\ \Rightarrow \log \frac{{{x_1}}}{{{x_2}}} = 0 \Rightarrow \frac{{{x_1}}}{{{x_2}}} = 1 \Rightarrow {x_1} = {x_2}\end{array}\)
پس تابع f يك به يك است.
ه(
\(f(0) = f(2\pi ) = - 1 \Rightarrow 0 \ne 2\pi \)
بنابراين تابع f يك به يك نيست.
توجه: توابع متناوب يك به يك نيستند.
و(
\(\begin{array}{l}f({x_1}) = f({x_2}) = \frac{{{3^{{x_1}}}}}{{{3^{{x_1}}} + 1}} = \frac{{{3^{{x_2}}}}}{{{3^{{x_2}}} + 1}} \Rightarrow {3^{{x_1}}} \times {3^{{x_2}}} + {3^{{x_1}}} = {3^{{x_2}}} \times {3^{{x_1}}} + {3^{{x_2}}}\\\\ \Rightarrow {3^{{x_1}}} = {3^{{x_2}}} \Rightarrow {x_1} = {x_2}\end{array}\)
پس تابع f يك به يك است
مثال
ثابت كنيد اگر تابع f يكنواي اكيد باشد آنگاه تابع f يك به يك است.
مثلاً فرض كنيم تابع f صعودي اكيد باشد آنگاه اگر \({x_1} \ne {x_2}\) دو حالت رخ ميدهد: حالت اول : اگر \({x_1} < {x_2}\) باشد، داريم:
\({x_1} > {x_2} \Rightarrow f({x_1}) < f({x_2}) \Rightarrow f({x_1}) \ne f({x_2})\)
لذا f يك به يك است.
حالت دوم اگر \({x_1} > {x_2}\) باشد، داريم:
\({x_1} > {x_2} \Rightarrow f({x_1}) > f({x_2}) \Rightarrow f({x_1}) \ne f({x_2})\)
لذا f يك به يك است.
مثال
اگر توابع f و g يك به يك باشند، يك به يك بودن هر يك از توابع f+g و fog را بررسي كنيد.
تابعf+g همواره نميتواند يك به يك باشد زيرا مثلاً اگر \(f = \left\{ {\left( {0,0} \right)} \right.,(1,1\left. ) \right\}\) و \(g = \left\{ {\left( {0,0} \right)} \right.,(1, - 1\left. ) \right\}\) را در نظر بگيريم، داريم \(f + g = \left\{ {\left( {0,0} \right)} \right.,(1,1\left. ) \right\}\) كه يك به يك نيست.
اما تابع fog يك به يك است زيرا:
\(\begin{array}{l}(fog)({x_1}) = (fog)({x_2}) \Rightarrow f(g({x_1})) = f(g({x_2}))\\\\g({x_1}) = g({x_2})\\\\{x_1} = {x_2}\end{array}\)
مثال
آيا يك تابع ميتواند هم فرد و هم يك به يك باشد.
بلي . مثلاً توابع \(y = {x^3}\) و\(y = x\) است، اما يك به يك نيست.ولی تابع \(y = \sin x\) فرد است امایک به یک نیست
مثال
آيا يك تابع ميتواند هم زوج و هم يك به يك باشد.
فرض كنيم f تابعي زوج و يك به يك باشد . داريم:
F \(x = - x \Rightarrow x = 0\) یک به یک است \(f \Rightarrow f(x) = f( - x)\) تابعی زوج است
پس تنها تابعي كه هم زوج و هم يك به يك است ، تابعی دلخواه با دامنه ي يك عضوي صفر ميباشد. f
يك تابع چند ضابطه اي در صورتي يك به يك است كه هر يك از ها يك به يك بوده و اشتراك برد دوبه دوي ضابطه ها مجموعه تهي باشد.
مثال
يك به يك بودن تابع \(f(x) = \left\{ \begin{array}{l}x + 1,x < 1\\\\2x + 3,x \ge 1\end{array} \right.\) را بررسی کنید.
\({f_1}({x_1}) = {f_1}({x_2}) \Rightarrow {x_1} + 1 \Rightarrow {x_2} + 1 \Rightarrow {x_1} = {x_2}\)
ضابطه اول يك به يك است.
\(\begin{array}{l}{f_2}({x_1}) = {f_2}({x_2}) \Rightarrow 2{x_1} + 3 \Rightarrow 2{x_2} + 3 \Rightarrow 2{x_1} = 2{x_2} \Rightarrow \\\\{x_1} = {x_2}\end{array}\)
ضابطه دوم يك به يك است
\(\left. \begin{array}{l}x < 1 \Rightarrow x + 1 < 2 \Rightarrow R = ( - \infty ,2)\\\\x \ge 1 \Rightarrow 2x \ge 2 \Rightarrow 2x + 3 \ge 5 \Rightarrow {R_2} = (5, + \infty )\end{array} \right\} \Rightarrow {R_1} \cap {R_2} = \emptyset \)
پس اشتراك برد ضابطه ها نيز تهي است . بنابراين f تابعي يك به يك است.
مثال
حدود k را طوري تعيين كنيد تا تابع \(f(x) = \left\{ \begin{array}{l}3x - 2,x > 1\\\\2x + k,x \le 1\end{array} \right.\) يك به يك باشد.
واضح است كه هر يك از ضابطه ها تابعي يك به يك هستند، كافي است اشتراك برد آنها نيز تهي باشد.
\(\left. \begin{array}{l}x > 1 \Rightarrow 3x > 3 \Rightarrow 3x - 2 > 1 \Rightarrow {R_1} = \left( {1, + \infty } \right)\\\\x \le 1 \Rightarrow 2x \le 3 \Rightarrow 2x + k \Rightarrow {R_2} = \left( { - \infty ,2 + k} \right)\end{array} \right\} \Rightarrow 2 + k \le 1 \Rightarrow k \le - 1\)
وارون تابع
اگر وارون \(f = \left\{ {(x,y\left. ) \right|} \right.x \in A,y \in \left. B \right\}\) يك تابع باشد، وارون تابع f به صورت تعريف ميشود. اگر تابع f به صورت \(\left\{ {(y,x\left. ) \right|} \right.(x,y) \in \left. f \right\}\) نمودار نمايش داده شده باشد، براي پيدا كردن وارون آن كافي است قرينه ي نقاط نمودار را نسبت به خط x = y رسم كنيم.
مثال
وارون هر يك از توابع زير را به دست آوريد.
الف) \(f = \left\{ {(1,2),} \right.(3,4),(5,6\left. ) \right\}\) ب) \(f = \left\{ {(1,3),} \right.(2,4),(5,3\left. ) \right\}\)
الف) \(f = \left\{ {(1,2),} \right.(3,4),(5,6\left. ) \right\}\) همانگونه كه مشاهده ميشود وارون تابع f يك تابع را مشخص ميكند.
ب( \(f = \left\{ {(1,3),} \right.(2,4),(5,3\left. ) \right\}\) همانگونه كه مشاهده ميشود وارون تابع g يك تابع نيست
اگر وارون تابع f خود يك تابع باشد، آن را تابع وارون f ميگويند و f را وارونپذير مينامند. بديهي است f وارون پذير است اگر و تنها اگر f يك به يك باشد و وارون f نمايش ميدهيم.
مثال
تابع وارون تابع \(f(x) = 3x + 5\) را در صورت وجود به دست آوريد.
ابتدا يك به يك بودن تابع را بررسي ميكنيم.
\(f({x_1}) = f({x_2}) \Rightarrow 3{x_1} + 1 = 3{x_2} + 5 \Rightarrow 3{x_1} = 3{x_2} \Rightarrow {x_1} = {x_2}\)
تابع f يك به يك است، پس وارون پذير ميباشد . براي به دست آوردن ضابطه ي تابع وارون كافي است y را به جاي قرار دهيم و x را برحسب y به دست آورده، سپس جاي x و y را با هم عوض كنيم.
\(y = 3x + 5 \Rightarrow 3x = y - 5 \Rightarrow x = \frac{{y - 5}}{3} \Rightarrow {f^{ - 1}}(x) = \frac{{x - 5}}{3}\)
مثال
اگر \(f = \left\{ {(1,2),} \right.(3,4\left. ) \right\}\) ، توابع \({f^{ - 1}}\) و \(\frac{1}{f}\) را محاسبه كنيد
f يك به يك است پس \({f^{ - 1}} = \left\{ {(2,1),} \right.(4,3\left. ) \right\}\) و \(\frac{1}{f} = \left\{ {(1,\frac{1}{2}),} \right.(3,\frac{1}{4}\left. ) \right\}\) واضح است كه \({f^{ - 1}}\) و \(\frac{1}{f}\) با هم مساوي نيستند.
مثال
تابع وارون هر يك از توابع وارون پذير زير را به دست آوريد.
الف) \(f(x) = {x^3} + 4\) ب) \(f(x) = {x^2} - 4,x < 0\)
ج) \(f(x) = 2{x^3} + 6{x^2} + 6x\) د) \(f(x) = \log _5^x\)
ه) \(f(x) = \sqrt {2 - 3x} \) و) \(f(x) = x + \frac{1}{x},x \ge 1\)
ز) \(f(x) = \frac{{2x + 1}}{{3x - 2}}\)
با توجه به اينكه روي وارون پذيري توابع داده شده تصريح شده است، بررسي وارون پذيري لازم نيست.
الف(
\(y = {x^3} + 4 \Rightarrow {x^3} = y - 4 \Rightarrow x{ = ^3}\sqrt {y - 4} \Rightarrow {f^{ - 1}}(x){ = ^3}\sqrt {y - 4} \)
ب)
\(\begin{array}{l}y = {x^2} - 4 \Rightarrow {x^2} = y + 4 \Rightarrow x = \pm \sqrt {y + 4} \\\\x = - \sqrt {y + 4} \Rightarrow {f^{ - 1}}(x) = - \sqrt {x + 4} \end{array}\)
ج)
\(y = 2({x^3} + 3{x^2} + 3x) \Rightarrow y = 2({x^3} + 3{x^2} + 3x + 1 - 1)\)
\(\begin{array}{l}y = 2({x^3} + 6{x^2} + 6x) \Rightarrow y = 2({x^3} + 6{x^2} + 6x + 1 - 1) \Rightarrow \\\\y = 2{(x + 1)^3} - 2 \Rightarrow {(x + 1)^3} = \frac{{y + 2}}{2} \Rightarrow x + 1{ = ^3}\sqrt {\frac{{y + 2}}{2} \Rightarrow } \\\\x = - 1{ + ^3}\sqrt {\frac{{y + 2}}{2} \Rightarrow } {f^1}(x){ = ^3}\sqrt {\frac{{x + 2}}{2}} \end{array}\)
د)
\(y = \log _5^x \Rightarrow x = {5^y} \Rightarrow {f^{ - 1}}\left( x \right) = {5^x}\)
ه)
\(\begin{array}{l}fy = \sqrt {2 - 3x} \to {y^2} = 2 - 3x \Rightarrow 2 - 3x - {y^2} \Rightarrow x = \frac{{2 - {y^2}}}{3} \Rightarrow \\\\{f^{ - 1}}(x) = \frac{{2 - {x^2}}}{3}\end{array}\)
و)
\(\begin{array}{l}y = x + \frac{1}{x} \Rightarrow y = \frac{{{x^2} + 1}}{x} \Rightarrow {x^2} - yx + 1 = 0 \Rightarrow \\\\\\x = \frac{{y \pm \sqrt {{y^2} - 4} }}{2}x = \frac{{y + \sqrt {{y^2} - 4} }}{2} \to {f^{ - 1}}(x) = \frac{{x + \sqrt {{x^2} - 4} }}{2}\end{array}\)
ز)
\(\begin{array}{l}f(x) = \frac{{2x + 1}}{{3x - 2}} \Rightarrow 3xy - 2y = 2x + 1 \Rightarrow 3xy - 2x = 2y + 1 \Rightarrow \\\\x(3y - 2) = 2y + 1 \Rightarrow \frac{{2y + 1}}{{3y - 2}} \Rightarrow {f^{ - 1}}(x) = \frac{{2x + 1}}{{3x - 2}}\end{array}\)
اگر دو تابع f و g وارون يكديگر باشند داريم:
\({D_g} = {R_f},{R_g} = {D_f}\)
و برای هر \(x \in {D_f}\) داریم :
\(g(f(x)) = x\)
و برای هر \(x \in {D_g}\) داریم :
\(f(g(x)) = x\)
مثال
نشان دهيد توابع \(f(x) = 2x + 5\) و \(g(x) = \frac{{x\_2}}{2}\) وارون يكديگرند.
\(x \in {D_g}:f(g(x)) = f\left( {\frac{{x - 5}}{2}} \right) = 2 \times \frac{{x - 5}}{2} + 5 = x\) دلخواه
\(x \in {D_F}:g(f(x)) = g\left( {2x + 5} \right) = \frac{{2x + 5 - 5}}{2} = x\) دلخواه
مثال
آيا دو تابع \(f(x) = \frac{{x + 1}}{2}\) و \(g(x) = 2x + 1\) وارون يكديگر هستند؟
روش اول:
\(x \in {D_g}:f(g(x)) = f(2x + 1) = \frac{{2x + 1 + 1}}{2} = x + 1 \ne x\)
بنابراين f و g وارون يكديگر نيستند.
مثال
برد تابع وارون تابع\(f(x) = \frac{x}{{\sqrt {x + 4 - 2} }}\) را به دست آوريد.
\(\begin{array}{l}\left\{ \begin{array}{l}x + 4 \ge 0\\\\\sqrt {x + 4} - 2 \Rightarrow \sqrt {x + 4} \ne 2 \Rightarrow x \ne 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x \ge 4\\\\x \ne 0\end{array} \right.\\\\{D_f} = \left( { - 4,0} \right) \cup (0, + \infty ) = {D_{{f^{ - 1}}}} = \left( { - 4,0} \right) \cup (0, + \infty )\end{array}\)
مثال
\(2 \le x < 4\), ,\(f(x) = \frac{{1 - 3x}}{4}\) داده شده است . دامنه تابع را بدست آورید
ميدانيم \({R_{{f^{ - 1}}}} = {R_f}\) پس كافي است برد تابع f را به دست آوريم.
\(\begin{array}{l}2 \le x < 4 \Rightarrow - 12 < - 3x < - 6 \Rightarrow - 11 \le 1 - 3x < - 5 \Rightarrow \\\\\frac{{ - 11}}{4} < \frac{{1 - 3x}}{4} < - \frac{5}{4} \Rightarrow \frac{{ - 11}}{4} < y < - \frac{5}{4} \Rightarrow {R_f} = (\frac{{ - 11}}{4},\left. { - \frac{{ - 5}}{4}} \right] \Rightarrow \\\\{D_f}^{ - 1} = (\frac{{ - 11}}{4},\left. { - \frac{{ - 5}}{4}} \right]\end{array}\)
براي به دست آوردن تابع وارون يك تابع چند ضابطه اي در صورت وجود وارون هر يك مياز ضابطه ها را به دست آوريم. بديهي است دامنه ،ي هر ضابطه برد ضابطهي نظير در تابع اصلي است.
مثال
تابع وارون تابع وارون پذير \(f(x) = \left\{ \begin{array}{l}x - 2,x < 1\\\\2x + 4,x \ge 1\end{array} \right.\) را بدست آورید .
برای ضابطه اول داریم:
\(x < 1 \Rightarrow x - 2 < - 1 \Rightarrow {R_1} = ( - \infty , - 1)\)
در نتیجه
\(y = x - 2 \Rightarrow x = y + 2 \Rightarrow f_1^{ - 1}(x) = x + 2\)
برای ضابطه دوم داریم
\(x \ge 1 \Rightarrow 2x \ge 2 \Rightarrow 2x + 4 \ge 6 \Rightarrow {R_2} = \left[ {6, + \left. \infty \right\}} \right.\)
در نتیجه
\(y = 2x + 4 \Rightarrow 2x = y - 4 \Rightarrow x = \frac{{y - 4}}{2} \Rightarrow f_2^{ - 1}(x) = \frac{{x - 4}}{2}\)
بنابراين ضابطه ي تابع وارون f به صورت زير خواهد بود.
\(f(x) = \left\{ \begin{array}{l}x + 2,x < - 1\\\\\frac{{x + 4}}{2},x \ge 6\end{array} \right.\)
اگر f تابع صعودي اكيد باشد، محل برخورد f و \({f^{ - 1}}\) در صورت وجود روی خط y=xقرار دارد.
مثال
اگر \(f(x) = {x^3} + x\_8\) فاصله ی نقطه ی fتلاقی و \({f^{ - 1}}\) تا مبدأ مختصات را محاسبه ، كنيد.
\(\begin{array}{l}{x_1} < {x_2} \Rightarrow \left\{ \begin{array}{l}x_1^3 < x_2^3\\\\{x_1} < {x_2}\end{array} \right. \Rightarrow x_3^1 + {x_1} < x_2^3 + {x_2} \Rightarrow x_3^1 + {x_1} - 8 < x_2^3 + {x_2} - 8\\\\ \Rightarrow f({x_1}) < f({x_2})\end{array}\)
در نتيجه تابع f صعودي اكيد است
بنابراين براي محاسبه محل تلاقي f و \({f^{ - 1}}\) كافي است محل تلاقي f و خط x = y را در صورت وجود محاسبه كنيم.
\(\begin{array}{l}\left\{ \begin{array}{l}y = {x^3} + x - 8\\\\y = x\end{array} \right. \Rightarrow {x^3} + x - 8 = x \Rightarrow {x^3} = 8 \Rightarrow x = 2,y = 2\\\\ \Rightarrow d = \sqrt {4 + 4} = 2\sqrt 2 \end{array}\)
مثال
نقاط برخورد تابع \(f(x) = x - \sqrt {x + 1} \) را با وارونش، در صورت وجود پيدا كنيد.
\(\begin{array}{l}{x_1},{x_2} \in \left[ { - 1, + \left. \infty \right)} \right.,{x_1} < {x_2}\\\\{x_1} < {x_2} \Rightarrow \left\{ \begin{array}{l}{x_1} < {x_2}\\\\{x_1} + 1 < {x_2} + 1 \Rightarrow \sqrt {{x_1} + 1} < \sqrt {{x_2} + 1} \end{array} \right.\\\\ \Rightarrow {x_1} + \sqrt {{x_1} + 1} < {x_2} + \sqrt {{x_2} + 1} \Rightarrow f({x_1}) < f({x_2})\end{array}\) دلخواه
تابع f صعودي اكيد است.
براي پيدا كردن نقطه ي برخورد داريم:
\(\left\{ \begin{array}{l}y = x\\\\y = x + \sqrt {x + 1} \end{array} \right. \Rightarrow x = x + \sqrt {x + 1} \Rightarrow \sqrt {x + 1} = 0 \Rightarrow x = - 1,y = - 1\)
تهیه کننده: حامد دلیجه
توابع متناوب
توابع متناوب
تابع f را متناوب ناميم هرگاه يك عدد حقيقي مثبت مانند T موجود باشد، كه برای هر \(x \in {D_f}\) داشته باشيم:
\(f(x + T) = f(x),x + T \in {D_f}\)
براي هر
كوچكترين عدد T با خاصيت هاي بالا را دوره تناوب f مينامند.
مثال
با استفاده از رسم نمودار دوره تناوب تابع \(y = \sin x\) را تعيين كنيد.
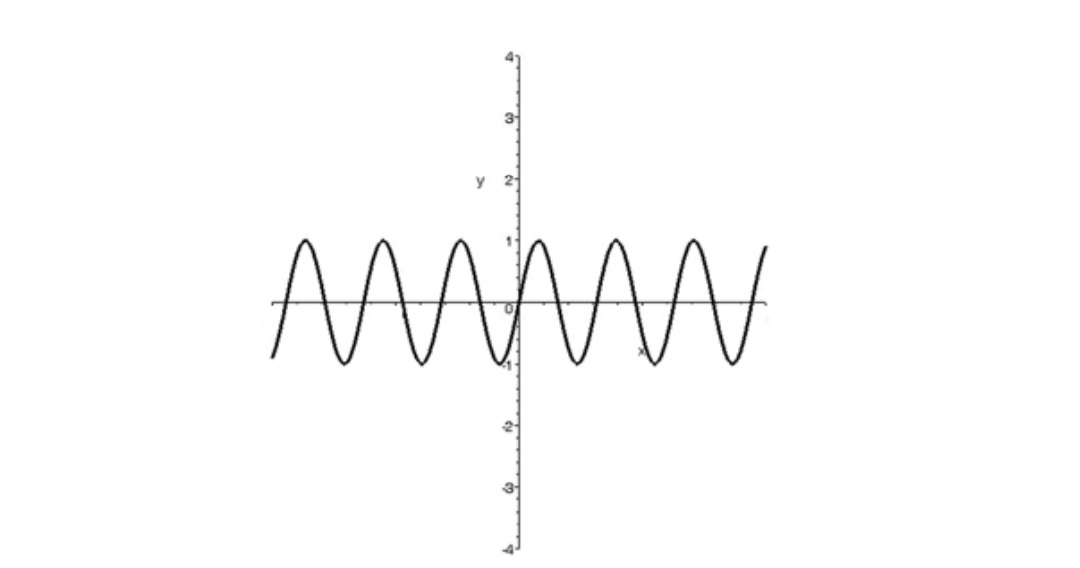
حل: همانگونه كه از نمودار مشاهده ميشود كمترين طولي كه نمودار تابع در آن عيناً تكرار ميشود \(2\pi \) است. پس دوره تناوب تابع \(T = 2\pi \) ميباشد.
مثال
دوره تناوب تابع \(y = 3\sin x - 1\) را تعيين كنيد.
با توجه به اينكه براي رسم نموار تابع \(y = 3\sin x - 1\) ميتوانيم ابتدا نمودار تابع \(y = \sin x\) را رسم و نمودار را با يك انبساط در جهت محور y ها و يك انتقال به راست، نمودار تابع را رسم كنيم در واقع دوره تناوب اين تابع با تابع \(y = \sin x\) يكسان است. اين مطلب در شكل زير به خوبي قابل مشاهده ميباشد.
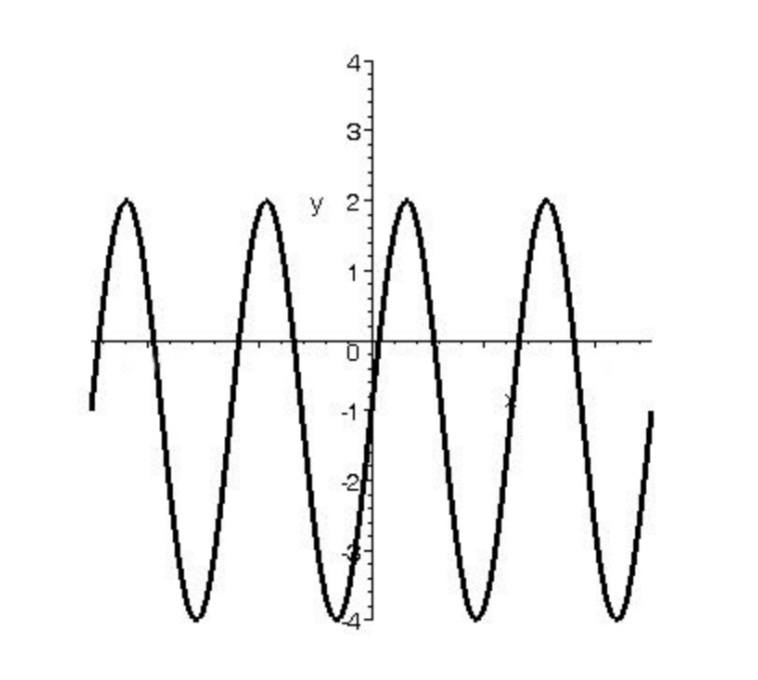
توجه: در حالت كلي اگر f تابعي متناوب با دوره تناوب T باشد توابع \(y = af(x) + b\) نيز متناوب با همان دوره تناوب T خواهند بود. ولي دوره تناوب تابع \(y = f(ax)\) برابر \(\frac{{2\pi }}{{\left| a \right|}}\) است ( . به علت π2 انقباض و انبساط در جهت محور x ها(
مثال
آيا تابع \(y = \sqrt {1 - {x^2}} \) متناوب است؟ چرا؟
خير - زيرا \({D_f} = \left[ { - 1,1} \right]\) و شرط \(x + T \in {D_f}\) نميتواند براي تابع برقرار باشد.
مثال
آيا تابع y=2متناوب است؟ در صورت متناوب بودن دوره تناوب آن را تعيين كنيد.
دامنه تعريف تابع برابر ℜ است. پس T هر عدد حقيقي مثبت كه باشد داريم
\(\left\{ \begin{array}{l}x + T \in {D_f}\\\\f(x + T) = f(x)\end{array} \right.\)
پس تابع متناوب است. اما چون كوچكترين عدد حقيقي مثبت وجود ندارد، پس دوره تناوب ندارد.
براي تعيين دوره تناوب ميتوانيم از دستورهاي زير استفاده كنيم:
\(\begin{array}{l}1)y = {\sin ^{2n - 1}}(ax).y = {\cos ^{2n - 1}}(ax)T = \frac{{2\pi }}{{\left| a \right|}}\\\\2)y = {\sin ^{2n - 1}}(ax).y = {\cos ^{2n - 1}}(ax)T = \frac{{2\pi }}{{\left| a \right|}}\\\\3)y = {\sin ^{2n}}(ax),y = {\cos ^{2n}}(ax),y = {\tan ^n}(ax),y = {\cot ^n}(ax)T = \frac{\pi }{{\left| a \right|}}\\\\y = \left| {\sin (ax)} \right|,y = \left| {\cos (ax)} \right|,y = \left| {A\sin (ax) + B\cos (ax)} \right| \Rightarrow T = \frac{\pi }{{\left| a \right|}}\\\\\end{array}\)
مثال
دوره تناوب توابع زير را تعيين مي کنیم
\(\begin{array}{l}1)y = {\sin ^3}(2x) \Rightarrow T = \frac{{2\pi }}{2} = \pi \\\\2)y = {\sin ^2}(2x) \Rightarrow T = \frac{\pi }{2}\\\\3)y = - 3\sin (2x) \Rightarrow T = \frac{{2\pi }}{2} = \pi \\\\4)y = {\sin ^3}(2x) \Rightarrow T = \frac{{2\pi }}{2} = \pi \\\\5)y = \frac{\pi }{4} - 3\sin (1 - 2x) \Rightarrow T = \frac{{2\pi }}{{\left| { - 2} \right|}} = \pi \\\\6)y = {\tan ^2}(3x) \Rightarrow T = \frac{\pi }{3}\\\\7)y = 4 - 2\cot (\frac{\pi }{4} - 3\pi x) \Rightarrow T = \frac{\pi }{{\left| { - 3\pi } \right|}} = \frac{1}{3}\end{array}\)
مثال
دوره تناوب تابع \({y_1} = \sin (\frac{2}{3}x + \frac{\pi }{6}) - 1\) چند برابر دوره تناوب تابع \({y_2} = {\sin ^2}(\frac{2}{3}x)\) است.
\({T_1} = \frac{{2\pi }}{{\frac{2}{3}}} = 3\pi ,{T_2} = \frac{{2\pi }}{{\frac{2}{3}}} = \frac{{2\pi }}{3} \Rightarrow \frac{{{T_1}}}{T} = \frac{{3\pi }}{{\frac{2}{3}}} = \frac{9}{2}\)
توابع زير متناوب نيستند:
توابع مثلثاتي كه در آن كمان x زير راديكال و يا تواني غير از يك داشته باشد متناوب نيستند.
هر گاه در تابع، كمان با يكي از چهار عمل اصلي با نسبت مثلثاتي قرار گيرد، تابع متناوب نيست.
مثال
توابع زير متناوب نيستند
الف)\(y = \cos \left| x \right|\) ب) \(y = x\cos x\)
ج) \(y = \sqrt x + \tan x\) د) \(y = x - \cos x\)
ه)\(y = \sin \left| x \right|\)
جزء صحيح
براي هر عدد حقيقي x جزء صحيح آن بزرگترين عدد صحيحي است كه از x بيشتر نيست. جزء صحيح x را با نماد \(\left[ x \right]\) يا \(\left\lfloor x \right\rfloor \) نمايش ميدهيم. يعني براي هر عدد حقيقي x يك عدد صحيح p موجود است به طوري که:
\(p \le x < p + 1 \Rightarrow \left[ x \right] = p\)
مثال
الف)\(\left[ x \right] < 2\) ب)\(\left[ x \right] \le 2\)
ج)\(\left[ x \right] < - \frac{1}{2}\) د)\(\left[ x \right] \le - \sqrt 2 \)
ه)\(\left[ {\frac{{3x + 1}}{2} < 4} \right]\) و)\({\left[ x \right]^2} - 3\left[ x \right] + 2 < 0\)
ز)\(\left[ {\log _2^x} \right] < 8\)
\(\left[ x \right] < 2 \Rightarrow \left[ x \right] \le 2 \Rightarrow x < 2\) (الف
\(\left[ x \right] \le 2 \Rightarrow x < 3\) (ب
\(\left[ x \right] < - \frac{1}{2} \Rightarrow \left[ x \right] < - \frac{1}{2} < 0 \Rightarrow x < 0\) (ج
\(\left| x \right| \le - \sqrt 2 \Rightarrow \left| x \right| \le - \sqrt 2 < - 1 \Rightarrow x < - 1\) (د
\(\left[ {\frac{{3x + 1}}{2}} \right] < 4 \Rightarrow \frac{{3x + 1}}{2} < 4 \Rightarrow 3x + 1 < 8 \Rightarrow x < \frac{7}{3}\) (ه
\(\begin{array}{l}{\left[ x \right]^2} - 3\left[ x \right] + 2 < 0{t^2} - 3t + 2 < 0 \Rightarrow 1 < t < 2\\\\ \Rightarrow 1 < \left[ x \right] < 2\end{array}\)
\(\left[ {\log _2^x} \right] < 9 \Rightarrow \log _2^x < 9 \Rightarrow x < {2^9}\) (ز
دستور های زیر برای جز صحیح همواره برقرار است
\(\begin{array}{l}\left[ {x + k} \right]\left[ x \right] \pm k\\\\\left[ x \right] + \left[ { - x} \right] = \left\{ \begin{array}{l}0,x \in z\\\\ - 1,x \notin z\end{array} \right.\\\\0 \le x - \left[ x \right] < 1\\\\x - 1 \le \left[ x \right] \le x\\\\\left[ x \right] + \left[ {x + \frac{1}{n}} \right] + \left[ {x + \frac{n}{2}} \right] + ... + \left[ {x + \frac{{n - 1}}{n}} \right] = \left[ {nx} \right]\\\\x > 0 \Rightarrow \left[ x \right] \ge 0\\\\x < 0 \Rightarrow \left[ x \right] < 0\end{array}\)
مثال
معادله ي \(\left[ x \right] + \left[ {x + 3} \right] - \left[ {x + 2} \right] = 5\) را حل كنيد.
\(\left[ x \right] + \left[ x \right] + 3 - \left[ x \right] - 2 = 5 \Rightarrow \left[ x \right] = 4 \Rightarrow 4 \le x < 5\)
مثال
معادله ی \(4\left[ x \right.\left. {^2} \right] + x = 5\) را حل كنيد.
\(\left\{ \begin{array}{l}\left\{ {4\left[ x \right.\left. {^2} \right]} \right. \in z\\\\\left\{ {4\left[ x \right.\left. {^2} \right]} \right. + x = 5\end{array} \right. \Rightarrow x \in z \Rightarrow {x^2} \in z \Rightarrow 4{x^2} + x - 5 = 0 \Rightarrow \left\{ \begin{array}{l}x = 1\\\\x = - \frac{5}{4}\end{array} \right.\)
مثال
معادله ي \(\left[ x \right] + \left[ { - x} \right] = \frac{1}{{x - \left[ x \right]}}\) را حل كنيد.
ميدانيم
\(\left[ x \right] + \left[ { - x} \right] = \left\{ \begin{array}{l}0,x \in z\\\\ - 1,x \notin z\end{array} \right.\)
باتوجه به اینکه صورت کسر طرف دوم عدد یک یک است پس طرف اول صفر نمی تواند باشد بنابراین \(x \in z\) و برابر 1- است و داریم :
مهادله جواب ندارد \( - 1 = \frac{1}{{x - \left[ x \right]}} \Rightarrow x - \left[ x \right] = - 1 \to 0 < x - \left[ x \right] < 1\)
مثال
دامنه و برد تابع \(y = \frac{1}{{\sqrt {x - \left| x \right|} }}\) را تعيين كنيد
لازم است \(x - \left| x \right| > 0\) باشد،
\(\begin{array}{l}0 \le x - \left| x \right| < 1x - \left| x \right| \ne 0 \Rightarrow x \ne z \Rightarrow {D_f} = R - Z\\\\x \in R - Z \Rightarrow 0 < x - \left| x \right| < 1 \Rightarrow \sqrt {x - \left| x \right| < 1} \Rightarrow \frac{1}{{\sqrt {x - \left| x \right|} }} > 1 \Rightarrow {R_f} = \left( {, + \infty } \right)\end{array}\)
مثال
نمودار تابع \(y = - 2\left| x \right| - 1\) را رسم كنيد.
ميدانيم نمودار تابع \(y = \left| x \right|\) به صورت مقابل است.
پس لازم است ابتدا y هاي نقاط اين نمودار در -2 ضرب شود، سپس تمام نقاط آن يك واحد به سمت پايين انتقال يابد. بنابراين نمودار به صورت زير در مي آيد.
مثال
نمودار تابع \(y = \left| {\sqrt x } \right|\) را در فاصله ي ( 90 ,0 ] رسم كنيد.
داريم
\(\begin{array}{l}0 \le x < 9 \Rightarrow 0 \le \sqrt x < 3 \Rightarrow \left| {\sqrt x } \right| = 0,1,2\\\\\left| {\sqrt x } \right| = 0 \Rightarrow 0 \le \sqrt x < 1 \Rightarrow 0 \le x < 1,y = 0\\\\\left| {\sqrt x } \right| = 1 \Rightarrow 1 \le \sqrt x < 2 \Rightarrow 1 \le \sqrt x < 4,y = 1\\\\\left| {\sqrt x } \right| = 2 \Rightarrow 2 \le \sqrt x < 3 \Rightarrow 4 \le \sqrt x < 9,y = 2\end{array}\)
و نمودار به صورت زير در مي آيد.
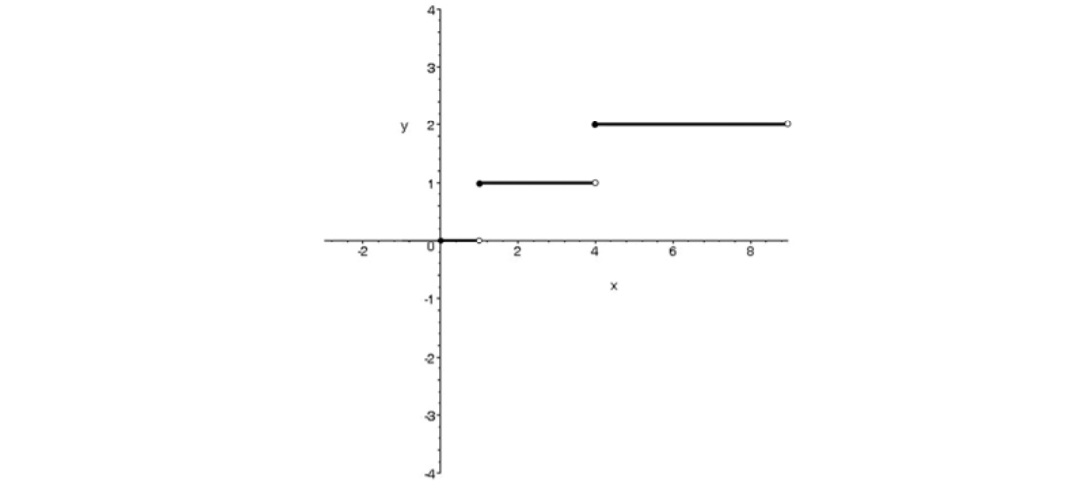
مثال
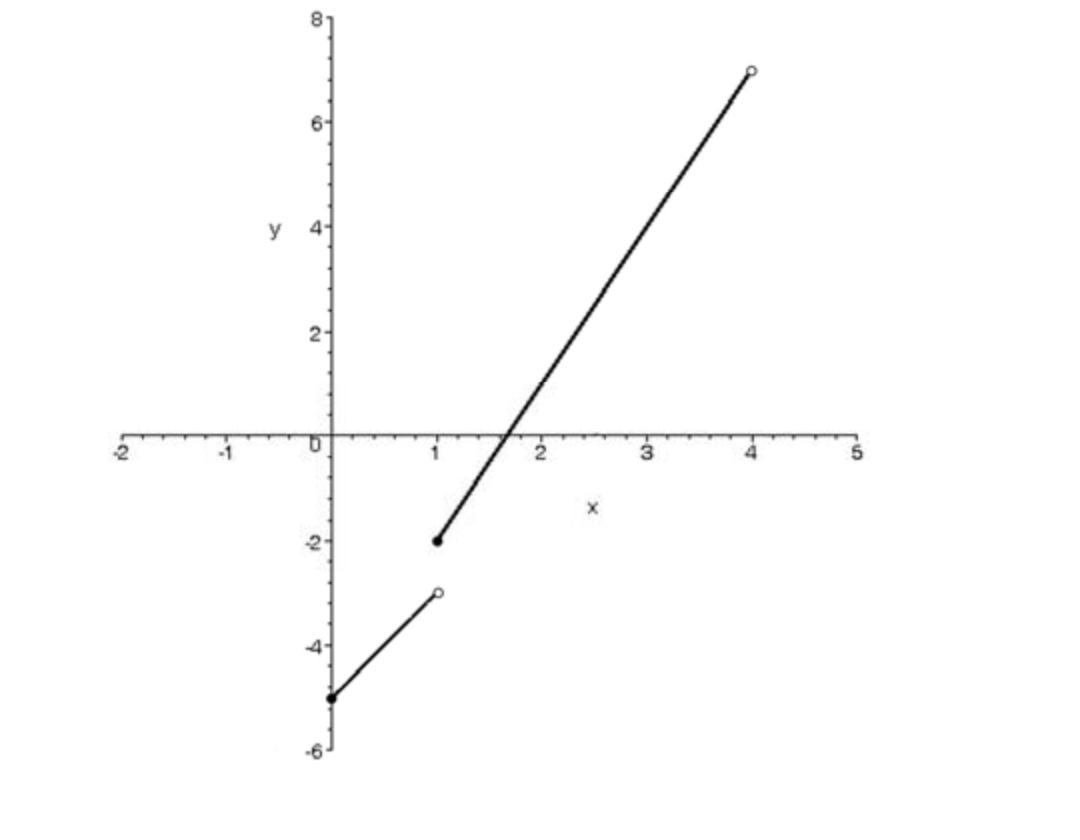
نمودار تابع \(y = x\left| {\sqrt x } \right| + 2x - 5\) را در فاصله ي ( 40 ,0 ] رسم كنيد.
\(0 \le x < 4 \Rightarrow 0 \le \sqrt x < 2 \Rightarrow \left[ {\sqrt x } \right] = 0,1 \Rightarrow \left\{ \begin{array}{l}\left[ {\sqrt x } \right] = 0 \Rightarrow 0 \le \sqrt x < 1 \Rightarrow \left\{ \begin{array}{l}0 \le x < 1\\\\y = 2x - 5\end{array} \right.\\\\\left[ {\sqrt x } \right] = 1 \Rightarrow 1 \le \sqrt x < 2 \Rightarrow \left\{ \begin{array}{l}1 \le x < 4\\\\y = 3x - 5\end{array} \right.\end{array} \right.\)
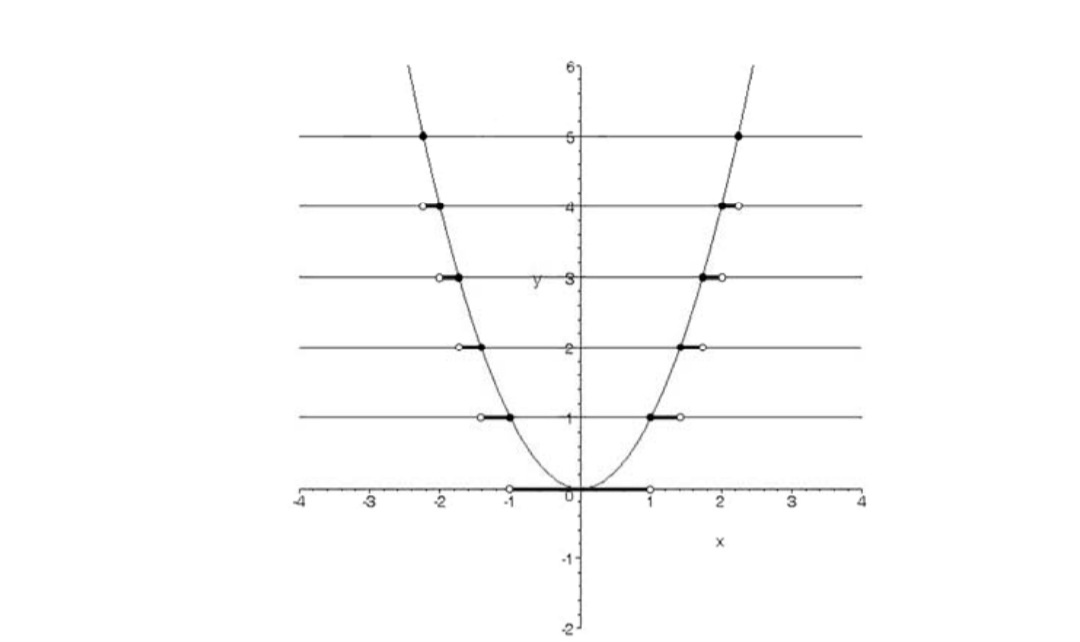
براي رسم نمودار تابع \(f(x) = \left[ {g(x)} \right]\) ميتوانيم ابتدا نمودار تابع \(y = g(x)\) را رسم كنيم. سپس خطوط\(y = k\) , \(k \in z\) را رسم نموده و در انتها هر قسمت از نمودار را كه بين دو خط افقي متوالي قرار گرفت را روي خط پاييني تصوير كنيم. محل تلاقي خطوط افقي با نمودار نقطه اي توپر ميباشد.
مثال
نمودار تابع \(y = \left| {{x^2}} \right|\) رارسم کنید
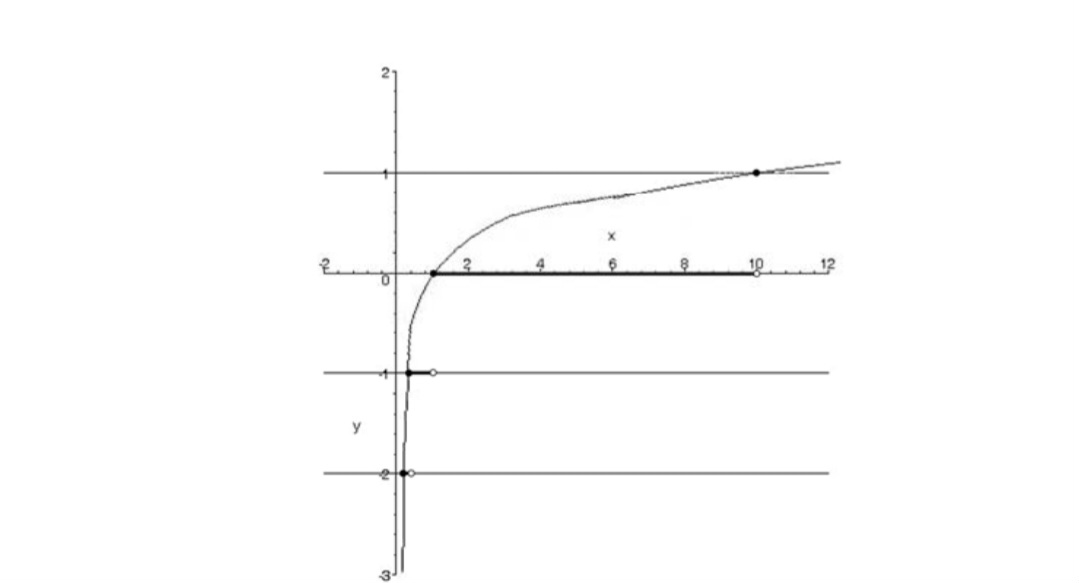
مثال
نمودار تابع \(y = \left| {\log x} \right|\) رارسم کنید
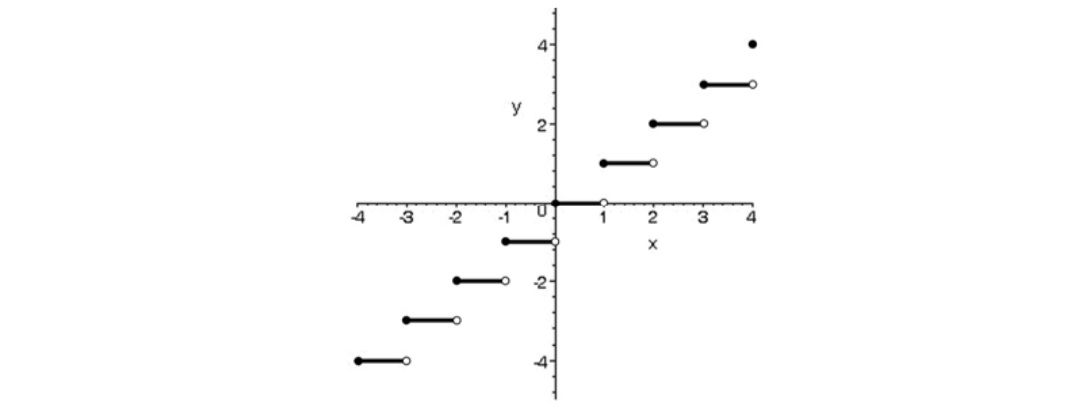
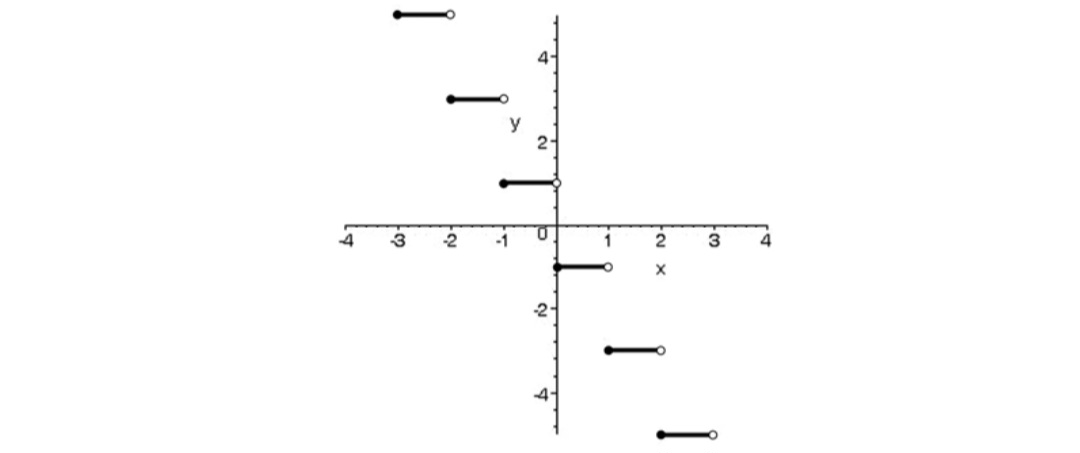
مثال
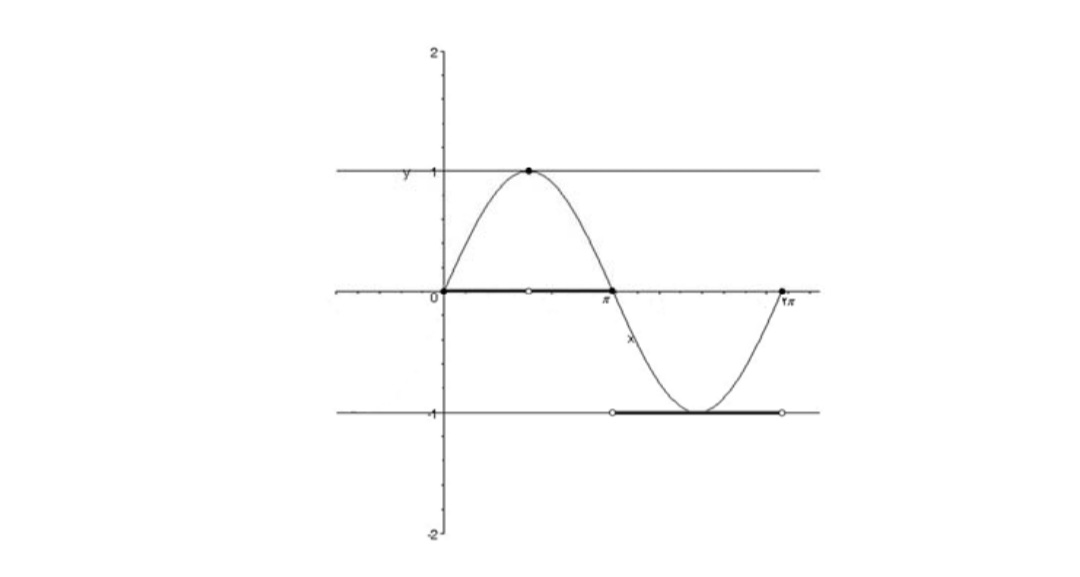
نمودار تابع\(y = \left[ {\sin x} \right]\) را در فاصله ی \(\left[ {0,2\pi } \right]\) رسم کنید
تهیه کننده: حامد دلیجه
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه یازدهم- آزمون آنلاین تمامی دروس پایه یازدهم
- گام به گام تمامی دروس پایه یازدهم
- ویدئو های آموزشی تمامی دروس پایه یازدهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه یازدهم
- فلش کارت های آماده دروس پایه یازدهم
- گنجینه ای جامع از انشاء های آماده پایه یازدهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه یازدهم



1736019749.png)















