درسنامه کامل حسابان یازدهم فصل 5 حد و پیوستگی
تعداد بازدید : 7.26Mخلاصه نکات حسابان یازدهم فصل 5 حد و پیوستگی - درسنامه شب امتحان حسابان یازدهم فصل 5 حد و پیوستگی - جزوه شب امتحان حسابان یازدهم نوبت اول فصل 5 حد و پیوستگی
همسايگي يك نقطه
همسايگي يك نقطه
اگر a عددي حقيقي و δ يك عدد مثبت باشد، بازه ي\((a - \delta + \delta )\) را يك همسايگي a مينامند a) مركز و δ شعاع همسايگي نام دارند(. اگر a را از اين همسايگي حذف كنيم، آن را يك همسايگي محذوف a مينامند.
مثال
هر يك از بازه هاي\(\left( {1/9,2/1} \right),\left( {0,4} \right),\left( {1,3} \right)\) يك همسايگي 2 هستند.
مثال
هر يك از مجموعه هاي \((0,2) \cup (2,4),(1,3) - \left\{ 2 \right\}\)و\(\left\{ {\left. x \right|} \right.1/9 < x < 2/1,x \ne \left. 2 \right\}\) يك همسايگي محذوف 2 هستند.
مثال
اگر \((3k - 2,k + 4)\)يك همسايگي 3 باشد، a و δ را به دست آوريد؟
عدد 3 نقطه ي وسط بازه است، پس
\(3 = \frac{{(3k - 2) + (k + 4)}}{2} \Rightarrow 4k + 2 = 6 \Rightarrow k = 1\)
بنابراين همسايگي به صورت \((1,5)\)در مي آيد و \(a = \frac{{1 + 5}}{2} = 3\) و\(\delta = 3 - 1 = 2\)
مثال
اگر مجموعه ی \(( - 3,y) \cup (2,{x^2} + 1)\)نمايشگر يك همسايگي محذوف باشد، حاصل \(3{x^2} + y\)را به دست آوريد؟
ابتدا طوري دو بازه را مينويسيم كه اعداد از كوچك به بزرگ مرتب شوند و داريم \(y = 2\) چون همسايگي محذوف 2 است، بايد:
\(2 = \frac{{ - 2 + {x^2} + 1}}{2} \Rightarrow {x^2} - 2 = 4 \Rightarrow x = \pm \sqrt 6 \)
بنابراين داريم:
\(3{x^2} + y = 3( \pm \sqrt 6 ) + 2 = 20\)
مثال
كداميك از مجموعه هاي زير يك همسايگي محذوف a را نمايش ميدهند؟
الف) \(\left\{ {x \in \left. R \right|} \right.0 < \left| {x - a} \right| < \left. \delta \right\}\) ب)\(\left\{ {x \in \left. R \right|} \right.\left| {x - a} \right| < \left. \delta \right\}\)
الف)
\(\begin{array}{l}0 < \left| {x - a} \right| < \delta \Rightarrow \left\{ \begin{array}{l}\left| {x - a} \right| < \delta \\\\\left| {x - a} \right| \ne 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l} - \delta < x - a < a + \delta \\\\x \ne a\end{array} \right.\\\\x \in (a - \delta ,a + \delta ) - \left\{ a \right\}\end{array}\)
بنابراين يك همسايگي محذوف a را نمايش ميدهد.
ب)
\(\left| {x - a} \right| < \delta \Rightarrow - \delta < x - a < \delta \Rightarrow a - \delta < x < a + \delta \)
بنابراین یک همسايگي هست ولی همسایگی محذوف نیست.
همسایگی چپ و راست یک نقطه
اگر a عددي حقيقي و δ يك عدد مثبت باشد، بازه به صورت\((a - \delta ,a)\) را يك همسايگي چپ a و بازه به صورت\((a,a + \delta )\) را يك همسايگي راست a ميناميم.
مثال
هر يك از بازه هاي\(\left( {3,3/1} \right)\) و \(\left( {3,4} \right)\) و\(\left( {3,5} \right)\) يك همسايگي راست 3 و هر يك از بازه هاي \(\left( {2/9,3} \right)\)و \(\left( {2,3} \right)\)و\(\left( { - 1,3} \right)\) يك همسايگي چپ 3 هستند.
مثال
همسايگي \(\left( {2,3} \right) \cup \left( {3,4} \right)\)در واقع از اجتماع يك همسايگي چپ 3 يعني \(\left( {2,3} \right)\) و يك همسايگي راست 3 يعني\(\left( {3,4} \right)\) تشكيل شده است.
اگر I يك همسايگي نقطه ي a باشد، گوييم تابع f در همسايگي I تعريف شده است، . هرگاه\(I \subseteq {D_f}\)
مثال
تابع \(y = \sqrt x \)در كداميك از همسايگي هاي زير تعريف شده است
الف) \(\left( {2,3} \right)\) ب) \(\left( {0,4} \right)\)
ج)\(\left( { - 2,1} \right)\) د) \(\left( { - 1, - 3} \right)\)
می دانیم پس داريم :
الف) \(\left( {2,3} \right) \subseteq {D_f}\)پس تابع در همسايگي \(\left( {2,3} \right)\) تعريف شده است.
ب)\(\left( {0,2} \right) \subseteq {D_f}\) پس تابع در همسايگي \(\left( {0,4} \right)\)تعريف نشده است.
ج)\(\left( { - 2,1} \right) \not\subset {D_f}\) پس تابع در همسايگي \(\left( { - 2,1} \right)\) تعريف نشده است
د) \(\left( { - 1, - 3} \right) \not\subset {D_f}\)پس تابع در همسایگی \(\left( { - 1, - 3} \right)\)تعریف نشده است.
مثال
تابع \(y = \sqrt {x - 1} \)در كداميك از همسايگي هاي عدد يك تعريف شده است.
الف)\(\left( {1,1 + \delta } \right)\) ب)\((1 - \delta ,1 + \delta )\) ج) \((1 - \delta ,1)\)
می دانیم\({D_f} = \left[ {1, + \infty )} \right.\) پس \(\delta \)هر عدد مثبتي كه باشد تابع در همسايگي\((1,1 + \delta )\) تعريف شده است . ولي به ازاي هيچ مقدار مثبتي از δ در همسايگي هاي \((1 - \delta ,1 + \delta )\)و \((1 - \delta ,1)\) تعريف نشده است.
مثال
نمودار تابع f زيربه صورت رسم شده است. با توجه به نمودار مشخص كنيد تابع f در كداميك از همسايگي هاي زير تعريف شده است.
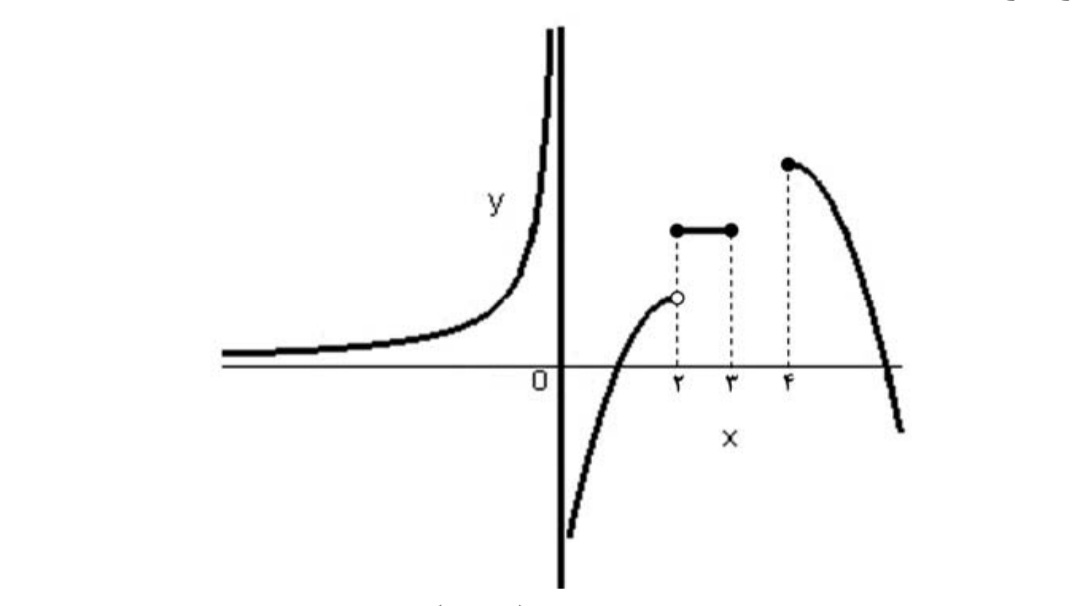
الف) \(\left( { - 3, - 1} \right)\) ب) \(\left( { - 2,2} \right)\)
ج) \(\left( {1,2} \right)\) د) \(\left( {0,3} \right)\)
هـ)\(\left( {0,7} \right)\) و) \(\left( {3,4} \right)\)
ز) \(\left( {2,3} \right)\)
با توجه به شكل داريم:
\({D_f} = \left( { - \infty ,0} \right) \cup \left( {0,3} \right) \cup \left( {4, + \infty } \right)\)
بنابراين تابع در همسايگي هاي\(\left( {0,3} \right),\left( {1,2} \right),\left( { - 3, - 1} \right)\) و \(\left( {2,3} \right)\) تعريف شده ولي در همسايگي هاي \(\left( {0,7} \right),\left( { - 2,2} \right)\)و \(\left( {3,4} \right)\)تعريف نشده است.
وقتي ميگوييم متغير مستقل x به عدد ثابت a نزديك ميشود . يعني هر اندازه كه بخواهيم متغير x به a نزديك ميشود ولي هيچگاه مساوي a نميشود. به بيان ديگر به ازاي هر عدد دلخواه و مثبت مانند ε داريم:
\(0 < \left| {x - a} \right| < \delta \)
مثال
با رسم يك جدول و نوشتن چند مقدار در آن مفهوم نزديك شدن متغير x را به عدد 2 نمايش دهيد.

مثال
با رسم یک جدول و نوشتن چند مقدار در آن مفهوم نزدیک شدن متغیر x رابه عدد ثابت -2نمایش دهید.

برای یک تابع fاگر مقادیر متغیر مستقل x(در دامنه f )به عددی مانند a نزدیک شوند و مشاهده شود که مقادیرf(x) به عددی مانندl نزدیک می شوند.(ممکن است مساوی l هم بشوند) گوییم تابعf در نقطه ی aحد داردو حد آن برابرl است و می نویسیم:
\(\mathop {\lim }\limits_{x \to a} f(x) = l\)
مثال
با رسم يك جدول حاصل حد تابع\(f(x) = 2x + 3\) را در\(x = 5\) محاسبه کنید.

همانگونه که از جدول مشاهده می شود بانزدیک شدن مقادیر متغیر x به عدد 5 مقادیر تابعf به عدد 13 نزدیک می شوند و داریم :
\(\mathop {\lim }\limits_{x \to 5} (2x + 3) = 13\)
توجه:تابع fدر\(x = 5\) تعریف شده است و \(f(5) = 13\)می باشد.
مثال
بارسم یک جدول حاصل حد تابع \(f(x) = \frac{{{x^2} - 4}}{{x - 2}}\)را در x=2محاسبه کنید.

همانگونه که از جدول مشاهده می شود با نزدیک شدن مقادیر متغیر x به عدد 2مقادیر تابع f به عدد 4 نزدیک می شوندو داریم:
\(\mathop {\lim }\limits_{x \to 2} \frac{{{x^2} - 4}}{{x - 2}}\)
توجه:تابعf در x=2 تعریف نشده است ولی حد دارد.
مثال
با رسم یک جدول رفتار تابع\(f(x) = \frac{1}{{x - 1}}\) را وقتی متغیر X به عدد یک نزدیک می شود بررسی کنید.

همانگونه که از جدول مشاهده می شود وقتی متغیر به عدد یک نزدیک می شودمقادیر تابع به هیچ عددی نزدیک نمی شوندو از نظر قدر مطلق مرتبا افزایش می یابند.بنابراین میگوییم تابع fدرx=1 حد ندارد.
توجه:تابع fدرx=1 نه تعریف شده است و نه حد دارد.
شرط لازم برای انکه بتوان درمورد حد تابع F درx=a صحبت کرد ان است که تابع F دست کم در یک همسایگی A تعریف شده باشد
مثال
در کدامیک از توابع زیرمیتوان از حد تابعf در نقطه ی داده شده صحبت کرد.
الف)  \(f(x) = \frac{1}{{\left| x \right|}},x = \frac{1}{2}\) ب) \(f(x) = x - \left| x \right|\)
\(f(x) = \frac{1}{{\left| x \right|}},x = \frac{1}{2}\) ب) \(f(x) = x - \left| x \right|\)
ج)\(f(x) = \left\{ \begin{array}{l}x - 1,x < 1\\\\1 - x,x > 1\end{array} \right.,x = 1\)
الف)
باتوجه به اینکه\({D_f} = ( - \infty ,0) \cup \left[ {1, + \infty )} \right.\) پس تابع f در هیچ همسایگی \(\frac{1}{2}\) تعریف نشده است.یعنی نمیتوان از حدتابع fدر\(x = \frac{1}{2}\) صحبت کرد.
\(\frac{1}{2}\) تعریف نشده است.یعنی نمیتوان از حدتابع fدر\(x = \frac{1}{2}\) صحبت کرد.
ب)
با توجه به اين كه \({D_f} = R\)پس میتوان درمورد حد تابع در x=2صحبت کرد
ج)
با توجه به اين كه \({D_f} = R - \left\{ 1 \right\}\)پس میتوان درمورد حد تابع در x=2 را بررسي کرد

همانگونه كه از جدول مشاهده ميشود داريم:
\(\mathop {\lim }\limits_{x \to 1} f(x) = 0\)
توجه: تابع f در x=1تعريف نشده است ولي حد دارد.
در تابع f اگر متغير x با مقدارهاي بزرگتر از عدد a به a نزديك شود و مقدارهايf(x) به عددي مانند l نزديك شوند، گوييم تابع f در نقطه يا به طول a حد راست دارد و مينويسيم:
\(\mathop {\lim }\limits_{x \to {a^ + }} f(x) = l\)
مثال
بارسم جدول اگر \(f(x) = \frac{{\left| x \right|}}{x}\)حاصل \(\mathop {\lim }\limits_{x \to {0^ + }} f(x)\)را محاسبه كنيد.

بنابراین داریم:
\(\mathop {\lim }\limits_{x \to {0^ + }} \frac{{\left| x \right|}}{x} = 1\)
مثال
اگر \(f(x) = \left\{ \begin{array}{l}3 - x,x < 1\\\\3,x = 1\\\\x + 1,x > 1\end{array} \right.\)مقدار\(\mathop {\lim }\limits_{x \to {1^ + }} f(x) = \) را با استفاده از رسم نمودار محاسبه کنید
نمودار تابع f در فاصله ی \((1, + \infty )\)به صورت زیر است.
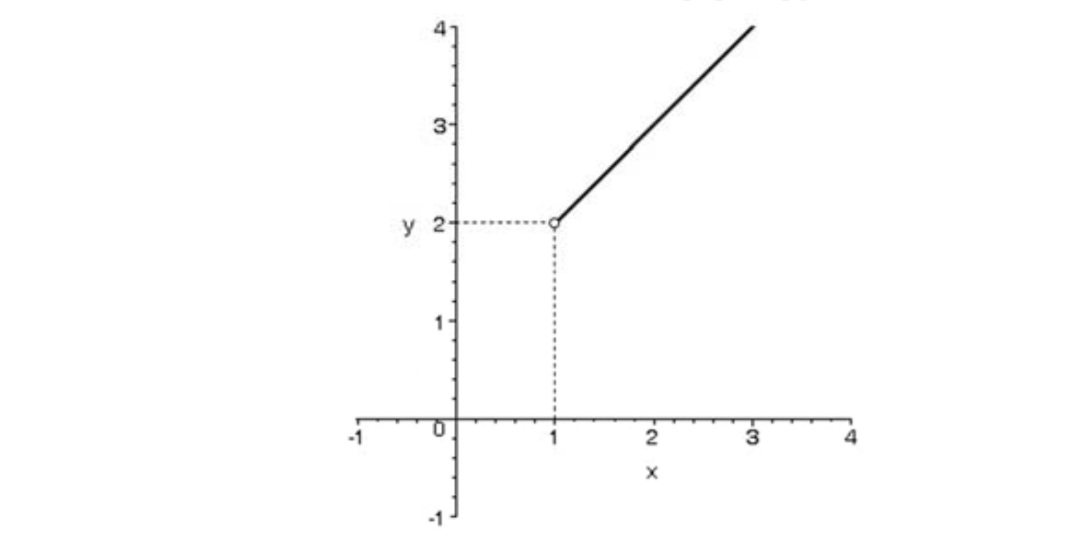
همانگونه كه از نمودار مشاهده مي شود با نزديك شدن مقادير x از طرف راست ( مقادير بزرگتر از يك ) به يك، مقادير f(x)به عدد 2 نزديك ميشوند. بنابراين داريم:
\(\mathop {\lim }\limits_{x \to {1^ + }} f(x) = 2\)
در تابع f اگر متغير x با مقدارهاي کوچک تر از عدد a به a نزديك شود و مقدارهاي f(x)به عددي مانند k نزديك شوند، گوييم تابع f در نقطه يا به طول a حد چپ دارد و مينويسيم:
\(\mathop {\lim }\limits_{x \to {a^ - }} f(x) = k\)
مثال
اگر\(f(x) = \frac{{\left| x \right|}}{x}\) با رسم جدول حاصل \(\mathop {\lim }\limits_{x \to {0^ - }} f(x)\)را محاسبه كنيد.

بنابراين داريم:
\(\mathop {\lim }\limits_{x \to {0^ - }} \frac{{\left| x \right|}}{x} = 1\)
مثال
اگر \(f(x) = \left\{ \begin{array}{l}3 - x,x < 1\\\\3,x = 1\\\\x + 1,x > 1\end{array} \right.\)حاصل\(\mathop {\lim }\limits_{x \to {1^ - }} f(x)\) را با استفاده از رسم نمودار تابع محاسبه كنيد.
نمودار تابع f در فاصله ي \(\left( { - \infty ,1} \right)\)به صورت زير است.

همانگونه كه از نمودار مشاهده مي شود با نزديك شدن مقادير x از طرف چپ ( مقادير كوچكتر از يك) به يك، مقادير f(x)به عدد 2 نزديك ميشوند. بنابراين داريم:
\(\mathop {\lim }\limits_{x \to {1^ - }} f(x) = 2\)
اگر حدهاي چپ و راست تابع در نقطه اي مساوي باشند، تابع در آن نقطه حد دارد و حد آن همان مقدار حد چپ و راست در آن نقطه است.
مثال
ابتدا نمودار هر يك از توابع زير را رسم كنيد و سپس با استفاده از نمودار، حدهاي چپ و راست و حد تابع را در صورت وجود در نقطه ي داده شده محاسبه كنيد
 الف) \(f(x) = \left\{ \begin{array}{l} - x,x < 0\\\\3,x = 0\\\\x + 1,x > 0\end{array} \right.,x = 0\)
الف) \(f(x) = \left\{ \begin{array}{l} - x,x < 0\\\\3,x = 0\\\\x + 1,x > 0\end{array} \right.,x = 0\)
نمودار تابع به صورت زير است.
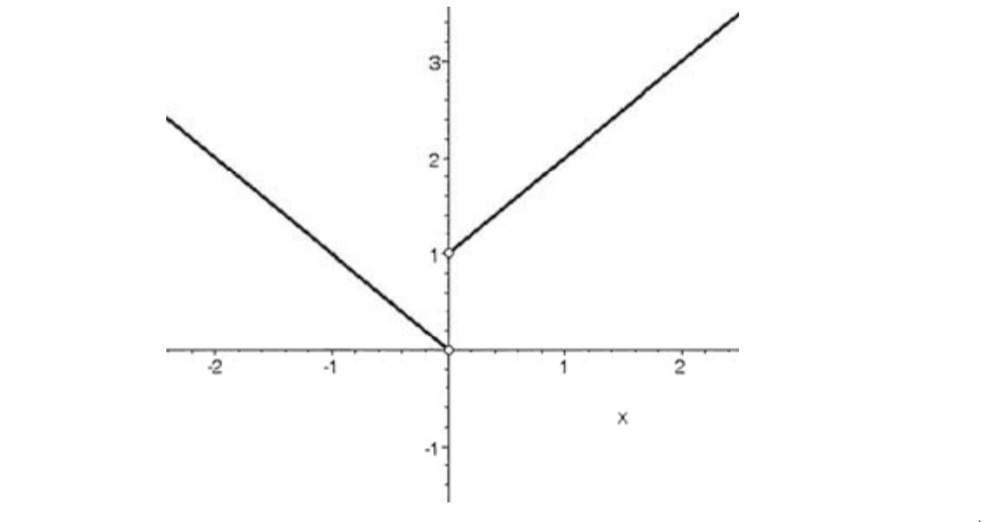
با توجه به نمودار داريم
\(\left\{ \begin{array}{l}\mathop {\lim }\limits_{x \to {0^ - }} f(x) = 0\\\\\mathop {\lim }\limits_{x \to {0^ + }} f(x) = 1\end{array} \right. \Rightarrow \mathop {\lim }\limits_{x \to 0} f(x)\)
وجود ندارد
ب)\(f(x) = \left\{ \begin{array}{l}{x^2} - 2x,x \ne 1\\\\0,x = 1\end{array} \right.,x = 1\)
نمودار تابع به صورت زير است.
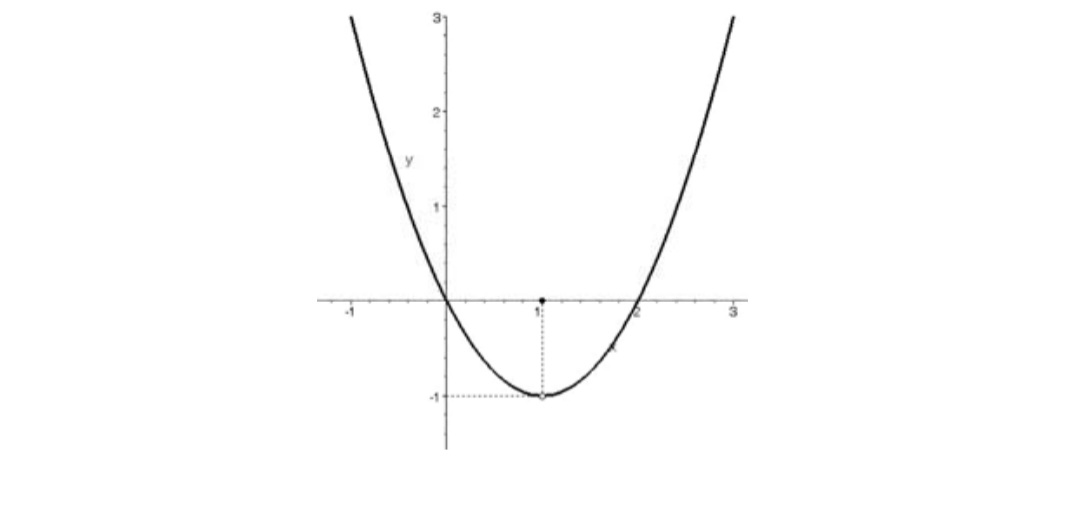
با توجه به نمودار داريم:
\(\left\{ \begin{array}{l}\mathop {\lim }\limits_{x \to {1^ - }} f(x) = - 1\\\\\mathop {\lim }\limits_{x \to {1^ + }} f(x) = - 1\end{array} \right. \Rightarrow \mathop {\lim }\limits_{x \to 1} f(x) = - 1\)
ج) \(=f(x) = \left[ x \right],x = 2\)
ج)نمودار تابع به صورت زير است.
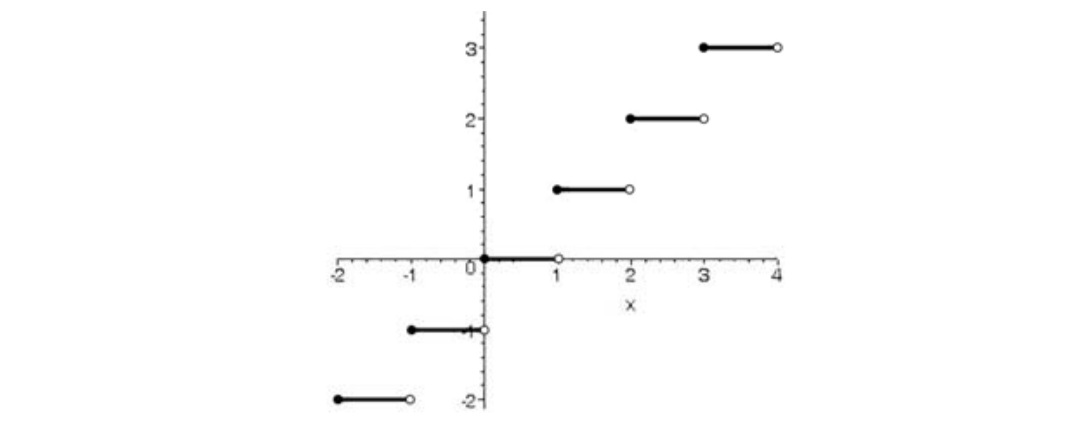
با توجه به نمودار داريم:
\(\left\{ \begin{array}{l}\mathop {\lim }\limits_{x \to {2^ - }} f(x) = 1\\\\\mathop {\lim }\limits_{x \to {2^ + }} f(x) = 2\end{array} \right. \Rightarrow \mathop {\lim }\limits_{x \to 2} f(x) = 1\)
وجود ندارد
مثال
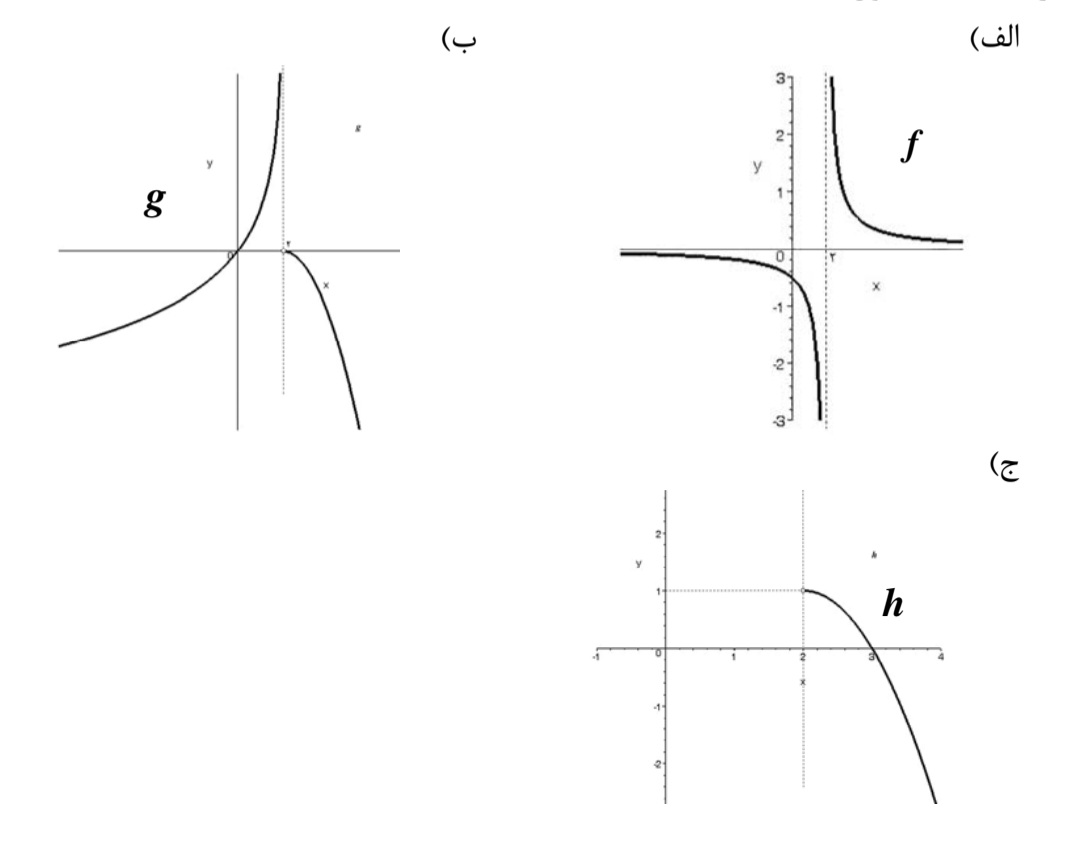
نمودار توابع f ، g و h به صورت زير رسم شده است. با استفاده از نمودار، حد توابع f ، g و h را در نقطه ای به طول x=2 محاسبه كنيد.
الف
با توجه به نمودار تابع در x=2از چپ حد ندارد و از راست نيز حد ندارد. بنابراين تابع در x=2حد ندارد .
ب)تابع g در x=2از چپ حد ندارد ولي \(\mathop {\lim }\limits_{x \to {2^ + }} f(x) = 0\) بنابراين g در x=2حد ندارد.
ج)به دليل عدم تعريف تابع h در يك همسايگي چپ ،2 بحث از وجود حد چپ در اين نقطه معنادار نيست. ازدر واقع منظور حد تابع h در x=2همان حد راست تابع h در x=2است. يعني:
\(\mathop {\lim }\limits_{x \to 2} h(x) = 1\)
مثال
اگر تابع \(f(x) = \left\{ \begin{array}{l}{x^2} + x,x > 2\\\\ax + b,x < 2\end{array} \right.\)در x=2 داراي حد باشد، چه رابطه اي بين a و b برقرار است.
\(\left. \begin{array}{l}\mathop {\lim }\limits_{x \to {2^ + }} f(x) = \mathop {\lim }\limits_{x \to {2^ + }} ({x^2} + x) = 6\\\\\mathop {\lim }\limits_{x \to {2^ - }} f(x) = \mathop {\lim }\limits_{x \to {2^ - }} (ax + b) = 2a + b\end{array} \right\}\)
مثال
نمودار تابع زوج f به صورت زير رسم شده است.
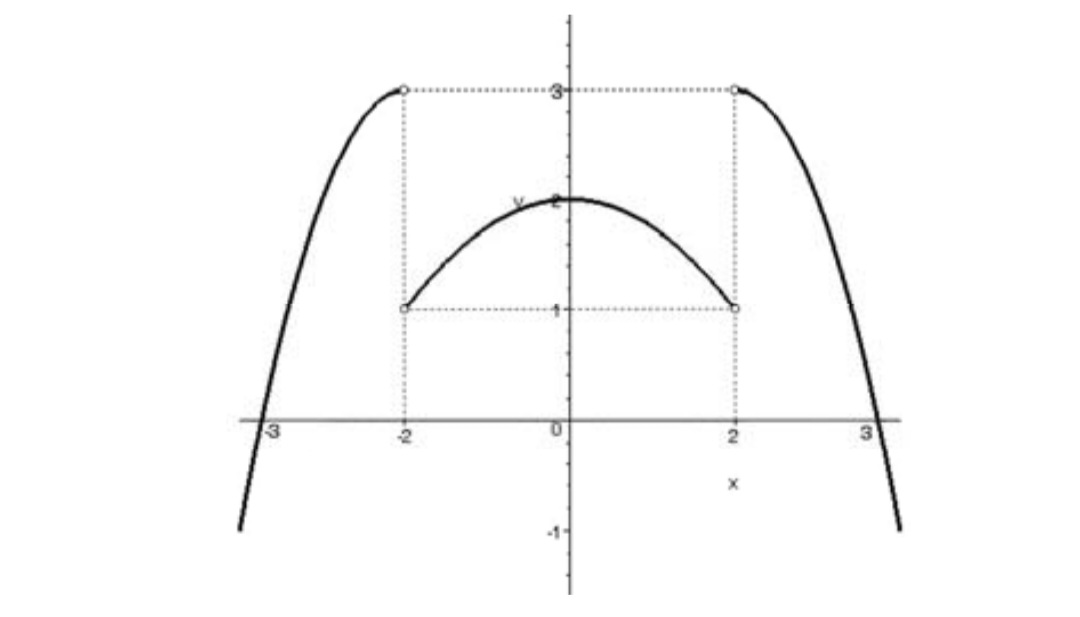
با توجه به نمودار، حدود زير را محاسبه كنيد.
الف) \(\mathop {\lim }\limits_{x \to - {2^ - }} f(x)\)ب) \(\mathop {\lim }\limits_{x \to - 3} f(x)\) ج) \(\mathop {\lim }\limits_{x \to - {2^ + }} f(x)\)
با توجه به اين كه f تابعي زوج است، نمودار آن نسبت به محور y ها متقارن است. بنابراين داريم:
\(\mathop {\lim }\limits_{x \to - {2^ - }} f(x) = \mathop {\lim }\limits_{x \to - {2^ + }} f(x) = 3\)(الف
\(\mathop {\lim }\limits_{x \to - 3} f(x) = \mathop {\lim }\limits_{x \to 3} f(x) = 0\)(ب
\(\mathop {\lim }\limits_{x \to - {2^ + }} f(x) = \mathop {\lim }\limits_{x \to - {2^ - }} f(x) = 1\)(ج
مثال
نمودار تابع زوج f به صورت زير رسم شده است.
با توجه به نمودار، حدود زير را محاسبه كنيد
الف)\(\mathop {\lim }\limits_{x \to - {2^ - }} f(x)\)
ب)\(\mathop {\lim }\limits_{x \to - 3} f(x)\)
ج) \(\mathop {\lim }\limits_{x \to - {2^ + }} f(x)\)
با توجه به اين كه f تابعي زوج است، نمودار آن نسبت به محور y ها متقارن است. بنابراين داريم:
\(\mathop {\lim }\limits_{x \to - {2^ - }} f(x) = \mathop {\lim }\limits_{x \to - {2^ + }} f(x) = 3\)(الف
\(\mathop {\lim }\limits_{x \to - 3} f(x) = \mathop {\lim }\limits_{x \to 3} f(x) = 0\)(ب
\(\mathop {\lim }\limits_{x \to - {2^ + }} f(x) = \mathop {\lim }\limits_{x \to {2^ - }} f(x) = 1\)(ج
تابع ثابت f(x)=cدر همه ی نقاط حد داردو حد آن در همه ی نقاط c است یعنی:
\(\mathop {\lim }\limits_{x \to a} c = c\)
تابع f(x)=x در همه ی نقاط حد داردو حد آن در هر نقطه به طول aبرابرa است یعنی:
\(\mathop {\lim }\limits_{x \to a} x = a\)
اگر\(\mathop {\lim }\limits_{x \to a} f(x) = l\) و\(\mathop {\lim }\limits_{x \to a} g(x) = k\) آنگاه:
\(\begin{array}{l}\mathop {\lim }\limits_{x \to a} (f(x) + g(x)) = \mathop {\lim }\limits_{x \to a} f(x) + \mathop {\lim }\limits_{x \to a} g(x) = l + k\\\\\mathop {\lim }\limits_{x \to a} (f(x) - g(x)) = \mathop {\lim }\limits_{x \to a} f(x) - \mathop {\lim }\limits_{x \to a} g(x) = l - k\\\\\mathop {\lim }\limits_{x \to a} (f(x) \times g(x)) = \mathop {\lim }\limits_{x \to a} f(x) \times \mathop {\lim }\limits_{x \to a} g(x) = l \times k\end{array}\)
اين قضايا را براي تعداد متناهي تابع نيز ميتوان تعميم داد.
اگر p(x) يك تابع چندجمله اي باشد، آنگاه:
\(\mathop {\lim }\limits_{x \to a} p(x) = p(a)\)
مثال
حدود زير را محاسبه كنيد.
الف)\(\mathop {\lim }\limits_{x \to 4} (2x + 3)\) ب)\(\mathop {\lim }\limits_{x \to 1} ({x^2} - 3x + 5)\)
ج)\(\mathop {\lim }\limits_{x \to \sqrt 2 } ({x^3} - 2{x^2} + x)\) د)\(\mathop {\lim }\limits_{x \to 7} \frac{{1 - 5x}}{3}\)
الف)
\(\mathop {\lim }\limits_{x \to 4} (2x + 3) = 1 \times 4 + 3 = 11\)
ب)
\(\mathop {\lim }\limits_{x \to 1} ({x^2} - 3x + 5) = {1^2} - 3(1) + 5 = 3\)
ج)
\(\mathop {\lim }\limits_{x \to \sqrt 2 } ({x^3} - 2{x^2} + x) = {\left( {\sqrt 2 } \right)^3} + 2{\left( {\sqrt 2 } \right)^2} + \sqrt 2 = 3\sqrt 2 + 4\)
د)
\(\mathop {\lim }\limits_{x \to 7} \frac{{1 - 5x}}{3} = \mathop {\lim }\limits_{x \to 7} ( - \frac{5}{3}x + \frac{1}{3}) = - \frac{5}{3}(7) + \frac{1}{3} = - \frac{{34}}{3}\)
اگر a عضوي از دامنه ي تابع باشد، آن گاه:
\(\begin{array}{l}{\mathop {\lim }\limits_{x \to a} ^k}\sqrt x { = ^k}\sqrt a ,\mathop {\lim }\limits_{x \to a} {b^x} = {b^a}\\\\\mathop {\lim }\limits_{x \to a} \sin x = \sin x,\mathop {\lim }\limits_{x \to a} \cos x = \cos a\end{array}\)
مثال
حدود زير را محاسبه كنيد(
الف) \(\mathop {\lim }\limits_{x \to 0} \sqrt x \) ب)\({\mathop {\lim }\limits_{x \to 0} ^3}\sqrt x \)
ج) \(\mathop {\lim }\limits_{x \to 8} (\sqrt x { + ^3}\sqrt x - 2)\) د)\(\mathop {\lim }\limits_{x \to \frac{\pi }{4}} \sin x\)
هـ)\(\mathop {\lim }\limits_{x \to \frac{\pi }{2}} {\sin ^2}x\) و)\(\mathop {\lim }\limits_{x \to \frac{\pi }{4}} (2\sin x - 3\cos x)\)
ز)\(\mathop {\lim }\limits_{x \to - 2} {3^x}\) ح)\(\mathop {\lim }\limits_{x \to 4} {2^x}\)
الف)
\(\mathop {\lim }\limits_{x \to 0} \sqrt x = \sqrt 0 = 0\)
توجه: منظور از\(\mathop {\lim }\limits_{x \to 0} \sqrt x \)درواقع\(\mathop {\lim }\limits_{x \to {0^ + }} \sqrt x \) است . زيرا تابع\(y = \sqrt x \) تنها در همسايگي راست صفر تعريف شده است.
ب(
\({\mathop {\lim }\limits_{x \to 0} ^3}\sqrt x { = ^3}\sqrt 0 = 0\)
ج)
\(\mathop {\lim }\limits_{x \to 8} (\sqrt x { + ^3}\sqrt x - 2) = \mathop {\lim }\limits_{x \to 8} \sqrt {x + } {\mathop {\lim }\limits_{x \to 8} ^3}\sqrt x - \mathop {\lim }\limits_{x \to 8} 2 = \sqrt 8 { + ^3}\sqrt 8 - 2 = 2\sqrt 2 + 2 - 2 = 2\sqrt 2 \)
د)
\(\mathop {\lim }\limits_{x \to \frac{\pi }{4}} \sin x = \sin x\frac{\pi }{4} = \frac{{\sqrt 2 }}{2}\)
هـ)
\(\mathop {\lim }\limits_{x \to \frac{\pi }{2}} {\sin ^2}x = \mathop {\lim }\limits_{x \to \frac{\pi }{2}} (\sin x\sin x) = \mathop {\lim }\limits_{x \to \frac{\pi }{2}} \sin x \times \mathop {\lim }\limits_{x \to \frac{\pi }{2}} \sin x = 1 \times 1 = 1\)
و)
\(\begin{array}{l}\mathop {\lim }\limits_{x \to \frac{\pi }{4}} (2\sin x - 3\cos x) = \mathop {\lim }\limits_{x \to \frac{\pi }{4}} 2\sin x - \mathop {\lim }\limits_{x \to \frac{\pi }{4}} 3\cos x\\\\2\mathop {\lim }\limits_{x \to \frac{\pi }{4}} \sin x - 3\mathop {\lim }\limits_{x \to \frac{\pi }{4}} \cos x\\\\2\sin x\frac{\pi }{4} - 3\cos \frac{\pi }{4}\\\\\sqrt 2 - 3\frac{{\sqrt 2 }}{2} = - \frac{{\sqrt 2 }}{2}\end{array}\)
ز)
\(\mathop {\lim }\limits_{x \to - 2} {3^x} = {3^{ - 2}} = \frac{1}{9}\)
ح)
\(\mathop {\lim }\limits_{x \to 4} {2^x} = {2^4} = 16\)
اگر توابع f و g در a حد داشته باشند و\(\mathop {\lim }\limits_{x \to a} g(x) \ne 0\) آنگاه تابع\(\frac{f}{g}\) نيز در a حد دارد و f داريم:
\(\mathop {\lim }\limits_{x \to a} \frac{{f(x)}}{{g(x)}} = \frac{{\mathop {\lim }\limits_{x \to a} f(x)}}{{\mathop {\lim }\limits_{x \to a} g(x)}}\)
مثال
حدود زير را محاسبه كنيد
الف)\(\mathop {\lim }\limits_{x \to 2} \frac{{{x^2} + 4x + 3}}{{2x - 1}}\) ب)\(\mathop {\lim }\limits_{x \to \frac{\pi }{2}} \frac{{\cos x + \sin x}}{{2\sin x - \cos x}}\)
ج)\(\mathop {\lim }\limits_{x \to 4} \frac{{\sqrt x + 2x}}{{{x^2} - 3}}\) (د \(\mathop {\lim }\limits_{x \to 1} \frac{1}{{x - 1}}\)
ه)\(\mathop {\lim }\limits_{x \to \frac{\pi }{4}} \tan x\)
الف )
\(\mathop {\lim }\limits_{x \to 2} \frac{{{x^2} + 4x + 3}}{{2x - 1}} = \frac{{4 + 8 + 3}}{{4 - 1}} = \frac{{15}}{3} = 5\)
ب)
\(\mathop {\lim }\limits_{x \to \frac{\pi }{2}} \frac{{\cos x + \sin x}}{{2\sin x - \cos x}} = \frac{{0 + 1}}{{2 - 0}} = \frac{1}{2}\)
ج)
\(\mathop {\lim }\limits_{x \to 4} \frac{{\sqrt x + 2x}}{{{x^2} - 3}} = \frac{{2 + 4}}{{16 - 3}} = \frac{6}{{13}}\)
د)
\(\mathop {\lim }\limits_{x \to 1} (x - 1) = 0\)پس وقتي x به 1 نزديك ميشود، قدرمطلق مقادير \(\frac{1}{{x - 1}}\)به طور نامحدود افزايش مييابد و به عدد خاصي نزديك نميشوند. بنابراين \(\mathop {\lim }\limits_{x \to 1} \frac{1}{{x - 1}}\) وجود ندارد.
هـ)
\(\mathop {\lim }\limits_{x \to \frac{\pi }{4}} \tan x = \mathop {\lim }\limits_{x \to \frac{\pi }{4}} \frac{{\sin x}}{{\cos x}} = \frac{{\sin \frac{\pi }{4}}}{{\cos \frac{\pi }{4}}} = 1\)
توجه: اگر داريم \(a \ne kz + \frac{\pi }{2}\)، داريم \(\mathop {\lim }\limits_{x \to a} \tan x = \tan a\)، اگر \(a \ne k\pi \)داریم\(\mathop {\lim }\limits_{x \to a} \cot a = \cot a\) و اگر \(\mathop {\lim }\limits_{x \to a} f\left( x \right) = 0\) و \(\mathop {\lim }\limits_{x \to a} g\left( x \right) = 0\) و اگر در يك همسايگي a ،\(f(x) \ne 0\) و \(g(x) \ne 0\)، در اين صورت گوييم \(\mathop {\lim }\limits_{x \to a} \frac{{f\left( x \right)}}{{g(x)}}\) مبهم است. براي محاسبه ي حد تابع \(\frac{{f\left( x \right)}}{{g(x)}}\) درx=a در صورت وجود، با ساده كردن و حذف عامل هاي مشترك \(\frac{{f\left( x \right)}}{{g(x)}}\)، به كسري تبديل ميشود كه حد آن را به كمك قضايايي كه ذكر آن رفت ميتوان محاسبه نمود.
مثال
الف)\(\mathop {\lim }\limits_{x \to 0} \frac{{{{\cos }^2}x}}{{1 - \sin x}}\) ب)\(\mathop {\lim }\limits_{x \to 0} \frac{{1 - \cos x}}{{{{\sin }^2}x}}\)
ج )\(\mathop {\lim }\limits_{x \to \frac{\pi }{4}} \frac{{1 - \sin 2x}}{{\sin x - \cos x}}\) د)\(\mathop {\lim }\limits_{x \to \frac{\pi }{2}} \frac{{\tan (x - \frac{\pi }{4})}}{{2\sin (\frac{\pi }{4} - x)}}\)
ه)\(\mathop {\lim }\limits_{x \to 0} \frac{{{{\sin }^2}x - {{\sin }^3}x}}{{{{\cos }^2}x - {{\cos }^3}x}}\) و)\(\mathop {\lim }\limits_{x \to \frac{\pi }{4}} \frac{{1 - \tan x}}{{\sin x - \cos x}}\)
ز)\(\mathop {\lim }\limits_{x \to \frac{{2\pi }}{3}} \frac{{\sin x + \sin 2x + \sin 3x}}{{2\cos x + 1}}\)
الف)
\(\mathop {\lim }\limits_{x \to 0} \frac{{{{\cos }^2}x}}{{1 - \sin x}}\mathop {\lim }\limits_{x \to 0} \frac{{1 - {{\sin }^2}x}}{{1 - \sin x}} = \mathop {\lim }\limits_{x \to 0} \frac{{(1 - {{\sin }^2}x)(1 + {{\sin }^2}x)}}{{1 - \sin x}} = \mathop {\lim }\limits_{x \to 0} (1 + \sin x) = 1\)
ب)
\(\mathop {\lim }\limits_{x \to 0} \frac{{1 - \cos x}}{{{{\sin }^2}x}}\mathop {\lim }\limits_{x \to 0} \frac{{1 - \cos x}}{{1 - {{\cos }^2}x}} = \mathop {\lim }\limits_{x \to 0} \frac{{1 - \cos x}}{{(1 - \cos )(1 + \cos )}} = \mathop {\lim }\limits_{x \to 0} \frac{1}{{1 + \cos }} = \frac{1}{2}\)
ج)
\(\begin{array}{l}\mathop {\lim }\limits_{x \to \frac{\pi }{4}} \frac{{1 - \sin 2x}}{{\sin x - \cos x}}\mathop {\lim }\limits_{x \to \frac{\pi }{4}} \frac{{\sin 2x + {{\cos }^2}x - 2\sin x\cos x}}{{\sin x - \cos x}} = \mathop {\lim }\limits_{x \to \frac{\pi }{4}} \frac{{{{(\sin x - \cos x)}^2}}}{{\sin x - \cos x}}\\\\\mathop {\lim }\limits_{x \to \frac{\pi }{4}} (\sin x - \cos x) = \sin \frac{\pi }{4} - \cos \frac{\pi }{4} = 0\end{array}\)
د)
\(\mathop {\lim }\limits_{x \to \frac{\pi }{2}} \frac{{\tan (x - \frac{\pi }{4})}}{{2\sin (\frac{\pi }{4} - x)}}\mathop {\lim }\limits_{x \to \frac{\pi }{2}} \frac{{\frac{{\sin (x - \frac{\pi }{4})}}{{\cos (x - \frac{\pi }{4})}}}}{{ - 2\sin (x - \frac{\pi }{4})}} = \mathop {\lim }\limits_{x \to \frac{\pi }{2}} \frac{1}{{ - 2\sin (x - \frac{\pi }{4})}} = - \frac{1}{2}\)
ه)
\(\begin{array}{l}\mathop {\lim }\limits_{x \to 0} \frac{{{{\sin }^2}x - {{\sin }^3}x}}{{{{\cos }^2}x - {{\cos }^3}x}}\mathop {\lim }\limits_{x \to 0} \frac{{{{\sin }^2}x(1 - \sin x)}}{{{{\cos }^2}x(1 - \cos x)}} = \mathop {\lim }\limits_{x \to 0} \frac{{(1 - {{\cos }^2}x)(1 - \sin x)}}{{{{\cos }^2}x(1 - \cos x)}}\\\\ = \mathop {\lim }\limits_{x \to 0} \frac{{(1 - {{\cos }^2}x)(1 + \cos x)(1 - \sin x)}}{{{{\cos }^2}x}}\\\\ = \mathop {\lim }\limits_{x \to 0} \frac{{(1 + \cos x)(1 - \sin x)}}{{{{\cos }^2}x}} = 2\end{array}\)
و)
\(\begin{array}{l}\mathop {\lim }\limits_{x \to \frac{\pi }{4}} \frac{{1 - \tan x}}{{\sin x - \cos x}}\mathop {\lim }\limits_{x \to \frac{\pi }{4}} \frac{{1 - \frac{{\sin x}}{{\cos x}}}}{{\sin x - \cos x}} = \mathop {\lim }\limits_{x \to \frac{\pi }{4}} \frac{{1 - \frac{{\cos x - \sin x}}{{\cos x}}}}{{\sin x - \cos x}}\\\\\mathop {\lim }\limits_{x \to \frac{\pi }{4}} \frac{{1 - \frac{{(\sin x - \cos x)}}{{\cos x}}}}{{\sin x - \cos x}}\end{array}\)
ز)
\(\begin{array}{l}\mathop {\lim }\limits_{x \to \frac{{2\pi }}{3}} \frac{{\sin x + \sin 2x + \sin 3x}}{{2\cos x + 1}}\mathop {\lim }\limits_{x \to \frac{{2\pi }}{3}} \frac{{(\sin x + \sin 3x) + \sin 2x}}{{2\cos x + 1}}\\\\ = \mathop {\lim }\limits_{x \to \frac{{2\pi }}{3}} \frac{{2\sin x2x\cos x + \sin 2x}}{{2\cos x + 1}}\\\\ = \mathop {\lim }\limits_{x \to \frac{{2\pi }}{3}} \frac{{\sin x(2x\cos x + 1)}}{{2\cos x + 1}}\\\\\mathop {\lim }\limits_{x \to \frac{{2\pi }}{3}} \sin 2x = \sin \frac{{4\pi }}{3} = - \frac{{\sqrt 2 }}{3}\\\end{array}\)
اگر P(x) وQ(x) دو چند جمله اي باشند و در محاسبه ي حد\(\frac{{P(x)}}{{Q(x)}}\) در نقطه اي به طول a به حالت مبهم\(\frac{0}{0}\)  برخورد كنيم، اين به معناي آن است كه \(P(a) = 0\) و\(Q(a) = 0\) يعني صورت 0 و مخرج برx-a بخش پذيرند و ميتوان عامل ( عامل هاي )x-a را در صورت و مخرج ظاهر ساخته، از صورت و مخرج حذف كنيم. سپس حد را در صورت وجود محاسبه كنيم.
برخورد كنيم، اين به معناي آن است كه \(P(a) = 0\) و\(Q(a) = 0\) يعني صورت 0 و مخرج برx-a بخش پذيرند و ميتوان عامل ( عامل هاي )x-a را در صورت و مخرج ظاهر ساخته، از صورت و مخرج حذف كنيم. سپس حد را در صورت وجود محاسبه كنيم.
مثال
حدود زير را محاسبه كنيد؟
الف)\(\mathop {\lim }\limits_{x \to 3} \frac{{{x^2} - 9}}{{{x^3} - 27}}\) ب)\(\mathop {\lim }\limits_{x \to - 2} \frac{{{x^5} + 32}}{{{x^3} + 8}}\)
ج)\(\mathop {\lim }\limits_{x \to 1} \frac{{{x^3}2x - 3}}{{{x^4} - 1}}\)
الف)
\(\mathop {\lim }\limits_{x \to 3} \frac{{{x^2} - 9}}{{{x^3} - 27}}\mathop {\lim }\limits_{x \to 3} \frac{{(x - 3)(x + 3)}}{{(x - 3)({x^2} + 3x + 9)}} = \mathop {\lim }\limits_{x \to 3} \frac{{x + 3}}{{{x^2} + 3x + 9}} = \frac{6}{{27}} = \frac{2}{9}\)
با توجه به اينكه x=3صورت و مخرج را صفر ميكند. صورت و مخرج بر x-3 بخشپذير هستند.
ب)
\(\begin{array}{l}\mathop {\lim }\limits_{x \to - 2} \frac{{{x^5} + 32}}{{{x^3} + 8}}\mathop {\lim }\limits_{x \to - 2} \frac{{{x^5} + {2^5}}}{{{x^3} + {2^3}}}\\\\\mathop {\lim }\limits_{x \to - 2} \frac{{(x + 2)({x^4}\_2{x^3} + 4{x^2} - 8x + 16)}}{{(x + 2)({x^2} - 2x + 4)}}\\\\\mathop {\lim }\limits_{x \to - 2} \frac{{{x^4}\_2{x^3} + 4{x^2} - 8x + 16)}}{{{x^2} - 2x + 4}} = \frac{{80}}{{12}} = \frac{{20}}{3}\end{array}\)
ج)
\(\mathop {\lim }\limits_{x \to 1} \frac{{{x^3}2x - 3}}{{{x^4} - 1}}\mathop {\lim }\limits_{x \to 1} \frac{{(x - 1)({x^2} + x + 3)}}{{(x - 1)(x + 1)({x^2} + 1)}} = \mathop {\lim }\limits_{x \to 1} \frac{{{x^2} + x + 3}}{{(x + 1)({x^2} + 1)}} = \frac{5}{4}\)
مثال
در تساوي زير مقادير a و b را به دست آوريد؟
\(\mathop {\lim }\limits_{x \to 1} \frac{{{x^2} - 6x + 5}}{{{x^2} + ax + b}} = 2\)
عدد يك، صورت را صفر ميكند. با توجه به اينكه جواب حد عدد 2 است. لازم است  x=1ريشه ي چندجمله اي مخرج نيز باشد. يعني \(1 + a + b = 0\)بنابراين صورت و مخرج هر دو عامل x-1دارند. پس داريم:
x=1ريشه ي چندجمله اي مخرج نيز باشد. يعني \(1 + a + b = 0\)بنابراين صورت و مخرج هر دو عامل x-1دارند. پس داريم:
\(\begin{array}{l}\mathop {\lim }\limits_{x \to 1} \frac{{{x^2} - 6x + 5}}{{{x^2} + ax + b}} = \mathop {\lim }\limits_{x \to 1} \frac{{{x^2} - 6x + 5}}{{{x^2} + ax + ( - a - 1)}}\\\\\mathop {\lim }\limits_{x \to 1} \frac{{(x - 1)(x - 5)}}{{(x - 1)(x + a + 1)}}\\\\ = \frac{{ - 4}}{{2 + a}}\\\\ \Rightarrow \frac{{ - 4}}{{2 + a}} = 2 \Rightarrow 4 + 2a = - 4 \Rightarrow a = - 4\\\\1 + a + b = 0b = 3\end{array}\)
مثال
اگر\(\mathop {\lim }\limits_{x \to 2} \frac{{{x^n} - {2^n}}}{{x - 2}} = 80\) ، مقدار n را به دست آوريد؟
\(\begin{array}{l}\mathop {\lim }\limits_{x \to 2} \frac{{{x^n} - {2^n}}}{{x - 2}}\mathop {\lim }\limits_{x \to 2} \frac{{(x - 2)({x^{n - 1}} + 2{x^{n - 2}} + 4{x^{n - 3}} + ... + {2^{n - 1}})}}{{x - 2}}\\\\ = \mathop {\lim }\limits_{x \to 2} ({x^{n - 1}} + 2{x^{n - 2}} + 4{x^{n - 3}} + ... + {2^{n - 1}})\\\\ = {2^{n - 1}} + {2^{n - 1}} + {2^{n - 1}} + ... + {2^{n - 1}}\\\\ = n \times {2^{n - 1}}\\\\ = 80\\\\ \Rightarrow n = 5\end{array}\)
اگر P(x) يا Q(x) عبارت هاي راديكالي باشند، براي محاسبه ي \(\mathop {\lim }\limits_{x \to a} \frac{{P(x)}}{{Q(x)}}\)در حالت مبهم \((\frac{0}{0})\) لازم است با گويا كردن و يا روش هاي ديگر عامل صفر كننده را ظاهر ساخته و پس از 0 حذف آن، حد را در صورت وجود محاسبه ميكنيم.
مثال
حدود زير را محاسبه كنيد؟
الف)\(\mathop {\lim }\limits_{x \to 1} \frac{{\sqrt {x + 3} - 2}}{{x - 1}}\) ب)\(\mathop {\lim }\limits_{x \to 1} \frac{{1 - \sqrt x }}{{{x^2} + x - 2}}\)
ج)\(\mathop {\lim }\limits_{x \to 1} \frac{{\sqrt {x + 2} - \sqrt 3 }}{{\sqrt {x + 3} - 2}}\) د)\(\mathop {\lim }\limits_{x \to 5} \frac{{^3\sqrt {x + 3} - 2}}{{{x^2} - 25}}\)
ه)\(\mathop {\lim }\limits_{x \to 27} \frac{{^3\sqrt {x + 3} }}{{\sqrt {x + 3} - 5}}\) و )\(\mathop {\lim }\limits_{x \to 16} \frac{{^4\sqrt {x - 2} }}{{\sqrt {x - 4} }}\)
الف)
\(\begin{array}{l}\mathop {\lim }\limits_{x \to 1} \frac{{\sqrt {x + 3} - 2}}{{x - 1}}\mathop {\lim }\limits_{x \to 1} \frac{{\sqrt {x + 3} - 2}}{{x - 1}} \times \mathop {\lim }\limits_{x \to 1} \frac{{\sqrt {x + 3} - 2}}{{\sqrt {x + 3} - 2}}\\\\ = \mathop {\lim }\limits_{x \to 1} \frac{{x - 1}}{{\left( {x - 1} \right)\left( {\sqrt {x + 3} + 2} \right)}}\\\\ = \mathop {\lim }\limits_{x \to 1} \frac{1}{{\sqrt {x + 3} + 2}} = \frac{1}{4}\end{array}\)
ب)
\(\begin{array}{l}\mathop {\lim }\limits_{x \to 1} \frac{{1 - \sqrt x }}{{{x^2} + x - 2}}\mathop {\lim }\limits_{x \to 1} \frac{{1 - \sqrt x }}{{{x^2} + x - 2}} \times \mathop {\lim }\limits_{x \to 1} \frac{{1 + \sqrt x }}{{1 + \sqrt x }}\\\\\mathop {\lim }\limits_{x \to 1} \frac{{1 - x}}{{(x - 1)(x + 2)(1 + \sqrt x )}}\\\\\mathop {\lim }\limits_{x \to 1} \frac{{ - 1}}{{(x + 2)(1 + \sqrt x )}} = \frac{{ - 1}}{6}\end{array}\)
ج)
\(\begin{array}{l}\mathop {\lim }\limits_{x \to 1} \frac{{\sqrt {x + 2} - \sqrt 3 }}{{\sqrt {x + 3} - 2}}\mathop {\lim }\limits_{x \to 1} \frac{{\sqrt {x + 2} - \sqrt 3 }}{{\sqrt {x + 3} - 2}} \times \mathop {\lim }\limits_{x \to 1} \frac{{\sqrt {x + 2} + \sqrt 3 }}{{\sqrt {x + 2} + \sqrt 3 }} \times \mathop {\lim }\limits_{x \to 1} \frac{{\sqrt {x + 2} + 2}}{{\sqrt {x + 3} + 2}}\\\\\mathop {\lim }\limits_{x \to 1} \frac{{(x - 1) - (\sqrt {x + 3} - 2)}}{{(x - 1) - (\sqrt {x + 3} - 2)}}\\\\\mathop {\lim }\limits_{x \to 1} \frac{{\sqrt {x + 3} + 2}}{{\sqrt {x + 2} + \sqrt 3 )}} = \frac{4}{{2\sqrt 3 }} = \frac{2}{{\sqrt 3 }}\end{array}\)
د)
\(\begin{array}{l}\mathop {\lim }\limits_{x \to 5} \frac{{^3\sqrt {x + 3} - 2}}{{{x^2} - 25}}\mathop {\lim }\limits_{x \to 5} \frac{{^3\sqrt {x + 3} - 2}}{{{x^2} - 25}} \times \frac{{{(^3}\sqrt {x + 3} ) + {2^3}\sqrt {x + 3} + 4}}{{{(^3}\sqrt {x + 3} ) + {2^3}\sqrt {x + 3} + 4}}\\\mathop {\lim }\limits_{x \to 5} \frac{{x - 5}}{{(x - 5)(x + 5)({{{(^3}\sqrt {x + 3} )}^2} + {2^3}\sqrt x + 4}} = \frac{1}{{10 \times 12}} = \frac{1}{{120}}\end{array}\)
ه)
\(\begin{array}{l}\mathop {\lim }\limits_{x \to 27} \frac{{^3\sqrt {x\_3} }}{{\sqrt {x + 3} - 5}}\mathop {\lim }\limits_{x \to 27} \frac{{^3\sqrt {x - 3} }}{{\sqrt {x + 2} - 5}} \times \frac{{{{{(^3}\sqrt x )}^2} + {3^3}\sqrt x + 9}}{{{(^3}\sqrt x ) + {3^3}\sqrt x + 9}} \times \frac{{\sqrt {x - 2} + 5}}{{\sqrt {x - 2} + 5}}\\\\\mathop {\lim }\limits_{x \to 27} \frac{{(x - 27)(\sqrt {x - 2} + 5)}}{{(x - 27)({(^3}\sqrt {x{)^2}} + {3^3}\sqrt x + 9}} = \frac{{10}}{{27}}\end{array}\)
و)با توجه به اتحاد \({a^4} - {b^4} = (a - b)({a^3} + {a^2}b + a{b^2} + {b^3})\)داریم:
\(\begin{array}{l}\mathop {\lim }\limits_{x \to 16} \frac{{^4\sqrt {x - 2} }}{{\sqrt {x - 4} }}\mathop {\lim }\limits_{x \to 16} \frac{{^4\sqrt {x - 2} }}{{\sqrt {x - 4} }} \times \frac{{{(^4}{{\sqrt {x)} }^3} + 2{(^4}{{\sqrt {x)} }^2} + {4^4}\sqrt {x + 8} }}{{{(^4}{{\sqrt {x)} }^3} + 2{(^4}{{\sqrt {x)} }^2} + {3^3}\sqrt x + 9}} \times \frac{{\sqrt {x + 4} }}{{\sqrt {x + 4} }}\\\\ = \mathop {\lim }\limits_{x \to 16} \frac{{(x - 16)(\sqrt x + 4)}}{{(x - 16)({(^4}{{\sqrt {x)} }^3} + 2{(^4}{{\sqrt {x)} }^{^2}} + {4^4}\sqrt x + 8}} = \frac{8}{{32}} = \frac{1}{4}\end{array}\)
هرگاه x زاويه اي بر حسب راديان باشد. آنگاه داريم:
\(\begin{array}{l}1)\mathop {\lim }\limits_{x \to 0} \frac{{\sin x}}{x} = 1\\\\2)\mathop {\lim }\limits_{x \to 0} \frac{x}{{\sin x}} = 1\end{array}\)
مثال
ثابت كنيد:
\(\mathop {\lim }\limits_{x \to \infty } \frac{{\tan x}}{x} = 1\)
\(\mathop {\lim }\limits_{x \to 0} \frac{{\tan x}}{x} = \mathop {\lim }\limits_{x \to 0} \frac{{\frac{{\sin x}}{{\cos x}}}}{x} = \mathop {\lim }\limits_{x \to 0} \frac{{\sin x}}{x} \times \frac{1}{{\cos x}} = \mathop {\lim }\limits_{x \to 0} \frac{{\sin x}}{x} \times \mathop {\lim }\limits_{x \to 0} \frac{1}{{\cos x}} = 1 \times 1 = 1\)
توجه : به طريق مشابه ميتوان ثابت كرد
\(\mathop {\lim }\limits_{x \to 0} \frac{x}{{\tan x}} = 1\)
مثال
حدود زير را محاسبه كنيد.
الف)\(\mathop {\lim }\limits_{x \to 0} \frac{{\sin 3x}}{x}\) ب)\(\mathop {\lim }\limits_{x \to 0} \frac{{\sin x + \sin 3x}}{{5x}}\)
ج)\(\mathop {\lim }\limits_{x \to 0} \frac{{x\sin 2x}}{{\tan {x^2}}}\) د)\(\mathop {\lim }\limits_{x \to 0} \frac{{1 - \cos 2x}}{{3{x^2}}}\)
ه)\(\mathop {\lim }\limits_{x \to 0} \frac{{1 - \cos 7x}}{{1 - \cos 4x}}\) و) \(\mathop {\lim }\limits_{x \to 0} \frac{{\tan x - \sin x}}{{4{x^3}}}\)
\(\mathop {\lim }\limits_{x \to 0} \frac{{\tan x - \sin x}}{{4{x^3}}}\)
ز)\(\mathop {\lim }\limits_{x \to 0} \frac{{\cos x - \cos 2x}}{{\cos 2x - \cos 3x}}\) ح)\(\mathop {\lim }\limits_{x \to 2} \frac{{\sin (x - 2)}}{{\tan ({x^2} - 3x + 2)}}\)
ط)\(\mathop {\lim }\limits_{x \to \frac{\pi }{2}} \frac{{\cos x}}{{2x - \pi }}\)
الف)
\(\mathop {\lim }\limits_{x \to 0} \frac{{\sin 3x}}{x}\mathop {\lim }\limits_{x \to 0} \frac{{\sin 3x}}{{3x}} \times 3 = 1 \times 3 = 3\)
ب)
\(\mathop {\lim }\limits_{x \to 0} \frac{{\sin x + \sin 3x}}{{5x}}\mathop {\lim }\limits_{x \to 0} \frac{{\frac{{\sin x}}{x} + \frac{{\sin 3x}}{x}}}{{\frac{{5x}}{x}}} = \frac{{1 + 3}}{5} = \frac{4}{5}\)
ج)
\(\mathop {\lim }\limits_{x \to 0} \frac{{x\sin 2x}}{{\tan {x^2}}}\mathop {\lim }\limits_{x \to 0} \frac{{x \times \frac{{\sin 2}}{{2x}} \times 2x}}{{\frac{{\tan {x^2}}}{{{x^2}}} \times {x^2}}} = 2\)
د)
\(\mathop {\lim }\limits_{x \to 0} \frac{{1 - \cos 2x}}{{3{x^2}}}\mathop {\lim }\limits_{x \to 0} \frac{{2{{\sin }^2}x}}{{3{x^2}}} = \mathop {\frac{2}{3}\lim }\limits_{x \to 0} {(\frac{{\sin x}}{x})^2} = \frac{2}{3} \times 1 = \frac{2}{3}\)
ه)
\(\mathop {\lim }\limits_{x \to 0} \frac{{1 - \cos 7x}}{{1 - \cos 4x}}\mathop {\lim }\limits_{x \to 0} \frac{{2{{\sin }^2}(\frac{{7x}}{2})}}{{2{{\sin }^2}x}} = \mathop {\lim }\limits_{x \to 0} \frac{{(\frac{{2{{\sin }^2}\frac{{7x}}{2}}}{{\frac{{7x}}{2}}}) \times {{(\frac{{7x}}{2})}^2}}}{{(\frac{{2{{\sin }^2}x}}{{2x}}) \times {{(2x)}^2}}} = \frac{{1 \times \frac{{49}}{4}}}{{1 \times 4}} = \frac{{49}}{{16}}\)
و)
\(\begin{array}{l}\mathop {\lim }\limits_{x \to 0} \frac{{\tan x - \sin x}}{{4{x^3}}}\mathop {\lim }\limits_{x \to 0} \frac{{\frac{{\sin x}}{{\cos x}} - \sin x}}{{4{x^3}}}\\\\\mathop {\lim }\limits_{x \to 0} \frac{{\sin x - \cos x\sin x}}{{4{x^3}\cos x}}\\\\\mathop {\lim }\limits_{x \to 0} \frac{{\sin x(1 - \cos x)}}{{4{x^3}\cos x}}\\\\\mathop {\lim }\limits_{x \to 0} \frac{{\sin x(2{{\sin }^2}x\frac{x}{2})}}{{4{x^3}\cos x}}\\\\\mathop {\frac{1}{2}\lim }\limits_{x \to 0} \frac{{\frac{{\sin x}}{x} \times x \times {{(\frac{{\sin \frac{x}{2}}}{{\frac{x}{2}}})}^2} \times {{\left( {\frac{x}{2}} \right)}^2}}}{{{x^3}\cos x}} = \frac{1}{2} \times \frac{{1 \times \frac{1}{4}}}{1} = \frac{1}{8}\end{array}\)
ز)
\(\begin{array}{l}\mathop {\lim }\limits_{x \to 0} \frac{{\cos x - \cos 2x}}{{\cos 2x - \cos 3x}}\mathop {\lim }\limits_{x \to 0} \frac{{ - 2\frac{{x - 2x}}{x}\sin \frac{{x + 2x}}{x}}}{{ - 2\frac{{x - 3x}}{2}\sin \frac{{x + 3x}}{2}}}\\\\ = \mathop {\lim }\limits_{x \to 0} \frac{{\sin \frac{x}{2}\sin \frac{{3x}}{2}}}{{\sin \frac{x}{2}\sin \frac{{5x}}{2}}}\\\\ = \mathop {\lim }\limits_{x \to 0} \frac{{\frac{{\sin \frac{{3x}}{2}}}{{\frac{{3x}}{2}}} \times \frac{{3x}}{2}}}{{\frac{{\sin \frac{{5x}}{2}}}{{\frac{{5x}}{2}}} \times \frac{{5x}}{2}}} = \frac{3}{5}\end{array}\)
ح)
\(\mathop {\lim }\limits_{x \to 2} \frac{{\sin (x - 2)}}{{\tan ({x^2} - 3x + 2)}}\mathop {\lim }\limits_{x \to 2} \frac{{\frac{{\sin (x - 2)}}{{(x - 2)}} \times (x - 2)}}{{\frac{{\tan ({x^2} - 3x + 2)}}{{({x^2} - 3x + 2)}} \times (x - 2)(x - 1)}} = 1\)
ط)
\(\mathop {\lim }\limits_{x \to \frac{\pi }{2}} \frac{{\cos x}}{{2x - \pi }}\mathop {\lim }\limits_{x \to \frac{\pi }{2}} \frac{{\sin (\frac{\pi }{2} - x)}}{{ - 2(\frac{\pi }{2} - x)}} = - \frac{1}{2}\sin \mathop {\lim }\limits_{x \to \frac{\pi }{2}} \frac{{\sin (\frac{\pi }{2} - x)}}{{(\frac{\pi }{2} - x)}} = - \frac{1}{2} \times 1 = - \frac{1}{2}\)
براي به دست آوردن \(\mathop {\lim }\limits_{x \to a} \left[ {f(x)} \right]\)ابتدا حاصل\(\mathop {\lim }\limits_{x \to a} f(x)\) را محاسبه ميكنيم، فرض ميكنيم\(\mathop {\lim }\limits_{x \to a} f(x) = l\) اگر عددي غير صحيح باشد آنگاه \(\mathop {\lim }\limits_{x \to a} \left[ {f(x)} \right] = \left[ l \right]\)و اگر عددي صحيح باشد، در صورت لزوم حد چپ و راست تابع را در x=a به دست مي آوريم.
عددي غير صحيح باشد آنگاه \(\mathop {\lim }\limits_{x \to a} \left[ {f(x)} \right] = \left[ l \right]\)و اگر عددي صحيح باشد، در صورت لزوم حد چپ و راست تابع را در x=a به دست مي آوريم.
اگر تابع f ميشامل جزء صحيح باشد ابتدا جزء صحيح را محاسبه كنيم و سپس حاصل حد را در صورت وجود مي یابيم .
مثال
حدود زير را محاسبه كنيد.
الف) \(\mathop {\lim }\limits_{x \to \frac{2}{2}} \left[ x \right]\) ب)\(\mathop {\lim }\limits_{x \to 2} \left[ x \right]\)
ج)\(\mathop {\lim }\limits_{x \to 0} \left[ {{x^2}} \right]\) د)\(\mathop {\lim }\limits_{x \to - 2} \left[ {3x - 1} \right]\)
ه)\(\mathop {\lim }\limits_{x \to \frac{3}{2}} \left[ {\sin x} \right]\) و)\(\mathop {\lim }\limits_{x \to 2} \left[ {\frac{{2x + 4}}{{x + 1}}} \right]\)
ز)\(\mathop {\lim }\limits_{x \to 1} \left[ {\frac{{2x + 4}}{{x + 1}}} \right]\) ح)\(\mathop {\lim }\limits_{x \to \frac{{3\pi }}{4}} \left[ {\sqrt 2 \cos x} \right]\)
ط) \(\mathop {\lim }\limits_{x \to 0} \left[ {\frac{{\sin x}}{x}} \right]\) ی)\(\mathop {\lim }\limits_{x \to 1} \left[ {\frac{{\left[ x \right] + 3 + x}}{{\left[ {x + \frac{1}{2}} \right] + \left[ { - 2x} \right] + 4 - x}}} \right]\)
الف)
\(\mathop {\lim }\limits_{x \to 0} \left[ {\sin x} \right]\)\(\mathop {\lim }\limits_{x \to \frac{3}{2}} x = \frac{3}{2} \Rightarrow \mathop {\lim }\limits_{x \to \frac{3}{2}} \left[ x \right] = \left[ {\frac{3}{2}} \right] = 1\)
ب)
\(\left\{ \begin{array}{l}x \to {2^ - } \Rightarrow 1 < x < 2 \Rightarrow \mathop {\lim }\limits_{x \to {2^ - }} \left[ x \right] = 1\\\\x \to {2^ + } \Rightarrow 2 < x < 3 \Rightarrow \mathop {\lim }\limits_{x \to {2^ + }} \left[ x \right] = 2\end{array} \right.\)
پس تابع \(\left[ x \right]\) در x=2حد ندارد.
ج)
\(x \to 0 \Rightarrow 0 < {x^2} < 1 \Rightarrow \mathop {\lim }\limits_{x \to 0} \left[ {{x^2}} \right] = 0\)
د)
\(\left\{ \begin{array}{l}x \to - {2^ - } \Rightarrow 3x \to - {6^ - } \Rightarrow 3x - 1 \to - {7^ - } \Rightarrow \mathop {\lim }\limits_{x \to - {2^ - }} \left[ {3x - 1} \right] = - 8\\\\x \to - {2^ + } \Rightarrow 3x \to - {6^ + } \Rightarrow 3x - 1 \to - {7^ + } \Rightarrow \mathop {\lim }\limits_{x \to - {2^ + }} \left[ {3x - 1} \right] = - 7\end{array} \right.\)
ه)
\(\left\{ \begin{array}{l}x \to {0^ - } \Rightarrow - 1 < \sin x < 0 \Rightarrow \mathop {\lim }\limits_{x \to {0^ - }} \left[ {\sin x} \right] = - 1\\\\x \to {0^ + } \Rightarrow 0 < \sin x < 1 \Rightarrow \mathop {\lim }\limits_{x \to {0^ + }} \left[ {\sin x} \right] = 0\end{array} \right.\)
پس تابع\(\left[ {\sin x} \right]\) در x=0حد ندارد
و)
\(\mathop {\lim }\limits_{x \to 2} \frac{{2x + 4}}{{x + 1}} = \frac{8}{3} \Rightarrow \mathop {\lim }\limits_{x \to 2} \frac{{2x + 4}}{{x + 1}} = \left[ {\frac{8}{3}} \right] = 2\)
ز)
\(\begin{array}{l}\frac{{2x + 4}}{{x + 1}} = \frac{{2x + 2 + 2}}{{x + 1}} = 2 + \frac{2}{{x + 1}}\\\\\\x > 1 \Rightarrow x + 1 > 2 \Rightarrow 0 < \frac{1}{{x + 1}} < \frac{1}{2} \Rightarrow 0 < \frac{2}{{x + 1}} < 1 \Rightarrow \mathop {\lim }\limits_{x \to {1^ + }} \left[ {\frac{2}{{x + 1}}} \right] = 0\\\\0 < x < 1 \Rightarrow 1 < x + 1 < 2 \Rightarrow \frac{1}{2} < \frac{1}{{x + 1}} < 1 \Rightarrow 1 < \frac{2}{{x + 1}} < 2 \Rightarrow \mathop {\lim }\limits_{x \to {1^ - }} \left[ {\frac{2}{{x + 1}}} \right] = 1\end{array}\)
بنابراین
\(\begin{array}{l}\mathop {\lim }\limits_{x \to {1^ + }} \left[ {\frac{{2x + 4}}{{x + 1}}} \right] = \mathop {\lim }\limits_{x \to {1^ + }} \left[ {2 + \frac{2}{{x + 1}}} \right]\\\\\mathop {\lim (2 + }\limits_{x \to {1^ + }} \left[ {\frac{2}{{x + 1}}} \right])\\\\2 + \mathop {\lim }\limits_{x \to {1^\_}} \left[ {\frac{{2x + 4}}{{x + 1}}} \right] = \mathop {\lim }\limits_{x \to {1^ - }} \left[ {2 + \frac{2}{{x + 1}}} \right])\\\\ = \mathop {\lim }\limits_{x \to {1^ - }} \left[ {\frac{{2x + 4}}{{x + 1}}} \right] = \mathop {\lim }\limits_{x \to {1^ - }} \left[ {2 + \frac{2}{{x + 1}}} \right]\\\\\mathop {\lim }\limits_{x \to {1^ - }} (2 + \left[ {\frac{2}{{x + 1}}} \right])\\\\2 + \mathop {\lim }\limits_{x \to {1^ - }} \left[ {\frac{2}{{x + 1}}} \right] = 3\end{array}\)
لذا تابع \(\left[ {\sqrt 2 \cos x} \right]\)در \(x = \frac{{3\pi }}{4}\)حد ندارد
ح)
\(\left\{ \begin{array}{l}x = \frac{{3{\pi ^ - }}}{4} \Rightarrow - \frac{{\sqrt 2 }}{2} < \cos x < 0 \Rightarrow - 1 < \sqrt 2 \cos x < 0 \Rightarrow \mathop {\lim }\limits_{x \to \frac{{3{\pi ^ - }}}{4}} \left[ {\sqrt 2 \cos x} \right] = - 1\\\\x = \frac{{3{\pi ^ + }}}{4} \Rightarrow - 1 < \cos x < - \frac{{\sqrt 2 }}{2} \Rightarrow - \sqrt 2 < \sqrt 2 \cos x < - 1 \Rightarrow \mathop {\lim }\limits_{x \to \frac{{3{\pi ^ + }}}{4}} \left[ {\sqrt 2 \cos x} \right] = - 2\end{array} \right.\)
لذا تابع \(\left[ {\sqrt 2 \cos x} \right]\)در \(x = \frac{{3\pi }}{4}\)حد ندارد
ط)وقتی\(x > 1\)میدانیم\(\sin x < x\)پس\(0 < \mathop {\lim }\limits_{x \to {0^ + }} \left[ {\frac{{\sin x}}{x}} \right] < 1\)بنابراین \(\mathop {\lim }\limits_{x \to {0^ + }} \left[ {\frac{{\sin x}}{x}} \right] = 0\)همچنین با توجه به زوج بودن تابع \(\frac{{\sin x}}{x}\)داریم \(\mathop {\lim }\limits_{x \to {0^ - }} \left[ {\frac{{\sin x}}{x}} \right] = 0\)و لذا\(\mathop {\lim }\limits_{x \to 0} \left[ {\frac{{\sin x}}{x}} \right] = 0\)
ی)اگر \(x \to {1^ - }\)داریم
\(\left\{ \begin{array}{l}\left[ x \right] = 0\\\\1 < x + \frac{1}{2} < \frac{3}{2} \Rightarrow \left[ {x + \frac{1}{2}} \right] = 1\\\\ - 2 < - 2x < - 1 \Rightarrow \left[ { - 2x} \right] = - 2\end{array} \right.\)
پس حد چپ به صورت زیر محاسبه می شود
\(\begin{array}{l}\mathop {\lim }\limits_{x \to {1^ - }} \frac{{\left[ x \right] + 3 + x}}{{\left[ {x + \frac{1}{2}} \right] + \left[ { - 2x} \right] + 4 - x}} = \mathop {\lim }\limits_{x \to {1^ - }} \frac{{0 + 3 + x}}{{1 - 2 + 4 - x}} = \frac{4}{2} = 2\\\end{array}\)
و اگر\(x \to {1^ + }\) داریم :
\(\left\{ \begin{array}{l}\left[ x \right] = 1\\\\\frac{3}{2} < x + \frac{1}{2} < 2 \Rightarrow \left[ {x + \frac{1}{2}} \right] = 1\\\\ - 3 < - 2x < - 2 \Rightarrow \left[ { - 2x} \right] = - 3\end{array} \right.\)
پس حد راست به صورت زیر محاسبه میشود
 \(\mathop {\lim }\limits_{x \to {1^ + }} \frac{{\left[ x \right] + 3 + x}}{{\left[ {x + \frac{1}{2}} \right] + \left[ { - 2x} \right] + 4 - x}} = \mathop {\lim }\limits_{x \to {1^ + }} \frac{{1 + 3 + x}}{{1 - 3 + 4 - x}} = \frac{5}{1} = 5\)
\(\mathop {\lim }\limits_{x \to {1^ + }} \frac{{\left[ x \right] + 3 + x}}{{\left[ {x + \frac{1}{2}} \right] + \left[ { - 2x} \right] + 4 - x}} = \mathop {\lim }\limits_{x \to {1^ + }} \frac{{1 + 3 + x}}{{1 - 3 + 4 - x}} = \frac{5}{1} = 5\)
لذا تابع در x=1حد ندارد
اگر \(\mathop {\lim }\limits_{x \to a} f(x) = l\)باشد آنگاه
\(\mathop {\lim }\limits_{x \to a} \left| {f(x)} \right| = \left| l \right|\)
اگر تابع f شامل قدرمطلق باشد، براي محاسبه ي \(\mathop {\lim }\limits_{x \to a} f(x)\)در صورت لزوم حدود چپ وراست را محاسبه ميكنيم.
مثال
حدود زير را محاسبه كنيد؟
الف)\(\mathop {\lim }\limits_{x \to 2} \left| {x - 2} \right|\) ب)\(\mathop {\lim }\limits_{x \to 1} \left| {x - 2} \right|\)
ج)\(\mathop {\lim }\limits_{x \to 2} \frac{{\left| {x - 2} \right|}}{{x - 2}}\) د)\(\mathop {\lim }\limits_{x \to 1} \frac{{\left| {x - 2} \right| - 3}}{{\left| {x - 2} \right| + 4}}\)
هـ)\(\mathop {\lim }\limits_{x \to \frac{\pi }{2}} \frac{{\left| {\cos x} \right|}}{{x - \frac{\pi }{2}}}\)
الف)
\(\mathop {\lim }\limits_{x \to 2} \left| {x - 2} \right| = \left| {2 - 2} \right| = 0\)
ب)
\(\mathop {\lim }\limits_{x \to 1} \left| {x - 2} \right| = \left| {1 - 2} \right| = 1\)
ج)
تابع در اینجا حد ندارد \(\mathop {\lim }\limits_{x \to 2} \frac{{\left| {x - 2} \right|}}{{x - 2}}\left\{ \begin{array}{l}\mathop {\lim }\limits_{x \to {2^ - }} \frac{{ - (x - 2)}}{{x - 2}} = - 1\\\\\mathop {\lim }\limits_{x \to {2^ + }} \frac{{ - x - 2}}{{x - 2}} = 1\end{array} \right. \Rightarrow x = 2\)
د)
\(\mathop {\lim }\limits_{x \to 1} \frac{{\left| {x - 2} \right| - 3}}{{\left| {x - 2} \right| + 4}} = \mathop {\lim }\limits_{x \to 1} \frac{{\left| {1 - 2} \right| - 3}}{{\left| {1 - 3} \right| + 4}} = \frac{{ - 3}}{6} = - \frac{1}{2}\)
ه)
تابع در \(x = \frac{\pi }{2}\)حد ندارد\(\mathop {\lim }\limits_{x \to \frac{\pi }{2}} \frac{{\left| {\cos x} \right|}}{{x - \frac{\pi }{2}}}\left\{ \begin{array}{l}\mathop {\lim }\limits_{x \to {{\frac{\pi }{2}}^ - }} \frac{{\cos x}}{{x - \frac{\pi }{2}}} = \mathop {\lim }\limits_{x \to {{\frac{\pi }{2}}^ - }} \frac{{\sin (\frac{\pi }{2} - x)}}{{ - (\frac{\pi }{2} - x)}} = - 1\\\\\mathop {\lim }\limits_{x \to {{\frac{\pi }{2}}^ + }} \frac{{ - \cos x}}{{x - \frac{\pi }{2}}} = \mathop {\lim }\limits_{x \to {{\frac{\pi }{2}}^ + }} \frac{{ - \sin (\frac{\pi }{2} - x)}}{{ - (\frac{\pi }{2} - x)}} = 1\\\end{array} \right.\)
قضيه فشردگي: اگر به ازاي هر x از يك همسايگي a داشته باشيم\(h(x) \le f(x) \le g(x)\) و \(\mathop {\lim }\limits_{x \to a} g(x) = \mathop {\lim }\limits_{x \to a} h(x) = L\)آنگاه.\(\mathop {\lim }\limits_{x \to a} f(x) = L\)
مثال
\(\mathop {\lim }\limits_{x \to 1} \left| {x - 1} \right|\cos \frac{1}{{x - 1}}\)را محاسبه كنيد.
\(\begin{array}{l} - 1 \le \cos \frac{1}{{x - 1}} \le 1 \Rightarrow - \left| {x - 1} \right| \le \left| {x - 1} \right|cos\frac{1}{{x - 1}} \le \left| {x - 1} \right|\\\\\\\mathop {\lim - }\limits_{x \to 1} \left| {x - 1} \right| = \mathop {\lim }\limits_{x \to 1} \left| {x - 1} \right| = 0 \Rightarrow \mathop {\lim }\limits_{x \to 1} \left| {x - 1} \right|\cos \frac{1}{{x - 1}} = 0\end{array}\)
مثال
اگر به ازاي هر \(x \in ( - 1,1)\)، داشته باشيم\(\left| {f(x) - 2} \right| \le {(x - 1)^2}\): حاصل \(\mathop {\lim }\limits_{x \to 1} \frac{1}{{f(x)}}\)را محاسبه كنيد.
\(\begin{array}{l}\left| {f(x) - 2} \right| \le {(x - 1)^2} \Rightarrow - {(x - 1)^2} \le f(x) - 2 \le {(x - 1)^2} \Rightarrow \\\\2 - {(x - 1)^2} \le f(x) \le 2 + {(x - 1)^2}\\\\\mathop {\lim }\limits_{x \to 1} (2 + {(x - 1)^2}) = \mathop {\lim }\limits_{x \to 1} (2 - {(x - 1)^2}) = \mathop {\lim }\limits_{x \to 1} f(x) = 2\mathop {\lim }\limits_{x \to 1} \frac{1}{{f(x)}} = \frac{1}{2}\end{array}\)
تهیه کننده: حامد دلیجه
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه یازدهم- آزمون آنلاین تمامی دروس پایه یازدهم
- گام به گام تمامی دروس پایه یازدهم
- ویدئو های آموزشی تمامی دروس پایه یازدهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه یازدهم
- فلش کارت های آماده دروس پایه یازدهم
- گنجینه ای جامع از انشاء های آماده پایه یازدهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه یازدهم
پیوستگی
پیوستگی
اگر \(a \in {D_f}\)و\(\mathop {\lim }\limits_{x \to a} f(x) = f(a)\)گوییم تابع در x=aپیوسته است.
مثال
نمودار تابعF به صورت زیر رسم شده است باتوجه به نمودار پیوستگی تابعF را در نقاط مشخص شده بررسی کنید.
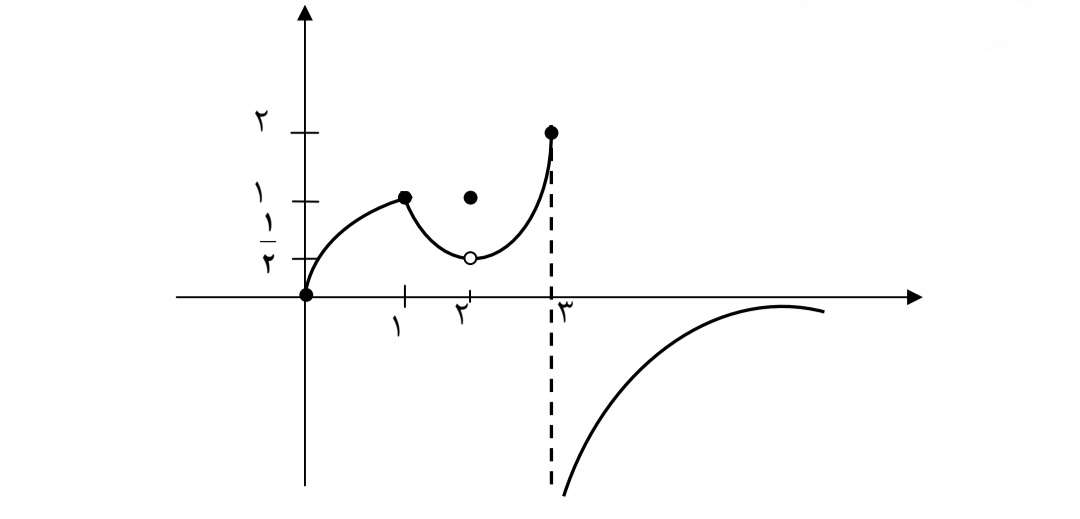
الف)X=0 ب)X=1 ج)X=2 د)X=3
الف)
\(\mathop {\lim }\limits_{x \to 0} f(x) = f(0) = 0\)
پس تابع در x=0پیوسته است.
توجه:در اصطلاح باتوجه به این که در واقع \(\mathop {\lim }\limits_{x \to {0^ + }} f(x) = f(0)\)میگویند تابع fدر x=0تنهااز راست پیوسته است.
ب)
\(\mathop {\lim }\limits_{x \to 1} f(x) = f(1) = 1\)
پس تابع fدرx=1 پیوسته است.
ج)
\(f(2) = 2\)ولی \(\mathop {\lim }\limits_{x \to 2} f(x) = \frac{1}{2}\)پس\(\mathop {\lim }\limits_{x \to 2} f(x) \ne f(2)\) بنابراین تابعf درx=2 پیوسته نیست
د)
تابع fدر x=3حدندارد پس دراین نقطه پیوسته نیست.
توجه:در اصطلاح می گویند تابع fدر x=3تنها پیوستگی چپ دارد.
مثال
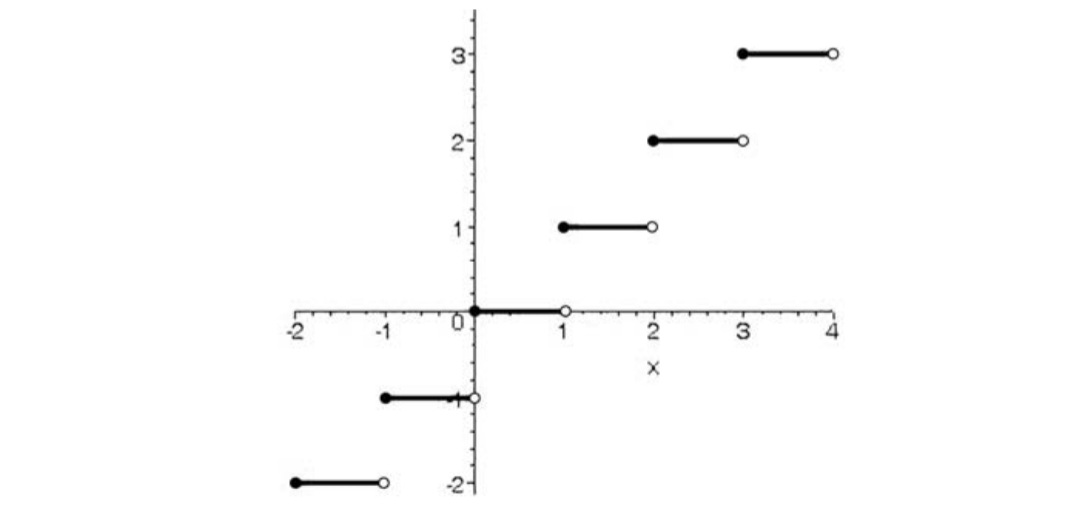
تابع \(y = \left| x \right|\)در چه نقاطی ناپیوسته است.
نمودارتابع \(y = \left| x \right|\) به صورت زیر می باشد باتوجه به نمودار تابع در zناپیوسته است (البته میتوان ثابت کرد تابع\(y = \left| x \right|\) در \(x \in z\)ناپیوسته ودر \(\)پیوسته است.)
مثال
پیوستگی هریک از توابع زیر رادر نقطه یا نقاط داده شده در صورت بامعنی بودن بررسی کنید.
الف)\(f(x) = \sqrt {x - 1,x = 0} \) ب)\(f(x) = {x^2} - 3x + 5,x = 2\)
ج)\(f(x) = \left\{ \begin{array}{l}{x^2} + 1,x < 1\\\\2.x = 1,x = 1\\\\\frac{{{x^2}1}}{{x - 1}},x > 1\end{array} \right.\) د)\(f(x) = \left\{ \begin{array}{l}{x^2} + 1,x < 1\\\\3,x = 1,x = 1\\\\\frac{{{x^2}1}}{{x - 1}},x > 1\end{array} \right.\)
ه) \(f(x) = \left\{ \begin{array}{l}\frac{{\sin x}}{x},x \ne 0\\\\1,x = 0\end{array} \right.,x = 0\)
و) \(\begin{array}{l}f(x) = \left\{ \begin{array}{l}{x^2} + 2,x < - 1\\\\ - 3x, - 1 < x < 1\\\\x - 4,x > 1\end{array} \right.,x = - 1,x = 1\\\end{array}\)
الف)
میدانیم \({D_f} = \left[ {1, + \infty )} \right.\)و \(0 \notin {D_f}\)بنابراین بحث از پیوستگی این تابع در x=0بی معنا است.
ب)
تابعf در x=2پیوسته است زیرا :\(\mathop {\lim }\limits_{x \to 2} f(x) = f(2) = 3\)
توجه :توابع چند جمله ای در هر نقطه ای ازR پیوسته هستند.
ج)
\(\left. \begin{array}{l}f(1) = 2\\\\f( - 1) = 3\\\\\mathop {\lim }\limits_{x \to {1^ - }} f(x) = \mathop {\lim }\limits_{x \to {1^ - }} f({x^2} + 1) = 2\\\\\mathop {\lim }\limits_{x \to {1^ + }} f(x) = \mathop {\lim }\limits_{x \to {1^ + }} \frac{{{x^2} - 1}}{{x - 1}} = 2\\\end{array} \right\} \Rightarrow \mathop {\lim }\limits_{x \to 2} f(x) = 2\)
تابع f در x=1پيوسته است زيرا\(\mathop {\lim }\limits_{x \to 1} f(x) = f(1)\)
د)
 \(\left. \begin{array}{l}f(1) = 3\\\\\mathop {\lim }\limits_{x \to {1^ - }} f(x) = \mathop {\lim }\limits_{x \to {1^ - }} f({x^2} + 1) = 2\\\\\mathop {\lim }\limits_{x \to {1^ + }} f(x) = \mathop {\lim }\limits_{x \to {1^ + }} \frac{{{x^2} - 1}}{{x - 1}} = \mathop {\lim }\limits_{x \to {1^ + }} \frac{{(x - 1)(x + 1)}}{{x - 1}} = 2\\\end{array} \right\} \Rightarrow \mathop {\lim }\limits_{x \to 1} f(x) = 2\)
\(\left. \begin{array}{l}f(1) = 3\\\\\mathop {\lim }\limits_{x \to {1^ - }} f(x) = \mathop {\lim }\limits_{x \to {1^ - }} f({x^2} + 1) = 2\\\\\mathop {\lim }\limits_{x \to {1^ + }} f(x) = \mathop {\lim }\limits_{x \to {1^ + }} \frac{{{x^2} - 1}}{{x - 1}} = \mathop {\lim }\limits_{x \to {1^ + }} \frac{{(x - 1)(x + 1)}}{{x - 1}} = 2\\\end{array} \right\} \Rightarrow \mathop {\lim }\limits_{x \to 1} f(x) = 2\)
تابع f در پيوسته نيست زيرا\(\mathop {\lim }\limits_{x \to 1} f(x) \ne f(1)\)
ه)
\(\begin{array}{l}f(1) = - 3\\\\\mathop {\lim }\limits_{x \to {1^ + }} f(x) = \mathop {\lim }\limits_{x \to {1^ + }} f( - 3x) = 3\\\\\mathop {\lim }\limits_{x \to - {1^ - }} f(x) = \mathop {\lim }\limits_{x \to - {1^ - }} ({x^2} + 1) = 2\end{array}\)
تابع f درx=0پيوسته است زيرا\(\mathop {\lim }\limits_{x \to 0} f(x) = f(0)\)
و)
\(\begin{array}{l}f( - 1) = 3\\\\\mathop {\lim }\limits_{x \to {1^ + }} f(x) = \mathop {\lim }\limits_{x \to {1^ + }} f( - 3x) = - 3\\\\\mathop {\lim }\limits_{x \to - {1^ - }} f(x) = \mathop {\lim }\limits_{x \to - {1^ - }} f({x^2} + 1) = 2\end{array}\)
تابع f در X=-1حد ندارد. بنابراين تابع f در X=-1 پيوسته نيست، زيرا در اين نقطه حد ندارد ( همانگونه كه بيان شد تابع f در X=-1تنها پيوستگي راست دارد)
\(\left. \begin{array}{l}f(1) = - 3\\\\\mathop {\lim }\limits_{x \to {1^ - }} f(x) = \mathop {\lim }\limits_{x \to {1^ - }} f( - 3x) = - 3\\\\\mathop {\lim }\limits_{x \to {1^ + }} f(x) = \mathop {\lim }\limits_{x \to {1^ + }} f(x - 4) = - 3\end{array} \right\} \Rightarrow \mathop {\lim }\limits_{x \to 1} f(x) = - 3\)
تابع f درx=1پيوسته است زيرا \(\mathop {\lim }\limits_{x \to 1} f(x) = f(1)\)
مثال
مقدار a را طوري بيابيد تا تابع \(f(x) = (x + a)\left[ {2x - 5)} \right.\) در x=2پيوسته باشد.
\(\begin{array}{l}f(2) = \left[ {2 + a)} \right.\left[ {4 - 5) = - a - 2} \right.\\\\\mathop {\lim }\limits_{x \to {2^ - }} (x + a)\left[ {2x - 5)} \right. = \mathop {\lim }\limits_{x \to {2^ - }} (x + a)( - 2) = - 4 - 2a\\\\\mathop {\lim }\limits_{x \to {2^ + }} (x + a)\left[ {2x - \left. 5 \right]} \right. = \mathop {\lim }\limits_{x \to {2^ + }} (x + a)( - 1) = 2 - a\end{array}\)
با توجه به اينكه بايد داشته باشيم \(\mathop {\lim }\limits_{x \to {2^ + }} f(x) = f(2)\)پس لازم است\( - a - 2 = - 4 - 2a\) بنابراينa=-2 ميباشد.
مثال
اگرتابع\(f(x) = \left\{ \begin{array}{l}\frac{{\sin x}}{{\sqrt {1 - \cos 2x} }},x < 0\\\\a,x = 0\\\\\left[ x \right] + b,x > 0\end{array} \right.\) در x=0 پیوسته باشد مقدار aو bرابدست آورید.
 \(\begin{array}{l}\mathop {\lim }\limits_{x \to {0^ - }} f(x) = \mathop {\lim }\limits_{x \to {0^ - }} \frac{{\sin x}}{{\sqrt {1 - \cos 2x} }} = \mathop {\lim }\limits_{x \to {0^ - }} \frac{{\sin x}}{{\sqrt {2{{\sin }^2}x} }} = \mathop {\lim }\limits_{x \to {0^ - }} \frac{{\sin x}}{{\sqrt {2\left| {\sin x} \right|} }} = \mathop {\lim }\limits_{x \to {0^ - }} \frac{{\sin x}}{{ - \sqrt {2\sin x} }} = \\\\\sqrt 2 \frac{{\sin x}}{{ - \sqrt {2\sin x} }} = \frac{{ - \sqrt 2 }}{2}\\\\\mathop {\lim }\limits_{x \to {0^ + }} f(x) = \mathop {\lim }\limits_{x \to {0^ + }} (\left| x \right| + b) = \mathop {\lim }\limits_{x \to {0^ + }} (0 + b) = b\end{array}\)
\(\begin{array}{l}\mathop {\lim }\limits_{x \to {0^ - }} f(x) = \mathop {\lim }\limits_{x \to {0^ - }} \frac{{\sin x}}{{\sqrt {1 - \cos 2x} }} = \mathop {\lim }\limits_{x \to {0^ - }} \frac{{\sin x}}{{\sqrt {2{{\sin }^2}x} }} = \mathop {\lim }\limits_{x \to {0^ - }} \frac{{\sin x}}{{\sqrt {2\left| {\sin x} \right|} }} = \mathop {\lim }\limits_{x \to {0^ - }} \frac{{\sin x}}{{ - \sqrt {2\sin x} }} = \\\\\sqrt 2 \frac{{\sin x}}{{ - \sqrt {2\sin x} }} = \frac{{ - \sqrt 2 }}{2}\\\\\mathop {\lim }\limits_{x \to {0^ + }} f(x) = \mathop {\lim }\limits_{x \to {0^ + }} (\left| x \right| + b) = \mathop {\lim }\limits_{x \to {0^ + }} (0 + b) = b\end{array}\)
براي اينكه تابع f در x=0 پيوسته باشد بايد\(\mathop {\lim }\limits_{x \to 0} f(x) = f(0)\) بنابراین داریم:
\(b = a = - \frac{{\sqrt 2 }}{2}\)
اگر تابعي در تمام نقاط دامنه ي خود پيوسته باشد، آن را تابعي پيوسته مي نامند.
مثال
كدام يك از توابع زير، تابع پيوسته ميباشند.
الف) \(f(x) = \sqrt {2x - {x^2}} \)ب)\(g(x) = \frac{{x + 1}}{{{x^2} - 4}}\)
ج) \(h(x) = \left\{ \begin{array}{l}\frac{{\tan x}}{x},x \ne 0\\\\2,x = 0\end{array} \right.\)
الف(
دامنه ي تابع f ، بازه ي \(\left[ {0,2} \right]\)ميباشد. اگر \(0 < x < 2\) ، آنگاه:
\(\)\(\)
اگر x=0 و \(\mathop {\lim }\limits_{x \to {0^ + }} = f(x) = 0 = f(0)\)واگر x=2، آنگاه. \(\mathop {\lim }\limits_{x \to {2^ - }} = f(x) = 0 = f(2)\) پس تابع f ، تابعي پيوسته ميباشد.
ب)
دلخواه
بنابراين g تابعي پيوسته است.
ج)
\(\begin{array}{l}{D_h} = R\\0 \in {D_h} = \left\{ \begin{array}{l}h(0) = 2\\\\\mathop {\lim h(x) = 1}\limits_{x \to 0} \end{array} \right. \Rightarrow \mathop {\lim h(x) \ne h(0)}\limits_{x \to 0} \end{array}\)
بنابراين h تابعي پيوسته نيست
توابع چندجمله ای \(y = {\tan ^{ - 1}}x,y = {\cos ^{ - 1}}x,y = {\sin ^{ - 1}}x\) و \(y = {\cot ^{ - 1}}x\)روی پیوسته اند
و \(y = {\cot ^{ - 1}}x\)روی پیوسته اند
توابع \(y = {\sin ^{ - 1}}x,y = \cot x,y = \tan x\)و \(y = {\cos ^{ - 1}}x\)در دامنه ی خود که زيرمجموعه اي از ℜ ميباشد تابعي پيوسته هستند.
اگر تابع h از جمع يا تفريق يا ضرب يا تقسيم چند تابع پيوسته تشكيل شده باشد روي دامنه خود تابعي پيوسته است.
اگر f تابعي پيوسته باشد، تابع باشد، تابع \(^n\sqrt f \)روي دامنه ي تعريف خود پيوسته است.
مثال
پيوستگي توابع زير را روي دامنه ي تعريف بررسي كنيد.
الف(\(f(x) = \frac{{{x^2} + 1}}{{{x^2} - 4}}\)
ب)\(g(x) = \sqrt {{x^2} - 4} \)
ج)\(h(x) = \tan x\cot x\)
الف)
صورت و مخرج توابع چند جمله اي هستند و در هر نقطه اي پيوسته، پس تابع f روي \({D_f} = R - \left\{ { - 2} \right\}\)پيوسته است.
ب) تابع \(y = {x^2} - 4\)چند جمله اي است و در هر نقطهاي پيوسته، پس تابع g در دامنه تعريف خود يعني \(\left( { - \infty ,2} \right) \cup \left[ {2, + \infty )} \right.\) تابع پيوسته است.
ج) تابع \(y = \tan x\)روی \(D = \left\{ {\left. x \right|} \right.x \ne k\pi + \left. {\frac{\pi }{2}} \right\}\)و تابع\(y = \cot x\) روی \({D_f} = \left\{ {\left. x \right|} \right.x \ne k\left. \pi \right\}\)پيوسته اند پس تابع h روي\({D_f} = \left\{ {\left. x \right|} \right.x \ne \left. {\frac{{k\pi }}{2}} \right\}\) است پيوسته است.
مثال
فاصله ي پيوستگي تابع\(f(x) = \left\{ \begin{array}{l}\frac{{x + 1}}{{x - 2}},x > 3\\\\\frac{{x + 1}}{{x + 2}},x \le 3\end{array} \right.\) را تعيين كنيد.
میدانیم \({D_f} = R - \left\{ { - 2} \right\}\)و هر يك از رابطه ها روي دامنه ي تعريف خود پيوسته اند. پس كافي است ض ميدانيم \(x = R - \left\{ 2 \right\}\)پيوستگي تابع در x=3را بررسي كنيم .
\(\begin{array}{l}\mathop {\lim }\limits_{x \to {3^ + }} f(x) = \mathop {\lim }\limits_{x \to {3^ + }} \frac{{x + 1}}{{x - 2}} = 4\\\\\mathop {\lim }\limits_{x \to {3^ - }} f(x) = \mathop {\lim }\limits_{x \to {3^ - }} \frac{{x + 1}}{{x + 2}} = \frac{4}{5}\end{array}\)
تابع در x=3پیوسته نیست بنابراین تابع f روي\(\left( { - \infty , - 2} \right) \cup \left( { - 2,3} \right) \cup \left( {3, + \infty } \right)\) پيوسته است.
مثال
حدود k را طوري تعيين كنيد تا تابع\(f(x) = \frac{{{x^2} + x + 7}}{{{x^2} + kx + 1}}\) در ℜ پيوسته باشد
صورت و مخرج توابع چند جمله اي هستند و در هر نقطهاي از ℜ پيوسته ميباشند. پس كافي است دامنه تعریف تابع برابرR باشد.یعنی باید معادله \({x^2} + kx + 1 = 0\)فاقد ريشه باشد بنابراين لازم است:
\(\Delta < 0 \Rightarrow {k^2} - 4 < 0 \Rightarrow \left| k \right| < 2 \Rightarrow - 2 < k < 2\)
اگر ترکیبfog امکان پذیر باشد و\(\mathop {\lim }\limits_{x \to a} g(x) = l\) و تابعی پیوسته در\(\) باشد،انگاه داریم:
\(\mathop {\lim }\limits_{x \to a} f(g(x)) = f\left( {\mathop {\lim g(x)}\limits_{x \to a} } \right)\)
مثال
الف)\(y = \sqrt x \)زیراتابعی پیوسته است\(\mathop {\lim }\limits_{x \to 1} \sqrt {{x^2} + 3} = \sqrt {\mathop {\lim ({x^2} + 3)}\limits_{x \to 1} } = \sqrt 4 = 2\)
ب)زیرا تابع \(y = \left| x \right|\)در  پیوسته نیست \(\mathop {\lim }\limits_{x \to 2} \left| x \right| \ne \left| {\mathop {\lim x}\limits_{x \to 2} } \right|\)
پیوسته نیست \(\mathop {\lim }\limits_{x \to 2} \left| x \right| \ne \left| {\mathop {\lim x}\limits_{x \to 2} } \right|\)
ج)\(\mathop {\lim }\limits_{x \to \frac{1}{2}} \left| {{x^2}} \right| = \left| {\mathop {\lim }\limits_{x \to \frac{1}{2}} {x^2}} \right| = \frac{1}{4} = 0\)
د)زیرا تابع \(y = \left| {\frac{{2x + 1}}{x}} \right|\)در  پیوسته نیست\(\mathop {\lim }\limits_{x \to 1} \left| {\frac{{2x + 1}}{x}} \right| \ne \mathop {\lim }\limits_{x \to 1} \left| {\frac{{2x + 1}}{x}} \right|\)
پیوسته نیست\(\mathop {\lim }\limits_{x \to 1} \left| {\frac{{2x + 1}}{x}} \right| \ne \mathop {\lim }\limits_{x \to 1} \left| {\frac{{2x + 1}}{x}} \right|\)
ه)\(\mathop {\lim }\limits_{x \to 2} \left| {\frac{{2x + 1}}{x}} \right| = \left| {\mathop {\lim \frac{{2x + 1}}{x}}\limits_{x \to 2} } \right| = \frac{5}{2} = 2\)
اگر تابع gدر x=aپیوسته و تابع fدر g(a)پیوسته باشد،تابع fogدر x=aپیوسته است.
مثال
ثابت کنید تابع\(f(x) = {\sin ^3}\sqrt x \) تابعی پیوسته است.
حل روش اول :
تابع y=xتابع چند جمله ای است ودر  دلخواه پیوسته است پس تابع \(g(x){ = ^3}\sqrt x \)در
دلخواه پیوسته است پس تابع \(g(x){ = ^3}\sqrt x \)در پیوسته است و تابع \(h(x) = \sin x\)در هر نقطه ای از جمله
پیوسته است و تابع \(h(x) = \sin x\)در هر نقطه ای از جمله پیوسته است پس تابع
پیوسته است پس تابع
\(f(x) = h(g(x)) = {\sin ^3}\sqrt x \)
در \(\mathop {\lim }\limits_{x \to 1} \sqrt {{x^2} + 3} = \sqrt {\mathop {\lim ({x^2} + 3)}\limits_{x \to 1} } = \sqrt 4 = 2\)پیوسته است.
روش دوم :
بنابراین تابع fروی \({D_f} = R\) تابعی پیوسته است.
تهیه کننده: حامد دلیجه
جزوات جامع پایه یازدهم
جزوه جامع حسابان یازدهم فصل 1 جبر و معادله
جزوه جامع حسابان یازدهم فصل 2 تابع
جزوه جامع حسابان یازدهم فصل 3 توابع نمایی و لگاریتمی
جزوه جامع حسابان یازدهم فصل 4 مثلثات
جزوه جامع حسابان یازدهم فصل 5 حد و پیوستگی
مشتق
مشتق
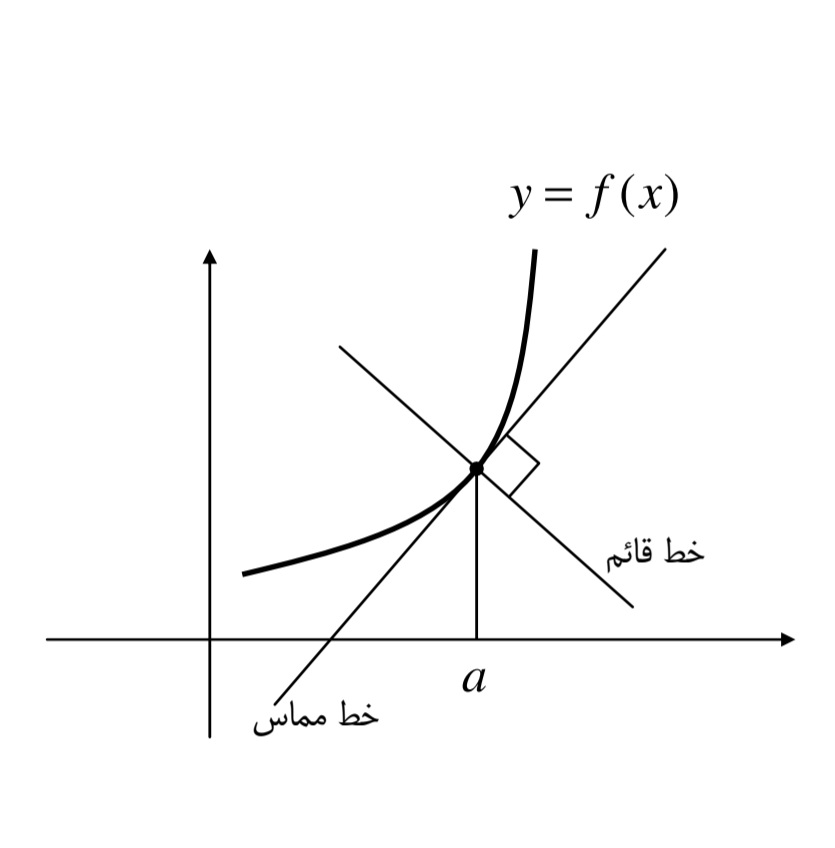
خط مماس و خط قائم بر منحنی از یک نقطه روی منحنی
با توجه به تغییرهندسی مشتق واضح است که مشتق تابع \( y = f(x)\)در نقطه ی a با شیب خط مماس بر منحنی در این نقطه برابر است.
\(m = {f^`}(a)\)=شیب خط مماس
حال اگر تعریف کنیم که خط قائم خطی است که در نقطه ی aبر خط مماس بر منحنی در این نقطه عمود باشد بدیهی است که اگر شیب خز مماس را عکس و قرینه کنیم شیب خط قائم به دست می اید.
\({m^`} = \frac{{ - 1}}{{{f^`}(a)}}\)شیب خط قائم
بنابراین معادله ی خط مماس و خط قائم بر منحنی در نقطه ی\(M(a,b)\) واقع بر نمودار ان به این شکل خواهند بود.
\(y = m(x - a) + b\)معادله ی خط مماس
\(y = {m^`}(x - a) + b\)معادله ی خط قائم
تهیه کننده: حامد دلیجه
آهنگ تغییرات
آهنگ تغییرات
واضح است که کمیت های زیادی وجود دارند که تغییر یکی وابسته به تغییر دیگری است. مانند:
الف:مساحت مربع تابعی از طول ضلع ان است.
ب:مساحت دایره تابعی از شعاع ان است.
ج:محیط دایره تابعی از شعاع مثال ان است.
د:حجم کره تابعی از شعاع ان است.
ه:شتاب حرکت یک متحرک تابعی از سرعت ان است.
حال اگر بین دو کمیت یا دو پدیده که تغییر یکی سبب تغییر در دیگری میشود یکی را به عنوان متغیر(متغیر مستقل یا) و دیگری را به عنوان تابعی از ان متغیر (متغیر وابسته یا )در نظر بگیریم خواهیم داشت:
\(y = f(x)\)
در این صورت تغییرات yنسبت به تغییرات را اهنگ تغییرy نسبت به تغییرx می گوییم.
اهنگ تغییر را میتوان به یکی از دو صورت زیر بررسی کرد.
آهنگ متوسط تغییرات
آهنگ تغییرات متوسط تابعf نسبت به تغییرات xوقتیx از\(x = a\) تا \(x = b\)تغییر کند برابر است با :
\(\frac{{y}}{{x}} = \frac{{f(b) - f(a)}}{{b - a}}\)
تذکر:اگر قرار دهیم \(x = h = b - a\)در این صورت \(b = a + h\)یعنی اگر مقدار کمیتa رابه اندازه یh واحد تغییر دهیم خواهیم داشت:
\(\frac{{y}}{{x}} = \frac{{f(a + h) - f(a)}}{h}\)
آهنگ تغییرات آنی(لحظه ای)
حد آهنگ تغییرات متوسط تابعf نسبت به تغییرات xوقتی تغییرx خیلی ناچیز\((h \to 0)\) باشد را آهنگ لحظه ای رابه اختصار آهنگ تغییر کمیت \(y = f(x)\)به کمیت xدر aمیگویند.
\(\mathop {\lim }\limits_{x \to 0} \frac{{y}}{{x}} = \mathop {\lim }\limits_{h \to 0} \frac{{f(a + b) - f(a)}}{h}\)
تذکر: با توجه به تعریف مشتق تابع در یک نقطه واضح است که
\(\mathop {\lim }\limits_{x \to 0} \frac{{y}}{{x}} = {f^`}(a)\)
مثال
آهنگ تغییرات متوسط حجم مکعبی به ضلع سانتی متر را نسبت به تغییرات وقتی از به تغییر می کند بیابید.
\(\begin{array}{l}v(x) = {x^3}\\\\\frac{{v}}{{x}} = \frac{{v(5) - v(2)}}{{5 - 2}} = \frac{{125 - 8}}{3} = 39\end{array}\)
مثال
اهنگ تغییر مساحت یک دایره را نسبت به تغییرات شعاع آن که \(r = 5\)سانتی متر باشد حساب کنید.
\(\begin{array}{l}s(r) = \pi {r^2} \to {s^`}(r) = 2\pi r\\\\{s^`}(5) = 2\pi r\left( 5 \right) = 10\pi \end{array}\)
مثال
اگر\(f(t) = 30 + 10{t^2}\) نمایش جمعیت یک نوع باکتری باشد (tبر حسب ساعت) آهنگ تغییرات متوسط افزایش جمعیت را در 5ساعت اول پس از زمان\({t_1} = 2\) را حساب کنید.
\(\begin{array}{l}f(t) = 30 + 10{t^2}\\\\f(2) = 30 + 10{(2)^2} = 70\\\\f(7) = 30 + 10{(7)^2} = 520\\\\\frac{{f}}{{x}} = \frac{{f(7) - f(2)}}{{7 - 2}} = \frac{{520 - 70}}{5} = 90\end{array}\)
مثال
طول دو ضلع مثلثی 1و2 و طول ضلع سوم برابر متغیرL است فرض کنید که زاویه ی مقابل به این ضلعa باشد
الف) Lرا برحسب aبنویسید
ب)مشتقL رابر حسب aبه دست اورید.
ج)آهنگ تغییرات L وقتی که \(\alpha = \frac{\pi }{4}\)رابه دست اورید.
\(\begin{array}{l}l = (1) + (2) - 2(1)(2)\cos \alpha \to l(\alpha ) = \sqrt {5 - 4\cos \alpha } \\\\{l^`}(\alpha ) = \frac{{4\cos \alpha }}{{2\sqrt {5 - 4\cos \alpha } }} = \frac{{2\sin \alpha }}{{\sqrt {5 - 4\cos \alpha } }}\\\\{l^`}(\frac{\pi }{4}) = \frac{{2\sin (\frac{\pi }{4})}}{{\sqrt {5 - 4\cos (\frac{\pi }{4})} }} = \frac{{2\sqrt {\frac{2}{2}} }}{{\sqrt {5 - 4(\frac{{\sqrt 2 }}{2})} }} = \frac{{\sqrt 2 }}{{\sqrt {5 - 2\sqrt 2 } }}\end{array}\)
مثال
مساحت هر دایره تابعی از محیط آن است .آهنگ تغییرات مساحت دایره را نسبت به محیط \(5\pi \)ان را برای دایره ای به محیط حساب کنید.
\(\begin{array}{l}s(r) = \pi {r^2}s(p) = \pi {(\frac{p}{{2\pi }})^2} = {\frac{p}{{4\pi }}^2}\\\\s(p) = {\frac{p}{{4\pi }}^2} \to {s^`}(p) = \frac{{2p}}{{4\pi }} = \frac{p}{{2\pi }}\\\\s(5\pi ) = \frac{{5\pi }}{2} = 2/5\end{array}\)
مثال
مخزنی که گنجایش 60لیتر آب را دارد می تواند در مدت200 ثانیه کاملا تخلیه شود لبریز از آب بود. در لحظه ی \(t = 0\)شیر این مخزن باز می شود. اگر حجم اب باقی مانده در مخزن پس ازt ثانیه از رابطه ی\(v = 60{(1 - \frac{t}{{200}})^2}\) به دست آید.
الف) آهنگ تغییرات متوسط تخلیه آب پس از یک دقیقه چقدر است؟
ب) آهنگ تغییرات تخلیه ی آب در\(t = 100\) ثانیه چقدر است ؟
تابع تخلیه آب
\(\begin{array}{l}v(t) = 60 - 60{(1 - \frac{t}{{200}})^2} = 60(1 - (1 - \frac{t}{{100}} + \frac{{{t^2}}}{{4000}}))\\\\ = 60(\frac{t}{{100}} - \frac{{{t^2}}}{{4000}})60 \times \frac{{400t - {t^2}}}{{4000}} = \frac{3}{{2000}}(400t - {t^2})\end{array}\)
الف
\(\begin{array}{l}v(t) = \frac{3}{{2000}}(400t - {t^2})\\\\v(0) = \frac{3}{{2000}}(400(0) - {(0)^2}) = 0\\\\v(60) = \frac{3}{{2000}}(400(60) - {(60)^2}) = 30/6\\\\\frac{{v}}{{t}} = \frac{{v(60) - v(0)}}{{60 - 0}} = \frac{{30/6 - 0}}{{60}} = 0/51\end{array}\)
ب
\(\begin{array}{l}v(t) = \frac{3}{{2000}}(400t - {t^2}) \to v(t) = \frac{3}{{2000}}(400 - 2t) = \frac{3}{{1000}} = (200 - t)\\\\{v^`}(100) = \frac{3}{{1000}}(200 - 100) = \frac{3}{{10}} = 0/3\end{array}\)
نتیجه : می دانیم که نسبت به تغییر مسافت یک متحرک نسبت به زمان را سرعت و همچنین نسبت تغییر سرعت را متحرک نسبت به زمان را شتاب می نامند.بنابراین اگر \(x = f(t)\)معادله ی حرکت یک متحرک باشد .داریم :سرعت اولی و شتاب دومی
مثال
معادله ی حرکت متحرکی به صورت\(x(t) = {t^2} - 5t + 6\) است. مطلوب است
الف)سرعت متوسط متحرک ببین لحظات \({t_1} = 3\)تا \({t_2} = 5\)ثانیه
ب) سرعت لحظه ای متحرک در لحظه ی\({t_0} = 2\)
\(x(t) = {t^2} - t + 6\)
الف
\(\begin{array}{l}x(3) = {(3)^2} - 5(3) + 6 = 9 - 15 + 6 = 0\\\\x(5) = {(5)^2}\_5(5) + 6 = 25 - 25 + 6 = 6\\\\v = \frac{{x}}{{t}} = \frac{{{x_2} - {x_1}}}{{{t_2} - {t_1}}} = \frac{{6 - 0}}{{5 - 3}} = 3\frac{m}{s}\end{array}\)
ب
\({x^`}(t) = 2t - 5 \to {x^`}(2) = 2(2) - 5 = - 1\frac{m}{s}\)
مثال
توپی را در راستای قائم از زمین به بالا پرتاب می کنیم .اگر جهت مثبت به طرف بالا و معادله ی حرکت توپ به صورت \(y(t) = - 5{t^2} + 20t\)باشد (tبرحسب ثانیه و yبر حسب متر)
1: نمودار\(y(t)\)را رسم کنید
2: دامنه ی\(y(t)\) را تعیین کنید
3:سرعت متوسط توپ را از لحظه ی پرتاپ\((t = 0)\) تا پایان ثانیه ی دوم \((t = 2)\)حساب کنید
4: سرعت لحظه ای توپ را در یک ثانیه پس از پرتاپ \((t = 1)\)را حساب کنید
5:سرعت لحظه ای توپ هنگام برخورد با زمین چقدر است ؟
6: در چه زمانی توپ به بالاترین ارتفاع خود می رسد.در این لحظه سرعت توپ چقدر است . معنای آن چیست .
1 معادله ی داده شده یک سهمی و چون در آن \(a = - 5\)پس نمودار سهمی رو به پایین بوده و دارای نقطه یmax است.
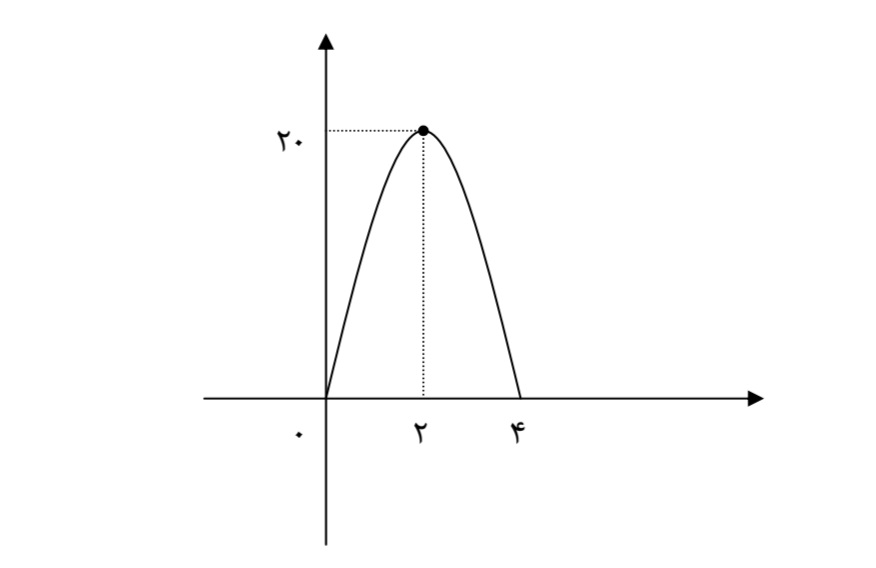
2 چون بعد از 4 ثانیه توپ مجددا به زمین بر میگردد .لذا دامنه ی تابع \(D = \left[ {0,4} \right]\)می شود.
3
\(\begin{array}{l}y(t) = - 5{t^2} + 20t\\\\y(0) = - 5{(0)^2} + 20(0) = 0\\\\y(2) = - 5{(2)^2} + 20(2) = - 20 + 4\\\\y(t) = - 5{t^2} + 20t\\\\\frac{{y}}{{t}} = \frac{{y(2) - y(0)}}{{2 - 0}} = \frac{{20 + 0}}{2} = 10\end{array}\)
4
\(\begin{array}{l}y(t) = - 5{t^2} + 20t \to {y^`}(t) = - 10t + 20t\\\\{y^`}(1) = - 10(1) + 20 = 10\frac{m}{s}\end{array}\)
5
\({y^`}(4) = - 10(4) + 20 = - 20\frac{m}{s}\)
6 بالاترین ارتفاع توپ زمانی است که\(t = 2\) باشد.لذا
\({y^`}(2) = - 10(2) + 20 = 0\frac{m}{s}\)
یعنی سرعت لحظه ای توپ در این لحظه برابر صفر است.(ایست لحظه ای )
تهیه کننده: حامد دلیجه
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه یازدهم- آزمون آنلاین تمامی دروس پایه یازدهم
- گام به گام تمامی دروس پایه یازدهم
- ویدئو های آموزشی تمامی دروس پایه یازدهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه یازدهم
- فلش کارت های آماده دروس پایه یازدهم
- گنجینه ای جامع از انشاء های آماده پایه یازدهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه یازدهم



1736019749.png)















