درسنامه کامل حسابان یازدهم فصل 4 مثلثات
تعداد بازدید : 7.26Mخلاصه نکات حسابان یازدهم فصل 4 مثلثات - درسنامه شب امتحان حسابان یازدهم فصل 4 مثلثات - جزوه شب امتحان حسابان یازدهم نوبت اول فصل 4 مثلثات
توابع مثلثاتي
توابع مثلثاتي
توابع \(y = \sin x\) و\(y = \cos x\) از ساده ترين توابع مثلثاتي هستند كه به ازاي هر مقدار x تعريف شده اند به عبارتي دامنه اين توابع، مجموعه اعداد حقيقي ℜ است و با تغيير x مقاديري كه براي \(\sin x\) و\(\cos x\) به دست مي آيد اعدادي بين 1 و1_ميباشند كه در حقيقت برد اين توابع \(\left[ { - 1,1} \right]\) می شود.
در حالت كلي تر، بيش ترين مقدار توابع \(a = \sin bx + c\) و \(a = \cos bx + c\)، \(\left| a \right|\)و كمترين \( - \left| a \right|\)مقدار و دوره تناوب آنها \(\frac{{2\pi }}{b}\)ميباشند.
همچنين بيش ترين و كمترين \(a = \sin bx + c\)مقدار و\(a = \cos bx + c\) عبارتست از
\(\min = - \left| a \right| + c\) و \(\max = \left| a \right| + c\)
مثال
در تابع \(f(x) = - 2\sin 3x\) مقادير حداقل و حداكثر و T، دوره تناوب تابع را مشخص كرده، نمودار آن را در بازه ي \(\left[ {0,T} \right]\) رسم كنيد.
\(\min f = - \left| 2 \right| = - 2,\max f = \left| { - 2} \right| = 2,T = \frac{{2\pi }}{3}\)
براي رسم، نقاطي كه تابع مقادير حداكثر و حداقل دارد را به دست آورده، همچنين نقاطي كه تابع صفر مي شود را نيز مشخص كنيم . سپس با توجه به نمودار توابع \(y = \sin x\) و \(y = \cos x\)شكل را كامل ميكنيم.
\(\begin{array}{l}2 = - 2\sin 3x \Rightarrow \sin 3x = - 1 \Rightarrow \frac{{3\pi }}{2} \Rightarrow x = \frac{{2\pi }}{3}\\\\ - 2 = - 2\sin 3x \Rightarrow \sin 3x = 1 \Rightarrow \frac{\pi }{2} \Rightarrow x = \frac{\pi }{3}\\\\0 = - 2\sin 3x \Rightarrow \sin 3x = 0 \Rightarrow 3x = 0 \Rightarrow x = 0\left\{ \begin{array}{l}3x = 0 \Rightarrow x = 0\\\\3x = \pi \Rightarrow x = \frac{\pi }{3}\\\\3x = 2\pi \Rightarrow x = \frac{{2\pi }}{3}\end{array} \right.\end{array}\)
نمودار تابع به صورت زير است:
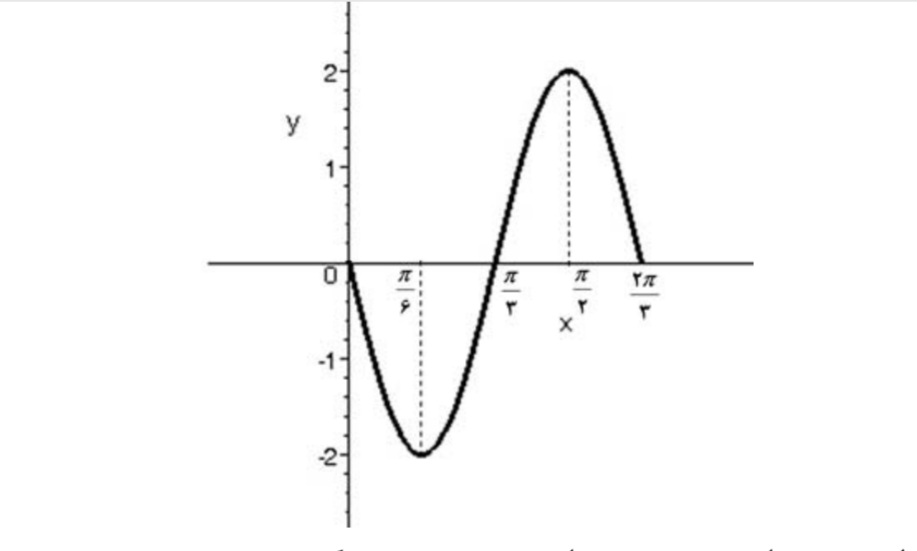
مثال
تابع مثلثاتي مربوط به نمودار رسم شده را بنويسيد (موج كسينوسي)
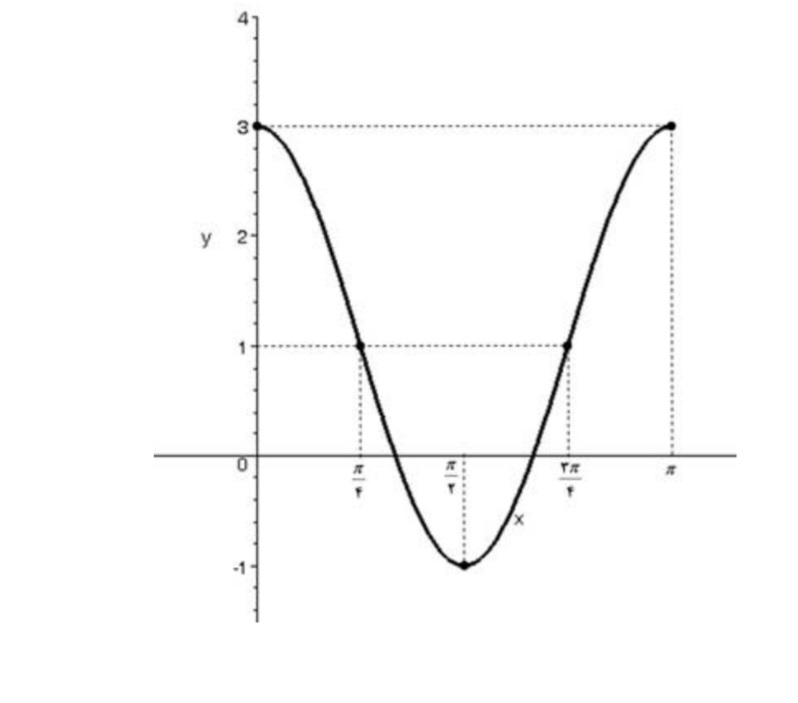
\(\left. \begin{array}{l}\min y = - 1 = - \left| a \right| + c\\\max y = 3 = \left| a \right| + c\end{array} \right\}c = 1,\left| a \right| = 2\)
باتوجه به شكل \(a = 2\) ميباشد چون موج كسينوسي از بالا شروع شده است. همچنين:
\(t = \pi \Rightarrow \pi = \frac{{2\pi }}{b} \Rightarrow x = 2 \Rightarrow y = 2\cos (2x) + 1\)
مثال
اگر آونگ يك ساعت بزرگ، نوسانات عمودي داشته باشد و ضابطه اين نوسانات \(d(t) = \frac{{\pi t}}{{10}}\) باشد (t بر حسب ثانيه و d برحسب متر)
الف) آونگ از حالت تعادل حداكثر چند متر بالا ميرود.
ب) چه مدت طول ميكشد تا يك نوسان كامل انجام گيرد.
ج) پاندول چند نوسان كامل در مدت 2 دقيقه انجام ميدهد
د ) نمودار تابع را در يك دوره تناوب رسم كنيد.
الف)
در واقع بايد بيشترين مقدار تابع را محاسبه نمود، بنابراين كافيست به جاي \(\cos \frac{{\pi t}}{{10}}\)
ب) در 20 ثانيه يك نوسان كامل انجام ميگيرد \(b = \frac{\pi }{{10}} \Rightarrow t = \frac{{2\pi }}{{\left| b \right|}} = \frac{{2\pi }}{{\frac{\pi }{{10}}}} = 20\)
ج) نوسان كامل ثانيه \(2 \times 60 = 120 \Rightarrow 12 + 2 = 6\)
د)
\(\begin{array}{l}\max d = 8 \Rightarrow 8 = 2\cos \frac{\pi }{{10}}t + 6 \Rightarrow \cos \frac{\pi }{{10}}t = 1 \Rightarrow \frac{\pi }{{10}}t = 0,\frac{\pi }{{10}}t = 2\pi \Rightarrow t = 0,t = 20\\\\\min d = 4 \Rightarrow 4 = 2\cos \frac{\pi }{{10}}t + 6 \Rightarrow \cos \frac{\pi }{{10}}t = - 1 \Rightarrow \frac{\pi }{{10}}t = \pi ,\pi = 20\\\\d = 0 \Rightarrow \cos (\frac{{\pi t}}{{10}}) = 0 \Rightarrow \frac{\pi }{{10}}t = \frac{\pi }{2},\frac{\pi }{{10}}t = \frac{{3\pi }}{2} \Rightarrow t = 5,t = 15\\\\\max d = 8 \Rightarrow 8 = 2\cos \frac{\pi }{{10}}t + 6 \Rightarrow \cos \frac{\pi }{{10}}t = 1 \Rightarrow \frac{\pi }{{10}}t = 0,\frac{\pi }{{10}}t = 2\pi \Rightarrow t = 0,t = 20\\\\\min d = 4 \Rightarrow 4 = 2\cos \frac{\pi }{{10}}t + 6 \Rightarrow \cos \frac{\pi }{{10}}t = - 1 \Rightarrow \frac{\pi }{{10}}t = \pi ,\pi = 20\\\\d = 0 \Rightarrow \cos (\frac{{\pi t}}{{10}}) = 0 \Rightarrow \frac{\pi }{{10}}t = \frac{\pi }{2},\frac{\pi }{{10}}t = \frac{{3\pi }}{2} \Rightarrow t = 5,t = 15\\\\\end{array}\)معادله ي توابع
سينوسي و كسينوسی در حالت كلي به صورت\(y = a\sin \left[ {b(t - c)} \right] + d\) و \(y = a\cos \left[ {b(t - c)} \right] + d\)ميباشد كه مقدار c نمايشگر تعداد واحدي است كه \(y = a\sin (bt)\) و\(y = a\cos (bt)\)در راستاي محور طولها انتقال می یابند . هرگاه \(a > 0\)انتقال به طرف راست محور طول ها و هرگاه\(a < 0\)انتقال در جهت چپ محور طول ها صورت ميگيرد d تعداد واحدي است كه توابع\(y = a\sin \left[ {b(t - c)} \right] + d\) و\(y = a\cos \left[ {b(t - c)} \right] + d\) در راستاي محور عرض ها منتقل ميشود. اگر \(a > 0\)انتقال به طرف بالا و اگر \(b < 0\)انتقال در جهت پايين صورت ميگيرد.
مثال
معادله تابع مربوط به نمودار مثلاتي زير كه در يك دورهي تناوب رسم شده است را بنويسيد ( با شرط\(a > 0\))
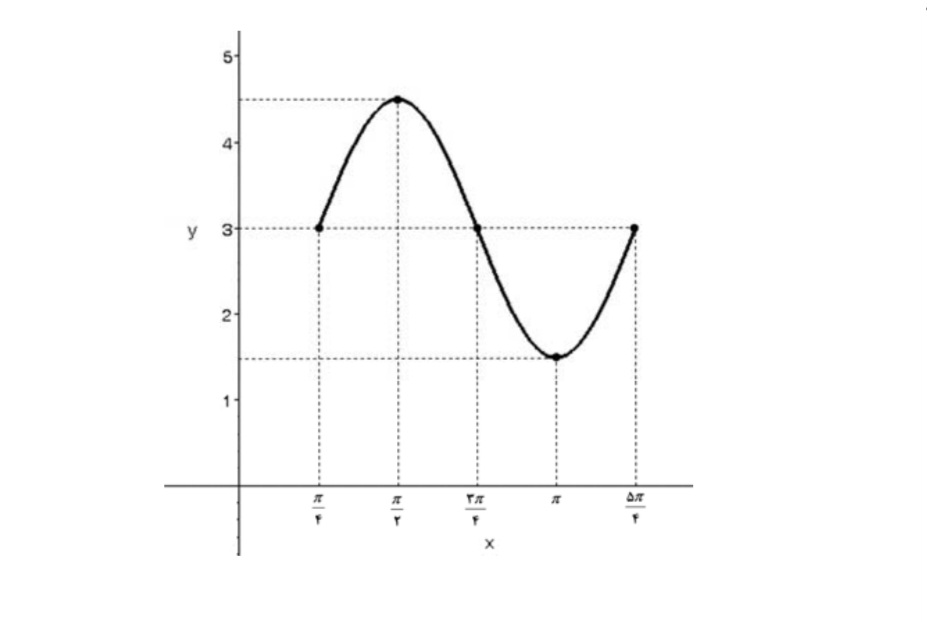
\(\begin{array}{l}a = \frac{{4/5 - 1/5}}{2} = 1/5\\\\t = \frac{{5\pi }}{4} - \frac{\pi }{4} = \pi \Rightarrow \frac{{2\pi }}{b} = \pi \Rightarrow b = 2\end{array}\)
همچنين با توجه به شكل، نمودار شبيه نمودار سينوسي است كه از\(\pi = \frac{\pi }{4}\) شروع شده است. يعني موج سينوسي به اندازه \(\frac{\pi }{4}\)به طرف راست منتقل شده است . پس \(c = \frac{\pi }{4}\)و مقدار d نيز برابر است با:
\(d = \frac{{\max y + \min y}}{2} = \frac{{4/5 + 1/5}}{2} = 3\)
در نتيجه معادله ي تابع به صورت زير است:
\(y = 1/5\sin \left[ {2(t - \frac{\pi }{4})} \right] + 3\)
مثال
ارتفاع يك موج سوار نسبت به سطح زمين در حركت بر روي آب از رابطه ی
\(h(t) = 10\sin \left[ {\frac{\pi }{{30}}\left( {t - 15} \right)} \right] + 12\)
بدست می آيد)hبرحسب متر و t برحسب ثانيه)
الف) بيشترين و كمترين ارتفاع موج سوار چقدر است؟
ب) چه مدت طول ميكشد تا موج سوار از نقطه با كمترين ارتفاع به نقطه با بيشترين ارتفاع برسد؟
ج)چه مدت طول ميكشد تا يك حركت نوساني كامل انجام گیرد؟
د ) در طول يك دقيقه در چه زمانهايي ارتفاع موج سوار نسبت به سطح زمين 17 متر خواهد بود؟
الف)
\(\begin{array}{l}\max h = 10 + 12 = 22\\\\\max h = 12 - 10 = 2\end{array}\)
ب)
\(\begin{array}{l}10\sin \left[ {\frac{\pi }{{30}}(t - 15)} \right] + 12 = 22 \Rightarrow \sin \left[ {\frac{\pi }{{30}}(t - 15)} \right] = 1\\\\ \Rightarrow \frac{\pi }{{30}}(t - 15) = \frac{\pi }{2} \Rightarrow t - 15 = 15 \Rightarrow 15 \Rightarrow at = 3\\\\10\sin \left[ {\frac{\pi }{{30}}(t - 15)} \right] + 12 = 2 \Rightarrow \sin \frac{\pi }{{30}}(t - 15) = 1\\\\\frac{\pi }{{30}}(t - 15) = - \frac{\pi }{2} \Rightarrow t - 15 = - 15 \Rightarrow t = 0\end{array}\)
ج)
\(t = \frac{{2\pi }}{b} = \frac{{2\pi }}{{\frac{\pi }{{30}}}} = 60s\)
با استفاده از قسمت ب نيز ميتوان تشخيص داد كه دوره تناوب \(2 \times 30 = 60\) ثانیه می شود
د)
\(h(t) = 17 \Rightarrow \left( {} \right)\sin \left[ {\frac{\pi }{{30}}(t - 15)} \right] = \frac{1}{2} \Rightarrow \frac{\pi }{{30}}(t - 15) = \frac{\pi }{6},\frac{\pi }{{30}}(t - 15) = \frac{{5\pi }}{6} \Rightarrow t = 20,t = 40\)
يكي ديگر از توابع مثلثاتي\(y = \tan x\)است كه از رابطه \(\tan x = \frac{{\sin x}}{{\cos x}}\)به دست مي آيد. بنابراين \(\tan x\)به ازاي x هايي که \(\cos x = 0\)تعريف نمي شود . يعني تانژانت زوايايي كه 2 كمان آن ها بر حسب راديان به صورت \(x = k\pi + \frac{\pi }{2}\)تعريف نمي شوند. بنابراين دامنه تابع تانژانت برابر است با\(R - \left\{ {\left. x \right|} \right.x = k\pi + \left. {\frac{\pi }{2}} \right\},k \in z\)،و با توجه به اینکه \(\tan (x + \pi ) = \tan x\)دوره تناوب تابع تانژانت \(t = \pi \) مي باشد.
يكي ديگر از توابع مثلثاتي \(y = \cot x\) است كه برابر است با \(y = \frac{1}{{\tan x}}\)و چون \(\cot x = \frac{{\cos x}}{{\sin x}}\)بنابراين تابع \(y = \cot x\)به ازاي هر x كه \(\sin x = 0\) تعريف نمي شود. يعني دامنه ي تابع كتانژانت برابر است با \(D = R - \left\{ {\left. x \right|} \right.x = k\left. \pi \right\},k \in z\)
نمودار تابع \(y = \tan x\)در فاصله ي \( - \frac{{3\pi }}{2} < x < \frac{{3\pi }}{2}\)به صورت زير ميباشد :
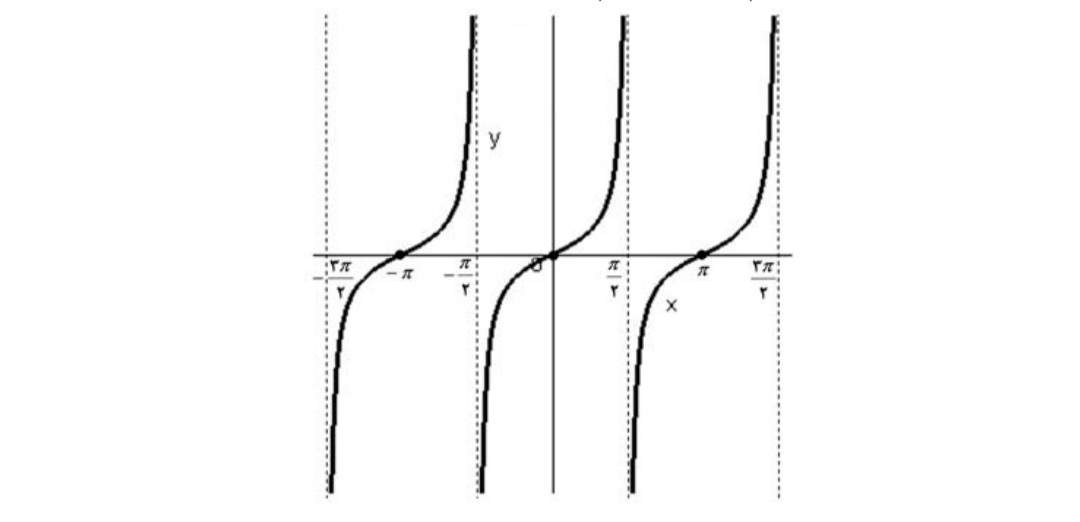
ديده ميشود كه هر شاخه در فاصله هاي به طول π تكرار ميگردد. واضح است كه هر شاخه از منحني صعودي است . اما تابع در دامنه اش نه صعودي و نه نزولي است
همچنين نمودار تابع\(y = \cot x\) در فاصله ي \( - \pi < x < \pi \)به صورت زير ميباشد:
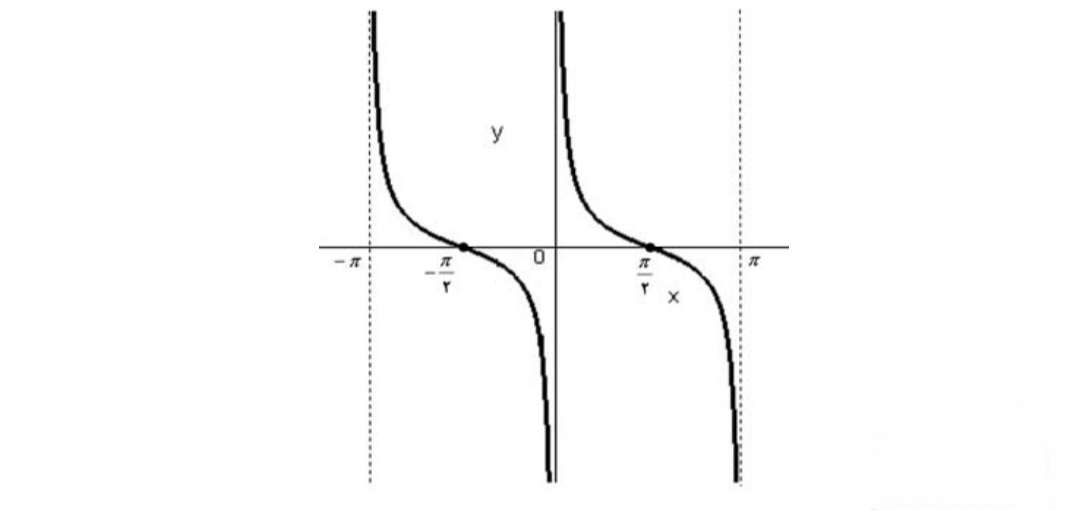
واضح است كه هر شاخه از منحني نزولي است
مثال
اگر \(0 < x < \frac{\pi }{2}\) و آنگاه مقادیر تابع \(y=tanx\) در بازه ی قرار دارند
مثال
اگر \( - \pi < x < \frac{{ - \pi }}{2}\)و \(\tan \alpha = \frac{2}{{m - 1}}\) آنگاه مقادیر تابع در بازه ي (∞ +, 0) قرار ميگيرند
روابط زير بين توابع مثلثاتي برقرار است ( اتحادهاي مثلثاتي)
\(\begin{array}{l}1)\sin 2\alpha = 2\sin \alpha \cos \alpha \\\\2)\cos 2\alpha = {\cos ^2}\alpha - {\sin ^2}\alpha = 1 - 2{\sin ^2}\alpha = 2{\cos ^2}\alpha - 1\\\\3){\sin ^2}\alpha = \frac{{1 - {{\cos }^2}\alpha }}{2}\\\\4){\cos ^2}\alpha = \frac{{1 + {{\cos }^2}\alpha }}{2}\\\\5){\mathop{\rm s}\nolimits} {\tan ^2}\alpha = \frac{{2{{\tan }^2}\alpha }}{2}\\\\6)\sin (\alpha \pm \beta ) = \sin \alpha \cos \beta \pm \cos \alpha \sin \beta \\\\7){\mathop{\rm s}\nolimits} \cos (\alpha \pm \beta ) = {\mathop{\rm s}\nolimits} \cos \alpha \sin \beta \pm \sin \alpha \sin \beta \\\\8)\tan (\alpha \pm \beta ) = \frac{{\tan \alpha \pm \tan \beta }}{{1 \pm \tan \alpha \tan \beta }}\end{array}\)
مثال
درستي اتحادهاي زير را بررسي كنيد.
\(\begin{array}{l}\sin 2x = \frac{{2\tan x}}{{1 + {{\tan }^2}x}}\\\\\cos 2x = \frac{{1 - {{\tan }^2}x}}{{1 + {{\tan }^2}x}}\\\\\frac{{2\sin 2x}}{{2{{\cos }^2}x + 1}} = \frac{{\sin x}}{{2\cos x - 1}} + \frac{{\sin x}}{{2\cos x + 1}}\end{array}\)
\(\begin{array}{l}\frac{{2\tan x}}{{1 + {{\tan }^2}x}} = \frac{{\frac{{2\sin x}}{{\cos x}}}}{{\frac{1}{{{{\cos }^2}x}}}}\\\\\frac{{1 - {{\tan }^2}x}}{{1 + {{\tan }^2}x}} = \frac{{\frac{{1 - {{\sin }^2}x}}{{{{\cos }^2}x}}}}{{\frac{1}{{{{\cos }^2}x}}}} = \frac{{{{\cos }^2}x - {{\sin }^2}x}}{{{{\cos }^2}x}} = {\cos ^2}x - {\sin ^2}x = {\cos ^2}x\\\\\frac{{\sin x}}{{2\cos x - 1}} + \frac{{\sin x}}{{2\cos x + 1}} = \frac{{2\sin x\cos x + 2\sin x\cos x - \sin x}}{{4{{\cos }^2}x - 1}} = \frac{{4\sin x\cos x}}{{4{{\cos }^2} - 1}} = \frac{{2\sin 2x}}{{2(2{{\cos }^2}x - 1) + 1}} = \frac{{2\sin 2x}}{{2\cos 2x + 1}}\\\\\cos 2x = \frac{{1 - {{\tan }^2}x}}{{1 + {{\tan }^2}x}}\\\\\frac{{2\sin 2x}}{{2{{\cos }^2}x + 1}} = \frac{{\sin x}}{{2\cos x - 1}} + \frac{{\sin x}}{{2\cos x + 1}}\end{array}\)
مثال
مقدار نسبت هاي مثلثاتي زاویه ی 75 درجه را بيابيد.
\(\begin{array}{l}\sin 75 = \sin (45 + 30) = \sin 45\cos 30 + \cos 45\sin 30 = \frac{{\sqrt 2 }}{2}(\frac{{\sqrt 3 }}{2} + \frac{1}{2}) = \frac{{\sqrt 6 + \sqrt 2 }}{4}\\\\\sin 75 = \sin (45 + 30) = \cos 45\cos 30 - \sin 45\sin 30 = \frac{{\sqrt 2 }}{2}(\frac{{\sqrt 3 }}{2} - \frac{1}{2}) = \frac{{\sqrt 6 - \sqrt 2 }}{2}\\\\\tan 75 = \sin (45 + 30) = \frac{{\tan 45 + \tan 30}}{{1 - \tan 45\tan 30}} = \frac{{1 + \frac{{\sqrt 3 }}{{\sqrt 3 }}}}{{1 - \frac{{\sqrt 3 }}{{\sqrt 3 }}}} = \frac{{3 + \sqrt 3 }}{{3 - \sqrt 3 }}\\\\\cot 75 = \frac{1}{{\tan 75}} = \frac{{3 - \sqrt 3 }}{{3 + \sqrt 3 }}\end{array}\)
روابط مثلثاتي زير همواره برقرار است:
قوانين ضرب به جمع
\(\begin{array}{l}1)\sin \alpha \cos \beta = \frac{1}{2}\left[ {\sin (\alpha + \beta ) + \sin (\alpha - \beta )} \right]\\\\2)\sin \alpha \cos \beta = \frac{1}{2}\left[ {\cos (\alpha - \beta ) - \cos (\alpha + \beta )} \right]\\\\3)\cos \alpha - \sin \beta = \frac{1}{2}\left[ {\cos (\alpha + \beta ) + \cos (\alpha - \beta )} \right]\end{array}\)
قوانين جمع به ضرب
\(\begin{array}{l}1)\sin \alpha + \cos \beta = 2\left[ {\cos (\frac{{\alpha + \beta }}{2})\cos (\frac{{\alpha - \beta }}{2})} \right]\\\\2)\sin \alpha + \sin \beta = 2\sin (\frac{{\alpha + \beta }}{2})\cos (\frac{{\alpha - \beta }}{2})\\\\3)\cos \alpha - \cos \beta = - 2\sin (\frac{{\alpha + \beta }}{2})\sin (\frac{{\alpha - \beta }}{2})\\\end{array}\)
اثبات روابط فوق به عنوان تمرين واگذار ميگردد.
مثال
\(\begin{array}{l}\sin x + \cos x = \sin x + \sin (\frac{\pi }{2} - x) = \\2\sin \frac{\pi }{4}\cos \frac{{x - \frac{\pi }{2} + x}}{2} = \sqrt 2 \cos (\frac{\pi }{4} - x) = \sqrt 2 \cos (\frac{\pi }{4} + x)\end{array}\)
مثال
\(\begin{array}{l}\sin x - \cos x = \sin x - \sin (\frac{\pi }{2} - x) = \sin x + \sin (x - \frac{\pi }{2})\\\\2\sin \frac{{x + x - \frac{\pi }{2}}}{2}\cos \frac{\pi }{4} = \sqrt 2 \sin (x - \frac{\pi }{4}) = \\\\\sqrt 2 \cos (\frac{{3\pi }}{4} - x)\end{array}\)
مثال
درستي اتحادهاي زير را تحقيق كنيد.
\(\begin{array}{l}\frac{{\sin 7x + \sin x}}{{\cos 7x + \cos x}} = \tan 4x\\\\\cos 5x\cos 2x + \sin 4x\sin 3x - \cos 4x\cos x = \sin 2x\sin 3x\end{array}\)
الف)
\(\begin{array}{l}\frac{{\sin 7x + \sin x}}{{\cos 7x + \cos x}} = \frac{{2\sin (\frac{{7x + x}}{2})\cos (\frac{{7x - x}}{2})}}{{2\cos (\frac{{7x + x}}{2})\cos (\frac{{7x - x}}{2})}} = \frac{{\sin 4x}}{{\cos 4x}} = \tan 4x\\\\\cos 5x\cos 2x + \sin 4x\sin 3x - \cos 4x\cos x = \sin 2x\sin 3x\\\\\\\\\\\cos 5x\cos 2x + \sin 4x\sin 3x - \cos 4x\cos x = \sin 2x\sin 3x\end{array}\)
ب)
\(\begin{array}{l}\cos 5x\cos 2x + \sin 4x\sin 3x - \cos 4x\cos x = \frac{1}{2}\left[ {\cos (5x + 2x) + \cos (5x - 2x)} \right]\\\\ + \frac{1}{2}\left[ {\cos (4x - 3x) + \cos (4x + 3x)} \right]\\ - \frac{1}{2}\left[ {\cos (4x + x) + \cos (4x - x)} \right]\\ = \frac{1}{2}\left[ {\cos 7x + \cos 3x + \cos x - \cos 7x - \cos 5x - \cos 3x} \right]\\\\ = \frac{1}{2}\left[ {\cos x - \cos 5x} \right]\\\\ = \frac{1}{2}( - 2)\sin (\frac{{x + 5x}}{2})\sin (\frac{{x0 - 5x}}{2})\\\\ - \sin 3x\sin ( - 2x)\\\\ = \sin 3x\sin 2x\end{array}\)
حل 4 معادله ي مثلثاتي اصلي به صورت هاي زير است:
\(\begin{array}{l}1)\sin x = \sin \alpha \Rightarrow x = 2k\pi + \alpha ,x = 2k\pi + \pi - \alpha \\\\2)\cos x = \cos \alpha \Rightarrow x = 2k\pi \pm \alpha \\\\3)\tan x = \tan \alpha \Rightarrow k\pi \pm \alpha \\\\4)\cot x = \cot \alpha \Rightarrow k\pi \pm \alpha \end{array}\)
مثال
معادلات مثلثاتي زير را حل كنيد
\(\begin{array}{l}2{\cos ^2}\theta + \cos \theta = 1\\\\1 - 3\cos 2x = 2{\sin ^2}x\\\\4\tan x + cotx = 5\end{array}\)
الف)
\(\begin{array}{l}2{\cos ^2}\theta + \cos \theta = 1 \Rightarrow 2{\cos ^2}\theta + \cos \theta - 1 = 0 \Rightarrow \\\\(2\cos - 1)(\cos \theta + 1) = 0 \Rightarrow \\\\\left\{ \begin{array}{l}2{\cos ^2}\theta - 1 = 0 \Rightarrow \cos \theta = \frac{1}{2} = \cos \frac{\pi }{3} \Rightarrow \theta = 2k\pi \pm \frac{\pi }{3}\\\\(\cos \theta + 1) = 0 \Rightarrow \cos \theta = - 1 = \cos \pi \Rightarrow \theta = 2k\pi + \pi \end{array} \right.\end{array}\)
ب)
 \(\begin{array}{l}1 - 3(1 - 2{\sin ^2}x) = 2{\sin ^2}x \Rightarrow 1 - 3 + 2 = 6{\sin ^2}x = 2{\sin ^2}x \Rightarrow + 4{\sin ^2}x = + 2\\\\ \Rightarrow {\sin ^2}x = \frac{1}{2} \Rightarrow \sin x = \pm \frac{{\sqrt 2 }}{2}\\\\\sin x = \frac{{\sqrt 2 }}{2} \Rightarrow \sin x = \sin \frac{\pi }{4} \Rightarrow x = 2k\pi + \frac{\pi }{4}\\\\\sin x = \frac{{ - \sqrt 2 }}{2} \Rightarrow \sin x = \sin ( - \frac{\pi }{4}) \Rightarrow x = 2k\pi - \frac{\pi }{4},x = 2k\pi + \frac{{5\pi }}{4}\\\end{array}\)
\(\begin{array}{l}1 - 3(1 - 2{\sin ^2}x) = 2{\sin ^2}x \Rightarrow 1 - 3 + 2 = 6{\sin ^2}x = 2{\sin ^2}x \Rightarrow + 4{\sin ^2}x = + 2\\\\ \Rightarrow {\sin ^2}x = \frac{1}{2} \Rightarrow \sin x = \pm \frac{{\sqrt 2 }}{2}\\\\\sin x = \frac{{\sqrt 2 }}{2} \Rightarrow \sin x = \sin \frac{\pi }{4} \Rightarrow x = 2k\pi + \frac{\pi }{4}\\\\\sin x = \frac{{ - \sqrt 2 }}{2} \Rightarrow \sin x = \sin ( - \frac{\pi }{4}) \Rightarrow x = 2k\pi - \frac{\pi }{4},x = 2k\pi + \frac{{5\pi }}{4}\\\end{array}\)
چهار جواب معادله ي مثلثاتي فوق را ميتوان به صورت زير خلاصه كرد:
\(x = k\pi + \frac{\pi }{4},k \in z\)
ج)
\(\begin{array}{l}4\tan x + \cot x = 5 \Rightarrow 4\tan x + \frac{1}{{\tan x}} = 5 \Rightarrow 4{\tan ^2}x + 1 = 5\tan x(x \ne \frac{{k\pi }}{2})\\\\ \Rightarrow 4{\tan ^2}x - 5\tan x + 1 = 0\left\{ \begin{array}{l}\tan x = 1 = \tan \frac{\pi }{4} \Rightarrow x = k\pi + \frac{\pi }{4}\\\\\tan x = \frac{1}{4} = \tan \alpha \Rightarrow x = k\pi + \alpha \end{array} \right.\end{array}\)
چون كوچكترين زاويه اي كه مقدار تانژانت آن برابر با\(\frac{1}{4}\)  است را بدون ماشين حساب نميتوان يافت از 1 زاويه αاستفاده كرديم.
است را بدون ماشين حساب نميتوان يافت از 1 زاويه αاستفاده كرديم.
تهیه کننده: حامد دلیجه
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه یازدهم- آزمون آنلاین تمامی دروس پایه یازدهم
- گام به گام تمامی دروس پایه یازدهم
- ویدئو های آموزشی تمامی دروس پایه یازدهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه یازدهم
- فلش کارت های آماده دروس پایه یازدهم
- گنجینه ای جامع از انشاء های آماده پایه یازدهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه یازدهم
حل معادلات مثلثاتي به روش نمودار
حل معادلات مثلثاتي به روش نمودار
بعضي از معادلات مثلثاتي از طريق جبري قابل حل نيستند و فقط با استفاده از رسم نمودار ميتوان تعداد جوابها را بدست آورد و مقدار آنها را تخمين زد.
مثال
معادله\(\sin x + 2x = 1\) را حل كنيد.
ابتدا معادله را به صورت \(\sin x = - 2x + 1\)مينويسيم . سپس نمودارهاي\(f(x) = \sin x\)و\(g(x) = - 2x + 1\)را رسم ميكنيم طول نقاط تلاقي اين دو نمودار جواب معادله مورد نظر ميباشد.
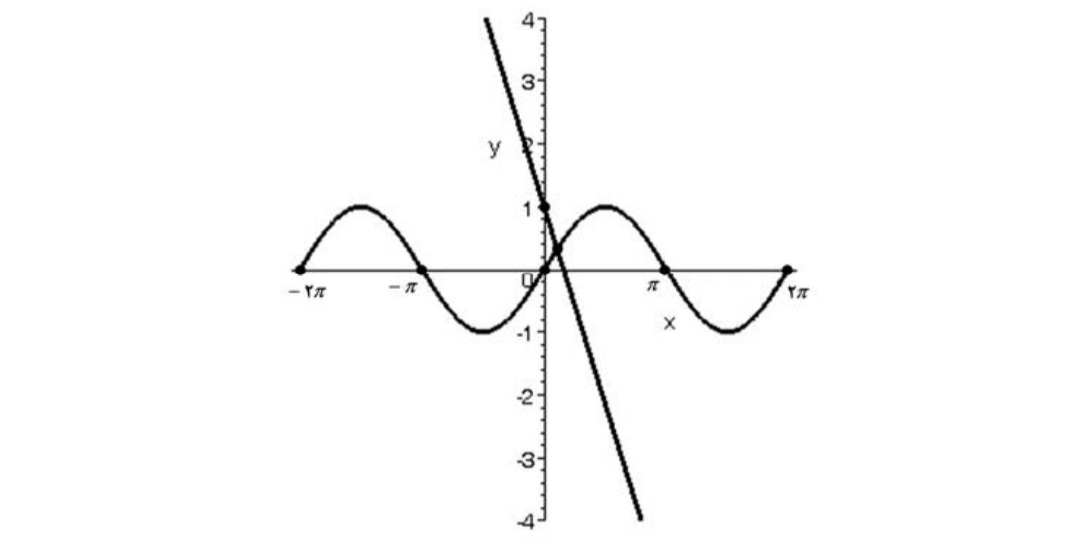
همانطوركه مشاهده ميكنيد معادله يك جواب دارد كه بين صفر و\(\frac{\pi }{2}\) است با روش آزمايش و خطا π ميتوان جواب تقريبي را بدست آورد .
مثلا:
\(\begin{array}{l}x = \frac{\pi }{4} \Rightarrow \left\{ \begin{array}{l}f(\frac{\pi }{4}) = \sin \frac{\pi }{4} = \frac{{\sqrt 2 }}{2} \approx \frac{{1/4}}{2} = 0/7\\\\g(x) = - \frac{\pi }{2} + 1 \approx \frac{{3/14}}{2} + 1 = - 0/75\end{array} \right.\\\\x = \frac{\pi }{6} \Rightarrow \left\{ \begin{array}{l}f(\frac{\pi }{6}) = \sin \frac{\pi }{6} = \frac{1}{2}\\\\g(x) = - \frac{\pi }{3} + 1 \approx - \frac{{3/14}}{2} + 1 = - 0/05\end{array} \right.\\x = 15^\circ = \frac{\pi }{{12}} \Rightarrow \left\{ \begin{array}{l}f(\frac{\pi }{{12}}) = \sin 15^\circ \approx 0/25\\g(x) - \frac{\pi }{6} + 1 \approx \frac{{2/86}}{6} = 0/48\end{array} \right.\end{array}\)
\(\)ً
لذا جواب معادله ي فوق نزديك به \(\frac{\pi }{{12}} \approx 026\) است و با ادامه ي اين روش و با استفاده از ماشين حساب ميتوان تقريب هاي بهتري يافت.
تهیه کننده: حامد دلیجه
جزوات جامع پایه یازدهم
جزوه جامع حسابان یازدهم فصل 1 جبر و معادله
جزوه جامع حسابان یازدهم فصل 2 تابع
جزوه جامع حسابان یازدهم فصل 3 توابع نمایی و لگاریتمی
جزوه جامع حسابان یازدهم فصل 4 مثلثات
جزوه جامع حسابان یازدهم فصل 5 حد و پیوستگی
وارون معادله مثلثاتی
وارون توابع مثلثاتي
ميدانيم تابعي وارون پذير است كه يك به يك باشد بنابراين براي بدست آوردن وارون توابع مثلثاتي كه يك به يك نيستند، بايد دامنه ي آنها را تحديد كنيم تا آنها تبديل به يك تابع يك به يك شوند.
تحديد تابع \(y = \sin x\)به بازه ي \(\left[ { - \frac{\pi }{2},\frac{\pi }{2}} \right]\)يك به يك بوده و معكوس پذير است.
\(y = \sin x,x \in \left[ { - \frac{\pi }{2},\frac{\pi }{2}} \right]\)
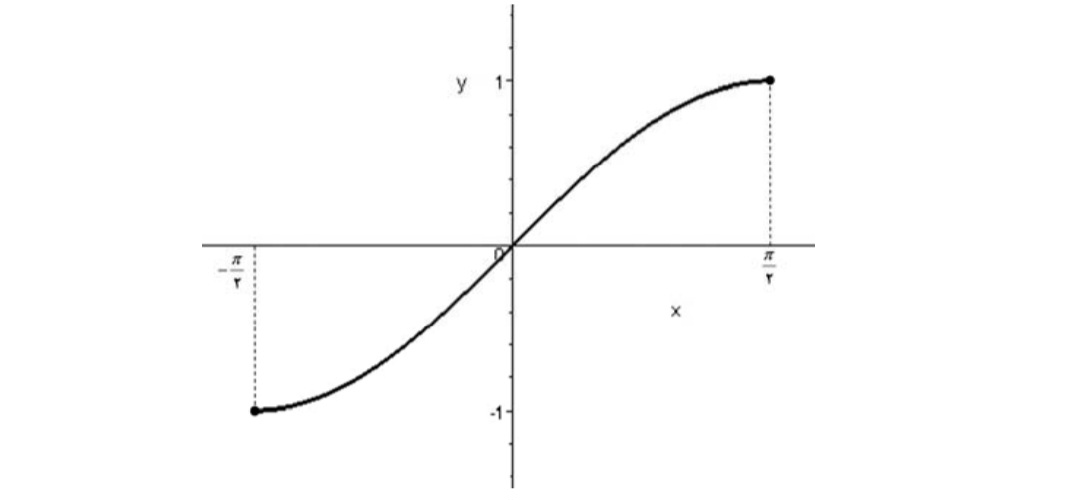
معكوس \(y = \sin x\)را با نمادهاي \(y = \arcsin x\)يا \(y = si{n^{ - 1}}\)
نمایش می دهیم پس:
\(y = si{n^{ - 1}}x:\left[ { - 1,1} \right] \to \left[ { - \frac{\pi }{2},\frac{\pi }{2}} \right]\)
نمودار آن بصورت زیر است:
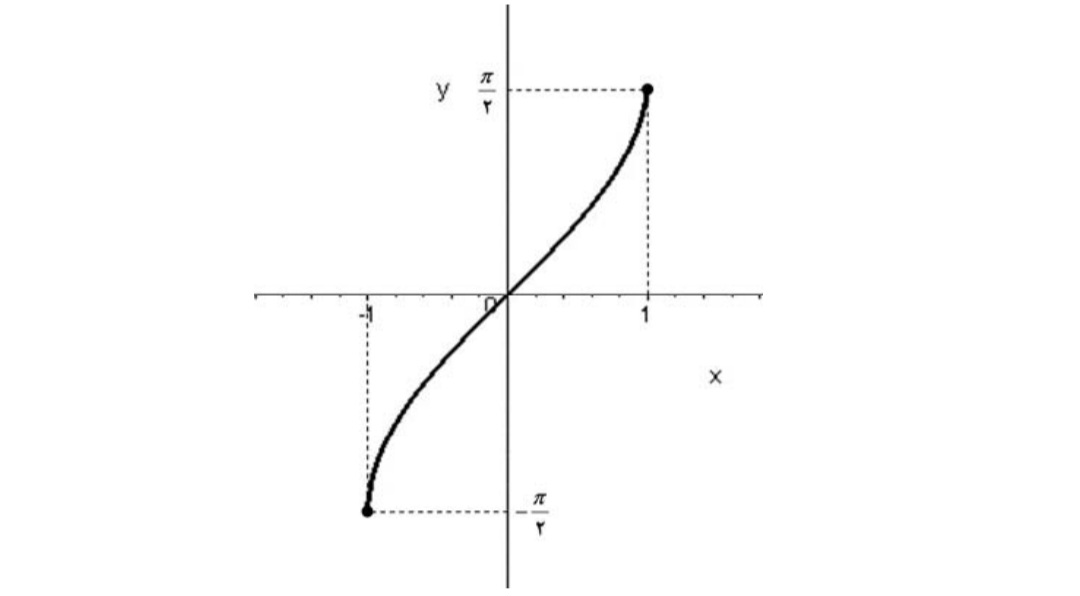
تحدید تابع \(y = \cos x\) به بازه ی \(( {-0,\pi } )\)یک به یک بوده و معکوس پذیر است.
\(y = \cos x,x \in \left[ {0,\pi } \right]\)
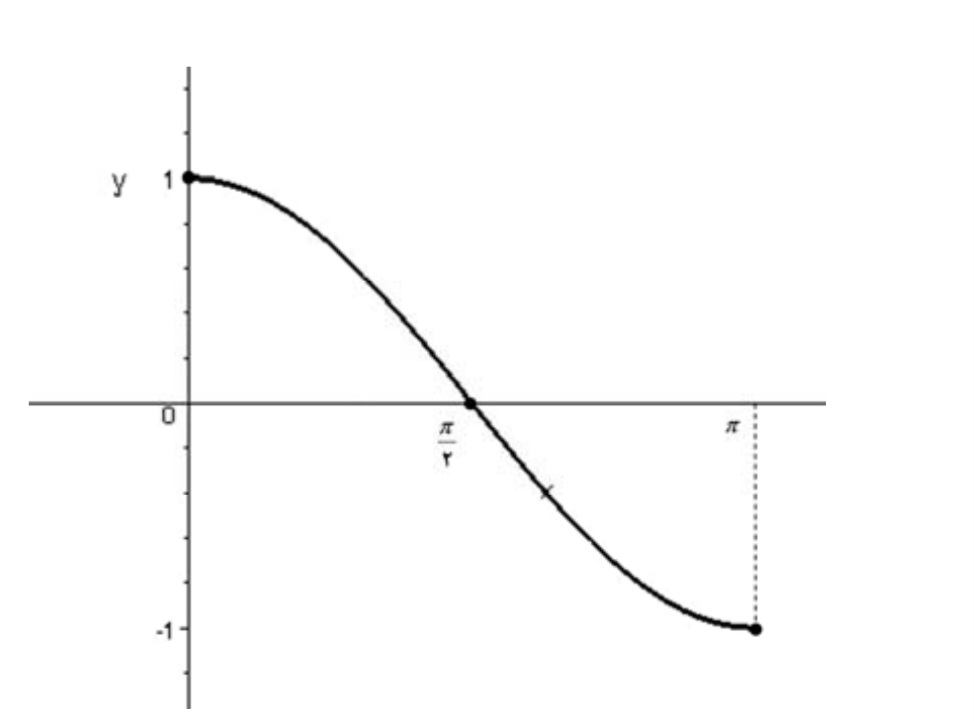
\(y = \cos x\)معکوس را با نماد های\(y = ars\cos x\)یا \(y = {\cos ^{ - 1}}x\)نمایش میدهیم پس
\(y = {\cos ^{ - 1}}x:\left[ { - 1,1} \right] \to \left[ {0,\pi } \right]\)
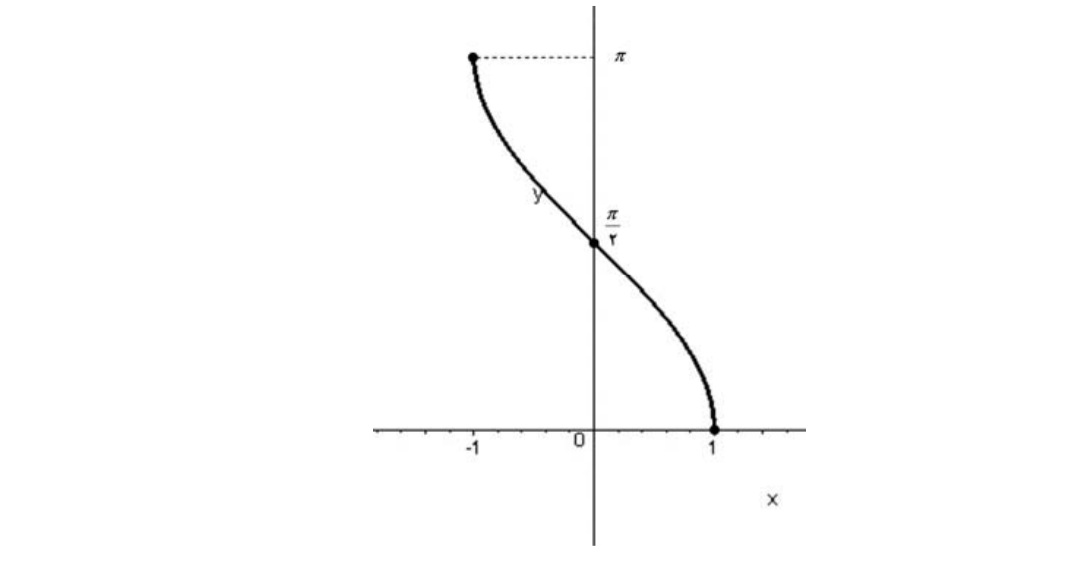
و نمودار آن به صورت زیر است:
تحدید تابع\(y=tanx\) به بازه ی \(( - \frac{\pi }{2},\frac{\pi }{2})\)یک به یک بوده و معکوس پذیر است
\(y = \tan x,x \in ( - \frac{\pi }{2},\frac{\pi }{2})\)
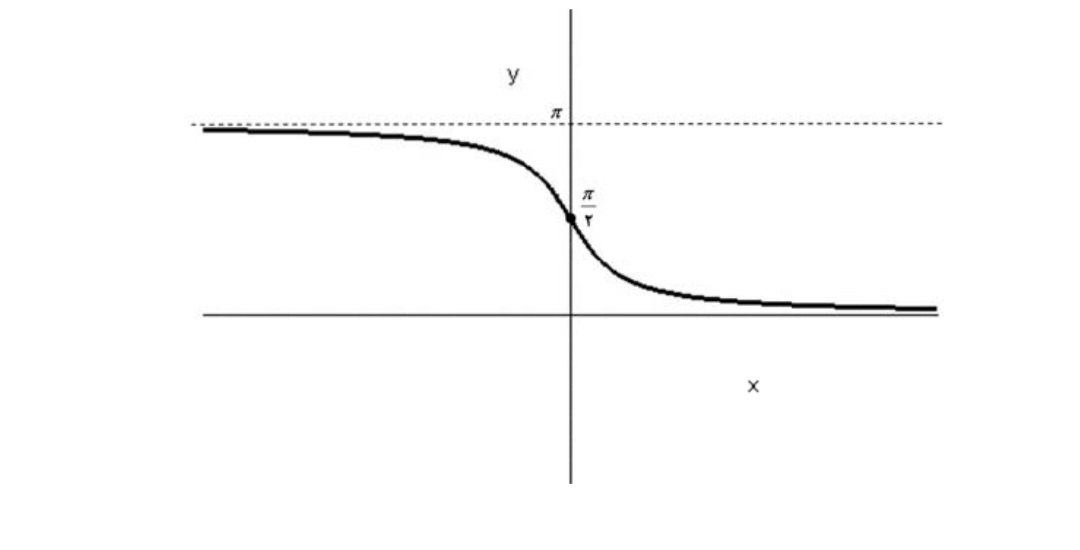
معکوس \(y = \tan x\)را با نماد های \(x = \arctan x\)یا \(y = {\tan ^{ - 1}}\) نمایش می دهیم
\(y = {\tan ^{ - 1}}x:R \to ( - \frac{\pi }{2},\frac{\pi }{2})\)
تابع \(y=cotx\)به بازه ی \((0,\pi )\)يك به يك بوده و معكوس پذير است.
\(y = \cot x,x \in \left( {0,\pi } \right)\)
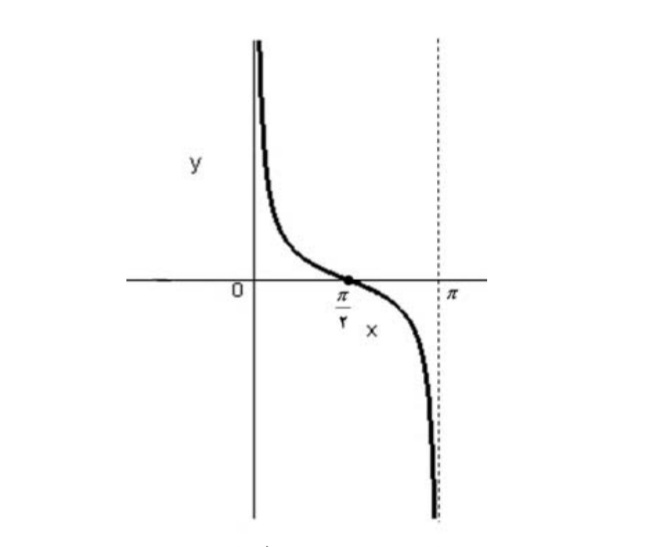
معكوس \(y = \cot x\) را با نمادهاي \(y = arc\cot x\)يا\(y = {\cot ^{ - 1}}x\)
\(y = \cot x\) را با نمادهاي \(y = arc\cot x\)يا\(y = {\cot ^{ - 1}}x\)
نمایش میدهیم پس:
\(y = {\cot ^{ - 1}}x:R \to (0,\pi )\)
و نمودار آن به صورت زير است:
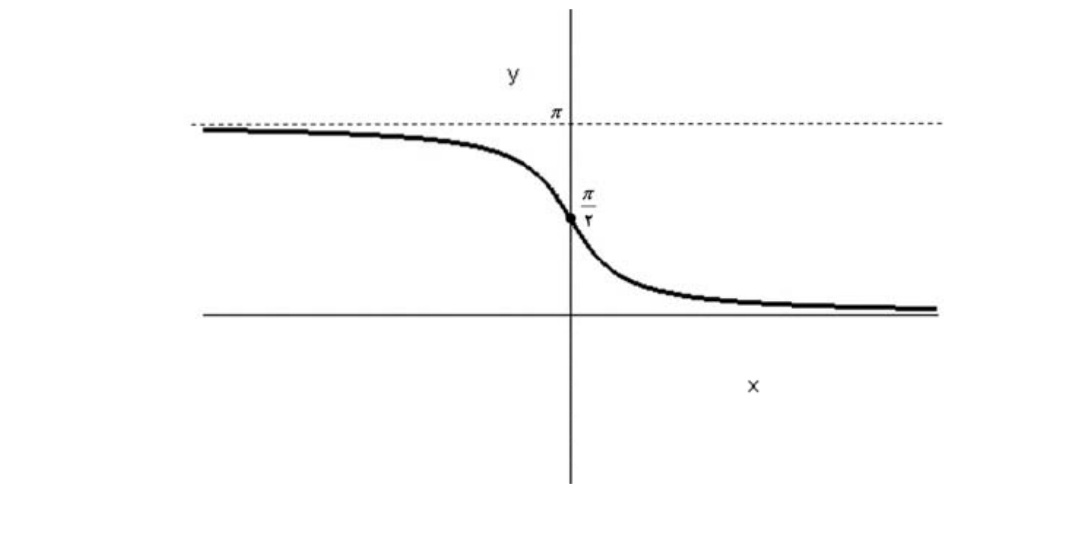
مثال
حاصل عبارتهاي زير را بدست آوريد.
\(\cos \left[ {2{{\sin }^{ - 1}}} \right.( - \frac{{\sqrt 3 }}{2}) + {\cos ^{ - 1}}(\frac{{ - 1}}{2}\left. ) \right]\)(الف
\(\cos \left[ {{{\sin }^{ - 1}}} \right.( - \frac{4}{2}))\)(ب
\({\sin ^{ - 1}}\left( a \right) = b\)یعنی\(\sin b = a\) به این توضیح داریم:
\({\cos ^{ - 1}}(\frac{{\sqrt 2 }}{2}) = \frac{\pi }{4}\) \({\sin ^{ - 1}}\left( 0 \right) = 0\)
\({\cot ^{ - 1}}( - 1) = \frac{{3\pi }}{4}\) \({\tan ^{ - 1}}(1) = \frac{\pi }{4}\)
تهیه کننده: حامد دلیجه



1736019749.png)















