درسنامه کامل ریاضی ششم فصل 2 کسر
تعداد بازدید : 7.26Mخلاصه نکات ریاضی ششم فصل 2 کسر - درسنامه شب امتحان ریاضی ششم فصل 2 کسر - جزوه شب امتحان ریاضی ششم نوبت اول فصل 2 کسر
کسرها
مفهوم کسر
به جزئی یا قسمتی از یک واحد ،کامل کسری از آن واحد گفته میشود بنابراین کسری از کل یعنی جزئی یا قسمتی از آن کل
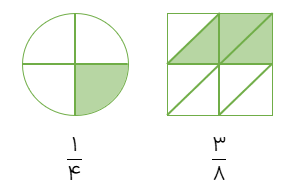
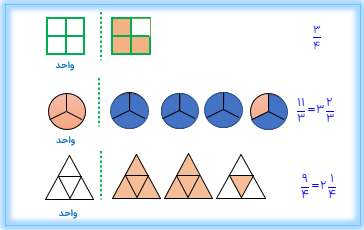
در شکل مقابل \(\frac{1}{4}\) دایره و \(\frac{3}{8}\)مربع رنگ شده است.
\(\frac{1}{4}\)یعنی یک قسمت از ۴ قسمت مساوی.
\(\frac{3}{8}\)یعنی سه قسمت از ۸ قسمت مساوی.
عدد مخلوط
اگر صورت کسر بزرگ تر از واحدی بر مخرجش بخش پذیر نباشد آن کسر را میتوان به صورت عدد مخلوط (ترکیبی از عدد صحیح و کسر) نوشت.
مثال
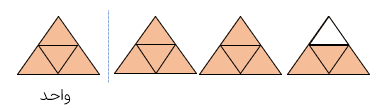
عدد مخلوط ۲۳ را به وسیله ی شکل نمایش دهید.
عدد مخلوط ۲۲ با کسر\(\frac{{11}}{4}\)برابر است.
شکل درست یک عدد مخلوط این است که حتما کسر نوشته شده در عدد مخلوط کوچک تر از واحد باشد.
مثال
شکل درست عدد مخلوط \(3\frac{5}{2}\) را بنویسید.
\(\frac{5}{2} = 2\frac{1}{2} \to 3\frac{5}{2} = 3 + 2\frac{1}{2} = 5\frac{1}{2}\)
کسرهای مساوی
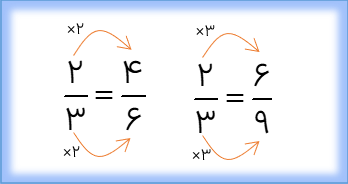
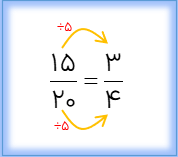
اگر صورت و مخرج کسری را در عدد طبیعی بزرگ تر از ۱ ضرب و یا بر عدد. ر عدد طبیعی بزرگ تر از یک تقسیم کنیم، کسری مساوی کسر اولیه به دست می آید.
کسر\(\frac{3}{4}\)با \(\frac{{15}}{{20}}\) کسر مساوی است.
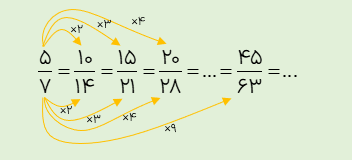
برای هر کسر، بی شمار کسر مساوی می توان نوشت:
\(\frac{{{3_{ \times 2}}}}{{{4_{ \times 2}}}} = \frac{6}{8} = \frac{9}{{12}} = \frac{{12}}{{16}} = \frac{{15}}{{20}} = \frac{{18}}{{24}} = \frac{{21}}{{28}} = ...\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه ششم- آزمون آنلاین تمامی دروس پایه ششم
- گام به گام تمامی دروس پایه ششم
- ویدئو های آموزشی تمامی دروس پایه ششم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ششم
- فلش کارت های آماده دروس پایه ششم
- گنجینه ای جامع از انشاء های آماده پایه ششم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ششم
مخرج مشترک
کوچک ترین مخرج مشترک دو یا چند کسر
اگر دو یا چند کسر داشته باشیم و بزرگترین مخرج این ،کسرها بر بقیه ی مخرجها بخش پذیر باشد، همان مخرج بزرگتر کوچک ترین مخرج مشترک کسرها می شود.
مثال
کوچک ترین مخرج مشترک کسرهای\(\frac{1}{2},\frac{5}{6},\frac{6}{7},\frac{3}{{14}},\frac{{11}}{{21}},\frac{5}{{42}}\) را بیابید.
چون ۴۲ بر تمامی مخرج ها بخش پذیر است پس کوچک ترین مخرج مشترک این کسرها، عدد ۴۲ است.
اگر مخرج بزرگ تر بر بقیه ی مخرجها بخش پذیر نبود میتوان با نوشتن کسرهای مساوی برای دو یا چند کسر داده شده، کوچک ترین مخرج مشترک آن ها را بیابیم.
مثال
کوچک ترین مخرج مشترک دو کسر \(\frac{5}{6},\frac{3}{4}\) را بنویسید.
\(\begin{array}{l}\frac{3}{4} = \frac{6}{8} = \frac{9}{{12}} = \frac{{12}}{{16}}\\\\\frac{5}{6} = \frac{{10}}{{12}} = \frac{{15}}{{18}}\end{array}\)
همان طور که میبینید عدد ۱۲ کوچک ترین مخرج مشترک دو کسر است.
روش بهتر برای یافتن کوچک ترین مخرج مشترک دو کسر این است که اگر بزرگ ترین مخرج بر دیگر مخرج ها بخش پذیر نبود آن را در عددهای ۲ ,۳ .۴, ۵ و ... به ترتیب ضرب کنیم تا جایی که بر مخرج یا مخرج های دیگر بخش پذیر شود.
مثال
کوچک ترین مخرج مشترک دو کسر\(\frac{4}{{15}},\frac{3}{{10}}\) را بیابید.
عدد ۳۰ بر ۱۰ بخش پذیر است، پس کوچک ترین مخرج مشترک\(\frac{4}{{15}},\frac{3}{{10}}\) عدد ۳۰ است.
۱۵×۲ = ۳۰
جزوات جامع پایه ششم
جزوه جامع ریاضی ششم فصل 1 عدد و الگوهای عددی
جزوه جامع ریاضی ششم فصل 2 کسر
جزوه جامع ریاضی ششم فصل 3 اعداد اعشاری
جزوه جامع ریاضی ششم فصل 4 تقارن و مختصات
جزوه جامع ریاضی ششم فصل 5 اندازه گیری
جزوه جامع ریاضی ششم فصل 6 تناسب و درصد
جزوه جامع ریاضی ششم فصل 7 تقریب
مقایسه ی کسرها
مقایسه ی کسرها
مثال
الف اگر دو کسر دارای مخرجهای مساوی باشند کسری بزرگ تر است که صورتش بزرگ تر باشد.
\(\begin{array}{l}\frac{5}{7} > \frac{2}{7}\\\\\frac{3}{{11}} < \frac{9}{{11}}\end{array}\)
ب اگر دو کسر دارای صورت های مساوی باشند کسری بزرگ تر است که مخرجش کوچک تر باشد.
\(\begin{array}{l}\frac{3}{4} > \frac{3}{5}\\\\\frac{9}{5} < \frac{9}{2}\end{array}\)
ج اگر دو کسر، نه صورتهای برابر و نه مخرجهای برابر داشته باشند ابتدا دو کسر را هم مخرج و یا هم صورت میکنیم و سپس آنها را مقایسه می کنیم
مثال

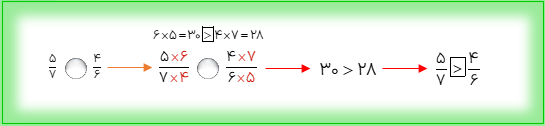
برای مقایسه ی دو کسر که صورتهای آنها برابر نباشند و مخرجهای آنها نیز برابر نباشند، از روش ساده تری به نام روش ضرب دری یا طرفین وسطین می توان استفاده کرد.
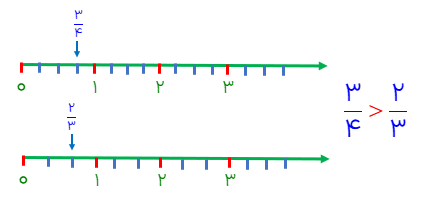
مقایسه ی کسرها توسط محور
در این روش دو محور رسم میکنیم که دقیقا واحدهای هم اندازه داشته باشند و صفرهای دو محور دقیقا زیر هم قرار گیرند.
مثال
کسرهای \(\frac{2}{3},\frac{3}{4}\) را روی محور مقایسه کنید.
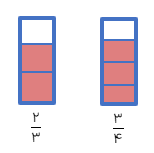
مقایسه ی دو کسر با شکل
در این روش دو واحد برابر انتخاب میکنیم و سپس با توجه به مخرج کسرها آنها را به قسمت های مساوی تقسیم کرده و سپس کسرها را روی شکل مشخص و مقایسه می کنیم
مثال
کسرهای \(\frac{2}{3},\frac{3}{4}\) را با شکل مقایسه کنید.
طبق شکل مقابل: \(\frac{2}{3} < \frac{3}{4}\)
جمع و تفریق کسرها
جمع و تفریق کسرها
به طور کلی در جمع و تفریق ،کسرها باید مخرجها مساوی باشند و اگر مخرجها مساوی نبودند، با استفاده از کوچک ترین مخرج مشترک آنها مخرجهایشان را مساوی می کنیم.
مثال
حاصل جمع و تفریق های زیر را حساب کنید.
الف \(\frac{2}{{13}} + \frac{4}{{13}}\)
\(\frac{2}{{13}} + \frac{4}{{13}} = \frac{{2 + 4}}{{13}} = \frac{6}{{13}}\)
ب \(\frac{4}{9} + \frac{2}{9}\)
\(\frac{4}{9} + \frac{2}{9} = \frac{{4 + 2}}{9} = \frac{6}{9}\)
مثال
حاصل عبارت زیر را حساب کنید و به ساده ترین صورت بنویسید.
\(\frac{2}{3} + \frac{1}{4} + \frac{5}{{12}}\)
\(\frac{2}{3} + \frac{1}{4} + \frac{5}{{12}} = \frac{8}{{12}} + \frac{3}{{12}} + \frac{5}{{12}} = \frac{{16}}{{12}} = \frac{4}{3} = 1\frac{1}{3}\)
جمع اعداد مخلوط
برای جمع اعداد مخلوط بهتر است عددهای صحیح را با هم و کسرها را نیز با هم جمع کنیم.
مثال
حاصل عبارت مقابل را حساب کنید.
\(2\frac{2}{5} + 3\frac{1}{3}\)
\(2\frac{2}{5} + 3\frac{1}{3} = (2 + 5) + (\frac{2}{5} + \frac{1}{3}) = 5 + \frac{6}{{15}} + \frac{5}{{15}} = 5\frac{{11}}{{15}}\)
تفریق اعداد مخلوط
مانند جمع اعداد مخلوط بهتر است که در تفریق ،هم عددهای صحیح را از هم کم کنیم و کسرها را نیز از هم تفریق کنیم.
مثال
حاصل عبارت زیر را حساب کنید.
\(5\frac{3}{4} - 2\frac{2}{3}\)
\(5\frac{3}{4} - 2\frac{2}{3} = (5 - 2) + (\frac{3}{4} - \frac{2}{3})3 + \frac{9}{{12}} - \frac{8}{{12}} = 3\frac{1}{{12}}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه ششم- آزمون آنلاین تمامی دروس پایه ششم
- گام به گام تمامی دروس پایه ششم
- ویدئو های آموزشی تمامی دروس پایه ششم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ششم
- فلش کارت های آماده دروس پایه ششم
- گنجینه ای جامع از انشاء های آماده پایه ششم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ششم
کسر های مساوی
کسر های مساوی
با مفهوم کسر در سال های گذشته آشنا شدید و آموختید که هرگاه جزئی از یک واحد مورد نظر باشد، آن را با کسر نشان میدهیم به مثال های زیر دقت کنید.
کسری که صورت آن بر مخرجش بخش پذیر باشد با یک عدد صحیح برابر است.
کسرهای مساوی
اگر صورت و مخرج کسری را در عددی طبیعی ضرب کنیم کسری مساوی با آن به دست می آید. به این ترتیب میتوانیم بی شمار کسر مساوی با یک کسر بنویسیم.
جمع و تفریق عددهای کسری
برای انجام جمع و تفریق بین دو یا چند کسر ابتدا باید آنها را با استفاده از یکی از روش های زیر هم مخرج کنیم، بعد از هم مخرج کردن ،کسرها یکی از مخرجها را می نویسیم و صورت کسرها را با توجه به علامت بین کسرها با هم جمع یا از هم کم می.کنیم دقت داشته باشید که گاهی اوقات یکی از مخرج ها بر دیگری بخش پذیر است، در این صورت به سادگی هر دو کسر هم مخرج می شوند.
هم مخرج کردن کسرها با استفاده از نوشتن کسرهای مساوی
در این روش از هم مخرج کردن دو ،کسر باید کسرهای مساوی با هر یک از کسرها را بنویسیم، تا جایی که به کسرهای هم مخرج برسیم.
مثال
به مثال های زیر توجه کنید.
\(\begin{array}{l}\frac{{{5_{ \times 3}}}}{{{4_{ \times 3}}}} + \frac{{{1_{ \times 2}}}}{{{6_{ \times 2}}}} = \frac{{15}}{{12}} + \frac{2}{{12}} = \frac{{15 + 2}}{{12}} = \frac{{17}}{{12}}\\\\\frac{{{5_{ \times 6}}}}{{{4_{ \times 6}}}} + \frac{{{1_{ \times 4}}}}{{{6_{ \times 4}}}} = \frac{{30}}{{24}} + \frac{4}{{24}} = \frac{{34}}{{24}} = \frac{{17}}{{12}}\end{array}\)
اگر نوشتن کسرهای مساوی را ادامه دهیم به کسرهای هم مخرج \(\frac{4}{{24}},\frac{{30}}{{24}}\) می رسیم که با جمع این دو کسر و ساده کردن جواب جمع مجددا به همان جواب قبلی می رسیم.
در مثال بالا، عددهای ۱۲ و ۲۴ مخرج های مشترک دو کسر و هستند ولی به عدد ۱۲، کوچک ترین مخرج مشترک دو کسر هم گفته میشود که استفاده از این عدد باعث ساده تر شدن محاسبات می گردد.
بنابراین برای انجام جمع و تفریق دو کسر با مخرجهای ،نابرابر بهتر است ابتدا کوچک ترین مخرج مشترک دو کسر را بیابیم، سپس جمع یا تفریق را انجام دهیم.
جزوات جامع پایه ششم
جزوه جامع ریاضی ششم فصل 1 عدد و الگوهای عددی
جزوه جامع ریاضی ششم فصل 2 کسر
جزوه جامع ریاضی ششم فصل 3 اعداد اعشاری
جزوه جامع ریاضی ششم فصل 4 تقارن و مختصات
جزوه جامع ریاضی ششم فصل 5 اندازه گیری
جزوه جامع ریاضی ششم فصل 6 تناسب و درصد
جزوه جامع ریاضی ششم فصل 7 تقریب
کوچک ترین مضرب مشترک
نوشتن مضرب های هر یک از مخرج ها
در این روش ابتدا مضرب های هر یک از مخرجها را مینویسیم اولین مضرب مشترک بین آن ها، همان کوچک ترین مخرج مشترک کسرها خواهد شد.
مثال
جمع زیر را انجام دهید.
الف)\(\frac{5}{9} + \frac{7}{6}\)
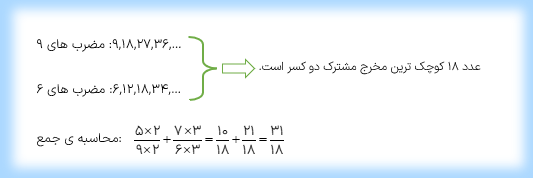
جمع و تفریق عددهای مخلوط
برای انجام جمع یا تفریق دو عدد ،مخلوط ابتدا قسمت صحیح هر دو عدد را با توجه به علامت بین عددها، با هم جمع یا تفریق میکنیم . سپس قسمت های کسری را پس از هم مخرج کردن با توجه به علامت عددها با هم جمع یا از هم کم میکنیم.
مثال
تفریق زیر را انجام دهید.
\(3\frac{1}{{24}} - 2\frac{3}{{16}}\)
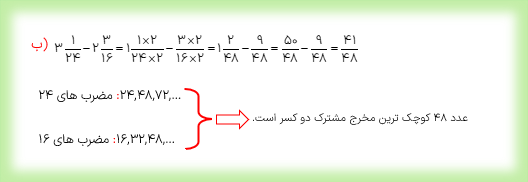
همان طور که ملاحظه نمودید گاهی اوقات در تفریق دو عدد مخلوط بعد از تفریق قسمت صحیح آن ها، قسمت کسری اولین عدد از قسمت کسری دومین عدد کوچک تر میشود و به این ترتیب تفریق امکان پذیر نمی باشد. در چنین مواقعی یک از روش های تفریق این است که مانند مثال بالا عدد مخلوط را به کسر تبدیل کنیم، سپس عملیات تفریق را انجام دهیم.
ضرب کسرها
ضرب کسرها
در ضرب دو یا چند کسر باید صورتها را در هم ضرب کنیم و در صورت کسر حاصل ضرب قرار دهیم و مخرج ها را نیز در هم ضرب کنیم و در مخرج کسر حاصل ضرب قرار دهیم.
مثال
حاصل ضرب زیر را حساب کنید.
الف \(\frac{4}{7} \times \frac{5}{{11}}\)
\(\frac{4}{7} \times \frac{5}{{11}} = \frac{{4 \times 5}}{{7 \times 11}} = \frac{{20}}{{77}}\)
ب\(\frac{2}{3} \times \frac{4}{5} \times \frac{6}{7}\)
\(\frac{2}{3} \times \frac{4}{5} \times \frac{6}{7} = \frac{{2 \times 4 \times 6}}{{3 \times 5 \times 7}} = \frac{{48}}{{105}}\)
در ضرب ،کسرها اگر بتوانیم صورت کسرها را با مخرج آنها ساده کنیم بهتر است که ابتدا این کار را انجام دهیم و سپس حاصل ضرب را حساب کنیم این کار سرعت و دقت محاسبه را افزایش می دهد و نیازی به ساده کردن کسر حاصل نیز نمی باشد.
مثال
حاصل ضرب زیر را حساب کنید.
\(\frac{{12}}{{15}} \times \frac{{25}}{{18}}\)
\(\frac{{12}}{{15}} \times \frac{{25}}{{18}} = \frac{2}{3} \times \frac{5}{3} = \frac{{2 \times 5}}{{3 \times 3}} = \frac{{10}}{9} = 1\frac{1}{9}\)
ضرب عددهای مخلوط
برای ضرب اعداد مخلوط از راه محاسبه ابتدا اعداد مخلوط را به کسر تبدیل میکنیم و سپس کسرها را در هم ضرب می کنیم و حاصل را به دست می آوریم.
مثال
حاصل ضرب زیر را بدست اورید.
\(3\frac{3}{5} \times 2\frac{2}{9}\)
\(3\frac{3}{5} \times 2\frac{2}{9} = \frac{{18}}{5} \times \frac{{20}}{9} = \frac{8}{1} = 8\)
هرگاه حاصل ضرب دو عدد مساوی ۱ ،باشد آن دو عدد را معکوس یکدیگر می.گویند. همه ی عددها به جز صفر، معکوس دارند.
برای مشخص کردن معکوس یک کسر، باید جای صورت و مخرج آن را عوض کنیم.
اگر بخواهیم معکوس یک عدد مخلوط را مشخص کنیم ابتدا باید آن را به شکل کسر در آوریم و سپس کسر را معکوس کنیم.
مثال
معکوس عدد \(3\frac{1}{4}\) را بنویسید.
\(3\frac{1}{4} = \frac{{13}}{4} \to \frac{4}{{13}}\)
مثال
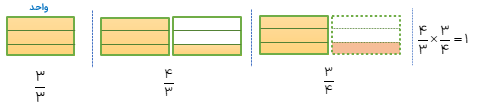
با استفاده از شکل تساوی های زیر را کامل کنید.
\(\frac{3}{4} \times \frac{4}{3}\)
نصف یک عدد یعنی آن عدد ضرب در\(\frac{1}{2}\)
مثال
نصف\(\frac{5}{6}\)یعنی:
\(\frac{5}{6} \times \frac{1}{2} = \frac{5}{{12}}\)
ربع یک عدد یعنی آن عدد ضرب در \(\frac{1}{4}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه ششم- آزمون آنلاین تمامی دروس پایه ششم
- گام به گام تمامی دروس پایه ششم
- ویدئو های آموزشی تمامی دروس پایه ششم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ششم
- فلش کارت های آماده دروس پایه ششم
- گنجینه ای جامع از انشاء های آماده پایه ششم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ششم
روش های محاسبه ضرب کسرها
روش های محاسبه ضرب کسرها
یادآوری
در سال قبل با سه روش محاسبه ی ضرب کسرها آشنا شدید که عبارت اند از:
۱ رسم شکل
۲ رسم محور
۳ محاسبات ریاضی
با توجه به این که روش محاسباتی سریع ترین و ساده ترین روش نسبت به دو روش دیگر است، لذا در سال ششم بیش تر از این روش استفاده می کنیم در این روش برای محاسبه ی حاصل ضرب دو ،کسر، ابتدا صورت های دو کسر را در همدیگر و مخرجهای دو کسر را نیز در همدیگر ضرب میکنیم و به عنوان صورت و مخرج جدید می نویسیم. بهتر است قبل از انجام ،ضرب صورت ها را با مخرج ها ساده کنیم دقت داشته باشید که در ضرب کسرها، نیازی به هم مخرج کردن کسرها نیست.
مثال
حاصل عبارت زیر رابدستت اورید.
الف\(\frac{8}{{21}} \times \frac{{14}}{{40}}\)
\(\frac{8}{{21}} \times \frac{{14}}{{40}} = \frac{{8 \times 14}}{{21 \times 40}} = \frac{2}{{15}}\)
عددهای ۸ و ۴۰ را به ۸ ساده کردیم و عددهای ۱۴ و ۲۱ را نیز به ۷ ساده کردیم و در آخر ساده شده ی عددها را در یک دیگر ضرب کردیم.
ب\(\frac{{27}}{{36}} \times \frac{{28}}{{21}}\)
\(\frac{{27}}{{36}} \times \frac{{28}}{{21}} = \frac{{27 \times 28}}{{36 \times 21}} = \frac{1}{1} = 1\)
در ابتدا عددهای ۲۷ و ۳۶ را به ۹ و عددهای ۲۸ و ۲۱ را نیز به ۷ ساده میکنیم و این عمل را مجددا برای ساده شده ی عددها تکرار می کنیم
ضرب عددهای مخلوط
برای انجام ضرب عددهای مخلوط ابتدا باید آنها را به عدد کسری تبدیل سپس مثل ضرب كسرها عمل کنیم.
مثال
عبارت زیر را حل کنید.
\(2\frac{3}{7} \times 2\frac{5}{8}\)
\(2\frac{3}{7} \times 2\frac{5}{8} = \frac{{24}}{7} \times \frac{{21}}{8} = \frac{{24 \times 21}}{{7 \times 8}} = \frac{9}{1} = 9\)
معکوس یک کسر
اگر جای صورت و مخرج یک کسر را تغییر دهیم معکوس آن کسر به دست می آید.
\(\frac{3}{5} \to \frac{5}{3}\,\,\,\,\,\,\,\,\,\,\,\,\frac{7}{2} \to \frac{2}{7}\,\,\,\,\,\,\,\,\,\,\,\,\frac{4}{3} \to \frac{3}{4}\,\,\,\,\,\,\,\,\,\,\,\,5 = \frac{5}{1} \to \frac{1}{5}\)
۱ همه ی اعداد به غیر از صفر معکوس دارند.
۲ برای تعیین معکوس یک عدد ،مخلوط ابتدا باید آن عدد را به کسر تبدیل، و سپس معکوس کنیم.
3 هرگاه حاصل ضرب دو عدد برابر یک شود آن دو عدد معکوس یک دیگر هستند. به عبارت دیگر، حاصل ضرب هر عددی در معکوسش همیشه مساوی یک می شود.
\(\frac{3}{5} \times \frac{5}{3} = 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,2\frac{1}{3} \times \frac{3}{7} = \frac{7}{3} \times \frac{3}{7} = 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,5 \times \frac{1}{5} = 1\)
مثال
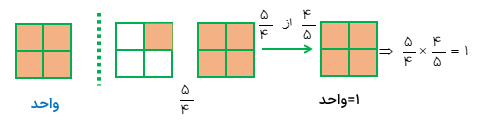
با رسم شکل نشان دهید که \(\frac{5}{4},\frac{4}{5}\) معکوس یک دیگر هستند.
کافی است که نشان دهیم حاصل ضرب این دو کسر برابر یک است. در ابتدا شکل \(\frac{5}{4}\)را رسم می کنیم، حالا برای مشخص کردن\(\frac{5}{4}\) از \(\frac{4}{5}\) باید ۴ خانه ی رنگ شده از شکل\(\frac{5}{4}\) را انتخاب کنیم. به این ترتیب ملاحظه می کنید که حاصل برابر یک واحد شد.
پس این دو کسر طبق نکته بالا معکوس یکدیگرند.
جزوات جامع پایه ششم
جزوه جامع ریاضی ششم فصل 1 عدد و الگوهای عددی
جزوه جامع ریاضی ششم فصل 2 کسر
جزوه جامع ریاضی ششم فصل 3 اعداد اعشاری
جزوه جامع ریاضی ششم فصل 4 تقارن و مختصات
جزوه جامع ریاضی ششم فصل 5 اندازه گیری
جزوه جامع ریاضی ششم فصل 6 تناسب و درصد
جزوه جامع ریاضی ششم فصل 7 تقریب
پیدا کردن مقدار نامعلوم در تساوی ها
پیدا کردن مقدار نامعلوم در تساوی ها
مثال
در تساوی \(\frac{3}{5} = \frac{{15}}{?}\) به جای علامت سؤال چه عددی باید نوشت؟
همان طور که ملاحظه میکنید عدد ۳ پنج برابر شده است پس باید ۵ هم پنج برابر شود.
\(\frac{{{3_{ \times 5}}}}{5} = \frac{{15}}{?}\)
به عبارت دیگر، اول ۱۵ را بر ۳ تقسیم میکنیم تا بفهمیم که ۳ چند برابر شده است و سپس ۵ را هم در همان عدد ضرب میکنیم .
برای حل این گونه سؤالات به روش زیر عمل می کنیم:
\(\frac{3}{5} = \frac{{15}}{?} \to ? = 5 \times \frac{{15}}{3} = \frac{{5 \times 15}}{3} = 25\)
در زنگ ورزش یک کلاس ۳۰ نفری،\(\frac{2}{5}\) از دانش آموزان فوتبال،\(\frac{1}{2}\) والیبال و بقیه ی آن ها تنیس روی میز بازی میکنند.
الف چند نفر فوتبال بازی می کنند؟
۱۲ نفر فوتبال بازی میکنند
\(\frac{2}{5} \times 30 = \frac{{2 \times 30}}{5} = 12\)
ب چند نفر والیبال بازی می کنند؟
۱۰ نفر والیبال بازی میکنند
\(\frac{1}{3} \times 30 = \frac{{1 \times 30}}{3} = 10\)
ج چند نفر تنیس روی میز بازی می کنند؟
۸ نفر تنیس روی میز بازی میکنند
\(30 - (10 = 12) = 30 - 22 = 8\)
تقسیم کسرها
تقسیم کسرها
برای محاسبه ی تقسیم کسرها از راه محاسبه یک روش کلی وجود دارد به این ترتیب که کسر اول را می نویسیم، عمل تقسیم را به ضرب تبدیل میکنیم و کسر دوم را معکوس میکنیم (یعنی جای صورت و مخرج را عوض می کنیم و سپس مانند ضرب کسرها، حاصل را به دست می آوریم.)
مثال
به عبارت زیر توجه کنید.
\(\frac{4}{5} \div \frac{2}{7} = \frac{4}{5} \times \frac{7}{2} = \frac{{14}}{5} = 2\frac{4}{5}\)
اگر در تقسیم ،کسرها صورت کسر سمت چپ بر صورت کسر سمت راست بخش پذیر باشد و مخرج کسر سمت چپ بر مخرج کسر سمت راست بخش پذیر باشد میتوانیم آنها را بر هم تقسیم کنیم و به سادگی جواب را به دست آوریم.
تقسیم کسرها به کمک شکل
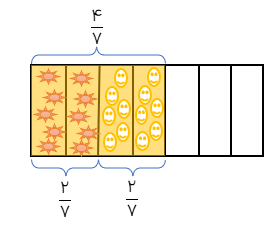
می خواهیم حاصل \(\frac{4}{7} \div \frac{2}{7}\) را به کمک شکل محاسبه کنیم.
ابتدا یک مستطیل را به عنوان واحد رسم میکنیم و آن را به ۷ قسمت مساوی تقسیم می کنیم ابتدا یک مستطیل را به عنوان واحد رسم میکنیم و ۴ قسمت آن را رنگ میکنیم اکنون هر دو قسمت آن را با رنگ های متفاوت مشخص می کنیم. دو تا\(\frac{2}{7}\)روی شکل مشخص میشود پس حاصل می شود ۲؛ یعنی :\(\frac{4}{7} \div \frac{2}{7} = 2\)
تقسیم کسرها به کمک محور اعداد
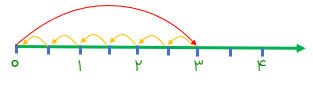
می خواهیم حاصل \(3 \div \frac{1}{2}\) را به کمک محور حساب کنیم ابتدا محور را رسم می کنیم و ۳ واحد را روی آن مشخص می کنیم چون مخرج کسر ۲ است هر واحد را به ۲ قسمت تقسیم میکنیم اکنون باید ببینیم که در ۳ واحد، چندتا\(\frac{1}{2}\)هست.
همان طور که روی محور می بینیم در ۳ واحد، ۶ تا\(\frac{1}{2}\)داریم، پس :\(3 \div \frac{1}{2} = 6\)
برای تقسیم اعداد مخلوط ابتدا باید آنها را به کسر تبدیل کنیم و سپس عمل تقسیم را انجام دهیم.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه ششم- آزمون آنلاین تمامی دروس پایه ششم
- گام به گام تمامی دروس پایه ششم
- ویدئو های آموزشی تمامی دروس پایه ششم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ششم
- فلش کارت های آماده دروس پایه ششم
- گنجینه ای جامع از انشاء های آماده پایه ششم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ششم
روش محاسبه در تقسیم کسرها
روش محاسبه در تقسیم کسرها
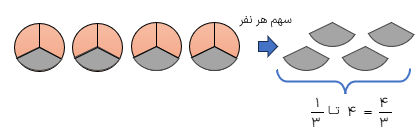
اگر بخواهیم چهار کلوچه را بین سه نفر تقسیم کنیم میتوانیم در ابتدا هر کلوچه را به سه قسمت تقسیم کنیم و سپس به هر نفر ۴ تا\(\frac{1}{3}\) کلوچه بدهیم؛ به این ترتیب سهم هر نفر\(\frac{4}{3}\)کلوچه می شود.
به عبارت دیگر:
\(4 \div 3 = 4 \times \frac{1}{3} = \frac{4}{3}\)
با توجه به عبارت بالا برای تقسیم دو عدد صحیح برهم کافی است که اولین عدد را در معکوس دومین عدد ضرب کنیم، سپس حاصل ضرب را به دست آوریم.
مثال
حاصل هر یک از تقسیم های زیر را به دست آورید.
\(7 \div 4\)الف
\(7 \div 4 = 7 \times \frac{1}{4} = 7\)
ب \(20 \div 9\)
\(20 \div 9 = 20 \times \frac{1}{9} = \frac{{20}}{9}\)
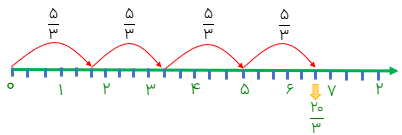
در محور بالا در\(\frac{{20}}{3}\) چهار تا\(\frac{5}{3}\)قرار دارد. به عبارت دیگر:
\(\frac{{20}}{3} \div \frac{5}{3} = \frac{{20}}{5} = 4\)
با توجه به عبارت بالا برای تقسیم دو کسر با مخرج های برابر کافی است که صورت اولین کسر را بر صورت دومین کسر تقسیم کنیم.
برای تقسیم دو عدد مخلوط بر یک دیگر ابتدا آنها را به صورت کسری می نویسیم، سپس حاصل تقسیم را به دست می آوریم.
اگر دو کسر هم مخرج ،باشند حاصل تقسیم آنها به سادگی قابل محاسبه است. پس از این خاصیت می توانیم برای تقسیم کسرهایی که مخرج آنها برابر نمی باشد هم استفاده کنیم به این ترتیب که ابتدا دو کسر را هم مخرج کنیم و سپس به روش بالا عمل کنیم.
مثال
حاصل تقسیم های زیر را به دست آورید.
الف \(\frac{9}{{14}} \div \frac{1}{2}\)
\(\frac{9}{{14}} \div \frac{{{1_{ \times 7 = 7}}}}{{{2_{ \times 7 = 14}}}} = \frac{9}{{14}} \times \frac{7}{{14}} = \frac{9}{7}\)
\(2\frac{1}{7} \div 3\frac{1}{2}\) ب
\(2\frac{1}{7} \div 3\frac{1}{2} = \frac{{15}}{7} \div \frac{7}{2} = \frac{{30}}{{14}} \div \frac{{49}}{{14}} = \frac{{30}}{{49}}\)
روش کلی محاسبه ی حاصل تقسیم دو عدد
کافی است که اولین عدد را در معکوس دومین عدد ضرب کنیم و حاصل ضرب را پس از ساده کردن صورت ها با مخرج ها به دست آوریم
مثال
حاصل عبارت زیر را بدست اورید.
الف\(\frac{9}{4} \div \frac{1}{2}\)
\(\frac{9}{4} \div \frac{1}{2} = \frac{9}{4} \times \frac{2}{1} = \frac{{9 \times 2}}{{4 \times 1}} = \frac{9}{7}\)
ب\(\frac{{20}}{9} + \frac{5}{6}\)
\(\frac{{20}}{9} + \frac{5}{6} = \frac{{20}}{9} \times \frac{6}{5} = \frac{8}{3}\)
حاصل عبارت \(\left( {2\frac{1}{8} - 1\frac{5}{6}} \right) \div 2\frac{5}{{12}}\)را به دست آورید.
ابتدا حاصل عبارت داخل پرانتز را به دست میآوریم سپس جواب آن را بر عدد مخلوط تقسیم می کنیم.
عبارت داخل پانتز=\(2\frac{1}{8} - 1\frac{5}{6} = 1\frac{1}{8} - \frac{5}{6} = 1\frac{3}{{24}} - \frac{{20}}{{24}} = \frac{{27}}{{24}} - \frac{{20}}{{24}} = \frac{7}{{24}}\)
\(\left( {2\frac{1}{8} - 1\frac{5}{6}} \right) \div 2\frac{5}{{12}} = \frac{7}{{24}} \div \frac{{29}}{{12}} = \frac{7}{{24}} \times \frac{{12}}{{29}} = \frac{7}{{58}}\)
\(\frac{3}{5}\)گنجایش ظرفی ۷۵ لیتر است. گنجایش باقی مانده ی ظرف چه قدر است؟
گنجایش باقی مانده ی ظرف \( \ 125 - 75 = 50\)
گنجایش کل ظرف \(75 \div \frac{3}{5} = \frac{{75}}{1} \times \frac{5}{3} = 125\)
جزوات جامع پایه ششم
جزوه جامع ریاضی ششم فصل 1 عدد و الگوهای عددی
جزوه جامع ریاضی ششم فصل 2 کسر
جزوه جامع ریاضی ششم فصل 3 اعداد اعشاری
جزوه جامع ریاضی ششم فصل 4 تقارن و مختصات
جزوه جامع ریاضی ششم فصل 5 اندازه گیری
جزوه جامع ریاضی ششم فصل 6 تناسب و درصد
جزوه جامع ریاضی ششم فصل 7 تقریب
محاسبات با کسر
محاسبات با کسر
برای محاسبه ی حاصل کسرهایی که صورت و مخرج آن ها دارای عملیات ریاضی است، مانند مثال زیر عمل می کنیم:
مثال
حاصل عبارت مقابل را حساب کنید.
\(\frac{{\frac{2}{3} - \frac{1}{4}}}{{\frac{1}{2} + \frac{1}{3}}}\)
\(\frac{{\frac{2}{3} - \frac{1}{4}}}{{\frac{1}{2} + \frac{1}{3}}} = \frac{{\frac{8}{{12}} - \frac{3}{{12}}}}{{\frac{3}{6} + \frac{2}{6}}} = \frac{{\frac{5}{{12}}}}{{\frac{5}{6}}} = \frac{5}{{12}} \div \frac{5}{6} = \frac{1}{2}\)
مثال
یک ویروس رایانه حافظه ی رایانه ای را پاک کند. این ویروس روز اول \(\frac{2}{8}\)حافظه و روز دوم \(\frac{2}{8}\)حافظه ی باقی مانده از روز اول و روز سوم \(\frac{3}{8}\)باقی مانده از روزهای قبل را پاک می کند. حساب کنید پس از ۳ روز هنوز چه کسری از حافظه پاک نشده است؟
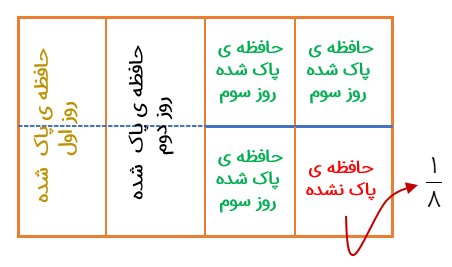
هنوز\(\frac{1}{8}\)حافظه پاک نشده است.
در انجام عملیات ریاضی باید به ترتیب و اولویت عملیات داده شده دقت کنیم به طور کلی در یک عبارت محاسباتی باید به ترتیب زیر عمل کنیم.
۱ محاسبه ی پرانتز ها از داخلی ترین آنها
۲ انجام ضرب یا تقسیم هر کدام که از چپ به راست عبارت، زودتر دیده شد.
3 انجام جمع یا ،تفریق هر کدام که از چپ به راست عبارت، زودتر دیده شد.
مثال
حاصل عبارت زیر را بدست اورید.
الف\(\left( {3\frac{3}{5} - 2\frac{{11}}{5}} \right) \div 1\frac{3}{{10}}\)
در ابتدا، حاصل عبارت داخل پرانتز را حساب کرده و عدد به دست آمده را بر\(1\frac{3}{{10}}\) تقسیم می کنیم.
محاسبه ی داخل پرانتز:\(3\frac{3}{5} - 2\frac{{11}}{5} = 1\frac{3}{5} - \frac{{11}}{{15}} = 1\frac{9}{5} - \frac{{11}}{{15}} = \frac{{24}}{{15}} - \frac{{11}}{{15}} = \frac{{13}}{{15}}\)
محاسبه ی کل عبارت:\(\left( {3\frac{3}{5} - 2\frac{{11}}{5}} \right) \div 1\frac{3}{{10}} = \frac{{13}}{{15}} \div \frac{{13}}{{10}} = \frac{{13}}{{15}} \times \frac{{10}}{{13}} = \frac{2}{3}\)
ب\(\frac{9}{{11}} - \frac{9}{{11}} \div \frac{{22}}{{27}}\)
در این عبارت، در ابتدا باید حاصل تقسیم \(\frac{9}{{11}} \div \frac{{22}}{{27}}\) را به دست آوریم. دقت داشته باشید که در هر عبارت محاسباتی، باید حاصل ضرب و تقسیم را زودتر از جمع و تفریق به دست آوریم.
\(\frac{9}{{11}} - \frac{9}{{11}} \div \frac{{22}}{{27}} = \frac{9}{{11}} - \frac{9}{{11}} \times \frac{{22}}{{27}} = \frac{{{9_{ \times 3}}}}{{{{11}_{ \times 3}}}} - \frac{{{2_{ \times 11}}}}{{{3_{ \times 11}}}} = \frac{{27}}{{33}} - \frac{{22}}{{33}} = \frac{5}{{33}}\)
ج\(\frac{{\frac{9}{{20}}}}{{\frac{3}{{25}}}}\)
\(\frac{{\frac{9}{{20}}}}{{\frac{3}{{25}}}} = \frac{9}{{20}} \div \frac{3}{{25}} = \frac{9}{{20}} \times \frac{{25}}{3} = \frac{{15}}{4}\)
برای حل چنین سؤالاتی ابتدا باید عبارت های موجود در صورت و مخرج کسر را به طور جداگانه محاسبه کنیم، سپس با استفاده از نکته ،قبل حاصل کل عبارت را به دست آوریم.
مقایسه ی کسرها
مقایسه ی کسرها
در مقایسه ی کسرها، سه حالت زیر اتفاق می افتد:
حالت اول در کسرهایی که مخرج آنها مساوی است کسری بزرگ تر است که صورت آن بزرگ تر باشد.
\(\frac{3}{7}\left\lfloor {\, < \,} \right\rfloor \frac{5}{7}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{{12}}{{13}}\left\lfloor {\, > \,} \right\rfloor \frac{9}{{13}}\)
حالت دوم در کسرهایی که صورت آنها مساوی است کسری بزرگ تر است که مخرج آن کوچک تر باشد.
\(\frac{3}{5}\left\lfloor {\, < } \right\rfloor \frac{3}{2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{{15}}{7}\left\lfloor {\, > \,} \right\rfloor \frac{{15}}{{20}}\)
حالت سوم برای مقایسه ی کسرهایی که نه صورت و نه مخرج های برابر دارند ابتدا هر دو کسر را هم مخرج یا هم صورت میکنیم سپس کسرها را مانند حالت اول یا دوم مقایسه میکنیم.
\(\frac{{25}}{{18}}\left\lfloor {\,\,} \right\rfloor \frac{{17}}{{12}} \to \frac{{{{25}_{ \times 2}}}}{{{{18}_{ \times 2}}}}\left\lfloor {\,\,} \right\rfloor \frac{{{{17}_{ \times 3}}}}{{{{12}_{ \times 3}}}} \to \frac{{50}}{{36}} < \frac{{51}}{{36}}\)
در مقایسه ی عددهای مخلوط ابتدا قسمت های صحیح سپس قسمت های کسری که کوچک تر از واحد هستند را با هم مقایسه میکنیم.
\(3\frac{4}{5} > 3\frac{3}{5}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,2\frac{7}{{10}} < 3\frac{1}{{10}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,7\frac{3}{7} < 7\frac{3}{4}\)
مثال
اعداد زیر را از کوچک به بزرگ مرتب کنید.
\(3\frac{1}{3},\frac{3}{5},\frac{2}{3},\frac{5}{4},1,\frac{{11}}{6},\frac{7}{2},\frac{4}{7}\)
برای حل چنین سؤالاتی بهتر است در ابتدا عددهای کوچک تر از واحد را جداگانه و عددهای بزرگ تر از واحد را نیز جداگانه مقایسه کنیم.
عددهای کوچک تر از واحد:
\(\begin{array}{l}\frac{3}{5},\frac{2}{3},\frac{4}{7} \to \frac{{{3_{ \times 21}}}}{{{5_{ \times 21}}}},\frac{{{2_{ \times 35}}}}{{{3_{ \times 35}}}},\frac{{{4_{ \times 15}}}}{{{7_{ \times 15}}}} \to \frac{{63}}{{105}},\frac{{70}}{{105}},\frac{{60}}{{105}}\\\\\frac{{60}}{{105}} < \frac{{63}}{{105}} < \frac{{70}}{{105}} \to \frac{4}{7} < \frac{3}{5} < \frac{2}{3}\end{array}\)
عددهای بزرگتر از واحد:
\(\begin{array}{l}3\frac{1}{3},\frac{5}{4},\frac{{11}}{6},\frac{7}{2} \to \frac{{{{10}_{ \times 4}}}}{{{3_{ \times 4}}}},\frac{{{5_{ \times 3}}}}{{{4_{ \times 3}}}},\frac{{{{11}_{ \times 2}}}}{{{6_{ \times 2}}}},\frac{{{7_{ \times 6}}}}{{{2_{ \times 6}}}} \to \frac{{40}}{{12}},\frac{{15}}{{12}},\frac{{22}}{{12}},\frac{{42}}{{12}}\\\\ \to \frac{{15}}{{12}} < \frac{{40}}{{12}} < \frac{{22}}{{12}} < \frac{{42}}{{12}} \to \frac{5}{4} < \frac{{11}}{6} < \frac{{10}}{3} < \frac{7}{2}\end{array}\)
بنابراین عددها به ترتیب مقابل هستند:
\(\frac{4}{7} < \frac{3}{5} < \frac{2}{3} < \frac{5}{4} < \frac{{11}}{6} < \frac{{10}}{3} < \frac{7}{2}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه ششم- آزمون آنلاین تمامی دروس پایه ششم
- گام به گام تمامی دروس پایه ششم
- ویدئو های آموزشی تمامی دروس پایه ششم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ششم
- فلش کارت های آماده دروس پایه ششم
- گنجینه ای جامع از انشاء های آماده پایه ششم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ششم



1736019749.png)