درسنامه کامل ریاضی ششم فصل 5 اندازه گیری
تعداد بازدید : 7.25Mخلاصه نکات ریاضی ششم فصل 5 اندازه گیری - درسنامه شب امتحان ریاضی ششم فصل 5 اندازه گیری - جزوه شب امتحان ریاضی ششم نوبت اول فصل 5 اندازه گیری
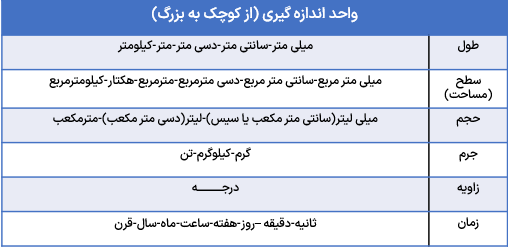
طول و سطح
طول و سطح
می دانیم که برای اندازه گیری مقداری از هر چیز نیاز به واحد داریم برای مثال برای اندازه گیری قد یک انسان از واحد متر یا سانتی متر و برای اندازه گیری سنگینی یک جسم از واحد گرم یا کیلوگرم استفاده می کنیم. معنی کلمات زیر را یاد بگیرید:
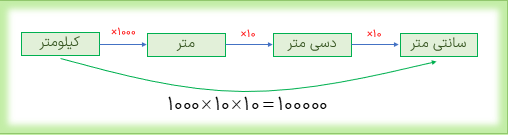
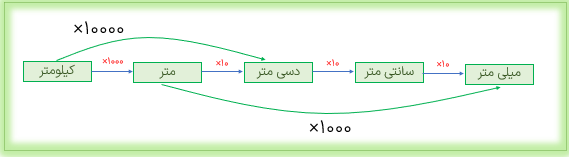
كيلو یعنی هزار : مثال: کیلوگرم یعنی هزار گرم - کیلومتر یعنی هزار متر.
دسی یعنی یک دهم: مثال: دسی متر یعنی یک دهم متر.
سانتی یعنی یک صدم : مثال: سانتی متر یعنی یک صدم متر.
میلی یعنی یک هزارم: مثال: میلی متر یعنی یک هزارم متر - میلی گرم یعنی یک هزارم گرم - میلی لیتر یعنی یک هزارم لیتر که معادل یک سی سی یا یک سانتی متر مکعب است.
در جدول زیر واحدهایی را که به طور معمول از آنها استفاده می کنیم، بیان شده است:
تبدیل واحدهای طول
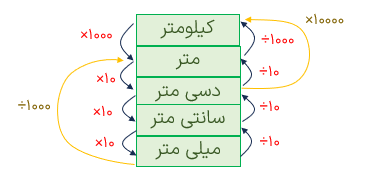
با استفاده از جدول زیر به راحتی میتوان واحدهای طول را تبدیل کرد.
مثال
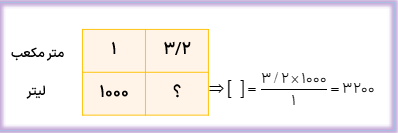
۳/۴ متر، چند سانتی متر است؟
با استفاده از جدول می دانیم که هر متر ۱۰۰ سانتی متر است و برای تبدیل از واحد بزرگ (متر) به واحد کوچک (سانتی متر) باید از عمل ضرب استفاده کنیم.
سانتی متر ۳۴۰ = ۱۰۰ × ۳/۴
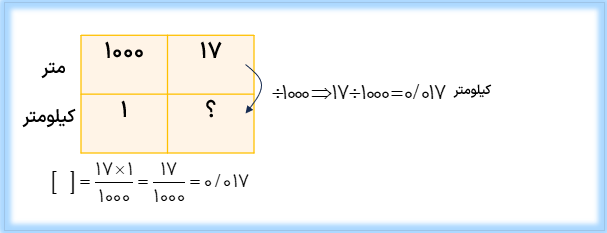
روش دیگر تبدیل واحدها استفاده از جدول تناسب است.
مثال
۱۷ متر چند کیلومتر است؟
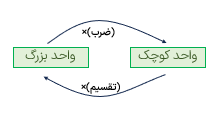
برای تبدیل واحدها از روش زیر استفاده می کنیم.
یعنی برای تبدیل واحد بزرگ به واحد کوچک از عمل ضرب و برای تبدیل واحد کوچک به واحد بزرگ از عمل تقسیم استفاده می شود.
مثال
یک کیلومتر چند سانتی متر است؟
(واحد کیلومتر از واحد سانتی متر بزرگ تر است.)
یعنی یک کیلومتر ۱۰۰۰00 سانتی متر است.
مثال
۰/۰۱۶ کیلومتر یعنی چند سانتی متر؟
سانتی متر ۱۶۰۰ = ۱۰۰۰۰۰ × ۰/۰۱۶
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه ششم- آزمون آنلاین تمامی دروس پایه ششم
- گام به گام تمامی دروس پایه ششم
- ویدئو های آموزشی تمامی دروس پایه ششم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ششم
- فلش کارت های آماده دروس پایه ششم
- گنجینه ای جامع از انشاء های آماده پایه ششم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ششم
واحدهای سطح (مساحت)
واحدهای سطح (مساحت)
می دانیم که مساحت مربع برابر است با یک ضلع ضرب در خودش.
اگر مربعی به ضلع یک سانتی متر داشته باشیم مساحت آن برابر است با ۱ سانتی متر مربع.
۱ سانتی متر مربع : ۱ سانتی متر × ۱ سانتی متر = مساحت مربع
اگر مربعی به ضلع یک متر داشته باشیم مساحت آن برابر است با ۱ متر مربع.
دسی متر مربع : دسی متر × ۱۰ دسی متر = ۱ متر × ۱ متر = ۱ متر مربع
دسی متر مربع ۱۰۰ = ۱ متر مربع
سانتی متر مربع: ۱۰۰۰۰ = ۱۰۰ سانتی متر × ۱۰۰ سانتی متر = ۱ متر × ۱ متر = ۱ متر مربع
سانتی متر مربع ۱۰۰۰۰=۱ متر مربع
میلی متر مربع: ۱۰۰۰۰ = ۱۰۰۰ میلی متر × ۱۰۰۰ میلی متر = ۱ متر × ۱ متر = ۱ متر مربع
میلی متر مربع ۱۰۰۰۰۰۰ = 1متر مربع
سانتی متر مربع: ۱۰۰ = ۱۰ سانتی متر × ۱۰ سانتی متر = ۱ دسی متر × ۱ دسی متر= ۱ دسی متر مربع
سانتی متر مربع ۱۰۰=۱ دسی متر مربع
میلی متر مربع: ۱۰۰۰۰ = ۱۰۰ میلی متر × ۱۰۰ میلی متر = ۱ دسی متر × ۱ دسی متر =۱ دسی متر مربع
میلی متر مربع ۱۰۰۰۰=۱ دسی متر مربع
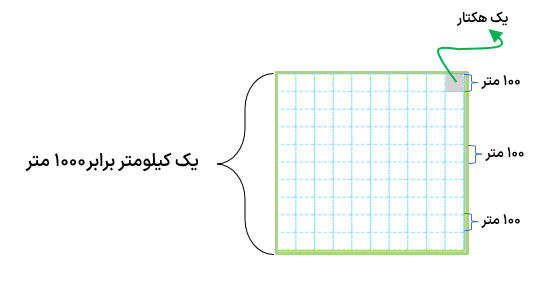
برای اندازه گیری مساحت مزرعه ها پارک ها و جنگل ها از واحد بزرگ تری به نام هکتار استفاده می شود.
یک هکتار مساحت مربعی است که اندازه ی هر ضلع آن ۱۰۰ متر است.
متر مربع ۱۰۰۰۰=۱ هکتار\( \Rightarrow \) متر مربع 10000 = 100 متر × 100 متر = 1 هکتار
برای اندازه گیری سطح های بزرگ تر مانند مساحت شهرها کشورها قاره ها و اقیانوس ها از واحد بزرگ تری به نام کیلومتر مربع استفاده میشود یک کیلومتر مربع مساحت مربعی است که اندازه ی هر ضلع آن یک کیلومتر یا ۱۰۰۰ متر است.
مساحت مربع شکل مقابل یک کیلومتر مربع است و مساحت مربعی که در بالا سمت راست رنگ شده، یک هکتار است.
متر مربع ۱۰۰۰۰۰۰ = ۱۰۰۰ متر × ۱۰۰۰ متر= ۱ کیلومتر ×۱ کیلومتر = ۱ کیلو متر مربع
متر مربع ۱۰۰۰۰۰۰ = ۱ کیلومتر مربع
تبدیل واحد
برای تبدیل واحدها دو روش وجود دارد:
۱- استفاده از ضرب و تقسیم
2- استفاده از تناسب
مثال
۲/۳ متر مربع چند سانتی متر مربع است؟
استفاده از ضرب و تقسیم
سانتی متر مربع ۲۳۰۰۰ = ۱۰۰۰۰ × ۲/۳\( \Rightarrow \) سانتی متر مربع 10000 = 1 متر مربع
استفاده از تناسب
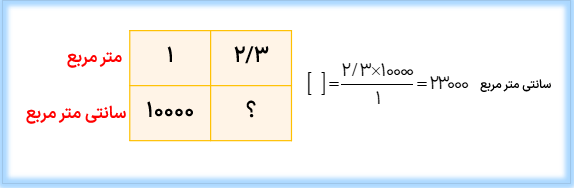
تبدیل واحدهای سطح
کیلومتر مربع مساحت مربعی به ضلع یک کیلومتر است از طرفی چون هر کیلومتر، برابر ۱۰۰۰ متر است بنابراین ۱ کیلومتر مربع، برابر ۱۰۰۰ × ۱۰۰۰ یعنی ۱۰۰۰۰۰۰ متر مربع می باشد. از واحد کیلومتر مربع برای بیان مساحت سطح های بزرگ مانند مساحت قاره،ها کشورها و شهرها استفاده می شود.
یک هکتار مساحت مربعی به ضلع ۱۰۰ متر است. پس هر هکتار برابر ۱۰۰ × ۱۰۰ یعنی ۱۰۰۰۰ متر مربع می باشد.
از واحد هکتار برای بیان مساحت زمین های کشاورزی و جنگل ها استفاده می شود.
هر کیلومتر مربع برابر ۱۰۰ هکتار است.
یک متر مربع مساحت مربعی به ضلع ۱ متر است. از طرفی چون هر دسی متر، برابر ۰/۱ متر است پس هر دسی متر مربع برابر ۰/۱ متر است.پس هر دسی متر مربع برابر 1/0×1/0 یعنی 0/01 متر مربع می باشد .از این واحد هم برای بیان مساحت اتاق ها استفاده می شود.
به طور مثال مساحت یک اتاق ۱۲ متر مربع و ۶ دسی متر مربع میباشد. که این مساحت با ۱۲/۰۶ متر مربع برابر است.
یک سانتی متر مربع مساحت مربعی به ضلع ۱ سانتی متر است. از طرفی چون هر سانتی متر، برابر ۰/۰۱ متر است، پس هر سانتی متر برابر ۰/۱۰/۰۱ یعنی ۰/۰۰۰۱ متر مربع میباشد. از این واحد برای بیان مساحت سطح های کوچک مانند سطح کتاب استفاده می شود.
پیشنهاد میشود که از الگوی زیر برای تبدیل واحدهای سطح به یک دیگر و با کمک از جدول تناسب استفاده کنید.
مثال
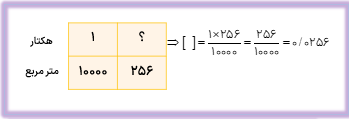
الف ۲۵۶ متر مربع، چند هکتار است؟
می دانیم که هر ۱۰۰۰۰ متر مربع برابر یک هکتار است بنابراین:
ب ۲۵۶ هکتار چند متر مربع است؟
از آن جا که هر هکتار برابر ۱۰۰۰۰ متر مربع است پس ۲۵۶ هکتار را برابر ۱۰۰۰۰ × ۲۵۶ یعنی ۲۵۶۰۰۰۰ متر مربع می باشد.
ج ۳۵۴ دسی متر مربع چند سانتی متر مربع است؟
می دانیم که هر دسی متر برابر ۱۰ سانتی متر است، پس با توجه به رابطه های زیر هر دسی متر مربع برابر۱۰۰ سانتی متر مربع است.
۱۰۰ سانتی متر مربع = ۱۰ سانتی متر × ۱۰ سانتی متر و ۱ دسی متر مربع = ۱ دسی متر × ۱ دسی متر
سانتی متر مربع ۳۵۴۰۰ = ۱۰۰ × ۳۵۴ = ۳۵۴ دسی متر مربع
د ۷۸۹ هکتار چند کیلومتر مربع است؟ میدانیم که هر ۱۰۰ هکتار برابر یک کیلومتر مربع است، بنابراین:
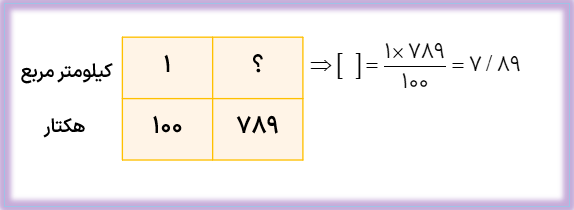
مثال
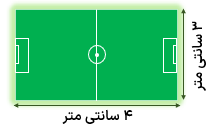
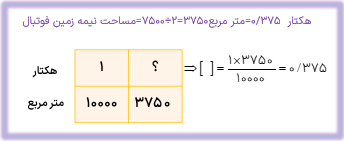
اگر مستطیل مقابل نقشه ی یک زمین فوتبال باشد و هر یک سانتی متر روی شکل برابر ۲۵ متر بر روی زمین باشد، به سؤالات زیر پاسخ دهید.
الف مساحت کل این زمین فوتبال چند متر است؟
با توجه به این که هر یک سانتی متر روی نقشه معادل ۲۵ متر در طبیعت (واقعیت) است پس طول و عرض زمین برابر است با:
متر ۱۰۰= ۴×۲۵ = طول زمین ، متر ۷۵ = ۲۵ × ۳ = عرض زمین
متر مربع ۷۵۰۰ = ۷۵ × ۱۰۰ = مساحت زمین فوتبال
ب مساحت نیمه ی زمین فوتبال چند هکتار است؟
جزوات جامع پایه ششم
جزوه جامع ریاضی ششم فصل 1 عدد و الگوهای عددی
جزوه جامع ریاضی ششم فصل 2 کسر
جزوه جامع ریاضی ششم فصل 3 اعداد اعشاری
جزوه جامع ریاضی ششم فصل 4 تقارن و مختصات
جزوه جامع ریاضی ششم فصل 5 اندازه گیری
جزوه جامع ریاضی ششم فصل 6 تناسب و درصد
جزوه جامع ریاضی ششم فصل 7 تقریب
واحدهای طول
واحدهای طول
در سال ها قبل با مفهوم اندازه گیری و واحدهای مختلف برای اندازه گیری مواردی از قبیل طول سطح و حجم و ... آشنا شدید. در این قسمت بعضی از واحدهای اندازه گری را یادآوری می کنیم:
واحد اندازه گیری طول: کیلومتر – متر - دسی متر – سانتی متر – میلی متر
واحدهای اندازه گیری زمان: سال - ماه - هفته - روز – ساعت – دقیقه – ثانیه
واحدهای اندازه گیری جرم (وزن): تن – کیلوگرم - گرم
واحدهای اندازه گیری سطح: کیلومتر مربع - هکتار - متر مربع - دسی متر مربع - سانتی متر مربع – میلی متر مربع
واحدهای اندازه گیری: حجم متر مکعب – دسی متر مکعب – سانتی متر مکعب
واحدهای اندازه گیری گنجانش: لیتر – میلی لیتر
واحدهای اندازه گیری زاویه: درجه
همان طور که میدانید برای اندازه گیری در هر یک از موارد بالا باید از واحد مناسب آن استفاده کنیم به طور مثال برای اندازه گیری طول یک اتاق بهتر است از واحد متر استفاده کنیم اما برای اندازه گیری فاصله ی بین دو شهر بهتر است از واحد کیلومتر و برای اندازه گیری ضخامت یک کتاب از واحد میلی متر استفاده کنیم.
پس انتخاب واحد مناسب در اندازه گیری از اهمیت زیادی برخوردار است. حال اگر در انتخاب واحدها دقت نکنیم، مجبوریم از عددهای خیلی بزرگ و یا خیلی کوچک استفاده کنیم به طور مثال فاصله ی تهران تا مشهد تقریبا ۹۰۰ کیلومتر است این فاصله با واحد متر برابر ۹۰۰,۰۰۰ متر و با واحد سانتی متر برابر ۹۰,۰۰۰,۰۰۰ سانتی متر است.
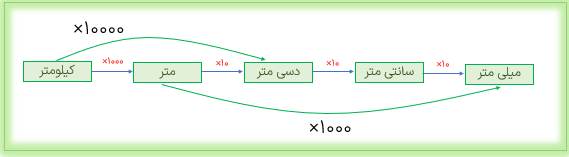
تبدیل واحدهای طول
هر کیلومتر، برابر ۱۰۰۰ متر است.
(۱متر) × ۱۰۰۰ = ۱
هر متر برابر ۱۰ دسی متر است.
(1دسی متر) × ۱۰ = ۱
هر دسی متر برابر ۱۰ سانتی متر است.
(1 سانتی متر) × ۱۰ = ۱ دسی
هر سانتی متر، برابر ۱۰ میلی متر است.
(1 میلی متر) × ۱۰ = ۱ سانتی متر
پیشنهاد میکنیم که از الگوی زیر برای تبدیل واحدهای طول به یک دیگر استفاده کنید. همچنین می توانید از جدول تناسب هم در تبدیل واحدهای طول به یک دیگر استفاده کنید.
مثال
الف ۴۳۲ کیلومتر چند متر است؟
می دانیم که هر کیلومتر برابر ۱۰۰۰ متر است. پس ۴۳۲ کیلومتر برابر ۱۰۰۰ × ۴۳۲ یعنی ۴۳۲۰۰۰ متر است.
ب ۵۲۷ متر چند کیلومتر است؟ میدانیم که هر کیلومتر برابر ۱۰۰۰ متر است، بنابراین:

ج ۵۲۷ دسی متر چند کیلومتر است؟
طبق الگوی بالا هر کیلومتر، برابر ۱۰ × ۱۰۰۰ ۱۰۰۰۰ دسی متر است بنابراین:
د ۳۷ دسی متر چند میلی متر است؟
طبق الگوی بالا هر دسی متر برابر ۱۰ × ۱۰ یعنی ۱۰۰ میلی متر است، پس ۳۷ دسی متر برابر ۱۰۰ × ۳۷ یعنی ۳۷۰۰ میلی متر است.
حجم و جرم
حجم و جرم
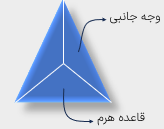
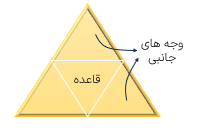
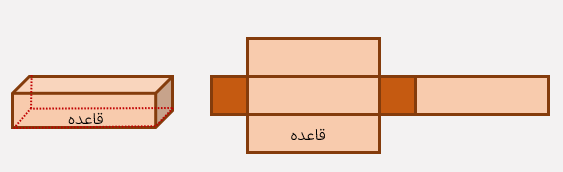
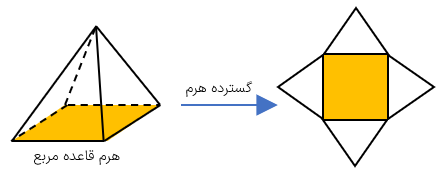
به شکل مقابل هرم می گویند.
قاعده ی هرم یک چندضلعی است (مانند: مثلث، مربع مستطیل، پنج ضلعی و ...)
به هر یک از سطح های تشکیل دهندهی هرم یک وجه می گویند.
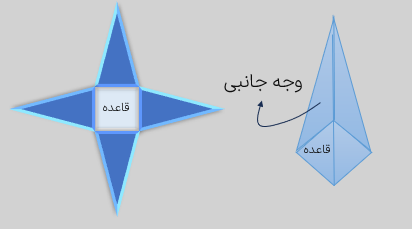
گسترده ی هرم بالا به صورت مقابل است.
اگر گسترده هرم از چهار مثلث متساوی الاضلاع هم اندازه تشکیل شده باشد به آن چهاروجهی منتظم هم گفته می شود.
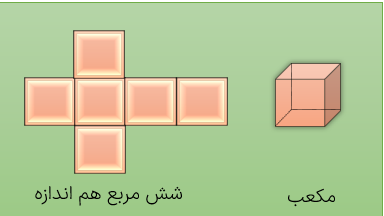
شکل زیر یک مکعب و گسترده ی آن را نشان می دهد.
ضلع ضلع x ضلع = حجم مکعب
ضلع × ضلع ×۶ = مساحت گسترده ی مکعب (مساحت کل مکعب)
همه ی ضلع های مکعب با هم برابرند.
برای اندازه گیری ،حجم واحدهایی مانند مترمکعب دسی مترمکعب (لیتر) و سانتی مترمکعب (سی سی) وجود دارد.
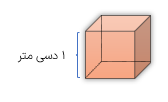
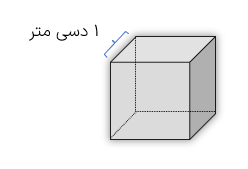
یک متر مکعب، حجم مکعبی است که اندازه ی هر ضلع آن یک متر باشد.
یک دسی مترمکعب (یا یک لیتر)، حجم مکعبی است که اندازه ی هر ضلع آن یک دسی متر یا ۱۰ سانتی متر باشد. این واحد برای اندازه گیری حجم مایعات بسیار مورد استفاده قرار می گیرد.
۱ لیتر یا یک دسی متر مکعب = حجم
یک سانتی متر مکعب حجم مکعبی است که اندازه ی هر ضلع آن یک سانتی متر باشد. نام های دیگر این واحد سی سی» و «میلی لیتر» است.
۱ سانتی متر مکعب = حجم
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه ششم- آزمون آنلاین تمامی دروس پایه ششم
- گام به گام تمامی دروس پایه ششم
- ویدئو های آموزشی تمامی دروس پایه ششم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ششم
- فلش کارت های آماده دروس پایه ششم
- گنجینه ای جامع از انشاء های آماده پایه ششم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ششم
واحدهای حجم
واحدهای حجم
دسی متر مکعب 1000=۱۰ دسی متر× ۱۰ دسی متر × ۱۰ دسی متر = ۱ متر × ۱ متر × ۱ متر = ۱ متر مکعب
لیتر ۱۰۰۰ = دسی متر مکعب ۱۰۰۰=۱ متر مکعب
سانتی متر مکعب ۱۰۰۰۰۰۰ = ۱۰۰ سانتی متر × ۱۰۰ سانتی متر × ۱۰۰ سانتی متر= ۱ متر× ۱ متر ×۱ متر = ۱ متر مکعب
میلی لیتر ۱۰۰۰۰۰۰ = سی سی ۱۰۰۰۰۰ = سانتی متر مکعب ۱۰۰۰۰۰۰=۱ متر مکعب
سانتی متر مکعب ۱۰۰۰ = ۱۰ سانتی متر × ۱۰ سانتی متر × ۱۰ سانتی متر = ۱ دسی متر× ۱ سی متر× ۱ دسی متر = ۱ دسی متر مکعب = ۱ لیتر
میلی لیتر ۱۰۰۰ = سی سی ۱۰۰۰ =سانتی متر مکعب ۱۰۰۰=۱ دسی متر مکعب = ۱ لیتر
برای تبدیل واحدهای حجم میتوان از دو روش ضرب و جدول تناسب استفاده کرد.
مثال
۳/۲ متر مکعب برابر چند لیتر است؟
روش ۱: میدانیم که هر متر مکعب مساوی ۱۰۰۰ لیتر است؛ پس
لیتر ۳۲۰۰ = ۱۰۰۰ × ۳/۲
روش ۲: استفاده از جدول تناسب
مثال
حجم و مساحت گسترده ی مکعبی به ضلع ۵ سانتی متر را حساب کنید.
سانتی متر مکعب ۱۲۵ = ۵ ×۵ × ۵ = حجم
سانتی متر مربع ۱۵۰ = ۵ × ۵ × ۶ = مساحت گسترده (مساحت کل)
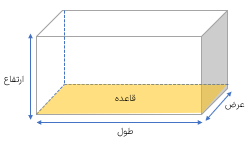
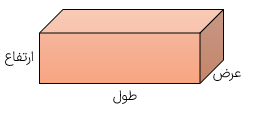
شکل زیر یک مکعب مستطیل و گسترده ی آن را نشان میدهد اضلاع برابر در گسترده ی شکل مشخص شده اند.
در گسترده ی مکعب مستطیل سطح هایی (وجه) هایی که هم رنگ هستند دارای مساحت های مساوی هستند. این سطح ها در مکعب مستطیل در مقابل هم قرار می گیرند.
اگر اضلاع مکعب مستطیل را به صورت مقابل نام گذاری کنیم حجم و مساحت گسترده ی مساحت کل آن به صورت زیر محاسبه می شود.
ارتفاع × عرض × طول = حجم مکعب مستطیل
(ارتفاع × عرض) + (ارتفاع × طول) + (عرض × طول ) × ۲ = مساحت گسترده ی مکعب مستطیل (مساحت کل)
مثال
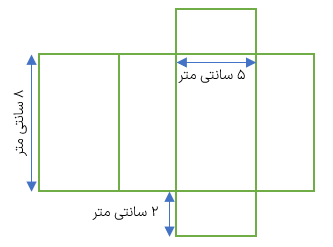
شکل مقابل گسترده ی یک مکعب مستطیل است با توجه به اندازه های روی آن، حجم و مساحت گسترده ی مکعب مستطیل را حساب کنید.
سانتی متر مکعب ۱۲۰ = ۳×۸×۵ = حجم
سانتی متر مربع ۱۵۸ = (۵×۳) + (3×8)+ (۸×۵)× ۲ = مساحت گسترده (مساحت کل)
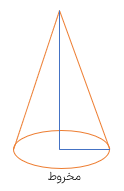
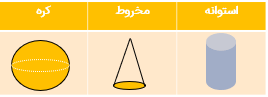
شکل مقابل یک مخروط است. مخروط شبیه هرم است فقط قاعده ی آن به شکل دایره است (چند ضلعی نیست).
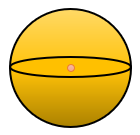
شکل مقابل یک کره است.
توپ فوتبال به شکل یک کره است کره را از هر طرف نگاه کنیم، یک دایره می بینیم.
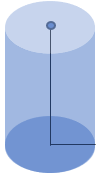
شکل مقابل یک استوانه است.
استوانه ی مقابل را اگر از بالا نگاه کنیم یک دایره می بینیم و اگر از راست یا روبه رو نگاه کنیم یک مستطیل می بینیم.
دو تصویر مختلف از این استوانه
واحدهای اندازه گیری :جرم واحدهای معمول اندازه گیری جرم از کوچک به بزرگ عبارت اند از:
میلی گرم - گرم - کیلوگرم - تن
جدول مقابل رابطه ی بین این واحدها را نشان می دهد.
واحد میلی گرم واحد بسیار کوچکی است و به طور معمول در صنایع داروسازی مورد استفاده قرار می گیرد.
یعنی هر ۱ تن مساوی ۱۰۰۰۰۰۰ گرم است.
جرم یک سی سی آب تقریبا یک گرم است و چون یک لیتر مساوی ۱۰۰۰ سی سی است، بنابراین جرم یک لیتر آب معادل ۱۰۰۰ گرم یا یک کیلوگرم است.
جزوات جامع پایه ششم
جزوه جامع ریاضی ششم فصل 1 عدد و الگوهای عددی
جزوه جامع ریاضی ششم فصل 2 کسر
جزوه جامع ریاضی ششم فصل 3 اعداد اعشاری
جزوه جامع ریاضی ششم فصل 4 تقارن و مختصات
جزوه جامع ریاضی ششم فصل 5 اندازه گیری
جزوه جامع ریاضی ششم فصل 6 تناسب و درصد
جزوه جامع ریاضی ششم فصل 7 تقریب
هرم و مکعب
هرم
هرم یک شکل فضایی (چندوجهی) است که همه ی وجه های آن به جز یکی از آن ها در یک رأس مشترک هستند. به شکل های زیر دقت کنید.
مكعب
مکعب یک شکل فضایی شش وجهی است که تمامی وجههای آن از مربع های برابر هستند. هر مکعب دارای گوشته (رأس) و ۱۲ لبه (ضلع) است.
اندازه ی لبه (ضلع) را سه مرتبه نوشته و در هم ضرب کنید = حجم مکعب
مساحت یک مربع × ۶ = مساحت یک وجه × ۶ = مساحت گسترده ی مکعب
مثال
یک مکعب به صورت مقابل است حجم و مساحت گسترده ی این مکعب چه قدر است؟
سانتی متر مکعب ۱۲۵ = ۵ ×۵× ۵ = حجم
سانتی متر مربع ۱۵۰ = ۶×۲۵ = (۵×۵) ×۶ = مساحت گسترده
مکعب مستطیل
مکعب مستطیل یک شکل فضایی شش وجهی است که تمامی وجه های آن به شکل مستطیل هستند. هر مکعب مستطیل دارای ۸ گوشه (رأس) و ۱۲ لبه (ضلع) است. شکل های زیر چند حالت گسترده ی مکعب مستطیل را نمایش می دهند.
ارتفاع × عرض × طول = حجم مکعب مستطیل
(ارتفاع × عرض) + (ارتفاع × طول) + (عرض × طول) × ۲ = مساحت گسترده ی مکعب مستطیل
مثال
حجم و مساحت گستردهی مکعب مستطیل مقابل را به دست آورید.
سانتی متر مکعب ۱۲۰ = ۸×۳×۵ = حجم
سانتی متر مربع ۱۵۸ = (15×40×24)×2= (۳×۵) + (۸×۵) + (۸×۳)]× ۲ = مساحت گسترده
معرفی چند شکل هندسی دیگر
معرفی و تبدیل واحدهای حجم
معرفی و تبدیل واحدهای حجم
یک متر مکعب اگر مکعبی به ضلع یک متر داشته باشیم حجم آن یک متر مکعب می باشد.
۱ متر × ۱ متر ×1 متر × ۱ متر = ۱ متر مکعب
یک دسی متر مکعب اگر مکعبی به ضلع یک دسی متر داشته باشیم حجم آن یک دسی متر مکعب می باشد.
یک سانتی متر مکعب اگر مکعبی به ضلع یک سانتی متر داشته باشیم حجم آن یک سانتی متر مکعب می باشد.
هر متر برابر ۱۰ دسی متر است پس:
۱۰۰۰ دسی متر مکعب = ۱۰ دسی متر × ۱۰ دسی متر × ۱۰ دسی متر = ۱ متر مکعب
هر متر برابر ۱۰۰ سانتی متر است پس:
۱۰۰۰۰۰۰ سانتی متر مکعب = ۱۰۰ سانتی متر × ۱۰۰ سانتی متر × ۱۰۰ سانتی متر = ۱ متر مکعب
۱ هر سانتی متر مکعب برابر یک سی سی است.
۲ هر دسی متر مکعب برابر یک لیتر است پس هر لیتر برابر ۱۰۰۰ سی سی می باشد.
3 هر متر مکعب برابر ۱۰۰ لیتر است.
مثال
مخزنی داریم به شکل مکعب مستطیل و به ابعاد ۱ متر، ۵ دسی متر و ۳۰ سانتی متر، حجم این مخزن چند دسی متر مکعب است؟ در این مخزن چند لیتر آب میتوان ریخت؟
ابتدا بهتر است تمامی واحدها را به دسی متر تبدیل کنیم:
۳ دسی متر = ۳۰ سانتی متر = ارتفاع مکعب مستطیل
۱۰ دسی متر = ۱ متر = طول مکعب مستطیل
دسی متر مکعب ۱۵۰ = ۳ × ۵ × ۱۰ = حجم مکعب مستطیل
می دانیم که هر دسی متر مکعب با ۱ لیتر برابر است پس گنجایش این مخزن همان ۱۵۰ لیتر است.
تبدیل واحدهای جرم
تن: هر هزار کیلوگرم برابر یک تن است. پس یک کیلوگرم برابر \(\frac{1}{{1000}}\) تن می باشد.
کیلوگرم: هر کیلوگرم برابر ۱۰۰۰ گرم است. پس یک گرم برابر \(\frac{1}{{1000}}\) کیلوگرم می باشد.
گرم: هر گرم برابر ۱۰۰۰ میلی گرم است. پس هر میلی گرم برابر \(\frac{1}{{1000}}\)گرم است.
برای تبدیل واحدهای جرم میتوان از الگوی زیر استفاده کرد:
مثال
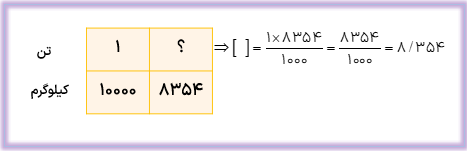
الف ۸۳۵۴ کیلوگرم چند تن است؟
ب ۵۴۹ میلی گرم چند کیلوگرم است؟
مساحت دایره
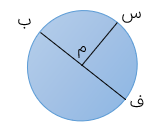
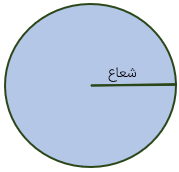
شکل مقابل یک دایره را نشان می دهد.
نقطه ی «م» مرکز دایره است.
پاره خط «م س» شعاع دایره است.
پاره خط «ف ب» قطر دایره است.
دایره دارای بی شمار شعاع و بی شمار قطر است.
شعاع های دایره با هم برابر و قطرهای دایره نیز با هم برابرند.
اندازه ی هر قطر دو برابر شعاع است یعنی اندازه ی شعاع نصف قطر است.
۳/۱۴ × قطر = محیط دایره
۳/۱۴ × شعاع × شعاع = مساحت دایره
عدد ۳/۱۴ را عدد پی می.گویند البته این عدد مقدار تقریبی عدد پی است.
محیط (ه ر ) شکل یعنی دوتا دور شکل یعنی طول خطی که دو شکل را تشکیل می دهد.
مثال
در شکل های زیر محیط هر شکل با خط قرمز مشخص شده است.
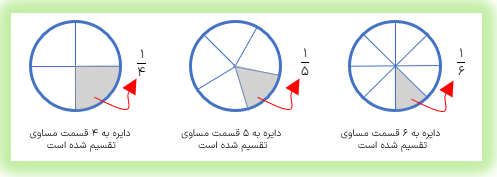
می دانیم که یک دایره کامل یک زاویه ی ۳۶۰ درجه را نشان میدهد. اکنون به شکل های زیر که در آن ها دایره ها به قسمتهای مساوی تقسیم شدهاند و اندازه ی زاویه های هر بخش دقت کنید.
مثال
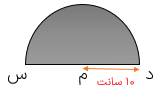
محیط و مساحت نیم دایره ی شکل مقابل را حساب کنید.
مساحت دایره ی کامل:
۱۰ × ۱۰ × ۳/۱۴ =314 سانتی متر مربع
مساحت نیم دایره:
سانتی متر مربع ۱۵۷ = ۲ ÷ ۳۱۴
اندازه ی قطر (د س) + طول خط منحنی = محیط نیم دایره
. \( = \frac{{2 \times 10 \times 3/14}}{2} = 31/4\)طول خط منحنی
31/4×20=51/4= محیط نیم دایره
مثال
محیط و مساحت شکل مقابل را حساب کنید.
شکل مقابل \(\frac{3}{4}\) یک دایره است.
. \(\frac{3}{4} \times 20 \times 20 \times 3/14 = 3 \times 100 \times 3/14 = 3 \times 31\)=مساحت شکل
.\(2 \times 30 \times 3/14 \times \frac{3}{4} + 2 \times 20 = 94/40 = 134/2\) = محیط شکل
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه ششم- آزمون آنلاین تمامی دروس پایه ششم
- گام به گام تمامی دروس پایه ششم
- ویدئو های آموزشی تمامی دروس پایه ششم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ششم
- فلش کارت های آماده دروس پایه ششم
- گنجینه ای جامع از انشاء های آماده پایه ششم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ششم
دایره و چند شکل مهم دیگر
محیط دایره
در سال های گذشته با محیط دایره و نحوه ی محاسبه ی آن آشنا شدید:
عدد پی × شعاع × ۲ = عدد پی × قطر = محیط دایره
با توجه به رابطه ی بالا نصف محیط دایره برابر است با حاصل ضرب شعاع در عدد بی، اما دقت داشته باشید که محیط یک نیم دایره از رابطه ی زیر به دست می آید.
قطر + (عدد پی × شعاع) =محیط نیم دایره
مساحت دایره
در کتاب درسی چگونگی اثبات رابطهی مساحت دایره بیان شده است و در این جا فقط به بیان این رابطه می پردازیم.
عدد پی × شعاع × شعاع = مساحت دایره
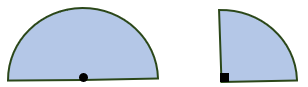
۲ + (عدد پی × شعاع × شعاع) = مساحت نیم دایره
۴ +(عدد پی × شعاع × شعاع) = مساحت ربع دایره
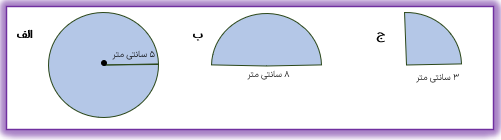
مثال
مساحت هر یک از شکل های زیر را به دست آورید.
الف)
سانتی متر مربع ۷۸/۵ = ۳/۱۴ × ۲۵ = ۳/۱۴ × ۵ × ۵ = مساحت دایره به شعاع ۵ سانتی
ب) دقت داشته باشید که در این نیم دایره اندازه ی قطر داده شده است لذا ابتدا باید اندازه ی شعاع را حساب کنیم:
دسی متر ۴ = ۲ ÷ ۸ = شعاع نیم دایره به قطر ۸ دسی متر
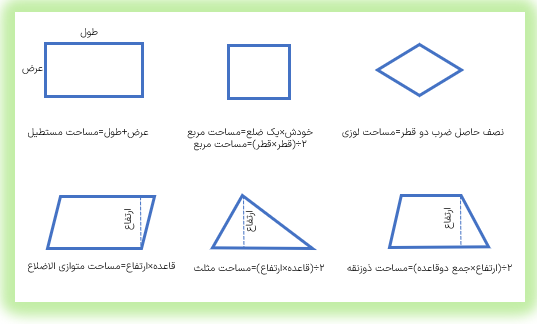
مساحت چند شکل مهم
جزوات جامع پایه ششم
جزوه جامع ریاضی ششم فصل 1 عدد و الگوهای عددی
جزوه جامع ریاضی ششم فصل 2 کسر
جزوه جامع ریاضی ششم فصل 3 اعداد اعشاری
جزوه جامع ریاضی ششم فصل 4 تقارن و مختصات
جزوه جامع ریاضی ششم فصل 5 اندازه گیری
جزوه جامع ریاضی ششم فصل 6 تناسب و درصد
جزوه جامع ریاضی ششم فصل 7 تقریب
خط و زاویه
خط و زاویه
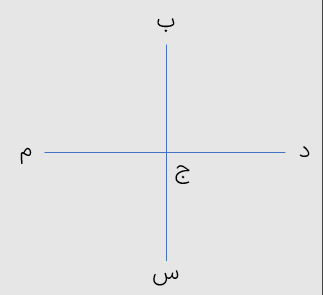
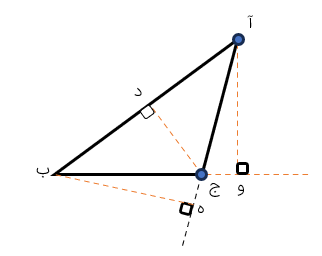
فاصله ی بین دو نقطه طول پاره خطی است که دو نقطه را به هم وصل می.کند در شکل روبه رو، فاصله ی دو نقطه ی و «س» برابر است با طول پاره خط «ب س».
فاصله ی یک نقطه تا یک خط پاره خط برابر است با طول پاره خط عمودی که از آن نقطه بر خط رسم می شود. در شکل زیر فاصله ی نقطه ی «م» از خط ب پ برابر است با طول پاره خط «م ج».
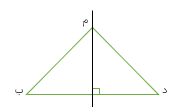
فاصله ی هر رأس مثلث از ضلع مقابل آن برابر است با : ارتفاع وارد بر آن ضلع
در شکل زیر (ب ج) فاصله ی نقطه ی «ب» از ضلع پت است بنابراین ب ج» ارتفاع وارد بر ضلع (پ ت) است.
از هر نقطه روی یک پاره خط فقط یک خط عمود بر آن می توان رسم کرد.
مثال
از نقطه ی «ج» روی خط «م د» فقط یک خط مانند بس را میتوان بر خط «د م» عمود رسم کرد.
عمود منصف یک پاره خط خطی است که از وسط پاره خط بگذرد و بر آن عمود رسم شود. در شکل مقابل خط «م ل » عمود منصف پاره خط س ده است.
دقت کنید چون هر پاره خط فقط یک نقطه ی وسط دارد بنابراین هر پاره خط فقط یک عمود منصف دارد.
هر نقطه روی عمود منصف پاره خط از دو سر پاره خط به یک فاصله است یعنی در شکل روبه رو اندازه «د م» با «م ب» برابر است.
دقت کنید چون خط و نیم خط اندازه ی مشخصی ندارند بنابراین نقطه ی وسط آن ها نیز مشخص نیست. پس برای نیم خط و خط نمی توان عمود منصف رسم کرد.
فاصله ی دو نقطه از هم
فاصله ی دو نقطه از هم
می دانیم که از دو نقطه شمار خط خمیده میگذرد اما از دو نقطه فقط یک خط راست عبور می کند که به این ترتیب طول پاره خطی که دو نقطه را به یک دیگر وصل میکند برابر فاصله ی بین این دو نقطه است. در شکل زیر طول پاره خط آب برابر فاصله بین دو نقطه ی (آ) و (ب) است.
فاصله ی دو نقطه طول کوتاه ترین پاره خطی است که دو نقطه را به هم وصل می کند.
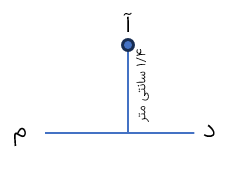
فاصله ی نقطه از خط
کوتاه ترین فاصله ی یک نقطه تا یک خط برابر طول پاره خطی است که از نقطه ی مورد نظر بر آن خط عمود میشود برای رسم پاره خط عمود از یک نقطه بر یک خط میتوانیم از گونیا استفاده کنیم. در شکل مقابل فاصله ی نقطه ی (آ) از خط (د م) برابر ۱/۴ سانتی متر است.
فاصله ای نقطه از خط طول پاره خطی است که از آن نقطه به خط عمود می شود
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه ششم- آزمون آنلاین تمامی دروس پایه ششم
- گام به گام تمامی دروس پایه ششم
- ویدئو های آموزشی تمامی دروس پایه ششم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ششم
- فلش کارت های آماده دروس پایه ششم
- گنجینه ای جامع از انشاء های آماده پایه ششم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ششم
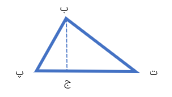
ارتفاع و عمود منصف
رسم ارتفاع در مثلث
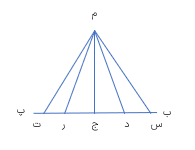
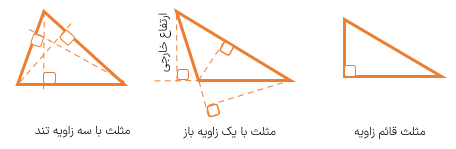
اگر در مثلثی از یک رأس بر ضلع مقابل آن عمود کنیم این پاره خط عمود همان ارتفاع مثلث و ضلع مقابل به آن نیز قاعده ی نظیر آن ارتفاع می باشد.. در شکل زیر از رأس (ج) بر ضلع مقابل آن یعنی ضلع آب پاره خط (ج) (د) را عمود کرده ایم به این ترتیب پاره خط (د ج) همان ارتفاع مثلث ضلع (آ ب) نیز قاعده ی متناظر با آن ارتفاع می باشد. توجه داشته باشید که گاهی مجبوریم ارتفاع وارد بر یک ضلع را در خارج از مثلث . بر امتداد آن ضلع رسم کنیم در شکل زیر پاره خط (آ و) ارتفاع هر مثلث دارای سه ارتفاع میباشد که همگی آنها یک دیگر را در یک نقطه قطع می کنند. در شکل های زیر ارتفاع های سه نوع مثلث را نشان داده ایم به ارتفاع هایی که در بیرون مثلث رسم می شوند ارتفاع خارجی می گوییم.
نظیر ضلع (ج) (ب) میباشد که برا امتداد ضلع (ج ب) عمود شده است و این اتفاق زمانی می افتد که مثلث زاویه ی بزرگ تر از ۹۰ درجه داشته باشد.
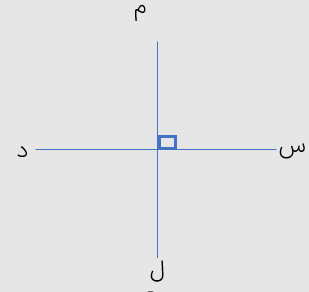
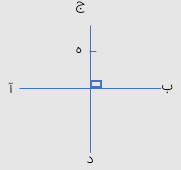
عمود منصف
در شکل مقابل خط (ج د) بر پاره خط (آ ب) عمود شده و آن را به دو قسمت مساوی تقسیم کرده است. به این خط یعنی خط (ج د)، عمود منصف پاره خط (ب آ) گفته می شود.
در شکل بالا نقطه ی (ه) روی عمود منصف پاره خط (ب آ) قرار دارد از طرفی فاصله ی دو نقطه (ه آ) با فاصله ی دو نقطه ی (ب ه) برابر است از این خاصیت میتوان برای تشخیص عمود منصف بودن یک خط استفاده کرد.
۱ عمود منصف، خطی است که از وسط پاره خط بگذرد و بر آن عمود باشد.
2 هر نقطه روی عمود منصف یک پاره خط از دو سر آن پاره خط به یک فاصله است.
جزوات جامع پایه ششم
جزوه جامع ریاضی ششم فصل 1 عدد و الگوهای عددی
جزوه جامع ریاضی ششم فصل 2 کسر
جزوه جامع ریاضی ششم فصل 3 اعداد اعشاری
جزوه جامع ریاضی ششم فصل 4 تقارن و مختصات
جزوه جامع ریاضی ششم فصل 5 اندازه گیری
جزوه جامع ریاضی ششم فصل 6 تناسب و درصد
جزوه جامع ریاضی ششم فصل 7 تقریب
زوایای مکمل و متمم و متقابل به رأس
انواع زاویه
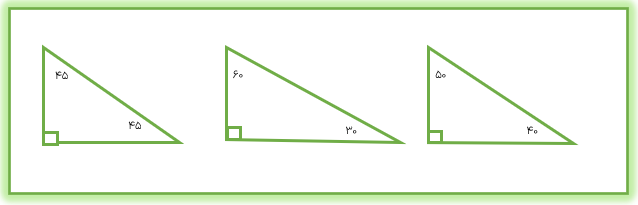
اندازه ی زاویه ی راست (قائمه)، برابر ۹۰ درجه است.
اندازه ی زاویه نیم صفحه برابر ۱۸۰ درجه است.
اندازه ی زاویه تند از صفر درجه بیشتر و از ۹۰ کم تر است.
اندازه ی زاویه ی باز از ۹۰ درجه بیشتر و از ۱۸۰ درجه کم تر است.
اندازه ی زاویه ی تمام صفحه مساوی ۳۶۰ درجه است.
یعنی:
زاویه ی تمام صفحه > زاویه ی نیم صفحه > زاویه ی باز > زاویه ی راست > زاویه ی تند
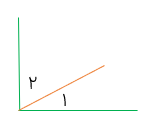
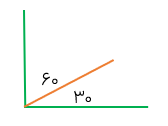
دو زاویه ی متمم اگر مجموع دو زاویه ۹۰ درجه باشد آن دو زاویه را متمم گویند.
در شکل مقابل زاویه های ۱ و ۲ متمم اند.
در مثلث قائم الزاویه دو زاویه ی تند متمم یکدیگرند.
مثال
اندازه ی متمم زاویه ی ۲۵ درجه را حساب کنید.
\(90^\circ - 25^\circ = 65^\circ \)
یعنی زاویه ی ۶۵ درجه متمم زاویه ی ۲۵ درجه است.
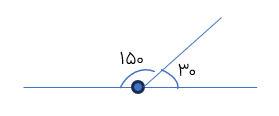
اگر مجموع دو زاویه ۱۸۰ درجه باشد آن دو زاویه را مکمل می گویند.
در شکل مقابل زاویه های ۱ و ۲ مکمل اند.
مثال
اندازه ی مکمل زاویه ۱۲۰ درجه را حساب کنید.
\(180^\circ - 120^\circ = 60^\circ \)
یعنی زاویه ۶۰ درجه مکمل زاویه ی ۱۲۰ درجه است.
در متوازی الاضلاع زاویه های مجاور مکمل اند، یعنی:

\(\begin{array}{l}1 + 2 = 180^\circ \\\\3 + 4 = 180^\circ \\\\1 + 4 = 180^\circ \\\\2 + 3 = 180^\circ \end{array}\)
مثال
الف اندازه ی زاویه ی متمم و مکمل زاویه ۳۵ درجه را حساب کنید.
مکمل زاویه \(180^\circ - 35^\circ = 145^\circ \)
متمم زاویه \(90^\circ - 35^\circ = 55^\circ \)
ب اختلاف مکمل و متمم این زاویه چند درجه است؟
\(145^\circ - 55^\circ = 90^\circ \)
اختلاف مکمل و متمم هر زاویه ای همیشه ۹۰ است.
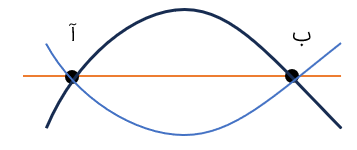
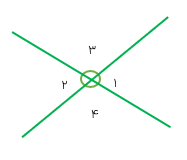
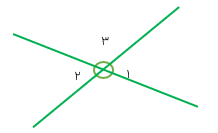
اگر دو خط راست یکدیگر را قطع کنند، ۴ زاویه درست میشود که زاویه های روبه رو، دوبه دو متقابل به رأس هستند یعنی در شکل مقابل زاویه های ۱ و ۲ متقابل به رأس هستند. زاویه های ۳ و۴ نیز متقابل به رأس هستند.
دو زاویه ی متقابل به رأس با هم برابرند، یعنی در شکل بالا:
\(\widehat 1 = \widehat 2\,\,\,\,,\,\,\,\,\,\,\widehat 3 = \widehat 4\)
مثال
در شکل مقابل مجموع ۱ و ۲ مساوی ۶۰ درجه است. اندازه ی زاویه ی ۳ چند درجه است؟
.\(\widehat 1,\widehat 2 \to 60^\circ \div 2 = 30^\circ \) اندازه ی
.\(\widehat 3 \to 180^\circ - 30^\circ = 150^\circ \) اندازه ی
دایره ی شکل مقابل به شش قسمت مساوی یا به شش کمان مساوی تقسیم شده است. اگر نقطه های کنار هم روی دایره را به هم وصل کنیم شش پاره خط به وجود آمده نیز مساوی اند یعنی پاره خط های مربوط به کمان های مساوی با هم برابرند.
۱ زاویه ی تند از زاویه راست (قائمه) کوچک تر است.
۲ زاویه ی باز از زاویه ی راست بزرگ تر و از زاویه ی نیم صفحه ۱۸۰( درجه) کوچک تر است.
3 زاویه ی نیم صفحه > زاویه ی باز زاویه ی راست > زاویه ی تند
دو زاویه ی متمم
به هر دو زاویه ای که مجموع آنها ۹۰ درجه باشد دو زاویه متمم میگویند به طور مثال دو زاویه ی ۳۰ درجه و ۶۰ درجه متمم یک دیگر هستند.
مثال
متمم زاویه ۳۷ درجه را حساب کنید.
چون مجموع دو زاویه ی متمم ۹۰ درجه است بنابراین با انجام تفریق زیر میتوانیم زاویه ی ۳۷ درجه را پیدا کنیم.
۵۳ = ۳۷ - ۹۰ = متمم زاویه ۳۷
مثال
دو زاویه ی متمم مشخص کنید که اندازه ی یکی از آن ها ۵ برابر دیگری باشد.
با توجه به این که اندازه ی یکی از زاویه،ها پنج برابر دیگری است لذا در ابتدا باید ۹۰ درجه را به ۶ قسمت مساوی تقسیم کنیم تا اندازه ی زاویه کوچک تر به دست آید.
اندازه ی زاویه کوچک تر ۱۵ = ۶ ÷۹۰
اندازه ی زاویه بزرگ تر ۷۵ = ۵× ۱۵
دو زاویه ی مکمل
به هر دو زاویه که مجموع آن ها ۱۸۰ درجه باشد دو زاویه ی مکمل میگویند به طور مثال دو زاویه ی ۳۰ درجه و ۱۵۰ درجه مکمل یک دیگر هستند.
مثال
مکمل زاویه ی ۳۷ درجه را حساب کنید.
چون مجموع دو زاویه مکمل ۱۸۰ درجه است بنابراین با انجام تفریق زیر میتوانیم مکمل زاویه ی ۳۷ درجه را پیدا کنیم.
۱۴۳ = ۳۷ - ۱۸۰ = مکمل زاویه ی ۳۷
مثال
دو زاویه ی مکمل مشخص کنید که اندازه ی یکی از آن ها پنج برابر دیگری باشد.
چون اندازه ی یکی از زاویه های مکمل پنج برابر دیگری است لذا در ابتدا باید ۱۸۰ درجه را بر ۶ قسمت مساوی تقسیم کنیم تا اندازه ی زاویه ی کوچک تر به دست آید.
۱۵۰ = ۵ × ۳۰ = اندازه ی زاویه بزرگتر و اندازه ی زاویه کوچکتر ۳۰ = ۶ ÷ ۱۸۰
اختلاف متمم و مکمل هر زاویه ای برابر ۹۰ درجه است به طور مثال متمم زاویه ی ۳۰ درجه برابر ۶۰ و مکمل این زاویه برابر ۱۵۰ درجه است و داریم:
150-60=90
دو زاویه ی متقابل به رأس
اگر دو خط هم دیگر را قطع کنند، چهار زاویه به وجود می آید که زاویه های روبه رو دو به دو با هم برابر هستند. به این زاویه ها متقابل به رأس می گویند. توجه داشته باشید که در زاویه های متقابل به رأس، ضلع ها باید در امتداد یک دیگر باشند.
با توجه به این که دو زاویه ی متقابل به رأس باید هم رأس باشند و همچنین اضلاع دو زاویه ی متقابل به رأس باید در امتداد یک دیگر باشد لذا در شکلهای زیر زاویه ی متقابل به رأس وجود ندارد.
مثال
مجموع دو زاویه ی متقابل به رأس ۶۴ درجه است اندازه ی هر یک از آن ها چند درجه است؟
با توجه به این که دو زاویه ی متقابل به رأس با هم برابرند، بنابراین:
۳۲ = ۲ ÷ ۶۴ = اندازه ی هر یک از زاویه ها
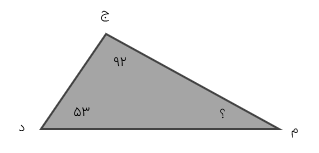
مجموع زاویه های داخلی هر مثلث ۱۸۰ درجه است.
مثال
در شکل زیر اندازه ی زاویه ی «م» چند درجه است؟
می دانیم که مجموع همه ی زاویه های داخلی این مثلث باید ۱۸۰ درجه باشد، بنابراین:
۳۵ = ۱۴۵ - ۱۸۰ = (۵۳ + ۹۲) – ۱۸۰= اندازه ی زاویه ی «م»



1736019749.png)