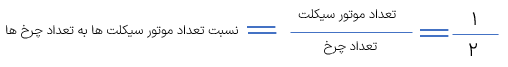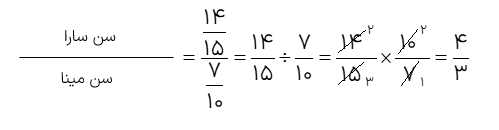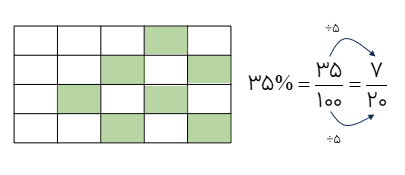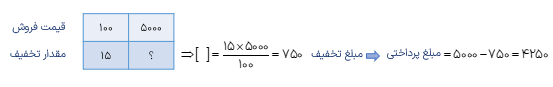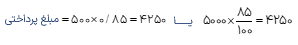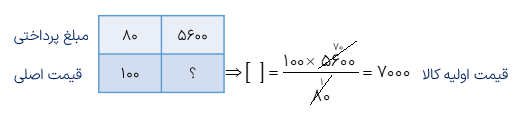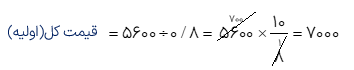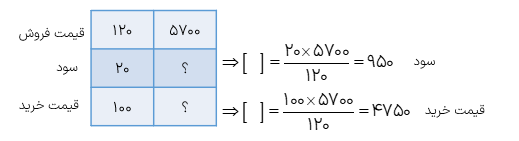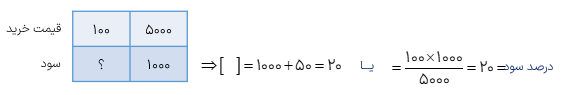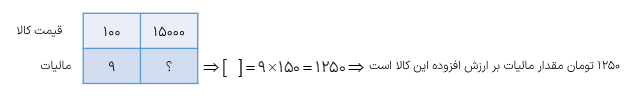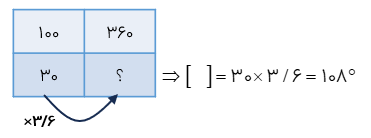درسنامه کامل ریاضی ششم فصل 6 تناسب و درصد
تعداد بازدید : 7.27Mخلاصه نکات ریاضی ششم فصل 6 تناسب و درصد - درسنامه شب امتحان ریاضی ششم فصل 6 تناسب و درصد - جزوه شب امتحان ریاضی ششم نوبت اول فصل 6 تناسب و درصد
کسر، نسبت و تناسب
کسر، نسبت و تناسب
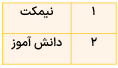
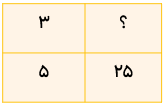
نسبت مقایسه ی بین دو چیز مختلف است. برای مثال اگر نسبت نیمکتها به دانش آموزان در یک کلاس ۱ به ۲ باشد یعنی روی یک نیمکت ۲ نفر مینشینند این نسبت را به صورت زیر در جدول قرار می دهیم و به صورت های «۱ به ۲» یا «۱ و ۲» یا «۲ : ۱» یا \(\frac{1}{2}\)نمایش می دهیم.
مثال
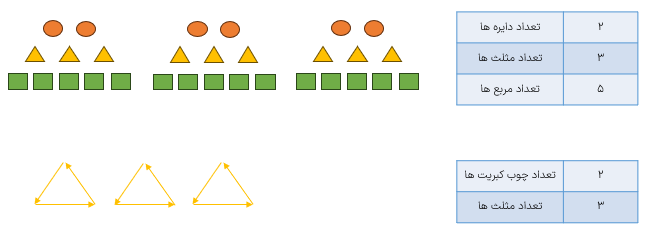
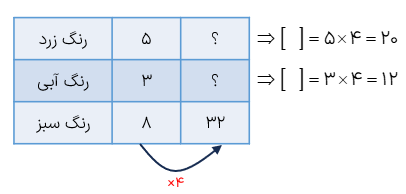
به شکل ها و جدول های زیر توجه کنید.
همان طور که صورت و مخرج کسری را در عددی ضرب میکنیم و کسری مساوی کسر اولیه به دست می آید، اگر نسبت ها را نیز در عددی ضرب کنیم تغییر نمی کنند و نسبت های حاصل با نسبت های اولیه برابرند؛ یعنی نسبت ۲ به ۳ با نسبت ۴ به ۶ برابر است.
مثال
نسبت پول رضا احمد و پرهام مانند \(\frac{5}{6},\frac{2}{3},\frac{1}{2}\) است نسبت ها را به صورت عدد صحیح بیان کنید.
هر سه عدد را در کوچک ترین مخرج مشترک آنها (عدد ۶) ضرب می کنیم.
پرهام:\(\frac{5}{6} \times 6 = 5\)
احمد:\(\frac{2}{3} \times 6 = 4\)
رضا:\(\frac{1}{2} \times 6 = 3\)
یعنی نسبت پول ،رضا احمد و پرهام مانند ۳ به ۴ به ۵ است.
در مسئله های مربوط به نسبت، ترتیب مهم است؛ یعنی وقتی که می گوییم نسبت سن آرش به روزمهر 3به ۵ است یعنی عدد ۳ مربوط به سن آرش و عدد ۵ مربوط به سن روز مهر است.
گاهی نسبت های بین چند مقدار به طور واضح بیان نمیشود که در این صورت باید نسبت بین عامل مشترک آن ها را یکسان کنیم تا بتوانیم نسبت هر یک از عامل های داده شده را تشخیص دهیم.
مثال
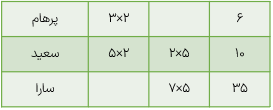
نسبت سن پرهام به سعید ۳ به ۵ و نسبت سن سعید به سارا ۲ به ۷ است نسبت سن پرهام به سارا را بیابید.
دقت کنید که در این مسئله نسبت سن پرهام به سارا واضح نیست و سعید در هر دو نسبت مشترک پس باید نسبت سن سعید در هر دو حالت به یک عدد تبدیل شود یعنی نسبت سن پرهام به سارا، مانند ۶ به ۳۵ است.
هرگاه تغییرات دو مقدار به صورتی باشد که نسبت حاصل تقسیم آنها مقدار ثابتی باشد، به آن دو مقدار، مقدارهای متناسب می گوییم.
مثال
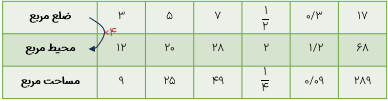
نسبت طول یک ضلع مربع به محیط آن، همواره ثابت و مساوی است؛ پس می گوییم طول ضلع یک مربع با محیط آن متناسب است به جدول زیر دقت کنید.
اندازه ی ضلع مربع با مساحت آن متناسب نیست؛ یعنی نسبت آن ثابت نیست.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه ششم- آزمون آنلاین تمامی دروس پایه ششم
- گام به گام تمامی دروس پایه ششم
- ویدئو های آموزشی تمامی دروس پایه ششم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ششم
- فلش کارت های آماده دروس پایه ششم
- گنجینه ای جامع از انشاء های آماده پایه ششم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ششم
تناسب
تناسب
دو نسبت مساوی یک تناسب را تشکیل میدهند حاصل تناسب یعنی یافتن مقدار مجهول در دو نسبت مساوی؛ یعنی اگر یکی از عددها در تناسب مشخص نباشد، مقدار آن را بیابیم.
جدولی که تناسب را نمایش میدهد جدول تناسب نامیده می شود.
مثال
در تساوی مقابل در جای خالی چه عددی را باید قرار داد؟
تناسب را به صورت دو کسر مساوی نیز نشان می دهند.
برای مثال جدول تناسب فوق را به صورت \(\frac{3}{4} = \frac{9}{{12}}\) نیز نشان می دهند.
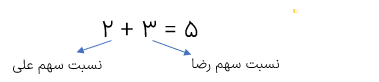
تسهیم به نسبت یعنی تقسیم کردن به نسبت سهم هر چیزی یا هر کسی از کل سهم. برای مثال وقتی که می گوییم می خواهیم ۵۰ تومان را نسبت ۲ به ۳ بین علی و رضا تقسیم کنیم یعنی می خواهیم این پول را طوری تقسیم کنیم که از ۵ قسمت کل ،پول ۲ قسمت به علی و ۳ قسمت به رضا برسد. این طوری:
مثال
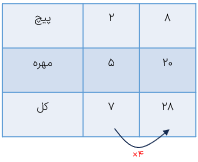
احمد ۲۸ عدد پیچ و مهره دارد. نسبت پیچها به مهرههای او است؛ او چند پیچ و چند مهره دارد؟
عدد ۲۸ نه تعداد پیچ ها است و نه تعداد مهره ها بلکه مجموع تعداد پیچها و مهره ها است، بنابراین باید مجموع نسبت ها را حساب کنیم
یعنی احمد ۸ پیچ و ۲۰ مهره دارد.
جزوات جامع پایه ششم
جزوه جامع ریاضی ششم فصل 1 عدد و الگوهای عددی
جزوه جامع ریاضی ششم فصل 2 کسر
جزوه جامع ریاضی ششم فصل 3 اعداد اعشاری
جزوه جامع ریاضی ششم فصل 4 تقارن و مختصات
جزوه جامع ریاضی ششم فصل 5 اندازه گیری
جزوه جامع ریاضی ششم فصل 6 تناسب و درصد
جزوه جامع ریاضی ششم فصل 7 تقریب
نسبت
نسبت
اگر بخواهیم در ریاضیات رابطه ی بین دو چیز یا دو عدد را نشان دهیم از نسبت استفاده . می کنیم به طور مثال هر موتورسیکلت دارای دو چرخ است بنابراین دو موتورسیکلت دارای چهار چرخ است و سه موتورسیکلت دارای شش چرخ می باشند به این ترتیب میتوان گفت که نسبت تعداد موتورسیکلت ها به تعداد چرخ ها ۱ به ۲ است که این نسبت را به صورت کسر با - و به صورت اعشاری با ۰/۵ هم نمایش می دهند. البته در بعضی از کتاب ها نسبت ۱ به ۲ را به صورت های (۱و۲) و همچنین (۲و ۱) هم نمایش میدهند. دقت داشته باشید که نسبت را به کسری نخوانید بلکه آن را به صورت (۱ به ۲) و یا (۱ و ۲) بخوانید.
۱ نسبت واحد ندارد اما باید دقت کنیم که در هر نسبت صورت و مخرج را بر حسب یک واحد معین بنویسیم.
2 صورت و مخرج هر نسبت را می توان ساده کرد.
مثال
قد علی ۱۷۵ سانتی متر است و قد مهدی ۱/۵ متر است نسبت قد علی به قد مهدی چه قدر است؟
با توجه به این که قد مهد ی برحسب متر بیان شده است ابتدا قد او را بر حسب سانتی متر بیان می کنیم، چون هر متر معادل صد سانتی متر است پس قد مهدی ۱۵۰ = ۱۰۰ × ۱/۵ سانتی متر می شود. بنابراین؛ در برخی از مسائل صورت یا مخرج و یا هر دوی آنها را به صورت کسری میدهند که برای ساده تر شدن نسبت باید صورت نسبت را بر مخرج آن تقسیم کنیم.
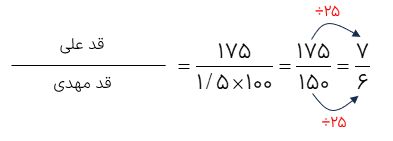
مثال
نسبت سن سارا به سن مینا مثل به است. نسبت سن این دو نفر را به ساده ترین شکل بیان کنید.
نسبت \(\frac{4}{3}\)ساده ترین شکل بیان نسبت سن این دو نفر است.
جدول تناسب
جدول تناسب
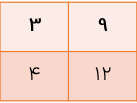
هرگاه دو نسبت با هم مساوی باشند میگوییم که این دو نسبت با هم دیگر متناسب هستند. به طور مثال با توجه به جدول زیر نسبت طول ضلع هر مربع به محیط آن\(\frac{1}{4}\)است و با کم تر یا بیش تر شدن ضلع مربع، محیط هم به همان نسبت تغییر میکند یعنی اگر طول ضلع را دو برابر کنیم محیط هم دو برابر می شود و یا اگر محیط را ۲۰ برابر کنیم طول ضلع هم ۲۰ برابر میشود پس محیط مربع با طول ضلع آن متناسب است و یا به عبارت دیگر طول ضلع مربع با محیط آن تناسب دارد به این جدول که تناسب را نشان می دهد جدول تناسب می گوییم.
در حل برخی مسائل می توانیم از جدول تناسب استفاده کنیم و جواب مسئله را به دست آوریم.
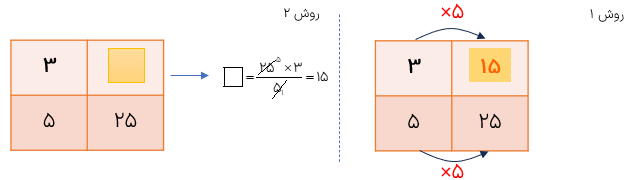
مثال
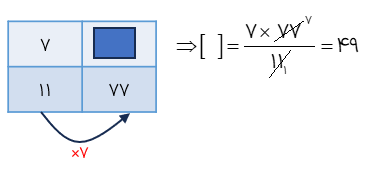
اگر نسبت ۷ به ۱۱ مانند نسبت جای خالی به ۷۷ باشد داخل دایره چه عددی باید بنویسیم؟
برای حل سؤال از جدول تناسب مقابل استفاده میکنیم چون ۱۱ را هفت برابر کردیم تا حاصل ۷۷ شود پس باید ۷ را هم هفت برابر کنیم، بنابراین؛
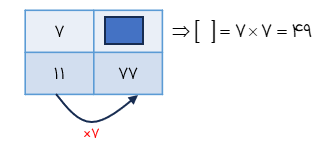
حل جدول تناسب
اگر مانند مثال قبل نتوانیم چند برابر شدن عددها را تشخیص دهیم بهتر است که از روش زیر که به روش طرفين وسطین معروف میباشد کمک بگیریم در جدول مقابل به عددهای ۷ و ۷۷، طرفین و به ۱۱ و هم وسطین گفته . شود. در هر جدول تناسب همواره حاصل ضرب طرفین با حاصل ضرب وسطین برابر است. می بنابراین برای پیدا کردن عدد داخل کافی است که حاصل ضرب طرفین را بر عدد ۱۱ تقسیم کنیم:
تسهیم به نسبت
تسهیم به نسبت یعنی سهیم بودن در نسبت به عبارت دیگر تسهیم به نسبت یعنی مشخص کردن سهم هر چیزی به نسبت معین از کل سهم ها به طور مثال در یک کلاس نسبت دانش آموزانی که به فوتبال علاقه مند هستند به دانش آموزانی که به والیبال علاقه مندند \(\frac{5}{3}\)است پس نسبت دانش آموزانی که به فوتبال علاقه مندند به کل دانش آموزان \(\frac{5}{{5 + 3}} = \frac{5}{8}\) است. همچنین نسبت دانش آموزانی که به والیبال علاقه مندند به کل دانش آموزان \(\frac{3}{{5 + 3}} = \frac{3}{8}\) است. البته به شرط این که این نسبت مربوط به کل دانش آموزان باشد و هر دانش آموز حتما به یکی از این دو ورزش علاقه مند باشد.
مثال
یک نقاش ساختمان برای تهیه ی رنگ سبز هر ۵ کیلوگرم رنگ زرد را با ۳ کیلوگرم رنگ آبی مخلوط میکند. او برای تهیه ۳۲ کیلو گرم رنگ سبز به چند کیلوگرم از هر رنگ نیاز دارد؟
8=3+5 = مجموع نسبت ها
یعنی اگر ۵ کیلوگرم رنگ زرد را با ۳ کیلوگرم رنگ آبی مخلوط کنیم ۸ کیلوگرم رنگ سبز به دست می آید.
مقایسه ی نسبت ها
برای مقایسه چند نسبت ابتدا هر نسبت را به صورت یک کسر می نویسیم و سپس آن ها را مانند مقایسه ی کسرها، از روش مخرج مشترک گیری و یا روشهای دیگر مقایسه می کنیم.
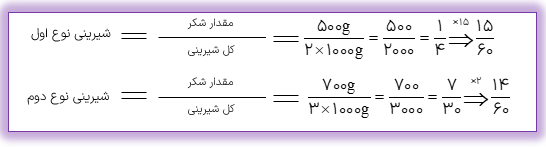
مثال
در ۲ کیلوگرم از یک نوع ،شیرینی ۵۰۰ گرم شکر و در ۳ کیلوگرم از نوع دیگری شیرینی، ۷۰۰ گرم شکر به کار رفته است کدام نوع ،شیرینی شکر بیش تری دارد؟ ابتدا نسبت شکر به شیرینی را در هر دو نوع سپس کسرهای حاصل را با هم مقایسه می کنیم.
با مقایسه \(\frac{{14}}{{60}},\frac{{15}}{{60}}\) نتیجه میشود که شیرینی نوع اول دارای شکر بیش تری است.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه ششم- آزمون آنلاین تمامی دروس پایه ششم
- گام به گام تمامی دروس پایه ششم
- ویدئو های آموزشی تمامی دروس پایه ششم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ششم
- فلش کارت های آماده دروس پایه ششم
- گنجینه ای جامع از انشاء های آماده پایه ششم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ششم
درصد
درصد
نسبت یا کسری که مخرج آن ۱۰۰ باشد، نشان دهنده ی درصد است. برای مثال، کسری \(\frac{{57}}{{100}}\) را به صورت% ۵۷ نشان میدهیم و میخوانیم: پنجاه و هفت درصد
وقتی که میگوییم شیر با چربی ۴% یعنی در هر ۱۰۰ گرم از این شیر ۴ گرم چربی است یا در ۱۰۰ کیلوگرم از این شیر، ۴ کیلوگرم چربی است.
اگر بخواهیم کسری را به صورت درصد بنویسیم باید کسری مساوی با آن و با مخرج ۱۰۰ پیدا کنیم.
\(\frac{3}{5},\frac{1}{4},\frac{{14}}{{25}}\)
مثال
کسرهای مقابل را به صورت درصد بنویسید.
\(\begin{array}{l}\frac{3}{5}\\\\\frac{1}{4}\\\\\frac{{14}}{{25}}\end{array}\)
\(\begin{array}{l}\frac{3}{5} = \frac{{60}}{{100}} = 60\% \\\\\frac{1}{4} = \frac{{25}}{{100}} = 25\% \\\\\frac{{14}}{{25}} = \frac{{56}}{{100}} = 56\% \end{array}\)
اگر بخواهیم کسری را به صورت درصد بنویسیم اما نتوانیم مخرج آن را به سادگی با ضرب کردن در یک عدد به ۱۰۰ تبدیل کنیم ابتدا صورت کسر را بر مخرجش تقسیم کرده و به صورت عدد اعشاری و سپس به شکل درصد می نویسیم.
مثال
کسر\(\frac{3}{8}\)را به صورت درصد بنویسید.
مخرج کسر باید ۱۰۰ باشد تا بتوانیم به صورت درصد بنویسیم.
\(\frac{3}{8} = 3 \div 8 = 0/375 = \frac{{375}}{{1000}} = \frac{{37/5}}{{100}} = 37/5\% \)
مثال
کسر\(\frac{{147}}{{500}}\) را به صورت درصد بنویسید.
توجه کنید که مخرج کسر باید ۱۰۰ باشد تا بتوانیم به صورت درصد بنویسیم.
\(\frac{{147}}{{500}} = \frac{{294}}{{1000}} = \frac{{29/4}}{{100}} = 29/4\% \)
کسرها یا عددهای بزرگ تر از واحد را نیز میتوان به صورت درصد نوشت به مثال های زیر دقت کنید.
مثال
عددهای مقابل را به صورت درصد بنویسید.
\(\frac{7}{5},3/4\)
\(\begin{array}{l}\frac{7}{5} = \frac{{140}}{{100}} = 140\% \\\\3/4 = 3/40 = 340\% \end{array}\)
دقت کنید: ۵/۷۶یعنی ۵۷۶%، ۲/۳ یعنی ۲/۳۰ یعنی ۲۳۰%.
دقت کنید:
دو برابر یعنی %۲۰۰, سه برابر یعنی %۳۰۰ ، هفت برابر یعنی ٪۷۰۰.
کل هر چیزی را ٪۱۰۰. در نظر میگیریم یعنی وقتی می گوییم کل دانش آموزان یک کلاس به اردو می روند، یعنی ۱۰۰% دانش آموزان یک کلاس به اردو میروند یا وقتی میگوییم مبلغ کالایی ۷۰۰۰ تومان است، یعنی ۱۰۰٪ مبلغ کالا ۷۰۰۰ تومان است.
مثال
%۳۰ دانش آموزان کلاسی به مسابقه ی فوتبال رفته اند چند درصد به مسابقه ی فوتبال نرفته اند؟
کل دانش آموزان کلاس ۱۰۰% است.
به مسابقه ی فوتبال نرفته اند ۷۰% = %۳۰ – ۱۰۰%
مثال
فروشنده ای برای فروش کالایش ۲۰% تخفیف می دهد، یعنی چند درصد آن را باید بپردازیم؟
کل مبلغ کالا %۱۰۰ است.
باید بپردازیم ۸۰% = %۲۰ – ۱۰۰%
توجه کنید که ۲۰% مبلغ کالا را تخفیف میدهد یعنی ۲۰% قیمت کالا گرفته نمی شود.
مثال
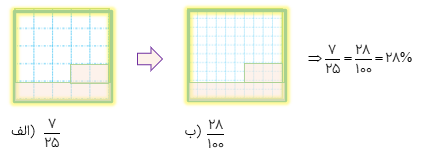
به شکل (الف) که به ۲۵ قسمت مساوی تقسیم شده است دقت کنید در این شکل ۷ قسمت رنگ شده است، پس\(\frac{7}{{25}}\) شکل (الف) رنگی است. حال اگر همان شکل را به ۱۰۰ قسمت مساوی تقسیم کنیم و به همان اندازه مانند شکل (الف) رنگ کنیم ملاحظه کنید که\(\frac{{28}}{{100}}\) شکل (ب) رنگ شده است این دو کسر نمایش مختلفی از یک چیز هستند در ضمن می توانیم\(\frac{{28}}{{100}}\) را به صورت ۲۸% (میخوانیم ۲۸ درصد) هم نمایش دهیم.
جزوات جامع پایه ششم
جزوه جامع ریاضی ششم فصل 1 عدد و الگوهای عددی
جزوه جامع ریاضی ششم فصل 2 کسر
جزوه جامع ریاضی ششم فصل 3 اعداد اعشاری
جزوه جامع ریاضی ششم فصل 4 تقارن و مختصات
جزوه جامع ریاضی ششم فصل 5 اندازه گیری
جزوه جامع ریاضی ششم فصل 6 تناسب و درصد
جزوه جامع ریاضی ششم فصل 7 تقریب
نمایش درصد روی یک شکل
نمایش درصد روی یک شکل
نسبتی که مخرج آن عدد ۱۰۰ باشد درصد نامیده می.شود به طور مثال اگر در نوعی گز (سوغاتی اصفهان) ۳۵ گرم از هر ۱۰۰ گرم پسته باشد در اصطلاح به آن گز ۳۵ درصد و یا ٪۳۵ گفته می شود.
۱ در صورتی که کسری بزرگ تر از واحد ،باشد درصد آن بیش تر از ۱۰۰ خواهد شد.
۲ مقایسه ی درصد از مقایسه ی کسرها ساده تر است.
از درصد برای درک بهتر از نسبت ها و یا کسرها استفاده میکنیم به این ترتیب که آن نسبت و یا کسر را به صورت کسری با مخرج ۱۰۰ تبدیل میکنیم و سپس آن را به صورت درصد مینویسیم. به طور مثال کسر\(\frac{3}{{30}}\) را می توان به صورت\(\frac{{3 \times 5}}{{20 \times 5}} = \frac{{15}}{{100}}\) یعنی ۱۵% نشان دهیم. بنابراین برای تبدیل و نمایش هر عدد کسری به شکل درصد کافی است که کسری مساوی با آن کسر با مخرج ۱۰۰ پیدا کنیم. حال اگر در یک کسر نتوانیم کسر مساوی با مخرج ۱۰۰ پیدا کنیم. حال اگر در یک کسر نتوانیم کسر مساوی با مخرج ۱۰۰ پیدا کنیم است که تقسیم صورت بر مخرج کسر را تا دو رقم اعشار حساب کنیم و درصد آن عدد را به صورت تقریبی به دست بیاوریم. مثلا در کسر\(\frac{5}{7}\):
\(\frac{5}{7} = 5 \div 7 \to 0/714285714 \simeq 0/71 = \frac{{71}}{{100}} = 71\% \)
نمایش درصد روی یک شکل
برای نمایش هر درصدی روی یک شکل ابتدا درصد را به شکل کسری نوشته و آن را تا جای ممکن ساده می کنیم به این ترتیب به کسری میرسیم که با نمایش آن روی شکل داده شده درصد آن نیز مشخص می شود. به طور مثال اگر بخواهیم ۳۵ درصد یک مستطیل را نشان دهیم ابتدا ۳۵% را به صورت\(\frac{{35}}{{100}}\) می نویسیم و آن را ساده می کنیم تا به کسر\(\frac{7}{{20}}\) برسیم حالا این کسر را روی یک مستطیل نشان می دهیم.
برای حل مسئله های درصد میتوانیم از جدول تناسب استفاده کنیم به مثالهای زیر دقت کنید.
مثال
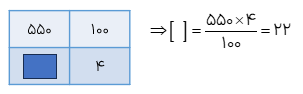
در یک کارگاه تولید قطعات اتومبیل ۴ درصد از محصولات معیوب هستند. اگر در این کارگاه و در یک روز ۵۵۰ قطعه تولید شود چند تا از قطعات معیوب هستند؟
كل قطعات تولید شده (یعنی ۵۵۰) را به عنوان ۱۰۰. در نظر گرفته و با کمک جدول تناسب جواب را به دست می آوریم.
مثال
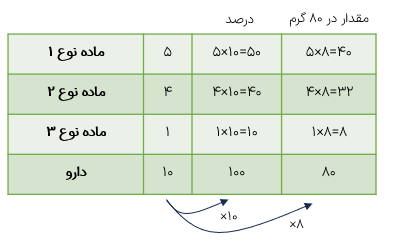
برای تهیه ی نوعی دارو سه ماده ی شیمیایی را به نسبت ۵، ۴ و ۱ مخلوط می کنند. در داروی به دست آمده چند درصد از هر نوع ماده وجود دارد؟ در هر ۸۰ گرم از این دارو چند گرم از هر ماده وجود دارد؟
برای حل سؤال از جدول تناسب زیر استفاده مي کنیم:
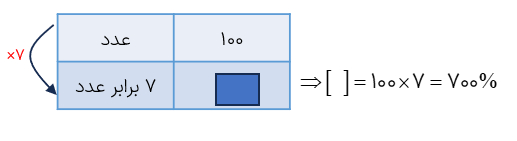
مثال
عددی را هفت برابر کرده ایم.
الف عدد جدید چند درصد عدد اولیه است؟
ب عدد اولیه چند درصد افزایش پیدا کرده است؟
افزایش ۶۰۰% = %۱۰۰ – ۷۰۰%
کاربرد درصد در محاسبات مالی
کاربرد درصد در محاسبات مالی
در محاسبات مالی همیشه درصد قیمت اصلی کالا یا قیمت اولیه ۱۰۰% در نظر گرفته می شود درصد مالیات و درصد سود همیشه به درصد قیمت اصلی کالا اضافه میشوند و قیمت کالا را افزایش می دهند.
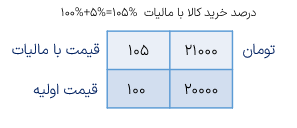
مثال
قیمت کالایی ۲۰۰۰۰ تومان است. اگر ۵ مالیات بر این کالا تعلق بگیرد خریدار برای خرید این کالا چند تومان باید بپردازد؟
قیمت کالا با مالیات ۲۱۰۰۰ تومان است.
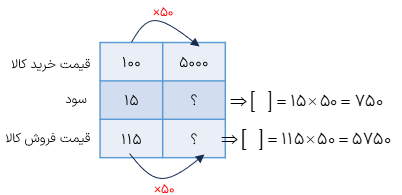
مثال
فروشنده ای کالایی را به قیمت ۵۰۰۰ تومان خرید اگر او کالا را با ۳۰% سود قیمت گذاری کند، قیمت فروش کالا چند تومان است؟
قیمت فروش کالا ۶۵۰۰ تومان است.
درصد تخفیف همواره از درصد قیمت اصلی (یعنی ۱۰۰%) کم میشود و قیمت کالا را کاهش می دهد.
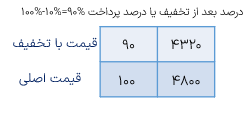
مثال
فروشنده ای کتابی را با ۱۰% تخفیف میفروشد. اگر قیمت اولیهی کالا ۴۸۰۰ تومان باشد، خریدار برای خرید این کالا چند تومان باید بپردازد؟
قیمت کالا پس از تخفیف ۴۳۲۰ تومان است.
سال گذشته قیمت کالایی ۴۰۰۰ تومان بوده و امسال همان کالا ۱۰۰۰۰ تومان شده است. قیمت این کالا چند درصد افزایش داشته است؟
درصد افزایش قیمت %۱۵۰ = %۱۰۰ – ۲۵۰%
تخفیف
منظور از تخفیف روی یک کالا این است که مبلغی از کل قیمت کالا را پرداخت نکنیم به طور مثال اگر قیمت کالایی ۵۰۰۰ تومان باشد و آن را با ۱۵% تخفیف خریداری کنیم آن گاه باید مبلغ ۴۲۵۰ تومان را جهت خرید این کالا پرداخت کنیم به روشهای زیر برای محاسبه ی این مبلغ دقت کنید.
روش اول
با استفاده از جدول تناسب ۱۵ قیمت کالا را حساب کنیم و عدد حاصل را از قیمت اصلی کم کنیم.
روش دوم
۱۵% از ۱۰۰% را تخفیف میگیریم پس %۸۵ = %۱۵ – ۱۰۰% از قیمت این کالا را پرداخت می کنیم از طرفی ۸۵% همان ۰/۸۵ است، بنابراین:
در بعضی از مسئله ها مقدار تخفیف و مبلغ پرداختی مشخص است و میخواهند قیمت اولیه را مشخص کنیم. به مثال زیر دقت کنید.
مثال
قیمت کالایی پس از تخفیف ۲۰ درصدی، ۵۶۰۰ تومان شده است قیمت اولیه این کالا چه قدر بوده است؟
روش اول
وقتی %۲۰ از قیمت کالا را تخفیف گرفته ایم یعنی %۸۰ = ۲۰% - %۱۰۰ قیمت آن را پرداخت کرده ایم، 5600 تومان همان ۸۰% قیمت کل است. بنابراین برای تعیین قیمت اولیه یا کل از جدول تناسب زیر کمک می گیریم:
روش دوم
همان طور که گفتیم %۸۰ همان ۵۶۰۰ تومان است از طرفی ۸۰% همان ۰/۸ می باشد، بنابراین:
در بعضی از مسئله ها قیمت اولیه و مبلغ پرداختی مشخص است و میخواهند تا مقدار تخفیف را مشخص کنیم به مثال زیر دقت کنید.
مثال
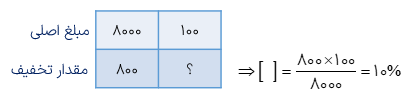
قیمت کالایی ۸۰۰۰ تومان بود اما فروشنده آن را به مبلغ ۷۲۰۰ تومان فروخت. او چند درصد تخفیف داده است؟
فروشنده ۷۲۰۰ - ۸۰۰۰ یعنی مبلغ ۸۰۰ تومان تخفیف داده است. لذا با استفاده از جدول تناسب زیر درصد تخفیف را مشخص می کنیم:
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه ششم- آزمون آنلاین تمامی دروس پایه ششم
- گام به گام تمامی دروس پایه ششم
- ویدئو های آموزشی تمامی دروس پایه ششم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ششم
- فلش کارت های آماده دروس پایه ششم
- گنجینه ای جامع از انشاء های آماده پایه ششم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ششم
سود
سود
منظور از سود در فروش یک کالا این است که مبلغی بیش تر از قیمت خریداری شده توسط خودمان دریافت کنیم. به طور مثال اگر کالایی را به قیمت ۵۰۰۰ تومان خریداری کنیم و بخواهیم آن را با ۱۵ درصد سود بفروشیم آن گاه باید قیمت این کالا را ۵۷۵۰ تومان اعلام کنیم به روشهای زیر برای محاسبه ی مقدار سود دقت کنید.
روش اول
باید ۱۵ درصد به قیمت کل (یعنی ۱۰۰ درصد) اضافه کنیم بنابراین باید ۱۱۵ = ۱۵ + ۱۰۰ درصد قیمت کالا را دریافت کنیم.
البته می توانیم قیمت فروش کالا را با جمع مقدار سود و مبلغ خریداری شده هم مشخص کنیم:
۵۰۰۰ + ۷۵۰ = ۵۷۵۰
روش دوم
۱۵٪ سود روی %۱۰۰ قیمت خریداری شده توسط خودمان گرفته ایم پس باید ٪۱۱۵ = ٪۱۵ + ٪۱۰۰ یا همان ۱/۱۵ قیمت خریداری شده را دریافت کنیم، بنابراین:
در بعضی از مسئله ها مقدار سود و مبلغ فروش مشخص است و میخواهند مبلغ خرید کالا را مشخص کنیم. به مثال زیر دقت کنید.
مثال
قیمت کالایی پس از افزودن ۲۰ به قیمت آن مبلغ . ۵۷۰۰ تومان اعلام شده است. قیمت خرید این کالا چه قدر بوده است؟
روش اول
وقتی %۲۰ به قیمت کالایی اضافه کرده ایم یعنی ۱۲۰% = %۲۰ + ۱۰۰% قیمت خریداری شده را برای فروش کالا اعلام کرده ایم پس ۵۷۰۰ تومان همان ۱۲۰% قیمت کالا است بنابراین برای تعیین قیمت خرید کالا از جدول تناسب زیر استفاده می کنیم:
البته برای حل این مسئله نیازی به رسم جدول تناسب سه طبقه نیست و بهتر ا است طبقه ی سود را در این جدول حذف کنیم اما این روش را با توجه به کتاب درسی بیان کرده ایم.
روش دوم
همان طور که گفتیم ۵۷۰۰ تومان یعنی ۱۲۰% قیمت خریداری شده از طرفی %۱۲۰ برابر\(\frac{{120}}{{100}}\) یا ۱/۲ است. با تقسیم ۵۷۰۰ بر \(\frac{{120}}{{100}}\) و یا ۱/۲ قیمت خرید مشخص می شود.
.\(5700 \div \frac{{120}}{{100}} = 5700 \times \frac{{100}}{{120}} = 4750 \) = قیمت خرید
در بعضی از مسئله ها قیمت خرید و قیمت فروش کالا را اعلام میکنند و میخواهند تا درصد سود را مشخص کنیم. به مثال زیر دقت کنید.
مثال
علی کالایی را به قیمت ۵۰۰۰ تومان خرید و آن را به قیمت ۶۰۰۰ تومان فروخت، او چند درصد سود کرده است؟
۵۰۰۰ تومان همان ۱۰۰ درصد قیمت خرید است از طرفی علی ۵۰۰۰ – ۶۰۰۰ یعنی مبلغ ۱۰۰۰ تومان سود کرده است لذا با استفاده از جدول تناسب زیر درصد سود او را مشخص می کنیم:
جزوات جامع پایه ششم
جزوه جامع ریاضی ششم فصل 1 عدد و الگوهای عددی
جزوه جامع ریاضی ششم فصل 2 کسر
جزوه جامع ریاضی ششم فصل 3 اعداد اعشاری
جزوه جامع ریاضی ششم فصل 4 تقارن و مختصات
جزوه جامع ریاضی ششم فصل 5 اندازه گیری
جزوه جامع ریاضی ششم فصل 6 تناسب و درصد
جزوه جامع ریاضی ششم فصل 7 تقریب
مالیات
مالیات
در کشور عزیزمان به بیشتر کالاها و خدماتی که ارائه میشود مالیات بر ارزش افزوده تعلق می گیرد. در واقع مالیات پولی است که باید به قیمت کالا اضافه شود و از مشتریان دریافت گردد و فروشنده باید این مبلغ اضافه را به خزانه ی دولت واریز نماید و حق ندارد آن را برای خودش بردارد به طور مثال اگر قیمت کالایی ۱۵۰۰۰ تومان باشد و به این کالا %۹ مالیات بر ارزش افزوده تعلق بگیرد باید مبلغ ۱۶۳۵۰ تومان به فروشنده پرداخت کنیم مسئله های مالیات را همانند مسئله های سود حل میکنیم به روش های محاسبه ی مقدار مالیات و مبلغ پرداختی در مثال بالا دقت کنید.
روش اول
روش دوم
%۹ مقدار مالیات بر ارزش افزوده این کالا است پس فروشنده باید 100%+9%=109% یا همان\(\frac{{109}}{{100}}\) قیمت کالا را دریافت کند بنابراین:
.\( = 15000 \times \frac{{109}}{{100}} = 16350\) مبلغ پرداختی توسط مشتری
مثال
فروشنده ای قیمت کالایی را پس از محاسبه ی8% مالیات بر ارزش افزوده مبلغ ۷۵۶۰ تومان اعلام کرد. قیمت اصلی این کالا قبل از مالیات چه قدر بوده است؟
۷۵۶۰ تومان همان ۱۰۸ درصد قیمت اصلی می باشد، بنابراین
\(7560 + \frac{{108}}{{100}} = 7560 \times \frac{{100}}{{108}} = 7000\) = قیمت کالا بدون مالیات
کاربرد درصد در آمار و احتمال
کاربرد درصد در آمار و احتمال
یک دایره کامل زاویه ۳۶۰ درجه را نشان می دهد.
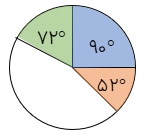
مثال
دایره ی مقابل به چند بخش با رنگهای مختلف تقسیم شده و اندازه ی زاویه ی مربوط به هر بخش نوشته شده است. درصد مساحت هر بخش را به کل دایره بنویسید.
\(\begin{array}{l}\frac{{90^\circ }}{{360^\circ }} = \frac{1}{4} = \frac{{25}}{{100}} \to 90^\circ \to 25\% \\\\\frac{{54^\circ }}{{360^\circ }} = \frac{{54^\circ \div 18}}{{360^\circ \div 18}} = \frac{3}{{20}} = \frac{{15}}{{100}} \to 54^\circ \to 15\% \\\\\frac{{72^\circ }}{{360^\circ }} = \frac{{72^\circ \div 18}}{{360^\circ \div 18}} = \frac{4}{{20}} = \frac{{20}}{{100}} \to 72^\circ \to 20\% \end{array}\)
مثال
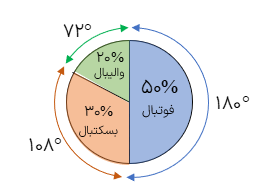
%۳۰ دانش آموزان کلاسی در رشته ی بسکتبال ۵۰% در رشته ی فوتبال و ٪۲۰ در رشته ی والیبال شرکت دارند. نمودار دایره ای مربوط به این داده ها را رسم کنید.
روش محاسبه ی دیگر:
اکنون دایره ای را رسم میکنیم و قسمتهای مختلف را با استفاده از نقاله معین می کنیم.
مثال
در نمودار دایره ای ٪۶۰ یعنی چند درجه؟
\(\frac{{60}}{{100}} \times 360^\circ = 216^\circ \)
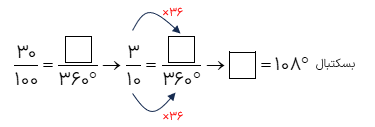
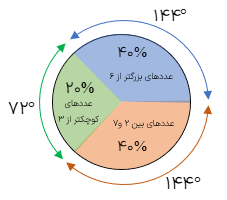
در داخل کیسه ای ۱۰ کارت وجود دارد که روی هر یک از آنها اعداد از ۱ تا ۱۰ نوشته شده است. اگر بدون نگاه کردن به داخل کیسه یک کارت را بیرون بیاوریم:
الف احتمال این که عدد روی کارت بزرگ تر از ۶ باشد، چه قدر است؟
اعداد بزرگ تر از ۶ یعنی ۷، ۸، ۹ یا ۱۰.
\(\begin{array}{l}\frac{4}{{10}} = \frac{{40}}{{100}} = 40\% \\\\\frac{4}{{10}} = \frac{{144^\circ }}{{360^\circ }}\end{array}\)
ب احتمال این که عدد روی کارت کم تر از ۳ باشد، چه قدر است؟
یعنی عدد ۱ یا ۲ روی کارت باشد، پس:
\(\begin{array}{l}\frac{2}{{10}} = \frac{{20}}{{100}} = 20\% \\\\\frac{2}{{10}} = \frac{{72^\circ }}{{360^\circ }}\end{array}\)
ج نمودار دایره ای مربوط به موارد بالا را رسم کنید.
د باقی ماندهی نمودار دایره ای مربوط به کدام اعداد روی کارت ها است؟
باقی ماندهی نمودار مربوط به عددهای بین ۲ و ۷ یعنی (۳، ۴، ۵ یا ۶) می باشد.
نمودار دایره ای
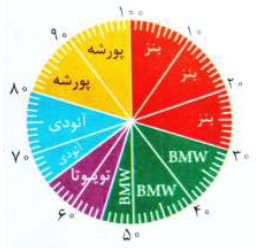
فرض کنید که در یک نظرسنجی از دوستان خود میزان علاقه مندی آنها به انواع برندهای معروف اتومبیل را پرسیده اید و اطلاعات به دست آمده را در جدول زیر وارد کرده اید.
همان طور که ملاحظه میکنید، در مجموع از ۲۰ نفر نظرسنجی شده است. حال اگر نسبت هر یک از عددها به ۲۰ را حساب کنیم و سپس در عدد ۱۰۰ ضرب کنیم درصد علاقه مندی به هر برند مشخص می شود.
\(\frac{6}{{100}} \times 100 = 30\,\,\,\,,\,\,\,\,\frac{5}{{20}} \times 100 = 25\% \,\,\,\,,\,\,\,\,\frac{2}{{20}} \times 100 = 10\% \,\,\,\,\,,\,\,\,\,\,\,\,\frac{3}{{20}} \times 100 = 15\% \,\,\,\,\,\,\,\,\,\,,\,\,\,\,\,\,\,\,\,\,\frac{4}{{20}} \times 100 = 20\% \)
حالا مانند شکل مقابل یک دایره را به ۱۰۰ قسمت مساوی تقسیم می کنیم.
هر قسمت نشان دهنده ی یک درصد است سپس درصد مربوط به هر کدام از اتومبیل ها را روی شکل مشخص می کنیم همان طور که ملاحظه میکنید تقسیم یک دایره به ۱۰۰ قسمت مساوی کمی سخت و دشوار است و شاید قسمتها به طور دقیق تقسیم نشوند لذا بهتر است روش دیگری را برای رسم چنین نموداری یاد بگیریم در این روش کافی است که زاویه ی مربوط به هر یک از درصدهای بالا را با استفاده از جدول تناسب زیر مشخص کنیم. دقت داشته باشید که یک دایره ی کامل یک زاویه ی ۳۶۰ درجه را نشان می دهد از طرفی دایره ی بالا را به ۱۰۰ قسمت مساوی تقسیم کردیم. پس حالا با استفاده از این جدول تناسب زاویه ها را مشخص می کنیم:
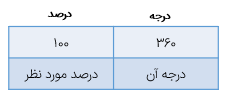
اکنون یک دایره رسم کرده و مرکز آن را مشخص میکنیم سپس با کمک یک نقاله و قرار دادن مرکز نقاله روی مرکز دایره زاویه ی مربوط به هر قسمت را مشخص میکنیم تا شکل موردنظر به دست آید.
پرتاب سکه
وقتی یک سکه را میاندازیم یا روی سکه بالا قرار میگیرد و یا پشت آن اما انتظار داریم تقریبا در نصف (یعنی ۵۰ درصد) پرتاب ها رو و در نصف ۵۰ (درصد دیگر پرتاب ها هم پشت سکه بیابید که در اصطلاح می گوییم احتمال رو آمدن و پشت آمدن سکه ۵۰ - ۵۰ است.
مثال
یک سکه را ۵۰۰ مرتبه انداخته ایم نتیجه این آزمایش در جدول زیر دیده می شود. در چند آزمایش سکه رو آمده است؟
برای پیدا کردن جواب کافی است که درصد رو آمدن یعنی (۴۷/۴) را در عدد ۵۰۰ ضرب کنیم.

پرتاب تاس
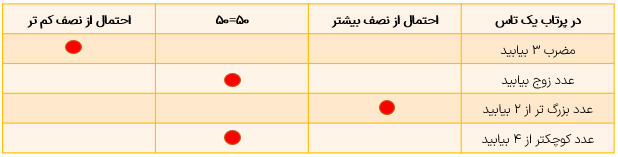
وقتی که یک تاس را می اندازیم حتما یکی از عددهای ۱ ۲ ۳ ۴ ۵ و یا ۶ در روی تاس ظاهر می شوند. پس در پرتاب ۳۰ مرتبه یک تاس انتظار داریم هر کدام از وجه ها (عددهای ۱ تا ۶) را تقریبا ۵ مرتبه مشاهده کنیم. در این آزمایش احتمال وقوع و یا ظاهر شدن هر یک از عددها از نصف یعنی ۵۰ درصد کم تر است.
به طور مثال احتمال ظاهر شدن عدد ۵ از نصف کم تر است اما احتمال ظاهر شدن عدد فرد، ۵۰ - ۵۰ می باشد. به جدول زیر دقت کنید.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه ششم- آزمون آنلاین تمامی دروس پایه ششم
- گام به گام تمامی دروس پایه ششم
- ویدئو های آموزشی تمامی دروس پایه ششم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ششم
- فلش کارت های آماده دروس پایه ششم
- گنجینه ای جامع از انشاء های آماده پایه ششم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ششم



1736019749.png)