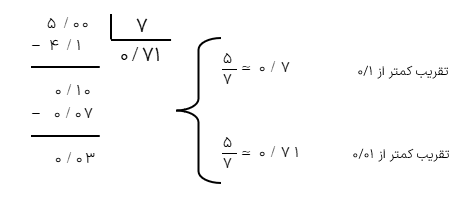درسنامه کامل ریاضی ششم فصل 7 تقریب
تعداد بازدید : 7.27Mخلاصه نکات ریاضی ششم فصل 7 تقریب - درسنامه شب امتحان ریاضی ششم فصل 7 تقریب - جزوه شب امتحان ریاضی ششم نوبت اول فصل 7 تقریب
تقریب به روش گردکردن
تقریب به روش گرد کردن
برای این که در استفاده از عددهای تقریبی خطای کم تری داشته باشیم از روش گرد کردن استفاده می کنیم. در این روش با توجه به تقریب مورد نظر عددی را به صورت تقریبی انتخاب میکنیم که به مقدار واقعی نزدیک باشد. برای مثال مقدار تقریبی عدد ۷۸۳ با تقریب کمتر از ۱۰۰ و روش گرد کردن برابر ۸۰۰ می شود، چون عدد ۸۰۰ به عدد ۷۸۳ نزدیک تر از عدد 70۰می باشد.
مثال
با تقریب کمتر از ۰/۱ به روش گرد کردن عدد ۴۳/۱۹ به عدد ۴۳/۲ نزدیک تر است تا عدد ۴۳/۱.
بنابراین گردشده ی عدد ۴۳/۱۹ با تقریب کم تر از ۰/۱ به روش گرد کردن، برابر است با ۴۳/۲.
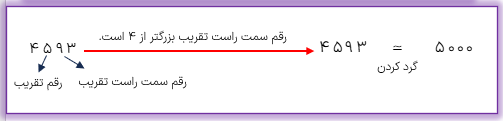
در روش گرد کردن ابتدا به رقم سمت راست تقریب توجه میکنیم اگر این رقم ۵ یا بزرگ تر از ۵ باشد (یعنی ۵، ،۶ ،۷ ،۸ یا ۹ باشد) یک واحد به رقم تقریب اضافه کنیم و سپس رقمهای سمت راست تقریب را با صفر جایگزین میکنیم و اگر رقم سمت راست تقریب کوچک تر از ۵ (یعنی ۴ ۳ ۲ ۱ یا صفر) باشد بدون این که به رقم تقریب چیزی اضافه کنیم رقم های سمت راست تقریب را با صفر جایگزین می کنیم.
مثال
عدد ۴۵۹۳ را با تقریب کم تر از ۱۰۰۰ گرد کنید.
مثال
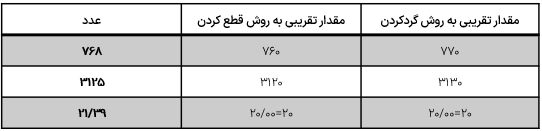
مقدار تقریبی عددهای داده شده را با تقریب کمتر از ۱۰ به دو روش بنویسید.
1 اگر رقم سمت راست تقریب کمتر از ۵ ،باشد پاسخ تقریبی به روش قطع کردن و گرد کردن یکسان می شود.
\(\begin{array}{l}7523/4 \simeq 7500\\\\7523/4 \simeq 7500\end{array}\)
2 برای محاسبه مقدار تقریبی کسرها به روش گرد کردن باید خارج قسمت تقسیم را تا یک رقم بیشتر از تقریب داده شده محاسبه کنیم؛ یعنی اگر بخواهیم مقدار تقریبی کسری را به روش گردکردن با تقریب کم تر از ۰/۰۱ محاسبه کنیم باید خارج قسمت را تا سه رقم اعشار یک رقم بیشتر از رقم های اعشاری (۰/۰۱) محاسبه کنیم و سپس عدد اعشاری به دست آمده را با تقریب داده شده گرد کنیم
مثال
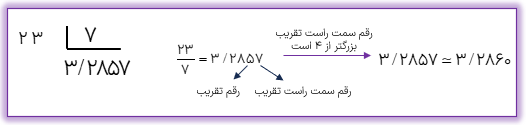
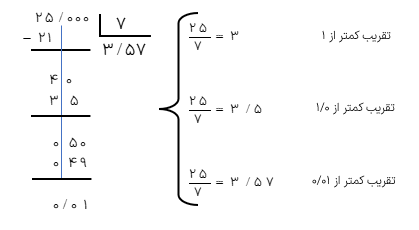
مقدار تقریبی عدد\(\frac{{23}}{7}\) را با تقریب کم تر از ۰/۰۰۱ به روش گردکردن محاسبه کنید.
باید حاصل تقسیم ۲۳ بر ۷ را تا چهار رقم اعشار یعنی یک رقم بیشتر از رقم های اعشار ۰/۰۰۱ حساب کنیم.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه ششم- آزمون آنلاین تمامی دروس پایه ششم
- گام به گام تمامی دروس پایه ششم
- ویدئو های آموزشی تمامی دروس پایه ششم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ششم
- فلش کارت های آماده دروس پایه ششم
- گنجینه ای جامع از انشاء های آماده پایه ششم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ششم
تقریب به روش قطع کردن
تقریب
در محاسبه های تقریبی برای نشان دادن مقدار تقریبی ،عددها به جای علامت مساوی از علامت \( \simeq \)استفاده می کنیم که یعنی « تقریبا برابر است با ».
برای تقریب زدن عددها، دو روش داریم:
۱ روش قطع کردن
۲ روش گرد کردن
روش قطع کردن
در این روش رقم های سمت راست ،تقریب یعنی عددهایی را که ارزش مکانی آنها از تقریب داده شده، کم تر باشد با صفر جایگزین می کنیم.
مثال
با تقریب کمتر از ۱۰ در روش قطع کردن یعنی تمامی رقم هایی که ارزش مکانی آنها کم تر از دهگان است، به صفر تبدیل شوند.
تقریب کمتر از 10 به روش قطع کردن:
\(293 \simeq 290\)
با تقریب کم تر از ۱۰۰۰ در روش قطع کردن، یعنی تمامی رقم هایی که ارزش مکانی آن ها کم تر از یکان هزار است رقم های سمت راست (۳) به صفر تبدیل شوند.
تقریب کمتر از 1000 به روش قطع کردن:
\(43591 \simeq 43000\)
با تقریب دهگان یعنی با تقریب کمتر از ۱۰ با تقریب ،صدگان یعنی با تقریب کم تر از 100 .
مثال
عدد ۳۹/۷۴۱ را با تقریب کم تر از ۱ قطع کنید.
این عدد را در جدول ارزش مکانی قرار می دهیم وقتی می گوییم با تقریب کم تر از یک یعنی رقم هایی که ارزش مکانی آنها کم تر از یکان است باید به صفر تبدیل شوند.

وقتی میگوییم با تقریب کم تر از ۰/۰۱ یعنی رقم هایی که در مرتبه ی هزارم و ده هزارم و ... قرار دارند، به صفر تبدیل شوند.
مثال
مقدار عدد\(\pi \)تا هشت رقم اعشار برابر است با:
\(\pi = 3/14159265\)
مقدار عدد 7 با تقریب کمتر از ۰/۰۱ تا دو رقم اعشار:
\(\pi = 3/14\)
مقدار عدد با تقریب کمتر از ۰/۰۰۰۱ تا چهار رقم اعشار:
\(\pi = 3/1415\)
مقدار عدد با تقریب کمتر از ۰/۱ تا یک رقم اعشار:
\(\pi = 3/1\)
با تقسیم صورت هر کسر بر مخرج آن میتوان آن کسر را به صورت عدد اعشار نوشت.
وقتی می گوییم تقسیم را تا یک رقم اعشار انجام دهید یعنی خارج قسمت را با تقریب کم تر از ۰/۱ به دست آورید و یا وقتی میگوییم تقسیم را تا دو رقم اعشار انجام دهید یعنی خارج قسمت را با تقریب کم تر از ۰/۰۱ حساب کنید.
در تقریب رقم دهگان اختلاف هر عدد با مقدار تقریبی آن کوچک تر از ۱۰ است.
مثال
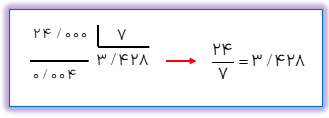
مقدار تقریبی کسر\(\frac{{24}}{7}\) را تا سه رقم اعشار حساب کنید.
برای محاسبه ی مقدار تقریبی کسرها به روش قطع کردن فقط کافی است که خارج قسمت تقسیم را به اندازه ی رقم های اعشاری عدد تقریب محاسبه کنیم. برای مثال اگر بخواهیم مقدار تقریبی کسر\(\frac{{19}}{{11}}\) را با تقریب کم تر از ۰/۰۱ به روش قطع کردن حساب کنیم باید خارج قسمت تقسیم صورت بر مخرج کسر را تا ۲ رقم اعشار حساب کنیم.
مثال
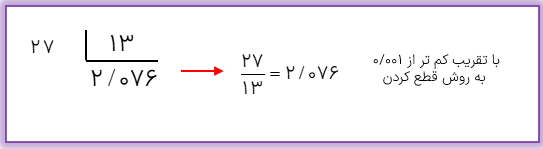
مقدار تقریبی عدد\(\frac{{27}}{{13}}\) را با تقریب کم تر از ۰/۰۰۱ به روش قطع کردن حساب کنید.
چون ۰/۰۰۱ دارای سه رقم اعشار است و باید به روش قطع کردن تقریب ،بزنیم، بنابراین خارج قسمت تقسیم ۲۷ بر ۱۳ را تا سه رقم اعشار حساب می کنیم.
وقتی صحبت از سن افراد میشود مجبوری از عددهای تقریبی استفاده کنیم به طور مثال اگر سن رضا ۱۲ سال و ۵ ماه و ۱۷ روز باشد میگوییم سن رضا ۱۲ سال است و یا اگر وزن رضا ۵۳/۳۵۰ کیلوگرم باشد، می گوییم وزن رضا ۵۳ کیلوگرم است به چنین بیانی از مقدارهای تقریبی که همواره مقدار کم تر مورد نظر است، روش قطع کردن گفته می شود.
در روش قطع کردن رقم های سمت راست تقریب را که ارزش مکانی کم تری نسبت به رقم تقریب دارند، با صفر جایگزین میکنیم (یعنی به صفر تبدیل میکنیم) و خود رقم تقریب و همچنین رقم های مرتبه های بالاتر را بدون تغییر می نویسیم
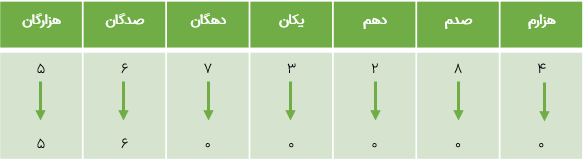
به طور مثال وقتی میخواهیم مقدار تقریبی عدد ۵۶۷۳/۲۸۴ را با تقریب کمتر از ۱۰۰، به روش قطع کردن حساب کنیم با توجه به جدول ارزش مکانی این عدد که در قسمت زیر ملاحظه می کنید، تمامی رقم هایی که در مرتبه ی پایین تری از صدگان قرار دارند؛ یعنی رقم هایی که در مرتبه ی دهگان یکان دهم، صدم و هزارم قرار دارند را به صفر تبدیل نموده و بقیه رقم ها را بدون تغییر می نویسیم.
به این ترتیب ۳ مقدار تقریبی این عدد با تقریب کم تر از ۱۰۰ برابر ۵۶۰۰ خواهد شد.
در نمایش تقریبی عددها از علامت استفاده می کنیم و این علامت را تقریبا مساوی می خوانیم.
مثال
با تقریب کمتر از صدگان ۵۶۰۰ = ۵۶۷۳/۲۸۴
می خوانیم عدد ۵۶۷۳/۲۸۴ با تقریب کم تر از صدگان تقریبا مساوی با ۵۶۰۰ است.
در تقریب به روش قطع کردن همیشه اختلاف هر عدد با مقدار تقریبی آن کوچک تر از مقدار رقم تقریب است به طور مثال در تقریب رقم صدگان اختلاف هر عدد با مقدار تقریبی آن کوچک تر از صد است و یا در تقریب رقم دهگان اختلاف هر عدد با مقدار تقریبی آن کوچک تر از ده است به همین دلیل است که از این به بعد به جای عبارت (با تقریب کم تر از صدگان دهگان ،یکان دهم و ..) از عبارت (با تقریب کم تر از ۱۰۰، ۱۰، ۱، ۰/۱ و . ) استفاده می کنیم.
مثال
مقدار تقریبی هر یک از عددهای زیر را به روش قطع کردن و با تقریب خواسته شده بنویسید.
(با تقریب کم تر از ۱۰۰)\(1999/9\) الف
\(1999/9 \simeq 1900\)
(با تقریب کم تر از ۱۰)\(199/9\) ب
\(199/9 \simeq 1990\)
(با تقریب کمتر از ۱)\(35/742\) ج
\(35/742 \simeq 35\)
(با تقریب کمتر از10/1 )\(35/742\) د
\(35/742 \simeq 35/7\)
جزوات جامع پایه ششم
جزوه جامع ریاضی ششم فصل 1 عدد و الگوهای عددی
جزوه جامع ریاضی ششم فصل 2 کسر
جزوه جامع ریاضی ششم فصل 3 اعداد اعشاری
جزوه جامع ریاضی ششم فصل 4 تقارن و مختصات
جزوه جامع ریاضی ششم فصل 5 اندازه گیری
جزوه جامع ریاضی ششم فصل 6 تناسب و درصد
جزوه جامع ریاضی ششم فصل 7 تقریب
تقریب عددهای کسری
تقریب عددهای کسری
برای تقریب زدن عددهای کسری مانند\(\frac{{25}}{7}\) به روش قطع کردن ابتدا صورت کسر را بر مخرج آن تقسیم می کنیم، اگر تقسیم را تا یک رقم اعشار در خارج قسمت انجام دهیم یعنی حاصل را با تقریب کم تر از ۰/۱ به دست آورده ایم و اگر تقسیم را تا دو رقم اعشار در خارج قسمت انجام دهیم؛ یعنی حاصل را با تقریب کم تر از ۰/۰۱ به دست آورده ایم به همین ترتیب اگر تقسیم را تا سه رقم اعشار انجام دهیم؛ یعنی حاصل را با تقریب کم تر از ۰/۰۰۱ حساب کرده ایم.
در کسرهایی مانند\(\frac{1}{2},\frac{1}{5}\) که مخرج آن ها فقط ۲ و یا فقط ۵ هستند، همه ی تقریب های آن ها مساوی اند زیرا مقدار دقیق تقسیم صورت این کسرها بر مخرج آنها تا یک رقم اعشار قابل محاسبه است.
مقدار تقریبی \(\frac{1}{2}\)با تمام تقریب های کم تر از ۰/۱ یا ۰/۰۱ یا ۰/۰۰۱ و ... برابر ۰/۵ است.
\(\frac{1}{2} = \frac{5}{{10}} = 0/5\)
مقدار تقریبی\(\frac{1}{5}\)با تمام تقریب های کم تر از ۰/۱ یا۰/۰۱ یا ۰/۰۰۱ و ... برابر ۰/۲ است.
\(\frac{1}{5} = \frac{2}{{10}} = 0/2\)
تقریب زدن به روش گرد کردن
در سال چهارم دبستان با تقریب زدن آشنا شدید و آموختید که برای تقریب زدن هر عددی با توجه به تقریب داده شده یک عدد رند قبل و یک عدد رند بعد از عدد مورد نظر می نویسیم و از بین آن ها عددی را که به عدد مورد نظر نزدیک تر است به عنوان مقدار تقریبی عدد در نظر میگیریم اما امسال می آموزیم که هرگاه بخواهیم مقدار تقریبی عددی را با (تقریب دهگان) و یا به عبارت دیگر با تقریب کمتر از ۱۰ به دست آوریم، باید به رقم يكان عدد دقت کنیم در صورتی که رقم یکان ۵ یا بیش تر از ۵ باشد ( یعنی ۵ ۶ ۷، ۸ و ۹)، به رقم دهگان یک واحد اضافه کرده و یکان را صفر میکنیم اما در صورتی که رقم یکان کم تر از ۵ باشد یعنی یکی از رقم های ۰، ۱، ۲، ۳ و ۴ در این صورت دهگان تغییر نمی کند و یکان هم صفر می.شود.
به مثال های زیر دقت کنید:
با تقریب دهگان ۵۷۰ = ۵۷۳ : روش سال ششم \( \Rightarrow \)۵۸۰ \( \Rightarrow \) ۵۷۳\( \Leftarrow \) ۵۷۰: روش سال چهارم
با تقریب دهگان ۱۴۳۰ = ۱۴۲۵ : روش سال ششم\( \Rightarrow \) ۱۴۳۰ \( \Rightarrow \) ۱۴۲۵ \( \Leftarrow \) ۱۴۲۰ : روش سال چهارم
هرگاه بخواهیم مقدار تقریبی عددی را با تقریب صدگان و یا به عبارت دیگر با تقریب کم تر از صد به دست آوریم باید به رقم دهگان عدد دقت کنیم در صورتی که رقم دهگان ۵ و یا بیش تر از ۵ (یعنی ۵ ۶ ۷، ۸و ۹) باشد به رقم صدگان یک واحد اضافه کرده و یکان و دهگان و قسمت اعشاری را صفر می کنیم. اما اگر رقم دهگان کم تر از ۵ ،باشد رقم صدگان تغییر نکرده و یکان و دهگان و قسمت اعشاری به صفر تبدیل می شوند.
به مثال های زیر دقت کنید:
با تقریب صدگان ۱۷۰۰ = ۱۷۴۳ : روش سال ششم۱۸۰۰\( \Rightarrow \)۱۷۴۳\( \Leftarrow \) ۱۷۰۰ : روش سال چهارم
با تقریب صدگان ۱۴۰۰ = ۱۳۵۲ : روش سال ششم۱۴۰۰\( \Rightarrow \) ۱۳۵۲ \( \Leftarrow \) ۱۳۰۰: روش سال چهارم
در تمامی مثال هایی که در قسمت قبل ملاحظه نمودید مقدار تقریبی عددها به روش گرد کردن به دست آمده اند. برای تقریب زدن عددها به روش گرد کردن به ترتیب زیر عمل می کنیم:
۱ رقمی را که باید گرد شود مشخص میکنیم به طور مثال در تقریب کمتر از ۱۰۰ باید زیر صدگان خط بکشیم.
2 به اولین رقم جلو سمت راست رقم مورد تقریب دقت میکنیم اگر این رقم ۵ یا بیش تر از ۵ (یعنی ۵، ۷،۶، ۸ و یا ۹) بود یک واحد به رقم مورد تقریب اضافه می کنیم در غیر این صورت رقم مورد تقریب تغییری نمی کند.
3 همه ی رقم های سمت راست رقم مورد تقریب را با صفر جایگزین میکنیم و یا به عبارت دیگر به صفر تبدیل می کنیم.
به مثال های زیر دقت کنید.
(با تقریب کم تر از ۱۰۰۰) با تقریب صدگان ۳۶۰۰۰ = ۳۵۸۴۵ (الف
رقم جلو هزارگان یعنی رقم صدگان برابر ۸ است پس یک واحد به رقم هزارگان اضافه نموده و تمامی رقم های
یکان دهگان و صدگان را به صفر تبدیل می کنیم.
(با تقریب کم تر از۱۰۰) با تقریب صدگان ۳۵۸۰۰ = ۳۵۸۴۵ (ب
رقم جلو صدگان یعنی دهگان برابر ۴ است پس رقم صدگان را بدون تغییر می نویسیم و تمامی رقم های یکان و دهگان را به صفر تبدیل می کنیم.
با تقریب دهگان ۳۵۸۵۰ = ۳۵۸۴۵ (ج
با تقریب یکان ۲۳۳۰ = ۲۳۲/۵ (د
مثال
مقدار تقریبی عدد ۱۷/۹۹۹ با تقریب کمتر از ۰/۰۱ مشخص کنید.
\(17/99 \simeq 18/000 = 18\)
۱ وقتی عددی را گرد میکنیم منظورمان گرد شده به نزدیک ترین عدد است. اگر رقم مربوط ۵ باشد، رقم مرتبه ی قبلی ) از سمت چپ را یک واحد افزایش می دهیم
2 در روش گرد کردن گاهی گرد کردن کاهشی (مانند مورد ب) و گاهی گرد کردن افزایشی (مانند مورد الف)می باشد.
3 در روش گرد کردن نیز اختلاف بین هر عدد و مقدار تقریبی آن (یعنی عدد بزرگ تر منهای عدد کوچک تر) همیشه از مقدار تقریب کم تر است.
محاسبه ی مقدار تقریبی کسرها به روش گردکردن
برای تقریب زدن اعداد کسری به روش گرد کردن ابتدا مقدار تقسیم صورت کسر بر مخرج آن را تا یک رقم بیش تر از تقریب داده شده به دست می آوریم، یعنی اگر تقریب کم تر از ۰/۱ باشد باید تقسیم را تا دو رقم اعشار حساب کنیم و سپس عدد به دست آمده را به روش گرد کردن تقریب می زنیم.
مثال
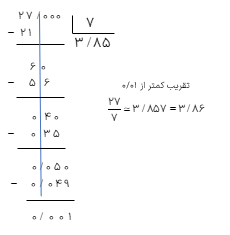
مقدار تقریبی کسر \(\frac{{27}}{7}\) به را با تقریب کمتر از ۰/۰۱ به روش گرد کردن حساب کنید.
ابتدا با توجه به این که روش گرد کردن و تقریب کمتر از ۰/۰۱ میباشد باید حاصل تقسیم را تا سه رقم اعشار در خارج قسمت حساب کنیم که برای این عمل میتوانیم از ماشین حساب هم کمک بگیریم سپس عدد به دست آمده (یعنی ۳/۸۵۷ ) را با تقریب داده شده گرد می کنیم.
تفاوت بین روش قطع کردن و گردکردن
تفاوت بین روش قطع کردن و گردکردن
در روش قطع کردن سرعت انجام محاسبات بیشتر است اما در روش گرد کردن جواب به دست آمده دقیق تر است. لذا استفاده از این روشها به اهمیت دقت پاسخ و سرعت انجام محاسبات بستگی دارد. در ضمن به یاد داشته باشید که اگر رقم جلوی تقریب کوچکتر از ۵ (یعنی ،۱۰، ۲، ۳ و یا ۴) باشد، مقدار تقریبی عدد با تقریب داده شده از هر دو روش یکسان است.
(قطع شده با تقریب کمتر از 10۰) ۵۳۰۰ = ۵۳۴۷
(گرد شده با تقریب کمتر از ۱۰۰) ۵۳۰۰ = ۵۳۴۷
(قطع شده با تقریب کمتر از ۱۰۰) ۲۷۰۰ = ۲۷۶۴
(گرد شده با تقریب کمتر از ۱0۰) ۲۸۰۰ = ۳۷۶۴
اگر رقم سمت راست تقریب کمتر از ۵ ،باشد جواب به دست آمده در هر دو روش قطع کردن و گرد کردن یکی می شود.
نمایش تقریبی عددها روی محور
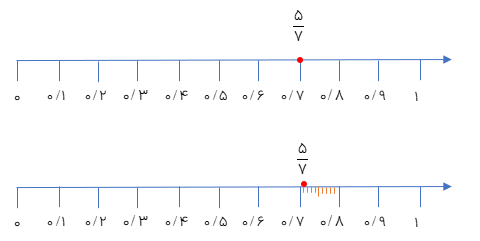
اگر بخواهیم عددی مانند\(\frac{5}{7}\) را روی محور نمایش دهیم به دلیل این که تقسیم یک واحد به ۷ قسمت مساوی کمی سخت است بهتر است که از نمایش تقریبی این عدد روی محور استفاده کنیم اگر حاصل تقسیم صورت کسر بر مخرج آن را تا یک رقم اعشار در خارج قسمت حساب کنیم مقدار تقریبی این عدد با تقریب ۰/۱ به دست می آید. حال اگر بخواهیم که موقعیت دقیق تری از این عدد روی محور نمایش دهیم کافی است که تقسیم را تا دو رقم اعشار ادامه دهیم تا مقدار تقریبی عدد با تقریب ۰/۰۱ به دست آید.
به این ترتیب موقعیت جدید از موقعیت قبلی دقیق تر میباشد و به همین ترتیب با پیشروی در تقسیم باز هم موقعیت های دقیق تری نسبت به قبل به دست می آید.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه ششم- آزمون آنلاین تمامی دروس پایه ششم
- گام به گام تمامی دروس پایه ششم
- ویدئو های آموزشی تمامی دروس پایه ششم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ششم
- فلش کارت های آماده دروس پایه ششم
- گنجینه ای جامع از انشاء های آماده پایه ششم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ششم
عدد پی
عدد پی
به مقدار تقریبی عددهای عدد \(\pi = \frac{{22}}{7}\) (بخوانید عدد پی) تا ۵ رقم اعشار دقت کنید مقدار تقریبی این دو عدد با تقریب کمتر از ۰/۱ و ۰/۰۱ دقیقا با هم برابر میباشد. لذا میتوانیم گاهی اوقات به جای عدد\(\pi \) از کسر \( \frac{{22}}{7}\)هم استفاده کنیم.
\(\frac{{22}}{7} = 3/14285\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\pi = 3/14159\)
مثال
۴ شعاع دایره ای ۷ سانتی متر است. محیط و مساحت این دایره را حساب کنید. ( ۳/۱۴ = \(\pi \))
روش اول
۴۳/۹۶ = ۳/۱۴×۷×۲ =\(\pi \)x قطر = محیط دایره محیط دایره
۱۵۳/۸۶ = ۳/۱۴× ۷ × ۷ =\(\pi \)x شعاع x شعاع = مساحت دایره
روش دوم
\(2 \times 7 \times \frac{{22}}{7} = 44\) =محیط دایره
\(7 \times 7 \times \frac{{22}}{7} = 154\) =مساحت دایره
همان طور که ملاحظه می کنید زمانی که به جای مقدار تقریبی عدد\(\pi \) از کسر\(\frac{{22}}{7}\)استفاده کردیم، مقادیر محیط و مساحت دایره با اختلاف بسیار ناچیزی نسبت به زمانی که مقدار تقریبی \(\pi \) را تقریبا مساوی ۳/۱۴ در نظر گرفتیم به دست آمد.
جزوات جامع پایه ششم
جزوه جامع ریاضی ششم فصل 1 عدد و الگوهای عددی
جزوه جامع ریاضی ششم فصل 2 کسر
جزوه جامع ریاضی ششم فصل 3 اعداد اعشاری
جزوه جامع ریاضی ششم فصل 4 تقارن و مختصات
جزوه جامع ریاضی ششم فصل 5 اندازه گیری
جزوه جامع ریاضی ششم فصل 6 تناسب و درصد
جزوه جامع ریاضی ششم فصل 7 تقریب
دقت اندازه گیری
دقت اندازه گیری
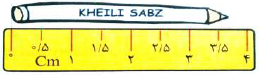
به خط کش مقابل دقت کنید.
کوچک ترین قسمتی که روی این خط کش مشخص شده ۰/۵ سانتی متر یا ۵ میلی متر است، بنابراین دقت اندازه گیری این خط کش ۵/ سانتی متر است؛ یعنی این خط کش اندازههای کم تر از ۰/۵ سانتی متر یا ۵ میلی متر را برای ما مشخص نمیکند اندازه ی مدادی که روی شکل دیده میشود بین ۳/۵ و ۴ سانتی متر است. چون خط کش نمی تواند بین این دو عدد را برای ما مشخص کند و اندازه ی مداد به ۳/۵ سانتی متر نزدیک تر است، ما اندازه ی مداد را به طور تقریبی ۳/۵ سانتی متر در نظر میگیریم اختلاف اندازه ی واقعی مداد و عدد ۳/۵ از 0/5 سانتی متر کم تر است بنابراین میگوییم این خط کش اندازه اشیا را با تقریب کم تر از ۰/۵ سانتی متر مشخص میکند در خط کشهای معمولی کوچک ترین قسمتی که روی آنها مشخص شده، ۱ میلی متر است؛ یعنی دقت اندازه گیری این خط کش ها ۱ میلی متر است؛ یعنی این خط کش ها اندازه ی اشیا را با تقریب کم تر از ۱ میلی متر مشخص می کنند.
برای هر نوع اندازه گیری با توجه به موضوع و اهمیت آن از ابزار مناسب استفاده می کنیم تا تقریب مورد نظر حاصل شود.
برای اندازه گیری وزن یک انسان به ترازویی با دقت تا ۱ کیلوگرم نیاز داریم.
برای اندازه گیری دمای بدن انسان به دماسنجی با دقت تا ۱ درجه نیاز داریم.
برای اندازه گیری وزن فلزات و سنگ های گرانبها به ترازویی با دقت تا ۰/۱ گرم نیاز داریم.
در محاسبه های تقریبی، با توجه به شرایط ابتدا عددها را تقریب میزنیم و سپس محاسبه را انجام می دهیم و یا در بعضی موارد ابتدا محاسبه را انجام می دهیم و سپس حاصل را تقریب میزنیم.
مثال
قیمت فروش نوعی ،تخته متر مربعی ۸۰۰۰ تومان است. قیمت تخته ای به ابعاد ۳/۴۴ و ۲/۸۳ متر چند تومان است؟
روش ۱ ابتدا ابعاد تخته را با تقریب کم تر از ۰/۱ گرد میکنیم و مساحت را حساب می کنیم.
\(2/8 \times 3/4 = 9/52\)متر مربع
روش ۲ ابتدا مساحت تخته را حساب می کنیم و سپس عدد حاصل را با تقریب کم تر از ۰/۰۱ گرد می کنیم.
متر مربع\(2/83 \times 3/44 = 9/7352\)
\(9/7352 \simeq 9/74\)
همان طور که ملاحظه می کنید در روش دوم مساحت به دست آمده به مساحت واقعی تخته نزدیک تر است؛ بنابراین در این مسئله بهتر است که ابتدا مساحت را به دست آورده و سپس عدد حاصل را تقریب بزنیم.
قیمت تخته تومان ۷۷۹۲۰ = ۸۰۰۰× ۹/۷۴
هر یک از عددهای مخلوط زیر را با تقریب کم تر از ۱ گرد کنید.
الف \(17\frac{1}{5}\)
چون \(\frac{1}{5}\)از نصف تقریب (نصف عدد ۱ یعنی\(\frac{1}{2}\) ) کم تر است، بنابراین:
\(17\frac{1}{5} \simeq 17 + 0 = 17\)
ب \(3\frac{4}{5}\)
چون\(\frac{4}{5}\) عدد از نصف بیشتر است، بنابراین:
\(3\frac{4}{5} \simeq 3 + 1 = 4\)
ج \(29\frac{7}{8}\)
چون \(\frac{7}{8}\)از نصف بیشتر است، بنابراین:
\(29\frac{7}{8} \simeq 29 + 1 = 30\)
ترتیب انجام عملیات
در محاسبات ریاضی، ترتیب انجام عملیات تقدم (محاسبات) به شکل زیر است:
۱ ابتدا حاصل پرانتزها را حساب میکنیم و اگر چندین پرانتز داخل هم باشند از داخلی ترین پرانتز محاسبه را شروع می کنیم.
۲ بعد از محاسبه ی پرانتزها، عملهای ضرب و تقسیم را انجام می دهیم. از چپ به راست
3 بعد از محاسبه های ضرب و تقسیم از چپ به راست محاسبه های جمع و تفریق را انجام می دهیم.
مثال
حاصل عبارت های زیر را به دست آورید.
الف \(2 + 3 \times 5\)
\(2 + 3 \times 5 = 2 + 15 = 17\)
ب\(2 + 4 \times (8 - 3)\)
\(2 + 4 \times (8 - 3) = 2 + 4 \times = 2 + 20 = 22\)
ج\(8 - 12 \div (1/2 + (3/6 \div 2)) \)
\(8 - 12 \div (1/2 + (3/6 \div 2)) = 8 - 12 \div (1/2 + 1/8) = 8 - 12 \div 3 = 8 - 4 = 4\)
اندازه گیری
هر وسیله ی اندازه گیری تا حدی میتواند عدد یا مقدار دقیق چیزی را که اندازه میگیریم، نشان دهد. برای مثال، اکثر خط کش هایی که در اختیار دانش آموزان قرار دارد تا واحد میلی متر را نشان می دهد. این خط کش ها طول های کم تر از یک میلی متر را مشخص نمیکنند بنابراین میگوییم خط کش طول اجسام و یا خط ها را با تقریب کم تر از ۱ میلی متر نشان میدهد از طرفی چون هر میلی متر مساوی ۰/۱ سانتی متر است. می توانیم بگوییم که دقت خط کش با تقریب کم تر از ۰/۱ سانتی متر است.
برای هر نوع اندازه گیری با توجه به موضوع و اهمیت آن از وسیله ی اندازه گیری مناسبی استفاده می کنیم تا تقریب مورد نظر ما حاصل شود.
به طور مثال برای اندازه گیری وزن اشخاص از واحد کیلوگرم استفاده میکنیم به عبارت دیگر، ترازوها معمولا وزن اشخاص را با تقریب کمتر از ۱ کیلوگرم نشان میدهد البته ترازوهای دیجیتال دقت بالاتری دارند یا برای اندازه گیری وزن یک قطعه طلا از ترازویی استفاده می کنند که دقت آن ۰/۰۱ گرم میباشد. به عبارت دیگر، این گونه ترازوها وزن اجسام را با تقریب کم تر از ۰/۰۱ گرم نشان می دهند.
کاربرد مقدار تقریبی
گاهی اوقات بهتر است اعداد را به صورت تقریبی بیان کنیم تا انجام محاسبه روی آنها ساده تر شود. در این صورت مقدار محاسبه شده با مقدار واقعی برابر نیست ولی به آن نزدیک است. به مثال زیر دقت کنید:
۵۲۷ × ۶۷۹ = ۳۵۷۸۳۳
همان طور که ملاحظه کنید حاصل ضرب دو عدد ۵۲۷ و ۶۷۹ دقیقا مساوی ۳۵۷۸۳۳ شد. حال اگر مقدار دقیق حاصل ضرب مورد نیاز نباشد و فقط بخواهیم مقدار تقریبی آن را به دست آوریم کافی است که مقدارهای تقریبی این دو عدد را در یک دیگر ضرب کنیم:
با تقریب صدگان ۵۰۰ = ۵۲۷
با تقریب صدگان ۷۰۰ = ۶۷۹
\( \Rightarrow 527 \times 679 = 500 \times 700 = 350000\)
بنابراین زمانی که هر یک از عددها را با تقریب صدگان گرد ،کنیم مقدار تقریبی حاصل ضرب برابر ۳۵۰۰۰۰ خواهد شد که این مقدار نزدیک به جواب واقعی همان ۳۵۷۸۳۳ میباشد. حال اگر عددها را تقریب دهگان گرد می کردیم جواب تقریبی به دست آمده نسبت به تقریب صدگان دقیق تر خواهد شد.
با تقریب دهگان ۵۳۰ = ۵۲۷
679 با تقریب دهگان ۶۸۰ =
\( \Rightarrow 527 \times 679 = 530 \times 680 = 360400\)
همان طور که ملاحظه می کنید مقدار تقریبی حاصل ضرب دو عدد در این حالت اختلاف کم تری نسبت به حالت قبل دارد.
محاسبه ی تقریبی
محاسبه ی تقریبی
برای انجام محاسبات تقریبی میتوانیم از روش های زیر استفاده کنیم:
روش اول ابتدا عددها را گرد کنیم سپس محاسبه را انجام دهیم.
روش دوم ابتدا حاصل را به دست آورده سر ، سپس پاسخ را گرد کنیم.
مثال
الف حاصل عبارت ۵۵ - ۲۹ + ۴۴ را به دست آورید. سپس جواب به دست آمده را با تقریب کم تر از ۱۰ گرد کنید.
\(44 + 29 - 55 = 73 - 55 = 18 = 20\)(با تقریب کمتر از ۱۰)
ب ابتدا مقدار تقریبی هر یک از عددهای بالا را با تقریب کم تر از ۱۰ به دست آورده سپس حاصل عبارت را به دست آورید.
مقدار تقریبی عددها با تقریب کم تر ۱۰
\(\begin{array}{l}44 \simeq 40\,\,,\,\,29 \simeq 30\,\,\,,\,\,\,\,55 \simeq 60\\44 + 29 - 55 \simeq 40 + 30 - 60 = 70 - 60 = 10\end{array}\)
همان طور که ملاحظه میکنید مقدار دقیق این عبارت برابر ۱۸ شد و وقتی که مقدار تقریبی جواب را با تقریب کم تر از ۱۰ گرد میکنیم حاصل ۲۰ می.شود پس اختلاف مقدار تقریبی با مقدار دقیق ۲ واحد است. اما اگر ابتدا عددها را گرد کنیم و سپس حاصل را به دست آوریم جواب برابر ۱۰ میشود که اختلاف این عدد با مقدار دقیق برابر ۸ = ۱۰ - ۱۸ واحد میباشد پس استفاده از روش اول بهتر است.
اگر ابتدا حاصل عبارت ۵۵ - ۲۹ + ۴۴ را به دست آوریم و سپس جواب به دست آمده را با تقریب کم تر از ۱۰ قطع کنیم خواهیم داشت:
قطع شده با تقریب کمتر از ۱۰
\(44 + 29 - 55 = 73 - 55 = 18 \simeq 10\)
حال اگر مقدار تقریبی هر یک از عددها را با روش قطع کردن و با تقریب کمتر از ۱۰ تقریب بزنیم و سپس محاسبه ی عبارت را انجام دهیم، خواهیم داشت:
مقدار تقریبی عددها با تقریب کمتر از10
\(\begin{array}{l}44 \simeq 40\,\,\,,\,\,\,\,29 \simeq 20\,\,\,,\,\,\,\,\,55 \simeq 50\\44 + 29 - 55 = 40 + 20 - 50 = 10\end{array}\)
به این ترتیب حاصل عبارت از هر دو روش یکسان خواهد شد لذا توصیه میکنیم که در محاسبات تقریبی برای این که جواب به دست آمده به مقدار واقعی نزدیک تر باشد از روش گرد کردن استفاده کنید.
وقتی هم باید عملیات انجام گیرد و هم تقریب بزنیم برای آن که پاسخ به مقدار واقعی نزدیک تر باشد، باید ابتدا عملیات را انجام دهیم و بعد از آن تقریب بزنیم.
الف حاصل ضرب ۱۱/۹ و ۲۵/۲ را به دست آورید.
\(25/2 \times 11/9 = 299/88\)
ب حاصل ضرب ۱۱/۹ × ۲۵/۲ را با قطع اعشار و با تقریب کم تر از ۱ به دست آورید.
۲۵/۲ = ۲۵/۲×۱۱/۹ = ۲۵×۱۱ = ۲۷۵
ج حاصل ضرب ۱۱/۹ × ۲۵/۲ را ابتدا با قطع اعشار و تقریب کم تر از ۱۰ به دست آورید.
۲۵/۲ = ۲۵/۲×۱۱/۹ = ۲۰×۱۰ = ۲۰۰
د در کدام ،حالت اختلاف با پاسخ واقعی کم ترین مقدار است؟
همان طور که دیده میشود، در حالت (ب)، یعنی حالتی که رقم مورد تقریب کوچک تر است مقدار تقریبی به مقدار واقعی نزدیک است. اختلاف جواب ها بسیار زیاد میباشد و جواب در حالت ،(ب) به مقدار واقعی نزدیک تر است. لذا باید در محاسبات خود از تقریب مناسب استفاده کنیم همچنین اگر به جای روش قطع کردن از روش گرد کردن استفاده می کردیم جواب ها با اختلاف بسیار کم تری نسبت به روش قطع کردن به دست می آمدند.
\(25/2 \simeq 25\,\,,\,\,11/9 \simeq 12\, \to 25/2 \times 11/9 = 25 \times 12 = 300\)
\(25/2 \simeq 30\,\,,\,\,\,\,11/9 \simeq 10 \to 25/2 \times 11/9 \simeq 30\,\, \times 10 \simeq 300\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه ششم- آزمون آنلاین تمامی دروس پایه ششم
- گام به گام تمامی دروس پایه ششم
- ویدئو های آموزشی تمامی دروس پایه ششم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه ششم
- فلش کارت های آماده دروس پایه ششم
- گنجینه ای جامع از انشاء های آماده پایه ششم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه ششم
ترتیب انجام عملیات
ترتیب انجام عملیات
در انجام عملیات محاسباتی باید به ترتیب زیر عمل کنیم:
۱) محاسبه ی عبارت داخل پرانتزها
۲) انجام ضرب یا تقسیم از چپ به راست عبارت هر کدام که زودتر دیده شد.
۳) انجام جمع یا تفریق از چپ به راست عبارت هر کدام که زودتر دیده شد.
بنابراین اگر ترتیب عملیات با پرانتز مشخص نشده باشد، ابتدا باید ضربها و تقسیم ها و سپس جمع ها و تفریق ها را از چپ به راست عبارت انجام دهیم.
مثال
به عبارات زیر دقت کنید.
الف \(5/2 + 1/3 \times 7/1 = 5/2 + (1/3 \times 7/1) = 5/2 + 9/23 = 14/43\)
ب \(20 - 20 \div 4 \times 2 = 20 - (20 \div 4) \times 2 = 20 - (5 \times 2) = 20 - 10 = 10\)
دقت داشته باشید که چون در این عبارت پرانتزی وجود ندارد پس ابتدا به سراغ محاسبه ی تقسیم و سپس ضرب می رویم چون تقسیم زودتر از ضرب دیده میشود و در آخر تفریق را انجام می دهیم.
عبارت زیر را حل کنید
\((5\frac{1}{4} - 3\frac{3}{{10}}) \div (7/1 + 0/7)\)
محاسبه پرانتز اول:
\(5\frac{1}{4} - 3\frac{3}{{10}} = 2\frac{{1 \times 5}}{{4 \times 5}} - \frac{{3 \times 2}}{{10 \times 2}} = 2\frac{5}{{20}} - \frac{6}{{20}} = \frac{{45}}{{20}} - \frac{6}{{20}} = \frac{{39}}{{20}}\)
محاسبه پرانتز دوم:
\(7/1 + 0/7 = 7/8 = \frac{{78}}{{10}}\)
محاسبه کل عبارت:
\(\frac{{39}}{{20}} \div \frac{{78}}{{10}} = \frac{{39}}{{20}} \times \frac{{10}}{{78}} = \frac{1}{4}\)



1736019749.png)