درسنامه کامل ریاضی دهم فصل 2 مثلثات
تعداد بازدید : 7.26Mخلاصه نکات ریاضی دهم فصل 2 مثلثات - درسنامه شب امتحان ریاضی دهم فصل 2 مثلثات - جزوه شب امتحان ریاضی دهم نوبت اول فصل 2 مثلثات
نسبت های مثلثاتی
نسبت های مثلثاتی
از کلاس نهم می دانید چنانچه دو زاویه از مثلثی با دو زاویه از مثلث دیگر برابر باشند دو مثلث متشابه اند. در شکل زیر دو مثلث \(ABC,A'B'C'\) متشابه اند.
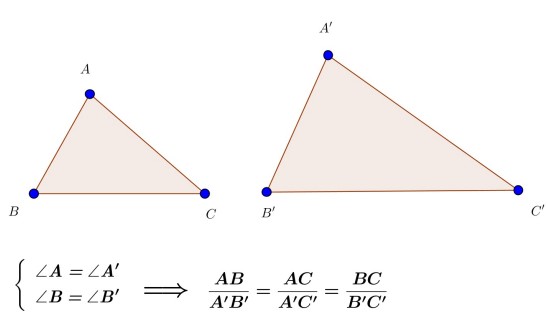
حال در دو مثلث قائم الزاویه برابری تنها یک زاویه حاده از مثلث اولی با یک زاویه حاده از مثلث دومی برای تشابه دو مثلث کفایت می کند.
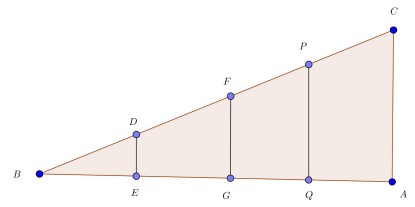
در شکل بالا داریم \(A = E = G = Q = {90^0}\) ولذا مثلث های قائم الزاویه ای که در راس B مشترک اند متشابه هستند. حال اگر نسبت تشابه را در این مثلث ها بنویسیم خواهیم داشت:
\(\frac{{DE}}{{BE}} = \frac{{FG}}{{BG}} = \frac{{PQ}}{{BQ}} = \frac{{GA}}{{BA}}\)
پس برای زاویه B همه این نسبت ها مقداری ثابت است . برای این نسبت ثابت نامی انتخاب می کنیم. این نام تانژانت زاویه B است. پس داریم:
\(\tan B = \frac{{AC}}{{AB}}\)
در مثلث، تانژانت هر زاویه ای از ضلع مقابل بر ضلع مجاور به دست می آید.
عکس نسبت تانژانت را کتانژانت می نامیم. پس داریم:
\(\cot B = \frac{{AB}}{{AC}}\)
در مثلث، کتانژانت هر زاویه ای از ضلع مجاور بر ضلع مقابل به دست می آید.
به همین ترتیب در این مثلث های متشابه نسبت های زیر نیز ثابت اند و باید نامی برای آنها انتخاب کرد.
\(\begin{array}{l}1)\frac{{DE}}{{BD}} = \frac{{FG}}{{BF}} = \frac{{PQ}}{{BP}} = \frac{{AC}}{{BA}}\\2)\frac{{BD}}{{DE}} = \frac{{BF}}{{FG}} = \frac{{BP}}{{PQ}} = \frac{{BA}}{{AC}}\end{array}\)
اولی را سینوس و دومی را کسینوس می نامند. پس داریم:
\(\sin B = \frac{{AC}}{{BC}}\)
\(\cos B = \frac{{AB}}{{AC}}\)
در مثلث، سینوس و کسینوس هر زاویه ای از ضلع مقابل بر وتر و ضلع مجاور بر وتر به دست می آید.
در یک مثلث قائم الزاویه نسبت های ، سینوس، کسینوس، تانژانت، کتانژانت را نسبت های مثلثاتی می نامیم.
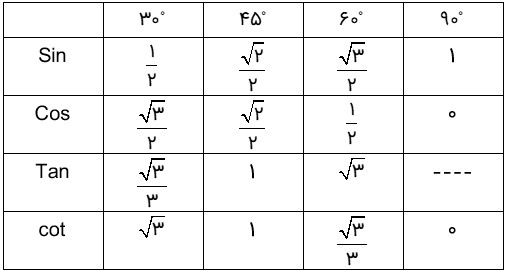
مقدار نسبت های مثلثاتی در درجاتی که نیاز خواهید داشت به صورت زیر است:
1 مقدار عددی عبارات زیر را بدست آورید.
الف \({{\mathop{\rm Sin}\nolimits} ^2}{45^0} + {{\mathop{\rm Cos}\nolimits} ^2}{45^0} = \)
\(\begin{array}{l}{\left( {\frac{{\sqrt 2 }}{2}} \right)^2} + {\left( {\frac{{\sqrt 2 }}{2}} \right)^2} = \frac{1}{2} + \frac{1}{2} = 1\\{{\mathop{\rm Sin}\nolimits} ^2}{45^0} + {{\mathop{\rm Cos}\nolimits} ^2}{45^0} = 1\end{array}\)
ب \(\frac{{\tan {{45}^0} - \tan {{60}^0}}}{{1 + \tan {{45}^0} \times \tan {{60}^0}}} = \)
\(\begin{array}{l}\frac{{1 - \sqrt 3 }}{{1 + \sqrt 3 }} = \frac{1}{1} = 1\\\frac{{\tan {{45}^0} - \tan {{60}^0}}}{{1 + \tan {{45}^0} \times \tan {{60}^0}}} = 1\end{array}\)
2 در شکل زیر طول نردبان را بیابید. (\({\mathop{\rm Cos}\nolimits} {36^0} \approx 0/8\))
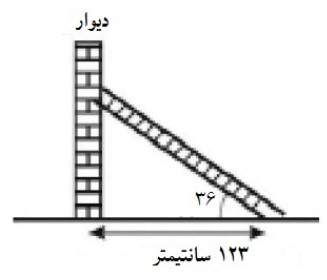
\({\mathop{\rm Cos}\nolimits} A = \frac{{AB}}{{AC}} \to 0/8 = \frac{{1/23}}{{AC}} \to AC = \frac{{1/23}}{{0/8}} \to AC = 1/5375\)
تهیه کننده: فرهاد صمدی
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه دهم- آزمون آنلاین تمامی دروس پایه دهم
- گام به گام تمامی دروس پایه دهم
- ویدئو های آموزشی تمامی دروس پایه دهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه دهم
- فلش کارت های آماده دروس پایه دهم
- گنجینه ای جامع از انشاء های آماده پایه دهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه دهم
مساحت مثلث بر حسب نسبت های مثلثاتی
مساحت مثلث بر حسب نسبت های مثلثاتی
از گذشته می دانیم مساحت یک مثلث برابر است با نصف حاصل ضرب ارتفاع در قاعده ی نظیر به آن ارتفاع؛ حال در شکل زیر می خواهیم مساحت مثلث ABC را محاسبه کنیم. برای این منظور می نویسیم:
\({S_{ABC}} = \frac{{AH \times BC}}{2} = \frac{{AB \times {\mathop{\rm Sin}\nolimits} \alpha \times BC}}{2} = \frac{1}{2}AB \times BC \times {\mathop{\rm Sin}\nolimits} \alpha \)
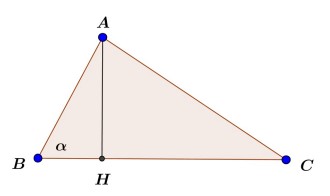
\(AH = AB \times {\mathop{\rm Sin}\nolimits} \beta = AB \times {\mathop{\rm Sin}\nolimits} \alpha \)
1 مساحت مثلث ABC را بیابید. (\(BC = 5\sqrt 3 ,\hat C = {30^0}\))
\(\begin{array}{l}AB = h \to \tan {30^0} = \frac{h}{{5\sqrt 3 }} \to h = 5\sqrt 3 \times \frac{{\sqrt 3 }}{3} \to h = 5\\{S_{ABC}} = \frac{1}{2}h \times BC = \frac{1}{2} \times 5 \times 5\sqrt 3 = \frac{{25}}{2}\sqrt 3 \end{array}\)
2 مساحت مثلث متساوی الساقین ABC برابر 9 است. اندازه x را بیابید. (\({\mathop{\rm Sin}\nolimits} A = {30^0}\) و طول ساق را x بگیرید.)
\({S_{ABC}} = \frac{1}{2}AB{\mathop{\rm Sin}\nolimits} \alpha \to {S_{ABC}} = \frac{1}{2}{x^2}{\mathop{\rm Sin}\nolimits} {30^0} = \frac{1}{2}{x^2} \times \frac{1}{2} = \frac{1}{4}{x^2} = 9 \to {x^2} = 36 \to x = 6\)
تهیه کننده: فرهاد صمدی
جزوات جامع پایه دهم
جزوه جامع ریاضی دهم فصل 1 مجموعه، الگو و دنباله
جزوه جامع ریاضی دهم فصل 2 مثلثات
جزوه جامع ریاضی دهم فصل 3 توان های گویا و عبارت های جبری
جزوه جامع ریاضی دهم فصل 4 معادله ها و نامعادله ها
جزوه جامع ریاضی دهم فصل 5 تابع
جزوه جامع ریاضی دهم فصل 6 شمارش، بدون شمردن
جزوه جامع ریاضی دهم فصل 7 آمار و احتمال
دایره مثلثاتی
دایره مثلثاتی
پرسشی که بطور طبیعی به ذهن می رسد این است که نسبت های مثلثاتی در مورد زوایای غیرحاده تعریف می شود؟ مثلا برای زاویه ١۵٠ درجه می توان سینوس تعریف کرد و چگونه؟ جواب مثبت است. اما مثلث قائم الزاویه دیگر جوابگوی این تعریف نیست. دایره مثلثاتی را برای این منظور معرفی می کنیم.دایره ای به شعاع یک و مرکز مبداء مختصات. اگر از نقطه \(A\left( {1,0} \right)\) و در خلاف جهت حرکت عقربه های ساعت سروع به حرکت کنیم زاویه ای مثبت تولید خواهد شد. در صورت چرخش در جهت عقربه های ساعت زاویه ی منفی حاصل می شود.
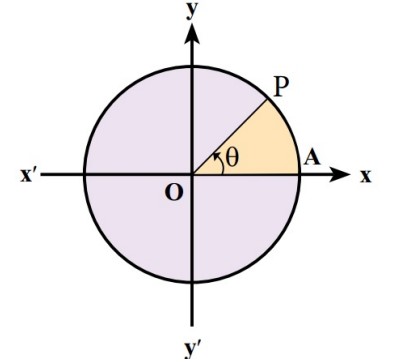
در شکل زیر چند زاویه مثبت و منفی در دایره مثلثاتی دیده می شود.
حال نقطه \(P\left( {x,y} \right)\) را در نظر بگیرید. از نقطه p عمودی بر محور طول ها رسم می کنیم. در مثلث قائم الزاویه ی حاصل نسبت های مثلثاتی زاویه \(\theta \) را محاسبه می کنیم.
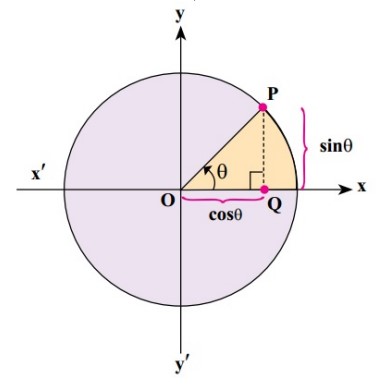
\(\begin{array}{l}{\mathop{\rm Sin}\nolimits} \theta = \frac{{PQ}}{{OP}} = y\\{\mathop{\rm Cos}\nolimits} \theta = \frac{{OQ}}{{OP}} = x\\{\mathop{\rm Tan}\nolimits} \theta = \frac{{PQ}}{{OQ}} = \frac{y}{x}\\Cot\theta = \frac{{OQ}}{{PQ}} = \frac{x}{y}\end{array}\)
علامت نسبت های مثلثاتی با توجه به هر ناحیه در جدول زیر گردآوری شده است.
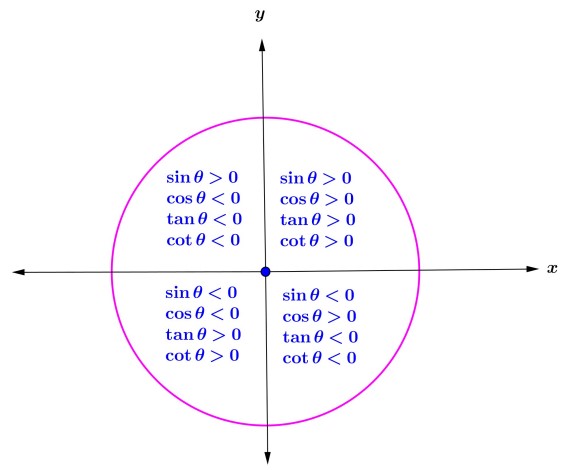
با توجه به دایره مثلثاتی و تعریف نسبت های مثلثاتی متوجه می شویم که همواره \( - 1 \le {\mathop{\rm Sin}\nolimits} \theta \le 1\) و همین طور \( - 1 \le {\mathop{\rm Cos}\nolimits} \theta \le 1\). اما در مورد دو نسبت دیگر یعنی \(\tan \theta ,\cot \theta \) این گونه نیست. در واقع این دو نسبت هر مقداری می توانند باشند، چه مثبت و چه منفی. به زبان ریاضی:
\({\mathop{\rm Sin}\nolimits} \theta \in \left[ { - 1,1} \right],{\mathop{\rm Cos}\nolimits} \theta \in \left[ { - 1,1} \right],\tan \theta ,\cot \theta \in \left( { - \infty , + \infty } \right)\)
شکلی دیگری از دایره مثلثاتی نیز مرسوم است که در آن چهار محور به نام نسبت های مثلثاتی بصورت زیر وجود دارد.
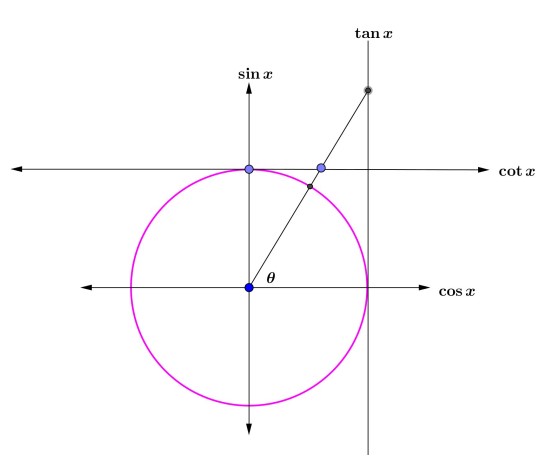
از روی شکل فوق بهتر متوجه خواهید شد که چرا مثلا \(\tan \theta \) می تواند هر مقداری را اختیار کند.
در کلاس نهم معادله خط و مفهوم شیب را خوانده اید. برای یک خط که از نقاط \(B\left( {{x_2},{y_2}} \right),A\left( {{x_1},{y_1}} \right)\) می گذرد شیب چنین تعریف می شود:
\(m = \frac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}\)
M شیب خط است.
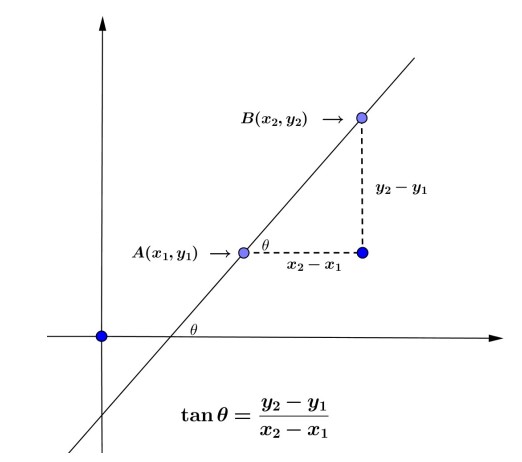
همان طور که در شکل بالا می بینید تانژانت زاویه ای که خط با جهت مثبت محور طول ها می سازد برابر شیب خط است.از این نکته می توان در نوشتن معادله خط استفاده کرد.
روابط بین نسبت های مثلثاتی
شاید تا الان متوجه شده باشید که چهار نسبت مثلثاتی علیرغم نام های متفاوت با هم ارتباط نزدیکی دارند. این روابط را در زیر فهرست کرده ایم.
\(\begin{array}{l}1)\tan x = \frac{{\sin x}}{{\cos x}}\\2)\cot x = \frac{{\cos x}}{{\sin x}}\\3){\sin ^2}x + {\cos ^2}x = 1\\{\sin ^2}x = 1 - {\cos ^2}x\\{\cos ^2}x = 1 - {\sin ^2}x\\4)1 + {\tan ^2}x = \frac{1}{{{{\cos }^2}x}}\\5)1 + {\cot ^2}x = \frac{1}{{{{\sin }^2}x}}\end{array}\)
1 \(\alpha \) زاویه ای در ربع دوم دایره مثلثاتی و \(\tan \alpha = - \frac{{12}}{5}\) است. با استفاده از روابط بین نسبت های مثلثاتی، مقدار \(\cos \alpha \) را به دست آورید.
\({\cos ^2}\alpha = \frac{1}{{1 + {{\tan }^2}\alpha }} = \frac{1}{{1 + \frac{{144}}{{25}}}} = \frac{{25}}{{169}} \to \cos \alpha = - \frac{5}{{13}}\)
2 با فرض با معنی بودن کسرها ، درستی تساوی مقابل را ثابت کنید.
\(\frac{1}{{\cos x}} - \tan x = \frac{{\cos x}}{{1 + sinx}}\)
\(\frac{1}{{\cos x}} - \tan x = \frac{1}{{\cos x}} - \frac{{sinx}}{{\cos x}} = \frac{{1 - \sin x}}{{\cos x}} \times \frac{{1 + \sin x}}{{1 + \sin x}} = \frac{{1 - {{\sin }^2}x}}{{\cos x\left( {1 + \sin x} \right)}} = \frac{{{{\cos }^2}x}}{{\cos x\left( {1 + \sin x} \right)}} = \frac{{\cos x}}{{1 + \sin x}}\)
3
الف معادله خط شکل زیر را بنویسید.
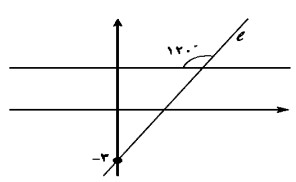
\(y = \sqrt 3 x - 3\)
ب اگر \(\tan \beta \) و \(\sin \beta \) هم علامت باشند، آنگاه \(\beta \) در کدام ربع مثلثاتی قرار دارد؟
\(\beta \) در ربع اول قرار دارد.
تهیه کننده: فرهاد صمدی



1736019749.png)















