درسنامه کامل ریاضی دهم فصل 4 معادله ها و نامعادله ها
تعداد بازدید : 7.27Mخلاصه نکات ریاضی دهم فصل 4 معادله ها و نامعادله ها - درسنامه شب امتحان ریاضی دهم فصل 4 معادله ها و نامعادله ها - جزوه شب امتحان ریاضی دهم نوبت اول فصل 4 معادله ها و نامعادله ها
معادله درجه دوم و روش های حل آن
معادله درجه دوم و روش های حل آن
به معادله ی \(a{x^2} + bx + c = 0\) یک معادله درجه دوم گوییم به شرطی که \(a \ne 0\) باشد. اعداد \(a,b,c \in \mathbb{R}\) را ضرائب معادله می نامیم. X مجهول معادله است و منظور از حل معادله فوق یعنی یافتن تمام اعداد حقیقی چون x که در معادله صدق کنند.
حال به معرفی روش های حل این معادله می پردازیم. برای این منظور با توجه به وضعیت ضرایب معادله روش هایی ارائه می شود.
روش ریشه گیری
اگر در معادله درجه دوم \(a{x^2} + bx + c = 0\) داشته باشیم \(b = 0\& c \le 0\) آنگاه با یک ریشه گیری جواب معادله بدست می آید.
مثال
معادله \(4{x^2} - 16 = 0\) را به روش ریشه گیری حل کنید.
\(4{x^2} - 16 = 0 \to 4{x^2} = 16 \to {x^2} = 4 \to x = \pm 2\)
روش فاکتورگیری
اگر در معادله درجه دوم داشته باشیم \(b = 0\) با یک فاکتورگیری ساده معادله حل می شود.
مثال
معادله \(3{x^2} + 12x = 0\) را به روش فاکتور گیری حل کنید.
\(3{x^2} + 12x = 0 \to 3x\left( {x + 4} \right) = 0 \to x = 0\& x = - 4\)
روش تجزیه
چنانچه هیچ یک از ضرائب صفر نباشد به کمک تجزیه کردن سه جمله ای می توان معادله را حل کرد. در این مورد توجه داریم که ازیکی از خواص اعداد حقیقی استفاده می کنیم که قبلا به آن اشاره کرده ایم :
\(ab = 0 \to a = 0 \vee b = 0\)
مثال
معادله \({x^2} - x - 12 = 0\) را به روش تجزیه حل کنید.
\(\begin{array}{l}{x^2} - x - 12 = \left( {x - 4} \right)\left( {x + 3} \right) = 0\\ \to x - 4 = 0 \to x = 4\\ \to x + 3 = 0 \to x = - 3\end{array}\)
روش مربع کامل کردن
تصور کنید می خواهید جواب معادله \({x^2} + 2x - 1 = 0\) را بدست آورید. هرچه تلاش کنید ، معادله به روش های معمول اشاره شده در بالا حل نخواهد شد. پس باید راهکار تازه ای بکار برد. بدین منظور می توان نوشت:
\(\begin{array}{l}{x^2} + 2x - 1 = 0 \to {x^2} + 2x = 1 \to {x^2} + 2x + 1 = 1 + 1\\ \to {\left( {x + 1} \right)^2} = 2 \to x + 1 = \pm \sqrt 2 \to x = \pm \sqrt 2 - 1\end{array}\)
اگر خوب به محاسبات نگاه کنید هدف از اضافه کردن عدد ١ به طرفین تساوی این بوده است که یک طرف معادله مربع کامل شود تا بتوان از طرفین جذر گرفت و جواب را یافت. چرا عدد ١؟ جواب در محاسبه زیر نهفته است. در حالت کلی برای اینکه عبارت \({x^2} + bx\) را به عبارتی تبدیل کنیم که شامل مربع کامل باشد به شکل زیر عمل می کنیم:
\({x^2} + bx = {x^2} + bx + \frac{{{b^2}}}{4} - \frac{{{b^2}}}{4} = {\left( {x + \frac{b}{2}} \right)^2} - \frac{{{b^2}}}{4}\)
مثال
جواب های معادله \(3{x^2} - 9x + 3 = 0\) را به روش مربع کامل پیدا کنید.
\(\begin{array}{l}3{x^2} - 9x + 3 = 0 \to {x^2} - 3x + 1 = 0 \to {x^2} - 3x + \frac{9}{4} - \frac{9}{4} + 1 = 0\\ \to {\left( {x - \frac{3}{2}} \right)^2} = \frac{9}{4} - 1 \to x - \frac{3}{2} = \pm \frac{{\sqrt 5 }}{2}\\ \to x = \pm \frac{{\sqrt 5 }}{2} + \frac{3}{2}\end{array}\)
روش کلی حل معادله درجه دوم
همان طور که مثال های حل شده بالا ملاحضه کردید،روش مربع کامل کردن کمی وقت گیر و پرمحاسبه است. به همین دلیل یکبار روش مربع کامل را روی فرم کلی معادله درجه دوم \(a{x^2} + bx + c = 0\) بکار می بریم تا دستوری کلی بر حسب رادیکال ها بیابیم و بعد از آن برای حل از دستور یافت شده استفاده کنیم. قبل از شروع محاسبات مبین معادله درجه دوم را بصورت \(\Delta = {b^2} - 4ac\) تعریف می کنیم. \(\Delta \) یک عدد حقیقی است و لذا هر سه حالت \(\Delta \langle 0,\Delta \rangle 0,\Delta = 0\) ممکن است اتفاق بیافتد.
\(\begin{array}{l}a{x^2} + bx + c = 0 \to {x^2} + \frac{b}{a}x + \frac{c}{a} = 0\\ \to {x^2} + \frac{b}{a}x + \frac{{{b^2}}}{{4{a^2}}} - \frac{{{b^2}}}{{4{a^2}}} + \frac{c}{a} = 0\\ \to {\left( {x + \frac{b}{{2a}}} \right)^2} = \frac{{{b^2}}}{{4{a^2}}} - \frac{c}{a} \to {\left( {x + \frac{b}{{2a}}} \right)^2} = \frac{{{b^2} - 4ac}}{{4{a^2}}}\\ \to x + \frac{b}{{2a}} = \pm \frac{{\sqrt \Delta }}{{2a}} \to x = \frac{{ - b \pm \sqrt \Delta }}{{2a}}\end{array}\)
به این ترتیب با فرض اینکه \(\Delta \rangle 0\) باشد معادله دارای دو جواب \({x_2} = \frac{{ - b - \sqrt \Delta }}{{2a}}\) و \({x_1} = \frac{{ - b + \sqrt \Delta }}{{2a}}\) می باشد. اگر \(\Delta = 0\) باشد هر دو جواب برابرند و داریم: \({x_1} = {x_2} = \frac{{ - b}}{{2a}}\) و سرانجام اگر \(\Delta \langle 0\) باشد، گوییم معادله جواب حقیقی ندارد.
1 معادله های زیر را به روش مربع کامل حل کنید.
الف \({x^2} - 6x = 7\)
\(\begin{array}{l}{x^2} - 6x = 7 \to {x^2} - 6x + 9 = 7 + 9 \to {\left( {x - 3} \right)^2} = 16 \to x - 3 = \pm 4\\x - 3 = 4 \to {x_1} = 7\\x - 3 = - 4 \to {x_2} = - 1\end{array}\)
ب \({r^2} + 4r + 4 = 0\)
\({r^2} + 4r + 4 = 0 \to {\left( {r + 2} \right)^2} = 0 \to r + 2 = 0 \to r = - 2\)
2 هر یک از معادله های زیر را به روش دلخواه حل کنید.
الف \(2{x^2} = 250\)
\(2{x^2} = 250 \to \div 2 \to {x^2} = 125 \to x = \pm \sqrt {125} \to x = \pm 5\sqrt 5 \)
ب \(4{x^2} - 13x + 3 = 0\)
\(\begin{array}{l}4{x^2} - 13x + 3 = 0 \to \Delta = {b^2} - 4ac \to \Delta = 169 - 48 \to \Delta = 121\\x = \frac{{ - b \pm \sqrt \Delta }}{{2a}}\\ \to {x_1} = \frac{{13 + 11}}{8} = 3\\ \to {x_2} = \frac{{13 - 11}}{8} = \frac{1}{4}\end{array}\)
3 طول یک مستطیل 3 سانتی متر بیشتر از 4 برابر عرض آن است. اگر مساحت این مستطیل 45 سانتی متر مربع باشد، ابعاد این مستطیل را مشخص کنید.
\(\begin{array}{l}S = a\left( {4a + 3} \right) \to 45 = a\left( {4a + 3} \right) \to 4{a^2} + 3a - 45 = 0 \to \Delta = {b^2} - 4ac \to \Delta = 729\\x = \frac{{ - b \pm \sqrt \Delta }}{{2a}}\\{x_1} = \frac{{ - 3 + 27}}{8} \to {x_1} = 3\\{x_2} = \frac{{ - 3 - 27}}{8} \to {x_2} = - \frac{{15}}{4}\end{array}\)
عرض مستطیل 3 و طول مستطیل 15 است.
تهیه کننده: فرهاد صمدی
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه دهم- آزمون آنلاین تمامی دروس پایه دهم
- گام به گام تمامی دروس پایه دهم
- ویدئو های آموزشی تمامی دروس پایه دهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه دهم
- فلش کارت های آماده دروس پایه دهم
- گنجینه ای جامع از انشاء های آماده پایه دهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه دهم
سهمی ها
سهمی ها
ساده ترین سهمی دارای معادله ی \(y = {x^2}\) است. اگر به متغیر x مقدار دهیم می توانیم نمودار آن را رسم کنیم. مثلا با فرض \(x = 0, \pm 1, \pm 2, \pm 3\) مقادیر حاصل عبارتند از \(y = 0,1,4,9\) اگر این نقاط را روی محورهای مختصات مشخص کنیم و نقاط حاصل را به هم وصل کنیم شکل زیر حاصل می شود.
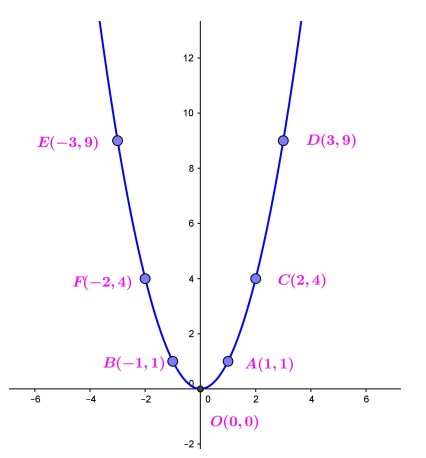
پایین ترین نقطه سهمی در شکل فوق مبداء مختصات است.
نقطه \(O\left( {0,0} \right)\) را مینیمم(کمینه) سهمی گوییم.
محور عرض ها سهمی را به دو قسمت یکسان تقسیم کرده است. محور عرض ها \(x = 0\) را محور تقارن سهمی گوییم.
منظور از یک سهمی معادله ای بصورت \(y = a{x^2} + bx + c\) است که \(a \ne 0\& a,b,c \in \mathbb{R}\) با مربع کامل کردن این عبارت بصورت:
\(y = a{\left( {x - h} \right)^2} + k\)
درمی آید که در این حالت راس سهمی یا مینیمم سهمی نقطه \(M\left( {h,k} \right)\) است و خط \(x = h\) را محور تقارن سهمی گوییم. اگر \(a\rangle 0\) باشد دهانه ی سهمی رو به بالا باز می شود و اگر \(a\langle 0\) باشد دهانه سهمی رو به پایین باز می شود.
رسم سهمی ساده تر می شود اگر بتوانیم دستوری صریح از راس سهمی بدست آوریم. برای این منظور داریم :
\(\begin{array}{l}y = a{x^2} + bx + c \to y = a\left( {{x^2} + \frac{b}{a}x + \frac{c}{a}} \right)\\ \to y = a\left( {{x^2} + \frac{b}{a}x + \frac{{{b^2}}}{{4{a^2}}} - \frac{{{b^2}}}{{4{a^2}}} + \frac{c}{a}} \right)\\ \to y = a{\left( {x + \frac{b}{{2a}}} \right)^2} - \frac{{{b^2}}}{{4a}} + c\\ \to y = a{\left( {x + \frac{b}{{2a}}} \right)^2} + \frac{{4ac - {b^2}}}{{4a}}\end{array}\)
با این حساب راس سهمی بصورت زیر بدست می آید:
\(M\left( { - \frac{b}{{2a}},\frac{{4ac - {b^2}}}{{4a}}} \right)\)
به این ترتیب با داشتن راس سهمی کافیست یک یا دو نقطه قبل و بعد از آن را در معادله منحنی جایگذاری کنیم تا عرض آن نقاط حاصل شده و سپس سهمی را رسم کنیم. همچنین توجه کنید که اگر \(a\rangle 0\) باشد سهمی مینیمم دارد و اگر \(a\langle 0\) باشد سهمی ماکزیمم (بیشینه) دارد.
1 اگر \(\left( { - 2,5} \right)\) و \(\left( {0,5} \right)\) دو نقطه از یک سهمی باشند، خط تقارن این سهمی را به دست آورید.
با توجه به اینکه عرض نقاط یکسان است، این دو نقطه نسبت به محور تقارن سهمی قرینه ی یکدیگرند، به عبارت دیگر محور تقارن از وسط طول های این دو نقطه می گذرد.
\(x = \frac{{ - 2 + 0}}{2} \to x = - 1\)
2 دو پرتابگر وزنه در یک مسابقه ورزشی، وزنه های خود را با زاویه های متفاوت \(\alpha \) و \(\beta \) که \(\alpha \langle \beta \) است، پرتاب کرده اند. پرتابگر A، زاویه \(\alpha \) را انتخاب می کند و مسیر طی شده از رابطه ی \(y = - \frac{{{x^2}}}{2} + \frac{3}{2}x + 2\) به دست می آید. پرتابگر B نیز زاویه \(\beta \) را انتخاب می کند و مسیر طی شده از رابطه ی \(y = - 2{x^2} + 3x + 2\) به دست می آید. در هر دو معادله، y ارتفاع وزنه از سطح زمین و x مسافت افقی طی شده، بر حسب متر است. کدام یک از وزنه ها ارتفاع بیشتری از سطح زمین پیدا کرده است؟ اندازه آنها را مشخص کنید.
\(\begin{array}{l}A)y = - \frac{{{x^2}}}{2} + \frac{3}{2}x + 2 = 0 \to \times 2 \to - {x^2} + 3x + 4 = 0 \to \Delta = 25\\{x_1} = - 1\& {x_2} = 4\end{array}\)
مسافتی که وزنه A طی کرده است 5 متر است.
\(\begin{array}{l}B)y = - 2{x^2} + 3x + 2 = 0 \to \Delta = 25\\{x_1} = - \frac{1}{2}\& {x_2} = 2\end{array}\)
مسافتی که وزنه B طی کرده است \(\frac{5}{2}\) متر است.
بنابراین وزنه پرتابگر A مسافت بیشتری پیموده است.
میزان ارتفاع هر دو وزنه یکی است که هر دو \(\frac{{25}}{8}\) را نشان می دهد.
تهیه کننده: فرهاد صمدی
جزوات جامع پایه دهم
جزوه جامع ریاضی دهم فصل 1 مجموعه، الگو و دنباله
جزوه جامع ریاضی دهم فصل 2 مثلثات
جزوه جامع ریاضی دهم فصل 3 توان های گویا و عبارت های جبری
جزوه جامع ریاضی دهم فصل 4 معادله ها و نامعادله ها
جزوه جامع ریاضی دهم فصل 5 تابع
جزوه جامع ریاضی دهم فصل 6 شمارش، بدون شمردن
جزوه جامع ریاضی دهم فصل 7 آمار و احتمال
تعیین علامت چندجمله ای ها
تعیین علامت چندجمله ای ها
به دقت به شکل زیر نگاه کنید. نمودار یک منحنی در دستگاه مختصات ترسیم شده است. نام منحنی \(p\left( x \right)\) است و در برخی بازه ها بالای محور x هاست و لذا مثبت است و در برخی بازه ها زیر محور x هاست و لذا منفی است. اگر دقت کنید نقاطی که منحنی محور طولها را در آن ها قطع کرده است نقشی اساسی در تعیین اینکه p مثبت است یا منفی بازی می کند. چنین نقاطی را ریشه های p گوییم. در حالت کلی نقاط حاصل از حل معادله \(p\left( x \right) = 0\) را ریشه های p گوییم.
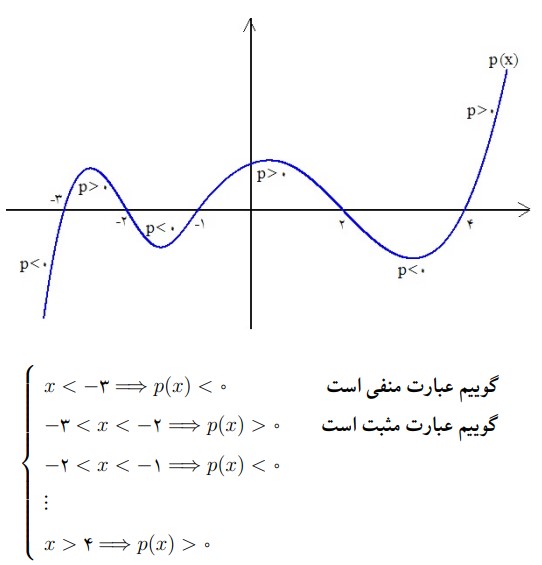
تعیین علامت دوجمله ای درجه اول
می خواهیم عبارت \(p\left( x \right) = ax + b\) را تعیین علامت کنیم. ابتدا ریشه یا ریشه های آن را بدست می آوریم:
\(p\left( x \right) = 0 \to ax + b = 0 \to x = - \frac{b}{a}\)
در حالت کلی نمودار \(p\left( x \right) = y = ax + b\) یکی از دو حالت زیر را دارد:
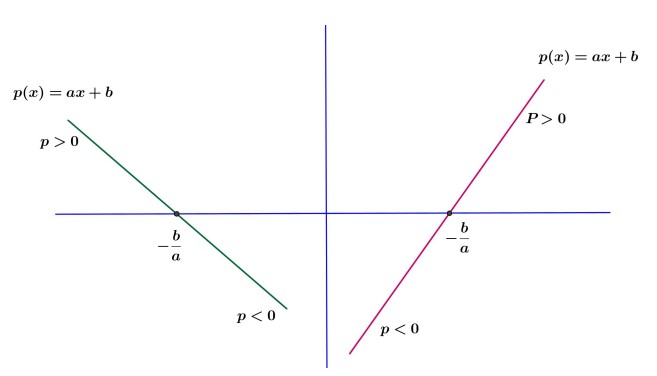
ازنمودار فوق می توان نتیجه گرفت:
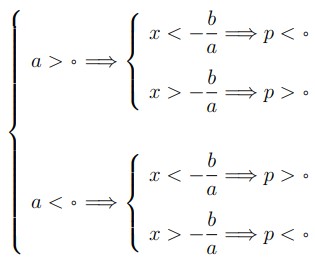
خلاصه بحث فوق در جدول زیر که آن را جدول تعیین علامت می نامیم آمده است.

چنانچه بخواهیم علامت یک عبارت جبری را که شامل چند دوجمله ای درجه اول است را تعیین کنیم، می توانیم در یک جدول همه ی دوجمله ایها را نوشته و ریشه تک تک آنها را یافته و هر کدام را تعیین علامت کنیم و دست آخر با ضرب علامت ها درهم علامت کل عبارت را بیابیم.
مثال
عبارت \(y = 5x - 2\) را تعیین علامت کنید.
ریشه عبارت \(5x - 2\) از معادله \(5x + 2 = 0\) به دست می آید که برابر \(x = \frac{2}{5}\) است.
با توجه به اینکه علامت ضریب x ؛ یعنی \(a = 5\) مثبت است، طبق جدول بالا، جدول تعیین علامت به صورت زیر است:
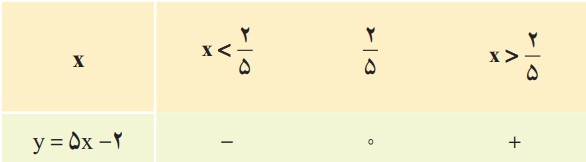
مقدار y را برای \(x = 3\) و \(x = - 1\) به دست آورید و صحت علامت اعداد به دست آمده را با جدول بالا بررسی کنید.
\(\begin{array}{l}x = 3 \to y = 5\left( 3 \right) - 2 = 13\\x = - 1 \to y = 5\left( { - 1} \right) - 2 = - 7\end{array}\)
تعیین علامت سه جمله ای درجه دوم
همان طور که تا الان متوجه شدید یک سه جمله ای درجه دوم را می توان با تجزیه به عامل های درجه اول تعیین علامت کرد. اما این زمانی شدنی است که عبارت تجزیه شود . در صورتیکه عبارت تجزیه نشود راه حل چیست؟ راه حل یافتن روشی است که به کمک آن بتوان سه جمله ای ها را مستقیما تعیین علامت کرد. در حالت کلی یک سه جمله ای درجه دوم یا همان سهمی به یکی از صورت های زیر است:
الف: اگر \(\Delta \rangle 0\)
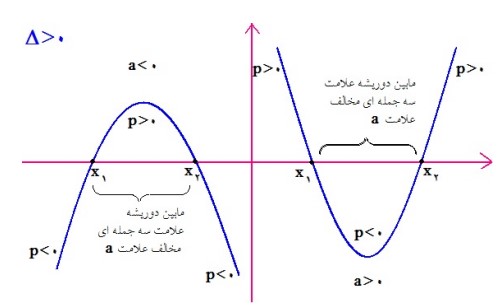
ب: اگر \(\Delta = 0\)
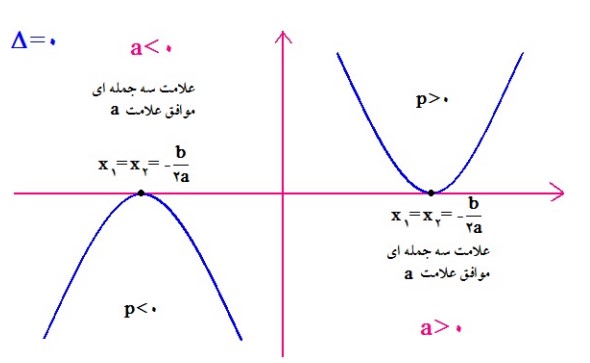
ج: اگر \(\Delta \langle 0\)
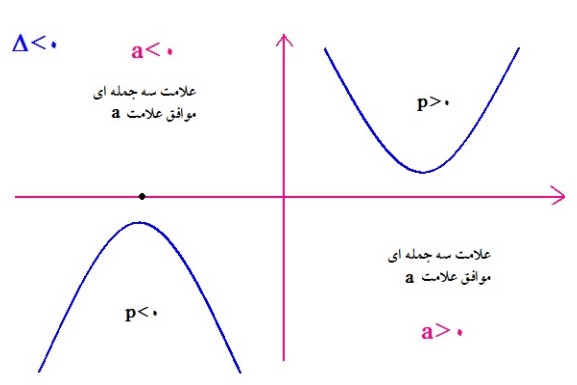
پس برای تعیین علامت سه جمله ای \(p\left( x \right)\) ابتدا باید \(p\left( x \right) = 0\) را حل کنیم. پس اولین گام یافتن مبین معادله درجه دوم است یعنی \(\Delta = {b^2} - 4ac\) است که بسته به علامت \(\Delta \) یکی از جداول زیر را تشکیل می دهیم.
اگر \(\Delta \rangle 0\) باشد:
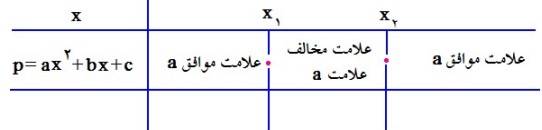
اگر \(\Delta = 0\) باشد:

اگر \(\Delta \langle 0\) باشد:

نتایج حاصل از بررسی نمودارهای یک سه جمله ای درجه دوم را می توان از روی معادله سه جمله ای درجه دوم \(p\left( x \right) = a{x^2} + bx + c\) نیز بدست آورد. برای این منظور فرم تبدیل شده ی عبارت p را که قبلا محاسبه کرده ایم بصورت زیر می نویسیم:
\(\begin{array}{l}p\left( x \right) = a{x^2} + bx + c = a\left( {{{\left( {x + \frac{b}{{2a}}} \right)}^2} - \frac{{{b^2} - 4ac}}{{4{a^2}}}} \right) = a\left( {{{\left( {x + \frac{b}{{2a}}} \right)}^2} - \frac{\Delta }{{4{a^2}}}} \right) \to \frac{{p\left( x \right)}}{a} = \left( {{{\left( {x + \frac{b}{{2a}}} \right)}^2} - \frac{\Delta }{{4{a^2}}}} \right)\\\end{array}\)
حال اگر \(\Delta \langle 0\) باشد عبارت \({\left( {x + \frac{b}{{2a}}} \right)^2} - \frac{\Delta }{{4{a^2}}}\) همواره مثبت است پس \(\frac{{p\left( x \right)}}{a}\) هم مثبت است و این یعنی اگر a مثبت باشد آنگاه \(p\left( x \right)\) هم مثبت است.و اگر a منفی باشد آنگاه \(p\left( x \right)\) هم منفی است.
حال اگر \(\Delta = 0\) باشد عبارت حاصل بصورت \({\left( {x + \frac{b}{{2a}}} \right)^2}\) درمی آید و باز \(\frac{{p\left( x \right)}}{a}\) مثبت است و مانند حالت قبل نتیجه حاصل می شود.
سرانجام اگر \(\Delta \rangle 0\) باشد، پس \(\sqrt \Delta \) با معنی است و داریم:
\(\begin{array}{l}1)\frac{{p\left( x \right)}}{a} = \left( {{{\left( {x + \frac{b}{{2a}}} \right)}^2} - \frac{\Delta }{{4{a^2}}}} \right)\\\frac{{p\left( x \right)}}{a} = \left( {x + \frac{b}{{2a}} - \frac{{\sqrt \Delta }}{{2a}}} \right)\left( {x + \frac{b}{{2a}} + \frac{{\sqrt \Delta }}{{2a}}} \right)\end{array}\)
عبارت های داخل پرانتز که بلافاصله بعد از x آمده اند همان ریشه های معادله \(p\left( x \right) = 0\) هستند. اگر قرار دهیم: \({x_2} = \frac{{ - b - \sqrt \Delta }}{{2a}}\) و \({x_1} = \frac{{ - b + \sqrt \Delta }}{{2a}}\)
آنگاه معادله (1) بصورت زیر تبدیل می شود:
\(\frac{{p\left( x \right)}}{a} = \left( {x - {x_1}} \right)\left( {x - {x_2}} \right)\)
بدون آنکه استدلال دچار نقصان شود می توان فرض کرد \({x_1}\langle {x_2}\) است. حال برای بررسی علامت \(\frac{{p\left( x \right)}}{a}\) باید حالات زیر را بررسی کرد.
1) اگر \({x_1}\langle x\langle {x_2}\) باشد عبارت \(\left( {x - {x_1}} \right)\left( {x - {x_2}} \right)\) منفی است و لذا \(\frac{{p\left( x \right)}}{a}\) منفی است و این یعنی \(p\left( x \right)\) و a از نظر علامت مخالف هم هستند.
2) اگر \({x_1}\langle x\langle {x_2}\) باشد و یا \({x_1}\langle {x_2}\langle x\) باشد عبارت \(\left( {x - {x_1}} \right)\left( {x - {x_2}} \right)\) مثبت است و لذا \(\frac{{p\left( x \right)}}{a}\) هم مثبت است و این یعنی \(p\left( x \right)\) و a هم علامت هستند.
همان طور که مشاهده کردید نتایج بدست آمده در این حالت منطبق بر نتایج بدست آمده از نمودارهای هندسی است.
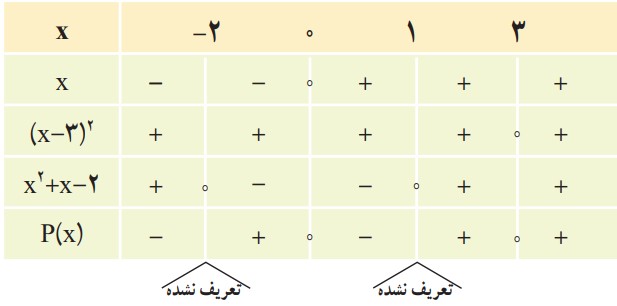
عبارت \(p\left( x \right) = \frac{{x{{\left( {x - 3} \right)}^2}}}{{{x^2} + x - 2}}\) را تعیین علامت کنید.
هریک از عبارت های موجود در صورت و مخرج را تعیین علامت می کنیم و نتایج را در یک جدول می نویسیم.
\(\begin{array}{l}x = 0\\{\left( {x - 3} \right)^2} = 0 \to x - 3 = 0 \to x = 3\\{x^2} + x - 2 = 0 \to \left( {x + 2} \right)\left( {x - 1} \right) = 0 \to x = - 2 \vee x = 1\end{array}\)
تهیه کننده: فرهاد صمدی
نا معادله
نا معادله
یکی از مهم ترین کاربردهای تعیین علامت حل نامعادلات جبری است. برای یافتن مقادیری از x که در شرط \(p\left( x \right)\rangle 0\) صدق می کند تنها راه تعیین علامت p است . حتی ممکن است p لزوما چندجمله ای نباشد. قبل از هر چیز خواص مقدماتی نامساوی ها را بیان می کنیم.
خواص اصلی نامساوی ها
\(\begin{array}{l}1)a \le b \to a + c \le b + c\\2)a \le b\\ \to c\rangle 0 \to ac \le bc\\ \to c\langle 0 \to ac \ge bc\\3)a \le b\& b \le c \to a \le c\\4)0\langle a \le b \to \frac{1}{a} \ge \frac{1}{b}\rangle 0\\5)a \le b\langle 0 \to \frac{1}{b} \le \frac{1}{a}\langle 0\\6)a\langle 0\langle b \to \frac{1}{a}\langle 0\langle \frac{1}{b}\end{array}\)
قدرمطلق و معادلات و نامعادلات قدرمطلقی
قدر مطلق x را که با نماد \(\left| x \right|\) نشان داده می شود بصورت زیر تعریف می کنیم:
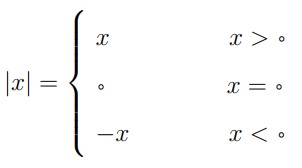
مثال
قدرمطلق عبارت های زیر را حساب کنید.
الف \(\left| {1 + \sqrt 2 } \right| = \)
\(\left| {1 + \sqrt 2 } \right| = 1 + \sqrt 2 \)
ب \(\left| {1 + {t^2}} \right| = \)
\(\begin{array}{l}\left| {1 + {t^2}} \right| = 1 + {t^2}\\\end{array}\)
پ \(\left| {1 - \sqrt 2 } \right| = \)
\(\left| {1 - \sqrt 2 } \right| = \sqrt 2 - 1\)
ج \(\left| {1 - \frac{\pi }{3}} \right| = \)
\(\left| {1 - \frac{\pi }{3}} \right| = \frac{\pi }{3} - 1\)
مهم ترین خواص قدرمطلق ها
\(\begin{array}{l}1)\left| u \right| = 0 \to u = 0\\2)\left| u \right| = a \to u = \pm a,a\rangle 0\\3)\left| u \right| \le a \to - a \le u \le a,a\rangle 0\\4)\left| u \right| \ge a \to u \ge a \vee u \le - a,a\rangle 0\\5){u^2} \le {a^2} \leftrightarrow \left| u \right| \le a \leftrightarrow - a \le u \le a,a\rangle 0\\6){u^2} \ge {a^2} \leftrightarrow \left| u \right| \ge a \leftrightarrow u \ge a \vee u \le - a,a\rangle 0\\7)\left| u \right| = u \leftrightarrow u \ge 0\& \left| u \right| = - u \leftrightarrow u \le 0\\8)\left| {\left| a \right| - \left| b \right|} \right| \le \left| {a \pm b} \right| \le \left| a \right| + \left| b \right|\\9)\left| {ab} \right| = \left| a \right|\left| b \right|\& \frac{{\left| a \right|}}{{\left| b \right|}} = \left| {\frac{a}{b}} \right|\end{array}\)
به خاصیت 8ام نامساوی مثلثی نیز می گویند.
1 تعداد ضربان قلب، پس از X دقیقه کار سنگین بدنی، طبق رابطه ی \(y = \frac{{15}}{8}{x^2} - 30x + 200\) به دست می آید. در چه زمان هایی پس از یک کار سنگین بدنی، تعداد ضربان قلب بیشتر است؟ آیا تمام جواب های به دست آمده قابل قبول اند؟
\(\begin{array}{l}\frac{{15}}{8}{x^2} - 30x + 200\rangle 110 \to y = \frac{{15}}{8}{x^2} - 30x + 90\rangle 0 \to \times 8 \to 15{x^2} - 240x + 720\rangle 0\\15{x^2} - 240x + 720 = 0 \to \Delta = 14400 \to {x_1} = 12\& {x_2} = 4\\ \to x\langle 4 \vee x\rangle 12\end{array}\)
2 معادلات و نامعادلات زیر را حل کنید.
الف \(\left| {{x^3} - 9x} \right| = 0\)
\(\begin{array}{l}\left| {{x^3} - 9x} \right| = 0 \to {x^3} - 9x = 0 \to x\left( {{x^2} - 9} \right) = 0\\{x_1} = 0 \vee {x_2} = 3\end{array}\)
ب \(\left| {3x - 5} \right| = 4\)
\(\left| {3x - 5} \right| = 4 \to 3x - 5 = 4 \to 3x = 9 \to x = \pm 3\)
ج \(\left| {2x - 1} \right|\langle 1\)
\(\left| {2x - 1} \right|\langle 1 \to - 1\langle 2x - 1\langle 1 \to 0\langle 2x\langle 2 \to 0\langle x\langle 1\)
3 یک نا معادله قدر مطلقی بنویسید که مجموعه جواب آن \(\left( { - \infty ,6} \right] \cup \left[ {6, + \infty } \right)\) باشد.
با توجه به اینکه \(\frac{9}{2}\) وسط فاصله \(\left[ {3,6} \right]\) است. شکل مجموعه نقاطی است که فاصله شان از \(\frac{9}{2}\) بیشتر از \(\frac{3}{2}\) می باشد بنابراین \(\left| {x - \frac{9}{2}} \right| \ge \frac{3}{2}\) جواب است.
تهیه کننده: فرهاد صمدی
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه دهم- آزمون آنلاین تمامی دروس پایه دهم
- گام به گام تمامی دروس پایه دهم
- ویدئو های آموزشی تمامی دروس پایه دهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه دهم
- فلش کارت های آماده دروس پایه دهم
- گنجینه ای جامع از انشاء های آماده پایه دهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه دهم



1736019749.png)















