درسنامه کامل ریاضی دهم فصل 6 شمارش، بدون شمردن
تعداد بازدید : 7.26Mخلاصه نکات ریاضی دهم فصل 6 شمارش، بدون شمردن - درسنامه شب امتحان ریاضی دهم فصل 6 شمارش، بدون شمردن - جزوه شب امتحان ریاضی دهم نوبت اول فصل 6 شمارش، بدون شمردن
اصل ضرب و جمع
اصل ضرب
فرض کنید کاری به دو جزء تقسیم شده است،چنانکه جز اول به m طریق انجام شدنی است و جزء دوم مستقل از اولی به n طریق انجام شدنی است. در این صورت این کار به mn طریق انجام شدنی است. البته این اصل قابل تعمیم است. اگر کاری به k طریق مجزا تقسیم شده باشد بطوریکه اولی به \({m_1}\) طریق انجام شدنی باشد، دومی به \({m_2}\) طریق انجام شدنی باشدو ... و k امی به \({m_k}\) طریق انجام شدنی باشد آنگاه کل کار به \({m_1} \times {m_2} \times ... \times {m_k}\) طریق شدنی است.
مثال
از شهر A به شهر B سه راه و از شهر B به شهر C چهار راه وجود دارد.
الف به چند طریق می توان از شهر A به شهر B رفت؟
به 3 طریق می توان رفت.
ب به چند طریق می توان از شهر A به شهر C رفت و به شهر A برگشت،بطوری که هر جاده حداکثر یک بار طی شود؟
به 6 طریق می توان رفت.
اصل جمع
فرض کنید کاری را بتوان به دو روش انجام داد طوری که در روش اول m انتخاب و در روش دوم n انتخاب موجود باشد. در این صورت برای انجام این کار \(m + n\) روش وجود دارد.مثل اصل ضرب این اصل نیز قابل تعمیم است.
مثال
بین شهرهای A و B سه جاده ،بین A و C ٢ جاده و بین B و C سه جاده احداث شده است.به چند طریق می توان با طی حداکثر دو جاده از A به B رفت؟
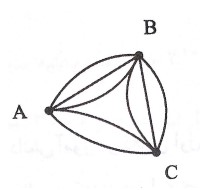
به 6 طریق می توان از A به B با طی حداکثر دو جاده رفت.
تکنیک به کار رفته در حل مسئله فوق ، استفاده از اصل متمم است. گاهی اوقات شمارش خاصیت ذکر شده در مسئله ای به مراتب مشکل تر از شمارش اعضایی است که خاصیت ذکرشده را ندارند. در این حالت بهتر است آنهایی که آن ویژگی معین را ندارند (متمم) شمارش شده و از کل اعضای مجموعه اصلی کم شوند.
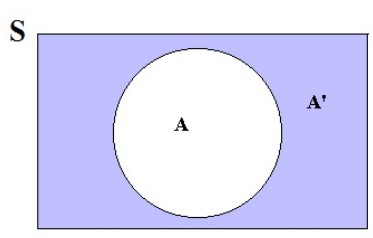
\(\left| S \right| = \left| A \right| + \left| {A'} \right|\)
1 به چند طریق می توان یک نفر را از بین ۶ زن و ٨ مرد انتخاب کرد؟
\(6 + 8 = 14\)
به 14 روش میتوان فرد را انتخاب کرد.
2 در یک شهرک صنعتی 5 بلوار اصلی و در هر بلوار، بین 8 تا 10 خیابان، و در هر خیابان بین 10 تا 12 کوچه و در هر کوچه بین 20 تا 30 کارخانه وجود دارد. حداقل و حداکثر تعداد کارخانه هایی که ممکن است در این شهرک وجود داشته باشد، چند تاست؟
\(\begin{array}{l}\max = 5 \times 10 \times 12 \times 30 = 18000\\\min = 5 \times 8 \times 10 \times 20 = 8000\end{array}\)
تهیه کننده: فرهاد صمدی
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه دهم- آزمون آنلاین تمامی دروس پایه دهم
- گام به گام تمامی دروس پایه دهم
- ویدئو های آموزشی تمامی دروس پایه دهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه دهم
- فلش کارت های آماده دروس پایه دهم
- گنجینه ای جامع از انشاء های آماده پایه دهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه دهم
جایگشت
جایگشت
سه نفر به چند صورت متفاوت می توانند در یک ردیف کنار هم ایستاده و عکس بگیرند؟ اگر این سه شخص را با حروف لاتین a و b و c نمایش دهیم، تمام حالات ممکنه در زیر آمده است:
abc, acb, bca, bac, cab, aba
هر یک از این ۶ حالت را یک جایگشت از سه حرف \(\left\{ {a,b,c} \right\}\) گوییم. حال اگر ۴ نفر بخواهند در یک ردیف و کنار هم عکس بگیرند چند حالت متفاوت پدید می آید؟
abcd , abdc , acbd , acdb , adcb , adbc
bacd , badc , bcad , bcda , bdac , bdca
cabd , cadb , cbad , cbda , cdab , cdba
dabc , dacb , dbac , dbca , dcab , dcba
به کمک اصل ضرب می توان تعداد جایگشت ها را بدون رسم کردن بدست آورد. تعداد جایگشت های ۴ شیء برابر است با \(4 \times 3 \times 2 \times 1 = 24\) و تعداد جایگشت های ٣ شیء برابر است با \(3 \times 2 \times 1 = 6\) در حالت کلی اگر n شیء متمایز داشته باشیم در این صورت تعداد جایگشت های این n شیء برابر است با: \(n \times \left( {n - 1} \right) \times \left( {n - 2} \right) \times ... \times 3 \times 2 \times 1\)
معرفی یک نماد: حاصل ضرب \(n \times \left( {n - 1} \right) \times \left( {n - 2} \right) \times ... \times 3 \times 2 \times 1\) را با نماد \(n!\) نشان می دهیم و n فاکتوریل خوانده می شود.
مثال
حاصل عبارت زیر را بدست آورید.
\(\frac{{8!}}{{5!}} = \)
\(\frac{{8!}}{{5!}} = \frac{{8 \times 7 \times 6 \times 5 \times 4}}{{5 \times 4 \times 3 \times 2 \times 1}} = \frac{{56}}{1} = 56\)
حال تصور کنید هفت شیء متمایز \({a_7},{a_6},{a_5},...,{a_1}\) داشته باشیم. می خواهیم تعداد جایگشت های بطول ٣ ( یعنی با سه شیء) را که می توان از ٧ شیء فوق ساخت محاسبه کنیم. یک جایگشت بطول ٣ را بصورت زیر در نظر می گیریم:
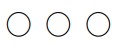
اولین خانه به هفت طریق ، دومین خانه به ۶ طریق و سومین خانه به ۵ طریق پر می شود. پس طبق اصل ضرب تعداد چنین جایگشت هایی برابر \(7 \times 6 \times 5\) است. می توان این عبارت را طور دیگری هم نوشت:
\(7 \times 6 \times 5 = 7 \times 6 \times 5 \times \frac{{4!}}{{4!}} = \frac{{7!}}{{7!}} = \frac{{7!}}{{\left( {7 - 3} \right)!}}\)
عدد ٣ و ٧ که نقشی اصلی در مسئله داشتند را در آخرین کسر می بینیم. در حالت کلی اگر باشد و بخواهیم تعداد جایگشت های r شیء را از n شیء بیابیم همانند مثال بالا عمل می کنیم:
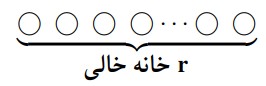
اولین خانه دارای n انتخاب،دومین خانه \(\left( {n - 1} \right)\) انتخاب، سومین خانه \(\left( {n - 2} \right)\) انتخاب .... و r امین خانه دارای \(\left( {n - r + 1} \right)\) نتخاب است. حال حاصلضرب این اعداد برابر است با:
\(n\left( {n - 1} \right)\left( {n - 2} \right)...\left( {n - r + 1} \right) = \frac{{n!}}{{\left( {n - r} \right)!}} = p\left( {n,r} \right)\)
عبارت \(p\left( {n,r} \right)\) را برای تعداد جایگشت های r شیء از n شیء انتخاب کرده ایم. پس تعداد جایگشت های rشیء از n شیء یا \(p\left( {n,r} \right)\) برابر است با :
\(p\left( {n,r} \right) = \frac{{n!}}{{\left( {n - r} \right)!}}\)
مثال
با حروف کلمه جهانگردی و بدون تکرار حروف:
الف) چند کلمه ٨ حرفی می توان نوشت؟ چند تا از آن ها به «ی» ختم می شود؟
\(8!,\frac{{8!}}{{7!}}\)
ب) چند کلمه ٨ حرفی می توان نوشت که در آن ها حروف «د» و «ی» کنار هم قرار گرفته باشند؟
\(\frac{{8!}}{{6!}}\)
پ) چند کلمه ۶ حرفی می توان نوشت؟ چند تا از آنها به «گردی» ختم می شوند؟
\(\frac{{6!}}{{4!}}\)
جایگشت های دوری
به هر روش قرار گرفتن n شیء دور یک دایره یک جایگشت دوری آن n شیء گوییم،با این ویژگی که اگر یک آرایش از دوران یک آرایش دیگر بدست آید این دو آرایش را هم ارز گوییم. در شکل زیر آرایش های ١ و ٢ از جایگشت های دوری \(E,D,E,B,A\) هم ارزند اما این دو با ٣ هم ارز نیست.
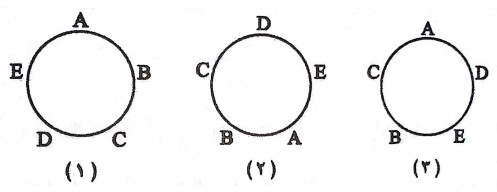
قضیه: تعداد جایگشت های دوری n شیء برابر است با \(\left( {n - 1} \right)!\) .
1 در یک لیگ فوتبال 18 تیم قرار دارند. در پایان این لیگ تیم های اول تا سوم به چند حالت مختلف می توانند مشخص شوند؟
\(\begin{array}{l}P\left( {18,3} \right)\\\frac{{n!}}{{\left( {n - r} \right)!}} = \frac{{18!}}{{15!}} = \frac{{18 \times 17 \times 16 \times 15!}}{{15!}} = 4896\end{array}\)
2 از بین تعدادی کتاب مختلف می خواهیم سه کتاب را انتخاب کنیم و در قفسه ای بچینیم. اگر تعداد حالت های مختلف برای این کار 210 تا باشد، تعداد کتاب ها چند تاست؟
\(\begin{array}{l}P\left( {n,3} \right)\\\frac{{n!}}{{\left( {n - r} \right)!}} = \frac{{n!}}{{\left( {n - 3} \right)!}} = n\left( {n - 1} \right)\left( {n - 2} \right) = 7 \times 6 \times 5 = 210 \to n = 7\end{array}\)
3 در یک نوع ماشین حساب کوچک که دارای 20 کلید است، برای انجام یک دستور خاص باید سه کلید مشخص با ترتیبی مشخص فشار داده شوند. اگر فردی نداند سه کلید مورد نظر کدام اند و بخواهد به طور تصادفی این کار را انجام دهد و فشردن هر سه کلید 2 ثانیه زمان بخواهد، این فرد حداکثر (در بدترین حالت) در چه زمانی می تواند دستور مورد نظر را اجرا کند؟
\(2 \times P\left( {20,3} \right) = 13680s\)
تهیه کننده: فرهاد صمدی
جزوات جامع پایه دهم
جزوه جامع ریاضی دهم فصل 1 مجموعه، الگو و دنباله
جزوه جامع ریاضی دهم فصل 2 مثلثات
جزوه جامع ریاضی دهم فصل 3 توان های گویا و عبارت های جبری
جزوه جامع ریاضی دهم فصل 4 معادله ها و نامعادله ها
جزوه جامع ریاضی دهم فصل 5 تابع
جزوه جامع ریاضی دهم فصل 6 شمارش، بدون شمردن
جزوه جامع ریاضی دهم فصل 7 آمار و احتمال
ترکیب
ترکیب
اگر در انتخاب r شیء از میان n شیء \(r \le n\) ترتیب انتخاب مهم نباشد با مسئله ترکیب روبرو هستیم. تعداد راه های انتخاب r شیء بدون اهمیت ترتیب آنها را ترکیب r شیء از n شیء گوییم و با نماد \(\left( {\begin{array}{*{20}{c}}n\\r\end{array}} \right)\) نشان می دهیم و برابر است با:
\(\left( {\begin{array}{*{20}{c}}n\\r\end{array}} \right) = C\left( {n,r} \right) = \frac{{n!}}{{r!\left( {n - r} \right)!}}\)
مثال
به چندطریق می توان از بین ده عضو شورای شهر دو نفر را به عنوان رئیس و معاون انتخاب کرد؟
\(\left( {\begin{array}{*{20}{c}}{10}\\2\end{array}} \right) = \frac{{10!}}{{2!\left( {8!} \right)}}\)
جایگشت با تکرار
فرض کنید \({m_1}\) شیء از نوع \({a_1}\) و \({m_2}\) شیء از نوع \({a_2}\) و ... و \({m_k}\) شیء از نوع \({a_k}\) داریم که \({m_1} + {m_2} + ... + {m_k} = n\) در اینصورت هر چیدن این n شیء را یک جایگشت با تکرار می نامیم. تعداد این جایگشت ها برابر است با :
\(\frac{{n!}}{{{m_1}!{m_2}!...{m_k}!}}\)
1 تعداد کلماتی یازده حرفی که با حروف کلمه ی Mississippi می توان نوشت را بیابید؟
\(\frac{{11!}}{{1!4!4!2!}}\)
2 چند عدد ده رقمی با استفاده از سه رقم ۴ و دو رقم ٢ و پنج رقم ٨ می توان نوشت؟
\(\frac{{10!}}{{3!2!5!}}\)
تهیه کننده: فرهاد صمدی



1736019749.png)















