جواب مرور فصل 6 صفحه 82 درس 6 ریاضی هفتم (سطح و حجم)
تعداد بازدید : 80.86Mپاسخ مرور فصل 6 صفحه 82 ریاضی هفتم
-گام به گام مرور فصل 6 صفحه 82 درس سطح و حجم
-مرور فصل 6 صفحه 82 درس 6
-شما در حال مشاهده جواب مرور فصل 6 صفحه 82 ریاضی هفتم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
مفاهیم و مهارت ها
در این فصل، اصطلاحات زیر به کار رفته اند. مطمئن شوید که می توانید با جملات خود، آنها را تعریف کنید.برای هر کدام مثال بزنید.
1 حجم هندسی
2 حجم منشوری
3 مساحت جانبی
4 مساحت کل
5 گسترده
1 حجم هندسی:
حجم هندسی به مقدار فضایی که توسط یک جسم سهبعدی که از شکل های هندسی شناخته شده مانند مکعب، استوانه، هرم، کُره، منشور و ... ایجاد شود یا اینکه ترکیبی از این ها باشد؛ مانند:
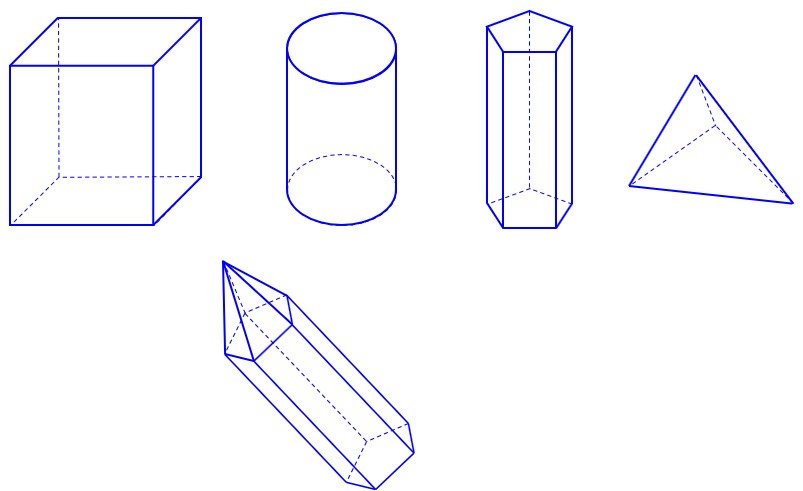
2 حجم منشوری:
حجم منشوری به فضایی که یک جسم منشوری اشغال میکند اشاره دارد. برای محاسبه حجم منشوری، باید مساحت قاعدهی منشور را در ارتفاع آن ضرب کنیم. حجم های منشوری، بین دو صفحۀ موازی قرار می گیرند. به این دو سطح موازی که سطح منشوری را قطع می کنند، قاعده و به سطح های اطراف آن وجه های جانبی می گویند. به محل برخورد سطح ها یال و به نقطۀ برخورد هر سه سطح رأس می گویند.
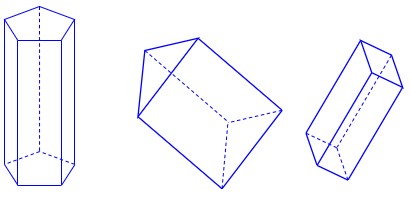
3 مساحت جانبی:
مساحت جانبی به مساحت کل سطوح جانبی یک جسم سه بعدی اشاره دارد، یعنی مساحت همه سطوحی که جسم را از کنارهها میپوشانند. برای محاسبه مساحت جانبی شکل های هندسی که در کتاب درسی خواندیم، کافی است که محیط قاعده را بدست آوریم و آن را در ارتفاع جسم ضرب کنیم. در این صورت مقدار مساحت جانبی جسم بدست می آید. به عنوان مثال، یک استوانه به شعاع 2 و ارتفاع 8، دارای مساحت جانبی زیر می باشد (برای راحتی مقدار عدد پی را برابر 3 در نظر می گیریم):
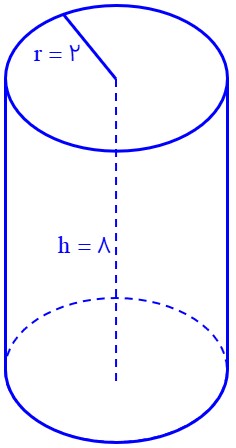
\(\begin{array}{l}\pi = 3\\\\h = 8\\\\r = 2\\\\P = 2 \times \pi \times r = 2 \times 3 \times 2 = 12\\\\S = P \times h = 12 \times 8 = 96\end{array}\)
4 مساحت کل:
مساحت کل به مجموع مساحتهای تمامی سطوح یک جسم سهبعدی اشاره دارد. به عبارت دیگر، مساحت کل شامل هم مساحتهای جانبی و هم مساحتهای دو قاعدۀ جسم میشود. به عنوان مثال می خواهیم مساحت کل استوانۀ بالا را بدست بیاریم. داریم:
\( = {S_J} = P \times h = \) مساحت جانبی
\(12 \times 8 = 96\)
\( = {S_{Gh}} = \pi \times r \times r = \) مساحت قاعده
\(3 \times 2 \times 2 = 12\)
اگر مساحت جانبی را با نماد \({S_J}\) و مساحت قاعده را با نماد \({S_{Gh}}\) نمایش دهیم، رابطه مساحت کل به صورت زیر می شود:
\( = 2 \times {S_{Gh}} + {S_J} = \) مساحت کل
\(2 \times 12 + 96 = 24 + 96 = 120\)
5 گسترده:
تبدیل یک شکل هندسی سه بعدی بر روی یک صفحه دو بعدی که این کار بوسیل، کشیدن تمام وجه های آن شکل هندسی بر روی صفحه دو بعدی (کاغذ) بدست می آید. لازم به ذکر است که همۀ این وجه ها به هم متصل هستند. به عنوان مثال، در شکل زیر بعضی از حجم های سه بعدی معروف را به صورت گستردۀ آن ها کشیده شده اند:
الف گسترده های یک مکعب:

ب گستردۀ یک مکعب مستطیل:
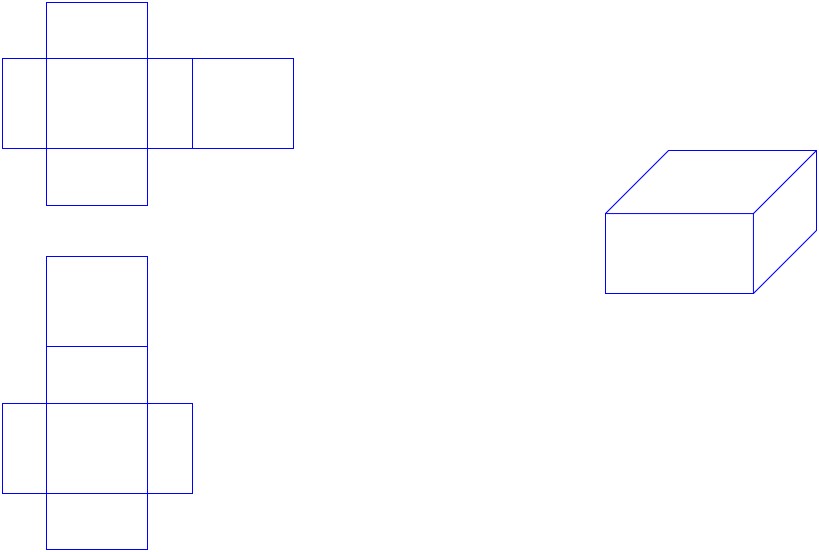
پ گستردۀ یک منشور پنج پهلو:
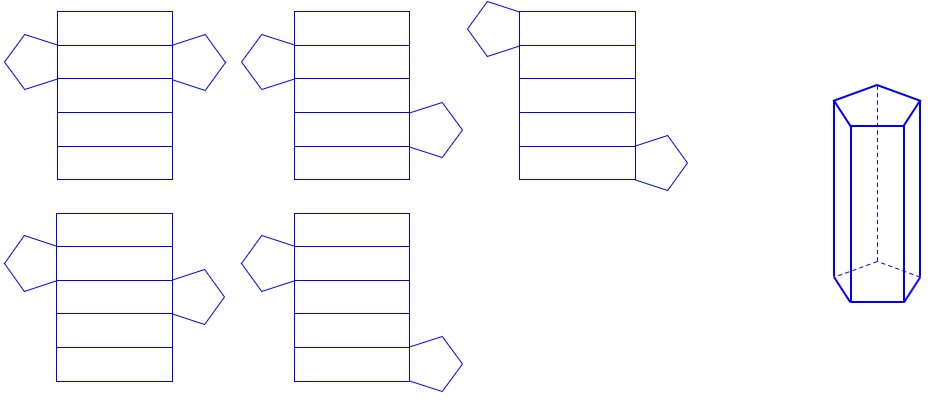
ت گستردۀ یک هِرَم:

ث گستردۀ یک مخروط:

در این فصل، روش های اصلی زیر مطرح شده اند.با یک مثال هر کدام را توضیح دهید و در دفتر خود یک خلاصه تهیه کنید.
1 انواع حجم های هندسی
2 حجم مخروطی و حجم منشوری
3 قاعده، وجه، یال و رأس حجم های منشوری
4 مقطع زدن یک حجم منشوری
5 رابطهٔ پیدا کردن حجم های منشوری
6 رابطهٔ پیدا کردن مساحت جانبی حجم های هندسی
7 رابطهٔ پیدا کردن مساحت کل حجم های منشوری
8 ساختن یک حجم به کمک گستردهٔ آن
9 دوران سطح حول یک محور و ساختن حجم
10 مقایسهٔ حجم هایی که با یک سطح مشخص درست شده اند.
1 انواع حجم های هندسی:
جسمی که دارای سه بعد، طول، عرض و ارتفاع باشد. در زیر برخی از حجمهای هندسی معروف را معرفی میکنیم:
الف مکعب:
جسمی با شش وجه مربع که طول، عرض و ارتفاع آن برابر است:
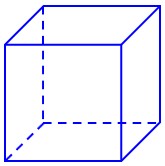
ب مکعب مستطیل:
جسمی با شش وجه مستطیلی که طول، عرض و ارتفاع آن متفاوت است:
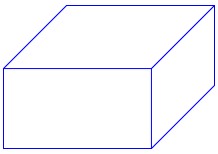
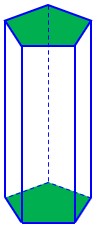
پ منشور:
جسمی با دو قاعده موازی و مسطح و وجوه جانبی مسطح می باشد؛ به عنوان مثال، شکل زیر یک منشور پنج پهلو را نشان می دهد:
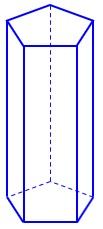
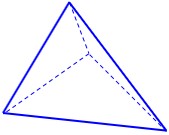
ت هِرَم:
جسمی با یک قاعده مسطح و وجوه جانبی که در یک نقطه به هم می رسند؛ به عنوان مثال، در شکل زیریک هرم چهار وجهی را می بینیم:
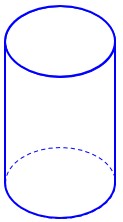
ث استوانه:
جسمی با دو قاعده دایرهای و سطح جانبی منحنی:
2 حجم مخروطی و حجم منشوری:
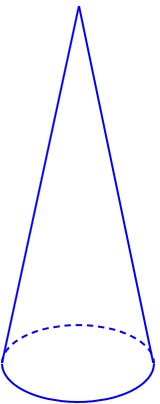
الف حجم مخروطی:
حجم مخروطی به حجم یک جسم سهبعدی با یک قاعده دایرهای و یک رأس در بالای آن اشاره دارد:
ب حجم منشوری:
حجمی با دو قاعده موازی و مسطح و وجوه جانبی مسطح می باشد؛ به عنوان مثال، شکل زیر یک منشور پنج پهلو را نشان می دهد:

3 قاعده، وجه، یال و رأس حجم های منشوری:
حجم منشوری زیر را در نظر بگیرید:

الف قاعده:
قاعده به سطح یا سطوح مسطحی گفته میشود که منشور بر آنها قرار گرفته و بهطور معمول دارای شکل خاصی مثل مثلث، مربع، مستطیل یا چندضلعیهای دیگر است. منشور دارای دو قاعده موازی و هم اندازه است:
ب وجه:
وجه به هر یک از سطوح مسطح منشور گفته میشود. یک منشور دارای چند وجه مسطح است که شامل دو قاعده و سایر سطوح جانبی میشود.
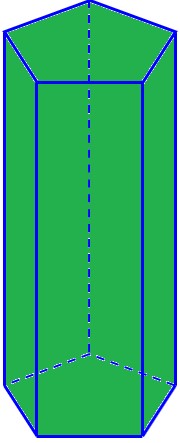
پ یال:
یال به لبههای منشور گفته میشود که دو وجه را به هم متصل میکنند. یالها خطوط مستقیمی هستند که در طول لبههای منشور قرار دارند.
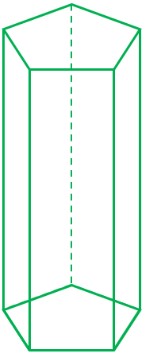
ت رأس:
رأس به نقاطی گفته میشود که در آنها چند یال به هم میرسند. رأسها نقاط گوشهای منشور هستند. در منشور، همواره تعداد رأس ها، دو برابر تعداد اضلاع شکل قاعده می باشد؛ مثلاً در منشور پنج پهلو که قاعدۀ آن یک پنج ضلعی می باشد، تعداد رأس ها برابر با 10 می باشد:
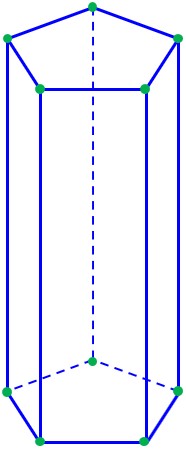
4 مقطع زدن یک حجم منشوری:
مقطع زدن یک حجم منشوری به معنی بریدن آن به طوری که سطح مقطع ایجاد شود. سطح مقطع به شکل جدیدی اشاره دارد که از تقاطع برش و حجم منشوری حاصل میشود. مقطع زدن یک حجم منشوری به سه روش انجام می شود:
الف برش عمودی:
برش از بالا به پایین و آن هم به صورت عمودی هست که حاصل آن شبیه به یک مستطیل می شود:
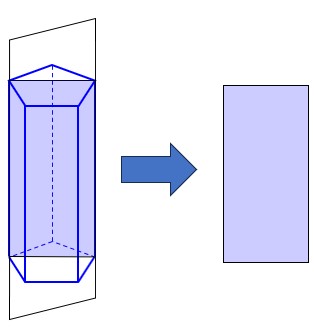
ب برش افقی:
برش از طرفین در یک راستای افقی صورت می گیرد که حاصل آن متشابه با شکل قاعده منشور خواهد بود.
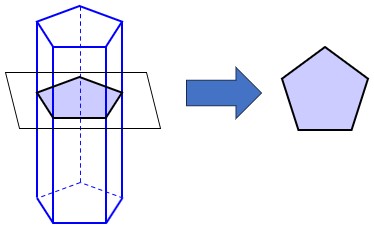
پ برش مورّب:
برش مورب در زاویهای انجام میشود که سطح مقطع جدید و متفاوتی ایجاد میکند.
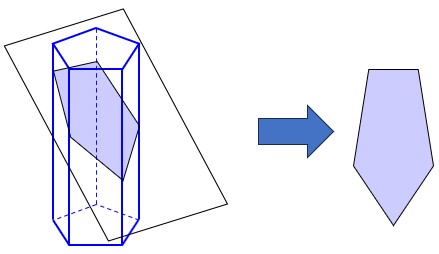
5 رابطهٔ پیدا کردن حجم های منشوری:
اگر مساحت یکی از قاعده های منشور با S و ارتفاع آن را با h نمایش دهیم، در این صورت کافی است که مساحت قاعده را پیدا کنیم و در ارتفاع آن ضرب کنیم:
\( = S \times h\) حجم منشور
6 رابطهٔ پیدا کردن مساحت جانبی حجم های هندسی:
اگر محیط یکی از قاعده های منشور با P و ارتفاع آن را با h نمایش دهیم، در این صورت کافی است که محیط قاعده را پیدا کنیم و در ارتفاع آن ضرب کنیم:
\( = P \times h\) مساحت جانبی منشور
7 رابطهٔ پیدا کردن مساحت کل حجم های منشوری:
اگر مساحت جانبی را با نماد \({S_J}\) و مساحت قاعده را با نماد \({S_{Gh}}\) نمایش دهیم، رابطه مساحت کل منشور به صورت زیر می شود:
مساحت کل منشور برابر است با مجموع مساحت دو تا قاعدۀ منشور و مساحت جانبی آن:
\( = 2 \times {S_{Gh}} + {S_J}\) مساحت کل
8 ساختن یک حجم به کمک گستردهٔ آن:
ساختن یک حجم (شکل سهبعدی) به کمک گستردهی آن، فرآیندی است که در آن یک شکل دوبعدی (گسترده) با تا کردن و اتصال لبهها به یک شکل سهبعدی تبدیل میشود. گستردهی یک حجم، نمایش دوبعدی تمام وجوه آن حجم است که به گونهای چیده شدهاند که با تا کردن و چسباندن لبهها، شکل سهبعدی اصلی بازسازی میشود؛ به عنوان مثال یکی از گسترده های شکل مکعب را در زیر آورده ایم که بعد از تا زدن، به صورت مکعب در می آید:
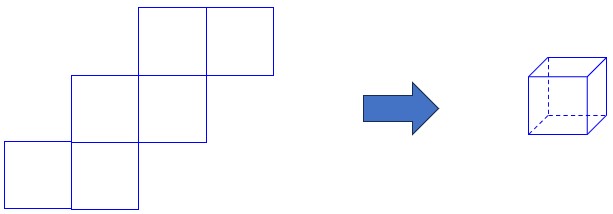
9 دوران سطح حول یک محور و ساختن حجم:
دوران یک سطح حول یک محور یک روش هندسی است که به کمک آن میتوان یک حجم سهبعدی ایجاد کرد. با این روش می توان با دوران یک شکل دو بعدی حول یک محور معین یک شکل هندسی ساخت. به عنوان مثال با چرخاندن یک مستطیل حول یکی از ضلع هایش، استوانه ایجاد می شود:
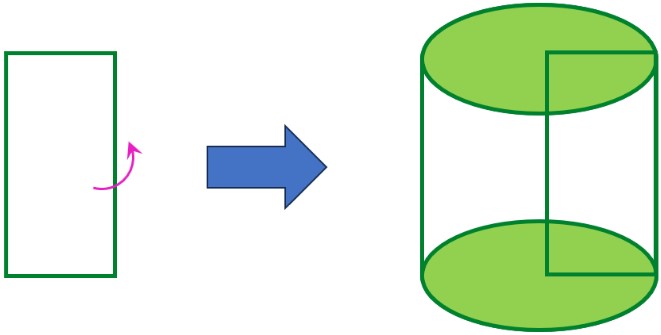
یا از چرخاندن یک مثلث قائم الزاویه حول یکی از ضلع های قائمه اش، مخروط بوجود می آید:
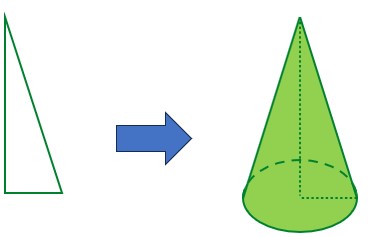
10 مقایسهٔ حجم هایی که با یک سطح مشخص درست شده اند:
منظور هنگامی که حجم های هندسیی هستند که از دوران یک سطح مشخص مثلاً مستطیل حول یکی از اضلاعش است. به این علت که اضلاع قائمه در مستطیل با یکدیگر برابر نیستند، به همین دلیل حجم هایی که درست می شوند دارای حجم متفاوت هستند. برای مقایسه حجم آن ها، حجم شان را محاسبه می کنیم. مثلا مستطیل شکل زیر را در نظر بگیرید که با دوران حول اضلاع متفاوتش، استوانه های زیر را ایجاد کرده است:
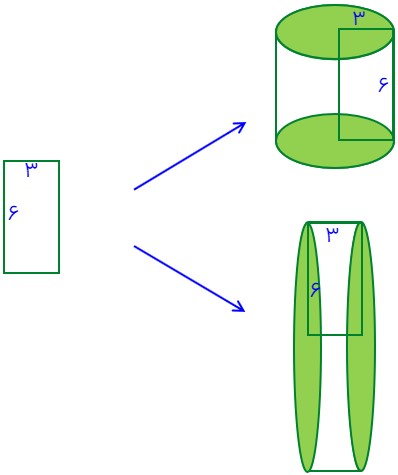
ابتدا میزان حجم استوانه بالایی را بدست می آوریم (با در برابر گرفتن عدد پی با 3):
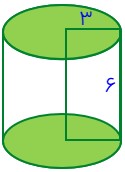
\(\begin{array}{l}h = 6\\\\r = 3\\\\S = \pi \times 3 \times 3 = 3 \times 3 \times 3 = 27\\\\V = S \times h = 27 \times 6 = 192\end{array}\)
حال میزان حجم استوانه پایینی را بدست می آوریم:
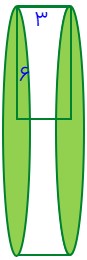
\(\begin{array}{l}h = 3\\\\r = 6\\\\S = \pi \times 6 \times 6 = 3 \times 6 \times 6 = 108\\\\V = S \times h = 108 \times 3 = 324\end{array}\)
با بررسی حجم دو استوانه متوجه می شویم که استوانه پایینی دارای حجم بیشتری می باشد.
تمرین های ترکیبی
1 حجم، مساحت جانبی و مساحت کل شکل های زیر را به دست آورید.
استوانه به شعاع قاعدهٔ 2 و ارتفاع 2
منشور چهارپهلو با قاعدهٔ مربع به ضلع 2 و ارتفاع 20
استوانه به شعاع قاعدهٔ 2 و ارتفاع 2
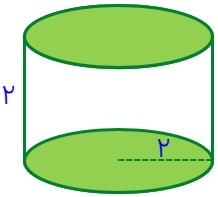
\(\begin{array}{l}h = 2\\\\r = 2\\\\P = 2 \times \pi \times r = 2 \times \pi \times 2 = 4\pi \end{array}\)
\( = {S_J} = P \times h = 4\pi \times 2 = \) مساحت جانبی
\(8\pi = 8 \times 3/14 = 25/12\)
\( = {S_{Gh}} = \pi \times r \times r = \) مساحت قاعده
\(3/14 \times 2 \times 2 = 12/56\)
\( = 2 \times {S_{Gh}} + {S_J} = \) مساحت کل
\(2 \times 12/56 + 25/12 = 50/24\)
\( = {S_{Gh}} \times h = 12/56 \times 2 = 25/12\) حجم
منشور چهارپهلو با قاعدهٔ مربع به ضلع 2 و ارتفاع 20
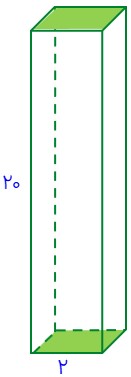
\(\begin{array}{l}h = 20\\\\a = 2\\\\P = 4 \times a = 4 \times 2 = 8\end{array}\)
\( = {S_J} = P \times h = \) مساحت جانبی
\(8 \times 20 = 160\)
\( = {S_{Gh}} = a \times a = 2 \times 2 = 4\) مساحت قاعده
\( = 2 \times {S_{Gh}} + {S_J} = \) مساحت کل
\(2 \times 4 + 160 = 168\)
\( = {S_{Gh}} \times h = 4 \times 20 = 80\) حجم
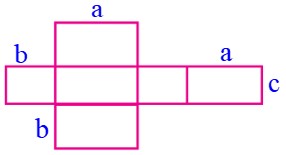
2 الف با توجه به شکل مکعب مستطیل، اندازهٔ ضلع های خواسته شده روی گستردهٔ آن را مشخص کنید.
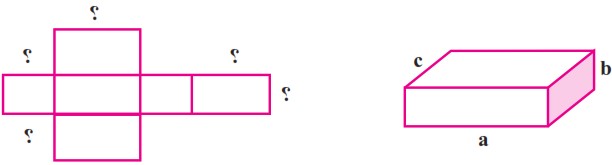
ب حجم شکل مقابل را به دست آورید.
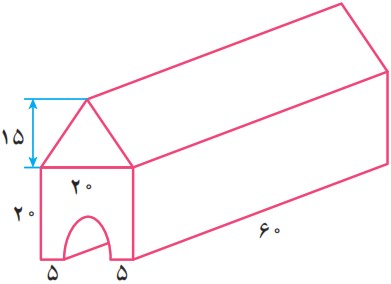
الف
ب
\( = {S_{triangle}} = \frac{{20 \times 15}}{2} = 150\) مساحت مثلث
\( = {S_{square}} = 20 \times 20 = 400\) مساحت مربع
\( = r = \frac{{20 - (5 + 5)}}{2} = 5\) شعاع نیم دایره
\( = {S_{semicircular}} = \frac{1}{2} \times 5 \times 5 \times \pi = \) مساحت نیم دایره
\(12/5 \times 3/14 = 39/25\)
\( = {S_{triangle}} + {S_{square}} - {S_{semicircular}} = \) مساحت قاعده
\( = 150 + 400 - 39/25 = 510/75\)
\( = 510/75 \times 60 = 30,645\) حجم شکل
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















