جواب تمرین صفحه 78 درس 6 ریاضی هفتم (سطح و حجم)
تعداد بازدید : 80.83Mپاسخ تمرین صفحه 78 ریاضی هفتم
-گام به گام تمرین صفحه 78 درس سطح و حجم
-تمرین صفحه 78 درس 6
-شما در حال مشاهده جواب تمرین صفحه 78 ریاضی هفتم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
1 در شکل زیر گستردۀ چند منشور نشان داده شده است. آنها را روی کاغذ بکشید و منشورها را درست کنید و به کلاس بیاورید.
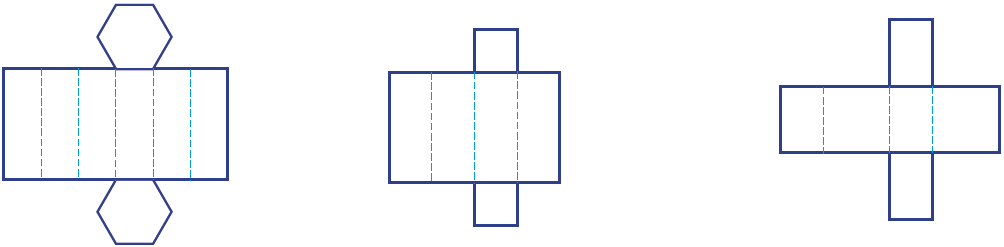
در چه صورت گستردهٔ شکل وسط به یک مکعب تبدیل می شود؟
گستردۀ شکل وسط هنگامی به صورت یک مکعب در می آید که عرض مستطیل ها با طول یکی از اضلاع مربع هم اندازه باشند.
2 یک غلتک باید ٤ بار روی زمین آسفالت شده غلت بزند تا سطح آن صاف شود. اگر شعاع غلتک 50 سانتی متر و ارتفاع استوانهٔ آن 1 متر باشد، برای آسفالت کردن سطح یک کوچه به طول ٢٠ و عرض ٤ متر، این غلتک باید به طور تقریبی چند دور بچرخد؟

ابتدا مساحت کوچه را به دست می آوریم:
\( = 20 \times 4 = \) مساحت کوچه
متر مربع 80
سپس مساحت جانبی استوانۀ غلتک را به دست می آوریم:
\( = 2\pi rh\) مساحت جانبی استوانۀ غلتک
متر مربع \( = 2 \times \pi \times 0/5 \times 1 = \pi \)
چون غلتک باید 4 بار مساحت کوچه را طی کند؛ بنابراین خواهیم داشت:
\( = 4 \times 80 = \) مساحت 4 بار طی شدن کوچه
متر مربع 320
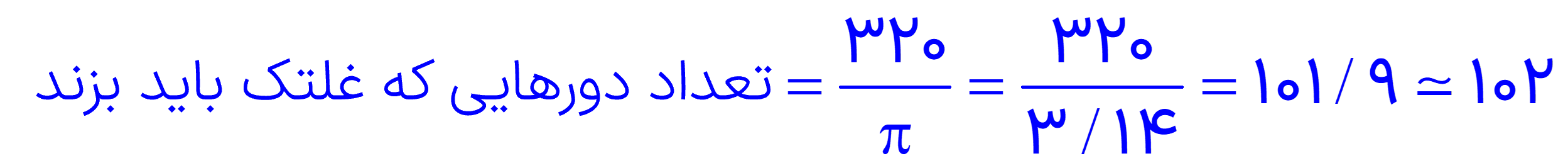
بنابراین این غلتک تقریبا 102 دور باید بزند.
3 یک چرخ ماشین که کاملاً خیس شده است، پس از 10 دور چرخیدن روی زمین جای خود را مشخص می کند و نهایتاً خشک می شود. اگر ضخامت این چرخ 20 سانتی متر و قطر آن 70 سانتی متر باشد، چه مساحتی از زمین را خیس خواهد کرد؟
ابتدا مساحت جانبی چرخ را بدست می آوریم:
ضخامت در اینجا ارتفاع استوانۀ چرخ است:
\(h = 20\,cm\)
\( = 70\,cm\) قطر چرخ
\( = r = 35\,cm\) شعاع چرخ
\(S = 2\pi rh = 2\pi \times 35 \times 20 = \)
\(1400\pi \) سانتی متر مربع
چون چرخ 10 دور می چرخد تا خشک شود، بنابراین خواهیم داشت:
\(\begin{array}{l}10 \times S = 10 \times 1400\pi = \\\\10 \times 1400 \times 3/14 = 43960\end{array}\)
در نتیجه 43960 سانتی متر مربع از زمین خیس خواهد شد تا چرخ خشک شود.
4 یک چادر مسافرتی به شکل مقابل داریم.چند متر پارچه برای ساخت آن به کار رفته است؟
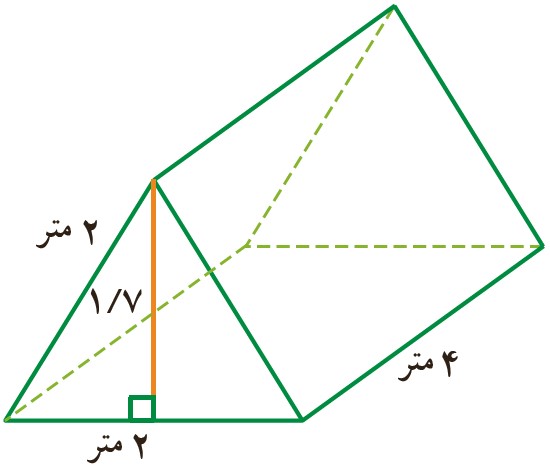
حجم این چادر چقدر است؟
این چادر در واقع به شکل یک منشور 3 پهلو با قاعده ای به شکل یک مثلث متساوی الاضلاع به ضلع 2 متر است و ارتفاع این منشور نیز 4 متر است.
ما ابتدا محیط و مساحت قاعدۀ این منشور را بدست می آوریم، چون قاعدۀ منشور به شکل مثلث است؛ پس:
\( = 3 \times 2 = \) محیط قاعدۀ منشور
متر 6
\( = S = \frac{{1/7 \times 2}}{2} = \) مساحت قاعدۀ منشور
متر مربع 1/7
حالا مساحت سطح جانبی منشور را بدست می آوریم:
\(\left\{ \begin{array}{l}h = 4\\\\P = 6\end{array} \right. \Rightarrow S = P \times h = 6 \times 4 = 24\)متر مربع
در نهایت چون این منشور 2 قاعده دارد، بنابراین مساحت قاعدۀ منشور 2 برابر شده و با مساحت سطح جانبی منشور جمع می شود تا مساحت کل منشور بدست بیاید:
\( = 1/7 \times 2 = \) مساحت 2 قاعدۀ منشور
متر مربع 3/4
\( = 24 + 3/4 = \) مساحت کل منشور
متر مربع 27/4
در نتیجه 27/4 متر مربع پارچه برای ساخت این چادر به کار رفته است.
برای پیدا کردن حجم چادر باید مساحت قاعده را در ارتفاع ضرب کنیم؛ پس خواهیم داشت:
\( = S = 1/7\) مساحت قاعده
\(h = 4\)
\( = V = S \times h = \) حجم منشور
متر مکعب \(1/7 \times 4 = 6/8\)
5 شعاع قاعدهٔ یک مخزن نفت به شکل استوانه ای 3 متر و ارتفاعش 5 متر است. می خواهیم بدنهٔ خارجی و سقف آن را رنگ بزنیم. اگر هزینهٔ رنگ کردن هر متر مربع 3000 تومان باشد، برای رنگ کردن این مخزن چقدر باید هزینه کرد؟
چون باید بدنۀ خارجی و سقف آن را رنگ بزنیم، پس باید ابتدا محیط قاعده و مساحت قاعده مخزن را بدست بیاوریم:
\( = P = 2\pi r = \) محیط قاعدۀ مخزن
\(2 \times \pi \times 3 = 6\pi \) متر
\( = {S_1} = r \times r \times \pi = \) مساحت قاعدۀ مخزن
\(3 \times 3 \times \pi = 9\pi \) متر مربع
حالا مساحت جانبی مخزن را به دست می آوریم:
\(h = 5\)
\( = {S_2} = P \times h = \) مساحت جانبی
متر مربع \(6\pi \times 5 = 30\pi \)
مساحتی که باید رنگ شود از جمع دو مساحت بدست می آید:
\(S = {S_2} + {S_2} = \)
\(9\pi + 30\pi = 39\pi \) متر مربع
در انتها هزینۀ رنگ آمیزی را از رابطۀ زیر بدست می آوریم:
\( = 39\pi \times 3000 = \) هزینۀ رنگ آمیزی
\(39 \times 3/14 \times 3000 = 367,300\) تومان
6 می خواهیم با مقوا مکعبی به ضلع 10 سانتی متر بسازیم. چند سانتی متر مربع مقوا به کار می رود؟
باید مساحت کل مکعب را بدست بیاوریم. برای این کار مساحت قاعده را بدست آورده و آن را دو برابر می کنیم و سپس مساحت جانبی مکعب را بدست آورده و در نهایت همۀ آن ها را با هم جمع می کنیم:
\( = 10 \times 10 = \) مساحت قاعده
سانتی متر مربع 100
چون دو تا قاعده داریم، مقدار بدست آمده را دو برابر می کنیم:
\(100 \times 2 = 200\)سانتی متر مربع
حال مساحت جانبی را بدست می آوریم:
\( = 4 \times (10 \times 10) = \) مساحت سطح جانبی
سانتی متر مربع \(4 \times 100 = 400\)
حال مساحت کل را بدست می آوریم:
\( = 400 + 200 = \) مساحت کل مکعب
سانتی متر مربع 600
بنابراین برای ساخت این مکعب، 600 سانتی متر مربع مقوا باید به کار ببریم.
7 یک جعبه به شکل مکعب مستطیل به ابعاد 30 و 50 و 40 سانتی متر را با کاغذ کادو پوشانده ایم. برای پوشاندن این جعبه حداقل چند سانتی مترمربع کاغذ کادو مصرف شده؟ چرا در این مسئله حداقل کاغذ لازم خواسته شده است؟
باید مساحت کل مکعب را بدست آوریم:
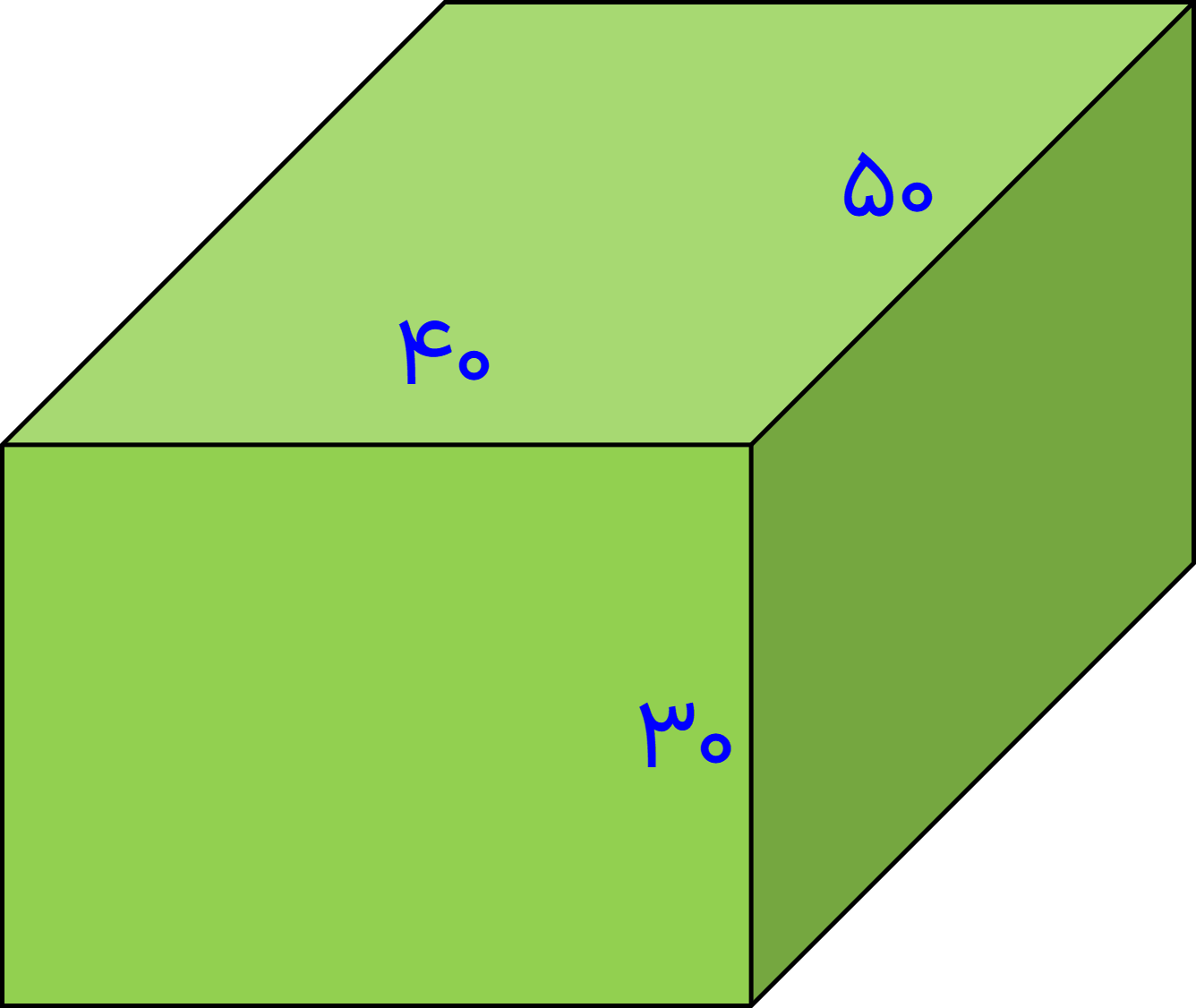
\( = {S_1} = 50 \times 40 = \) مساحت قاعده
سانتی متر مربع 2000
\( = P = 2 \times (50 + 40) = \) محیط قاعده
سانتی متر 180
سانتی متر \( = h = 30\) ارتفاع
\( = {S_2} = P \times h = \) مساحت وجه جانبی
\(180 \times 30 = 5400\) سانتی متر مربع
مساحت وجه جانبی + مساحت قاعده × 2 = مساحت کل شکل
\( = 5400 + 4000 = \) مساحت کل شکل
سانتی متر مربع 9400
چون مقدار کاغذ کادوی لازم نباید کمتر از مساحت کل مکعب باشد، به همین دلیل از کلمۀ حداقل استفاده شده است.
8 الف با مکعب های به ضلع 1 واحد حجم مقابل را ساخته ایم. اگر تمام سطح های این حجم را رنگ کنیم، چند مکعب رنگ نمی شود؟
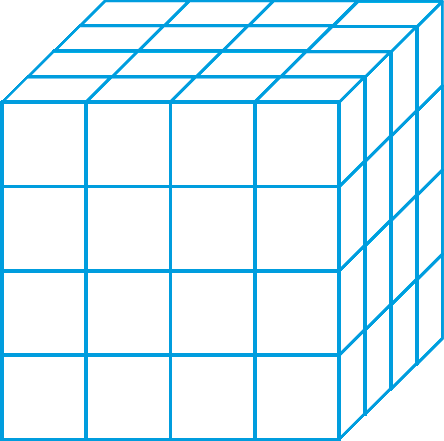
ب چند مکعب رنگ می شود؟
پ چند مکعب 2 وجهشان رنگ می شود؟
ت چند مکعب 3 وجهشان رنگ می شود؟
الف 8 مکعبی که در مرکز قرار دارند، رنگ نمی شوند:

= تعداد مکعب های این شکل
\(4 \times 4 \times 4 = 64\) مکعب
رنگ آبی مربوط به مکعب هایی هستند که یک وجه آن ها رنگ می شود که برابر 24 مکعب می باشد.
رنگ سبز مربوط به مکعب هایی هستند که دو وجه آن ها رنگ می شود که برابر 8 مکعب می باشد.
رنگ نارنجی مربوط به مکعب هایی هستند که سه وجه آن ها رنگ می شود که برابر 8 مکعب می باشد.
= تعداد مکعب های رنگ شده
مکعب 56 = 8 + 24 + 24
= تعداد مکعب های رنگ نشده
مکعب 8 = 56 – 64
ب 56 مکعب رنگ می شود.
پ 24 مکعب
ت 8 مکعب
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















