گام به گام تمرین صفحه 75 درس 6 ریاضی هفتم (سطح و حجم)

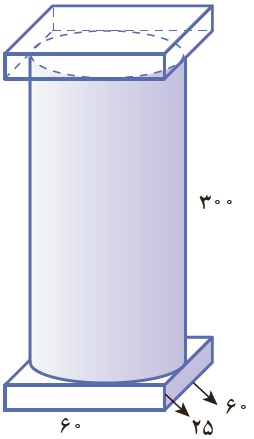
\(\begin{array}{l}\left\{ \begin{array}{l}S = 60 \times 60 = 3600\\\\h = 25 + 300 + 25 = 350\end{array} \right.\\\\ \Rightarrow V = 3600 \times 350 = 1,260,000\end{array}\)

\( = \frac{{60}}{2} = 30\) شعاع استوانه

\(V = 60 \times 60 \times 25 = 90,000\) مکعب پایین

\(V = (30 \times 30 \times 3/14) \times 300 = 847,800\) استوانه

\(V = 60 \times 60 \times 25 = 90,000\) مکعب بالا

\( = 90,000 + 847,800 + 90,000 = 1,027,800\) حجم شکل

\( = 1,260,000 - 1,027,800 = 232,200\) تفاوت

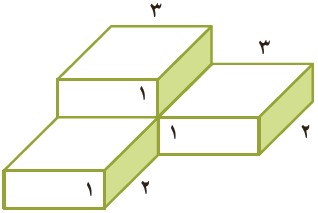
در این شکل 4 تا مکعب یکسان داریم. پس با بدست آوردن حجم یکی از مکعب ها می توان حجم کل شکل را بدست آورد:

\( = 3 \times 2 \times 1 = 6\) حجم یک مکعب

\( = 4 \times 6 = 24\) حجم شکل

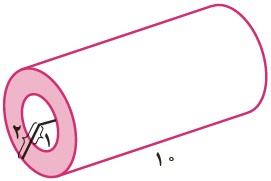
برای بدست آوردن حجم این شکل، بایستی مساحت قاعده را در ارتفاع ضرب کنیم. برای بدست آوردن مساحت قاعده نیز بایستی مساحت دایره بیرونی را منهای مساحت دایره داخلی کنیم:

\( = 2 \times 2 \times 3/14 = 12/56\) مساحت دایره بیرونی

\( = 1 \times 1 \times 3/14 = 3/14\) مساحت دایره داخلی

\( = 12/56 - 3/14 = 9/42\) مساحت قاعده

\( = 9/42 \times 10 = 94/2\) حجم شکل

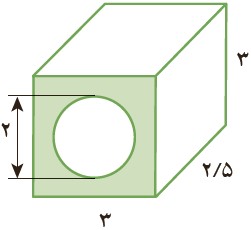
برای بدست آوردن حجم این شکل، بایستی مساحت قاعده را بدست آوریم و سپس در عدد 2/5 ضرب کنیم. برای بدست آوردن مساحت قاعده نیز بایستی مساحت مربع را منهای مساحت دایره کنیم (قطر دایره برابر 2 است؛ بنابراین شعاع آن برابر 1 می باشد):

\( = 3 \times 3 = 9\) مساحت مربع

\( = 1 \times 1 \times 3/14 = 3/14\) مساحت دایره

\( = 9 - 3/14 = 5/86\) مساحت قاعده

\( = 5/86 \times 2/5 = 14/65\) حجم شکل

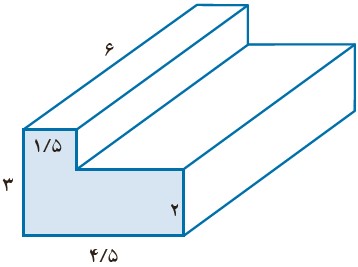
برای محاسبه حجم شکل، بایستی مساحت قاعده را در عدد 6 ضرب کنیم. برای بدست آوردن مساحت قااعده نیز بایستی مساحت دو مستطیل را محاسبه نماییم و آن ها را با هم جمع کنیم:

\( = 4/5 \times 2 = 9\) مساحت مستطیل بزرگ

\( = 1/5 \times (3 - 2) = 1/5 \times 1 = 1/5\) مساحت مستطیل کوچک

\( = 9 + 1/5 = 10/5\) مساحت قاعده

\( = 10/5 \times 6 = 63\) حجم شکل

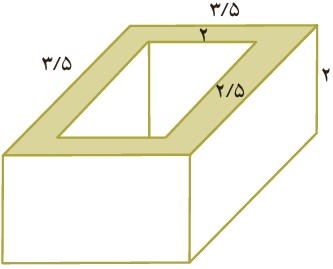
برای بدست آوردن حجم شکل بایستی مساحت قاعده را در ارتفاع ضرب کنیم. برای بدست آوردن مساحت قاعده نیز بایستی مساحت مستطیل بزرگ را منهای مساحت مستطیل کوچک کنیم:

\( = 3/5 \times 3/5 = 12/25\) مساحت مستطیل بزرگ

\( = 2/5 \times 2 = 5\) مساحت مستطیل کوچک

\( = 12/25 - 5 = 7/25\) مساحت قاعده

\( = 7/25 \times 2 = 14/5\) حجم شکل

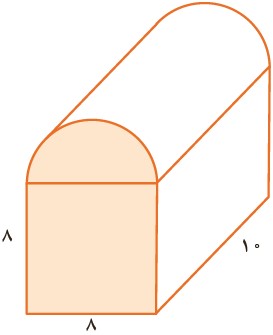
برای بدست آوردن حجم شکل بایستی مساحت قاعده را در عدد 10 ضرب کنیم. برای بدست آوردن مساحت قاعده نیز بایستی مساحت مربع را با مساحت نیم دایره به قطر 8 جمع کنیم (چون قطر نیم دایره برابر 8 است، بنابراین شعاع نیم دایره برابر 4 می شود):

\( = 8 \times 8 = 64\) مساحت مربع

\( = \frac{1}{2}(4 \times 4 \times 3/14) = 25/12\) مساحت نیم دایره

\( = 64 + 25/12 = 89/12\) مساحت قاعده

\( = 89/12 \times 10 = 891/2\) حجم شکل

ابتدا حجم چاه را محاسبه می کنیم:

\(\begin{array}{l}\left\{ \begin{array}{l}S = 0/4 \times 0/4\pi = 0/16\pi \\\\h = 12\end{array} \right.\\\\ \Rightarrow V = 0/16\pi \times 12 = 1/92\pi \end{array}\)

حالا حجم خاکی که از این چاه بدست آوردیم را بعد از افزایش محاسبه می کنیم (حتماً برای ساده تر شدن محاسبات از تقریب استفاده می کنیم):

\( = 1/3 \times 1/92\pi \simeq 2/5\pi \) حجم خاک

مکعب مستطیلی به قاعده ی 4×5=20 و ارتفاع H را در نظر می گیریم و این مقدار خاک را در این مکعب مستطیل می ریزیم:

حجم خاک = حجم مکعب مستطیل

\( = 20 \times H\) حجم مکعب مستطیل

\(\begin{array}{l}20 \times H = 2/5\pi \Rightarrow \\\\H = \frac{{2/5\pi }}{{20}}\\\\H = \frac{{2/5 \times 3/14}}{{20}} \simeq 0/39\end{array}\)

ارتفاع مکعب مستطیل بر حسب متر بدست می آید؛ به این علت که تمام محاسبات حجم و مساحت را بر حسب متر بدست آوردیم. اگر بخواهیم ارتفاع را بر حسب سانتی متر بدست آوریم، کافی است که این مقدار را در عدد 100 ضرب کنیم:

\(H = 0/39 \times 100 = 39\)سانتی متر 

هر متر مکعب برابر 1000 لیتر است. ابتدا حجم حوض را حساب می کنیم:

\(V = 1/5 \times 3 \times 4 = 18\)متر مکعب 

\(V = 18 \times 1000 = 18,000\)لیتر 

حالا زمان پر شدن حوض را محاسبه می کنیم:

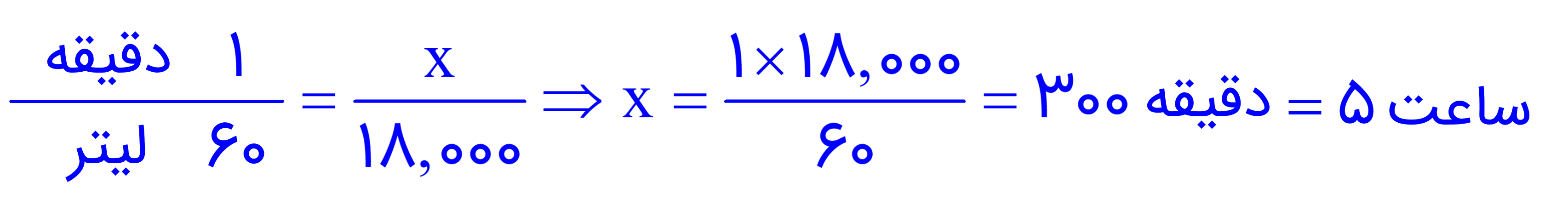
5 ساعت طول می کشد تا این حوض پر شود.

ابتدا حجم پارچ را محاسبه می کنیم:

\(V = (8 \times 8 \times \pi ) \times 30 = 1920\pi \)سانتی متر مکعب 

حالا حجم لیوان را محاسبه می کنیم:

\(V = (4 \times 4 \times \pi ) \times 10 = 160\pi \)سانتی متر مکعب 

حالا حجم پارچ را بر حجم یک لیوان تقسیم کرده تا تعداد لیوان ها به دست بیاید:

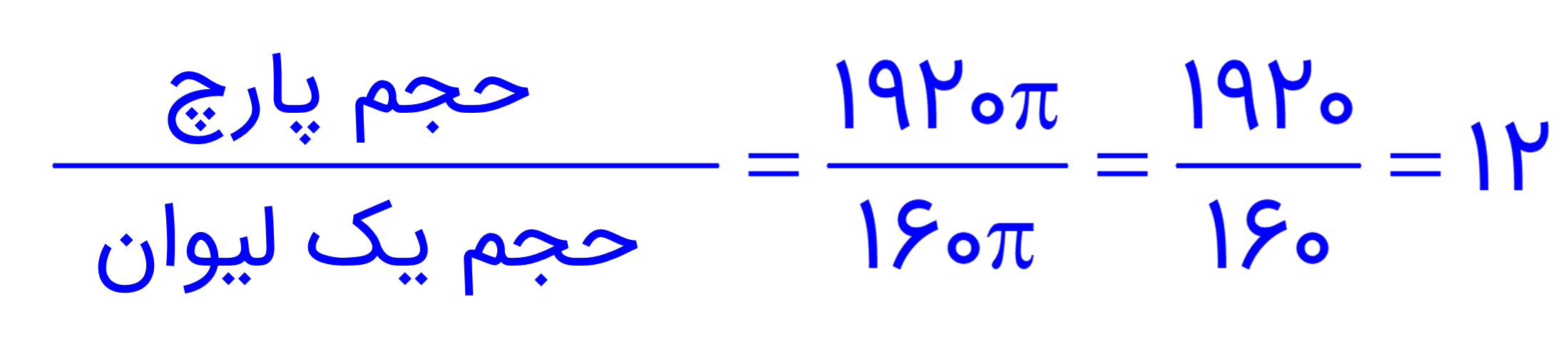
این پارچ می تواند 12 لیوان را پُر کند.