جواب تمرین صفحه 81 درس 6 ریاضی هفتم (سطح و حجم)
تعداد بازدید : 80.83Mپاسخ تمرین صفحه 81 ریاضی هفتم
-گام به گام تمرین صفحه 81 درس سطح و حجم
-تمرین صفحه 81 درس 6
-شما در حال مشاهده جواب تمرین صفحه 81 ریاضی هفتم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
1 یک مقوا به طول و عرض 5 × 20 را به شکل استوانه ای به ارتفاع 5 در آورده ایم. یک مقوای دیگر به ابعاد 10 × 10 را نیز به شکل استوانه درآورده ایم. با توجه به اینکه مساحت مقواها در دو حالت برابر است، کدام استوانه حجم بیشتری دارد؟
ابتدا شعاع استوانۀ اول را بدست می آوریم (در اینجا عدد پی را برابر 3 می گیریم):
\( = 20 \times 5 = 100\) مساحت مقوای اول
= مساحت جانبی استوانۀ اول
\(\begin{array}{l}100 = 2\pi {r_1}{h_1}\\\\{h_1} = 5 \Rightarrow 2\pi {r_1}{h_1} = 100 \Rightarrow 2\pi \times {r_1} \times 5 = 100\\\\ \Rightarrow 10\pi \times {r_1} = 100 \Rightarrow {r_1} = \frac{{100}}{{10\pi }} = \frac{{10}}{\pi } = \frac{{10}}{3}\end{array}\)
حال شعاع استوانۀ دوم را بدست می آوریم:
\( = 10 \times 10 = 100\) مساحت مقوای دوم
= مساحت جانبی استوانۀ دوم
\(\begin{array}{l}100 = 2\pi {r_2}{h_2}\\\\{h_2} = 10 \Rightarrow 2\pi {r_2}{h_2} = 100 \Rightarrow 2\pi \times {r_2} \times 10 = 100\\\\ \Rightarrow 20\pi \times {r_2} = 100 \Rightarrow {r_2} = \frac{{100}}{{20\pi }} = \frac{5}{\pi } = \frac{5}{3}\end{array}\)
اکنون حجم دو استوانه را بدست می آوریم:
حجم استوانۀ اوّل
\(\begin{array}{l}{h_1} = 5\\\\{r_1} = \frac{{10}}{3}\\\\{V_1} = \pi \times {r_1} \times {r_1} \times {h_1} = 3 \times \frac{{10}}{3} \times \frac{{10}}{3} \times 5 = \frac{{500}}{3} \simeq 166/67\end{array}\)
حجم استوانۀ دوم
\(\begin{array}{l}{h_2} = 10\\\\{r_2} = \frac{5}{3}\\\\{V_2} = \pi \times {r_2} \times {r_2} \times {h_2} = 3 \times \frac{5}{3} \times \frac{5}{3} \times 10 = \frac{{250}}{3} \simeq 83/33\end{array}\)
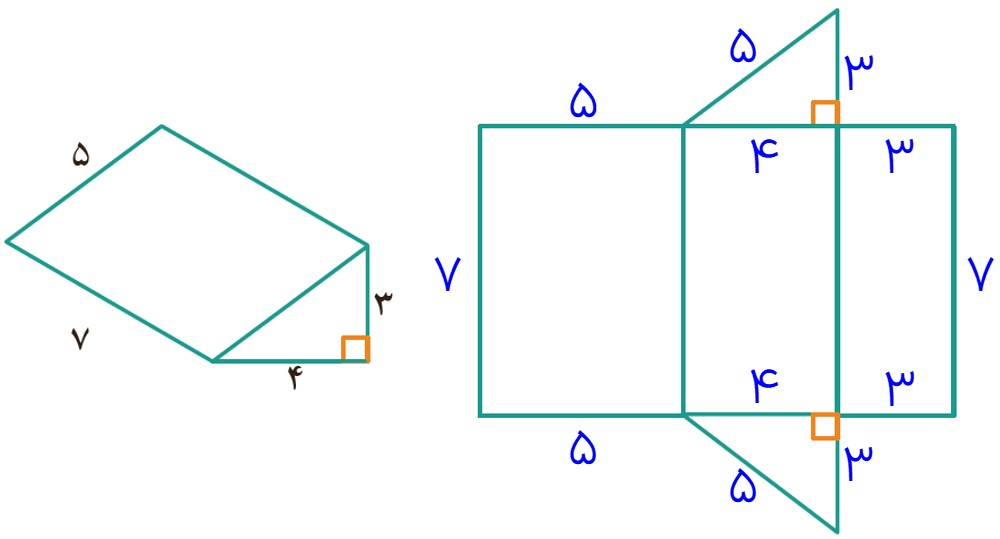
2 با شکل مقابل یک منشور درست کرده ایم. مساحت جانبی آن را پیدا کنید.
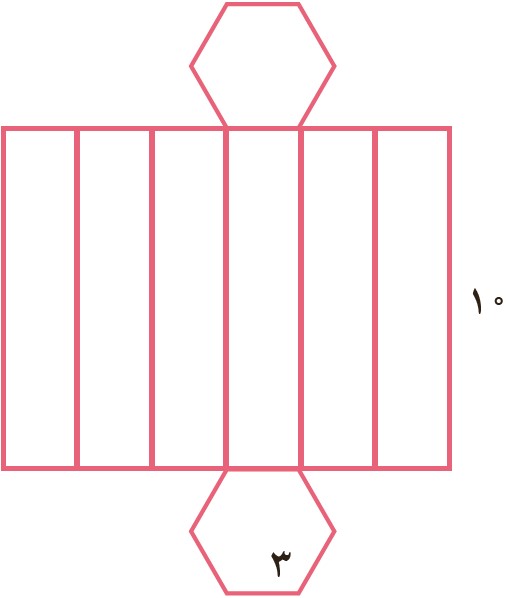
= مساحت مستطیل بزرگ = مساحت جانبی منشور
= عرض مستطیل بزرگ × طول مستطیل بزرگ
واحد مکعب \((6 \times 3) \times 10 = 18 \times 10 = 180\)
3 یک صابون مکعب مستطیل شکل به حجم 32 سانتی متر مکعب پس از چند بار مصرف، کوچک شده و ابعاد آن، به \(2\frac{1}{2}\) و 4 و \(1\frac{1}{2}\) سانتی متر کاهش یافته است. چند درصد این صابون استفاده شده است؟
ابتدا حجم صابون قبل از مصرف را بدست می آوریم:
\({V_1} = 32\)سانتی متر مکعب
حال حجم صابون پس از مصرف را بدست می آوریم:
\({V_2} = 2\frac{1}{2} \times 4 \times 1\frac{1}{2} = \frac{5}{2} \times 4 \times \frac{3}{2} = \)
\(\frac{{60}}{4} = 15\)سانتی متر مکعب
حالا حجم صابون مصرف شده را بدست می آوریم:
\(32 - 15 = 17\)سانتی متر مکعب
در نهایت درصد صابون مصرف شده را به دست می آوریم:
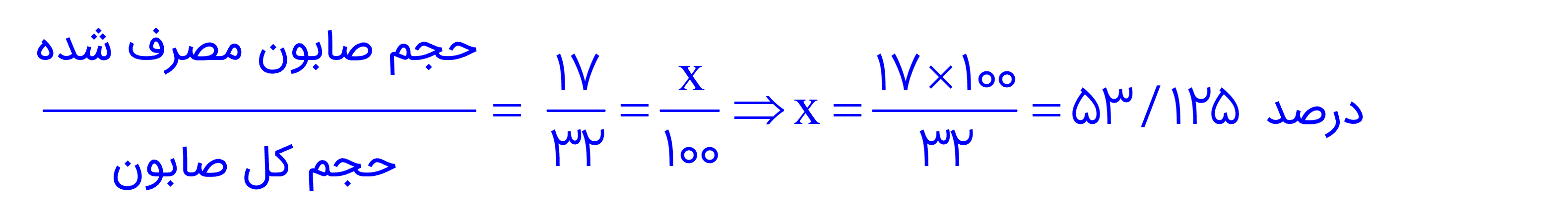
4 یک استوانه که با یک مقوا به طول 20 و عرض 10 سانتی متر ساخته شده به طور تقریبی چه حجمی دارد؟ (ارتفاع استوانه 20 است.)
ابتدا شعاع استوانه را بدست می آوریم (در اینجا عدد پی را برابر 3 می گیریم):
\( = 20 \times 10 = 200\) مساحت مقوا
\( = 2\pi rh\) مساحت جانبی استوانه
\(\begin{array}{l}h = 20 \Rightarrow 2\pi rh = 200 \Rightarrow 2\pi \times r \times 20 = 200\\\\ \Rightarrow 40\pi \times r = 200 \Rightarrow r = \frac{{200}}{{40\pi }} = \frac{5}{\pi } = \frac{5}{3}\end{array}\)
حالا حجم استوانه را محاسبه می کنیم:
\(V = \pi \times r \times r \times h = 3 \times \frac{5}{3} \times \frac{5}{3} \times 20 = \frac{{500}}{3} \simeq 166/67\)
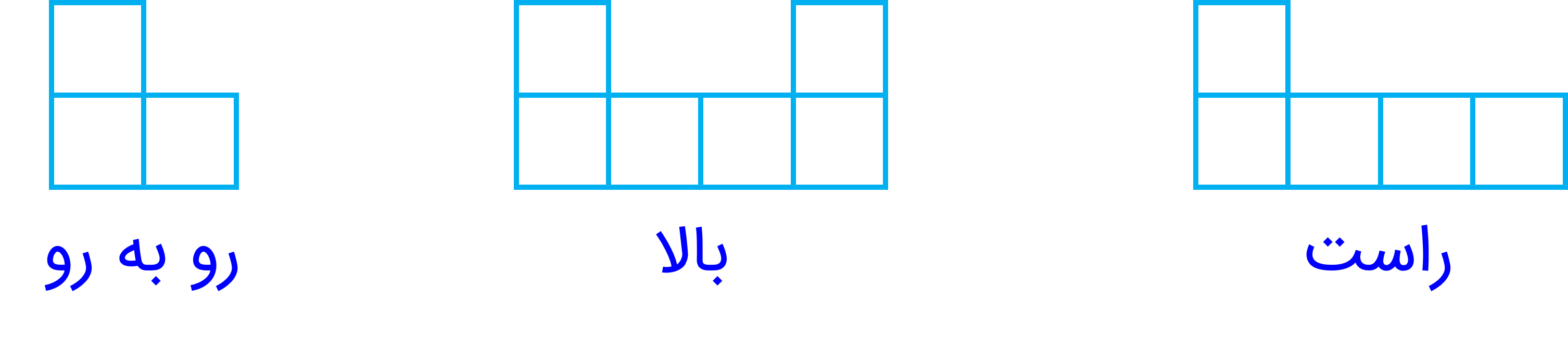
5 یک حجم از بالا و سمت راست و روبه رو به صورت زیر دیده می شود؛ آن را رسم کنید.


6 شکل مقابل، گستردهٔ یک منشور را نشان می دهد. مساحت جانبی منشور را پیدا کنید.
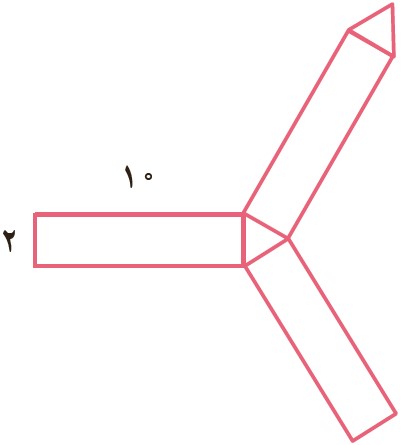
این منشور یک منشور سه پهلو به ارتفاع 10 و قاعده ای به شکل مثلث متساوی الاضلاع به ضلع 2 است.
\(\begin{array}{l}P = 3 \times 2 = 6\\\\h = 10\\\\S = P \times h = 6 \times 10 = 60\end{array}\)
7 با توجه به حجم منشور و ابعاد آن، اندازهٔ ضلع های گستردهٔ آن را بنویسید.
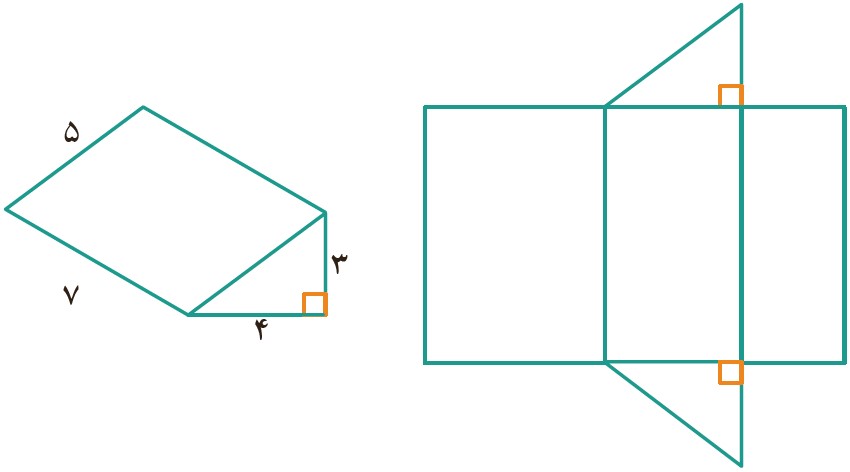
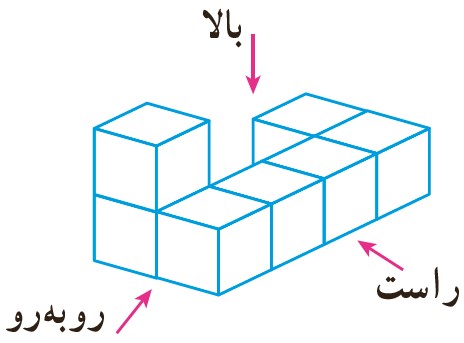
8 حجم مقابل از راست، بالا و روبه رو چگونه دیده می شود؟
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















