آیا تمام سوالات تمرین صفحه 35 ریاضی نهم، مطابق با آخرین تغییرات کتب درسی پاسخ داده شده است ؟

بله، تمام جواب ها به تمرین صفحه 35 ریاضی نهم مطابق با آخرین تغییرات کتب درسی 1402 - 1401 است.

آیا جواب ها به صورت آموزش محور و کامل بیان شده اند ؟

بله، جواب سوالات به صورت کاملا تشریحی و با هدف یادگیری و تسلط به مبحث بیان شده اند.

جواب تمرین صفحه 35 درس 3 ریاضی نهم (استدلال و اثبات در هندسه)

تعداد بازدید : 80.73M

پاسخ تمرین صفحه 35 ریاضی نهم

گام به گام تمرین صفحه 35 درس استدلال و اثبات در هندسه

تمرین صفحه 35 درس 3

شما در حال مشاهده جواب تمرین صفحه 35 ریاضی نهم هستید. ما در تیم مای درس، پاسخ‌نامه‌های کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کرده‌ایم. اگر به دنبال به‌روزترین پاسخ‌ها برای این صفحه هستید و می‌خواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخ‌های گام به گام، به گنجینه‌ای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مای‌درس را نصب نمایید.

📥 دانلود اپلیکیشن مای‌درس

برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینه‌ای از گام‌به‌گام‌ها و نمونه سوالات، اپلیکیشن را نصب کنید.

نصب رایگان اپلیکیشن

1 در شکل های زیر عمودمنصف های سه ضلع مثلث ها را رسم کنید:

آیا فقط با توجه به این شکل ها، می توان نتیجه گرفت که محل برخورد عمودمنصف های هر مثلث همیشه درون مثلث قرار دارد؟ چگونه می توانید درستی ادعای خود را نشان دهید؟

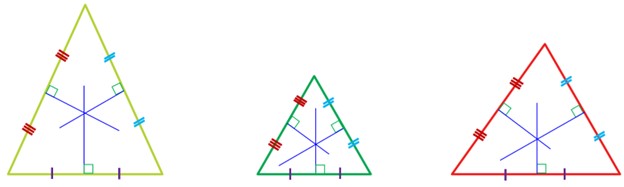
خیر؛ نمی توان نتیجه گرفت، زیرا:

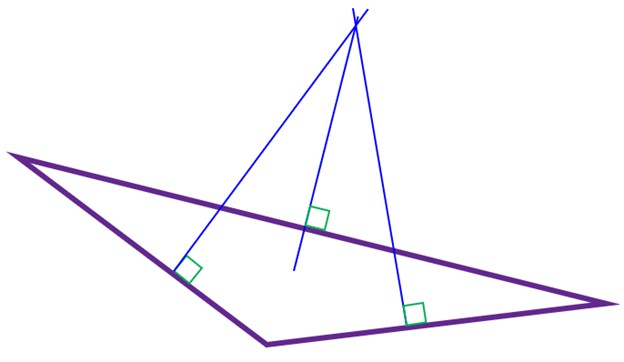
نتیجه

همانطور که مشاهده می کنیم عمود منصف ها ممکن است لیرون مثلث یکدیگر را قطع کنند.

نکته ی مهم

1 اگر هر سه زاویه ی یک مثلث حاده باشد عمود منصف ها درون مثلث یکدیگر را قطع می کنند.

2 اگر یکی از زاویه های مثلث 90 درجه باشد (مثلث قائم الزاویه) آنگاه عمود منصف ها روی وتر مثلث یکدیگر را قطع می کنند.

3 اگر یکی از زاویه های مثلث بیشتر از 90 درجه باشد آنگاه عمود منصف ها بیرون مثلث یکدیگر را قطع می کنند.

2 نیما و پژمان مشغول دیدن مسابقات وزنه برداری بودند. وزنه برداری می خواست وزنه ای 100 کیلویی را بلند کند. آنها هر دو عقیده داشتند که او نمی تواند وزنه را بلند کند؛ برای ادعای خود استدلال های متفاوتی می کردند.

نیما: زیرا هفتهٔ پیش این وزنه بردار تمرینات بهتری انجام داده بود، با این حال نتوانست وزنهٔ 90 کیلویی را بلند کند.

پژمان: امروز دوشنبه است. من بارها مسابقات این وزنه بردار را دیده ام. او هیچ گاه در روزهای زوج موفق نبوده است.

استدلال کدام یک قابل اعتمادتر است؟ دربارهٔ استدلال ها بحث کنید.

استدلال هیچ کدام کاملا دقیق نیست، ولی استدلال نیما منطقی تر است زیرا وقتی یک نفر با تمرینات بهتر، نتوانسته است وزنه ی 90 کیلویی را بلند کند، پس با احتمال زیادی وزنه ی 100 کیلویی را هم نمی تواند بالا ببرد. استدلال پژمان، دلیل منطقی ندارد.

3 چون من تا به حال هیچ وقت تصادف نکرده ام، در سفر آینده نیز تصادف نخواهم کرد. این استدلال مشابه کدام یک از استدلال های زیر است؟

الف چون برخی مثلث ها قائم الزاویه اند؛ پس مثلث های متساوی الاضلاع هم قائم الزاویه اند.

ب همهٔ فیلم های جنگی که تاکنون دیده ام، جذاب بوده اند. فیلمی که دیروز دیدم جذاب بود، پس فیلم جنگی بوده است.

ج چون تمام بچه های خاله های من دختر هستند، پس بچهٔ خالهٔ کوچکم هم که به زودی به دنیا می آید دختر خواهد بود.

د چون همهٔ قرص های مسکن خواب آور است، پس در این قرص ها ماده ای هست که باعث خواب آلودگی می شود.

پاسخ صحیح، گزینه (ج) است.

تحلیل و دلیل انتخاب:

۱ بررسی استدلال سوال اصلی: جمله «چون من تا به حال هیچ وقت تصادف نکرده‌ام، در سفر آینده نیز تصادف نخواهم کرد» چه منطقی دارد؟ این فرد دارد بر اساس تکرار یک اتفاق در گذشته (تصادف نکردن)، یک پیش‌بینی قطعی برای آینده می‌کند. در واقع می‌گوید: «چون قبلاً نشده، پس بعداً هم نمی‌شود.» این یک استدلال نادرست است چون گذشته تضمین‌کننده آینده نیست.

۲ چرا گزینه (ج) پاسخ درست است؟ در گزینه (ج) آمده: «چون تمام بچه‌های خاله‌های من دختر هستند، پس بچه خاله کوچکم هم که به زودی به دنیا می‌آید دختر خواهد بود.» این جمله دقیقاً همان الگوی غلط را دارد: مشاهده اتفاقات گذشته (تولد دخترها) و پیش‌بینی قطعی برای آینده (نوزاد بعدی). به همین دلیل، این شبیه‌ترین استدلال به سوال است.

۳ چرا بقیه گزینه‌ها نیستند؟

گزینه (الف): این یک نتیجه‌گیری هندسی اشتباه است (تعمیم دادن یک ویژگی خاص به همه)، اما ربطی به پیش‌بینی آینده بر اساس گذشته ندارد.

گزینه (ب): این نتیجه‌گیری درباره سلیقه است (چون فیلم‌های قبلی جذاب بودند، این هم جذاب است). اگرچه شبیه به نظر می‌رسد، اما گزینه (ج) به دلیل پیش‌بینی یک رخداد طبیعی (جنسیت نوزاد / تصادف) شباهت بیشتری دارد.

گزینه (د): این یک استدلال علمی و علت و معلولی است. فرد می‌گوید چون قرص اثر خواب‌آور دارد، پس حتماً ماده‌ای داخلش هست که باعث آن شده. این استدلال منطقی است و مثل سوال اصلی، یک پیش‌بینی بی‌دلیل نیست.

4 حمید و وحید می دانستند که علی، حسن، حسین و باقر برادرند و: علی از حسین بزرگ تر و حسن از باقر کوچک تر است و باقر از علی کوچک تر و حسن نیز از حسین کوچک تر است. هر دو نفر اعتقاد داشتند که علی از حسن بزرگ تر است؛ اما استدلال های متفاوتی می کردند.

حمید: در تمام خانواده هایی که دو فرزند به نام های علی و حسن داشته اند، علی فرزند بزرگ تر بوده است.

وحید: چون علی از حسین بزرگ تر و حسن از حسین کوچک تر است، پس علی از حسن بزرگ تر است.

استدلال کدام یک درست است؟ دربارهٔ درستی استدلال ها بحث کنید.

بیایید با هم استدلال حمید و وحید را زیر ذره‌بین ببریم تا ببینیم کدام‌ یک «منطق ریاضی» دارد.

۱ تحلیل استدلال حمید

استدلال حمید: «در تمام خانواده‌هایی که دو فرزند به نام‌های علی و حسن داشته‌اند، علی فرزند بزرگ‌تر بوده است.»

آیا درست است؟ خیر، استدلال حمید نادرست و غیرقابل اطمینان است.

چرا؟ حمید دارد بر اساس مشاهدات گذشته و تجربیات شخصی خودش نتیجه‌گیری می‌کند. اینکه در چند خانواده دیگر، پسری به نام علی بزرگ‌تر بوده، هیچ ربط منطقی به این خانواده خاص ندارد. نام افراد تعیین‌کننده سن آن‌ها نیست. این دقیقاً همان دامی است که در مثال‌های قبلی (مثل تیم فوتبال) هم وجود داشت.

۲ تحلیل استدلال وحید

استدلال وحید: «چون علی از حسین بزرگ ‌تر و حسن از حسین کوچک‌ تر است، پس علی از حسن بزرگ‌ تر است.»

آیا درست است؟ بله، استدلال وحید کاملاً درست و منطقی است.

چرا؟ وحید از اطلاعات داده شده در مسئله (فرض‌ها) استفاده کرده و با یک زنجیره منطقی به جواب رسیده است. بیایید حرف وحید را به زبان ریاضی بنویسیم تا زیبایی‌اش را ببینید:

1 می‌دانیم: علی > حسین (علی بزرگ‌تر از حسین است)

2 می‌دانیم: حسن < حسین (پس یعنی: حسین > حسن)

3 نتیجه‌گیری: وقتی علی از حسین بزرگ‌تر است و خود حسین هم از حسن بزرگ‌تر است، پس قطعاً علی > حسن.

نتیجه‌گیری نهایی

استدلال وحید درست است. در ریاضیات و هندسه، ما همیشه مثل وحید عمل می‌کنیم: استفاده از داده‌های معلوم برای رسیدن به مجهول از طریق یک مسیر منطقی. ما هرگز مثل حمید به حدس و گمان یا اسم‌ها تکیه نمی‌کنیم.

5 معلم از دانش آموزان خواست با استدلال ریاضی ثابت کنند که در مثلث متساوی الساقین زاویه های مجاور به قاعده با هم برابرند. احمد زاویه ها را با نقاله اندازه گیری کرد و نتیجه گرفت که زاویه ها مساوی هستند. چرا این روش برای اثبات کردن درست نیست؟ چرا اندازه گیری روش مناسبی برای نتیجه گیری نیست؟

احمد فقط یک مورد خاص را بررسی کرده است.

مشکل تعمیم: وقتی احمد یک مثلث خاص را روی کاغذ می‌کشد و اندازه می‌گیرد، فقط ثابت کرده که زاویه‌ها در همان یک مثلث خاص (تقریباً) برابرند. در ریاضیات، وقتی می‌خواهیم حکمی بدهیم (مثلاً بگوییم در همه مثلث‌های متساوی‌الساقین این قانون برقرار است)، نمی‌توانیم با بررسی یک یا چند نمونه محدود، آن را به میلیاردها مثلث دیگری که وجود دارند تعمیم دهیم.

اندازه‌گیری دو ایراد بزرگ دارد که اعتبار آن را برای «اثبات» از بین می‌برد:

خطای ابزار و دید:

چشم انسان و ابزارهایی مثل نقاله و خط‌کش، هرگز دقیقِ مطلق نیستند. ممکن است دو زاویه به اندازه 0/001 درجه با هم اختلاف داشته باشند و نقاله آن را نشان ندهد. اما در ریاضیات، برابری باید دقیق و مطلق باشد، نه تقریبی.

نبودِ دلیل منطقی:

اندازه‌گیری فقط به ما می‌گوید «چه هست»، اما نمی‌گوید «چرا این‌طور است». اثبات ریاضی باید بر اساس منطق و دلیل باشد تا نشان دهد چرا امکان ندارد که این دو زاویه نابرابر باشند.

خلاصه کلام:

همان‌طور که در صفحات قبل دیدیم (مثل خطای دید در دایره‌ها یا مثال محسن)، حواس ما و ابزارهای اندازه‌گیری می‌توانند خطا کنند و برای اطمینان کامل کافی نیستند. ریاضیات به دنبال دلیلی است که حتی بدون دیدن و اندازه‌گیری، درستی آن ۱۰۰٪ تضمین شده باشد.