جواب کار در کلاس صفحه 46 درس 3 ریاضی نهم (استدلال و اثبات در هندسه)
تعداد بازدید : 80.71Mپاسخ کار در کلاس صفحه 46 ریاضی نهم
-گام به گام کار در کلاس صفحه 46 درس استدلال و اثبات در هندسه
-کار در کلاس صفحه 46 درس 3
-شما در حال مشاهده جواب کار در کلاس صفحه 46 ریاضی نهم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
می خواهیم ثابت کنیم که در هر متوازی الاضلاع، مانند شکل روبه رو، ضلع های مقابل، همواره با هم برابرند.

الف مفروضات و داده های مسئله چیست؟ تمام آنها را بنویسید؛ حکم مسئله چیست؟ نظر دو دانش آموز را دربارهٔ این مسئله ببینید و به سؤال های مطرح شده پاسخ دهید.
شهرزاد: معلوم است که ضلع های روبه رو با هم مساوی است؛ با چشم هم می توان دید!
شبنم: می دانیم که در تعریف متوازی الاضلاع، برابری ضلع های روبه رو آورده شده است. علاوه بر آن با اندازه گیری هم می توانیم این موضوع را نشان دهیم.
ب آیا می توانیم در حل مسائل هندسه فقط به چشم هایمان اعتماد کنیم؟ چرا؟
پ به تعریف متوازی الاضلاع در کتاب سال گذشته مراجعه کنید. آیا برابری اضلاع مقابل در این تعریف وجود داشت؟ آیا اگر با اندازه گیری اضلاع مقابل، برابری آنها را ببینیم، درستی حکم را ثابت کرده ایم؟ چرا؟
ترانه: به نظر من باید دو مثلث هم نهشت بیابیم و با اثبات هم نهشتی آنها به برابری اضلاع مقابل در متوازی الاضلاع برسیم؛ امّا در شکل دو مثلث نداریم، پس با اضافه کردن یک خط، یعنی یکی از قطرها، دو مثلث ایجاد می کنیم.
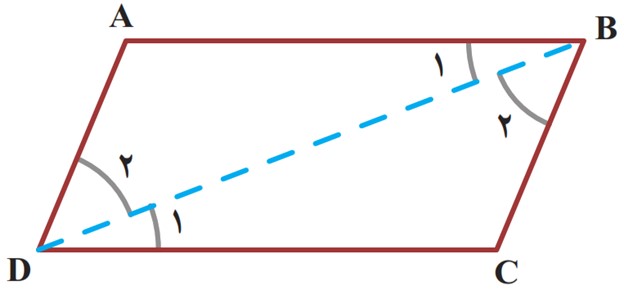
ت اثبات را به صورت زیر کامل کنید:
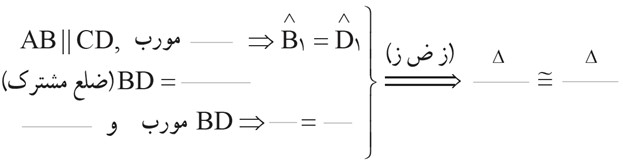
ث با توجه به هم نهشتی دو مثلث ABD و CBD، تساوی های زیر را کامل کنید.
دیدیم که \({\hat B_1} = {\hat D_1}\) است؛ بنابراین داریم: \(AD = …………\)
و \({\hat B_2} = {\hat D_2}\) است؛ بنابراین داریم: \(AB{\rm{ }} = {\rm{ }} \ldots \ldots \ldots \ldots \)
ج چرا برای اثبات هم نهشتی مثلث های ایجاد شده، نمی توانیم از حالت های (ض ز ض) و (ض ض ض) استفاده کنیم؟
چ با توجه به مباحث درس قبل (هندسه و استدلال) بگویید آیا می توانستیم همین نتیجه را با رسم قطر AC به دست آوریم؟
ح از هم نهشتی مثلث های ایجاد شده در متوازی الاضلاع، به جز برابری ضلع های مقابل، نتیجهٔ دیگری هم دربارهٔ زاویه های متوازی الاضلاع به دست می آید؛ این نتیجه را بنویسید.
خ در هر متوازی الاضلاع ....................... روبه رو، مساوی اند.
الف
مفروضات و دادههای مسئله (فرض): شکل ما متوازیالاضلاع است (یعنی ضلعهای روبهرو با هم موازیاند):
ریاضی: AB || DC و AD || BC
خواسته مسئله (حکم): ضلعهای روبهرو با هم برابرند:
ریاضی: AB = DC و AD = BC
ب
خیر! در هندسه و ریاضیات، «دیدن» و «اندازهگیری» اثبات محسوب نمیشوند:
1 چشم خطا میکند (خطای دید).
2 اندازهگیری خطا دارد و دقیق نیست.
3 مهمتر از همه، اندازهگیری فقط برای همان یک شکل که کشیدهایم ثابت میکند، اما ما میخواهیم برای همه متوازیالأضلاعهای دنیا ثابت کنیم. پس نیاز به اثبات منطقی داریم (روش ترانه).
پ
خیر؛ برابری اضلاع در تعریف وجود نداشت:
اگر به کتاب سال گذشته (ریاضی هشتم) مراجعه کنی، تعریف متوازیالاضلاع این است: «چهارضلعیای است که اضلاع روبهروی آن دو به دو با هم موازی باشند»
نکته کلیدی
در «تعریف» فقط صحبت از موازی بودن است (AB || CD و AD || BC). صحبت از مساوی بودن اندازه اضلاع نیست. مساوی بودن، یک «ویژگی» یا «نتیجه» است که ما باید آن را با استدلال ثابت کنیم (کاری که در تمرین قبل با همنهشتی مثلثها انجام دادیم).
خیر؛ اندازهگیری، درستی حکم را ثابت نمیکند:
همانطور که در بحثهای قبلی (مثل استدلال حسین و حامد) دیدیم، اندازهگیری برای اثبات ریاضی کافی نیست.
چرا؟ (دلایل اصلی):
1 عدم تعمیم (مهم ترین دلیل):
وقتی شما اضلاع یک متوازیالاضلاع خاص را اندازه میگیرید و میبینید برابرند، فقط برای همان یک شکل مطمئن شدهاید. در ریاضیات، حکم باید برای تمام متوازیالاضلاعهای دنیا (کوچک، بزرگ، کج، راست) برقرار باشد. ما نمیتوانیم همه را اندازه بگیریم.
2 خطای اندازهگیری:
ابزارهای اندازهگیری (خطکش) و چشم انسان همیشه خطا دارند. در ریاضیات ما به دنبال دقت ۱۰۰٪ و منطقی هستیم، نه تقریبی.
ت

ث
دیدیم که \({\hat B_1} = {\hat D_1}\) است؛ بنابراین داریم: AD = BC
و \({\hat B_2} = {\hat D_2}\) است؛ بنابراین داریم: AB = DC
ج
چون برای استفاده از این حالتها نیاز داریم بدانیم که ضلعها برابرند؛ در حالی که "برابری ضلعها" همان چیزی است که میخواهیم ثابت کنیم (حکم مسئله است) و هنوز نمیدانیم برابرند یا نه! تنها چیزی که میدانیم موازی بودن آنهاست که به ما برابری زاویهها را میدهد.
چ
بله، دقیقاً با همین روش. اگر قطر AC را رسم میکردیم، دو مثلث دیگر (ABC و ADC) تشکیل میشد و با اثبات همنهشتی آنها، باز هم به همین نتیجه میرسیدیم.
ح
از همنهشتی این مثلثها، یک نتیجه مهم دیگر هم به دست میآید:
چون دو مثلث همنهشت هستند، زاویه سوم آنها نیز با هم برابر است \(.(\hat A = \hat C)\)
همچنین مجموع زاویههای B و D هم برابر میشود.
خ
زاویه های
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















