جواب فعّالیت صفحه 45 درس 3 ریاضی نهم (استدلال و اثبات در هندسه)
تعداد بازدید : 80.71Mپاسخ فعّالیت صفحه 45 ریاضی نهم
-گام به گام فعّالیت صفحه 45 درس استدلال و اثبات در هندسه
-فعّالیت صفحه 45 درس 3
-شما در حال مشاهده جواب فعّالیت صفحه 45 ریاضی نهم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
در نزدیکی منزل ترانه و شهرزاد، بوستانی هست که در آن یک پل فلزی به شکل نیم دایره وجود دارد بچه ها برای بازی از پله های آن بالا می روند. می دانیم فاصلهٔ ابتدای پل (نقطۀ A) از انتهای آن (نقطۀ B) 10 متر است. ترانه روی پلۀ C نشسته است که از انتهای پل 6 متر فاصله دارد (BC = 6) و شهرزاد روی پلۀ D نشسته است که از ابتدای پل همین مقدار فاصله دارد. آن ها حدس می زنند که باید فاصله شان از پایه های مقابل برابر باشد؛ یعنی AC = BD. درستی حدس آن ها را به دو روش ثابت کنید.
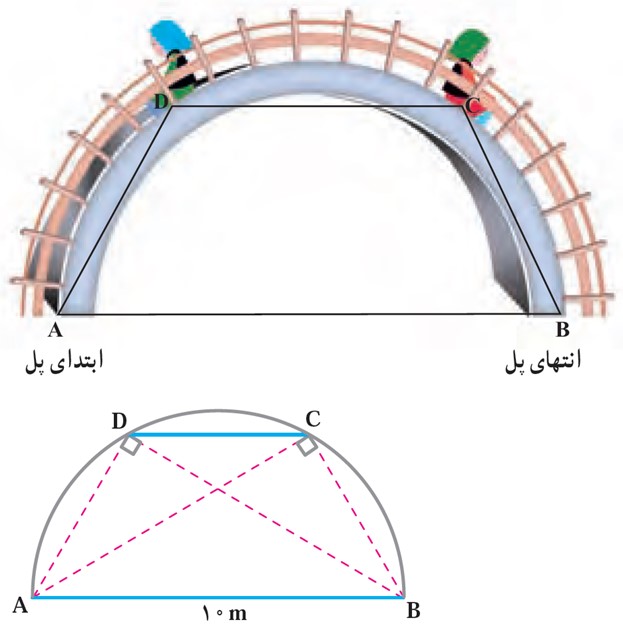
1 نشان دهید زاویه های \(\hat C\) و \(\hat D\) در شکل، قائمه است. طول های AC و BD را به کمک قضیهٔ فیثاغورس محاسبه کنید و نشان دهید: AC = BD
\(AB \Rightarrow \hat C = \hat D = \frac{{{{180}^ \circ }}}{2} = {90^ \circ }\) قطر نیم دایره است
می دانیم زاویه محاطی نصف کمان مقابل به آن می باشد بنابراین داریم:
\(\begin{array}{l}\hat C = {90^ \circ }\\\\ \Rightarrow A{C^2} = A{B^2} - B{C^2}\\\\ \Rightarrow AC = \sqrt {{{10}^2} - {6^2}} = \sqrt {100 - 36} = 8\\\\\hat D = {90^ \circ }\\\\ \Rightarrow B{D^2} = A{B^2} - A{D^2}\\\\ \Rightarrow BD = \sqrt {{{10}^2} - {6^2}} = \sqrt {100 - 36} = 8\end{array}\)
2 به کمک هم نهشتی مثلث های ACB و ADB، نشان دهید AC = BD.
می دانیم کمان های نظیر وتر های مساوی با هم مساوی اند بنابراین داریم:
\(\begin{array}{l}BC = AC = 6\\\\ \Rightarrow BC = AD \Rightarrow \frac{{BC}}{2} = \frac{{AD}}{2}\\\\ \Rightarrow {{\hat A}_1} = {{\hat B}_1} \Rightarrow C\hat AB = D\hat BA\end{array}\)
\({\hat A_1}\) و \({\hat B_1}\) دو زاویه محاطی رو به رو به کمان های BC و AD است
از طرفی با توجه به قسمت اول (سوال 1) داریم \(\hat C = \hat D = {90^ \circ }\) بنابراین داریم:
\(\left. \begin{array}{l}\hat C = \hat D = {90^ \circ }\\\\{{\hat A}_1} = {{\hat B}_1}\\\\AB = AB = 10\end{array} \right\} \Rightarrow \) بنا به حالت (و ز) \(A\mathop B\limits^\Delta C \cong A\mathop B\limits^\Delta D \Rightarrow AC = AD\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















