1736019749.png)
جواب تمرین صفحه 51 درس 3 ریاضی نهم (استدلال و اثبات در هندسه)
تعداد بازدید : 80.71Mپاسخ تمرین صفحه 51 ریاضی نهم
-گام به گام تمرین صفحه 51 درس استدلال و اثبات در هندسه
-تمرین صفحه 51 درس 3
-شما در حال مشاهده جواب تمرین صفحه 51 ریاضی نهم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
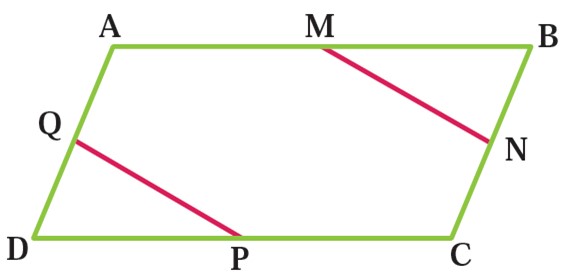
1 در شکل مقابل ABCD متوازی الاضلاع است و M و N و P و Q وسط های اضلاع متوازی الاضلاع اند، ثابت کنید: MN = PQ
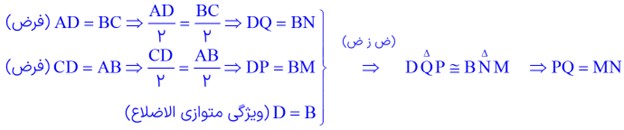
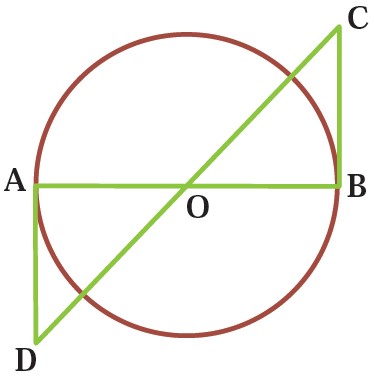
2 در شکل مقابل O مرکز دایره است و BC و AD بر دایره مماس اند، نشان دهید که AD و BC برابرند.
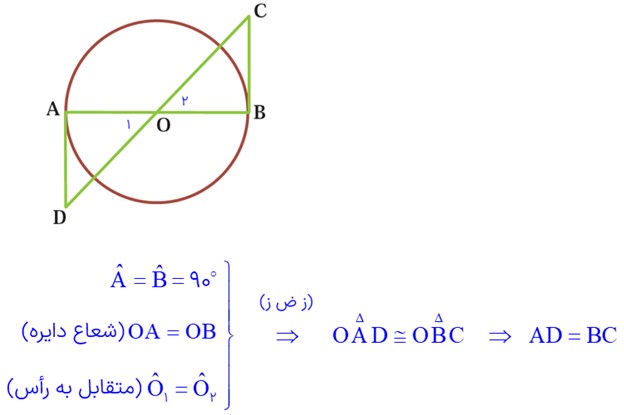
نکته
می دانیم خط مماس بر دایره در نقطه ی تماس بر آن، بر شعاع دایره عمود است.
3 در شکل مقابل، مثلث ABC متساوی الساقین است و M و N روی قاعدۀ BC طوری قرار دارند که BM = NC .
نشان دهید مثلث AMN هم متساوی الساقین است.
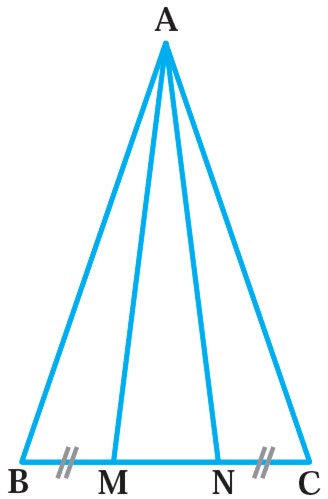
اضلاع AM و AN، ضلع های مثلث AMN می باشد. بنابراین مثلث AMN یک مثلث متساوی الساقین است.
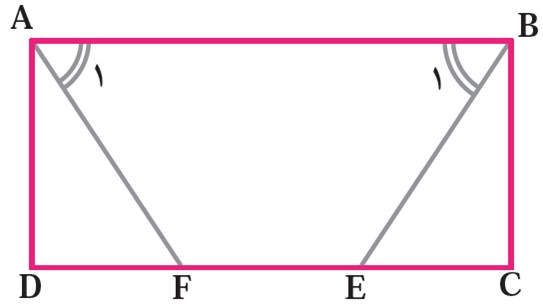
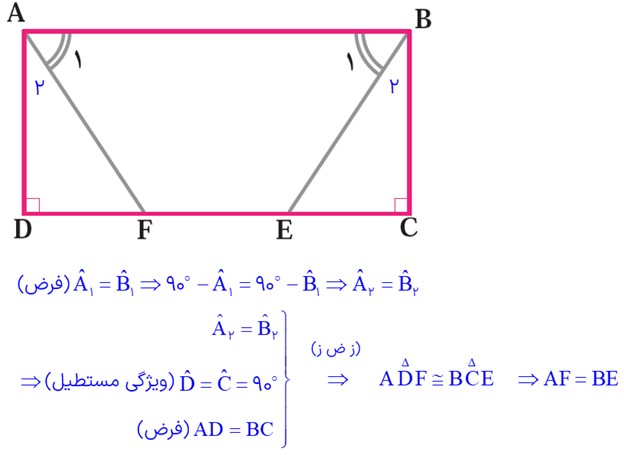
4 در مستطیل ABCD، پاره خط های BE و AF طوری رسم شده که دو زاویۀ A1 و B1 برابرند. ثابت کنید BE و AF مساوی اند.
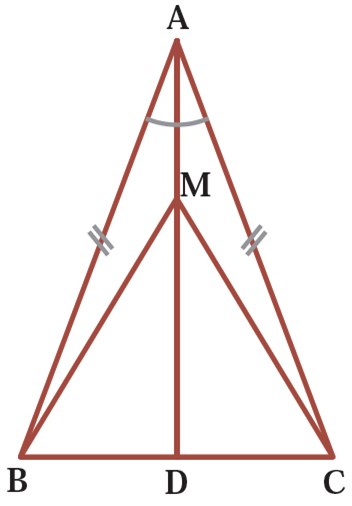
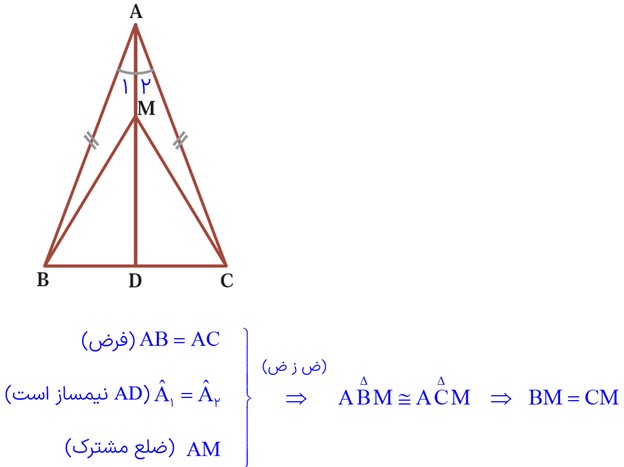
5 نشان دهید در هر مثلث متساوی الساقین، فاصلهٔ هر نقطهٔ دلخواه روی نیمساز زاویهٔ رأس از دو سر قاعده، برابر است: MB = MC .
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه
همین حالا نصب کن
