جواب تمرین صفحه 48 درس 3 ریاضی نهم (استدلال و اثبات در هندسه)
تعداد بازدید : 80.83Mپاسخ تمرین صفحه 48 ریاضی نهم
-گام به گام تمرین صفحه 48 درس استدلال و اثبات در هندسه
-تمرین صفحه 48 درس 3
-شما در حال مشاهده جواب تمرین صفحه 48 ریاضی نهم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
1 ثابت کنید قطرهای هر متوازی الاضلاع یکدیگر را نصف می کنند. یعنی در شکل مقابل نشان دهید: OA = OC و OB = OD.
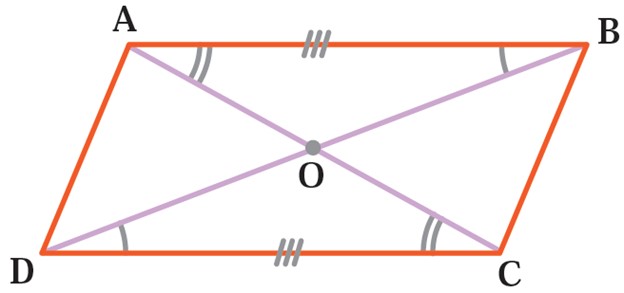

بنابراین نقطه O وسط دو پاره خط AC و BD می باشد.
نتیجه
قطر ها در متوازی الاضلاع یکدیگر را نصف می کنند.
2 ثابت کنید در هر مستطیل، قطرها با یکدیگر برابرند. (مستطیل نوعی متوازی الاضلاع است!)
مستطیل زیر را در نظر بگیرید:
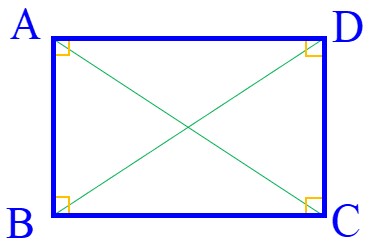
فرض: چهار ضلعی ABCD مستطیل است
حکم: AC = BD
اثبات:
برای اینکه ثابت کنیم AC = BD، باید دو مثلث انتخاب کنیم که این دو پارهخط، ضلعهای آنها باشند. بهترین انتخاب، مثلثهای ADC و BCD هستند (دو مثلث قائمالزاویه که روی ضلع DC نشسته اند).
حال ویژگی های این دو مثلث را بررسی می کنیم:

بنابراین در هر مستطیل، قطرها با یکدیگر برابرند.
3 در مثلث متساوی الساقین ABC، میانۀ AM را رسم کرده ایم. مثلث های AMB و AMC به چه حالتی هم نهشت اند؟ چرا AM نیمساز زاویۀ \(\hat A\) است؟ چرا AM بر BC عمود است؟
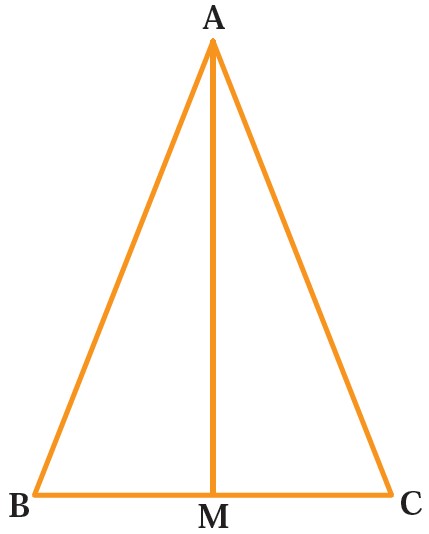
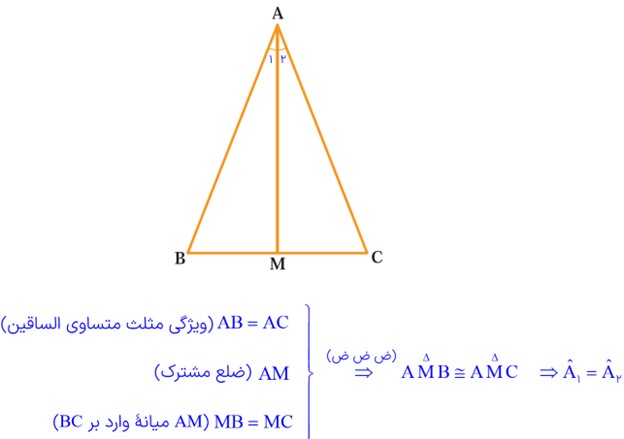
برای اثبات عمود بودن AM بر BC داریم:
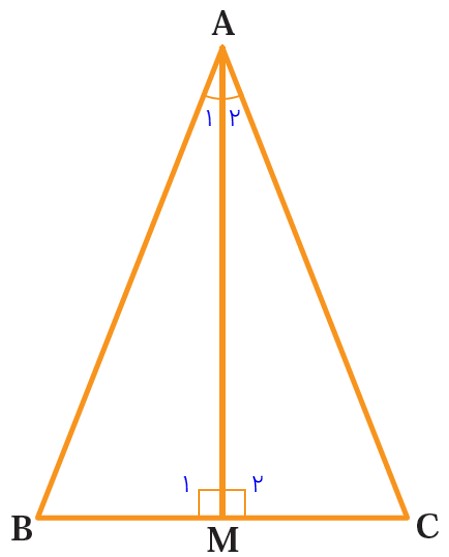
\(\begin{array}{l}{{\hat M}_1} = {{\hat M}_2}\\\\ \Rightarrow \hat M = {180^ \circ }\\\\ \Rightarrow {{\hat M}_1} + {{\hat M}_2} = {180^ \circ }\\\\ \Rightarrow {{\hat M}_1} + {{\hat M}_1} = {180^ \circ }\\\\ \Rightarrow 2{{\hat M}_1}_1 = {180^ \circ }\\\\ \Rightarrow {{\hat M}_1} = {{\hat M}_2} = {90^ \circ }\\\\ \Rightarrow AM \bot BC\end{array}\)
بنابراین AM بر BC عمود است.
4 از نقطۀ M خارج از دایره، دو مماسِ MA و MB را بر دایره رسم کنید. آیا اندازهٔ این دو مماس با هم برابر است؟ درستی ادعای خود را نشان دهید. (راهنمایی: از مرکز دایره به نقطه های M، A و B وصل کنید.)

از تساوی AM = BM نتیجه می گیریم اگر از نقطه ی خارج دایره دو مماس بر دایره رسم کنیم طول دو مماس با هم برابر است.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















